1 引言
水下噪声源的高分辨率识别具有重大意义[1-3]。基于阵列的阵元域声源定位方法已经被研究得比较透彻[4-11]。与阵元域方法不同,模态域声源定位方法需要对声场做空间谐波分解,将信号变换到圆谐波域或球谐波域[12]。这种处理方式使得模态域方法具有分辨相干声源的能力[13]。另外,因为模态域的导向矢量具有频率无关特性,可以不经过频率聚焦直接实现频域的平滑[12]。由于大多数水声环境都可以看作是一个缓慢时变的相干多途径信道,使得模态域声源定位方法尤为适合水下环境。本文将围绕球谐波域的模态阵列信号处理方法展开。
Meyer and Elko[14]基于声场分解提出了球形阵列的波束形成器设计,可以在不改变波束形状的前提下瞄准三维空间中任意方向。Abhayapala和Ward[15]研究了如何用球形阵列记录声场的高阶球谐波成分。Rafaely[16]在球谐波域设计延时求和波束形成器,并和相位模式方法进行比较。球谐波域的延时求和是以牺牲低频指向性为代价换取高鲁棒性。 Rafaely[17]在球谐波域用Dolph-Chebychev波束图设计方法实现了旁瓣控制。Li and Duraswami[18]将球形阵列波束形成器设计问题转换为最小二乘问题,并将白噪声增益约束引入到设计过程中。鄢社峰[19]将球形阵列波束形成器设计问题转化为多约束的二阶锥规划问题。Gao[20]在水下波导环境中分析了球谐波域声源定位方法的性能。
上述球谐波域声源定位方法的空间分辨能力受限于阵列孔径。因此对于一个尺寸确定的球形阵列,其极限定位性能也随之确定,这一点在频率较低时尤为明显。增加阵列尺寸能够提高阵列的空间分辨率,但是这在实际应用中是不现实的。此外,大孔径球形阵列因系统庞大导致不易制作、运输和使用。为了解决上述问题,我们基于声场的球谐波表达和变换提出了一种适用于分布式阵列的球谐波域声源定位方法。通过该方法,我们可以使用多个小型球形阵列代替大孔径球形阵列来实现优异的声源定位性能。
本文的核心思路为:在平面波激励的声场中,推导出球谐波系数的表达式,并根据球谐波函数的正交性设定滤波器系数,使得滤波器具有良好的空间选择性。通过定量地分析本文所提定位方法的可靠性,我们能得到如下结论:当阵元数量和阵列数量受限时,将阵列合理地分布在较大的区域内能够提高该定位方法的低频准确性,在高频则与之相反;当可使用的阵列数量较多时,该方法能够在较宽的频率范围内保证定位的准确性。在后续的仿真中,我们分析了不同频率下该方法的方位谱估计性能和对阵元位置误差的鲁棒性,结果说明了该方法的优异性能。
2 球谐波系数矢量
2.1 声场的球谐波表达和变换
假设Z为球心位于坐标系原点的球形有界区域,令r=(r,θ,φ)表示该区域内的任一观测点。则任意三维声场x(r,k)可以表示为球谐波展开的形式[21]:
(1)
其中k=2pf/c为波数,r0∈Z为展开中心,![]() 为球谐波系数,基函数
为球谐波系数,基函数![]() 定义为:
定义为:
(2)
其中jn为n阶球贝塞尔函数,![]() 为球谐波函数。
为球谐波函数。
以不同中心展开的球谐波系数![]() 与
与![]() 之间存在如下关系[22]:
之间存在如下关系[22]:
(3)
其中:
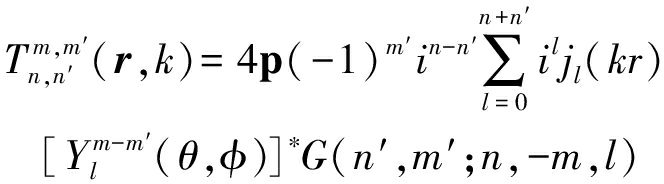
(4)
其中![]() 表示Gaunt系数[23]。定义
表示Gaunt系数[23]。定义![]() 为球谐波系数矢量,则公式(3)可以写成矩阵形式:
为球谐波系数矢量,则公式(3)可以写成矩阵形式:
α(r,k)=T(r-r′,k)α(r′,k)
(5)
其中矩阵T(r,k)∈C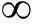 ×
×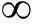 的元素由
的元素由![]() 构成。
构成。
2.2 球谐波系数估计方法
可以通过最小二乘法或谐波系数的坐标变换来估计区域Z的球谐波系数[22,24-25]。N.Ueno[22]提出了适用于任意阵型和阵元指向性的全局谐波系数估计方法。定义阵元指向性函数和它的球谐波分解系数分别为c(θ,φ)和![]() 令c∈C
令c∈C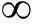 表示系数
表示系数![]() 组成的矢量。在区域Z中放置指向性为c1,...,cM的M个阵元在位置r1,...,rM处。通过贝叶斯准则,将后验均值作为该区域球谐波系数矢量的估计[22]:
组成的矢量。在区域Z中放置指向性为c1,...,cM的M个阵元在位置r1,...,rM处。通过贝叶斯准则,将后验均值作为该区域球谐波系数矢量的估计[22]:
![]()
![]() (r0,k)(
(r0,k)(![]() (k)+l
(k)+l![]() )-1xe
)-1xe
(6)
其中l是与球谐波系数矢量的先验分布有关的常数,![]() ∈CM×M是噪声的互功率谱密度矩阵,
∈CM×M是噪声的互功率谱密度矩阵,![]() (r0)∈C
(r0)∈C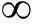 ×M和
×M和![]() (k)∈CM×M定义为:
(k)∈CM×M定义为:
![]() (r,k)=[T(r0-r1,k)c1,...,T(r0-rM,k)cM]
(r,k)=[T(r0-r1,k)c1,...,T(r0-rM,k)cM]
(7)
![]() (k)=
(k)=![]() (r0,k)H
(r0,k)H![]() (r0,k)
(r0,k)
(8)
对于全方向阵元,将c(θ,φ)=1带入式(1),则相应的谐波系数:
(9)
将式(9)带入式(7),则T(r,k)c相当于提取矩阵T(r,k)的第一列,对应的元素为:
![]()
G(0,0;n,-m,l)
(10)
将式(7)带入式(8),矩阵![]() 的元素可以表示为:
的元素可以表示为:
[![]()
![]()
(11)
将式(9)带入式(11)可得:
[![]()
![]()
(12)
在本文中,我们仅使用低阶的球谐波系数进行声源定位(n≤N)。定义有限阶的球谐波系数组成的矢量为![]() 其中
其中![]() 对式(6)做截断可得:
对式(6)做截断可得:
![]()
![]() N(r0,k)(
N(r0,k)(![]()
![]()
![]() )-1xe
)-1xe
(13)
其中![]() 是矩阵
是矩阵![]() (r0,k)的截断形式。
(r0,k)的截断形式。
2.3 球谐波系数估计量的可靠性
本文对球谐波系数的估计量做处理以实现声源定位。因此球谐波系数的估计量的可靠性直接影响本文声源定位方法的准确性。式(6)对应的后验协方差矩阵∑(k)具有如下形式[22]:
∑(k)=I-![]() (r0,k)(
(r0,k)(![]() (k)+lIM)-1
(k)+lIM)-1![]() (r0,k)H
(r0,k)H
(14)
由于本文仅使用了低阶的球谐波系数,因此对式(14)进行截断可得:
![]()
![]() N(r0,k)(
N(r0,k)(![]() (k)+lIM)-1
(k)+lIM)-1![]() N(r0,k)H
N(r0,k)H
(15)
矩阵∑N(k)的对角元素是对应阶次的球谐波系数估计量的方差,方差大意味着式(13)所示的估计量在真值附近波动较大,估计结果的可靠性较低;方差小则意味着估计量的可靠性较高。在本文中,我们取矩阵∑N(k)的迹作为球谐波系数估计的可靠性的描述:
![]()
![]() (k)+l IM)-1
(k)+l IM)-1![]() N(r0,k)H
N(r0,k)H![]() N(r0,k))
N(r0,k))
(16)
该物理量表示![]() 个球谐波系数估计值的方差的累加。从式(16)可以看出:球谐波系数估计量的可靠性是阵元位置和频率的函数。所以我们可以根据tr(∑N(k))的相对大小,确定某种分布式结构适用的频段或者根据处理频段确定分布式结构。需要注意的是,式(14)中省略了一个常数项,但是这并不影响对球谐波系数估计的可靠性的描述。
个球谐波系数估计值的方差的累加。从式(16)可以看出:球谐波系数估计量的可靠性是阵元位置和频率的函数。所以我们可以根据tr(∑N(k))的相对大小,确定某种分布式结构适用的频段或者根据处理频段确定分布式结构。需要注意的是,式(14)中省略了一个常数项,但是这并不影响对球谐波系数估计的可靠性的描述。
3 基于球谐波系数的方位谱估计
考虑幅度为S(ω)的单频平面波从方向(θ0,φ0)入射到区域Z,定义波矢k=(k,θ0,φ0),则在r处的频域观测信号为:
x(r,k)=S(ω)eik·r
(17)
其中k·r=kr cos Θ0,cos Θ0=cos θ cos θ0+cos(φ-φ0)sin θ sin θ0。对公式(17)做球谐波展开[12]:
(18)
将公式(18)所示的平面波展开带回到公式(1)中,能够确定在该声场中的球谐波系数具有如下形式:
(19)
其中o为球坐标系原点,也为球谐波系数的展开中心。若是多个平面波入射的情况,则有[12]:
(20)
其中Sd(ω)和(θd,φd)分别为dth平面波的幅度和入射方向。
我们希望从公式(20)所示的球谐波系数中提取信号的方位信息(θd,φd)。定义滤波器h(θ,φ)∈C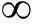 ,根据球谐波函数的正交性,令滤波器系数为:
,根据球谐波函数的正交性,令滤波器系数为:
(21)
则该滤波器输出为:
y(θ,φ)=h(θ,φ)Hα(o,k)=![]()
![]()
(22)
其中δ(·)是Dirac δ函数。假设各声源均值为零且互不相关,则该滤波器的输出功率为:
P(θ,φ)=E{y(θ,φ)y(θ,φ)*}=![]()
(23)
其中![]() 为dth信号功率。从公式(19)可以看出,该滤波器具有理想的空间选择特性。因此通过改变滤波器的瞄准方向,我们就可以得到方位谱的估计值,从而确定信号的入射方向。
为dth信号功率。从公式(19)可以看出,该滤波器具有理想的空间选择特性。因此通过改变滤波器的瞄准方向,我们就可以得到方位谱的估计值,从而确定信号的入射方向。
在实际应用中,我们仅用![]() 阶的球谐波系数估计方位谱:
阶的球谐波系数估计方位谱:
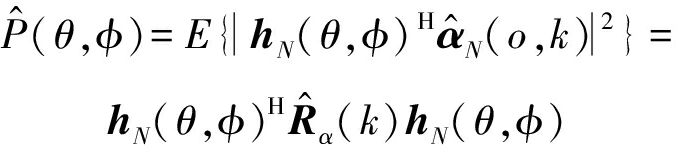
(24)
其中![]() 是h(θ,φ)的截断,
是h(θ,φ)的截断,![]() 是球谐波系数矢量的样本协方差矩阵:
是球谐波系数矢量的样本协方差矩阵:
(25)
其中![]() 是用lth数据快拍的估计结果,L为估计协方差矩阵所用的快拍数。
是用lth数据快拍的估计结果,L为估计协方差矩阵所用的快拍数。
图1总结了我们提出算法的流程。
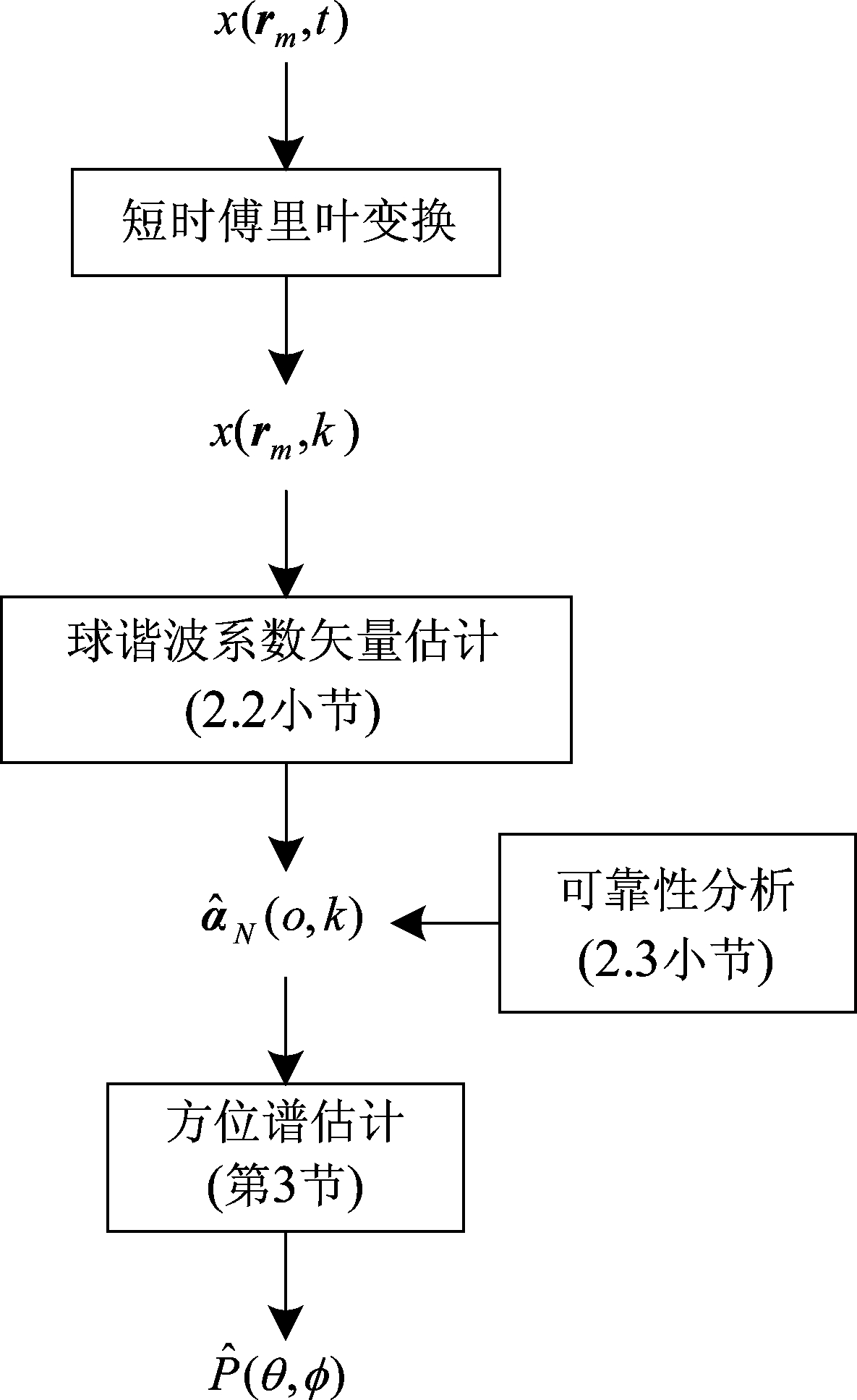
图1 算法流程示意图
Fig.1 The processing steps of the proposed algorithm
4 分布式阵列的方位谱估计性能仿真分析
下面考虑图2所示的阵型:四个全指向性阵元放置在正四面体的顶点上,其中正四面体的外接球半径为4 cm。下文将用SA来表示这种四阵元声透明球形阵列。用多个SA组成分布式球形阵列系统,用DSA表示。若无特殊说明,后续仿真的截断阶次N=4。
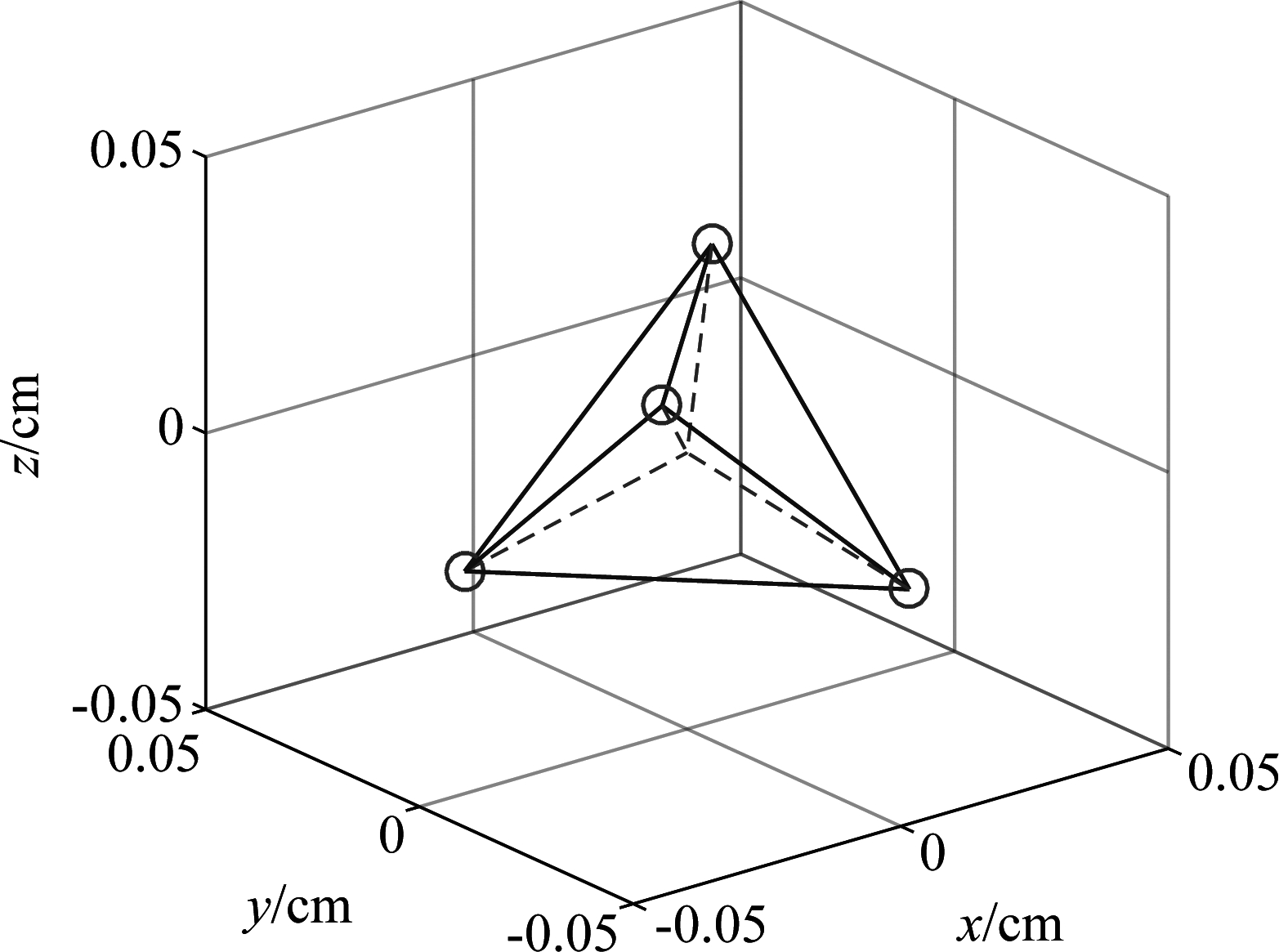
图2 四阵元声透明球形阵列结构示意图
Fig.2 Geometry model of a unbaffled spherical array with 4 elements
4.1 球谐波系数估计量的可靠性分析
首先假设DSA是由8个SA组成,其球心位于正六面体的8个顶点上,正六面体的外接球半径为R。此时DSA的阵元数量为32。我们首先分析在不同的频率点上,球谐波系数估计量的可靠性随半径R的变化情况。首先根据式(10)和式(12)分别计算矩阵![]() N和
N和![]() ,然后将结果带入式(16)中计算tr(∑N),其中l=10-3。图3给出tr(∑N)在500 Hz和2000 Hz频率点上随分布半径R的变化情况。如图3(a)所示,在500 Hz的频率点上,当R约为1.6 m时tr(∑N(k))最小。这说明:当可使用的传声器数量较少时,将SA分布在较大的区域能够降低低频球谐波系数的估计误差。我们从图3(b)中也能得到相似的结论:当可使用的传声器数量较少时,将SA分布在较小的区域能够降低高频球谐波系数的估计误差(当R约为0.3 m时tr(∑N(k))最小)。
,然后将结果带入式(16)中计算tr(∑N),其中l=10-3。图3给出tr(∑N)在500 Hz和2000 Hz频率点上随分布半径R的变化情况。如图3(a)所示,在500 Hz的频率点上,当R约为1.6 m时tr(∑N(k))最小。这说明:当可使用的传声器数量较少时,将SA分布在较大的区域能够降低低频球谐波系数的估计误差。我们从图3(b)中也能得到相似的结论:当可使用的传声器数量较少时,将SA分布在较小的区域能够降低高频球谐波系数的估计误差(当R约为0.3 m时tr(∑N(k))最小)。
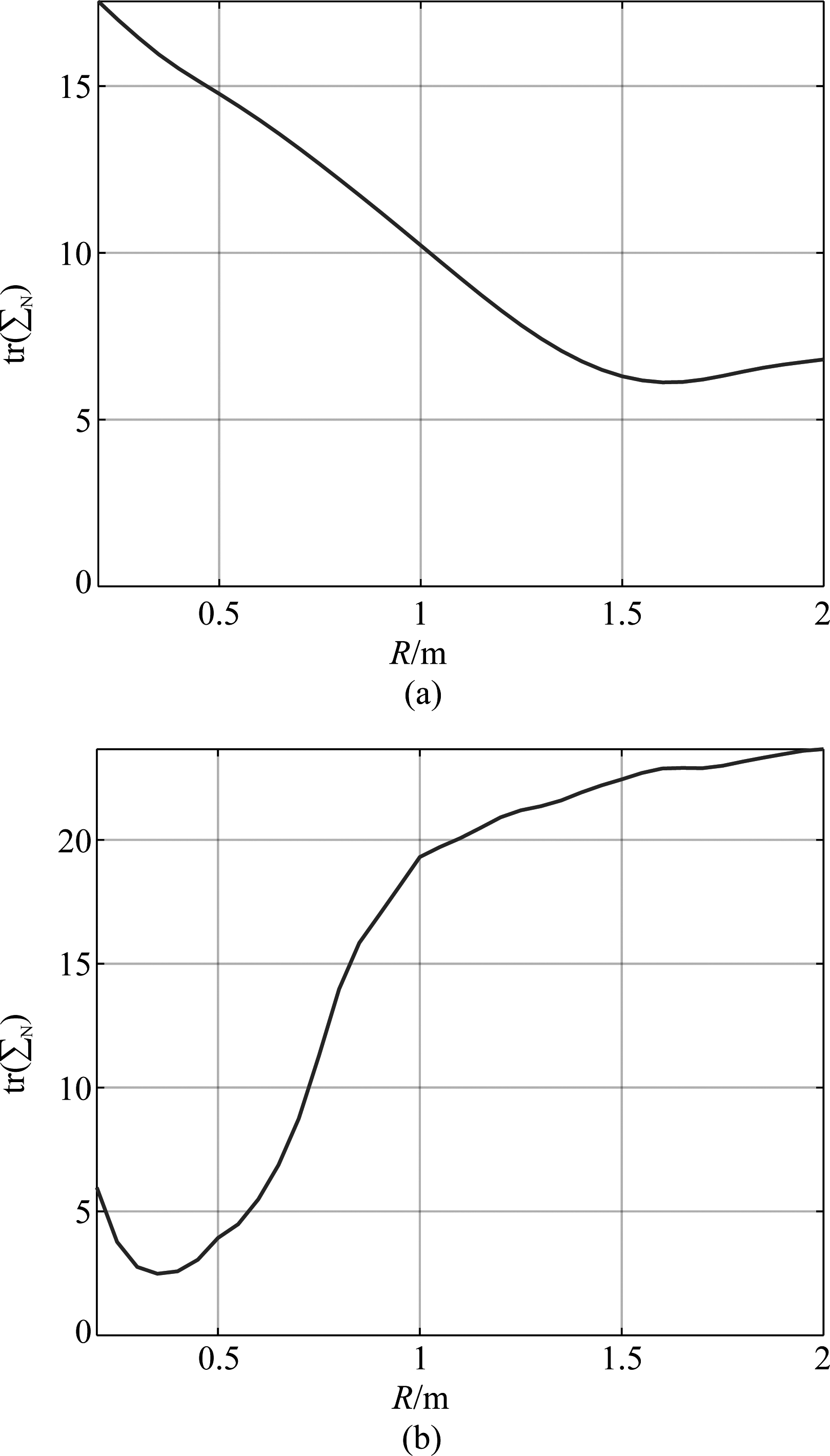
图3 在不同频率点上球谐波系数的估计误差随分布半径的变化曲线: (a) 500 Hz和(b) 2000 Hz
Fig.3 The reliability of the estimated spherical harmonic coefficients versus radius of the spherical region at (a) 500 Hz and (b) 2000 Hz
增加阵元数量或分布式阵列的数量能有效地控制球谐波系数的估计误差,使得分布式阵列系统在一定的频率范围内正常工作。为了验证这一点,我们增加SA的数量至16个,其中8个SA的球心位于半径为R的正六面体的8个顶点上,另外8个SA的球心与半径为R/2的正六面体的八个顶点重合。图4给出当区域半径为R=0.5 m和R=1.2 m时,tr(∑N)随频率的变化情况。经验证:图4(a)对应的分布式结构在1000~4000 Hz的频率范围内,图4(b)对应的分布式结构在500~2000 Hz的频率范围内,均具有良好的定位性能。
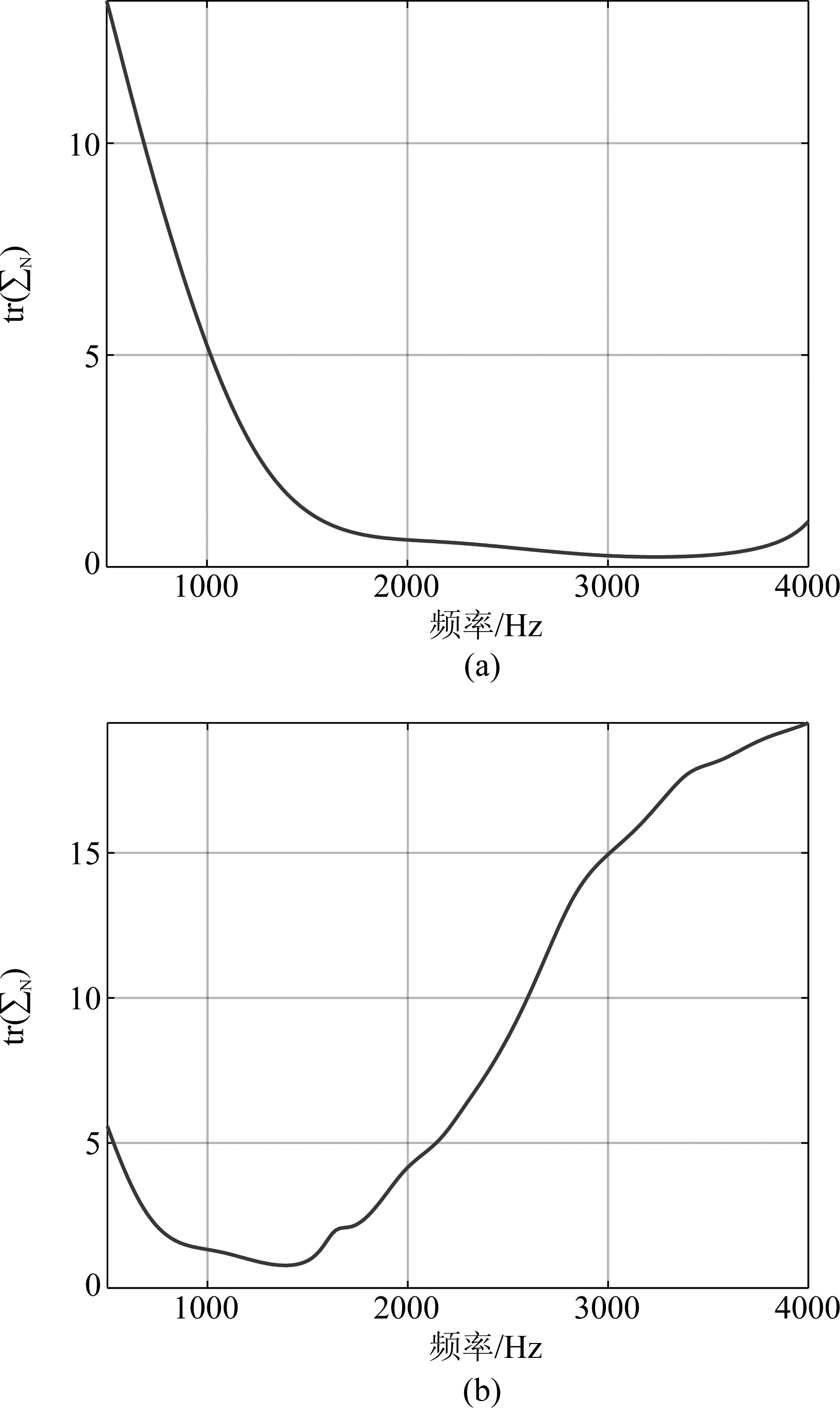
图4 在不同区域半径条件下,球谐波系数的估计误差随频率的变化曲线: (a) R=0.5 m和(b) R=1.2 m
Fig.4 The reliability of the estimated spherical harmonic coefficients versus frequency with the radius of (a) R=0.5 m and (b) R=1.2 m
4.2 不同频率下方位谱估计结果分析
在后续仿真中,我们考虑4.1节所述的由8个SA组成的DSA结构,采用本文提出的方位谱估计方法,对位于(70°,-10°)和(100°,60°)方位上的相干平面波进行定位。阵列接收的噪声是功率为20 dB的高斯白噪声。按照图1所示的流程在不同的频率点上做方位谱估计,其中球谐波系数的展开中心为坐标系原点,正则化参数为l=10-3,快拍数L=100。
针对不同频率范围,需要调整半径R使得分布式阵列系统的参数kR在一个合理的范围内。即当系统在测量低频范围时,SA的分布区域需要增大以保证系统的有效性,反之亦然。图5给出了不同频率和半径下的方位谱估计结果。仿真结果表明,算法在低至500 Hz频率处仍然能提供相当可观的空间分辨率,如图5(a)所示,但是要以较大的分布区域面积为代价。图5(b)~(d)是频率为1000 Hz、2000 Hz和4000 Hz时的空间谱扫描结果,算法均提高良好的空间分辨能力。
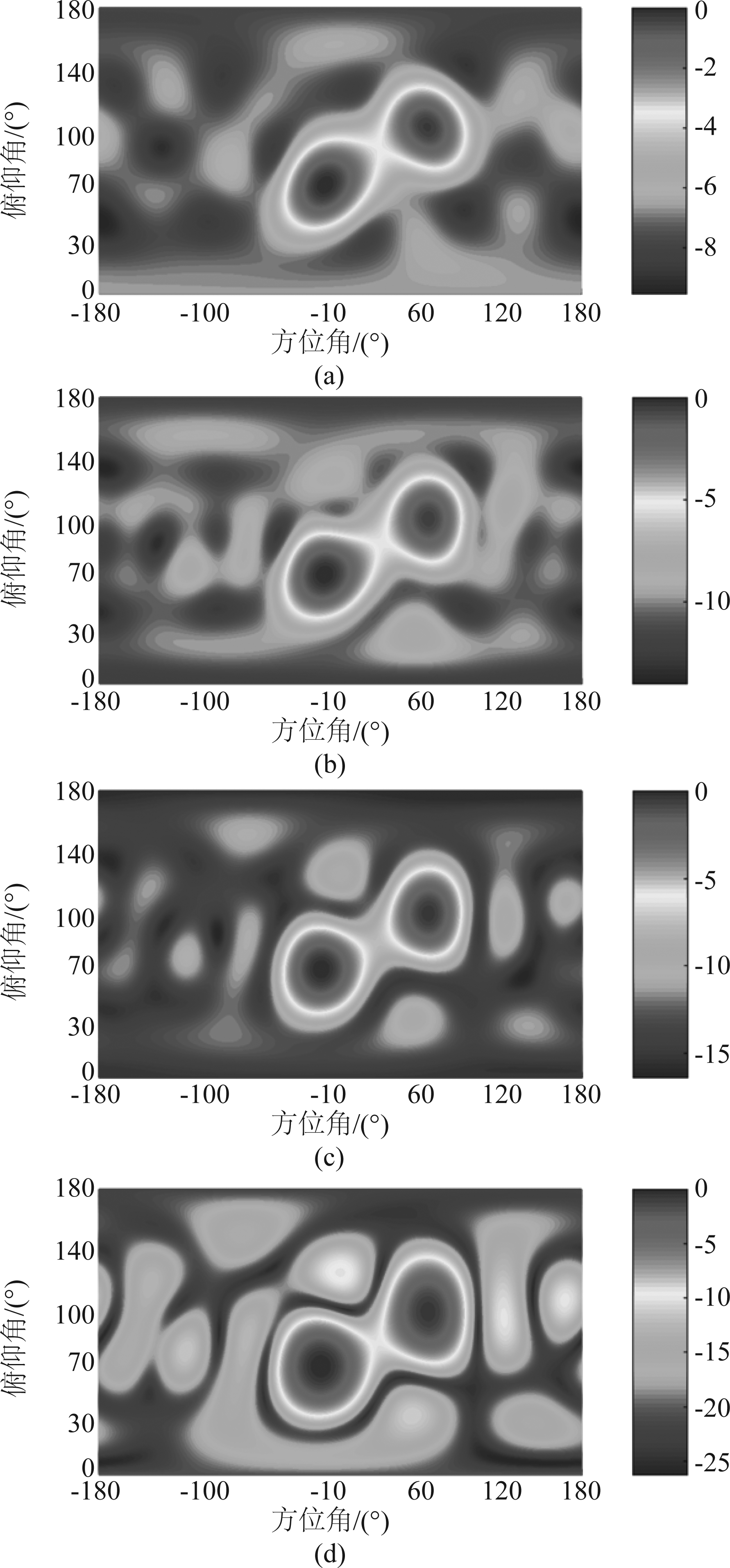
图5 不同频率的空间谱估计结果. (a) 500 Hz, R=1.2 m,(b) 1000 Hz, R=0.6 m,
(c) 2000 Hz, R=0.3 m,(d) 4000 Hz, R=0.2 m
Fig.5 Spatial spectrum estimation with different frequencies and distances. (a) 500 Hz, R=1.2 m, (b) 1000 Hz, R=0.6 m, (c) 2000 Hz, R=0.3 m, (d) 4000 Hz, R=0.2 m
4.3 阵元不一致性和位置误差对500 Hz声源定位性能的影响
在实际应用中,我们先将小型阵列合理地分布在一定大小的空间区域内,然后借助位置标定设备,能够获取较为精确的阵元的空间位置坐标,借此来实现本文算法。但是在实际应用中,阵列信号处理算法往往遭受由阵元位置误差和阵元不一致性带来的性能损失。在本节仿真中我们将引入如下三种误差:(1)SA的每个阵元均存在1 cm位置误差;(2)在测量各SA的中心位置坐标时存在±1 cm位置误差;(3)各阵元存在5%的幅度和相位的不一致性。八个SA被放置在外接球半径为R=1.2 m的正六面体顶点上,阵列接收的噪声是功率为0~20 dB的高斯白噪声,空间网格的间隔为1°,检测频率为500 Hz,正则化参数为l=10-1。
我们将借助定位结果的均方根误差(RMSE)分析本文提出的分布式定位算法的鲁棒性,RMSE可以表示为:
(26)
其中D为待检测位置的个数,对应的位置为(θd,φd),在每个待检测位置进行W次Monte-Carlo实验次数,本文选择![]() 为相应的估计结果。仿真中D=3个待检测位置分别为(45°,0°)、(90°,0°)和(90°,30°)。
为相应的估计结果。仿真中D=3个待检测位置分别为(45°,0°)、(90°,0°)和(90°,30°)。
图6给出不同信噪比条件下,存在与不存在上述三种误差时,使用本文提出的算法在500 Hz频率点上进行声源定位的RMSE结果。从图6中可以发现,当信噪比较低时(0~5 dB),阵元位置误差和阵元不一致性对该算法的定位性能影响有限;随着信噪比的提高,由于误差引起的定位性能的损失开始显现。在20 dB信噪比条件下,误差导致RMSE升高约0.7°。
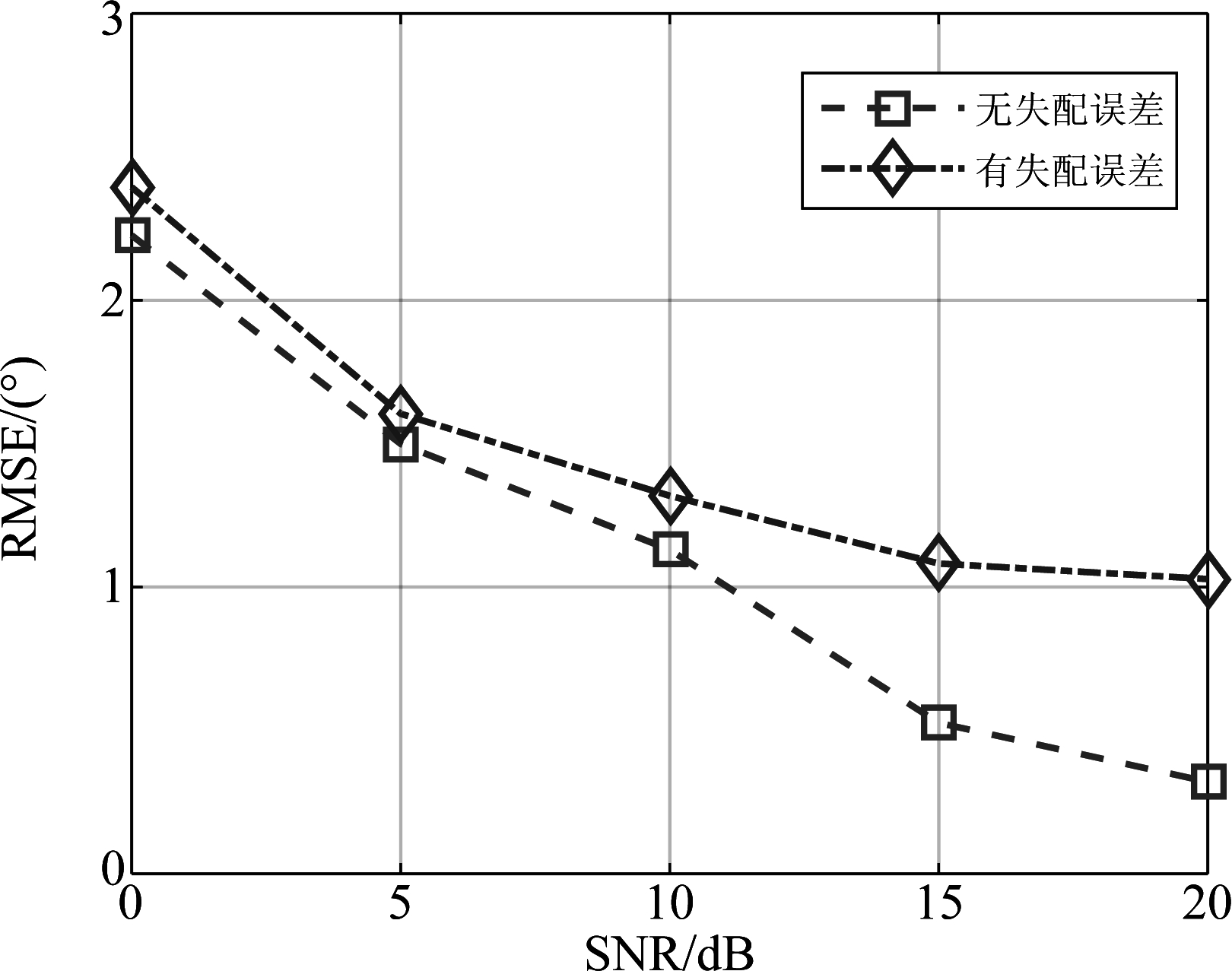
图6 存在和不存在阵元位置误差和阵元不一致性时,算法在不同信噪比条件下的RMSE
Fig.6 Results of root mean absolute error versus the SNR in the absence and presence of mismatch
5 结论
本文提出一种适用于任意阵型和阵元指向性的球谐波域声源定位方法。该方法以声场的球谐波分解和变换为基础,对声场的球谐波系数进行信号处理,获取声场的方位信息。该方法的优势在于:利用合理分布在一定区域内的多个小型阵列,可以在较宽的频率范围内,尤其是在低频,实现较高的空间分辨率。仿真结果说明了该方法的有效性以及对阵元位置误差和阵元不一致性的鲁棒性。
[1] 刘月婵. 水下噪声高分辨率定位识别技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
Liu Y C. High-resolution Localization and Identification Method of Underwater Noise[D]. Harbin: Harbin Engineering University, 2014.(in Chinese)
[2] 孙超. 有限空间水下结构近场声全息技术及应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
Sun C. Theoretical and its Application Investigation on Near Field Acoustic Holography for Underwater Structures in Confined Space[D]. Harbin: Harbin Engineering University, 2013.(in Chinese)
[3] 刘佳. 水下目标噪声源近场定位方法研究[D]. 哈尔滨:哈尔滨工程大学, 2012.
Liu J. Research on Near-field Localization Method of Underwater Target Noise Sources[D]. Harbin: Harbin Engineering University, 2012.(in Chinese)
[4] Wang Y L, Wu Y. An Efficient Semidefinite Relaxation Algorithm for Moving Source Localization Using TDOA and FDOA Measurements[J]. IEEE Communications Letters, 2017, 21(1): 80- 83.
[5] Wan L T, Han G J, Jiang J F, et al. DOA Estimation for Coherently Distributed Sources Considering Circular and Noncircular Signals in Massive MIMO Systems[J]. IEEE Systems Journal, 2017, 11(1): 41- 49.
[6] Qu X M, Xie L H, Tan W R. Iterative Constrained Weighted Least Squares Source Localization Using TDOA and FDOA Measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(15): 3990- 4003.
[7] Cobos M, Garcia-Pineda M, Arevalillo-Herraez M. Steered Response Power Localization of Acoustic Passband Signals[J]. IEEE Signal Processing Letters, 2017, 24(5): 717-721.
[8] Kaveh M, Barabell A. The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(2): 331-341.
[9] Grondin F, Michaud F. Noise mask for TDOA sound source localization of speech on mobile robots in noisy environments[C]∥IEEE International Conference on Robotics and Automation. Sweden: IEEE, 2016: 4530- 4535.
[10] Grondin F, Michaud F. Time difference of arrival estimation based on binary frequency mask for sound source localization on mobile robots[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg: IEEE, 2015: 6149- 6154.
[11] Evers C, Dorfan Y, Gannot S, et al. Source tracking using moving microphone arrays for robot audition[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. LA: IEEE, 2017: 6145- 6149.
[12] Teutsch H. Modal array signal processing: principles and applications of acoustic wavefield decomposition[M]. Germany: Springer, 2007: 5-38.
[13] Teutsch H, Kellermann W. Acoustic source detection and localization based on wavefield decomposition using circular microphone arrays[J]. J.Acoust.Soc.Am., 2006, 120(5): 2724-2736.
[14] Meyer J, Elko G. A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing. Orlando: IEEE, 2002: 1781-1784.
[15] Abhayapala T D, Ward D B. Theory and design of high order sound field microphones using spherical microphone array[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing. Orlando: IEEE, 2002: 1949-1952.
[16] Rafaely B. Phase-mode versus delay-and-sum spherical microphone array processing[J]. IEEE Signal Processing Letters, 2005, 12(10): 713-716.
[17] Koretz A, Rafaely B. Dolph-Chebyshev Beampattern Design for Spherical Arrays[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2417-2420.
[18] Li Z, Duraiswami R. Flexible and Optimal Design of Spherical Microphone Arrays for Beamforming[J]. IEEE Transactions on Audio, Speech and Language Processing, 2007, 15(2): 702-714.
[19] Yan S F, Sun H H, Svensson U P, et al. Optimal Modal Beamforming for Spherical Microphone Arrays[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(2): 361-371.
[20] Gao W J, Zhao H F, Xu W. Direction of arrival estimation based on spherical harmonics decomposition[C]∥MTS/IEEE Oceans Conference. Monterey: MTS/IEEE, 2016: 1-5.
[21] Williams E G, Mann J A. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography[M]. California: Elsevier, 1999: 101-103.
[22] Ueno N, Koyama S, Saruwatari H. Sound Field Recording Using Distributed Microphones Based on Harmonic Analysis of Infinite Order[J]. IEEE Signal Processing Letters, 2018, 25(1): 135-139.
[23] Martin P A. Multiple scattering: interaction of time-harmonic waves with N obstacles[M]. New York: Cambridge Univ., 2006: 325-328.
[24] Wu Y J, Abhayapala T D. Spatial Multizone Soundfield Reproduction: Theory and Design[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(6): 1711-1720.
[25] Han Z R, Wu M, Zhu Q X, et al. Two-dimensional multizone sound field reproduction using a wave-domain method[J]. J Acoust Soc Am., 2018, 144(3): 185-190.



