1 引言
合成孔径声呐利用小孔径基阵沿方位向的移动合成虚拟大孔径,然后根据空间位置和相位关系对不同位置处的接收回波进行相干叠加处理,获得高分辨率的图像[1]。合成孔径声呐对运动状态要求比较苛刻,要想实现高分辨率成像,需要做理想的匀速直线运动。但在实际外场环境中,受海浪、暗涌和母船等因素影响,合成孔径声呐不可避免地会产生运动误差,并且距离向越远的地方,合成孔径长度越长,受运动误差影响就越严重。运动误差将会引起声呐回波的幅度和相位发生变化,从而导致目标出现散焦、重影等现象,严重时甚至不能成像[2-3]。因此,需要对回波进行运动补偿。
运动补偿包括运动误差估计和运动误差补偿两个步骤。根据运动误差数据源的不同,运动误差估计方法主要分为基于运动测量系统的运动误差估计[4-5]、基于回波数据的运动误差估计[6-9]和基于图像域自聚焦的运动误差估计[10-11]。根据对运动误差斜距向空变性处理程度的不同,运动误差补偿方法主要包括距离门逐点补偿[12]、斜距向统一补偿和斜距向分段补偿[13-15]。
距离门逐点补偿原理简单,但运算量巨大,可实现精确补偿。文献[12]先依照场景中心线对回波数据进行统一补偿,然后对每个距离单元进行空变相位补偿,结合多子阵RD成像算法给出了仿真分析。斜距向统一补偿只需要根据参考中心计算一次相位误差,原理简单,运算量小,但由于引入了窄带假设忽略了距离向空变效应,存在较大的补偿误差。斜距向分段运动补偿考虑了运动误差在斜距向的空变性,计算略微复杂,运算量较小,存在一定程度的补偿误差。文献[13-14]研究了斜距向均匀分段补偿方法,将宽测绘带回波数据沿斜距向分块,然后依照等效相位中心相对每个距离块中心线视线偏移对回波数据进行补偿,结合多子阵RD成像算法给出了仿真分析。文献[15]研究了斜距向非均匀分段补偿方法,考虑运动误差在斜距向空变“先快后慢”的特性,设置相位误差容忍值的约束条件,对回波数据沿着斜距向非均匀分段,对各段数据使用DPC(Displaced Phase Center)算法估计运动误差,最后依段进行补偿,不过该方法的难点在于选取合适的阈值。
基于以上背景,本文提出一种斜距向非均匀分段补偿方法,充分考虑运动误差斜距向空变特点,通过对地距向均匀分段换取斜距向的非均匀子段,顺应运动误差的空变规律,达到准确补偿的目的。
2 多子阵合成孔径声呐运动误差分析
合成孔径声呐的理想航迹是沿着直线运动,实际工作时,受水介质和自身运动影响,往往会出现6自由度的运动误差。运动误差分为两类,角度误差和平动误差,如图1所示。角度误差包括偏航(yaw),俯仰(pitch),横滚(roll),平动误差包括横荡(sway),纵荡(surge),升沉(heave)。纵荡是由前向速度不均匀引起的,相比于横荡误差和升沉误差对成像影响较小,本文仅考虑平动误差中的横荡误差和升沉误差[7]。而多子阵合成孔径声呐由多个接收子阵组成,相比于单子阵合成孔径声呐,受角度误差影响更严重,因此对多子阵运动误差分析时需要考虑角度误差[14]。
大测绘带合成孔径声呐成像具有大距离向开角的特点,空变效应明显。运动误差在近距处和远距处的空变性有所不同[15]。
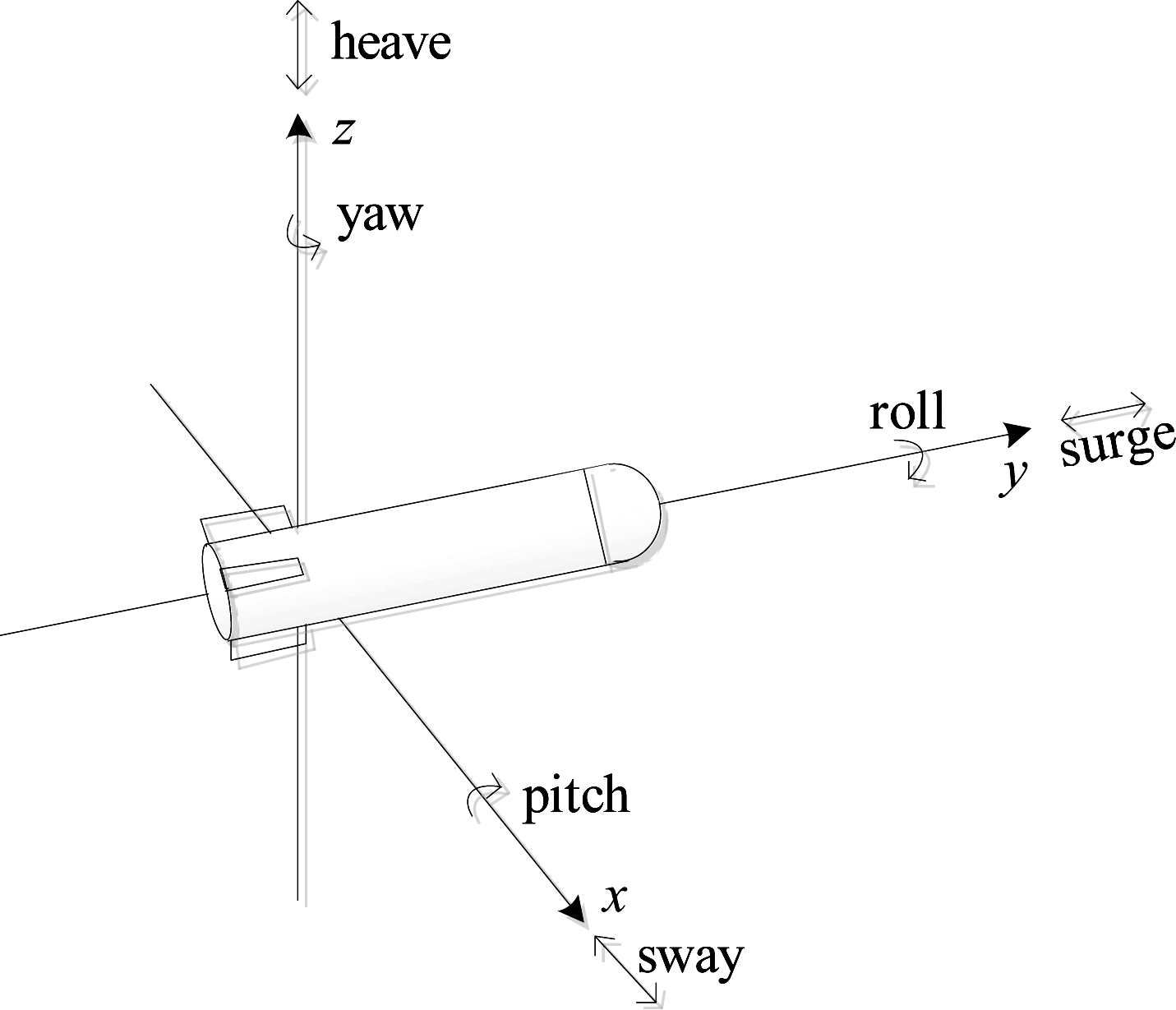
图1 合成孔径声呐6自由度运动误差示意图
Fig.1 Schematic diagram of synthetic aperture sonar motion error in six degrees of freedom
2.1 多子阵运动误差模型
为了简化模型方便分析,引入等效相位中心假设,取发射阵和接收阵的中点为等效相位中心,声波被认为从等效相位中心发射,并由等效相位中心接收,即收发同置。多子阵运动误差几何图如图2所示,理想情况下,多子阵各阵元保持一致的匀速直线运动轨迹,而当实际情况存在角度误差和平动误差时,阵元运动误差各不相同。以右起第一个阵元为参考点,假设阵元间距为
阵元n与参考点的间距为l,则
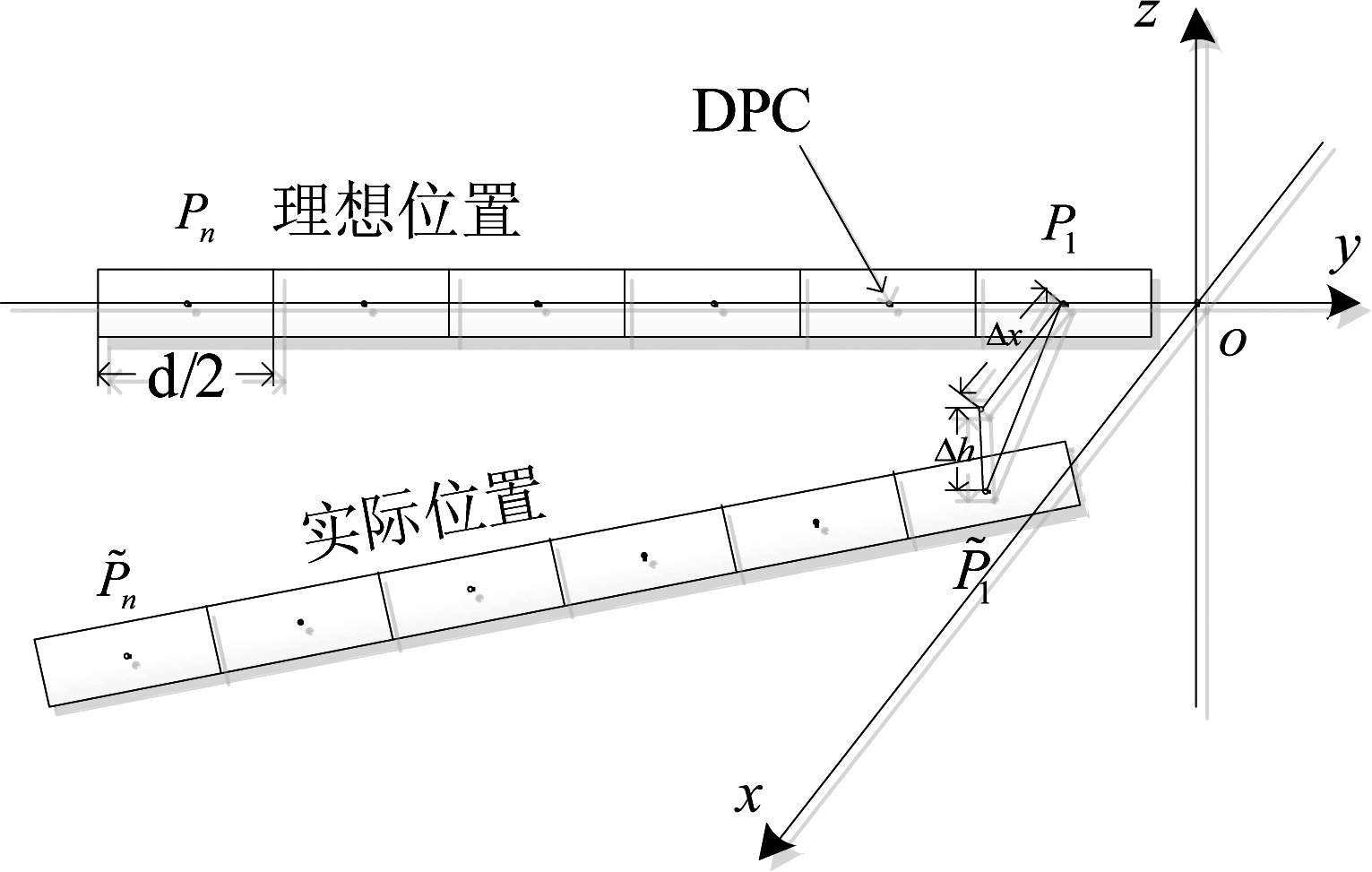
图2 多子阵运动误差几何图
Fig.2 Geometry of multi-element motion error
(1)
在图2oxyz坐标系下,假设t时刻,第一个阵元理想坐标为P1(x0,y0+νt,z0),而实际坐标为
分别指的是阵元1的横荡误差和升沉误差,ν代表声呐沿y轴方向前行的速度。
阵元n理想坐标为Pn(x0,y0+νt-l,z0),把角度误差考虑在内,阵元n实际坐标可表示为
其中,
(2)
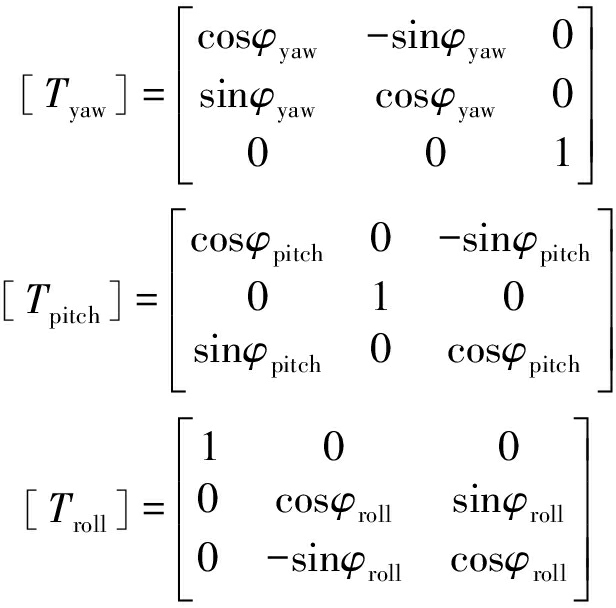
分别对应坐标点
在x,y,z方向的坐标值,Pnx,Pny,Pnz分别对应坐标点Pn相对于P1在x,y,z方向的坐标值,Tyaw,Tpitch,Troll分别代表偏航角、俯仰角和横滚角的转换矩阵,φyaw,φpitch,φroll分别为偏航角,俯仰角和横滚角。
由此,可计算出阵元n实际位置与理想位置之间存在的运动误差
将运动误差
换算成声程差后通过时域移位或频域补相的方式实现对阵元n接收的回波的补偿。
2.2 运动误差斜距向空变性
以上分析了阵元间的空间位置关系,下面以第一个阵元为参考,考虑存在横荡误差和升沉误差的情况下,运动误差在斜距向的空变效应。
图3是成像几何端射图,在xoz坐标系下,假设某时刻阵元理想位置处于点A,坐标为(0,h),由于横荡误差和升沉误差的影响,阵元实际处于点B,坐标为(-Δx,h+Δh)。在声呐波束照射范围内,由近及远依次排列3个目标M1,M2,M3,坐标分别为(x1,0),(x2,0),(x3,0)。声呐与目标M1的理想斜距为
(3)
而实际斜距为
(4)
斜距差可近似为
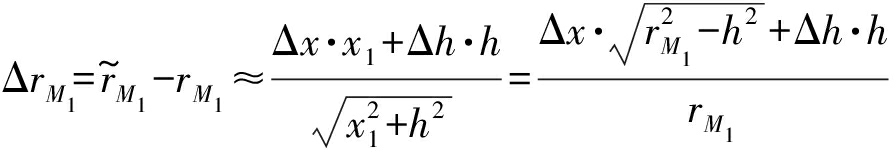
(5)
类似地,目标M2,M3的斜距差分别表示为
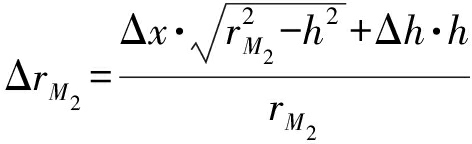
(6)
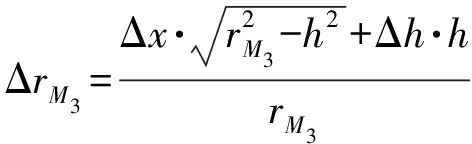
(7)
图3 存在横荡误差和升沉误差时成像声呐几何端射图
Fig.3 Imaging geometry of sonar with sway and heave errors
可以发现,斜距差不仅仅是关于横荡误差和升沉误差的函数,同时也是关于斜距的函数,不同斜距处的目标,斜距差各不相同,这就是运动误差在斜距向的空变性。对于窄测绘带合成孔径声呐,可以忽略运动误差随目标斜距变化的空变特性,直接利用场景中心线的运动误差对整个场景进行补偿。但对于大测绘带,近距和远距相差较大,空变效应更加明显,不能忽略。
3 分段运动补偿分析
对阵元n分析,将斜距差写成通式如下,r表示斜距长度,
(8)
以斜距为自变量,对斜距差求导,可得
(9)
为了描述Δr′的变化规律,需要对导数分子中的
重点讨论。不妨假设当
则导数的取值恒大于零,随着r的增大,导数单调递减,趋近于零。表明斜距小的地方,空变程度越大;随着斜距增加,空变程度逐渐减小。
当
时,则导数的取值恒小于零,随着r的增大,导数单调递增,趋近于零。同样表明斜距小的地方,空变性越大;随着斜距增加,空变程度逐渐减小。
当的取值有正有负时,导数变化不再单调,而是先减后增。但是前段近距处的变化率大于后段远距处的变化率。表明了斜距近的地方,空变程度较大,斜距大的地方,空变程度较小。
图4给出了参数在某些取值下的斜距差的变化曲线,可以看出,斜距差曲线基本服从“先快后慢”的变化规律,在近距处的变化率明显大于远距处。
理论上讲,为了精确补偿大测绘带SAS具有空变性的运动误差,需要对每一个距离单元计算其运动误差并分别补偿,文献[12,16]均采用了这种补偿方法。但该方法运算量巨大,补偿复杂,不利于实时系统实现。
另一种解决办法是将成像区域划分为多个子段,当子段足够窄时,段内的运动误差基本相同,这样可大大节省运算量,也非常方便,文献[13-14]采用了均匀分段的分段策略。但是根据上文的分析,运动误差在不同斜距处的空变程度不同。按照均匀分段策略,各子段的长度相同,空变性却差异较大。均匀分段对它们做一致的处理,势必会造成近距处的子段残留相对较大的补偿误差,因此有必要区别处理近距处和远距处的子段。
由于近距处的子段空变程度大于远距处的子段,为了顺应运动误差空变规律,实现更精确的补偿,应当缩短近距处空变性较大的子段长度,适当延长远距处空变性较小的子段长度,即采用非均匀分段策略,图5给出了分段策略的对比图。
利用斜距成像声呐的距离压缩效应,可通过对地距向均匀分段,换取斜距向的非均匀子段,且距离声呐越近的目标,在斜距向上的投影被压缩越严重,与运动误差的空变规律相似。如图3所示,以M1,M2,M3为中心的3个相同长度的子段,映射在斜距向后的长度变化依次减弱。
下面对子段的非均匀性进行分析,假设σX为
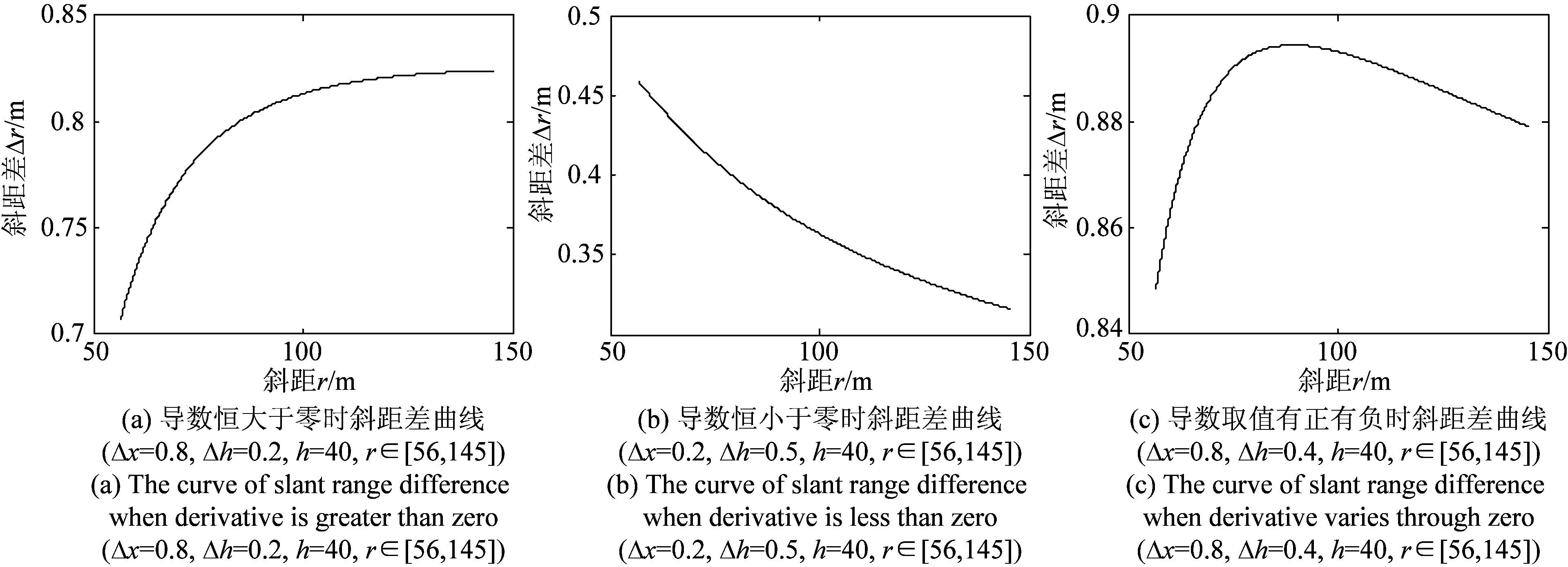
图4 斜距差变化曲线图
Fig.4 The curve of slant range difference
图5 斜距向分段策略对比图
Fig.5 Comparison diagram of segmenting strategies
地距向均匀分段的子段长度,σX′是地距向长度为σX的子段映射到斜距向的长度,以地距x为变量,对斜距向的子段σX′求导,即
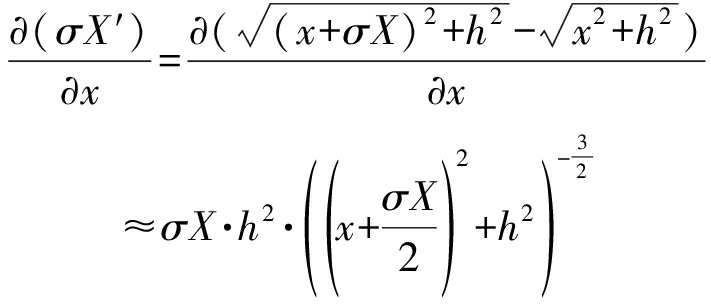
(10)
由式(10)可以看出导数单调递减,随着地距x的增大,导数越来越小,趋近于零。说明了地距向子段映射到斜距向子段的长度非均匀变化;地距向长度为σX的子段在近距处映射到斜距向的长度较短,随着地距x的增长,映射到斜距向的子段的长度逐渐增长,但增速变慢。图6给出了斜距向子段长度变化率的曲线。
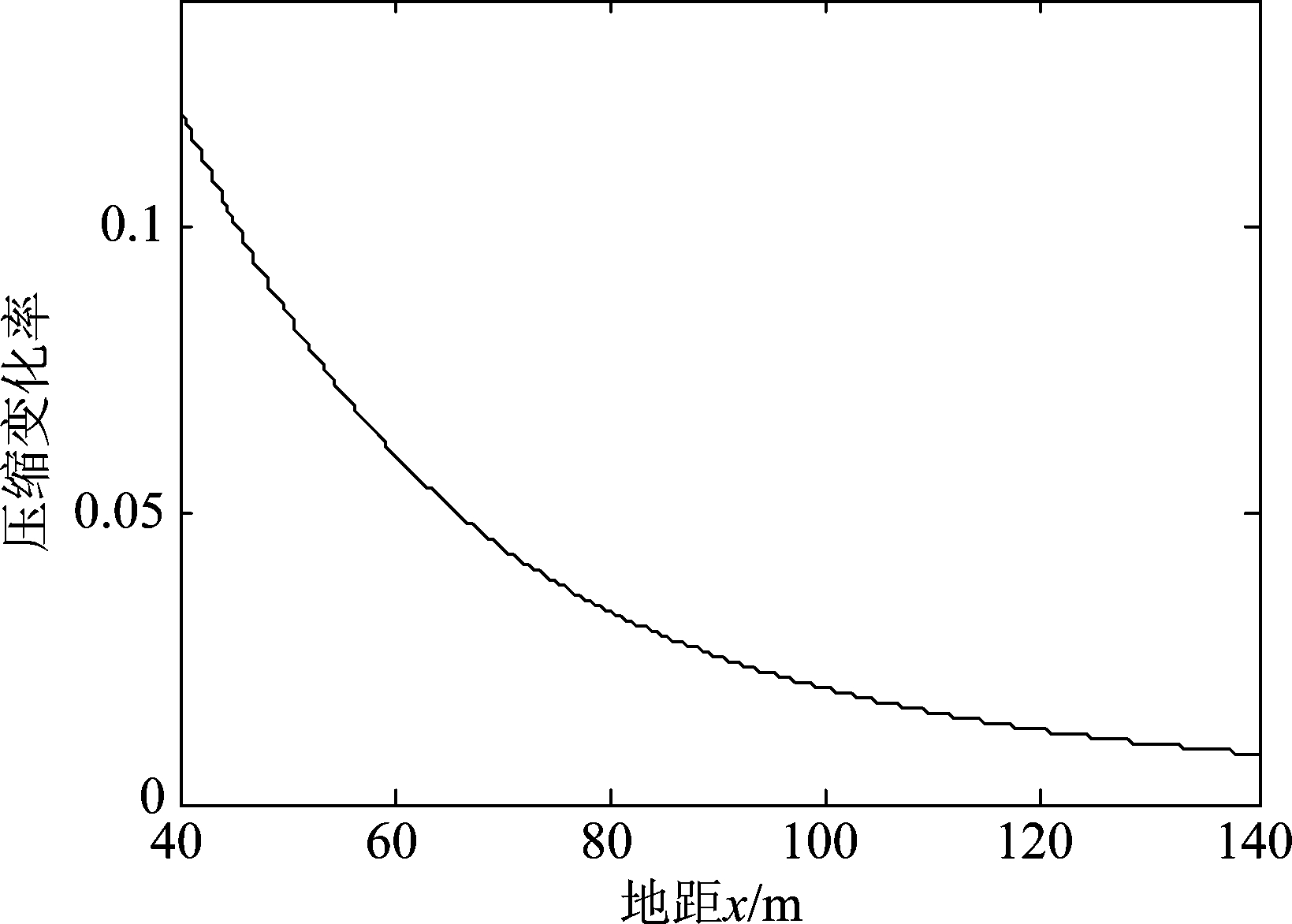
图6 地距子段沿斜距向投影的变化率
Fig.6 Rate of length of the segments
假设将回波数据非均匀分成N个子段,利用上述方法分别计算出各子段的斜距差后,通过时域移位或频域补相的方式补偿阵元n的原始回波,如下式所示。
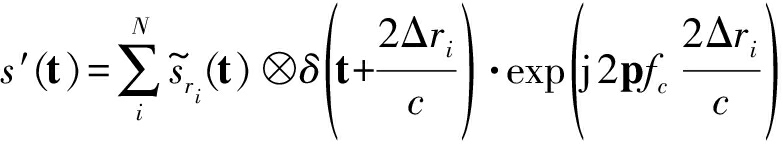
(11)
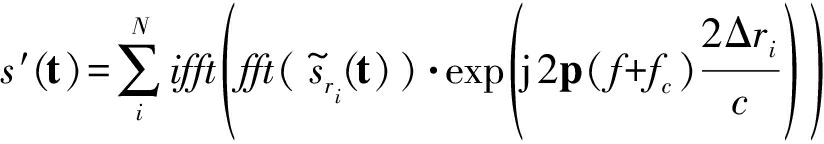
(12)
其中,t为距离向时间,
为第i段包含运动误差的基带回波数据,s′(t)为补偿后的回波数据,c为声速, fc为载波频率,Δri为第i段的斜距差。
4 数据分析
4.1 仿真分析
多子阵合成孔径声呐系统仿真参数设置见表1。采用点阵目标成像进行分析,成像算法使用多子阵ωK算法[17],共设54个点目标,点目标地距向间隔4 m,方位向间隔10 m。设置测绘带宽为80 m,运动误差为正弦形式。第1个阵元的横荡误差和升沉误差,以及角度误差(偏航角、俯仰角和横滚角)变化曲线如图7所示。
表1 多子阵合成孔径声呐系统仿真参数
Tab.1 Simulation parameters of multi-element SAS
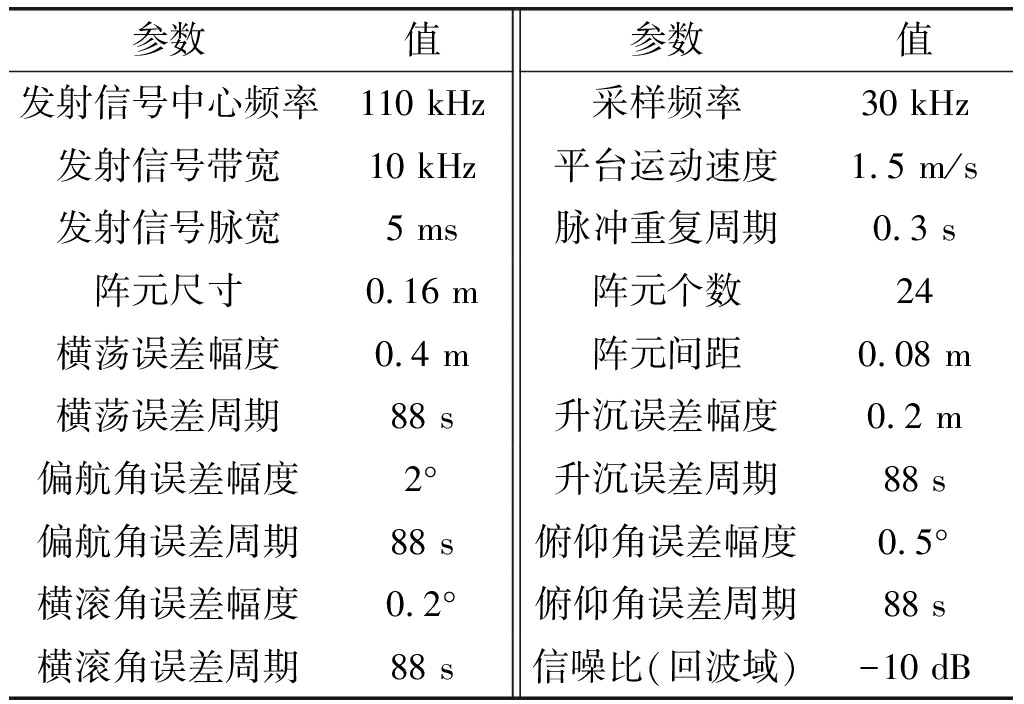
参数值参数值发射信号中心频率110 kHz采样频率30 kHz发射信号带宽10 kHz平台运动速度1.5 m/s发射信号脉宽5 ms脉冲重复周期0.3 s阵元尺寸0.16 m阵元个数24横荡误差幅度0.4 m阵元间距0.08 m横荡误差周期88 s升沉误差幅度0.2 m偏航角误差幅度2°升沉误差周期88 s偏航角误差周期88 s俯仰角误差幅度0.5°横滚角误差幅度0.2°俯仰角误差周期88 s横滚角误差周期88 s信噪比(回波域)-10 dB
点阵目标的成像结果如下图8所示,图8(a)是不存在运动误差的成像结果,图8(b)是存在运动误差不补偿的成像结果。通过比较可以明显看出,图8(b)中的大部分目标受运动误差影响出现了散焦现象;远端的目标因为合成孔径长度较长,受影响程度更大,在运动误差较大的方位向0 m的位置处,远端目标甚至不能成像。
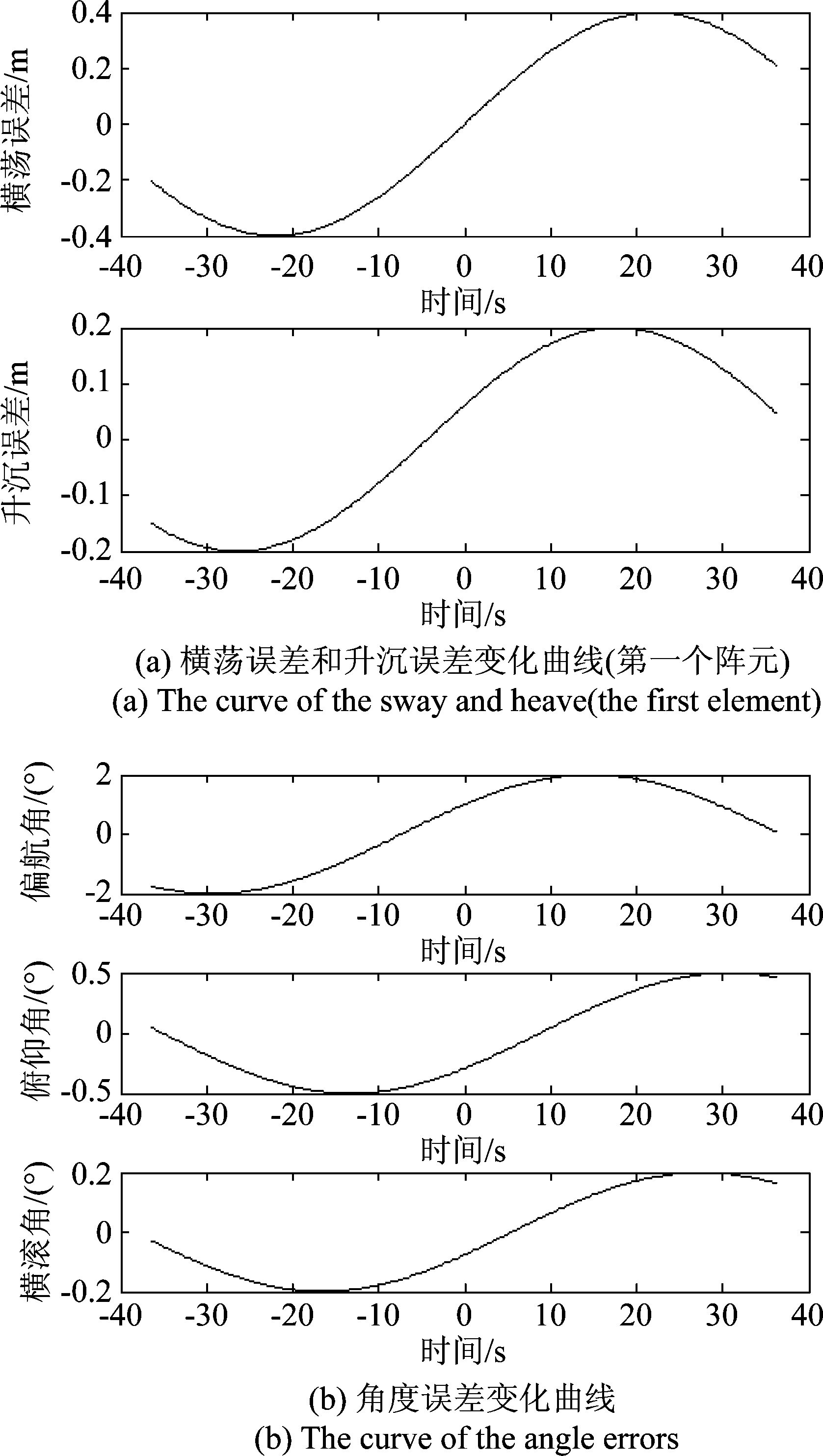
图7 运动误差变化曲线
Fig.7 The curve of the motion error
图9给出了经过4种不同补偿方法补偿后的点阵成像结果,其中,斜距向均匀分段和斜距向非均匀分段补偿方法是将回波划分成5段,斜距向固定阈值非均匀分段方法是以斜距向均匀分段的远距处子段的相位差作为阈值进行迭代。图9(a)采用统一补偿方法,将测绘带中心(110 m)当作参考点计算运动误差,不分段,对全测绘带回波数据统一补偿,这样做的弊端是没有考虑运动误差的空变性,所以图中近处目标的亮度特别低,聚焦效果不好。图9(b)采用文献[13-14]的均匀分段补偿方法,图9(c)采用了文献[15]的斜距向固定阈值非均匀分段补偿方法,图9(d)采用了斜距向非均匀(地距向均匀)分段补偿方法。这3种方法相比于统一补偿虽然增加了计算量,但成像质量均有所改善。仔细观察图9(b)、(c)、(d)3幅分段补偿成像图,能够看出一些细微的差异,比如图9(d)的近处目标亮度比图9(b)略高,图9(c)由于最佳阈值较难确定、子段长度不固定,一部分近处的目标聚焦效果较差。
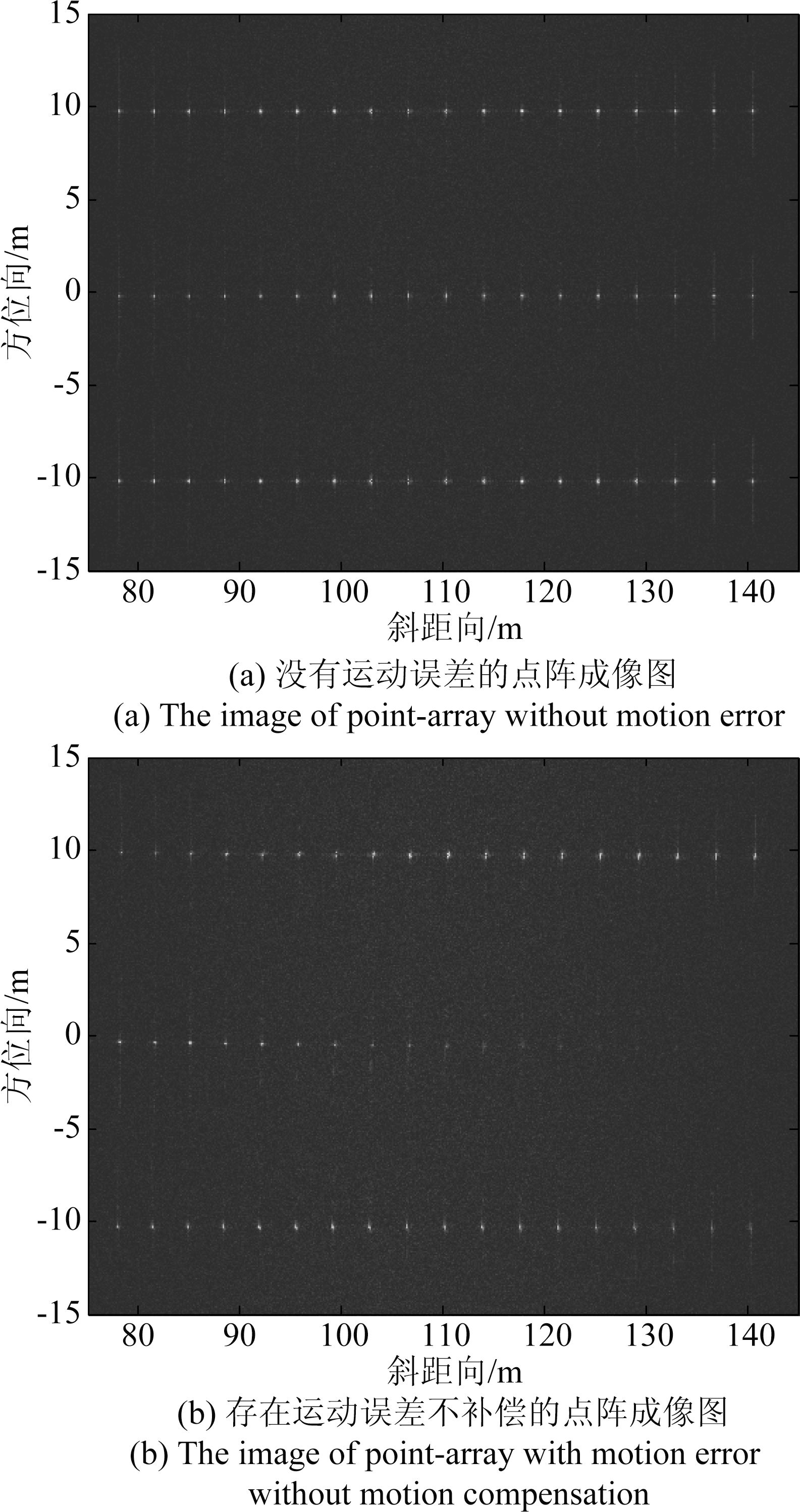
图8 不存在运动误差和存在运动误差不补偿的点阵成像图
Fig.8 Imaging results without motion error and with motion error without motion compensation
为了进一步比较补偿效果,给出斜距向近距离处的4列点目标成像结果,如图10所示。从图中可以看出,统一补偿的近距处点目标亮度较低,说明能量不集中。目标离测绘带中心(110 m)越远,能量越微弱。斜距向均匀分段由于没有考虑运动误差斜距向空变规律,子段内目标空变差异较大,所以部分目标出现散焦情况,比如斜距向约88.5 m处的目标。相比之下,本文提出的斜距向非均匀补偿方法就改善了段内目标空变差异大的问题,使补偿细腻而准确,目标聚焦效果更好。而斜距向固定阈值非均匀分段运动补偿在迭代过程中,由于阈值受运动误差大小影响而不断变化,导致近距处子段长度不断变化,很有可能积累补偿误差,影响了最终目标成像质量。
有必要对斜距向固定阈值非均匀分段补偿进行讨论。根据文献[15]的表述,其分段策略是首先设置相位误差阈值,根据运动误差计算子段长度,从而实现非均匀分段。依旧对阵元n进行分析,假设声呐信号波长为l,声呐距底高度为h,第k帧时刻,阵元n横荡误差为Δx,升沉误差为Δh,斜距为r处的目标对应的相位误差为
(13)
以斜距r为自变量,对相位误差Δφk求导,可得到相位误差随斜距的变化率为
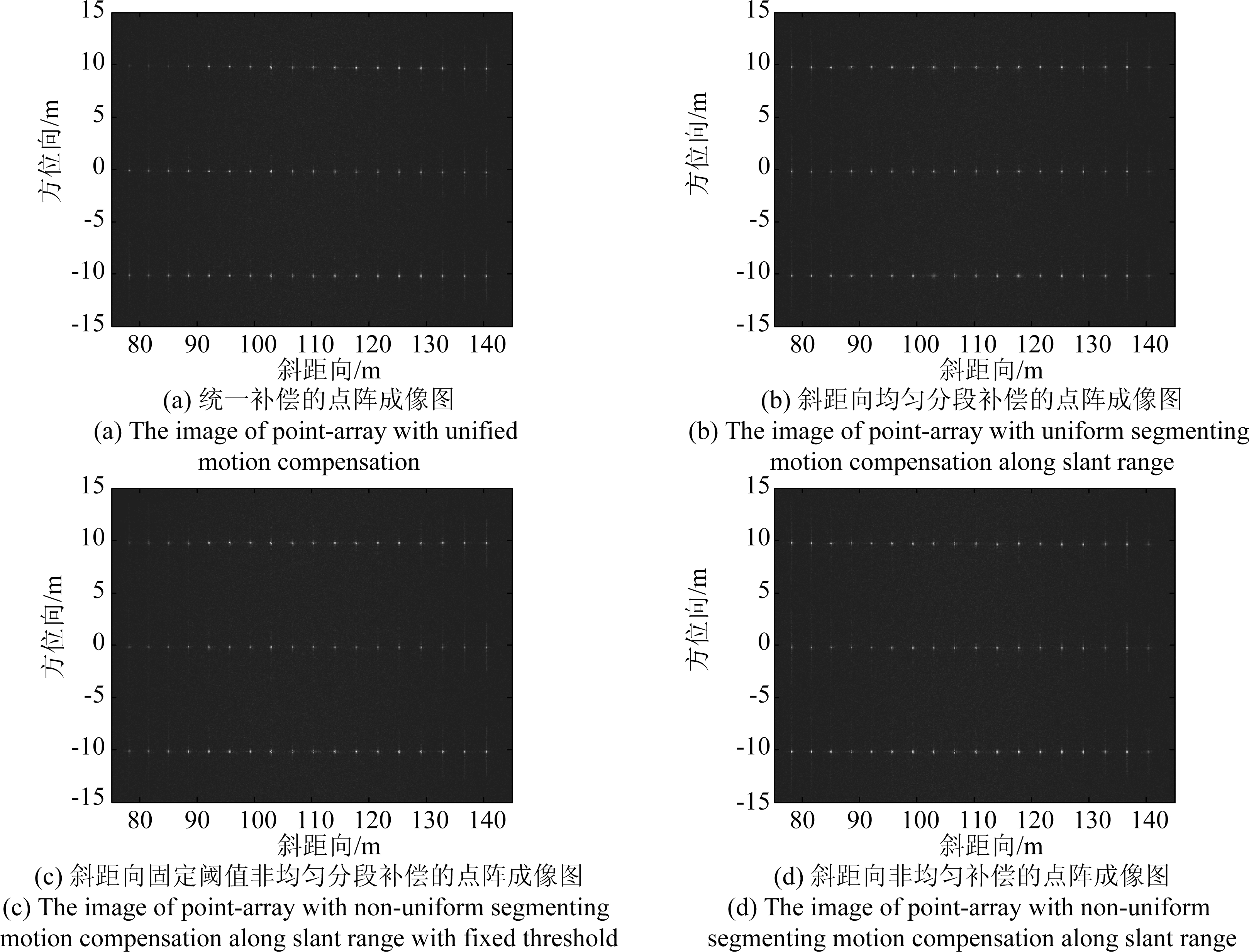
图9 采用4种补偿方法补偿后的点阵成像图
Fig.9 Imaging results with four different methods
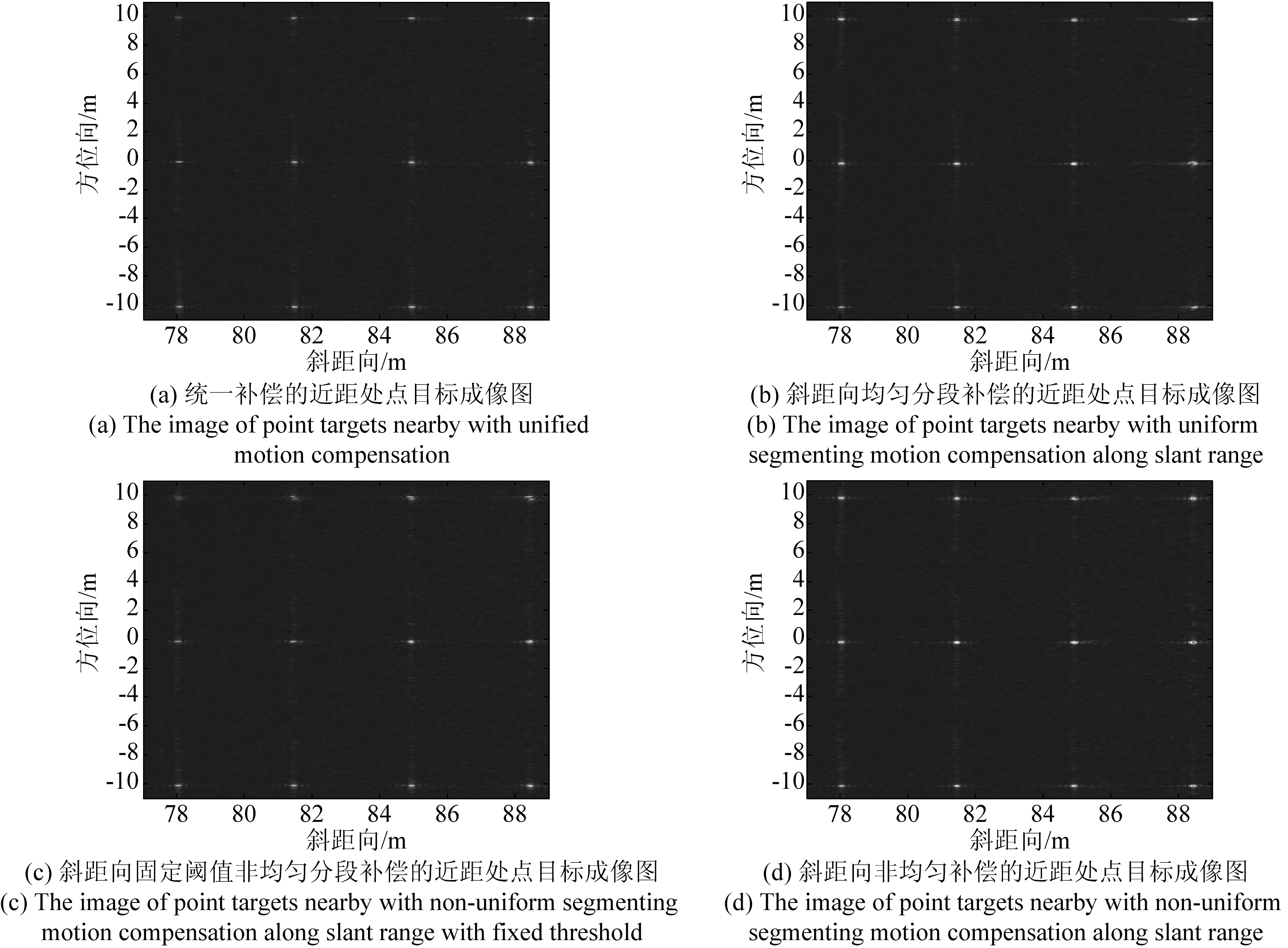
图10 采用4种补偿方法补偿后的近距处点目标成像图
Fig.10 Imaging results with four different methods at the near range
(14)
设定相位差阈值为Φ,则以斜距r为中心的回波子段长度为
(15)
由公式(15)可以看出,第k帧时刻,以斜距r为中心的回波子段长度不仅与设定的相位误差阈值有关,还与横荡误差和升沉误差有关,相比于斜距向均匀分段和斜距向非均匀分段,其子段长度具有不确定性。这样就很有可能出现以下情况:在第k帧处于以斜距r为中心的子段范围
内的点Q,在第k+1帧就处于以斜距r′为中心的子段范围
内,子段中心点的改变势必会影响点Q相比于中心点的相位差的偏移量,从而引起更大的相位差,如下图所示。其中,εφk是第k帧时点Q相比于斜距向距离为r点的相位偏移,εφk+1是第k+1帧时点Q相比于斜距向距离为r点的相位偏移。值得说明的是偏移量有可能增加,也有可能减小,但只要变化,就会影响点Q合成孔径长度内能量聚焦。
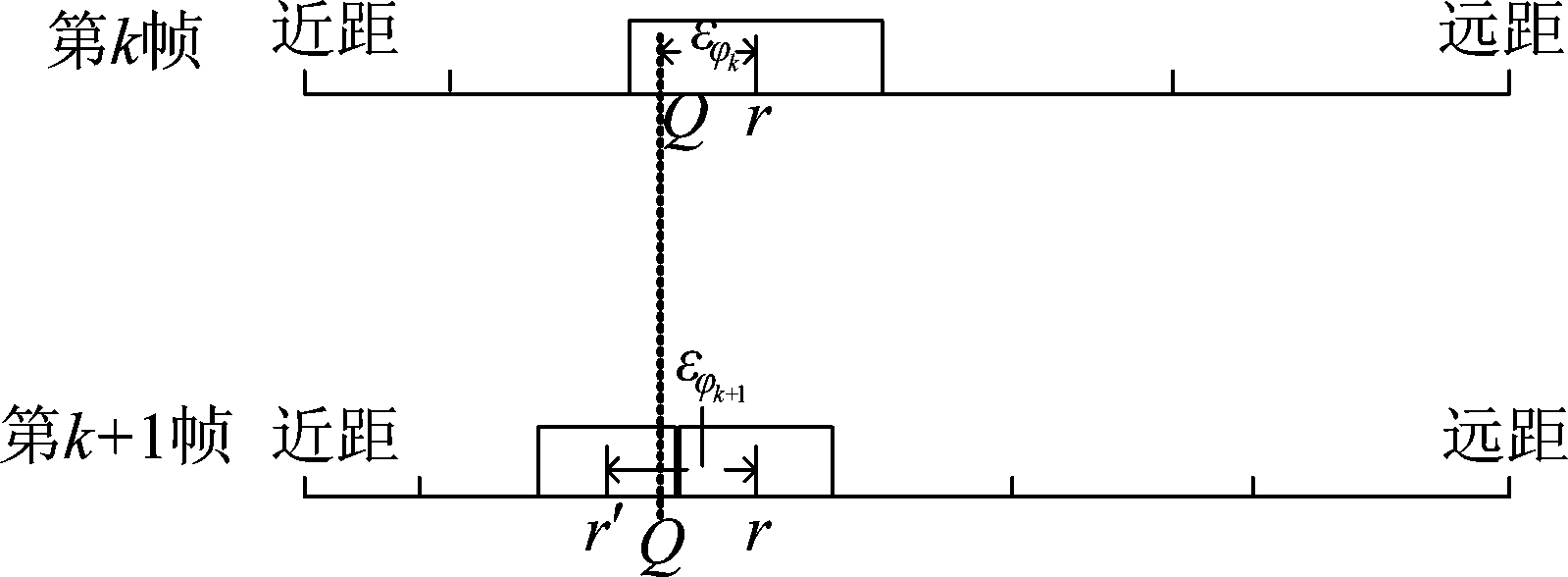
图11 斜距向固定阈值非均匀分段示意图
Fig.11 Diagram of non-uniform segmenting along slant range with fixed threshold
采用对比度和峰值旁瓣比指标[18]评价图10点阵目标的补偿结果。由上文分析可知,运动误差在近距处的空变程度较大,所以沿斜距向选择方位向0 m位置处的前四个点目标进行分析,统计结果见表2、表3。
表2统计了目标与背景的对比度结果
目标与背景对比度越大,表明目标越突出,成像效果越好。由表2中数据可得斜距向非均匀分段补偿后目标更加突出,相比于斜距向均匀分段补偿,对目标成像效果有所改善。
表2 目标与背景对比度
Tab.2 Contrast between target and background
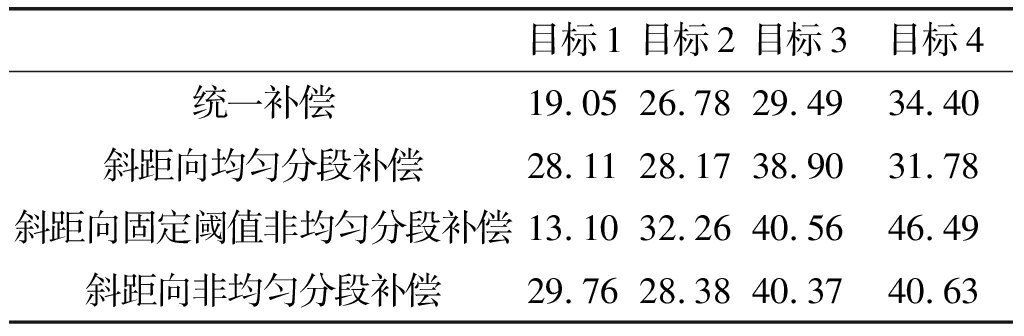
目标1目标2目标3目标4统一补偿19.0526.7829.4934.40斜距向均匀分段补偿28.1128.1738.9031.78斜距向固定阈值非均匀分段补偿13.1032.2640.5646.49斜距向非均匀分段补偿29.7628.3840.3740.63
值得一提的是,当运动补偿存在偏差,合成孔径时间内能量没有以目标为中心均匀聚焦,而是扭曲地分散这个中心点的周围时,就有可能会导致目标中心点亮度升高,但目标整体聚焦质量却下降。“斜距向固定阈值非均匀分段补偿”几乎每一帧回波数据的子段数量和长度都会因运动误差而改变,这种差异使得补偿后的回波在进行相干叠加时极易产生补偿误差,导致目标聚焦后出现扭曲的现象。因此,为了更客观地评价成像质量,引入峰值旁瓣比指标。
表3统计了目标方位向峰值旁瓣比的结果。斜距向均匀分段和斜距向非均匀分段相比于统一补偿对峰值旁瓣比改善较大。目标4处于子段边缘,受“段间接缝”影响,斜距向均匀分段结果较差,而斜距向非均匀分段由于对近距目标补偿更精确,有效减小了“段间接缝”影响。斜距向固定阈值非均匀分段补偿由于其最佳阈值很难确定,每帧子段长度与运动误差有关,对回波一致性影响较大,导致补偿并不能达到最优。
表3 方位向峰值旁瓣比
Tab.3 Peak side lobe ratio along azimuth
目标1目标2目标3目标4统一补偿/dB-11.11-9.39-8.95-8.26斜距向均匀分段补偿/dB-12.03-12.22-13.55-6.17斜距向固定阈值非均匀分段补偿/dB-7.77-11.94-9.32-7.02斜距向非均匀分段补偿/dB-12.75-12.83-12.99-13.18
4.2 实测数据分析
选用2018年项目组在某水库采集的合成孔径声呐湖试数据检验本文算法,主要针对浮球串目标成像结果进行分析。图12给出了该航次声呐姿态角变化曲线,从图中可知,声呐航行过程中始终存在运动误差。其中,航向角变化了约3°,俯仰角在-1°到-1.75°之间波动,横滚角基本保持在1°左右。
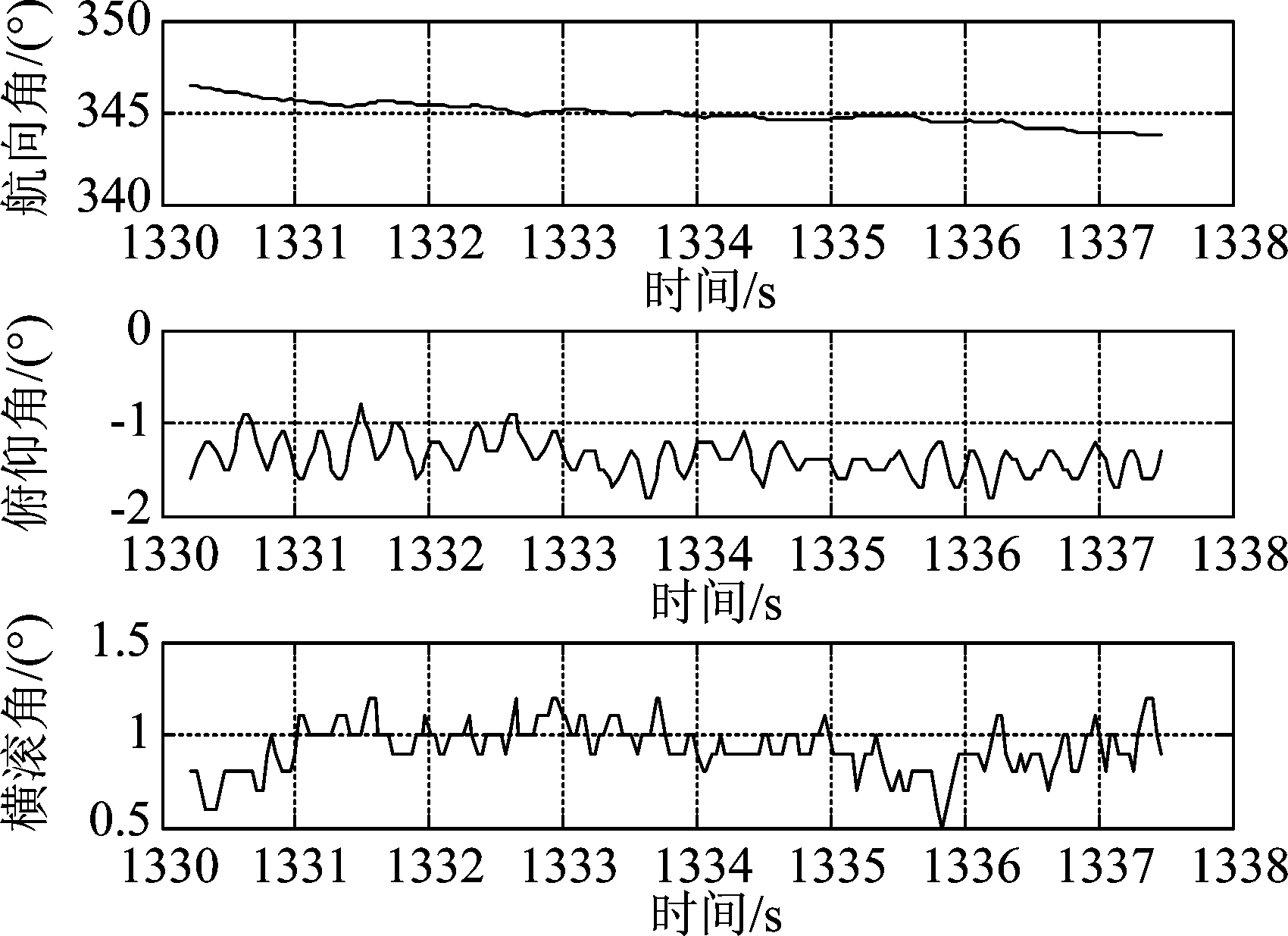
图12 某航次角度误差变化曲线
Fig.12 The curve of the angle errors during a voyage
声呐成像区域图像如图13(a)所示,可以看出水底地势比较平坦,没有异常的凸起和凹陷。在图像左侧有一处(框选区域)比较明亮的点阵为浮球串目标,浮球串由3个标准球形浮球不等间距排列组成,与声呐实际距离约87 m,而整个测绘带宽度为225 m。图13(b)显示了浮球串的成像结果,浮球串目标在方位向存在散焦,拖尾比较严重。
由于分段运动补偿相比于统一补偿主要改善了近距处和远距处目标的成像效果,且斜距向非均匀(地距向均匀)分段补偿相比于斜距向均匀分段补偿尤其改善了空变性较大的近距处目标的成像结果,所以选用该航次数据验证4种补偿算法是合理的。通过比较浮球串成像结果,能够反映出各方法之间的差异。4种补偿结果如图14所示,其中图14(a)是统一补偿的结果,图14(b)是斜距向均匀分段补偿的结果,图14(c)是斜距向固定阈值非均匀分段补偿结果,图14(d)是斜距向非均匀分段(地距向均匀分段)补偿结果。
图13 声呐原始成像结果
Fig.13 Imaging results of SAS without motion compensation
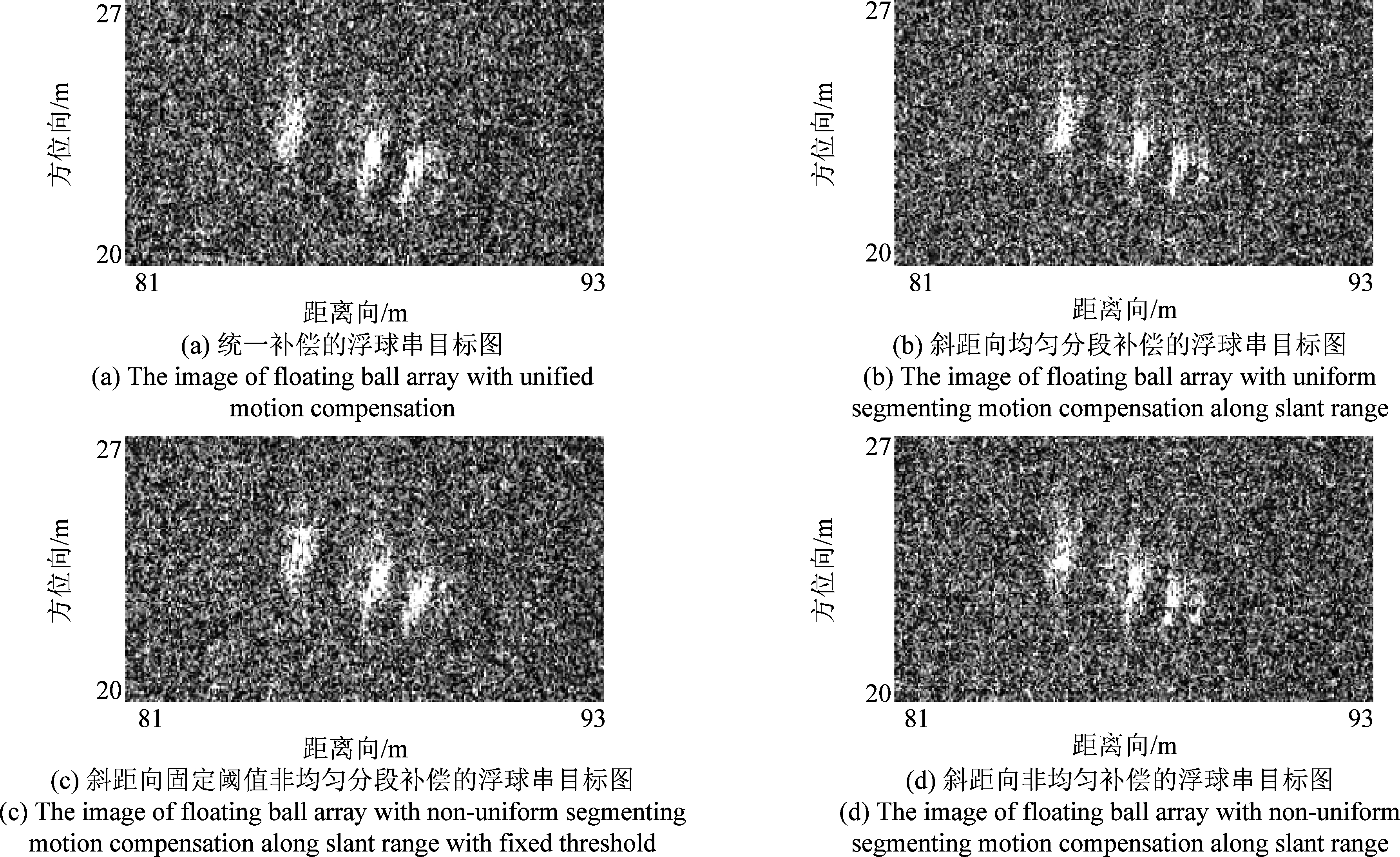
图14 采用4种补偿方法补偿后的浮球串目标图
Fig.14 Imaging results of floating ball array with four different methods
联合图13(b),对比图14中4幅图像可以看出,经过运动补偿后,浮球串目标聚焦情况均得到改善,拖尾现象有所抑制,说明了运动补偿的有效性。图14(b)、(c)、(d)中的浮球串比图14(a)中的浮球串目标更聚焦,能量更加集中,说明了分段补偿比统一补偿更加精准。而3种分段补偿中的斜距向非均匀分段补偿效果最佳,尤其是左起第一个浮球,成像结果更像球形,与真实情况吻合,体现了斜距向非均匀分段补偿的优势。
5 结论
运动误差会导致多子阵合成孔径声呐成像质量下降,运动误差的补偿方式也会对成像结果产生影响。本文考虑了角度误差、横荡误差和升沉误差,研究了大测绘带合成孔径声呐运动误差空变性特点,提出一种斜距向非均匀分段运动补偿方法。采用多子阵ωK成像算法对点阵目标和浮球串目标进行分析,并与统一补偿、斜距向均匀分段和斜距向固定阈值非均匀分段补偿方法进行了对比。研究结果表明:
(1)运动误差在斜距向具有空变性,不同斜距处的误差空变程度也有所不同,基本表现为“先快后慢”。
(2)沿地距向对回波数据进行均匀分段,借助距离压缩效应,映射到斜距向即为非均匀子段,能够顺应运动误差的空变规律,可实现更准确的误差补偿。
(3)仿真与实测数据分析结果表明,斜距向非均匀分段对空变性较大的近距目标补偿效果尤其明显。经过补偿后,目标聚焦效果得到改善,对比度得到增强。同时操作简单,较易实现。
另外需要说明的是子段长度越短,斜距向非均匀分段和斜距向均匀分段补偿结果差异越小。
[1] Hayes M P, Gough P T. Synthetic aperture sonar: a review of current status[J]. IEEE Journal of Oceanic Engineering, 2009, 34(3): 207-224. DOI:10.1109/JOE.2009.2020853.
[2] Hansen R E, Callow H J. Challenges in seafloor imaging and mapping with synthetic aperture sonar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3677-3687. DOI:10.1109/TGRS.2011.2155071.
[3] 刘纪元. 合成孔径声呐技术研究进展[J]. 中国科学院院刊, 2019, 34(3): 283-288. DOI:10.16418/j.issn.1000-3045.2019.03.005.
Liu Jiyuan. Advancement of synthetic aperture sonar technique[J]. Bulletin of the Chinese Academy of Sciences, 2019, 34(3): 283-288. DOI:10.16418/j.issn.1000-3045.2019.03.005.(in Chinese)
[4] 李厚全, 刘莫尘, 伍志海, 等. 球面单形平方根无迹粒子滤波在拖曳合成孔径声纳组合导航中的应用[J]. 中国惯性技术学报, 2014, 22(4): 531-535. DOI:10.13695/j.cnki.12-1222/o3.2014.04.020.
Li Houquan, Liu Mochen, Wu Zhihai, et al. Spherical simplex square-root unscented particle filter used in integrated navigation system of synthetic aperture sonar[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 531-535. DOI:10.13695/j.cnki.12-1222/o3.2014.04.020.(in Chinese)
[5] 张羽, 李更祥, 张鹏飞, 等. 基于多传感器数据融合的合成孔径声纳运动补偿算法[J]. 北京邮电大学学报, 2017, 40(5): 82- 86. DOI:10.13190/j.jbupt.2017- 061.
Zhang Yu, Li Gengxiang, Zhang Pengfei, et al. Motion compensation algorithm of synthetic aperture sonar based on multisensor data fusion[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(5): 82- 86. DOI:10.13190/j.jbupt.2017- 061.(in Chinese)
[6] 刘纪元, 唐劲松, 孙宝申, 等. 基于回波信号的一种合成孔径声纳运动补偿方法[J]. 电子学报, 2003, 31(1): 75-77.
Liu Jiyuan, Tang Jinsong, Sun Baoshen, et al. A receiving-Data-Based motion compensation method of synthetic aperture sonar[J]. Acta Electronica Sinica, 2003, 31(1): 75-77.(in Chinese)
[7] 江泽林, 刘维, 李保利, 等. 一种基于分段 DPC 和拟合的合成孔径声呐运动补偿方法[J]. 电子与信息学报, 2013, 35(5): 1185-1189. DOI:10.3724/SP.J.1146.2012.01096.
Jiang Zelin, Liu Wei, Li Baoli, et al. A motion compensation method for synthetic aperture sonar based on segment displaced phases center algorithm and errors fitting[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1185-1189. DOI:10.3724/SP.J.1146.2012.01096.(in Chinese)
[8] 张学波, 方标, 应文威. 多子阵合成孔径声纳系统中的侧摆运动误差补偿[J]. 电讯技术, 2018, 58(2): 138-144. DOI:10.3969/j.issn.1001- 893x.2018.02.004.
Zhang Xuebo, Fang Biao, Ying Wenwei. Motion compensation of sway error for multireceiver synthetic aperture sonar system[J]. Telecommunication Engineering, 2018, 58(2): 138-144. DOI:10.3969/j.issn.1001- 893x.2018.02.004.(in Chinese)
[9] Wei B, Li H, Zhou T, et al. Joint Motion Error Estimation Algorithm for Multibeam Synthetic Aperture Sonar[J]. IEEE Access, 2018, 6: 40519- 40529. DOI:10.1109/ACCESS.2018.2858259.
[10] 张友文. 条带式合成孔径声呐相位梯度自聚焦算法[J]. 哈尔滨工业大学学报, 2009, 41(5): 156-160. DOI:10.3321/j.issn:0367- 6234.2009.05.037.
Zhang Youwen. Phase gradient autofocus algorithm applied to stripmap SAS[J]. Journal of Harbin Institute of Technology, 2009, 41(5): 156-160. DOI:10.3321/j.issn:0367- 6234.2009.05.037.(in Chinese)
[11] 段江涛, 黄勇, 刘纪元. PGA算法在条带式SAS场景目标成像中的应用[J]. 应用声学, 2017, 36(2): 175-181. DOI:10.11684/j.issn.1000-310X.2017.02.013.
Duan Jiangtao, Huang Yong, Liu Jiyuan. The application of phase gradient autofocus algorithm to stripmap SAS imaging for scene targets[J]. Journal of Applied Acoustics, 2017, 36(2): 175-181. DOI:10.11684/j.issn.1000-310X.2017.02.013.(in Chinese)
[12] 张远彪, 朱三文. 多子阵合成孔径声纳空变运动补偿[J]. 计算机应用, 2014, 34(S1): 352-355.
Zhang Yuanbiao, Zhu Sanwen. Space-variant motion compensation for multi-element synthetic aperture sonar[J]. CODEN JYIIDU, 2014, 34(S1): 352-355.(in Chinese)
[13] Zhu S, Tang J, Chen M. Segment DPCA motion compensation for SAS[C]∥International Congress on Image & Signal Processing 2009. DOI:10.1109/CISP.2009.5304520.
[14] 朱三文, 胡金华, 唐劲松, 等. SAS角运动补偿仿真研究[J]. 系统仿真学报, 2009, 21(20): 6564- 6567.
Zhu Sanwen, Hu Jinhua, Tang Jinsong, et al. Simulation of SAS angular motion compensation[J]. Journal of System Simulation, 2009, 21(20): 6564- 6567.(in Chinese)
[15] 李保利, 江泽林, 刘维, 等. 一种大测绘带合成孔径声纳运动补偿方法[P]. 中国: ZL201010112241.7,2010.06.30.
Li Baoli, Jiang Zelin, Liu Wei, et al. A motion compensation method in the application of wide-swath synthetic aperture sonar[P]. Chinese: ZL201010112241.7,2010.06.30.(in Chinese)
[16] 张鹏飞, 江泽林, 刘维, 等. 一种适用于大测绘带合成孔径声呐的运动补偿方法[J]. 声学学报, 2015, 40(2): 153-161. DOI:10.15949/j.cnki.0371- 0025.2015.02.006.
Zhang Pengfei, Jiang Zelin, Liu Wei, et al. A motion compensation method for wide-swath synthetic aperture sonar[J]. ACTA ACUSTICA, 2015, 40(2): 153-161. DOI:10.15949/j.cnki.0371- 0025.2015.02.006.(in Chinese)
[17] 刘维, 刘纪元, 张春华. 多子阵合成孔径声呐波数域算法不均匀采样问题研究[J]. 声学学报, 2009, 34(3): 203-210.
Liu Wei, Liu Jiyuan, Zhang Chunhua. Research on non-uniform sampling problem when adapting wave number algorithm to multiple-receiver synthetic aperture sonar[J]. ACTA ACUSTICA, 2009, 34(3): 203-210.(in Chinese)
[18] 王建国, 邱会中, 黄顺吉. 合成孔径雷达图像质量的评估指标[J]. 电子科技大学学报, 1992, 21(5): 485- 490.
Wang Jianguo, Qiu Huizhong, Huang Shunji. The evaluating parameter system of the synthetic aperture radar images[J]. Journal of University of Electronic Science and Technology of China, 1992, 21(5): 485- 490.(in Chinese)
