1 引言
随着我国对海洋技术的研究由浅海步入深海,深海目标定位成为研究热点。深海目标定位对水下军事侦察和水下作战具有重要意义,传统的深海被动定位方法为匹配场定位法。20世纪80年代,Fizell和Wales[1]用垂直阵对260 km远处的低频声源进行匹配场定位;1991年,Transfer和Hodgkiss[2]在太平洋东北部进行了深海匹配场定位实验,结果在估计声源深度时存在较大模糊;1992年,Westwood[3]对墨西哥湾4500 m深海中43 km内的声源进行了匹配场定位,实验结果表明增加信号带宽可以提高定位精度;2013年,陈连荣[4]等人对位于深海海底反射声区的声源进行匹配场定位。尽管匹配场方法在深海被动定位中有一定的有效性,但是匹配场方法存在模型失配的问题,计算量较大,并且在实际中往往需要大孔径阵列提高定位精度,这在工程上难以实现。因此,匹配场方法在深海被动定位应用中受到限制。
由于匹配场定位存在局限性,近年来声纳工作者研究基于多途到达角和多途时延的被动定位方法。2006年,Tiemann[5]等人根据单水听器接收信号的多途时延差追踪到抹香鲸的运动轨迹,但由于海底反射损失太大,与海底作用的声线相关的多途到达时间差难以分离;2014年,段睿[6]等人根据接收信号自相关函数提取直达波和海面反射波到达时间差,通过扩展卡尔曼滤波对目标初始状态进行估计;2016年孙梅[7- 8]等人分析了大深度矢量水听器的接收信号,分别利用水平振速和垂直振速的能量差以及直达波和海面反射波的到达角实现了近水面声源的距离估计;2018年,高飞[9]等人研究了当声源和接收器都位于深海浅水表层时,根据首达波和次达波的声到达时间差,构建扩展卡尔曼模型,对移动声源进行定位。其中,多途到达角定位方法对声源深度不敏感,而多途时延定位方法对声源深度和声源距离均较敏感,但时延信息较难获得,对信号带宽和信噪比要求较高。
深海直达声区是指未经海底反射或者未经海底附近反转的声线所覆盖的区域[7]。本文在多途被动定位研究的基础上,对深海直达声区水下声源距离和深度进行联合估计。首先根据直达波到达两个不同深度水听器的时间差估计声源水平距离,然后利用单个水听器直达波与海面反射波的时延差估计声源深度,将两个估计结果相结合进一步提高声源距离估计精度,并通过实验数据验证了方法的有效性。
2 理论分析
2.1 双水听器接收信号互相关函数
如图1所示,在深海中两个接收水听器的深度分别为z1和z2,声源S的深度为zs,声源到垂直阵的水平距离为r,假设声源信号为s(n),则接收信号xk(n)为:
xk(n)=hk(n)*s(n)+ek(n) k=1,2
(1)
其中,k代表水听器序号,深度较浅的水听器序号为1,深度较深的水听器序号为2,hk(n)为传输函数,可表示为:
(2)
其中,ak,i(n)和nk,i分别代表到达第k个水听器的第i条本征声线的幅度和时延,δ(n)为单位脉冲序列,ek(n)代表噪声。假设信号与噪声不相关,两个接收水听器接收信号的互相关函数可以表示为[10]:
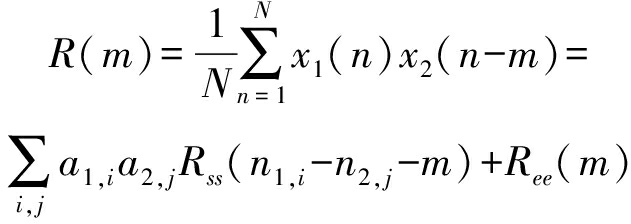
(3)
其中,
(4)
(5)
假设噪声为独立同分布,则Ree(m)≈0。若声源信号为宽带信号,则接收信号互相关函数会在m=n1,i-n2, j位置处出现峰值。由于在深海直达声区,声场主要由直达波和海面反射波构成[8],若将直达波和海面反射波分别视作到达接收水听器的第1、2条本征声线,则式(3)可近似为[10]:
R(m)≈a1,1a2,1Rss(n1,1-n2,1-m)+
a1,1a2,2Rss(n1,1-n2,2-m)
a1,2a2,1Rss(n1,2-n2,1-m)+
a1,2a2,2Rss(n1,2-n2,2-m)
(6)
由式(6)可以看出,互相关函数有四组峰值,但由于直达波没有海面反射损失且幅度相对较大,因此互相关函数的最大值出现在n1,1-n2,1处。设信号采样率为fs,则直达波到达两个接收水听器的时间差为:
(7)
假设声线直线传播,则声信号到达两个接收器的时间差Δt1可近似表示为:
(8)
其中,c1为两个接收水听器之间的平均声速,对Δt1关于声源深度zS求导可得:
![]() =
=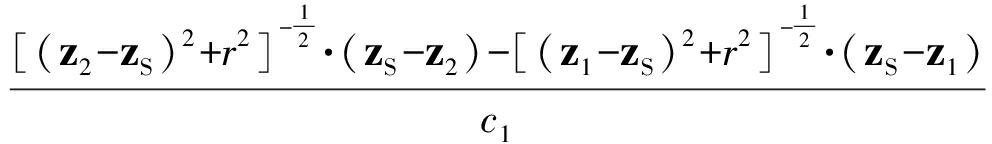 ≈
≈
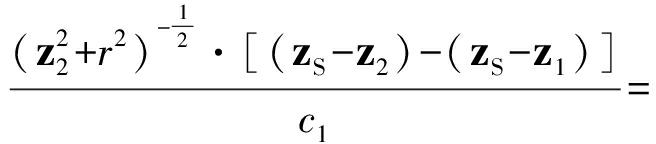
![]()
(9)
其中,Δz为两个接收水听器的深度差,相对于![]() 较小,说明直达声到达两接收水听器的时间差受声源深度变化影响不大。因此,可以根据接收水听器互相关函数提取直达声到达时间差,先假定声源深度在某一合理范围内,再与射线模型计算的时间差相匹配得到水下声源水平距离的初步估计结果。
较小,说明直达声到达两接收水听器的时间差受声源深度变化影响不大。因此,可以根据接收水听器互相关函数提取直达声到达时间差,先假定声源深度在某一合理范围内,再与射线模型计算的时间差相匹配得到水下声源水平距离的初步估计结果。
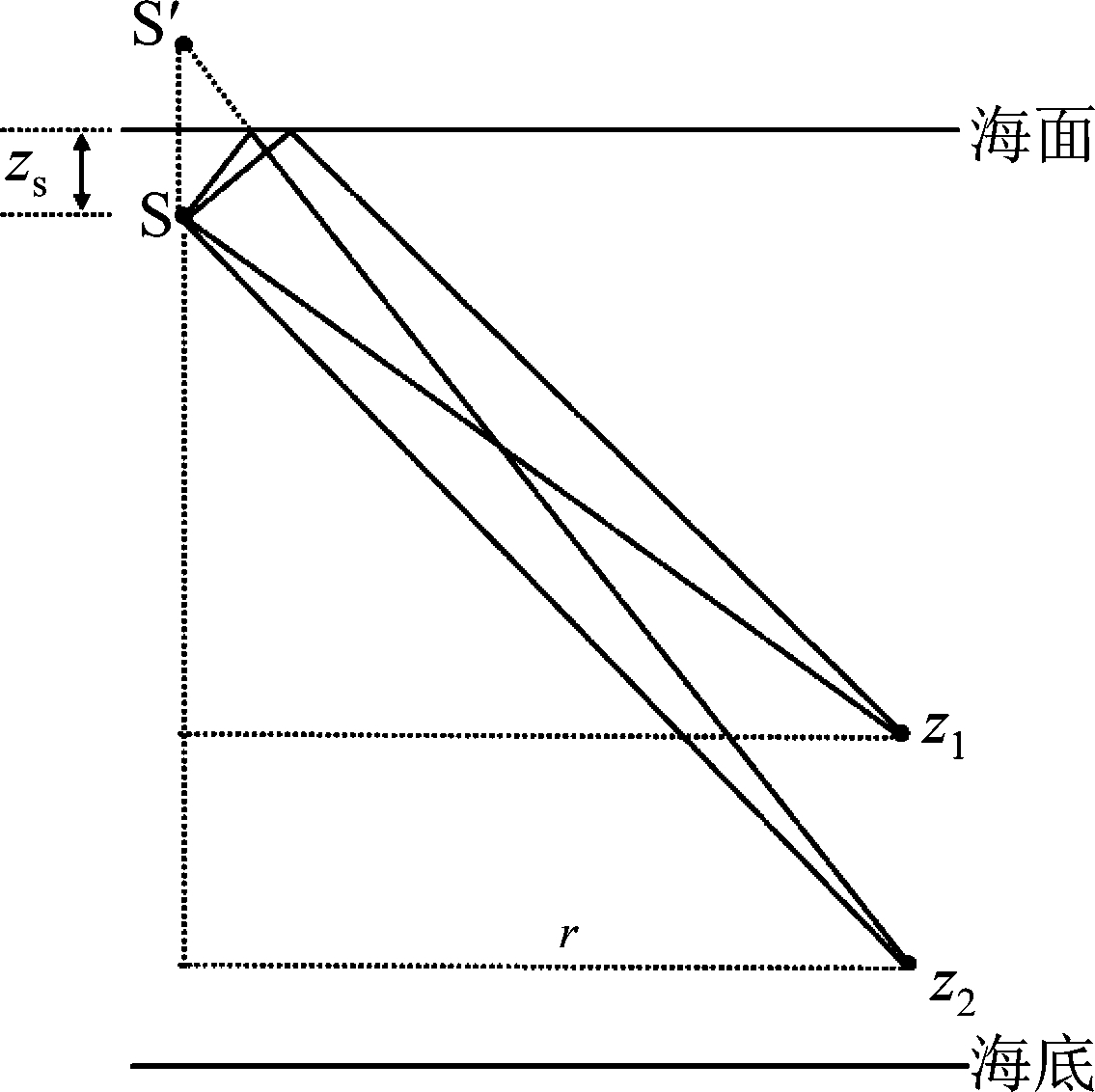
图1 声源与接收器相对位置示意图
Fig.1 The position of the sound source relative to the receiver
2.2 单水听器接收信号自相关函数
声源与接收器的相对位置如图1所示,接收信号形式如式(1)所示,则接收信号的自相关函数可以表示为:
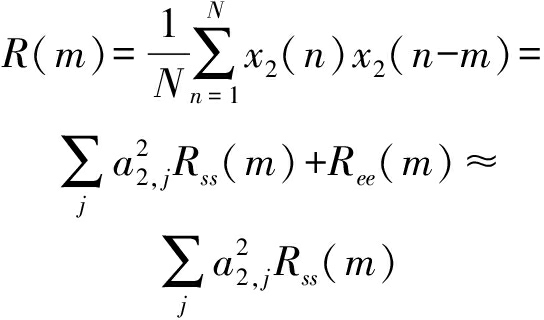
(10)
由式(10)得到直达波和海面反射波的时间差为:
(11)
假设声线直线传播,则直达波和海面反射波的到达时间差还可以表示为:
(12)
其中,c2是指声源到海表面间的平均声速,对Δt2关于r求导可得:
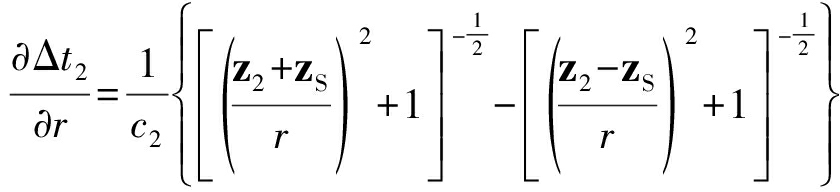
(13)
由式(13)可以得出Δt2随着水平距离r变化较小。当声源深度zS不变,水平距离较大时,![]() 趋于0,即直达波与海面反射波的时间差近似不变。因此可以结合声源水平距离估计结果以及由接收信号自相关函数提取直达波和海面反射波的到达时间差,再与射线模型计算的时延差匹配估计声源深度。
趋于0,即直达波与海面反射波的时间差近似不变。因此可以结合声源水平距离估计结果以及由接收信号自相关函数提取直达波和海面反射波的到达时间差,再与射线模型计算的时延差匹配估计声源深度。
3 实验数据
2016年11月,声场声信息国家重点实验室在南海深海进行了一次深海声传播实验,实验采用图2所示的单船结合潜标的方式,实验船为“实验一号”,接收阵为18阵元的自容式水听器阵,非均匀地分布在99 m~ 4152 m的深度范围内,其中最深的两个水听器布放深度为1972 m和4152 m。实验中拖曳声源的平均深度约120 m,拖曳换能器发射双曲调频信号,信号中心频率为300 Hz,带宽100 Hz。发射信号时序如图3所示,发射时长为20 s,间隔10 s发射下一个信号,每四个信号为一个组,间隔50 s发射下一组,发射信号声源级为193 dB。不同自容式水听器及其与发射系统之间的时间同步是通过高精度CPT原子钟实现,通过GPS对銣钟源进行同步授时,可保证在传播实验的两周内的时间精度误差控制在50 ns以内。实验过程中海深较为平坦,平均海深约为4312 m,最远传播距离为182 km。实验期间用抛弃式温盐深探头(XCTD)测量声速剖面如图4所示,得到声道轴大约位于1151 m深度处,声速为1484 m/s,海面声速为1540 m/s,大于海底附近的声速1533 m/s,为典型的深海不完全声道。
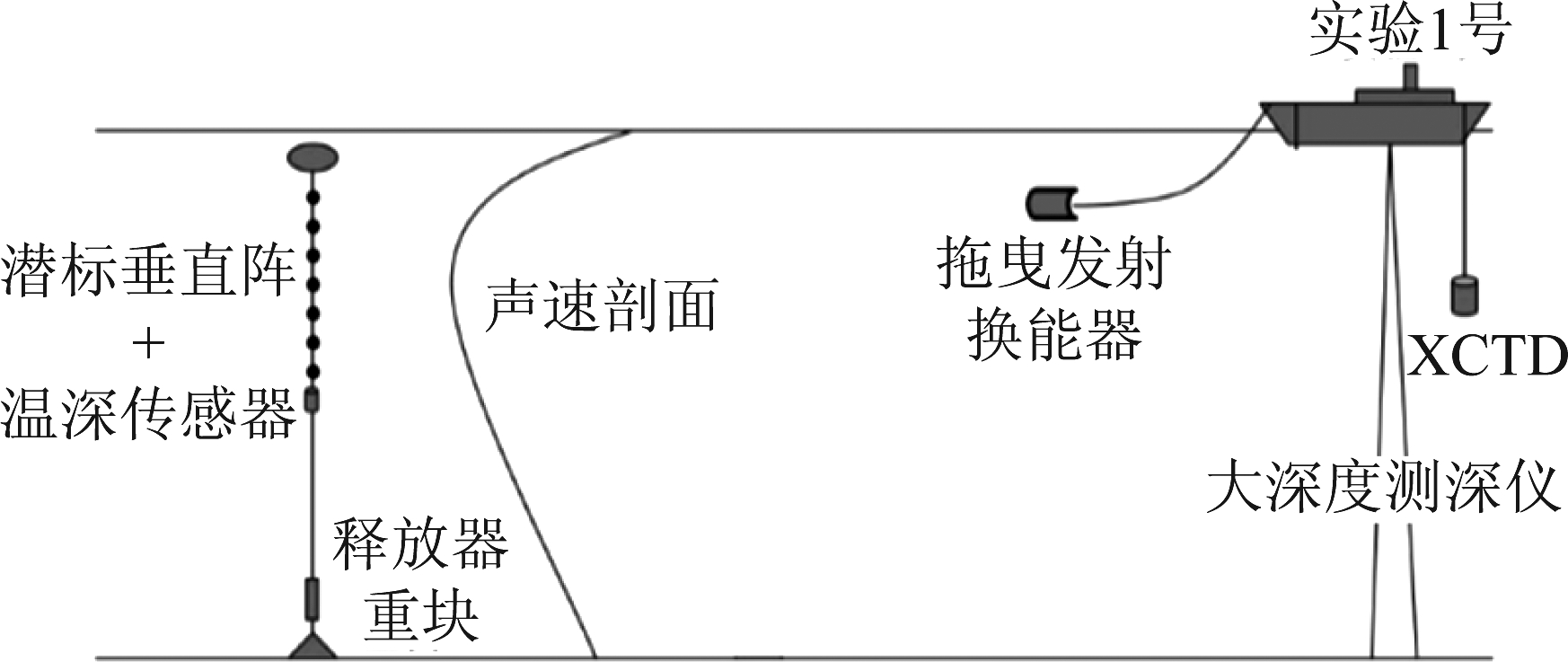
图2 声传播实验海上示意图
Fig.2 Experimental configuration

图3 发射信号序列示意图
Fig.3 The acoustic emission signal during the experiment
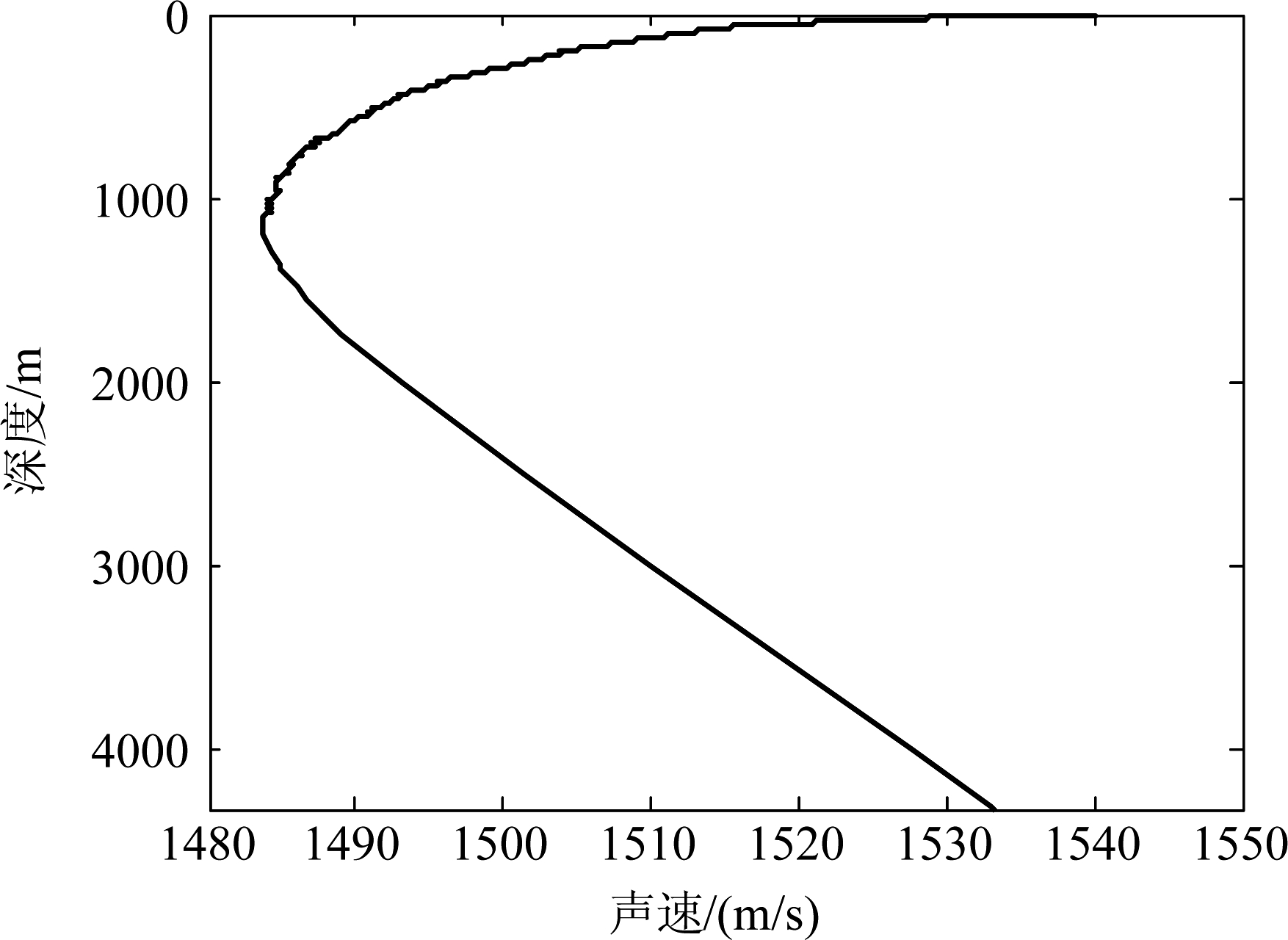
图4 实验期间用XCTD测量的海水声速剖面
Fig.4 Sound speed profile measured by XCTD near the receiving array
对深度为1972 m和4152 m的两个水听器的接收信号进行处理,得到的声传播损失如图5和图6中点线所示,用抛物方程近似声场模型RAM-PE[11]仿真的声传播损失如图5和图6中实线所示,计算中所用的海底声学参数为:声速1565 m/s,密度1.6 g/cm3,吸收系数0.3 dB/l[12]。可以看出仿真结果与实验结果在直达声区、影区和会聚区内均符合较好,而且直达声区的声传播损失相对影区来说较小。由图5和图6还可以看出,当接收深度为1972 m时,直达声区的宽度约为11 km,当接收深度为4152 m时,直达声区的宽度约为30 km。图7给出了RAM-PE模型计算的不同深度和距离的声传播损失,从图中可以看出接收深度越深,直达声区的水平距离越宽。
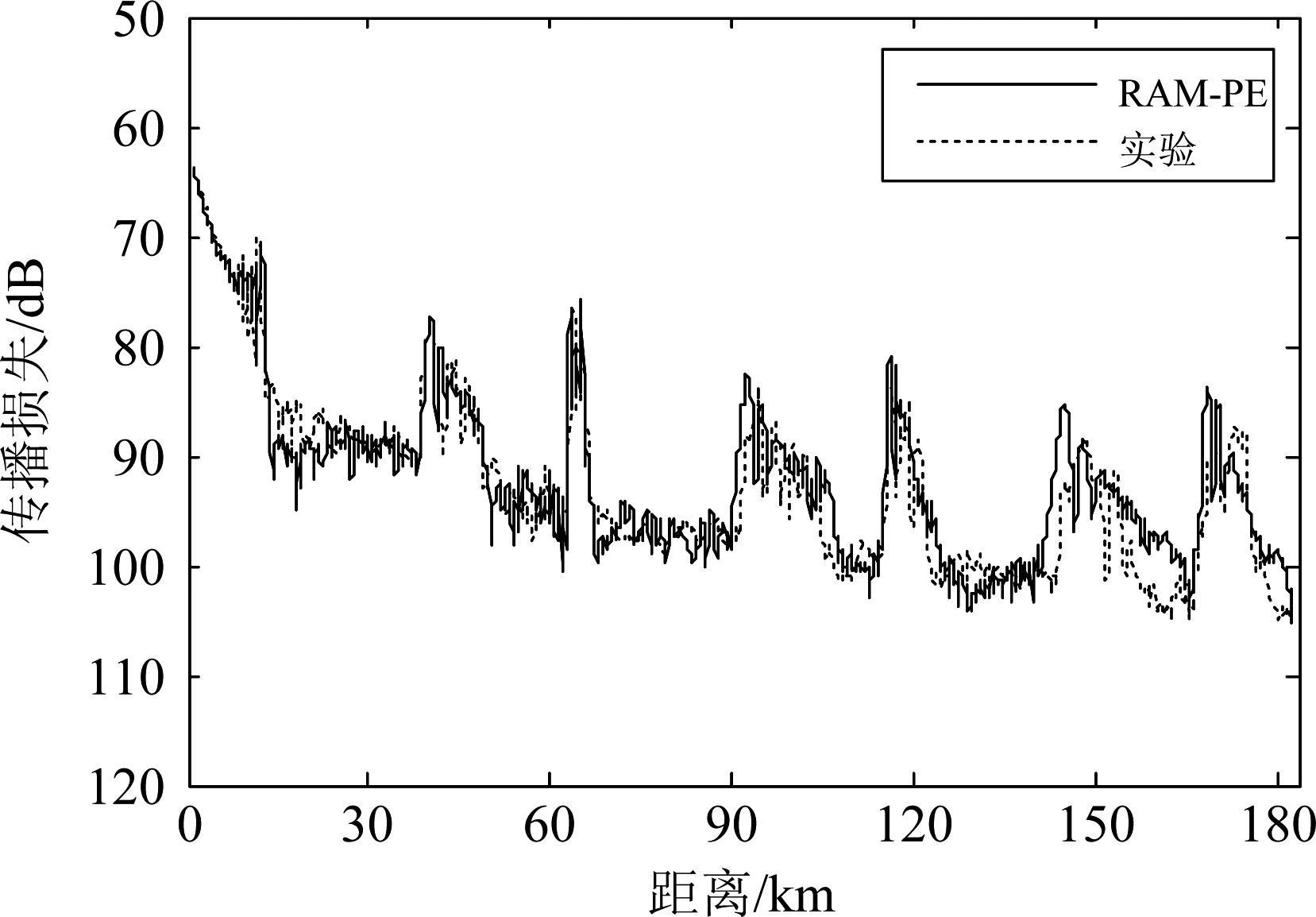
图5 接收深度为1972 m时声传播损失实验仿真对比图
Fig.5 Comparison of the experimental transmission losses (TLs) with numerical results at the depth of 1972 m
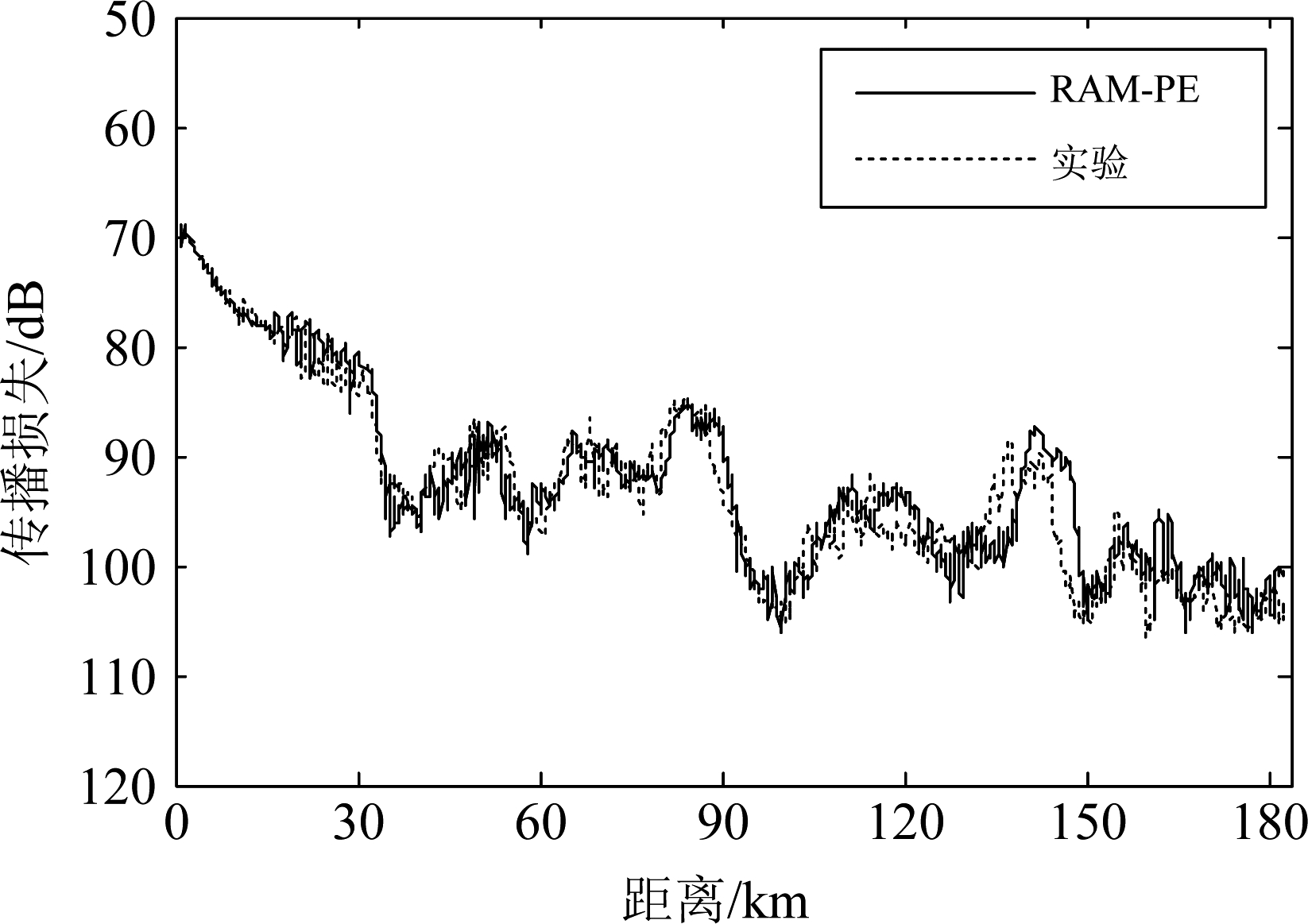
图6 接收深度为4152 m时声传播损失实验仿真对比图
Fig.6 Comparison of the experimental TLs with numerical results at the depth of 4152 m

图7 RAM-PE计算的二维传播损失图
Fig.7 Two-dimensional TL calculated by RAM-PE
在深海中,接收潜标与拖曳声源之间的距离需要特别标定。一般拖曳声源的位置通过“实验一号”的GPS位置和放出去的拖缆长度进行标定,而潜标的位置通过重块入水点的GPS位置和潜标顶端信标出水的GPS位置进行综合标定,此外,接收水听器与拖曳声源的水平距离还可以通过图6中大深度水听器接收直达声区与声影区传播损失急剧下降的距离来进行标校,而接收水听器的深度则通过绑在其附近的压力计进行标定。
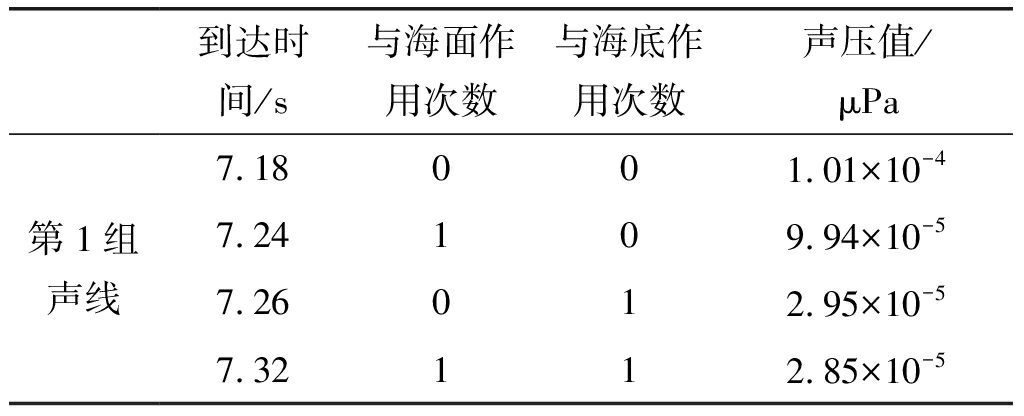
为了进一步分析深海直达声区的脉冲多途到达结构,采用以高斯波束追踪法为基础的BELLHOP射线模型[13]计算深海直达声区信号的声线轨迹、到达时间和声压。图8给出了接收深度为4152 m、接收水平距离为9977 m时的本征声线图。由图8可以看出声线主要分为三组:第一组用实线表示,分别与海面和海底作用的次数不超过一次;第二组用虚线表示,分别与海面和海底作用的次数不超过两次;第三组用点线表示,分别与海面和海底作用至少两次。表1给出了接收深度为4152 m、距离为9977 m时第一组声线的到达时间、与海面海底作用次数及声压值,第二组和第三组声线传播路径相对第一组较长,声压值较小,不再列出。对比第一组声线的声压值可以看出能量较强的为直达波和海面反射波,说明在深海直达声区接收信号的主要成分为直达波和海面反射波。因此,可以利用深海直达声区大深度水听器接收到的声信号对水下声源距离深度进行联合估计。
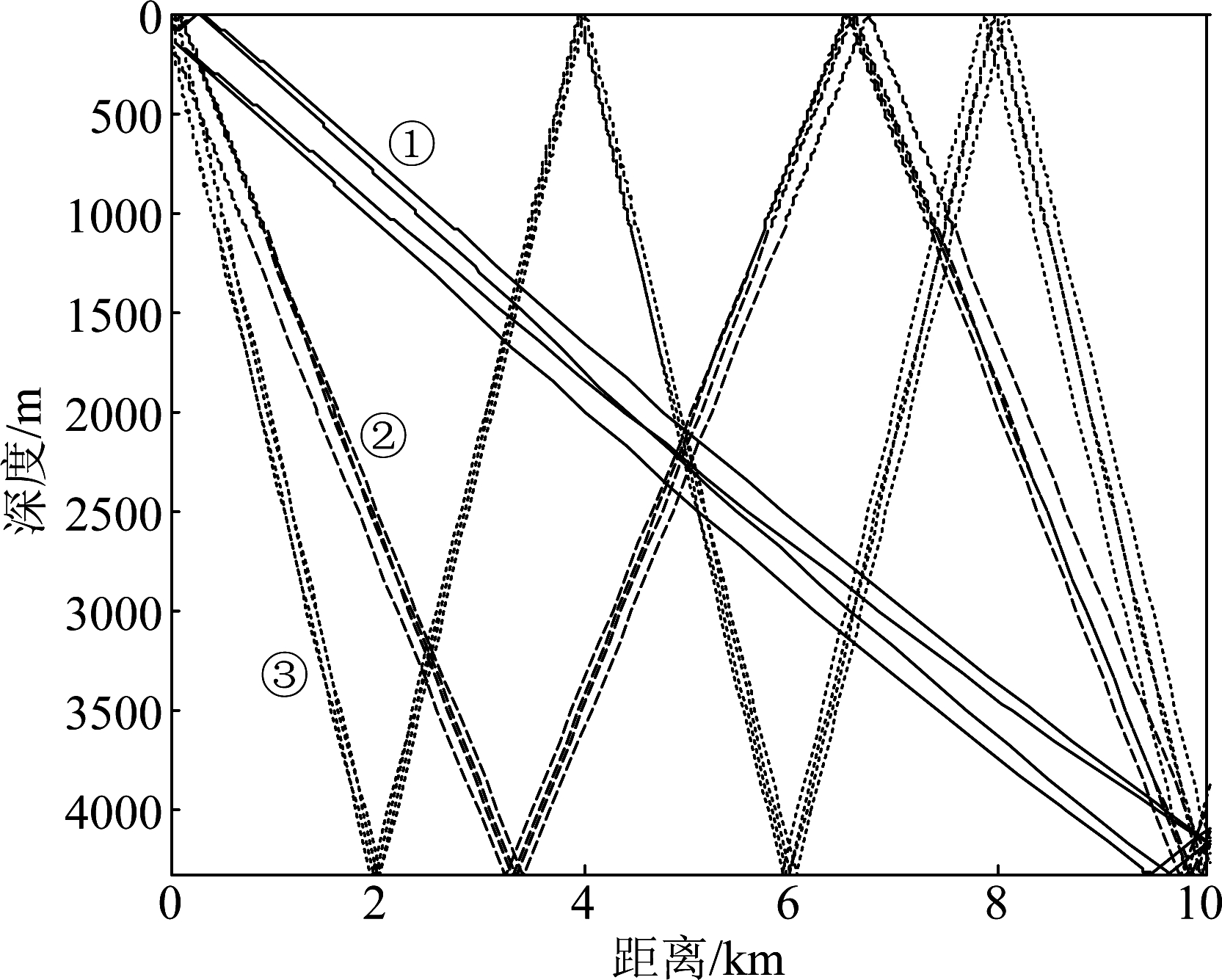
图8 接收深度为4152 m、水平距离为9977 m时的本征声线
Fig.8 The eigenray when the receive depth is 4152 m and the range is 9977 m
表1 接收深度为4152 m、距离为9977 m时第一组声线的到达时间、与海面海底作用次数及声压值
Tab.1
到达时间/s与海面作用次数与海底作用次数声压值/μPa第1组声线7.18001.01×10-47.24109.94×10-57.26012.95×10-57.32112.85×10-5
4 距离深度联合估计
对深海直达声区水下声源距离深度进行联合估计的流程图如图9所示。
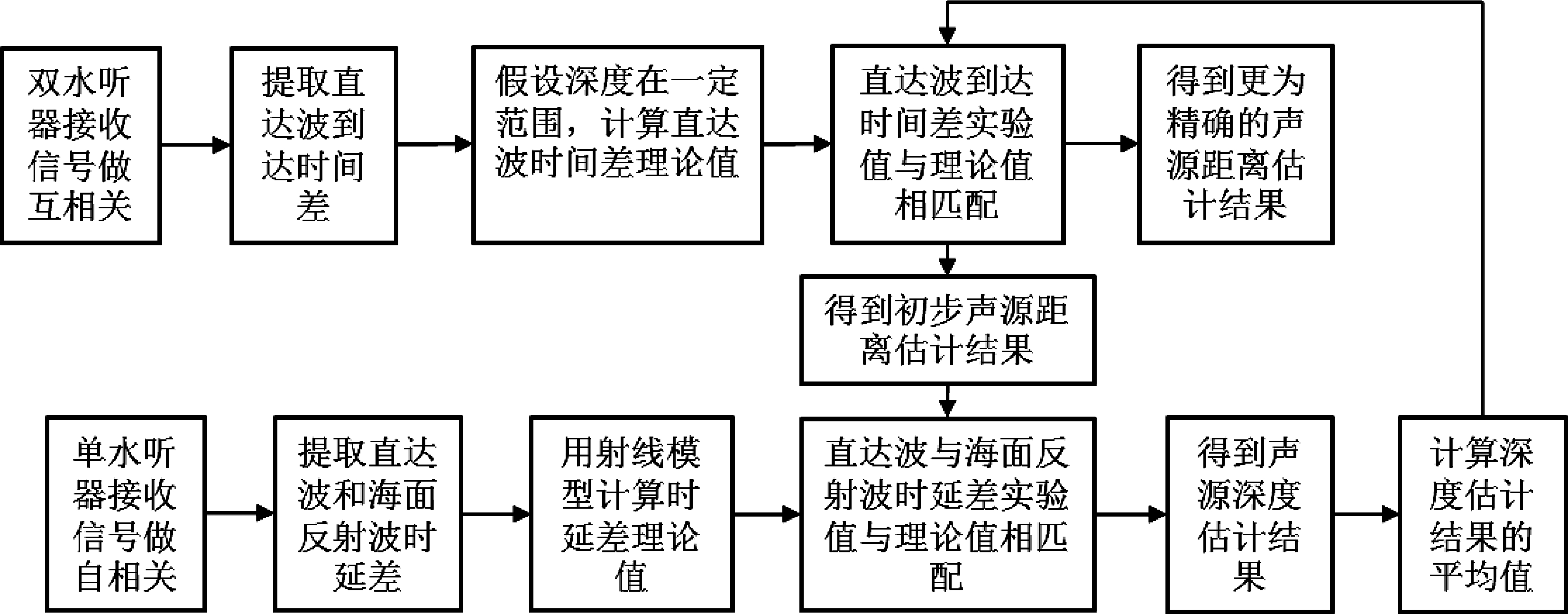
图9 距离深度联合估计流程图
Fig.9 Combined estimation flowchart of range and depth
根据上述流程图,首先对上一节中接收深度为1972 m和4152 m的两个水听器的接收信号做互相关,得到互相关函数随距离的变化如图10所示。由于当接收深度为1972 m时直达声区的宽度大约只有11 km,因此这里只给出了11 km内的互相关函数图。由图10可以看出互相关函数有四组峰值,这与2.1节中的理论分析一致。根据图10提取到的直达波到达时间差如图11中黑色圆圈所示,黑色实线是用BELLHOP模型仿真的理论值,仿真时声源深度取平均值120 m。由图11可以看出,两个水听器接收到直达波的到达时间差随水平距离的增大而减小,而且到达时间差的实验值与理论值符合较好。若假设声源深度在50 m~300 m之间变化,则

图10 双水听器接收信号互相关函数图
Fig.10 Cross-correlation function of signals received by two hydrophones
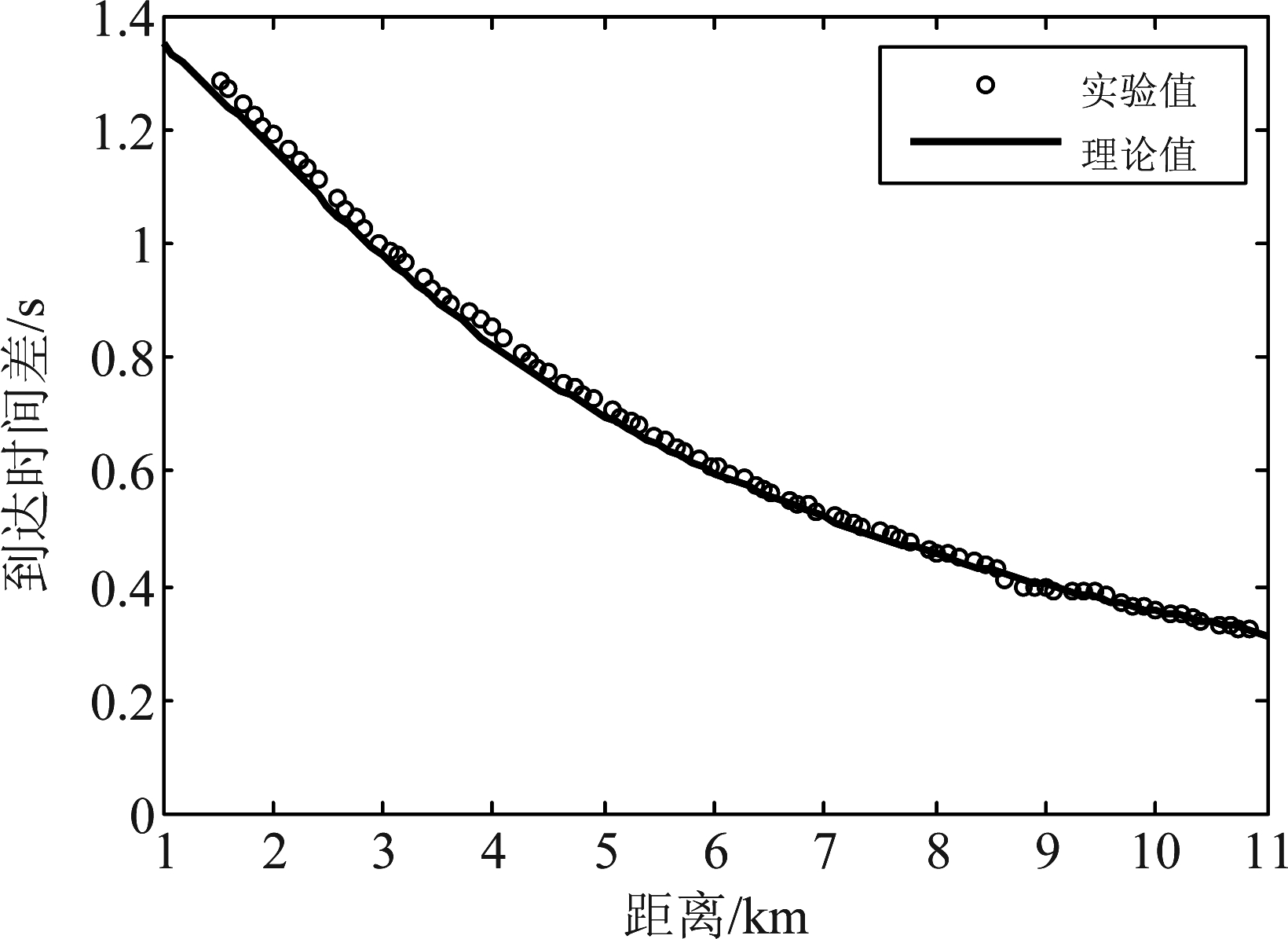
图11 直达波到达时间差实验理论对比图
Fig.11 Comparison of the experimental arrival times of the direct wave and numerical results

图12 不同深度不同水平距离下直达波到达时间差等高线图
Fig.12 The arrival time delay contour of direct waves for sources at different depths and ranges

图13 距离估计均方误差和相对误差限随声源深度的变化
Fig.13 Mean square error and relative error limit of range estimation vary with the source depth
用BELLHOP仿真得到直达波到达两个接收水听器的时间差如图12所示,从图12可以看出直达波到达时间差随声源深度变化较小,而随距离变化较大。将直达波到达时间差的实验值与理论值相匹配得到的距离估计均方误差和相对误差限如图13所示,可以看出当假设声源深度在50 m~300 m之间时,距离估计的均方误差在0.01 km~0.06 km之间,相对误差限在7.8%~16.5%之间。可以看出,当假设深度与实际深度偏差较大时,距离估计相对误差较大。
然后对深度为4152 m的水听器的接收信号做自相关,得到声源在不同距离时的自相关函数如图14所示,从图中可以看出自相关函数存在一组明显的峰值,总体上峰值位置对应的时间随距离增大单调递减,接收水平距离在2.5 km到5 km之间时峰值位置扰动较大,这是由于这段距离上拖曳声源的实际深度变化较大。根据图14提取到的直达波与海面反射波的时延差如图15中黑色圆圈所示,黑色实线是BELLHOP模型计算结果,计算时声源深度保持在120 m,所以时延差单调变化。图16给出了接收深度为4152 m时,BELLHOP模型计算的不同声源深度不同距离下直达波与海面反射波时延差,其中声源深度取值范围为50 m~300 m。结合由双水听器接收信号互相关函数估计的声源距离结果,得到声源深度估计结果的平均值和相对误差限如图17所示,可以看出声源深度估计结果的平均值在117 m~125 m之间,相对误差限在10.4%~13.3%,相对误差限变化较小,所以声源距离估计结果对声源深度估计结果影响不大。由图13可以得到,当声源深度在117 m~125 m时,距离估计的相对误差限在10.1%~10.5%之间,说明可以根据声源深度估计结果的平均值结合双水听器互相关函数可较好实现距离估计。

图14 深度在4152 m单水听器接收信号的自相关函数随距离变化
Fig.14 Autocorrelation function of signals received by hydrophone at 4152 m
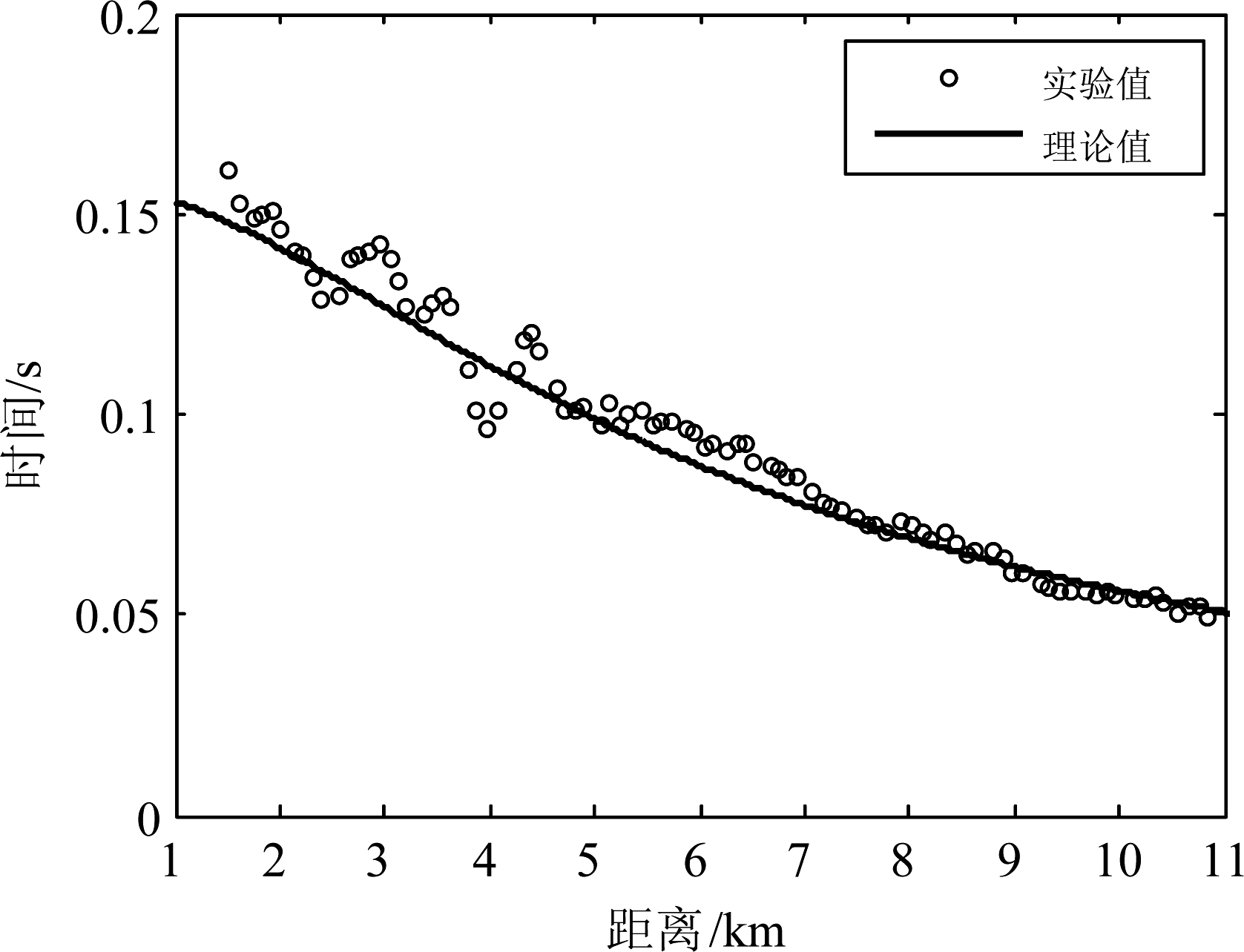
图15 直达波与海面反射波时延差实验结果与射线模型计算结果对比图
Fig.15 Comparison of the experimental time delay of the direct wave and the surface reflection wave with the numerical results
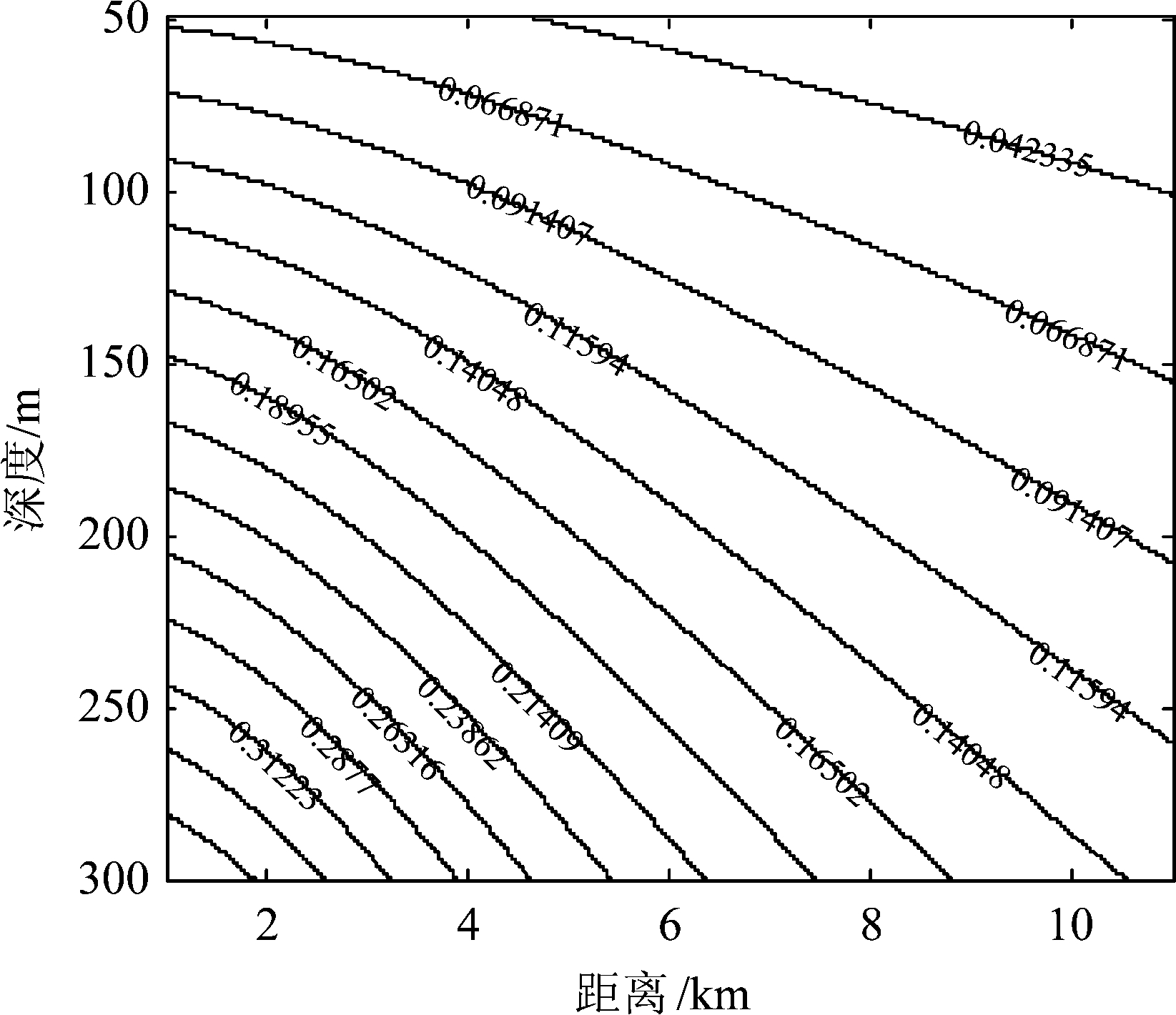
图16 不同深度不同距离下直达波与海面反射波时延差等高线图
Fig.16 The time delay contour of the direct wave and surface reflection wave for sources at different depths and ranges
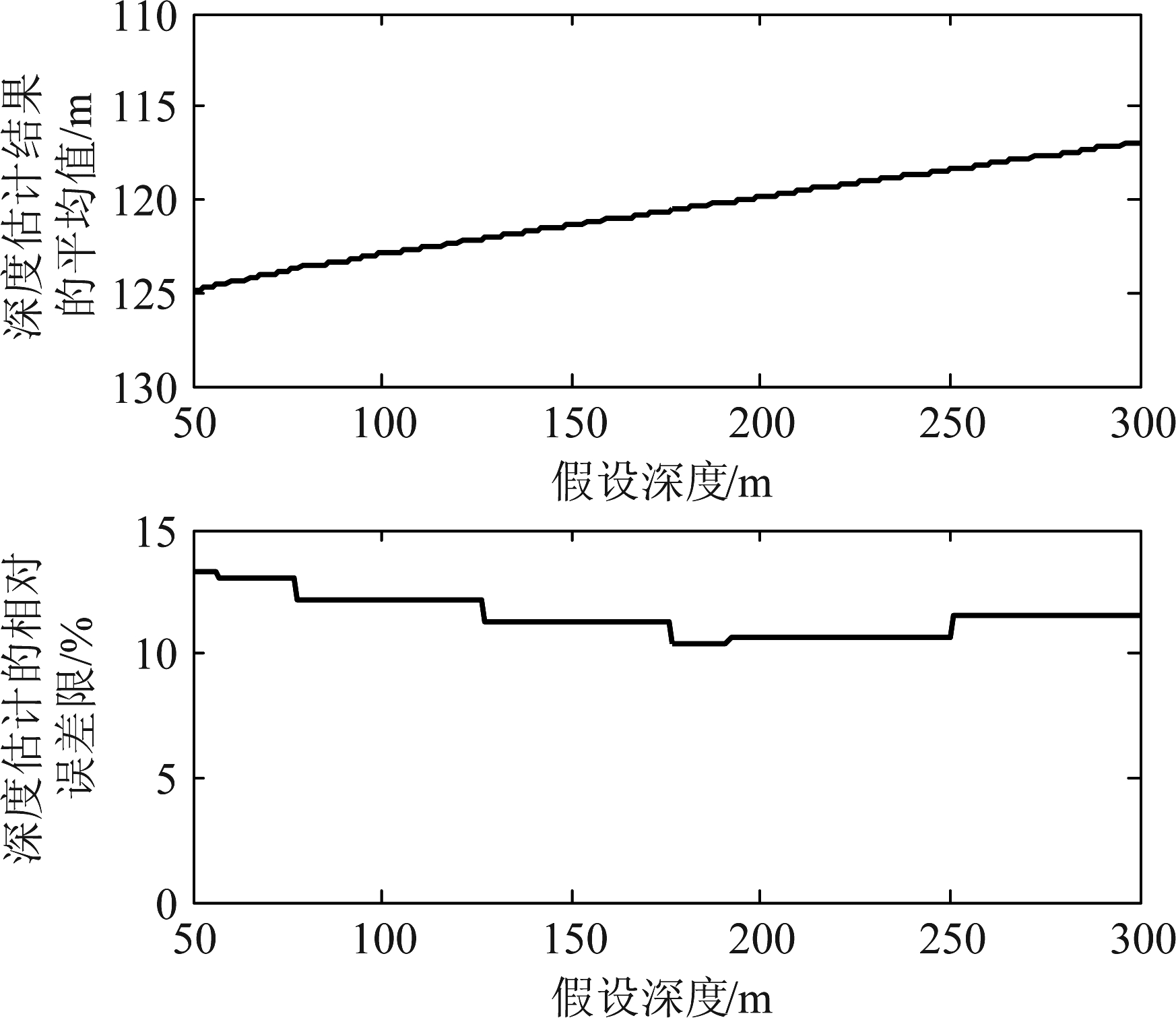
图17 深度估计结果的平均值和相对误差限
Fig.17 Mean value and relative error of depth estimation
图18给出了由假设深度为300 m时估计的距离结合单水听器自相关函数得到的声源深度估计结果,平均值为117 m,图19是对应的深度估计的绝对误差和相对误差。图20给出了声源假设深度取117 m并结合双水听器互相关函数得到的声源距离估计结果,图21是对应的距离估计的绝对误差和相对误差。从图19和图21可见,除了个别信号外,联合估计给出的大部分信号的深度和距离相对误差小于10%,能较好的实现对水下目标测距和测深。
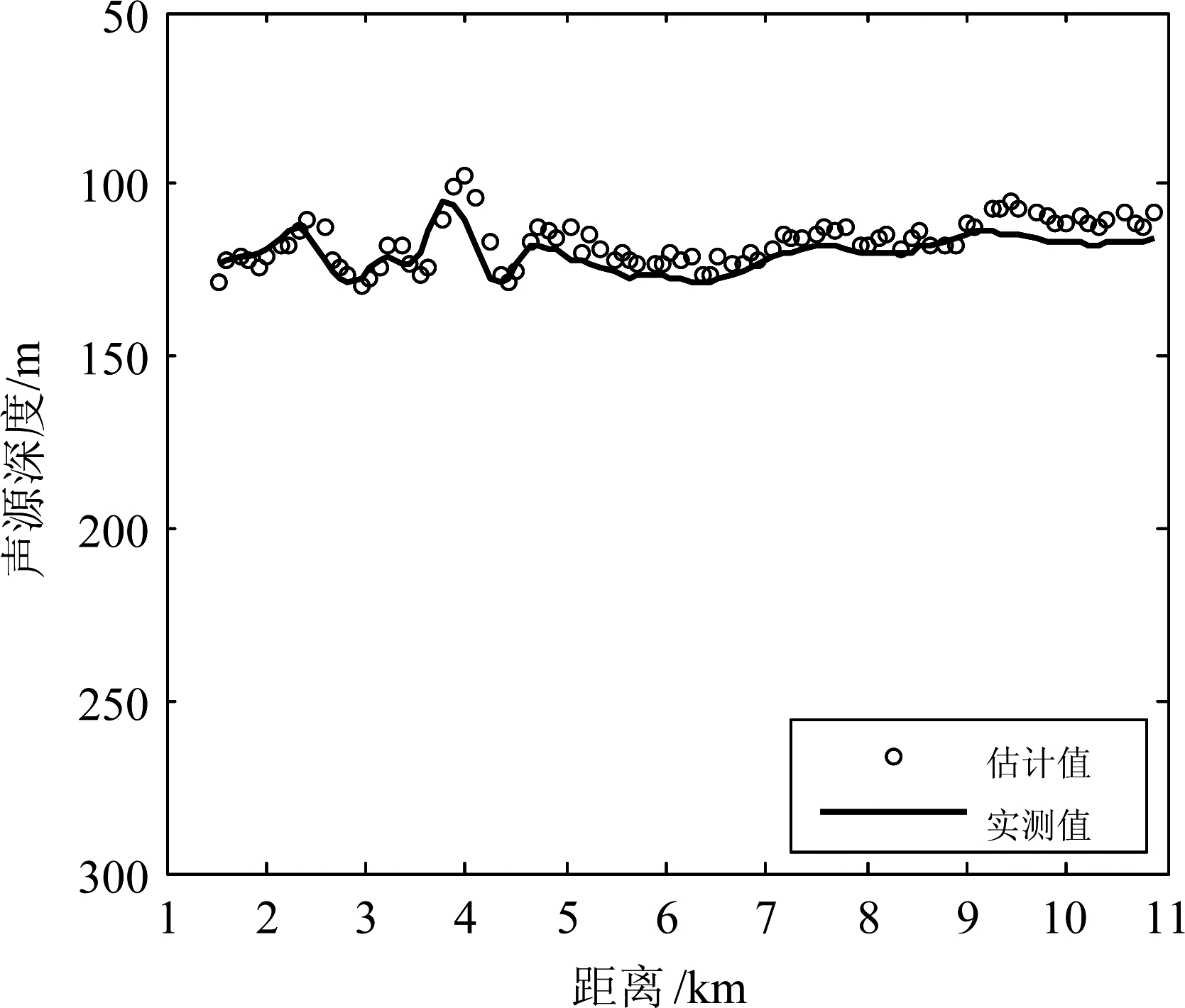
图18 声源深度估计结果
Fig.18 Source depth estimation result
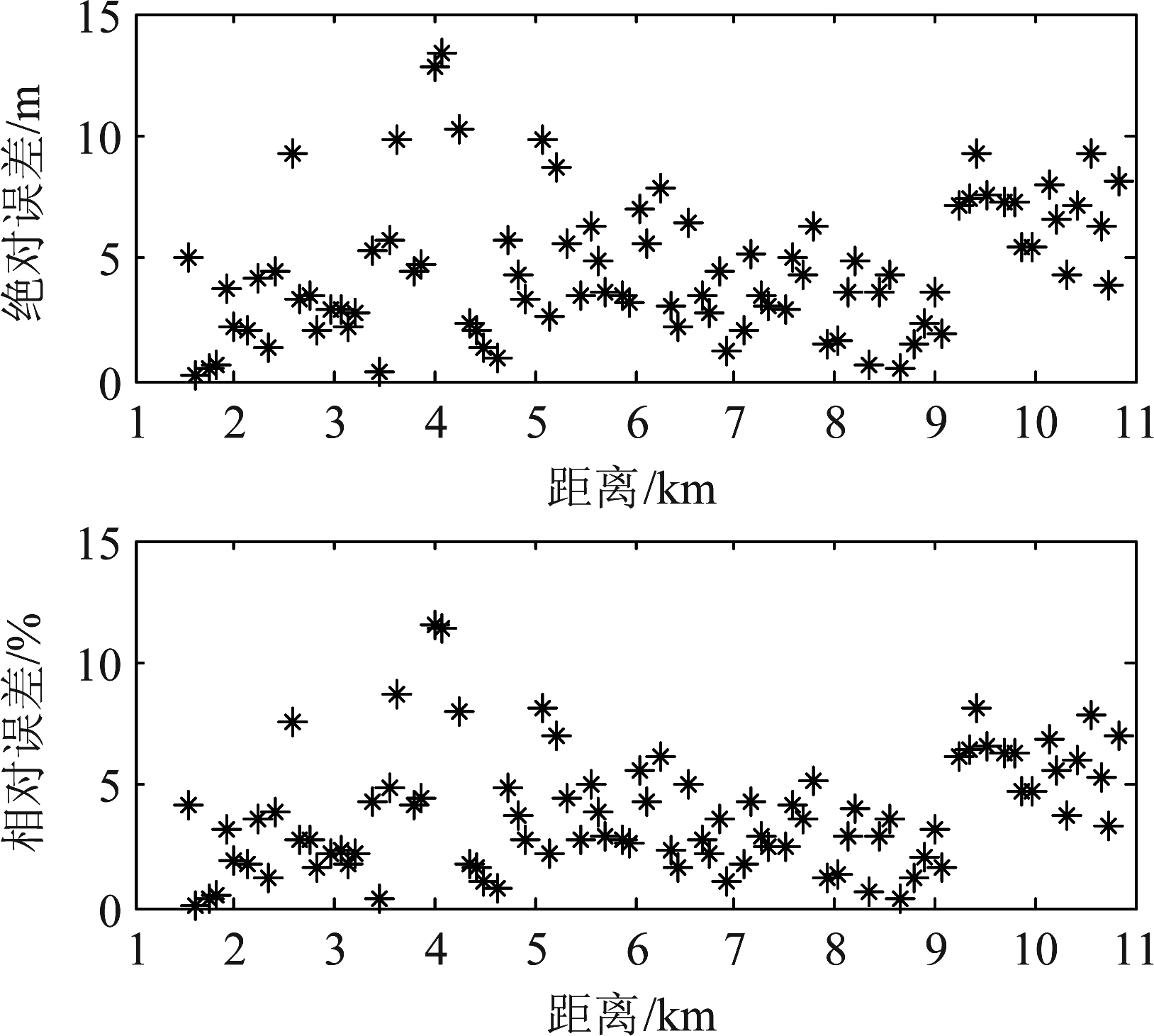
图19 声源深度估计误差
Fig.19 Source depth estimation errors
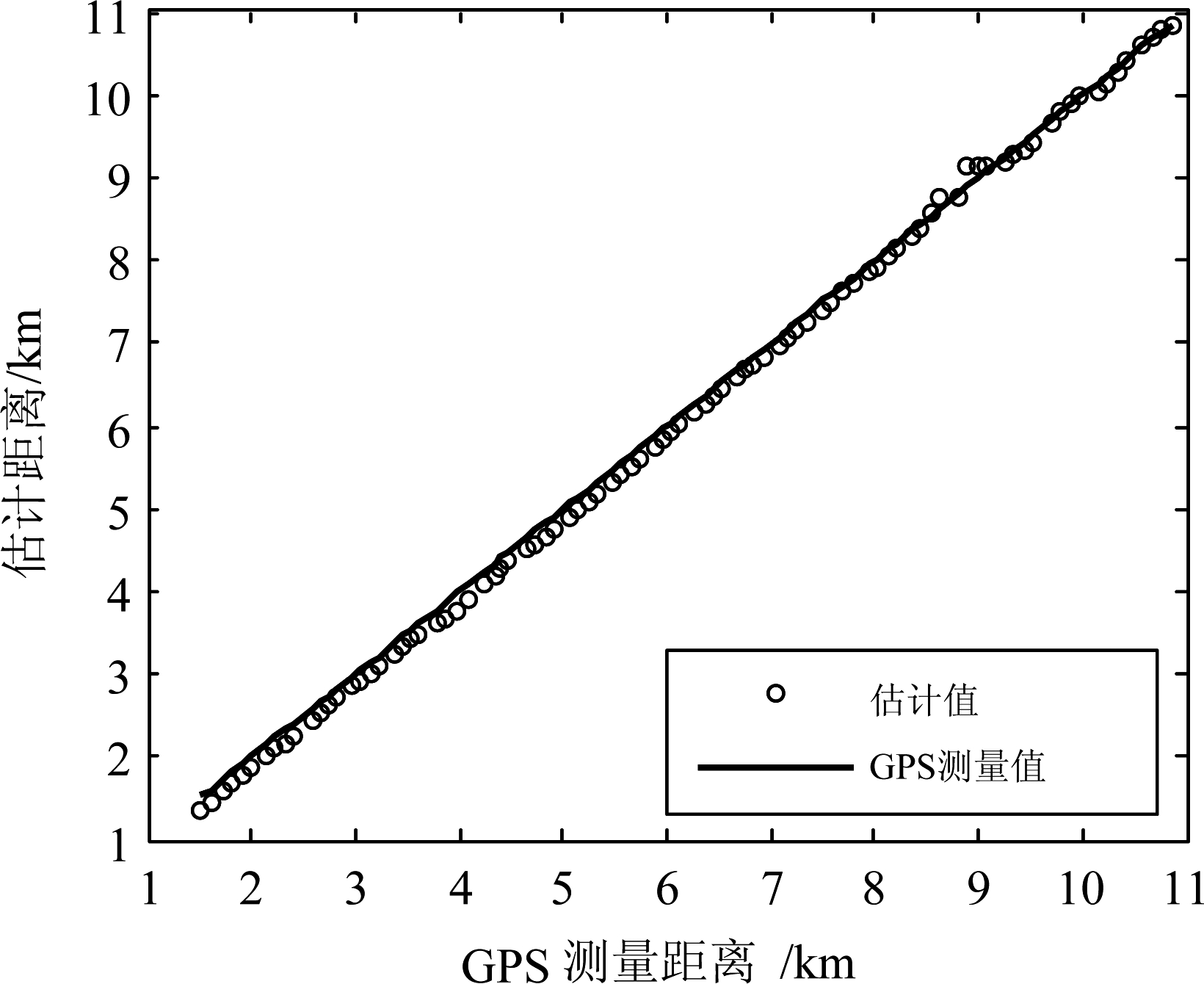
图20 声源距离估计结果
Fig.20 Source range estimation result
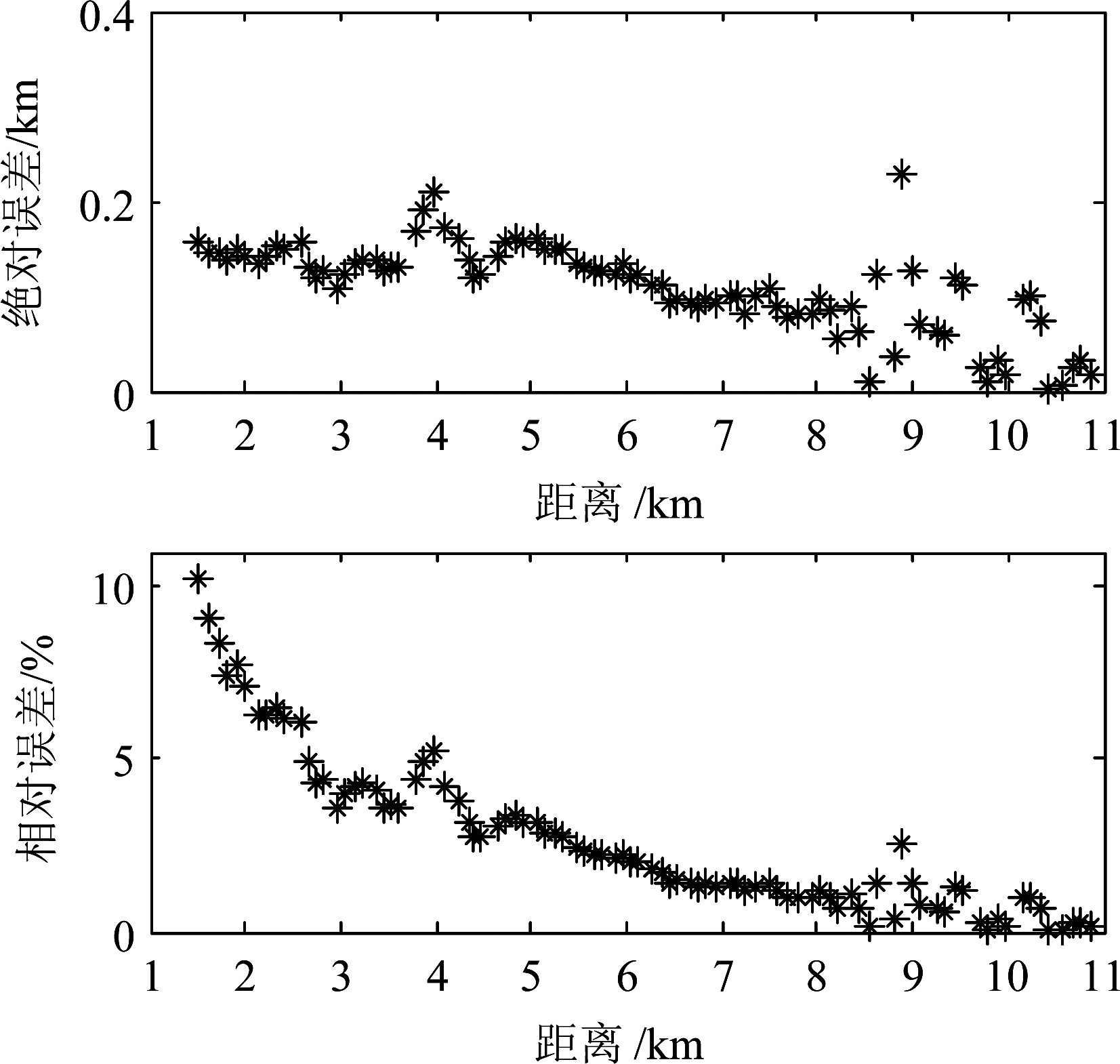
图21 声源距离估计误差
Fig.21 Source range estimation error
5 结论
针对深海直达声区水下目标定位问题,研究了深海直达声区水下声源距离和深度的联合估计方法,利用一次深海实验中大深度水听器接收的声信号,分析了双水听器接收信号互相关函数和单水听器接收信号自相关函数。得到由双水听器接收信号的互相关函数提取直达波到达时间差随距离增大单调递减,而受声源深度变化影响较小,所以先假定声源深度在一定范围内,得到初步距离估计结果;根据单水听器接收信号的自相关函数提取直达波和海面反射波时延差受声源深度变化影响较大,可以将此时延差与距离结果相结合估计出水下声源深度,得到声源深度的估计结果与实际值符合较好,并根据深度估计结果的平均值反馈到双水听器互相关函数测距方法中以得到了更为精确的距离估计结果。由于文中所用的接收器为单水听器,所以声源采用拖曳声源发射的强信号来验证方法的有效性,对于声纳对深海直达声区水下实际的弱目标定位,可以先通过水平阵阵列波束形成提高信噪比,然后再利用此距离深度联合估计方法,可对水下声源进行有效定位,研究结果对深海水下目标探测有一定参考价值。利用布放在深海海底的水平阵列对弱目标的定位实验将是以后的研究重点。
[1] Fizell R G, Wales S C. Source localization in range and depth in an Arctic environment[J]. Journal of the Acoustical Society of America, 1985, 78(S1): S57-S58.
[2] Tran J Q D, Hodgkiss W S. Matched‐field processing of 200-Hz continuous wave (cw) signals[J]. Journal of the Acoustical Society of America, 1991, 89(2): 745-755.
[3] Westwood E K. Broadband matched source localization[J]. Journal of the Acoustical Society of America, 1992, 91(5): 2777-2789.
[4] 陈连荣, 彭朝晖, 南明星. 高斯射线束方法在深海匹配场定位中的应用[J]. 声学学报, 2013, 38(6): 715-723.
Chen Lianrong, Peng Zhaohui, Nan Mingxing. The application of Gaussian bean method in deep ocean matched-field localization, 2013, 38(6): 715-723.(in Chinese)
[5] Tiemann C O, Thode A M, Straley J, et al. Three-dimensional localization of sperm whales using a single hydrophone[J]. The Journal of the Acoustical Society of America, 2006, 120(4): 2355.
[6] Duan R, Yang K, Ma Y, et al. Moving source localization with a single hydrophone using multipath time delays in the deep ocean[J]. Journal of the Acoustical Society of America, 2014, 136(2): 159-165.
[7] 孙梅, 周士弘, 李整林. 基于矢量水听器的深海直达波区域声传播特性及其应用[J]. 物理学报, 2016, 65(9): 139-147.
Sun Mei, Zhou Shihong, Li Zhenglin. Analysis of sound propagation in the direct-arrival zone in deep water with a vector sensor and its application[J]. Acta Phys Sin, 2016, 65(9): 139-147.(in Chinese)
[8] 孙梅, 周士弘. 大深度接收时深海直达波区的复声强及声线到达角估计[J]. 物理学报, 2016, 65(16): 134-143.
Sun Mei, Zhou Shihong. Complex acoustic intensity with deep receiver in the direct-arrival zone in deep water and sound-ray-arrival-angle estimation[J]. Acta Phys Sin, 2016, 65(16): 134-143.(in Chinese)
[9] 高飞, 孙磊. 基于首达波与次达波到达时差的深海浅层移动声源定位[J]. 兵工学报, 2018, 39(11): 2243-2248.
Gao Fei, Sun Lei. Localization of moving acoustic source in shallow Layer of deep ocean based on the time difference of arrival between the first and second waves[J]. Acta Armamentarii, 2018, 39(11): 2243-2248.(in Chinese)
[10] Lei Z, Yang K, Ma Y. Passive localization in the deep ocean based on cross-correlation function matching[J]. The Journal of the Acoustical Society of America, 2016, 139(6): EL196-EL201.
[11] Collins M D. A split-step Padé solution for the parabolic equation method[J]. Journal of the Acoustical Society of America, 1993, 93(93): 1736-1742.
[12] Wu S L, Li Z L, Qin J X. Geoacoustic Inversion for Bottom Parameters in the Deep-Water Area of the South China Sea[J]. Chin. phys. lett, 2015, 32(12): 70-73.
[13] Porter M B, Bucker H P. Gaussian beam tracing for computing ocean acoustic fields[J]. Journal of the Acoustical Society of America, 1987, 82(4): 1349-1359.



