1 引言
传感器阵列已广泛应用于声呐、雷达、语音和通信等领域[1-2],阵列信号处理算法利用阵元的空间位置关系与各阵元接收数据的相干特性提高输出信噪比并抑制其他方向干扰,与单个定向传感器相比具有明显的优势。阵列流形向量是指阵列对空间某一具有单位能量的窄带点源信号的复响应,当阵列的几何结构固定时,阵列对空间方位和信号频率的响应也随之固定。高分辨率的阵列算法如MVDR(Minimum Variance Distortionless Response)波束形成算法、MUSIC(Multiple Signal Classification)方位估计算法在提高信噪比和方位分辨方面更是具有显著的性能优势,但是这些算法对阵列流形向量误差敏感,即流形向量存在误差或扰动时,算法的性能会严重恶化,甚至失效[3]。实际装配完成的阵列由于各阵元的性能指标差异、阵列的空间位置误差以及阵元之间的耦合作用等影响,流形向量偏离理论值一定距离。如果直接用理论流形向量对阵列接收数据进行高分辨率算法应用,算法性能将大打折扣,因此阵列在装配完成后需要对阵列的实际阵列流形向量进行估计。
最直接的阵列系统流形向量估计方法是对流形向量进行测量、内插并存储,该方法计算量大、精度低且测量成本高[3]。针对这个缺陷,学者们尝试从阵列空间几何结构、声场分布等反映阵列具体特征的方面分析阵列流形响应,对阵列流形进行建模并估计模型参数。阵列误差可分为幅相误差、互耦误差和幅相互耦混合误差三种,而误差参数可分为方位依赖参数和固定参数。常见的阵列误差模型有:由阵列信号采集通道幅度相位响应偏差产生的误差对应固定参数的幅相误差模型、由各阵元的性能指标差异和各阵元位置扰动产生的误差对应方位依赖的幅相误差模型、由阵元间互耦作用产生的误差对应固定参数的互耦误差模型、当幅相误差和互耦作用同时存在时则对应幅相互耦误差混合模型。在参数估计方面,文献[4]提出一种利用多个方位已知的单信源数据估计阵列互耦参数的方法;文献[5]提出一种适用于任意形状阵列的利用多个方位已知的单信源数据估计阵元位置扰动参数和幅度相位扰动参数的方法;基于最大似然估计法,文献[6- 8]利用多个方位已知的辅助单信源数据联合估计幅度相位扰动参数、阵元位置扰动参数和互耦参数;利用阵列流形向量与单信源的接收数据协方差矩阵的主特征矢量的线性相关特性,文献[9-12]提出了几种联合估计幅度相位扰动参数、阵元位置扰动参数和互耦参数的估计方法。以上文献中的阵列误差模型和模型参数类型都是已知,然而实际中阵列模型是未知的,且没有模型参数的先验信息。
为了将文献中的估计算法应用到实际阵列,需要先测量实际阵列流形,再将实际值与现有模型进行拟合,从而得到最合适的误差参数模型,因此阵列流形的测量是阵列误差参数估计的第一步。高分辨率的方位估计算法(如MUSIC算法)能在低信噪比环境下准确的估计目标方位,但是当阵列流形向量失配时算法的估计精度下降,而流形向量引起的误差与阵列协方差矩阵估计的误差可以等价[14],高信噪比环境下阵列信号协方差矩阵估计误差小,所以高信噪比环境下算法的估计方位是可参考的,具体方位估计过程本文不作介绍。阵列流形具体的测量过程为:在高信噪比环境下,用方位估计算法估计信号入射方位,再用单频信号幅度相位算法估计某单频信号从该方位入射阵列时各阵元相对参考点的幅度相位响应,将此响应作为该入射方位和频率下的阵列流形向量,遍历所有方位和频率网格点,最后得到阵列的实际流形向量。在直接定义法中,单频信号幅度可利用能量定理估计得到、两个相关信号的相位差可以用共轭相关法获得。这种方法思路简单,但是相位差估计的精度低。而最小二乘法是通过特定长度的快拍信号联合估计某阵元接收信号的幅度与初相位[13]。该方法估计精度高,但是实际接收信号快拍数有限且很难满足算法要求。本文提出一种基于子空间分解的阵列流形向量估计方法,利用方位估计步骤中已获取的信号子空间基向量估计实际阵列流形向量。该方法不再约束快拍数为特定值,参数估计精度是最小二乘法的一倍同时计算复杂度比直接定义法和最小二乘法低一个数量级。
本文内容安排如下:第2节给出阵列系统的接收数据模型,第3节介绍现有阵列流形向量参数的估计方法,第4节详细阐述了本文所提出的基于子空间分解的阵列流形估计方法,第5节对所有提及方法进行蒙特卡罗仿真并比较各种方法性能,最后总结全文。
2 接收阵列模型
考虑一个由M个全向传感器组成的接收阵列,以第1号阵元所在位置作为阵列参考点[0,0,0],第m号阵元的位置坐标为pm=[pxm,pym,pzm]。当一个远场平面波窄带信号从球面角(θ,φ)入射到阵列,其中θ和φ分别为信号入射的方位角和俯仰角,窄带信号频率为f0,理想情况下阵列对该来波的响应为
a(θ,φ, f0)=
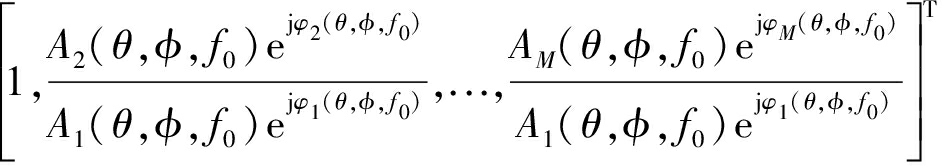
(1)
其中[·]T表示向量转置,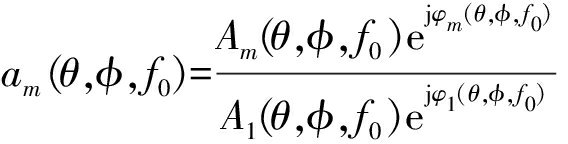
表示第m号阵元相对于第1号阵元对该窄带信号的响应。对于全向传感器阵元,有Am(θ,φ, f0)=A1(θ,φ, f0),第m号阵元幅度响应为
相位响应为
其中,c为信号在介质中的传播速度。由此可见,阵列各阵元的相位响应与波达方向和入射信号频率有关。
实际中的阵列由于各种误差因素(如阵元位置偏差、阵元间互耦作用等)的影响,各阵元对来波信号的幅度响应和相位响应与理想情况相比都有较大误差,阵列流形向量变为
因此阵列在装配后会对阵列流形向量进行测量,具体过程为:在远场放置一个信号源,在高信噪比条件下发射单频矩形脉冲信号,信号频率为f0,阵列接收到测试信号后估计来波方向(θ,φ)和阵列流形向量
遍历所有感兴趣的来波方向和接收频带从而得到阵列系统的实际阵列流形
阵列系统第m号阵元接收到的实信号可以表示为[13]
(2)
其中m=1,2,...,M;k=1,2,...,K,K为接收数据快拍数。若用s(k)表示参考点处的第1号阵元的接收信号,则阵列的输出向量为[6]
(3)
其中
表示k时刻各阵元输出复信号组成的M×1维向量,n(k)是M×1维噪声向量。假设噪声为空间高斯白噪声,即
则阵列协方差矩阵期望为[14]
(4)
其中,
为信号能量,且有
利用矩阵特征分解运算,接收信号的协方差矩阵可分解为
(5)
其中,Λ为按降序排列后的特征值构成的对角矩阵,最大特征值λS对应的特征向量
S构成信号子空间US,剩下(M-1)个特征值(λ1,λ2,...,λM-1)对应的特征向量(1,2,...,M-1)构成噪声子空间UN。分解得到的子空间可用于阵列流形向量测量中的方位估计以及本文提出的阵列幅度相位响应估计算法。
3 现有的阵列流形向量估计方法
本节主要介绍两种估计阵列幅度相位响应值的方法,包括直接定义法、最小二乘法。
3.1 直接定义法估计
根据电学定义,正弦信号峰值A是其有效值的
倍,而有效值是指时变量的瞬时值在给定时间间隔内均方根值。因此第m号阵元接收实信号的峰值Am无偏估计表达式为
(6)
定义K×K维的DFT变换矩阵为F,第m号阵元相对于第1号阵元的相位差为
(7)
(8)
其中,x1和xm分别表示第1号和第m号阵元K个快拍组成的1×K维接收数据向量,angle(·)表示取复数相角,abs(·)表示取复数模值,(·)*表示共轭运算,⊙表示矩阵对应元素相乘。直接定义法思路简单,幅度估计是无偏估计,但是相位差估计受快拍长度影响且估计精度低。
3.2 最小二乘法估计(LSE, Least Square Estimation)
根据文献[13],高信噪比环境下,发射单频信号的频率f0已知时,可利用K个快拍的阵列接收实信号数据X=[x(1),x(2),...,x(K)]对各阵元的幅度初相位做联合最小二乘估计
z=arg min‖X-Hz‖2
(9)
其中,H=[h1,h2,...,hM]T;hm=[ej2πf0/fs,ej2π2f0/fs,...,ej2πKf0/fs]T,联合估计值满足特定要求时有
0.5Amejφm|K=fs/(2f0)
(10)
此时,第m号阵元接收信号的幅度和初相位的估计分别为
Am=2abs(zm)
(11)
φm=angle(zm)
(12)
最小二乘法估计的幅度和相位差精度高,但是实际数据的快拍数很难是
的整数倍,一般取尽可能大且靠近的整数倍的整数,即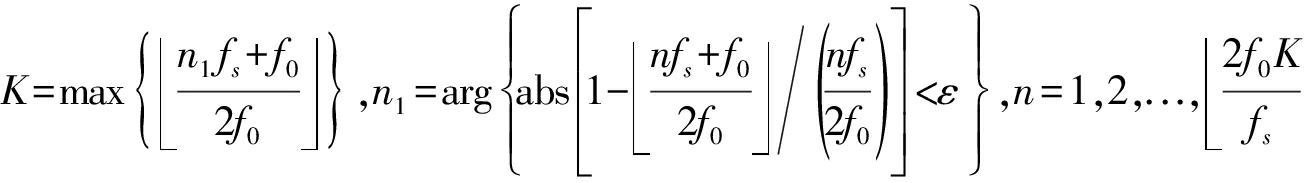
,其中,⎣·」表示向下取整运算,ε为预设极小量。这种近似取法使得联合估计的结果为有偏估计,会导致最小二乘法估计阵列幅度相位响应的精度下降。
4 本文提出的流形向量估计方法
现有方法的估计精度都随快拍数波动,这是因为它们都从频域角度计算各阵元相对相位。单频信号的初相位信息保留在频域的对应信号频率的频点f0上,当信号样本长度不是
的整数倍时,频域的频点不包含信号频率,此时初相位的估计值是从频率f0附近的频点上得到,估计结果偏离真实值。与现有方法不同,本文从阵列阵元域角度估计流形向量:当接收信号是只包含一个目标的单频信号时,阵列接收数据协方差矩阵的信号子空间US与阵列流形向量
张成的空间相同[16],因此阵列的实际流形向量与信号子空间的基向量线性相关,即满足
(13)
其中,
为信号子空间US的特征向量,μ为线性相关系数。
由文献[17]可知,阵列M个阵元接收复信号的K次快拍数据,这些数据对应的样本协方差矩阵
服从复Wishart分布
其中Rx为期望协方差矩阵。特征分解该矩阵后得到最大特征值λS对应的特征向量
服从均值为S的复高斯分布
S,CγS),CγS为特征向量的协方差矩阵。因此,样本协方差矩阵的特征向量是向量S的无偏估计,第m号阵元接收信号相对于第1号阵元的幅度Am1和相位差估计分别为
(14)
(15)
最后,基于子空间的阵列流形向量估计方法整体计算流程如下:
(1)利用Hilbert变换计算阵列接收实信号x(k)对应的复信号
(2)计算复信号
的样本协方差矩阵
(3)对协方差矩阵进行特征分解,求得特征向量和噪声子空间UN;
(4)利用MUSIC算法估计信号的波达方向(θ,φ);
(5)依据式(14)和式(15) 估计相对幅度Am1与相对相位差(φm-φ1);
(6)估计流形向量
由于协方差矩阵的估计对快拍数没有定量约束,本文所提方法从阵列的协方差矩阵角度利用信号子空间估计各阵元的相位差,快拍数越多,矩阵估计越精确,估计的流形向量与实际值越接近。另外,现有方法是根据空间-时间二维接收数据估计幅度相位响应,计算复杂度为
而本文方法利用方位估计时已求得的特征向量估计阵列流形空间的基向量,再得到阵列的幅度相位响应,计算复杂度为
5 性能仿真分析
本节首先仿真了高信噪比时,不同误差模型下的阵列流形向量对MUSIC算法方位估计的影响,再对比直接定义法、最小二乘法以及本文提出的子空间分解法在不同信噪比、不同快拍数条件下的相对相位估计均方根误差,最后比较了最小二乘法与本文提出的子空间分解法在不同阵元数时估计的平均耗时。
仿真参数按照阵列实物,考虑一个半径为r=7.83 cm均匀圆环阵,阵元数M=16,发射信号频率f0=23 kHz,信号以球面角(-60°,90°)入射到阵列,接收系统采样频率fS=200 kHz,阵列接收信号信噪比(Signal to Noise Ratio, SNR)为SNR=20 dB,信号快拍长度为K=1024。定义实际阵列流形向量atrue与理论值a的距离为
准确估计是指方位扫描时,方位谱峰值所在位置与预设值相同。
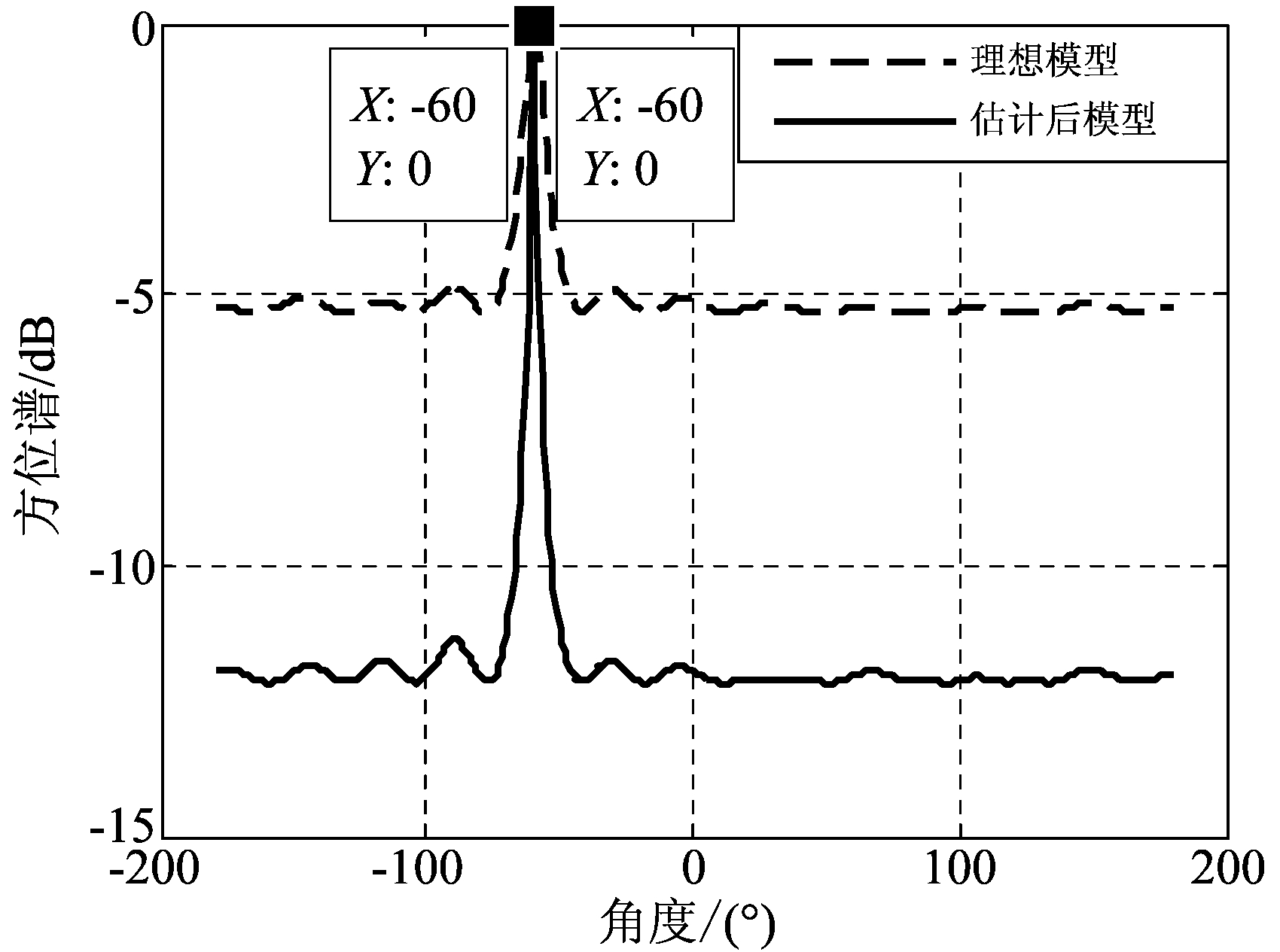
图1(a) 本文算法估计流形向量前后MUSIC方位估计性能对比
Fig.1(a) The performance of MUSIC algorithm comparison using the ideal and estimated MV
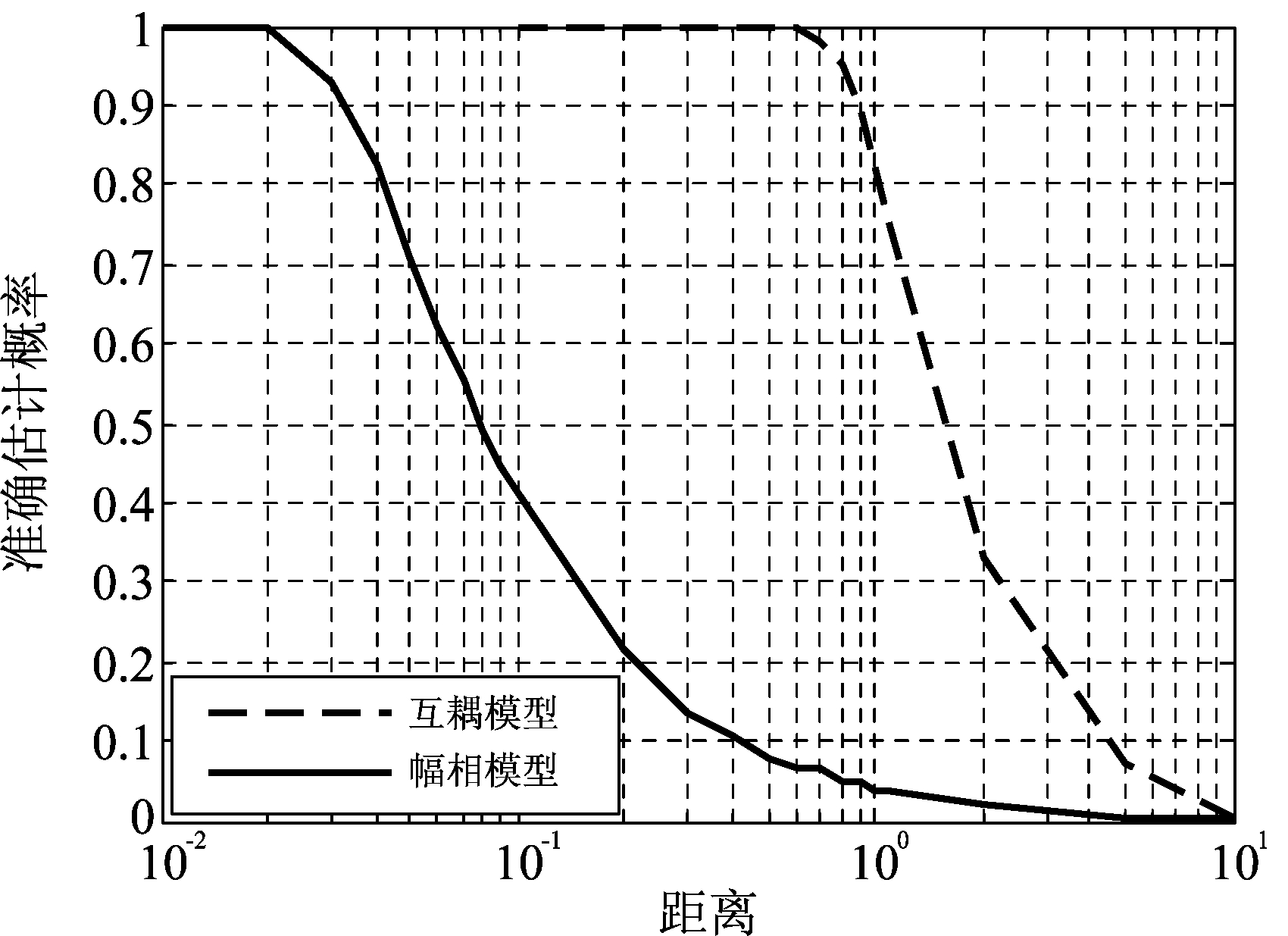
图1(b) 流形向量距离与MUSIC算法方位估计准确性关系
Fig.1(b) The relationship between MV distance and MUSIC algorithm DOA estimation accuracy
图1(a)为入射信噪比为0 dB,俯仰角已知为90°,流形向量存在幅相误差且误差距离为0.6时,MUSIC算法利用本文算法估计流形向量和理论值时方位估计性能对比,可以看出,正确估计后的方位估计性能提升了7 dB。图1(b)为幅相误差模型和互耦误差模型两种阵列误差模型下,5000次蒙特卡罗仿真实验中目标方位正确估计概率结果。可以看出,阵列在不同误差影响下的方位估计性能不同,阵列流形向量误差距离较小时,估计方位算法估计精度影响较小,具有一定的稳健性,距离超过门限后算法估计能力迅速下降。圆环阵对互耦作用产生的流形向量误差具有更好的宽容性而对幅度相位偏移的误差敏感。因此,实际阵列装配后需要对阵列流形模型进行拟合,使估计的流形向量与真实值之间的距离在门限值以下,而本文研究的高精度流形向量测量即为模型拟合的第一步。
图2 相对相位估计的均方根误差与信噪比关系
Fig.2 The relationship between relative phase estimation RMSE and SNR
由于高信噪比情况下,直接定义法、最小二乘法和本文提及算法估计接收信号的幅度偏差很小,三种算法估计精度几乎重合,因此以下仿真主要研究三种算法相对相位估计的精度。图2为阵列接收信号信噪比8 dB～24 dB变化时,本文算法与其他算法估计相对相位的均方根误差性能对比。可以看出,本文算法与最小二乘法的相对相位估计性能相近优于直接定义法;在相同均方根误差情形下,本文算法与最小二乘法的输入信噪比比直接定义法的输入信噪比小1 dB。
图3 相对相位估计的均方根误差与快拍数关系
Fig.3 The relationship between relative phase estimation RMSE and snapshot
图3是阵列接收数据以64快拍为步长且依次增加快拍数时,本文算法与其他算法估计相位参数的均方根误差性能对比。可以看出,本文算法与其他算法的估计均方根误差都随快拍数的增加而减少,而且本文算法和最小二乘法的估计性能相同;当快拍长度满足式(10)要求时,三种算法性能相近,快拍长度不满足式(10)要求时直接定义法与最小二乘法和本文算法性能差别较大。综合图2和图3可知,本文算法和最小二乘法的相位估计性能方面优于直接定义法。
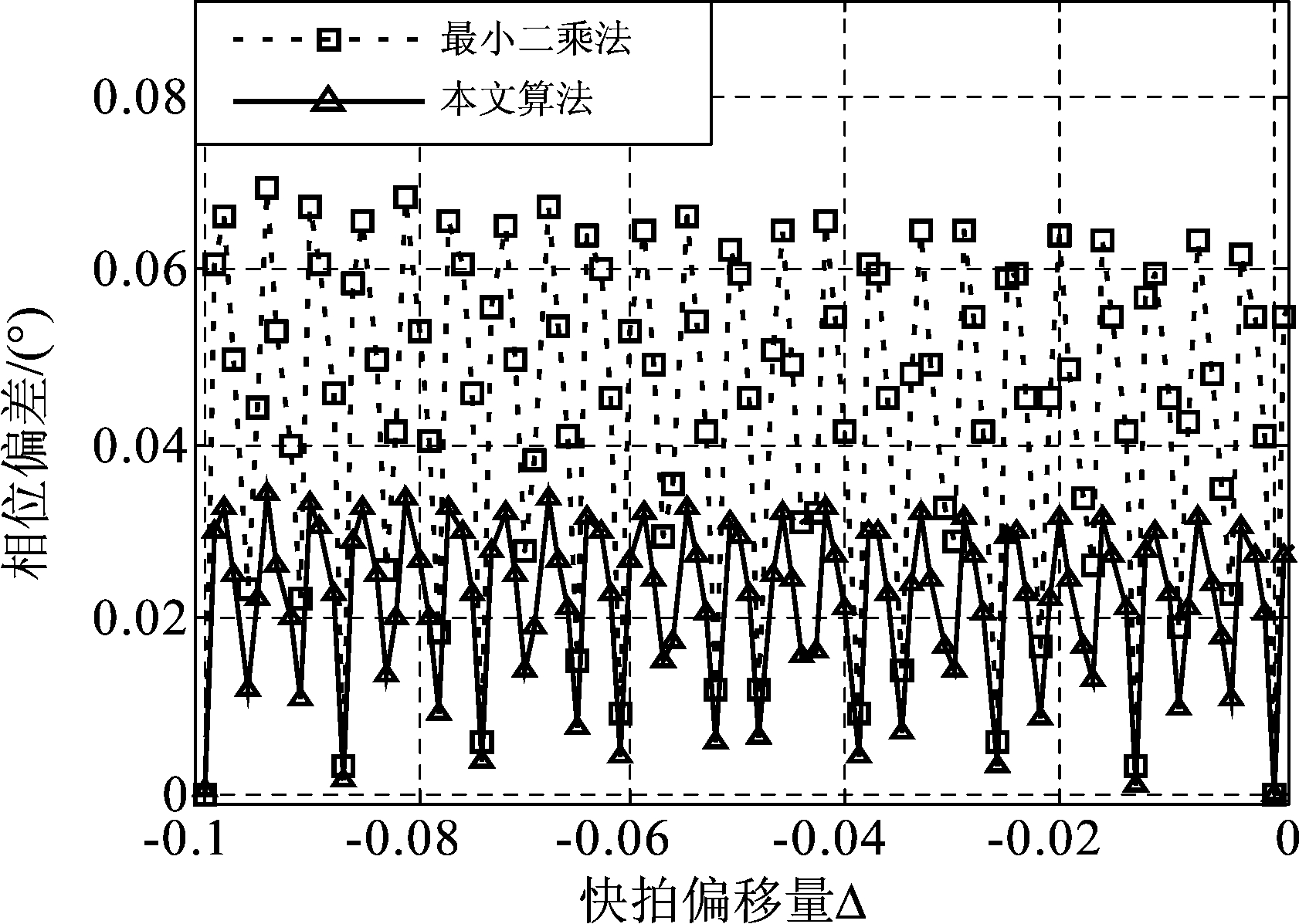
图4 相位估计偏差与快拍偏移关系
Fig.4 The relationship between phase estimation deviation and snapshot offset
图4是快拍数不满足式(10)时,本文算法与最小二乘法估计相对相位的偏差对比。快拍数取900和1000时都满足式(10)要求,其他参数与上文相同。取快拍数从900开始以1个快拍为步长逐渐增加,快拍数参考值为1000,于是偏移量Δ取值区间为-0.1～0。可以看出,两种算法估计的相对相位偏差都随偏移量Δ波动,且最小二乘法估计偏差比本文算法大,当快拍长度满足式(10)要求时,两种算法估计偏差都最小。因此,本文算法比最小二乘法具有更稳定的估计性能。
图5为不同阵元数情况下,最小二乘法与本文算法估计幅度相位响应耗时比的10000次蒙特卡罗仿真结果,仿真环境为CoreTM i5- 8400处理器,主频为2.8 GHz,仿真软件为Matlab R2014a。可以看出,本文算法的耗时远小于最小二乘法。随着阵元数的增加,最小二乘法与本文算法估计幅度相位响应的耗时比越来越大。
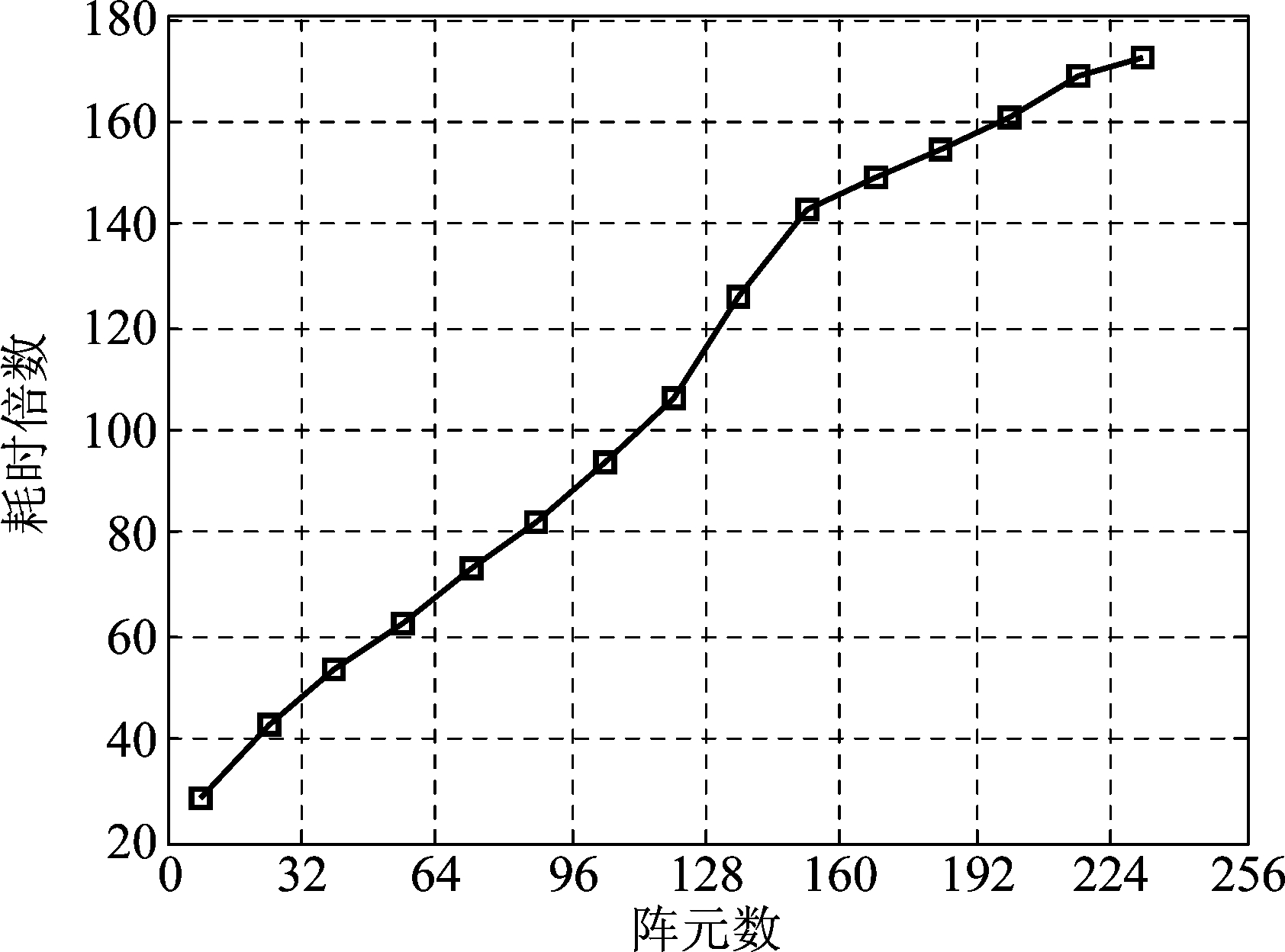
图5 最小二乘法与本文算法估计幅度相位响应耗时比
Fig.5 The time-consuming ratio of estimating the amplitude phase response using LSE and the proposed algorithm
6 结论
现有的直接定义法和最小二乘法在估计信号幅度相位参数时,算法复杂度高而且相位参数估计精度受观测数据快拍数影响。针对这些问题,本文利用信号子空间与阵列流形的线性相关特性,提出一种基于子空间分解的阵列流形向量估计方法。仿真结果表明,本文算法对观测数据快拍数无定量要求,算法相位参数估计方差与最小二乘法相同,偏差比它低一倍,复杂度也比现有两种方法低一个数量级,具有更好的实际应用价值。下一步将研究实际阵列流形产生误差的原因,并用方位依赖型参数模型拟合实际阵列。
[1] Krim B H, Viberg M. Two decades of array signal processing research[C]∥IEEE Sig.Proc.Magazine, 1996.
[2] Trees H L. Optimum Array Processing-Part IV of Detection, Estimation, and Modulation Therory[J]. A Papoulis Probability Random Variables & Stochastic Processes, 2002, 8(10): 293-303.
[3] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.
Wang Yongliang, Chen Hui, Peng Yingning, et al. Spatial spectrum estimation theory and algorithm[M]. Beijing: Tsinghua University Press, 2004.(in Chinese)
[4] 侯青松, 郭英, 王布宏, 等. 阵列天线散射条件下的互耦校正[J]. 信号处理, 2011, 27(1): 128-135.
Hou Qingsong, Guo Ying, Wang Buhong, et al. Mutual coupling calibration of array antenna in the presence of scattering[J]. Signal Processing, 2011, 27(1): 128-135.(in Chinese)
[5] 苗锦. 一种任意空间结构阵列的有源校准方法[J]. 水雷战与舰船防护, 2013, 21(1): 75-79.
Miao Jin. An active calibration method of arbitrary spatial structure array[J]. Mine Warfare & Ship Self-defence, 2013, 21(1): 75-79.(in Chinese)
[6] 王敏, 马晓川, 鄢社锋, 等. 阵列幅度相位误差的有源校正新方法[J]. 信号处理, 2015, 31(11): 1389-1395.
Wang Min, Ma Xiaochuan, Yan Shefeng, et al. New calibration method for array gain and phase errors with signal sources[J]. Journal of Signal Processing, 2015, 31(11): 1389-1395.(in Chinese)
[7] See C M S. Method for array calibration in high-resolution sensor array processing[J]. IEEE Proceedings-Radar, Sonar and Navigation, 2002, 142(3): 90-96.
[8] Ng B C, See C M S. Sensor-array calibration using a maximum-likelihood approach[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(6): 827- 835.
[9] See C M S. Sensor array calibration in the presence of mutual coupling and unknown sensor gains and phases[J]. Electronics Letters, 2002, 30(5): 373-374.
[10] Xie J, Yang X, Li H, et al. A hybrid algorithm for multiple parameters estimation with UCA of electromagnetic vector sensors[C]∥Signal & Information Processing Association Summit & Conference. IEEE, 2017.
[11] Zhang C, Huang H, Liao B. Direction Finding in MIMO Radar With Unknown Mutual Coupling[J]. IEEE Access, 2017, 5:4439- 4447.
[12] Ikram M Z, Ali M, Wang D. Joint antenna-array calibration and direction of arrival estimation for automotive radars[C]∥2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, 2016: 1-5.
[13] Yan S, Hovem J M. Array Pattern Synthesis With Robustness Against Manifold Vectors Uncertainty[J]. IEEE Journal of Oceanic Engineering, 2008, 33(4): 405- 413.
[14] 鄢社锋. 优化阵列信号处理:波束优化理论与方法[M]. 北京: 科学出版社, 2018.
Yan Shefeng. Optimal array signal processing: beamformer design theory and methods[M]. Beijing: Science Press, 2018.(in Chinese)
[15] Liu S, L Y, Xie Y. Robust calibration of mutual coupling effect for a Uniform Circular Array[C]∥IEEE, International Conference on Signal Processing. IEEE, 2017: 452- 456.
[16] Liu S, Yang L, Yang S. Robust Joint Calibration of Mutual Coupling and Channel Gain/Phase Inconsistency for Uniform Circular Array[J]. IEEE Antennas & Wireless Propagation Letters, 2016, 15: 1191-1195.
[17] Jeffries D J, Farrier D R. Asymptotic results for eigenvector methods[J]. Communications, Radar and Signal Processing, IEE Proceedings F, 1985, 132(7): 589-594.
[18] Kaveh M, Barabell A. The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise[J]. Acoustics Speech & Signal Processing IEEE Transactions on, 1986, 34(2): 331-341.
