1 引言
主动声纳在浅海区域进行沉底、掩埋目标探测中,通常采用大掠射角的信号发射方式,由此形成了强的海底混响,这严重干扰了线性调频(LFM)信号的回波检测。混响具有非平稳、非高斯的特性,其频谱结构与发射信号具有很强的相似性,因此难以用常规的带通滤波器滤除[1]。对比于海洋环境、舰船辐射等背景噪声,混响的形成机理更复杂,在时频域都与目标回波有较强的耦合性和相似性,因此对基于匹配滤波的回波检测方法有更强的干扰。针对该热点问题,近年来不少国内外研究学者开展了相关研究工作。
文献[1]视混响为局部平稳信号,对混响分段并分别采用自回归(AR)模型构造白化滤波器,预白化去色操作后,再进行匹配滤波以达到最优的检测性能。文献[2]用形态学方法对经AR预白化滤波的波束图进行处理,提高了检测效果。文献[3]将经AR预白化后的信号进行二分奇异值分解(SVD)处理,信混比提高约3 dB,匹配检测效果得到了改善。文献[4]运用分数阶傅里叶变换(FRFT),对经滑动窗截取的信号与发射信号在分数域做峰值匹配,以提取回波信号的起始位置。文献[5]先对信号作平稳化处理,再用滑动窗截取,变换到分数域滤波后进行逆变换,使混响得到了抑制,实现混响背景下的信号检测。文献[6]提出将混响视为一类信源与目标回波盲分离的方法,经时域二阶统计、时频域盲源分离处理,提高了目标回波的信混比。
基于AR模型预白化的方法,虽然能将信号中的有色混响变白,使其更适应于匹配检测器,但是该方法并不能改变信混比,因此相关特性较强的混响仍然会使匹配滤波出现伪峰,干扰目标回波的检测。基于分数阶傅里叶变换的方法能够通过分数域去混,有效地改善信混比,不过其前提是能准确地在分数域选择滤波窗,而强混响又会影响窗的选取。盲源分离方法是一种能在信源、信道未知的情况下,仅依据信源间的弱相关性,凭多个接收信号分离得到所有信源的方法;当观测信号数目较大时,这无疑会耗费大量的计算资源;当我们只对一个或某几个信号感兴趣时,这种处理又会造成大量计算资源的浪费。
针对以上问题,本文提出一种改进的基于线性预测的盲源提取算法(LP-BSE)。较预白化与分数域方法,本文算法匹配检测性能更好;较盲源分离方法,本文算法具有提取某一特定信号的能力更简单高效。在进一步串联LP-BSE与FRFT形成联合算法后,有着强混响背景下更佳的匹配检测效果,且性能稳定。
2 算法描述
盲源提取算法(BSE)能够从线性混合的信号源中抽取单个信号,特别地,当对源信号有某些先验知识的时候,利用BSE技术能够保证分离信号的唯一性和确定性[7]。本文算法正是利用了所期望的目标回波信号与发射LFM信号高度相关的先验知识,将构造出的具有双变量的全局自适应滤波算法转变为常规的LMS算法,完成对该期望信号的提取进而大幅抑制混响实现回波检测。
2.1 信号预处理
信号预处理包括信号去均值和白化处理,目的是改善算法的收敛特性,并消除冗余或减少噪声,预白化后的信号处理通常变得容易些,很少出现病态[8]。观测信号X(t)由源信号S(t)混叠而成
X(t)=AS(t)
(1)
其中X(t)=[x1(t),x2(t),…,xn(t)]T为n维观测信号;S(t)=[s1(t),s2(t),…,sm(t)]T为m维源信号;A为n×m阶混合矩阵。本文将混响看作一类信号源,并且假设满足线性瞬态混合模型。观测信号去均值过程为
(2)
式中,N为观测信号采样点数。记
对其协方差矩阵作特征值分解
(3)
然后经过白化得到预处理后的信号
(4)
式中,V为白化矩阵,V=D-1/2ET,白化后有
盲源提取的目的是找到一个合适的解混向量w,使得提取到的信号接近所期望的源信号。从观测信号X(t)里抽取第i个源信号yi(t),表达式如下
(5)
式中,wi是提取第i个信号对应的解混向量,i=1,2,…,m。
2.2 线性预测器
线性预测指随机信号s的采样值s[n],可以由其过去P个采样值s[n-1],s[n-2],…,s[n-P]预测,并且预测公式是一个线性方程:
(6)
其中,P为预测阶数,bn-k为预测系数,k=1,2,…,P,P<n;采样点n处的预测误差
当信号s能以极小的预测误差被一组参数向量b=[b1,b2,…,bP]T预测时,那么信号s是具有可预测性的。直觉上,一切有规律的信号都是可以预测的,LFM回波信号在时频图上呈一条规则的直线,因而其应该满足某个参数向量b下的线性预测模型。确实,经实验验证,存在着参数
能够以非常小的误差对信号作出预测。
于是,采用最小二乘法估计自回归模型参数[11],记单个观测信号为x,构造
Y=[xP+1,xP+2,…,xN]T
(7)
b=[b1,b2,…,bP]T
(8)
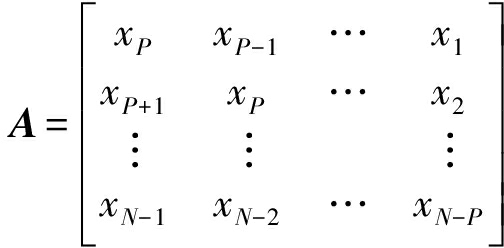
(9)
xP代表x样本的第P个观测值,则P阶自回归模型表示如下
Y=Ab+ε
(10)
ε为预测误差向量,由最小二乘原理可估计模型参数
(11)
根据式(11)估计的自回归参数
可构造对应的线性预测器。
2.3 算法主体
基于线性预测的盲源提取算法[12-14],分为盲源提取与线性预测器两个部分,前者基于回波信号的可分离性,后者的选取决定了前者的性能。文献[9]验证了,当发射信号为LFM信号时,换能器接收回波信号具有可分离性,即存在着2.1中所述的某个解混向量wi能从观测信号里抽取特定的信源。基于线性预测的盲提取算法结构图见图1。
不妨记解混向量为w1,从预处理信号
中抽取的信号为y1(t)。解混向量的选择影响了盲提取的效果,我们认为,如果提取信号y1(t)在k时刻的信号瞬时值与线性预测器在k时刻的预测值越接近,就代表构造的解混向量越优,二者差值如下:
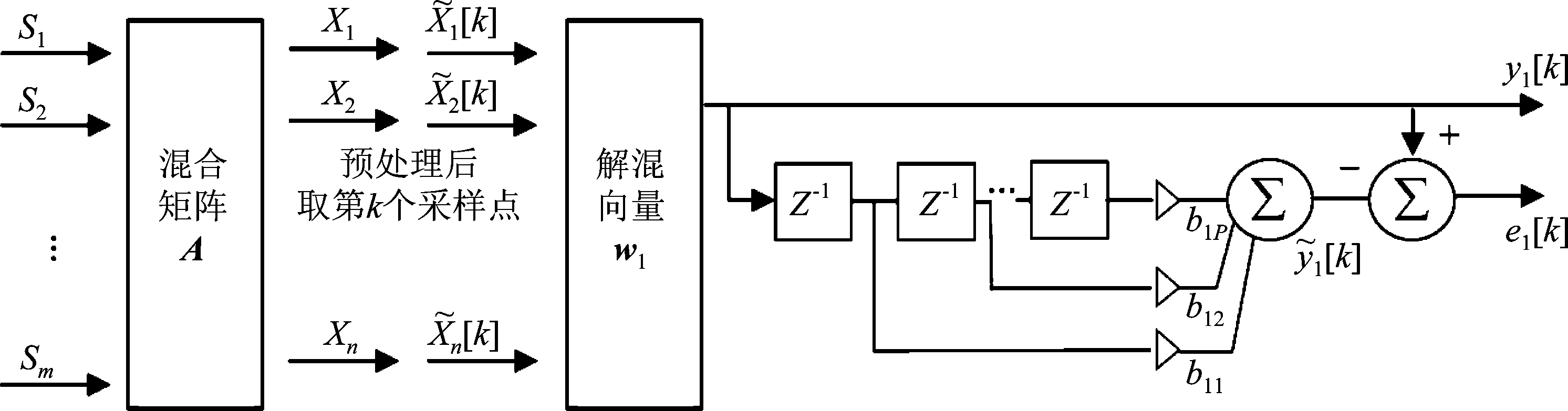
图1 基于线性预测的盲提取结构图(双变量:w1与b1)
Fig.1 Blind extraction structure based on linear prediction (Two variables:w1and b1)
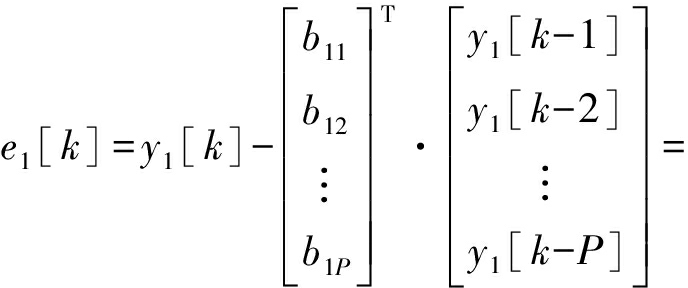
(12)
以k时刻的预测均方误差作为代价函数
(13)
代价函数同时与w1,b1有关,形式上是一种结合了并联与串联两种结构的、具有双变量的全局自适应滤波。对于随机给定的预测器参数b1,只要不同信源间有不同的最小均方预测误差(MSPE),那么存在w1优先将最小误差的提取出来[15],并且实际盲源提取的性能取决于参数b1的选取[15]。本文利用发射信号与目标回波具有相似时序特性的先验知识,用式(11)估计并固定该预测器参数,此时目标回波与混响信号对应的MSPE会出现差异,并且目标回波有着更小的MSPE,因此率先提取出的是所期望的目标回波。在固定参数b1之后,代价函数J只对解混向量w1求梯度:
(14)
其中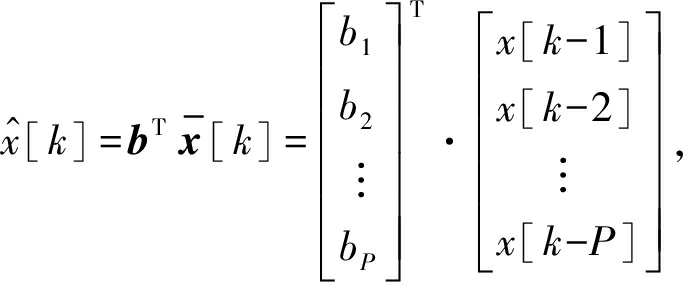
可以得到w1的在线更新规则:
(15)
μ代表更新速率,同时为了避免w1[k+1]趋于零向量,在每一次更新完之后都要将解混向量归一化到单位长度
(16)
在M步收敛或k=N-1,令K=min{M,k},得到最终提取信号
(17)
总结本节内容,归纳算法步骤为:
1)对接收信号X(t)进行去均值、白化预处理,得到信号
2)利用发射信号根据式(11)估计线性预测器参数,得到
3)随机初始化参数w1,取k=P。
4)k=k+1,用w1更新
代入得到e1[k]。
5)根据式(15)对w1进行迭代,并根据式(16)对w1进行归一化。
6)w1收敛或者k=N-1满足其一,根据式(17)得到y1,否则回到4)。
3 仿真实验分析
本节通过仿真实验,对比验证本文算法的有效性与鲁棒性。设主动声纳发射频率为5～14 kHz的LFM信号,脉宽为5 ms。信号经海洋信道传输照射到大片的海底底质及沉底点目标上,其反射和散射波再次经由海洋信道传输最终被接收端接收,采样率为160 kHz。
海底混响是海底底质对声探测系统的发射信号产生的散射在接收点叠加而成的,其强度与发射信号的能量成正比关系;频谱和发射信号的频谱具有一致性,有一定的频谱扩展;散射点足够多时,其瞬时值呈高斯分布,包络呈瑞利分布[17]。按文献[17]方法产生符合上述理论统计特性的混响信号,如图2所示,混响强度随时间逐渐衰减,为了得到充分的信息,采样8000个点至混响幅值衰减到足够低,此时混响长度50 ms。
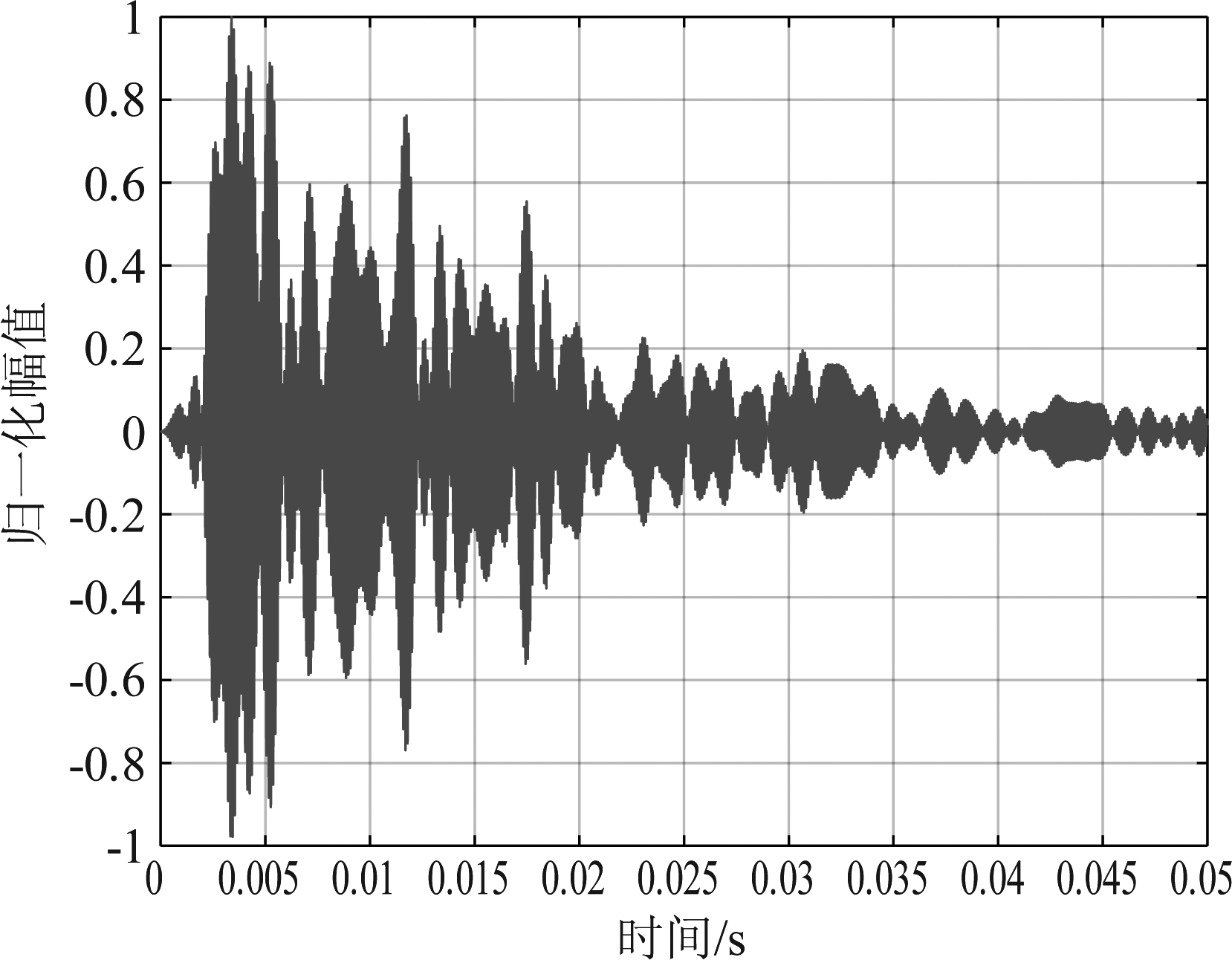
图2 仿真的混响时域波形
Fig.2 Simulation of reverberation time-domain waveform
不考虑脉冲展宽,将目标回波叠加到混响信号的1001～1800处,并模拟实际探测中信号掠射角接近90°、探测深度较浅的强混响情况,设置信混比SRR=-10 dB。将混响与目标回波看成两类信号,采用近场模型,生成接收阵列数据。以发射信号作为匹配滤波器的匹配波形,对不同处理的波形进行脉压处理。为了定量地对比不同方法下的回波检测效果,提出一种检测性能指标PI(单位分贝):
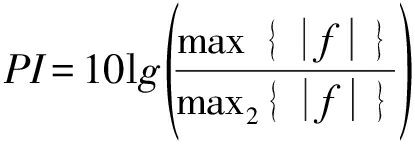
(18)
其中f为脉压幅值,max2算子表示选取次大项,因此PI指的是在脉压图中主峰(峰1)超出次级峰(峰2)的分贝值,其衡量了目标峰与干扰峰间的差异。PI越大,代表匹配检测效果越好,意味着更低的虚警率;若不能正确检测,则PI=0。
如图3所示,整体上看,各方法对应的匹配检测图均在采样点1800处出现最高峰,该采样位置与仿真构造一致,代表均能正常检出点目标。分别来看,不同方法有着不同的匹配检测能力。不经处理的匹配检测图(a)峰值几乎淹没在混响背景之中,这在很大程度上会造成虚警;经AR预处理后的检测图(b)有较高的伪峰,比起不处理的结果略有改善,并且存在部分信号丢失;经FRFT去混操作的检测图(c),伪峰降得更多但是主峰旁出现了旁瓣;本文的LP-BSE过后的匹配检测结果(d),没有出现具有模糊性的伪峰,次峰也已降至相对较低水平,检测效果改善明显;采用本文联合方法(e),检测图与FRFT去混结果类似,但旁瓣被进一步拉低,有着上述方法中最好的匹配检测性能。
表1为设置信混比-10 dB,上述不同方法分别试验1000次对PI值求取均值后的结果。本文提出的改进LP-BSE算法对比前两种方法,检测效果有了一定的改善,PI均值达到了4.68 dB;联合方法则展示了更良好的性能,PI值达到了10.69 dB。
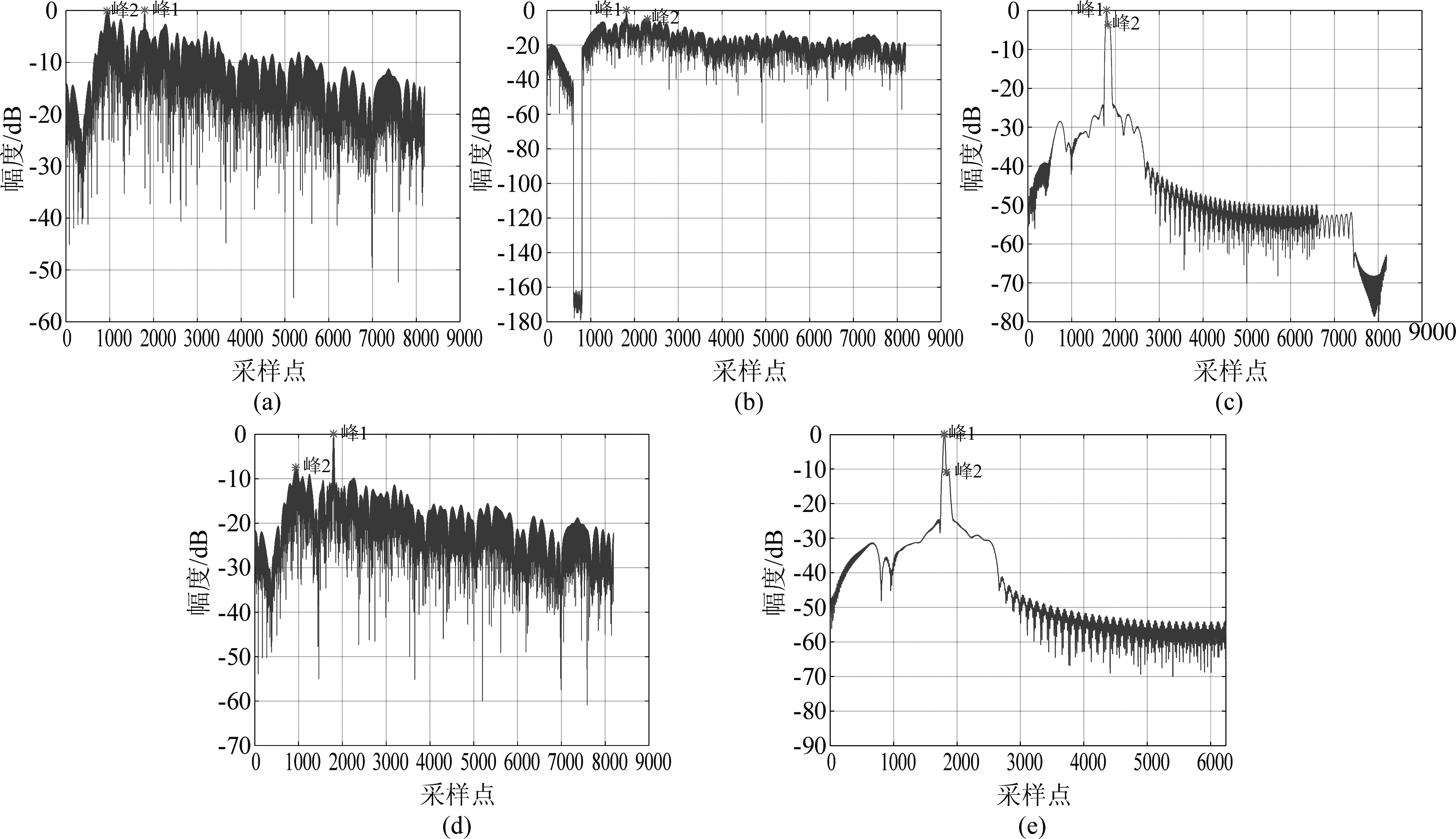
图3 匹配检测结果:(a)不处理;(b)AR预白化;(c)FRFT; (d)本文LP-BSE; (e)本文联合方法
Fig.3 Matching detection results: (a) no processing; (b) AR pre-whitening; (c) FRFT; (d) LP-BSE of this paper; (e)Joint method of this paper
表1 各方法1000次匹配检测的平均PI值
Tab.1 Average PI value of 1000 matching detections by different methods
不处理AR预白化FRFTLP-BSE(本文)联合(本文)PI(单位dB)0.030.923.154.6810.69
图4展示了在不同信混比下,各方法的平均检测性能,依此进一步衡量了各方法的鲁棒性。可见,在混响占优势的情况下,应用AR预白化方法会略有改善,但随着信混比的不断下降,方法逐渐失效;在高信混比下,FRFT具有较优性能,但是随着混响的增强,其性能急剧降低,稳定性较差;LP-BSE方法在信混比高于-5 dB时与FRFT方法有着相似的检测性能和变化趋势,但是当信混比接着下降直至-20 dB过程中,LP-BSE方法的PI值始终能稳定在4 dB之上,而联合方法的PI值几乎能在所有信混比条件下(-20～0 dB)维持在8 dB之上。综上所述,LP-BSE和联合方法在强混响背景下均展示了很强的鲁棒性以及良好的检测性能。
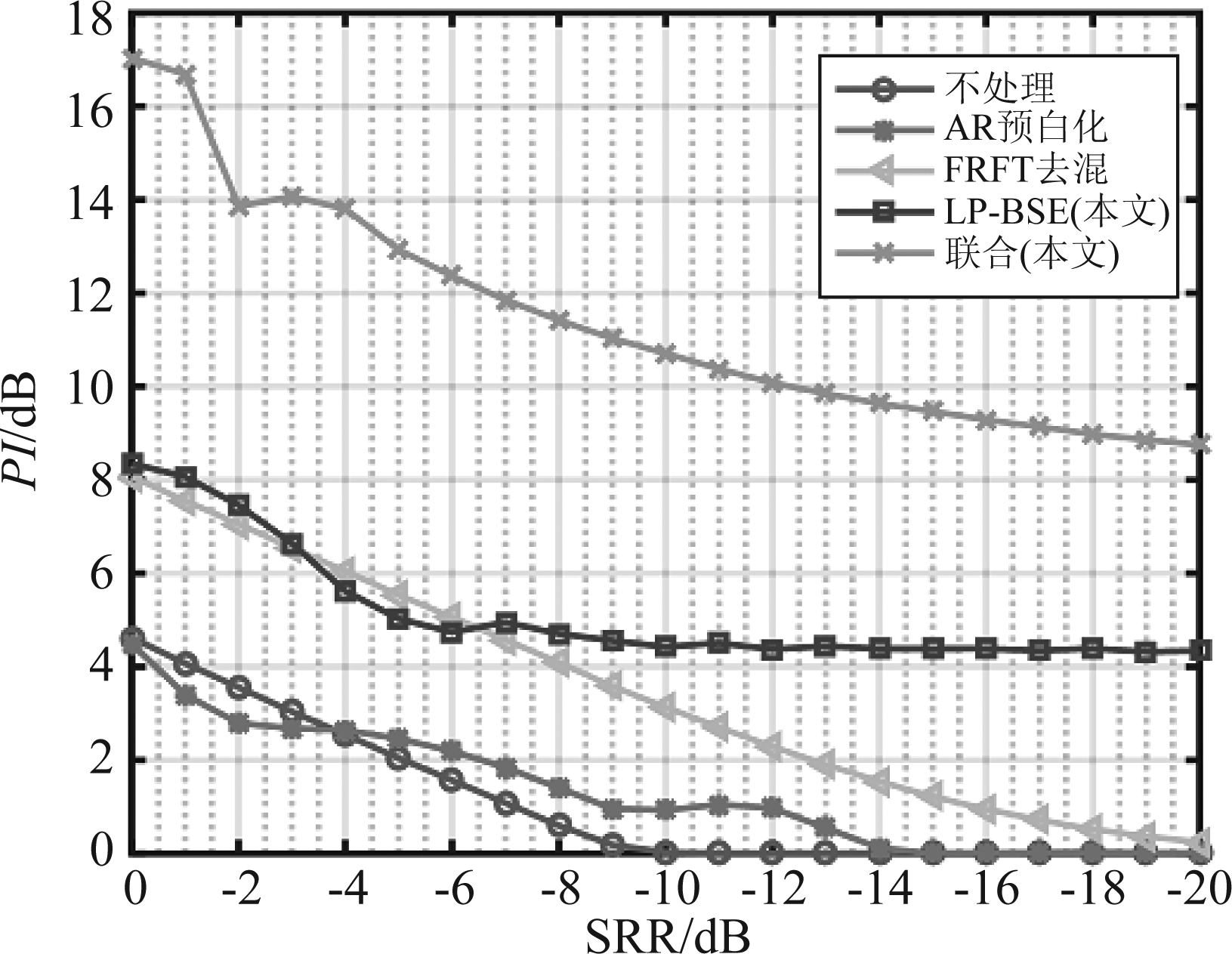
图4 不同信混比下不同方法的检测性能图
Fig.4 Detection performance of different methods under different signal-to-mix ratios
4 结论
本文提出了一种改进的基于线性预测的盲提取算法应用于水声信号处理,其有着在强混响背景下提取期望信号的能力,进而获得更佳的匹配检测性能且拥有更强的鲁棒性。本文利用期望信号与发射信号相似的自回归特性,构造对应线性预测器,预测器参数由最小二乘法估计;然后在LFM回波可分离的基础上,构建最小预测均方误差作为代价函数,迭代求得解混向量从而得到高信混比回波。本文方法对单目标下的信号回波,有着良好的检测效果,关于多目标的回波检测,则需要多次进行提取与紧缩操作,有待进一步研究完善。
[1] 赵航芳, 祝献, 宫先仪. 混响背景下的信号检测[J]. 哈尔滨工程大学学报, 2004, 25(1): 34-37.
Zhao Hangfang, Zhu Xian, Gong Xianyi. Detection of signals in reverberation noise[J]. Journal of Harbin Engineering University, 2004, 25(1): 34-37.(in Chinese)
[2] 王志强, 安良, 陆佶人. 基于数学形态学的海洋混响背景下的信号检测[J]. 信号处理, 2008, 24(6): 1004-1007.
Wang Zhiqiang, An Liang, Lu Jiren. Signal Detection Based on Mathematical Morphology in Ocean Reverberation[J]. Signal Processing, 2008, 24(6): 1004-1007.(in Chinese)
[3] 舒象兰, 孙荣光, 马鑫. 强混响背景下信号回波检测[J]. 电讯技术, 2016, 56(1): 82- 87.
Shu Xianglan, Sun Rongguang, Ma Xin. Echo Detection of LFM Signal under Strong Reverberation Background[J]. Telecommunication Engineering, 2016, 56(1): 82- 87.(in Chinese)
[4] 张宗堂, 杨锡铅, 戴卫国. 混响背景下回波信号起始位置提取[J]. 舰船电子工程, 2014, 34(11): 73-75,79.
Zhang Zongtang, Yang Xiqian, Dai Weiguo. Pick-up of Echo Starting Location in Reverberation[J]. Ship Electronic Engineering, 2014, 34(11): 73-75, 79.(in Chinese)
[5] 陈文剑, 孙辉, 朱建军, 等. 基于分数阶傅里叶变换混响抑制的目标回波检测方法[J]. 声学学报中文版, 2009, 34(5): 408- 415.
Chen Wenjian, Sun Hui, Zhu Jianjun, et al. A method for detecting target echo in reverberation based on fractional Fourier transform[J]. Acta Acustica(Chinese), 2009, 34(5): 408- 415.(in Chinese)
[6] 李秀坤, 夏峙, 王向红, 等. 混响背景下水底目标回波盲分离[J]. 哈尔滨工程大学学报, 2015, 36(1): 62- 67.
Li Xiukun, Xia Zhi, Wang Xianghong, et al. Blind separation of underwater target echoes in reverberation background[J]. Journal of Harbin Engineering University, 2015, 36(1): 62- 67.(in Chinese)
[7] Li Changli, Liao Guisheng, Shen Yuli. An improved method for independent component analysis with reference[J]. Digital Signal Processing, 2010, 20(2): 575-580.
[8] Yin Hongwei, Li Guolin, Lu Cuihua. Step adaptive normalization blind source separation algorithm[J]. Modern Technologies in Materials. Mechanics and Intelligent Systems, 2014, 51(3): 1407-1412.
[9] 许策, 赵相霞, 章新华, 等. 混响背景下主动声纳接收信号的可分离性探讨[J]. 声学技术, 2010, 29(3): 327-330.
Xu Ce, Zhao Xiangxia, Zhang Xinhua, et al. The separability of active sonar signals in the presence of reverberation[J]. Acoustic Technology, 2010, 29(3): 327-330.(in Chinese)
[10] Laura Frølich, Dowding I. Removal of muscular artifacts in EEG signals: a comparison of linear decomposition methods[J]. Brain Informatics, 2018, 5(1): 13-22.
[11] 林正华, 冯仁忠. 自回归模型参数的最小二乘估计[J]. 吉林大学自然科学学报, 2001, 47(2): 1- 4.
Lin Zhenghua, Feng Renzhong. Least Square Estimation of Autoregressive Model Parameters[J]. Acta Scientiarum Naturalium Universitatis Jilinensis, 2001, 47(2): 1- 4.(in Chinese)
[12] 连彦泽, 林臻, 李皓伟, 等. 一种针对具有时间结构的源信号盲源提取算法[J]. 信息技术, 2017, 41(8): 86- 89.
Lian Yanze, Lin Zhen, Li Haowei, et al. Blind source extraction algorithm for the source signals that own temporal structure[J]. Information Technology, 2017, 41(8): 86- 89.(in Chinese)
[13] Barros A K, Cichocki A. Extraction of Specific Signals with Temporal Structure[J]. Neural Computation, 2001, 13(9): 1995-2003.
[14] Taha L Y, Abdel-Raheem E. Efficient blind source extraction of noisy mixture utilising a class of parallel linear predictor filters[J]. IET Signal Processing, 2018, 12(8): 1009-1016.
[15] 李飞, 李国林, 张健, 等. 一种基于极大似然估计的信号盲抽取算法[J]. 海军航空工程学院学报, 2015, 30(3): 211-214, 252.
Li Fei, Li Guolin, Zhang Jian, et al. A Blind Signal Extraction Method Based on Maximum Likelihood Estimation[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(3): 211-214, 252.(in Chinese)
[16] Liu W, Mandic D P, Cichocki A. Blind source extraction based on a linear predictor[J]. IET Signal Processing, 2007, 1(1): 29-34.
[17] 王新晓, 黄建国, 张群飞. 海洋混响仿真技术研究[J]. 声学与电子工程, 2002, 17(3): 27-30.
Wang Xinxiao, Huang Jianguo, Zhang Qunfei. Research on simulation technology of ocean reverberation[J]. Acoustic and Electronic Engineering, 2002, 17(3): 27-30.(in Chinese)
[18] Li Changli. Improved cost functions for blind source separation based on linear prediction[J]. Optik -International Journal for Light and Electron Optics, 2016, 127(21): 10189-10194.
