1 引言
在水声通信中,不同水文环境、同一环境不同的时刻、不同频点对应的水声信道衰落特性不尽相同,导致固定的通信模式很难满足高质量的通信需求[1-2]。自适应技术是使水声通信系统提高通信效率的关键技术,它需要根据信道状态信息(Channel State Information, CSI)调整通信参数[3-5]。但由于北极冰水混合水域下声场的特殊性和复杂的多途结构[6-7],导致通过在接收端进行信道估计获得的CSI相对于即将发射数据时刻的水声信道已经过时[8-9],系统性能严重下降。因此必须对水声信道预测方法进行研究,解决时变水声环境下的可靠自适应通信问题。
信道预测一直是自适应通信系统的关键技术,它最早被提出于1998年,当时研究方向主要分为两种:一种是文献[10-11]中提出的基于复指数函数参数估计的信道预测方法;另一种是文献[12]中提出的基于AR模型对快速移动衰落信道进行大范围线性预测的方法。之后,Forenza A和Heath J R W等人将自适应技术与基于Burg的信道预测技术相结合应用到OFDM通信系统当中[13]。Yang T和Duel-Hallen A等人针对CSI的可靠反馈问题,提出了一种简化的频域信道预测的解决方法[14-15],而不同时刻频域子信道的相关性相对较小,因此通常对预测阶数的要求较高。文献[16]中提出了一种基于迭代信道估计算法的水声稀疏信道大范围自适应平滑预测方法,仿真中采用线性自回归模型,信道多途结构固定,并没有外场试验数据加以佐证。Radosevic A和Stojanovic M等人基于时变水声信道的建模对未来一段时间内的水声信道进行预测,只进行了信道主要路径权系数的预测,没有考虑多途结构变化和多普勒扩展的影响[17]。文献[18-19]将基于压缩感知信道估计的稀疏水声信道预测技术应用于自适应编码调制OFDM水声通信系统,为其提供有效的CSI反馈。由于近年自适应技术在水声领域的兴起,信道预测技术也以此为基础得到一定发展,但理论研究和试验成果依然少有。
在时变环境下获得精确的信道状态信息一直是一个难题,尤其在水声信道预测方面目前极少有公开文献对此进行研究和试验验证。本文主要针对时域水声信道预测技术进行研究,利用水声信道的稀疏特性,研究了一种时域预测器,保留重要的路径系数,减小噪声对预测精度的影响,进一步提高CSI的有效性,在稀疏水声信道环境中比频域预测更有优势。同时由于时域信道结构更为简单且相关性更强,因此时域预测器在保证预测性能的情况下可以降低预测阶数,减少计算复杂度。分析研究了几种信道预测方法用于时域稀疏水声信道预测,并基于在北极水声通信试验数据对所用的预测方法进行了验证和性能分析,还考虑了多普勒频移的存在,得到了比较好的预测结果,证明了本方法的有效性。
2 水声信道时域预测技术
2.1 自适应预测器模型及其原理
在时变自适应水声通信系统中,仅用传统方式在接收端进行信道估计是不够的,还须通过对未来的CSI进行预测来跟踪水声信道在传输时间内的变化,以提高自适应系统的通信稳健性。根据信道估计方法可以得到过去n个时刻的水声信道冲激响应,然后将这些已知的信道数据作为信道预测的基础,用来预测时域水声信道,最后将信道预测结果反馈给发送端。
自适应预测器的预测器参数可以按照一定准则不断进行调整,实时跟踪信道变化,然后利用这些参数来预测未来的信道响应。图1给出了自适应时域预测器的基本结构。
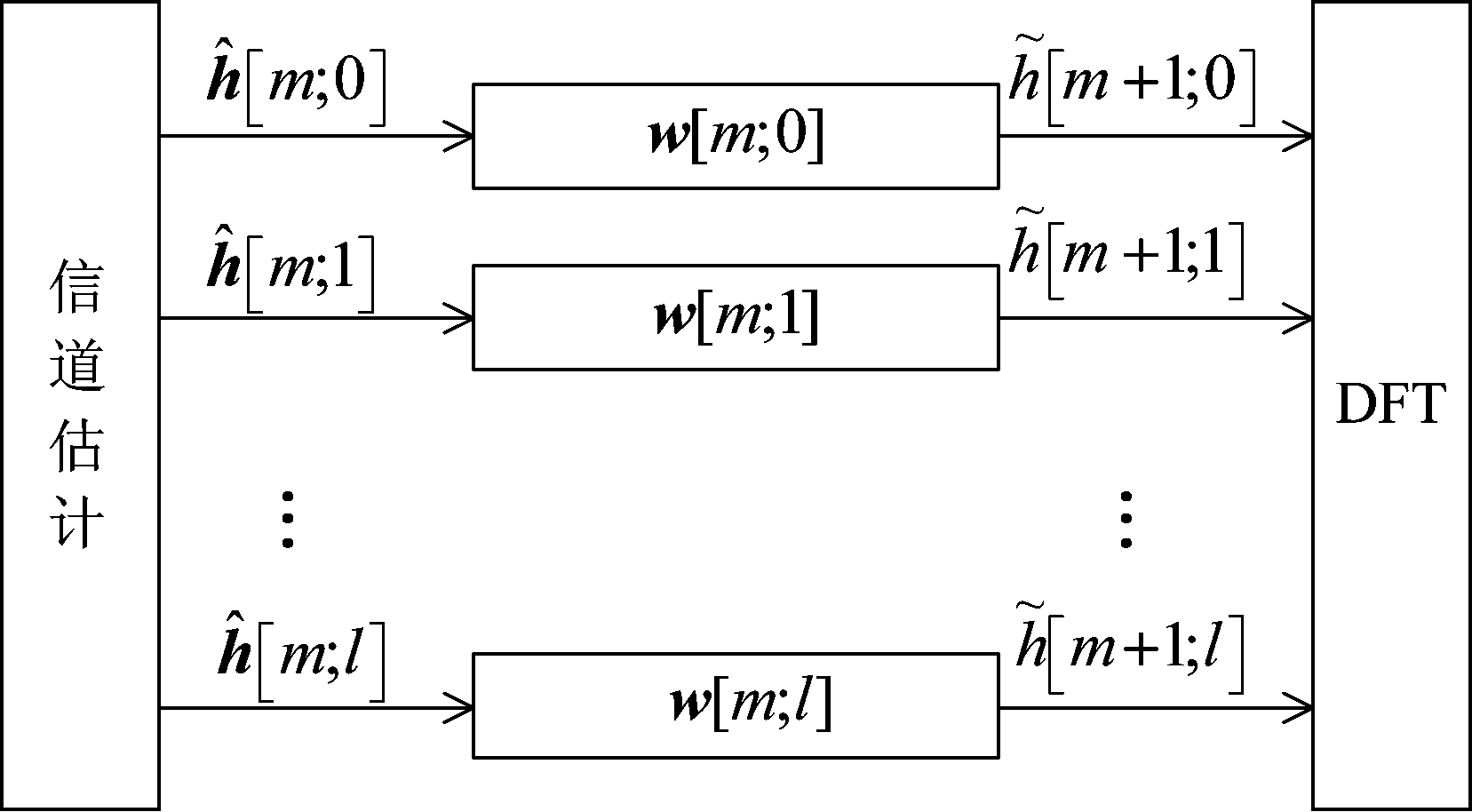
图1 自适应时域预测器结构
Fig.1 Adaption time domain predictor structure
从图中可以看出,预测器对接收到的数据进行信道估计,得到自适应系统所需的时域信道估计值![]() 若通信体制是单载波,则信道估计在时域执行;若通信体制是多载波,尤其是OFDM,则信道估计依然在频域执行,再通过IFFT将频域信道估计值转换到时域。这样做的优点有两个:一是可以在不改变原有的系统结构下,使信道预测技术应用于大多数的OFDM系统之中;二是由于OFDM的信号结构使得系统在频域对信道进行估计和均衡的运算复杂度更小。然后利用估计结果在时域进行信道预测,将当前和过去时刻的信道信息作为信道预测器的输入,对信道的时间抽头l分别进行预测,通过信道预测算法得到最佳预测系数w[m;l],计算出未来时刻的信道数据
若通信体制是单载波,则信道估计在时域执行;若通信体制是多载波,尤其是OFDM,则信道估计依然在频域执行,再通过IFFT将频域信道估计值转换到时域。这样做的优点有两个:一是可以在不改变原有的系统结构下,使信道预测技术应用于大多数的OFDM系统之中;二是由于OFDM的信号结构使得系统在频域对信道进行估计和均衡的运算复杂度更小。然后利用估计结果在时域进行信道预测,将当前和过去时刻的信道信息作为信道预测器的输入,对信道的时间抽头l分别进行预测,通过信道预测算法得到最佳预测系数w[m;l],计算出未来时刻的信道数据![]() 最后将预测结果通过使用DFT转换到频域,从而获得自适应传输所需的CSI。
最后将预测结果通过使用DFT转换到频域,从而获得自适应传输所需的CSI。
假设信道估计和时频域转换已经完成,得到时域信道估计结果为
(1)
式中,l=0,1,…,K-1,K为信道长度,p为预测模型阶数,![]() 为m-p时刻的信道估计值。然后在l个信道时间抽头上,用当前和过去的p个信道采样值依次进行信道预测,则信道预测的更新方程为
为m-p时刻的信道估计值。然后在l个信道时间抽头上,用当前和过去的p个信道采样值依次进行信道预测,则信道预测的更新方程为
(2)
式中,w[m;l]为预测系数向量,即
(3)
式中,wp[m;l]为m时刻第l个信道时间抽头上的第p个预测系数。
实际的水声信道结构通常是稀疏的,只有少数信道权系数具有较大的响应值。这些路径往往对通信系统性能有着关键性的影响,而其他权值很小的信道抽头大部分由噪声构成,并不包含实际的信道分量。由于自适应系统信道预测的目标是提前预测每个频域子载波信道值,即CSI,所以根据声信道的稀疏特性筛选出预测时域信道的主要路径后,还要通过DFT转到频域再供自适应传输的发射端使用。
2.2 水声信道预测算法
2.2.1 MMSE信道预测算法
MMSE算法是一种固定预测系数的方法,预测器的系数与已知信道数据的相关矩阵有关,需要矩阵求逆运算,所以算法复杂度高。MMSE信道预测原理是通过求得一个时域信道冲激响应,使得预测结果与实际信道响应的均方误差最小,以此准则来获得最佳信道预测系数。表1给出了MMSE信道预测算法的具体步骤。
表1 MMSE信道预测算法
Tab.1 MMSE channel prediction algorithm

初始化: p=预测阶数, l=信道长度。迭代步骤(对m=1,2,3,…):1.根据已知信道数据求得自相关矩阵Rh^m,l为Rh^m,l=rh^m,l(0)rh^m,l(1)…rh^m,l(p-1)rh^m,l(1)rh^m,l(0)…rh^m,l(p-2)︙︙⋱︙rh^m,l(p-1)rh^m,l(p-2)…rh^m,l(0)éëêêêêêêùûúúúúúú(4)自相关量rh^m,l为rh^m,l=E{h^[m+i;l]h^∗[m;l]},i=0,1,…,p(5)2.计算预测系数w[m;l]=(Rh^m,l)-1rh^m,l(6)3.求得下一时刻信道冲激响应h~[m+1;l]=∑p-1j=0wj[m;l]h^[m-j;l](7)4.计算预测误差E[e[m;l]2]=1-∑p-1j=0wp[m;l]h^[m-j;l](8)5.直到迭代次数=m, 根据式(2)求出预测时刻的信道响应。
因为MMSE算法的预测系数固定,所以在信道时不变或者缓慢时变时,算法预测性能较好。但由于这种方法并不能自适应更新预测系数来跟踪信道变化,故在水声信道变化较快时受时延、多普勒、预测阶数等因素影响严重,容易导致预测误差累积。
2.2.2 LMS自适应信道预测算法
LMS算法是一种系数随着已知数据自我更新的方法,与MMSE算法相比,它的算法性能有所提升。该算法可被看作是对可能的权值空间进行梯度下降,预测系数根据误差函数进行自适应调节,即性能函数误差均方值E[|e[m;l]|2]最小。该算法不需要矩阵求逆运算,计算复杂度小;且进一步精化了预测系数,加入一个收敛步长μ来控制预测系数的跟踪性能,μ是一个常数,取值范围为0<μ<1。然而实际求梯度值的过程很复杂,难以求解,因此在LMS算法中用梯度估计值代替梯度值,使算法能够快速收敛。表2给出了LMS信道预测算法的具体步骤。
表2 LMS信道预测算法
Tab.2 LMS channel prediction algorithm

初始化:μ=收敛步长, p=预测阶数, l=信道长度, w(0)=0。迭代步骤(对m=1,2,3,…):1.计算m时刻的信道预测结果h~[m;l]=wH[m-1;l]h^[m-1;l](9)2.m时刻的预测误差为e[m;l]=h^[m;l]-h~[m;l](10)3.更新预测系数w[m;l]=w[m-1;l]+2μh^[m-1;l]e[m;l](11)4.直到迭代次数=m, 根据式(2)求出预测时刻的信道响应。
由式(11)可以看出,LMS自适应算法当前时刻的预测系数由前一时刻的预测系数加上以预测误差和收敛步长为比例因子的p个时刻的信道信息得到,更新过程比MMSE算法简单得多。收敛步长μ越小,算法的收敛误差越小,稳态性能更好,但收敛速度变慢。因此μ的取值对于LMS算法的收敛速度和预测性能十分重要,应当取一个合适的值平衡μ值对二者的影响。
2.2.3 RLS自适应信道预测算法
RLS算法是一种典型的根据观测数据推断未知参量的数据处理方法,其目标函数是使实际信道响应与预测信道响应之差的平方和最小,即每个时刻预测系数的平方误差达到最小。它的自适应预测系数更新方法比LMS算法更复杂,通过调节过去一段时间内不同时刻的信道信息所占的比重来获得更好的预测效果。在对RLS算法初始化时,若已知水声信道的先验知识,可以用它来为预测系数w[m;l]选择适当的初值w(0),否则令w(0)=0。令RLS算法增益矢量k(0)中的矩阵p(0)=δ-1I,其中δ为平稳因子,是一个小的正值常数,取值范围为0<δ<1。表3给出了RLS信道预测算法的具体步骤。
表3 RLS信道预测算法
Tab. 3 RLS channel prediction algorithm

初始化:w(0)=0, p(0)=δ-1I, k(0)=h^[m;l]δ+h^[m;l]2,p=预测阶数, l=信道长度。迭代步骤(对m=1,2,3,…):1.更新增益矢量k[m;l]=p[m-1;l]h^[m;l]l+h^H[m;l]p[m-1;l]h^[m;l](12)2.根据式(2)求得下一时刻信道预测结果;3.m时刻的预测误差为e[m;l]=h^[m;l]-wH[m-1;l]h^[m-1;l](13)4.更新预测系数w[m;l]=w[m-1;l]+k[m-1;l]e∗[m;l](14)5.更新矩阵p[m;l]=1l(I-k[m;l]h^H[m;l])p[m-1;l](15)6.直到迭代次数=m, 根据式(2)求出预测时刻的信道响应。
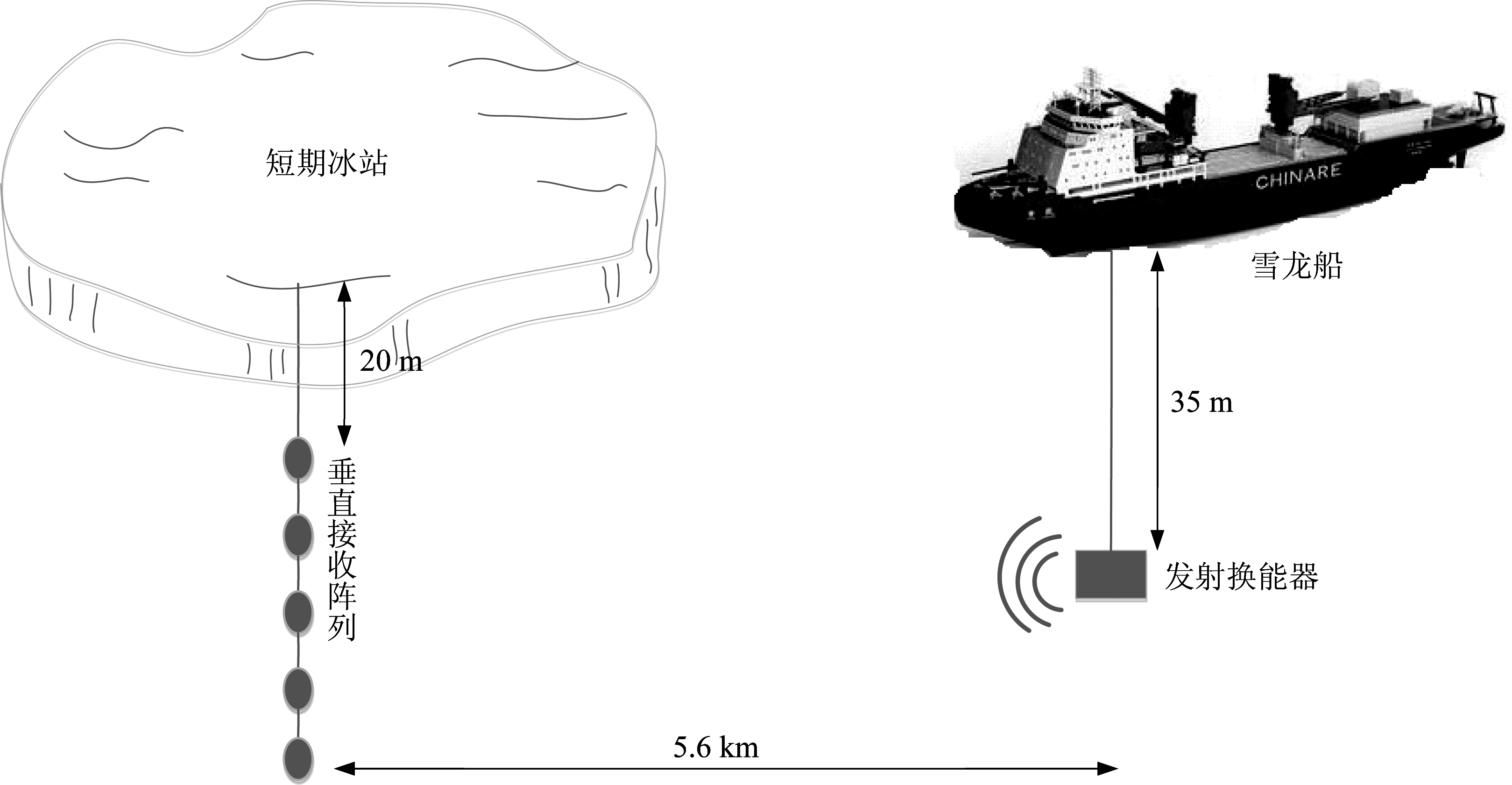
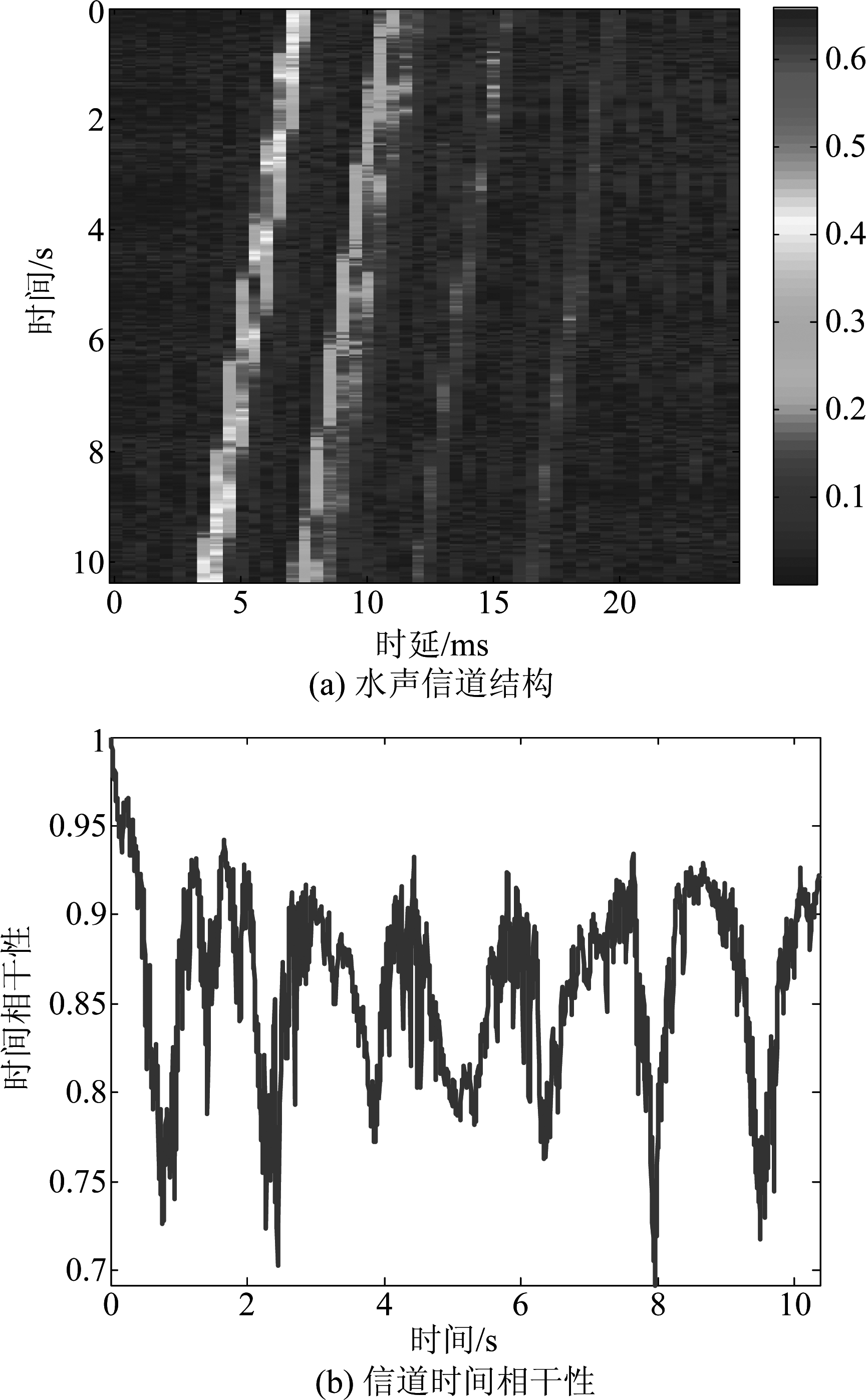
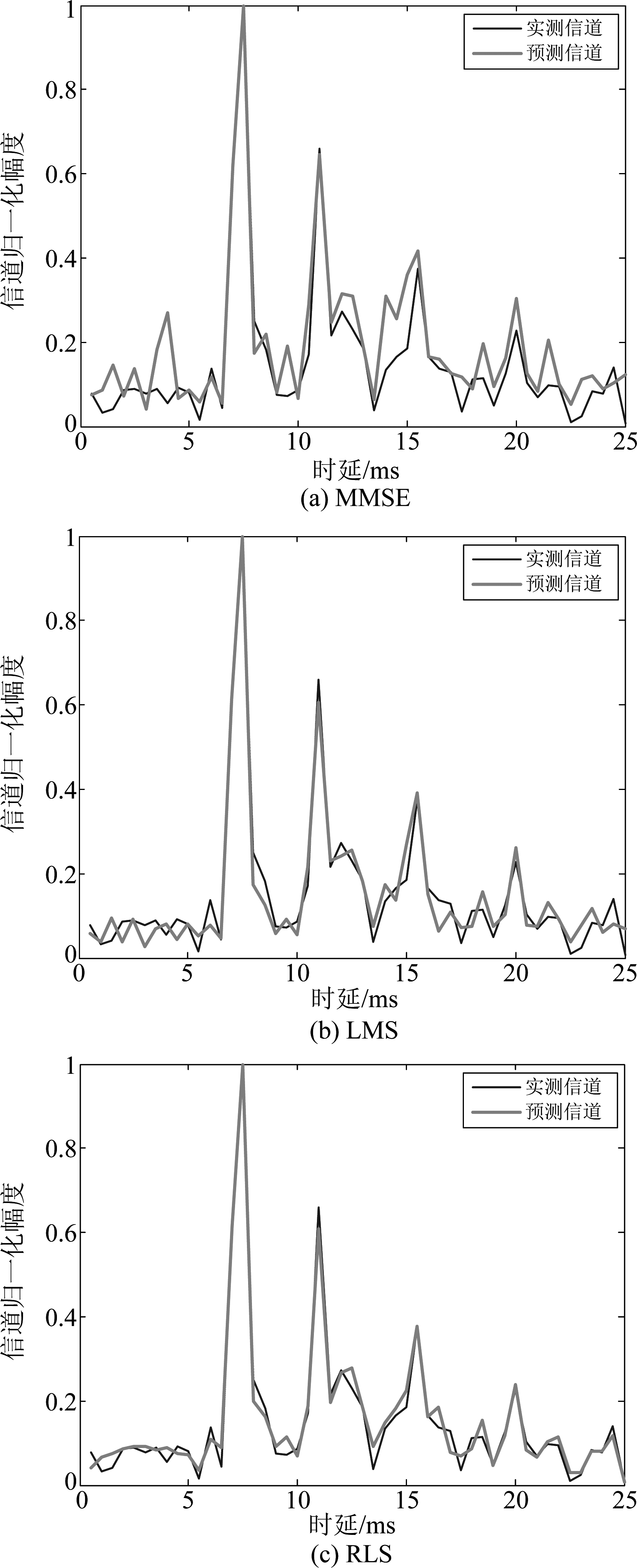
在RLS算法中以一个较小的权重l确保距离当前较远时刻的观测数据被“遗忘”,仅保留最近的数据,故l(0 第九次北极科学考察期间于2018年8月12日在短期冰站开展了水声通信试验,试验场景如图2所示。其中发声站位坐标为79°55′26.97″N 168°48′48.86″W,接收站位坐标为79°55′44.436″N 169°06′12.252″W,通信距离为5.6 km。5个自容水听器组成的垂直接收阵列从短期冰站吊放,阵元布放深度分别为20 m、30 m、40 m、50 m、60 m。发射换能器从雪龙船舯部甲板布放,布放深度为35 m,发射换能器频带为2~8 kHz。发送信号参数如下:采样频率为48 kHz,载波频率为3 kHz,映射方式为QPSK,采用开方升余弦滤波器进行脉冲成型,滚降系数为1。水声通信试验过程中雪龙船周边(500 m范围内)基本为开阔水域,但与短期冰站之间仍有大量的尺度不均匀的冰层覆盖,因此水声通信环境为冰水混合水域。 图2 北极水声通信试验场景 Fig.2 The scene of underwater acoustic communication test in Arctic 图3 北极水声通信试验实测水声信道 Fig.3 Measured results of under-ice acoustic channel in Arctic 图3给出了本次水声通信试验布放深度为40 m的接收阵元实测水声信道结果。从图3(a)可以看出该信道表现出较强的稀疏特性,包含4条主要的路径,且各路径信道幅值随时间起伏变化。此外,还可以观察到明显的多普勒效应,且多普勒随时间基本保持稳定,这主要是由于试验当天风速较大导致雪龙船与短期冰站之间存在相对运动。图3(b)为水声信道的时间相干性曲线,水声信道结构在观测时间内较为稳定,在10 s的时间长度内信道的时间相干性大于0.7。 表4给出了北极水声通信试验信道数据的具体参数,共包含2074组不同时刻的时域信道数据,每组信道之间的时间间隔为5 ms,每组信道长度为50个码元间隔(每个码元24个采样点),即信道长度为25 ms。 表4 北极水声通信试验信道数据参数 Tab.4 Data parameters of under-ice acoustic channel in Arctic 采样频率/kHz48信道长度/ms25通信频带/kHz2~4信道数据/组2074信道采样频率/Hz200 接下来,根据上节北极水声通信试验的实测信道数据分析论证三种信道预测算法的性能。图4给出了在北极水声信道下通过三种信道预测方法得到的预测信道与同一时刻北极实测信道的结果比较。对于MMSE算法,预测阶数p=20。对于LMS算法,预测阶数p=10,自适应跟踪步长μ=0.05。对于RLS算法,预测阶数p=1,遗忘因子l=0.75,平衡因子δ=0.99。 图4 北极水声信道下三种预测算法的信道预测结果 Fig.4 Under-ice channel prediction results of three prediction algorithms 从图中可以看出,本文所采用的三种预测算法均可以有效地预测出水声信道的主要路径结构,信道主要路径有四条,最大时延约为17 ms。但MMSE算法的预测曲线与LMS和RLS算法相比对信道跟踪能力稍差,对信道结构的预测不够精准,这是由于MMSE算法的预测系数不具备自适应更新能力所致。LMS预测算法和RLS预测算法均可以对水声信道的结构和衰落状况进行准确预测,但对幅值较小的信道抽头存在一些偏差。 图5中给出了在北极水声信道下,MMSE、LMS和RLS预测算法单次运算和50次平均的误差学习曲线,其中各个参数的取值与图4相同。三幅图中的信道预测误差均可以达到-20 dB以下,证明本文所用方法的预测结果可以实际有效的应用于自适应水声通信系统之中[14]。从图5(a)中可以看出,MMSE预测算法的误差曲线不收敛,与图5(b)和图5(c)相比,算法预测性能更差,随着水声信道多途强度和多普勒频移的变化,算法的预测误差逐渐增大,难以持续跟踪信道变化。从图5(b)和图5(c)中可以看出,由于LMS预测算法和RLS预测算法的预测系数可以自适应更新,因此预测精度受水声信道时变的影响不大。RLS算法的收敛速率比LMS算法更快,且信道预测误差相比LMS算法大约有3 dB的增益。这是由于RLS算法的目标函数是指数加权的误差平方和,利用遗忘因子l调整预测系数,确保最近的采样数据被重用。因此,对于时变水声信道来说,RLS算法的预测性能更好。 图5 北极水声信道下三种预测算法的信道预测误差曲线 Fig.5 Variation curves of under-ice channel prediction errors of three prediction algorithms 本节将针对预测阶数p、收敛步长μ、遗忘因子l三个参数对LMS和RLS算法预测误差性能的影响进行分析(由于MMSE算法不能有效跟踪时变,曲线无法收敛,研究参数对算法预测性能的影响意义不大,因此本节不对其进行研究)。 图6给出了预测阶数p=1,p=5,p=10,p=15,p=17,p=20时LMS算法在100次平均后的预测误差曲线,自适应跟踪步长μ=0.05。可以看出,当预测阶数变大时,预测误差减小,收敛速度变快。但是当预测阶数增大到一定值时(图中p=20时),由于收敛步长并没有调整,预测误差反而增大。因此需要选取合适的预测阶数与收敛步长,从而得到最优预测系数。另外,如果预测阶数过大会使算法的复杂度增大,但对预测误差性能的改善并不大。 图6 不同的预测阶数对LMS算法的影响 Fig.6 The effect of different prediction order on LMS algorithm 图7给出了收敛步长μ=0.005,μ=0.01,μ=0.03,μ=0.05,μ=0.08,μ=0.09时LMS算法在100次平均后的预测误差曲线,预测阶数p=10。可以看出,算法性能受限于收敛步长的选择。收敛步长的范围有限,越接近μ的上界,预测精度越好,收敛速度变快;若是超过上界,预测性能又会下降。因此根据图6和图7可以得出结论,在此时变水声信道条件下,当预测阶数取10,收敛步长取0.08时,可以兼顾算法复杂度、收敛速度和精度。 图7 不同的收敛步长对LMS算法的影响 Fig.7 The effect of different convergence step length on LMS algorithm 图8给出了l=0.6,l=0.7,l=0.75,l=0.9,l=0.93,l=0.96时RLS算法在100次平均后的预测误差曲线。预测阶数p=1,平衡因子δ=0.99。由图可以看出,当l减小时,收敛过程缩短,减小到一定程度时(图中l=0.75时),预测系统稳定性变差,预测误差增加。因此RLS算法的遗忘因子也是有范围的,需要根据经验调节,在此时变水声信道条件下,预测阶数取1,遗忘因子取0.9时,可以很好的平衡收敛速度、稳态误差、系统稳定性和算法复杂度。 图8 不同的遗忘因子对RLS算法的影响 Fig.8 The effect of different forgetting factor on RLS algorithm 研究了时变水声信道的信道预测技术,利用水声信道的稀疏特性,对结构更简单的时域信道预测器进行研究,仅保留重要的路径权系数,相比频域信道预测方法减少系统反馈冗余的同时提高预测精度。分析了三种信道预测算法的预测性能,根据北极冰水混合区域的实测信道数据对本文方法进行了验证,考虑了多普勒频移的存在,结果表明本文所用方法能够有效地预测出时变水声信道的主要路径结构,且收敛后的预测误差最优能够达到-30 dB,预测结果可以为冰水混合水域的自适应水声通信提供可靠的CSI。还分析了影响信道预测算法性能的参数,给出了在此水声信道条件下的预测参数参考值,可以为以后的冰水混合水域的水声信道预测技术研究提供依据。 [1] Freitag L, Koski P, Singh S, et al. Acoustic Communications Under Shallow Shore-fast Arctic Ice[C]∥In Oceans. Anchorage, AK, USA, 2017: 1-5. [2] 岳强, 孙亮, 王彬. 水声稀疏时变SIMO信道盲均衡算法[J]. 信号处理, 2017, 33(11):1486-1496. Yue Qiang, Sun Liang, Wang Bin. Blind Equalization Algorithm of Underwater Acoustic Sparse Time-Varying SIMO Channel[J]. Journal of Signal Processing, 2017, 33(11): 1486-1496.(in Chinese) [3] Radosevic A, Duman T M, Proakis J G, et al. Adaptive OFDM for Underwater Acoustic Channels with Limited Feedback[J]. In Proc.45th Asilomar Conf.Signals Syst.Comput., Nov., 2011: 975-980. [4] Radosevic A, Ahmed R, Duman T M, et al. Adaptive OFDM Modulation for Underwater Acoustic Communications: Design Considerations and Experimental Results[J]. IEEE J. Oceanic Eng., 2014, 39(2): 357-370. [5] 李鑫滨, 黄志鹏, 韩松, 等. 基于博弈论的分布式水声通信网络功率分配算法[J]. 信号处理, 2017, 33(5): 758-765. Li Xinbin, Huang Zhipeng, Han Song, et al. Power allocation algorithm for distributed underwater acoustic communication network based on game theory[J]. Journal of Signal Processing, 2017, 33(5): 758-765.(in Chinese) [6] Liu Chonglei, Huang Haining, Yin Li, et al. Multipath Structure of the Typical Under-ice Sound Channel in the Arctic: Theory and Experiment[J]. Chinese Journal of Acoustics, 2019, 38(1): 21-34. [7] 朱广平, 殷敬伟, 陈文剑, 等.北极典型冰下声信道建模及特性[J].声学学报, 2017, 42(2): 152-158. Zhu Guangping, Yin Jingwei, Chen Wenjian, et al. Modeling and Characterizing the Typical Under-ice Acoustic Channel for the Arctic[J]. Acta Acustica, 2017, 42(2): 152-158.(in Chinese) [8] Qiao Gang, Song Qingjun, Ma Lu, et al. Sparse Bayesian Learning for Channel Estimation in Time-Varying Underwater Acoustic OFDM Communication[J]. IEEE ACCESS, 2018, 6: 56675-56684. [9] Qiao Gang, Gan Shuwei, Liu Songzuo, et al. Self-Interference Channel Estimation Algorithm Based on Maximum-Likelihood Estimator in In-Band Full-Duplex Underwater Acoustic Communication System[J]. IEEE ACCESS, 2018, 6: 62324- 62334. [10] Hwang J K, Winters J H. Sinusoidal Modeling and Prediction of Fast Fading Processes[C]∥IEEE Global Telecommunications Conference, Globecom 1998, 1998: 667- 672. [11] Andersen J B, Jensen J, Jensen S H, et al. Prediction of Future Fading Based on Past Measurements[C]∥IEEE Vehicular Technology Conference, VTC 1999, Netherlands, Sep. 1999: 151-155. [12] Eyceoz T, Duel-Hallen A, Hallen H. Deterministic Channel Modeling and Long Range Prediction of Fast Fading Mobile Radio Channels[J]. IEEE Communications Letter, Sep. 1998, 2(9): 254-256. [13] Forenza A, Heath J R W. Link Adaptation and Channel Prediction in Wireless OFDM Systems[C]∥IEEE International Midwest Symposium on Circuits and Systems, Tulsa, Oklahoma, Aug. 2002: 211-214. [14] Yang T, Duel-Hallen A, Hallen H. Enabling Adaptive OFDM for Mobile Radio Channels[C]∥IEEE Military Communications Conference, MILCOM 2004, Monterey, CA, 2004: 704-710. [15] Duel-Hallen A, Hallen H, Yang T-S. Long Range Prediction and Reduced Feedback for Mobile Radio Adaptive OFDM Systems[J]. IEEE Transactions on Wireless Communications, Oct. 2006, 5(10): 2723-2733. [16] 姜喆, 王海燕, 赵瑞琴, 等.水声稀疏信道估计与大范围自适应平滑预测研究[J].西安工业大学学报, 2012, 32(10): 844- 852. Jiang Zhe, Wang Haiyan, Zhao Ruiqin, et al. Underwater Acoustic Sparse Channel Estimation and Long-range Adaptive Smooth Prediction[J]. Journal of Xi'an Technological University, 2012, 32(10): 844- 852.(in Chinese) [17] Radosevic A, Duman T M, Proakis J G, et al. Channel Prediction for Adaptive Modulation in Underwater Acoustic Communications[C]∥In Proc. IEEE OCEANS Conf., Santander, Spain, Jun. 2011: 1-5. [18] Kuai Xiaoyan, Sun Haixin, Qi Jie, et al. CSI Feedback-based CS for Underwater Acoustic Adaptive Modulation OFDM System with Channel Prediction[J]. China Ocean Eng., 2014, 28(3): 391- 400. [19] Lin Na, Sun Haixin, Cheng En, et al. Prediction based Sparse Channel Estimation for Underwater Acoustic OFDM[J]. Applied Acoustics, Apr. 2015, 96: 94-100.3 北极水声通信试验数据处理及结果分析
3.1 北极水声通信试验条件及信道结构

3.2 水声信道预测方法性能分析
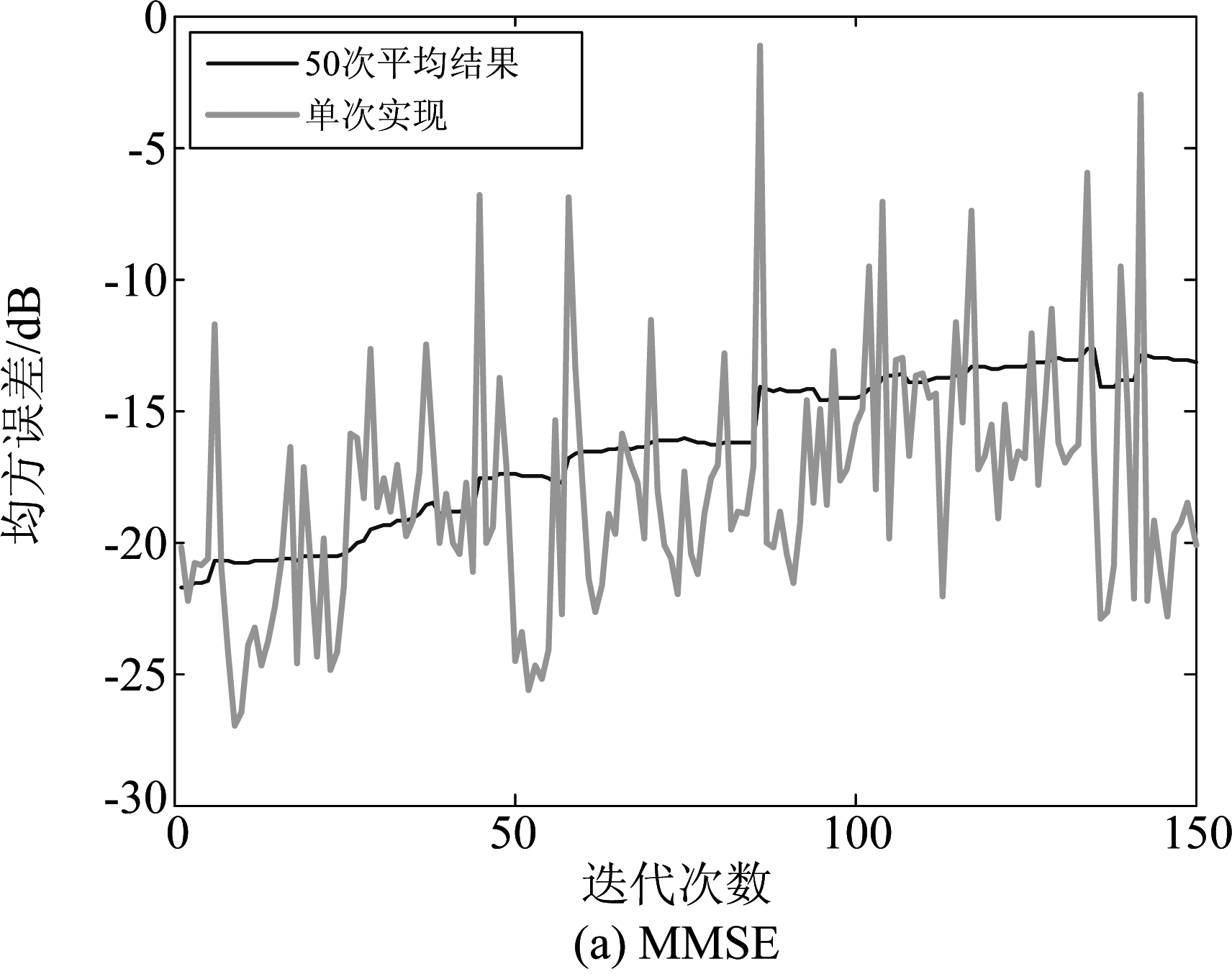

3.3 不同自适应算法参数对预测性能的影响
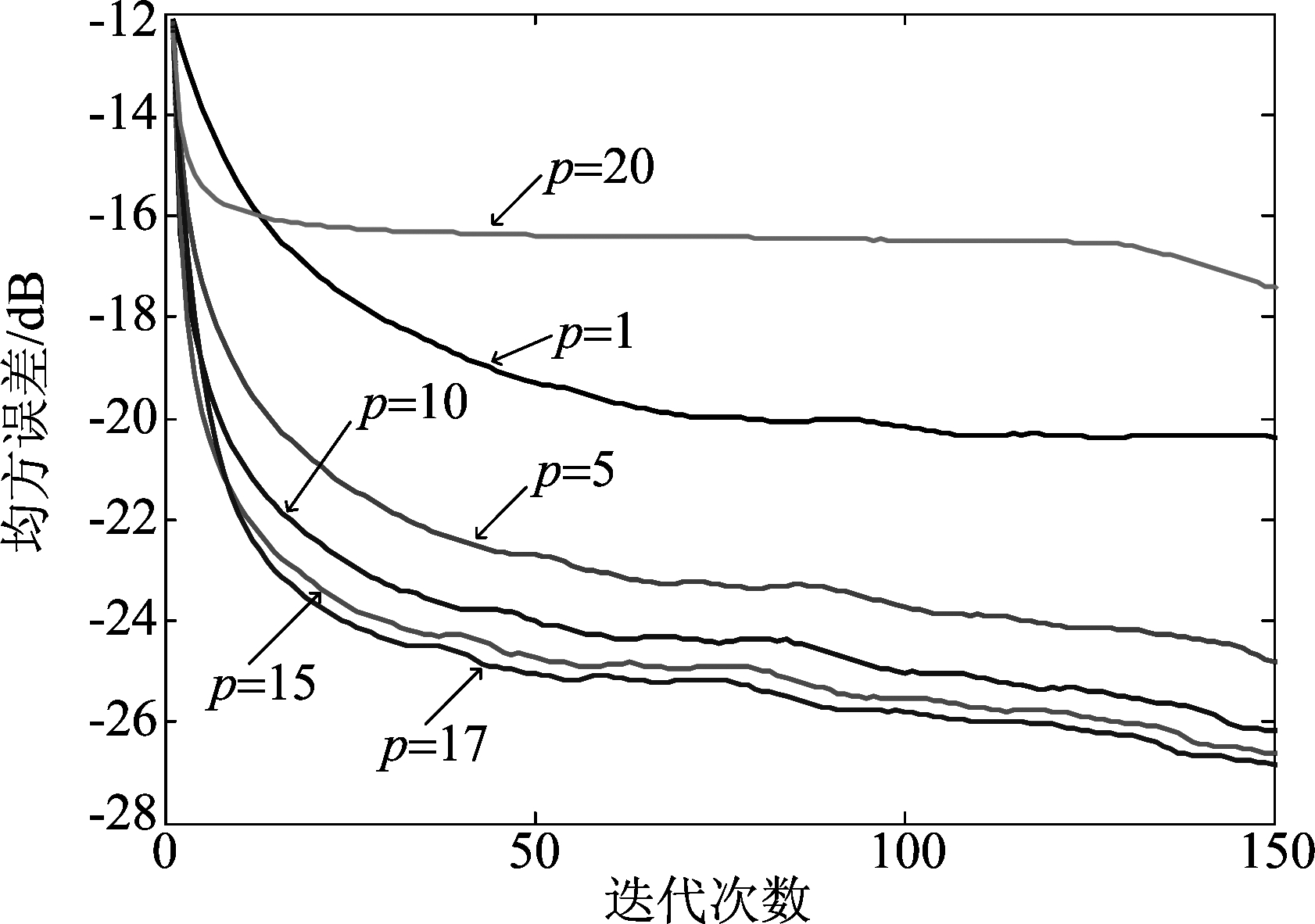
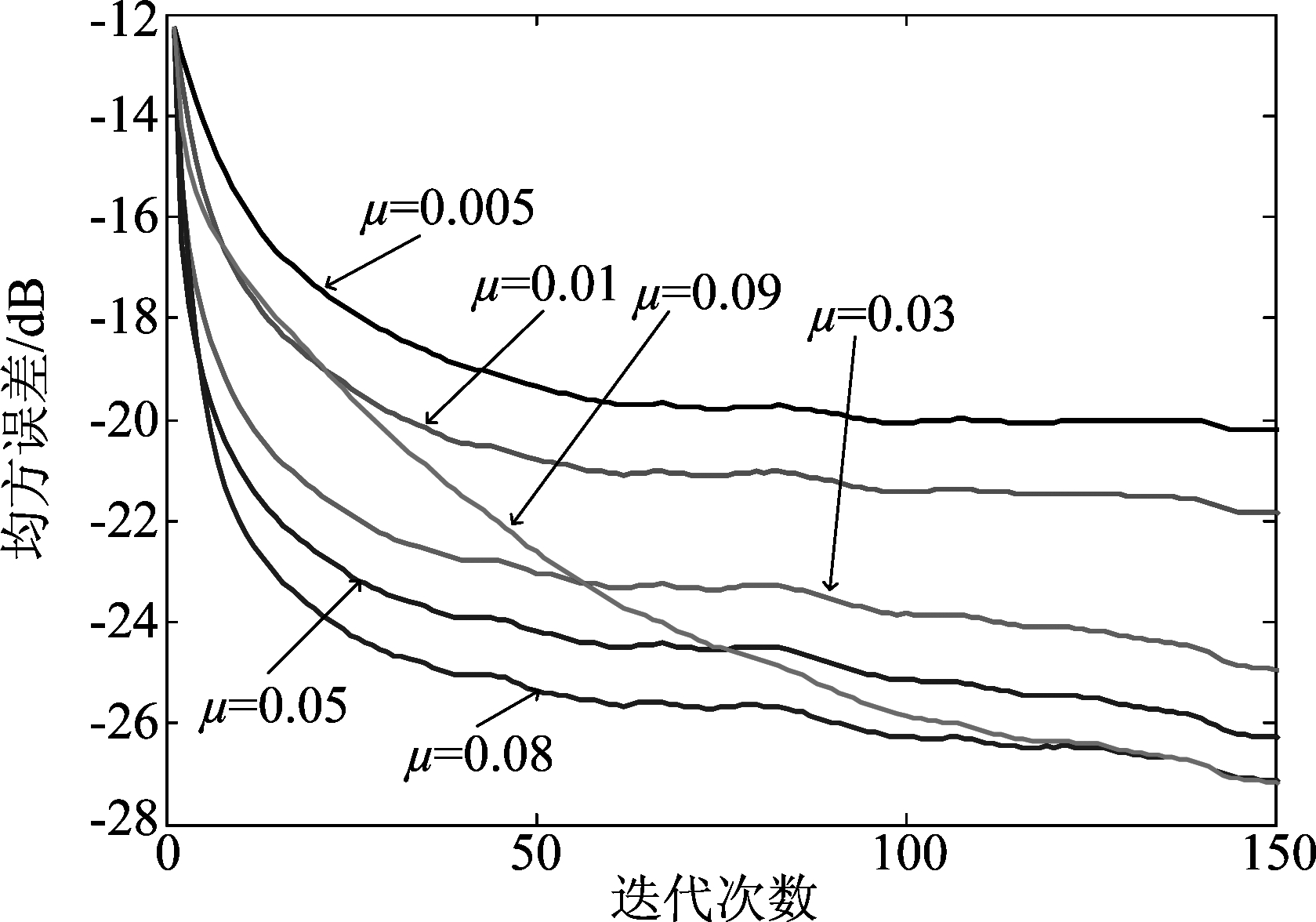
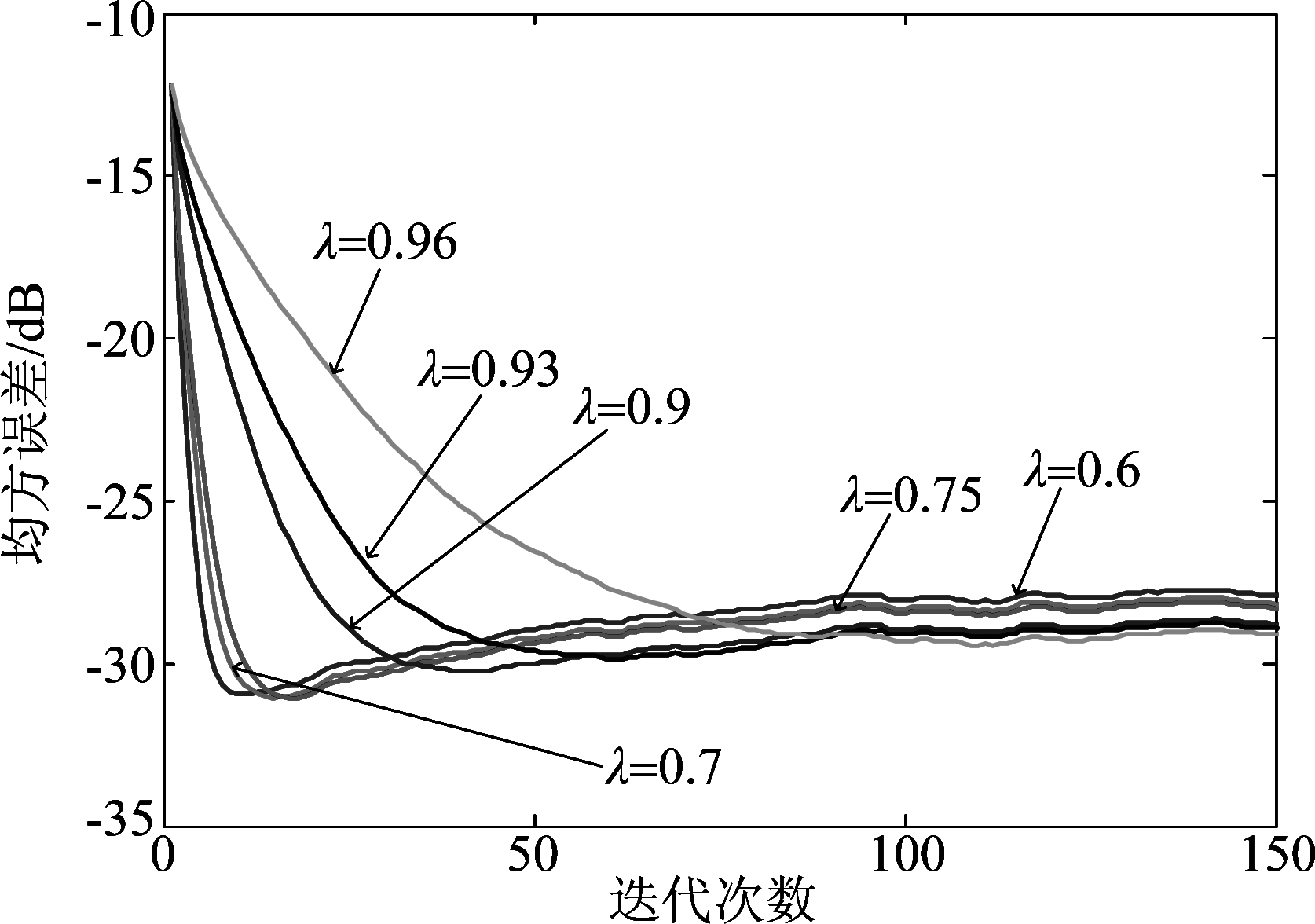
4 结论



