1 引言
近几年,机器学习方法(尤其是深度学习方法)在语音识别[1]、图像处理[2]、自然语言理解[3]等科学领域取得了突破性进展,促进了自动驾驶、人脸识别、语音个人助理、医学影像分析等领域的技术变革。不仅如此,机器学习方法也在深刻影响着其他自然科学领域(如地球物理学[4-7])的发展方向。从统计学的角度看,机器学习方法是一种最优化方法。利用大量统计数据对具有特定结构、包含未知参数的数学模型进行训练,可生成含有训练数据内在统计特征的拟合器。从这个角度看,机器学习方法是一种可应用于最优化问题求解的普适性的框架。因此,其可被应用于其他多个自然科学领域。水声远程被动定位问题是根据观测到的远距离声源辐射的声压数据,通过合适的信号处理算法,在空域内寻找声源最优或最可能的位置。显然,给定合适的经过预处理之后的训练数据,该问题可用机器学习方法进行求解。例如,将机器学习用于分类问题时,模型的输出为可能类型的概率分布。类似地,寻找最优声源位置也可作为机器学习的分类问题进行求解,此时模型输出为声源距离或深度的概率分布。本文对基于机器学习的水声被动定位算法进行综述,通过对目前最新的研究成果进行引述,重点讨论和给出所涉及到的算法理论基础、单阵元及阵列的前端信号预处理算法、模型选择和训练及性能评价等。
将机器学习方法应用到水声被动定位,可以追溯到上世纪九十年代。1991年,Steinberg[8]等人将神经网络用于对均匀介质中点声源的定位。同年,Ozard[9]等人仿真研究了在匹配场处理中利用神经网络进行距离和深度判别。之后,Caiti[10-11]等人(1994、1996)利用径向基函数神经网络估计海底沉积层的特性。另外,Michalopoulou[12](1995)、Stephan[13](1998)和Benson[14](2000)等人分别将神经网络用于海底分类和地声参数反演。总的来说,以上工作为神经网络在水声学中的应用作了探索性的研究。但是,受限于当时的计算资源及缺乏高效的训练算法,加之当时主流的被动定位算法——匹配场定位[15-19],正处于飞速发展阶段,在之后的很长一段时间,机器学习方法在水声学领域并没有受到足够重视,而基于物理场声学建模的匹配场处理方法则成为水声被动定位的研究热点。然而,尽管匹配场处理方法经过几十年的发展取得了巨大的进步,目前也被广泛应用于相关的工程实践,但是匹配场处理方法在实际应用中仍然面临着诸多困难和挑战,如典型的环境失配问题。海洋是一种时变、空变的复杂声信道,导致实测声场与理论建模声场之间必然存在一定的偏差和失配,这种失配有时会给匹配场定位造成较大影响。为克服和降低海洋环境参数不确定性对匹配场定位的影响,研究人员相继提出了一些将环境参数纳入未知参数集的改进的匹配场处理方法,如环境聚焦匹配场处理[20-24]或贝叶斯匹配场定位[25-26]。但同时这些方法带来的问题是计算量显著增加,增加了实时处理的难度。
由于匹配场处理方法的局限性及近几年机器学习理论和技术的新发展,一些基于机器学习的水声被动定位方法开始重新崭露头角,相关研究和报道也陆续出现。2017年,Lefort[27]等人利用水箱实验数据模拟研究了在起伏海洋环境下非线性回归算法的定位性能,表明机器学习算法在水声目标定位中有一定的优势和潜力。同年,Niu[28-29]等人提出了一类可行的基于机器学习算法的水下声源定位方法,系统性研究了前馈神经网络、支持向量机和随机森林三种机器学习模型的声源定位性能,并首次通过海试实测实验数据验证了机器学习算法的定位性能。2018年,Wang[30]等人将实测数据作为实验数据,利用广义回归神经网络对声源进行定位。同年,Huang[31]等人尝试将仿真声场作为训练数据,利用多层的深度卷积神经网络对声源进行定位。2019年,Liu[32]等人利用集合卷积网络对深海直达声区进行声源测距。Niu[33]等人利用50层残差卷积神经网络和单水听器对不确知环境条件下的声源进行定位。所有这些工作都表明了机器学习方法在水声被动定位中的应用潜力。同时,值得注意的是,相关研究在国际水声学领域也开始显示出影响力,越来越多的学者投入到相关研究中。以美国声学学会年会为例,基于机器学习的水声定位或反演研究在2016年的两次会议上还较为少见。到2018年11月的秋季年会,相关的会议报告[34- 40]已明显增加。由此可见,该研究方向正处于快速发展阶段,并逐步在整个水声学领域产生影响力。
2 定位算法
到目前为止,水声远程被动定位中所涉及的机器学习方法,绝大多数属于有监督学习类算法。即利用有标注的数据对机器学习模型进行训练。若机器学习模型的输出为连续的,则为回归器。若模型输出为多个离散值,则将这种机器学习模型称之为分类器。理论上,利用回归器或分类器对声源距离和深度进行估计都是可行的。定位算法的框图如图1所示。定位算法分为两个阶段:训练阶段和预测阶段。
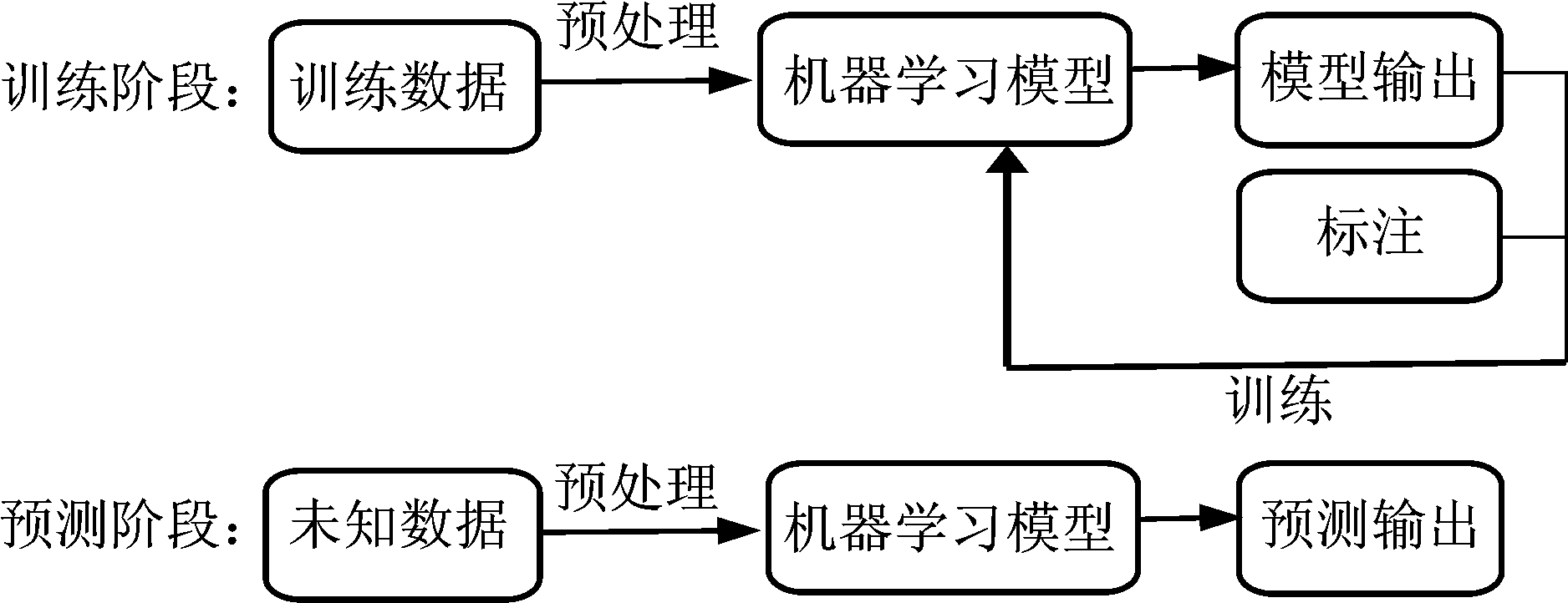
图1 机器学习定位算法框图
Fig.1 Localization algorithm using machine learning
在图1所示的训练阶段,原始声压数据经过前端预处理(见第2.2节)之后作为机器学习模型的输入。用于训练的标注数据为声源位置或与声源位置相关的量。对于回归器,标注为连续的声源距离或深度[28],对于分类器,标注一般采用位向量[28](即组成元素为0和1)对声源距离或深度进行编码表示。给定对应的标注之后,结合模型输出,就可以利用特定的训练损失函数对机器学习模型进行训练,目的是得到模型中的未知参量。几种典型的机器学习模型及对应的训练损失函数见第2.3节。在训练阶段训练好的机器学习模型可用于预测阶段对未知数据的预测,预测阶段机器学习模型的输入为经过同样预处理之后的测量数据。对于回归器,模型的输出为声源距离或深度;对于分类器,输出为声源距离或深度的概率分布,一般取概率最大值为声源位置的估计值。
2.1 理论基础
虽然在某些应用中机器学习模型被认为是无法解释的“黑盒子”模型,但是将机器学习方法应用到水声被动定位中,是有合理的物理理论基础的。如引言所述,机器学习模型实际上是一个函数拟合器,它将输入按照一定的规则映射为输出。在水声学中,不同位置(距离和深度)处的声源所产生的声场是不同的。具体来说,不同位置处声源对应的信道响应是不同的,而声源激励一般来说与位置无关。因此,我们可以将预处理之后的物理量映射为声源位置或与声源位置相关的量。以某浅海环境下单阵元为例,图2所示为仿真得到的单个阵元接收信号幅度的距离-频率图,可见不同距离处对应不同的频率干涉结构。同样,在深海直达声区,也存在类似的干涉结构[32]。因此,这种特征[32-33]可用来作为机器学习模型的输入。阵列信号的采样协方差矩阵也包含类似的信息(矩阵的对角线元素对应每个阵元信号的幅度,非对角线元素对应不同阵元信号间的相位差)。第2.2节所述的前端预处理算法的目的是将原始测量信号转换为信道响应或近似信道响应,从而尽量减小训练数据和预测数据可能存在的差异。在实际应用中,二者差异一般由声源激励不同引起,包括相位和幅度差异。对于阵列信号采用的归一化采样协方差矩阵[28-29]以及单阵元信号采用的分段归一化幅度[32-33],就是为了减小这种差异。
图2 接收信号的干涉结构(距离-频率图)
Fig.2 Interference structure of received signals (range-frequency)
2.2 前端预处理算法
对于海洋声信道,记L个水听器接收的频域声压数据为p( f )=[p1( f ),…,pL( f )]T,其可表示为
p( f )=S( f )g(f,r)+ε( f )
(1)
其中,S( f )为复数声源激励项,g(f,r)为与声源位置有关的信道响应或格林函数,ε( f )为噪声。因为一般情况下声源激励项与声源位置无关,并且训练数据与预测数据的声源激励可能会存在差异,为使机器学习模型的输入数据保持相同的特征,预处理算法的目的是消除或减小声源激励谱幅度和相位的影响[28-29]。
首先,复声压数据被归一化为[28-29]
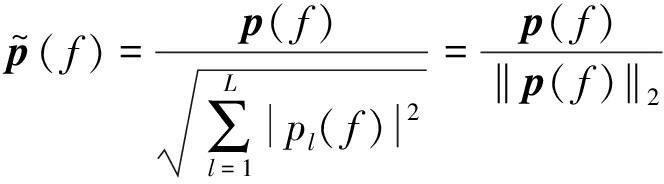
(2)
若噪声为零,公式(2)的归一化方法可将声源激励的幅度谱的影响完全消除。在较高信噪比情况下,声源幅度谱的影响可被有效抑制。
然后,利用归一化后的复声压,可得到多次快拍平均的采样协方差矩阵(SCM)[28-29]:
(3)
其中,Ns为快拍数。由公式(1)和(3)可见,在较高信噪比的条件下,声源激励相位的影响可被有效抑制和减弱。公式(2)和(3)保证了将与声源激励近似无关的物理量作为用于水声被动定位的机器学习模型输入,而非原始测量的声压。由于公式(3)计算得到的采样协方差矩阵是共轭对称的,因此为提高计算效率和较少内存占用,可取上三角矩阵对应元素的实部和虚部作为机器学习模型的输入。对于单频信号,L个水听器数据经预处理之后每个样本点的输入维数为L×(L+1)。若考虑输入为多频信号,可将多个频点的数据拼接为一个长向量作为模型输入。
公式(2)和(3)是针对阵列信号的预处理方法。对于单阵元信号,水声被动定位也是可行的,比如典型的利用波导不变量原理进行测距。基于波导不变量的测距方法,实际上是利用宽带信号的干涉结构,即不同距离上干涉结构不同。从另一个角度出发,波导不变量测距方法利用的是宽带信号的幅度谱,基于机器学习的定位方法也可借鉴这一点。因此,类似于阵列信号预处理方法的出发点,对于单阵元的宽带信号,预处理算法使得训练数据和预测数据的特征分布保持一致。记单阵元接收到的F个频率的复声压矢量为p=[p1,…,pf,…,pF],对应的幅度谱可写为:
q=[|p1|,…,|pf|,…,|pF|]
(4)
然后,将公式(4)向量中的元素归一化到[0, 1]区间[33]:
(5)
与阵列信号预处理相似,为降低训练数据和测试数据声源谱不一致造成的影响,对于缓变的声源谱,可用如下的分段归一化方法[33]:
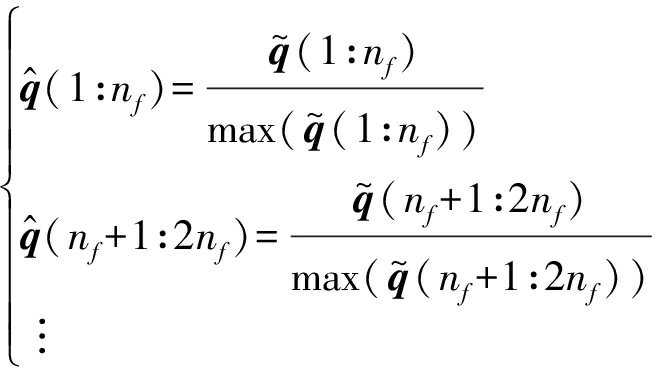
(6)
其中,nf为每一分段的频点数。向量
即为预处理之后机器学习模型输入的单个样本点。
另外,除了以上预处理算法外,还可以利用协方差矩阵的本征向量[31]作为模型的输入。该方法将多次快拍平均的采样协方差矩阵进行分解,理论上可将整个空间分解为模态信号空间和噪声空间。然后取前M个较大本征值(即理想情况下的前M阶简正波)对应的本征向量作为机器学习模型的输入。理想情况下,由于只取前M个特征向量,故该方法可抑制部分噪声。但同时存在的问题是若采样协方差矩阵统计不充分,子空间的分解可能存在一定的问题。另外,信号有效模态数M的值不太好确定,与海洋传播环境及信号频率等密切相关。总之,机器学习模型输入特征的提取和构造是一个非常值得研究的问题,关系到机器学习模型的学习效率和稳健性。
2.3 典型机器学习模型
根据现有文献,用于水声被动定位的机器学习模型有支持向量机、随机森林、前馈神经网络、深度神经网络以及集成神经网络模型等。其中,支持向量机、随机森林和单隐层的前馈神经网络属于浅层模型,对于小训练数据集具有很好的定位性能。而深度神经网络属于深度学习模型,学习能力更强,可构建高度复杂的机器学习模型,但同时需要的训练数据也越多。在训练数据不足的情况下,机器学习模型可能会出现过拟合的现象。选择哪种模型取决于训练数据集的大小及水声被动定位具体的应用场景(见第3节中对海试试验结果的概述)。下面对这几种模型进行简要介绍。
支持向量机[41]是一种典型的分类模型,它通过使间隔(margin)最大化的策略寻找一个超平面实现输入样本的分类。如果训练数据空间是线性可分的,可通过硬间隔最大化得到线性支持向量机分类器;若输入空间是近似线性可分时,可通过引入松弛变量即软间隔最大化,得到线性分类器;当训练数据为线性不可分时,可通过核技巧实现非线性支持向量机。以二分类为例,首先假设输入样本空间{xn; n=1,2,…,N}是线性可分的,对应的类型为sn∈{1, -1},则分类模型具有以下的形式:
yn=wTxn+b
(7)
其中,w和b是待求解的权重和偏置项。用于分类的超平面满足wTxn+b=0,若估计值yn在超平面之上(yn>0),则对应的估计类型为
相反,若yn位于超平面之下(yn<0),则估计类型为
样本点xn到超平面的垂直距离d等于点xn与其在超平面上投影点x0之间的距离,满足:
(8)
因此,距离d可写为[28]:
(9)
间隔距离dM定义为从超平面到间隔边界上最近的样本点(即支持向量)的距离。模型参数可由最大化间隔求解得到:
(10)
公式(10)等价于求解如下优化问题:
(11)
若训练数据是线性不可分的,可引入松弛变量ξn≥0,使得部分样本点有一定的误分类。此时对应的优化问题为[41]:
n=1,…,N
(12)
其中,参数C>0控制间隔最大化和误分类之间的权重。另外,对于非线性的分类问题,公式(7)可写为:
yn=wT
(xn)+b
(13)
其中(xn)表示特征空间的变换。对于该类问题,可通过核函数的技巧进行求解。与支持向量机分类器不同,支持向量回归器则是最小化如下ε敏感度的误差函数[41]:
(14)
其中,rn是样本xn对应的真实的声源位置。
随机森林模型[42- 43]是决策树模型的推广,它将输入数据划分到不同的特征空间中。即从根节点开始,对样本的某一特征进行测试,根据测试结果将样本分配到相应的子节点(每个子节点对应特征的一个取值),然后依次递归,最终将样本划分到不同叶节点。若输入样本{xn; n=1,2,…,N}是D维空间中的向量。按照决策树的思想,通过在第i维空间上定义一个截止门限c,输入数据可被划分到左右两个区域(或特征空间):
(15)
在每个分支处的代价函数可写为:
(16)
nleft和nright分别为划分到左右两个区域中的样本点数,H(·)为纯净度函数。对于分类问题,一种表达纯净度的函数为基尼指数(Gini Index):
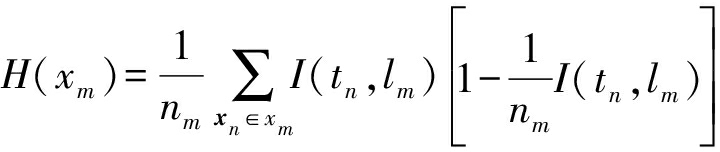
(17)
nm为区域xm内的样本点数,lm为区域xm对应的标注预测,表示区域内样本数量最多的类型标注:
(18)
其中,rk为声源位置对应的预测类型,tn为样本xn对应的标注,且
(19)
对于回归算法,区域的标注预测lm和纯净度函数H(·)为:
(20)
(21)
其中rn为对应样本的声源位置(标注)。单个决策树模型容易产生过拟合的问题,而随机森林则是一种通过统计自助抽样集成,综合多个决策树的模型,稳健性更好。对于给定的训练集,随机森林模型通过自助法产生Mr个训练集,在每个训练集上训练产生一个决策树。最终通过多个决策树的统计结果,样本被归为出现频次最多的类型。
另一类机器学习模型是前馈神经网络[41],一般也被称之为多层感知机,它具有前向直连的非循环结构。记输入层L1为D维的向量x=[x1,…,xD]T,与输入层相连的第二层L2含有M个神经元,每个神经元的激活值为输入层单元的线性组合:
(22)
其中,
和
被称之为权重和偏置,上标代表当前的层数。该层神经网络的输出为激活值经过一个激活函数f(·)的变换:
zj=f(aj)
(23)
激活函数有多种选择,包括sigmoid函数、tanh函数、ReLU函数等。以sigmoid函数为例,其数学形式为:
(24)
可以看出该函数为单调递增函数,当a→+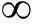
, f(a)→1,当a→-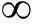, f(a)→0。以此类推,第三层L3中K个神经元对应的激活值为:
(25)
若该层为输出层,对于多分类问题,一般采用softmax函数作为激活函数,对应的K个输出为:
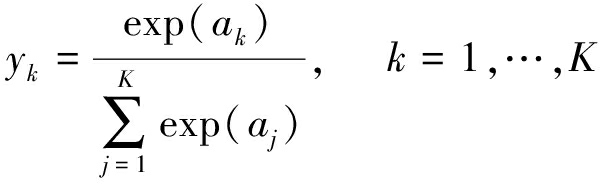
(26)
yk表示样本属于第k个类型的概率,满足0≤yk≤1且∑kyk=1。记tn为二进制的位向量(one-hot vector),向量中仅有一个数为非零,其在向量中的位置代表相应的类型。训练神经网络时,互熵一般作为训练的代价函数:
(27)
对于N个样本,对应的平均互熵及最优的权重分别为[41]:
(28)
(29)
对于回归问题,一般将平方误差函数作为最小化的代价函数[41]:
(30)
其中,rn为声源位置(标注)。神经网络的训练一般采用误差反向传播算法进行权重的更新。
深度神经网络一般被认为是在深度方向上拥有许多层结构的神经网络。例如,上文介绍的具有多个隐层的前馈神经网络也是一种深度神经网络,层与层之间通过全连接的方式进行互连。除了前馈神经网络,在图像和语音处理领域,被广泛采用的深度神经网络还有深度卷积神经网络及循环神经网络。深度卷积神经网络的基本组成单元为卷积层,通过权值参数共享的方式极大地减少了待求解的参数数量。循环神经网络则主要用来对序列进行建模,典型特点为具有有向环的结构。到目前为止,循环神经网络还未在水声被动定位中有所应用,因此本文仅简要介绍卷积神经网络。对于卷积层,记输入样本I的维度为W×H×D,在图像处理中代表宽、高及通道数,对于水声定位,输入可为一维或二维。卷积操作即为输入I与卷积核K的卷积(convolution),在卷积网络算法实现中,经常用互相关(cross-correlation)代替卷积,二者的区别在于是否对卷积核进行翻转。对于单个通道D=1,数学表达式为:
(31)
卷积操作后的输出经常被称之为特征图(feature map),卷积核的维度通常远小于输入的维度。然后,与其他神经网络类似,卷积之后的输出经过一个激活函数(卷积网络中一般为修正线性单元ReLU),最后经过一个池化层(pooling)对输出进行进一步修正处理。例如,常见的两种池化操作为最大池化和平均池化,分别对某一矩形区域内的元素取最大值或平均值。多个卷积层的级联可构成深度卷积神经网络,深度越深,模型的表达能力越强,但同时带来的问题是梯度消失问题,导致模型越难训练。为此,有研究人员提出残差神经网络(ResNet)[44]来缓解深度模型的训练问题。与常规卷积神经网络模拟输入x与输出H(x)之间的映射不同,残差网络模拟的是输入输出的残差函数F(x),即H(x)=F(x)+x。图3所示的瓶颈(bottleneck)结构[44]是一种实现残差网络的基本单元。
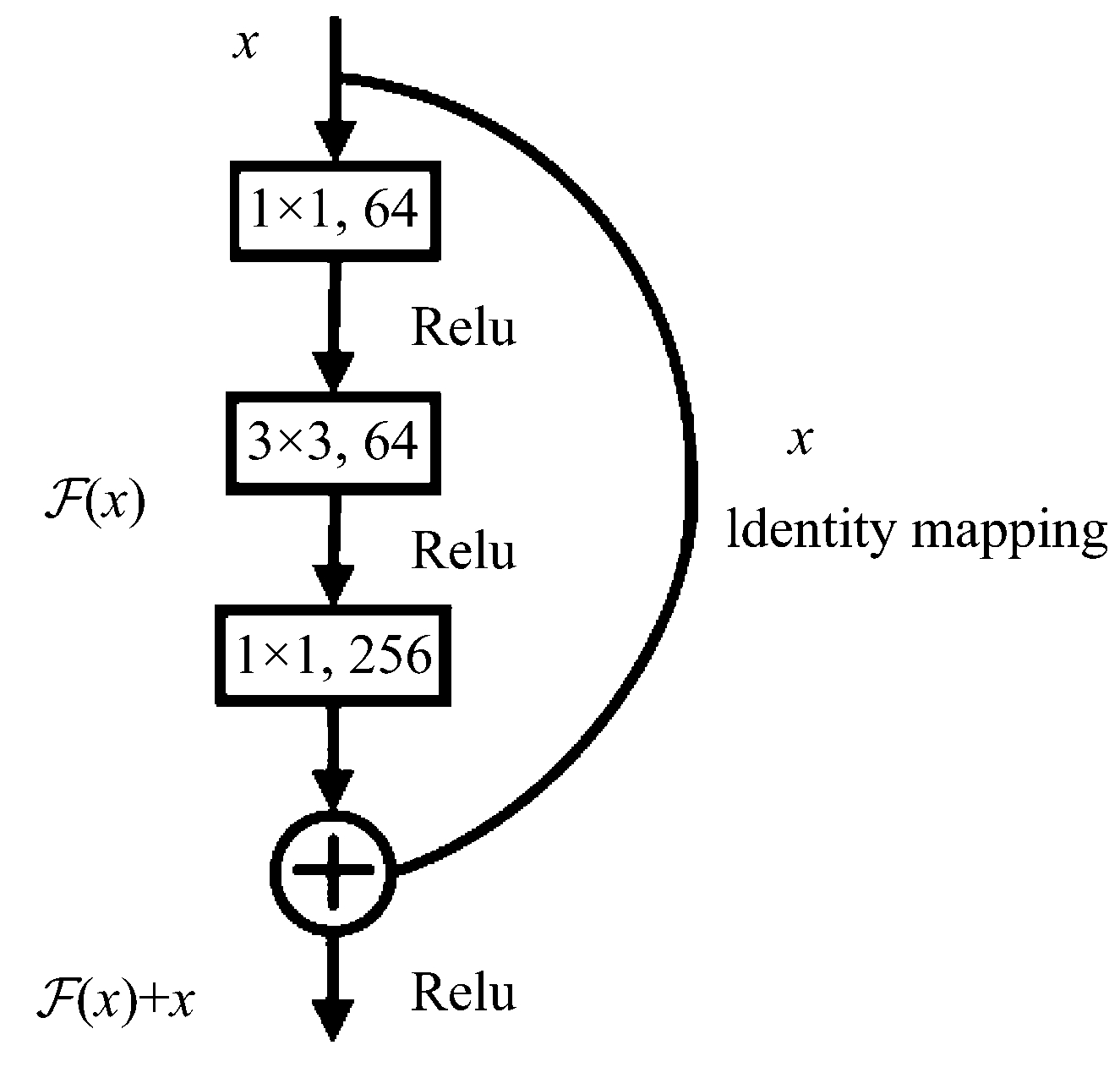
图3 残差网络中的瓶颈结构
Fig.3 Bottleneck structure in ResNet
另外,还有研究人员利用集成神经网络对声源进行测距[32]。集成神经网络模型是利用集成学习的思想(类似单个决策树和随机森林之间的关系),并综合多个神经网络模型,对结果进行统计预测,可在一定程度上提高模型的稳健性和性能。
机器学习模型的训练可在现有主流框架上进行高效地训练,如TensorFlow[45]和Scikit-learn[46]等。
2.4 性能评价
为度量机器学习方法的定位性能,有三种常见的评价准则,分别是均方误差(MSE)、平均绝对值误差(MAE)以及平均绝对百分比误差(MAPE)。记测试样本数为N、第i个样本对应的距离或深度的真实值为gi、第i个样本对应的距离或深度的预测值为yi,则均方误差的计算公式为:
(32)
平均绝对误差的计算公式为:
(33)
平均绝对百分比误差的计算公式为:
(34)
对于同一数据集,这三种评价准则的结果并不完全一致,一般情况下,可选择一种或多种度量对定位结果进行比较和评价。
2.5 与匹配场定位的区别
基于机器学习的水声定位方法,与经典的匹配场定位相比,有以下几点明显区别:
(1)算法的执行策略和效率不同。机器学习方法可以被认为是一种离线训练、在线预测的策略。大量密集的计算集中在模型的训练阶段,训练好的模型在预测阶段进行轻量级的计算,因此可较为容易地实现数据的实时处理。相反,匹配场处理方法采用的则是在一个参数空间内进行在线匹配的策略,如果参数空间较大(如同时包含环境参数),则计算效率会显著降低,导致无法进行实时处理。
(2)用于定位的代价函数不同。机器学习方法根据回归或者分类任务,大多采用最小均方误差或最小化互熵等训练的代价函数。而匹配场处理大多采用相关处理的方式。
(3)大数据处理的能力。机器学习方法可以很自然的采用大数据集结合深度学习模型进行训练,数据量越大,在统计意义上越有可能逼近真实的数据分布,并且可以同时利用仿真数据和实测数据作为训练数据。匹配场处理方法一般情况下无法有效处理大数据。
3 部分海试实验数据概述
本节对近几年公开发表文献中所涉及的海试实验数据处理中用到的机器学习模型和应用场景进行总结和概括,以便于读者了解目前机器学习方法应用于水声被动定位的概况。表1总结给出了对应的试验海域及类型、传感器和训练数据类型、机器学习模型及定位类型。在文献[28-30]中,实际测量数据被用于机器学习模型的训练,由于训练数据规模较小,模型均为结构较为简单的浅层模型。采用实验数据作为训练数据的好处是可避免对未知环境的声场理论建模,从而最大限度避免了环境失配造成的影响,但同时对应用场景有较大的限制,即训练好的机器学习模型仅适用于某一特定海域相似环境条件下(如固定式阵列的岸基系统)的声源定位。对于缺乏实验数据的场景,文献[31-33]利用环境参数生成的仿真声场作为模型的训练数据,结果表明深度学习算法的定位性能优于传统的匹配场处理定位算法。在文献[31-32]中,由于环境参数的先验信息较为准确,因此仿真声场数据集的规模不大。而文献[33]的应用场景是不确知海底参数情况下的声源定位。为降低海底参数的不确定性,训练数据采用基于多种假定海洋环境参数生成的仿真声场,训练数据样本数超过上千万个,对应的深度学习模型也更加复杂,采用了50层的深度残差网络,可适用于多种不同海底环境参数下的声源被动定位。由表1也可以看出,水声被动定位中用到的机器学习模型逐渐向大数据集、深度学习模型演进。究其原因,主要是在推向实际应用中,针对实测数据集有限和环境不确定性的应对策略。
表1 部分海试实验机器学习定位方法总结
Tab.1 Summary of machine learning methods in sea experimental data processing
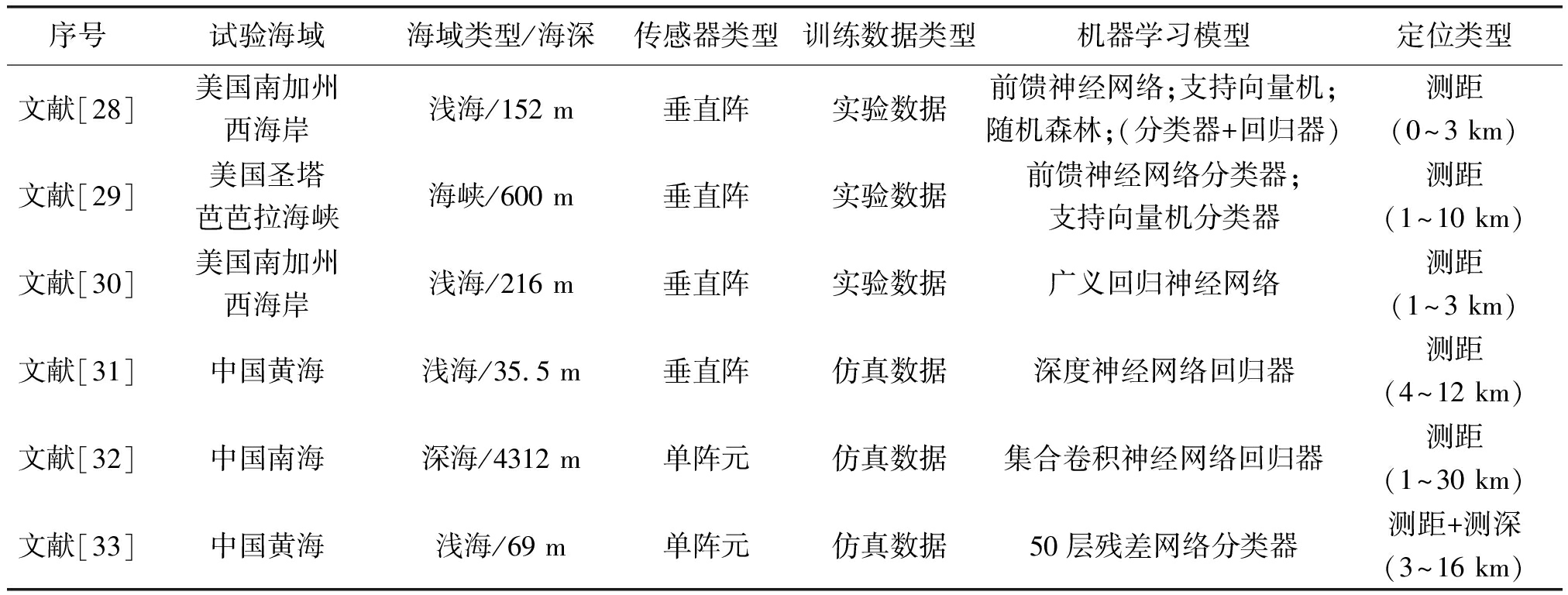
序号试验海域海域类型/海深传感器类型训练数据类型机器学习模型定位类型文献[28]美国南加州西海岸浅海/152 m垂直阵实验数据前馈神经网络;支持向量机;随机森林;(分类器+回归器)测距(0～3 km)文献[29]美国圣塔芭芭拉海峡海峡/600 m垂直阵实验数据前馈神经网络分类器;支持向量机分类器测距(1～10 km)文献[30]美国南加州西海岸浅海/216 m垂直阵实验数据广义回归神经网络测距(1～3 km)文献[31]中国黄海浅海/35.5 m垂直阵仿真数据深度神经网络回归器测距(4～12 km)文献[32]中国南海深海/4312 m单阵元仿真数据集合卷积神经网络回归器测距(1～30 km)文献[33]中国黄海浅海/69 m单阵元仿真数据50层残差网络分类器测距+测深(3～16 km)
4 现有模型存在的问题及解决思路
从近期公开发表的相关文献来看,基于机器学习的水声被动定位方法具有较好的应用前景和潜力。但同时,这类方法作为水声学领域中一种新兴的技术,尚处于起步阶段,在推向实际应用时还面临着多个问题和挑战。具体来说有以下几点:
(1)不确知海洋环境下的声源被动定位。对于实际应用,海洋环境是时变和空变的,海底参数的准确获取也具有相当大的难度。在不确知海洋环境条件下,如何训练机器学习模型成为关键。一种思路是收集不同水文、不同海底参数条件下的实测数据,将实测数据作为训练数据,对机器学习模型进行训练。但难点在于不同环境条件下、不同声源位置的实测数据获取难度较大。另外一种思路是利用仿真声场数据作为训练数据,这种方法的好处是可以低成本地获取足够多环境条件下的训练数据样本,不足之处是训练数据的质量依赖于声场建模的准确度,如目前复杂的二维或三维海洋声场的准确建模仍然具有挑战性。
(2)低信噪比条件下的声源被动定位。目前的研究都集中在较高信噪比条件下的定位,现有模型在低信噪比条件下定位性能会急剧下降。相应的解决思路是利用传统的阵列信号处理方法(如波束形成或空域滤波等)提高信噪比[33],或者通过将带噪声的数据作为训练数据,也可能提高机器学习模型在低信噪比条件下的定位稳健性。
(3)多声源同时定位。在实际应用中,存在多声源同时存在(或在同一方向上)的可能性。现有的机器学习模型目前考虑仅有一个声源存在,如何建立针对多声源情况的机器学习模型,也是水声被动定位中亟待解决的问题。
5 结论
本文对目前基于机器学习的水声被动定位方法进行了综述和回顾,介绍了前端信号预处理算法、几种典型的机器学习模型、评价准则,并对部分海试试验结果进行了概述。作者还简要讨论了基于机器学习的水声被动定位与经典的匹配场处理方法之间的区别。同时针对目前机器学习方法存在的问题,给出了相应的解决思路。基于机器学习的水声被动定位具有很好的发展潜力和工程化应用前景,该研究方向开始逐渐引起国际水声学界的兴趣,正处于快速发展时期。以作者的观点看,针对第4节所述的难点,未来的几个潜在的研究方向为:大数据和深度学习模型相结合的定位方法;低信噪比条件下的机器学习定位方法;适用于多声源定位的机器学习模型和方法。
[1] Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
[2] Krizhevsky A, Sutskever I, Hinton G. Imagenet classification with deep convolutional neural networks[C]∥Advances in Neural Information Processing Systems, 2012: 1097-1105.
[3] Collobert R, Weston J, Bottou L, et al. Natural language processing (almost) from scratch[J]. Journal of Machine Learning Research, 2011, 12(Aug): 2493-2537.
[4] Sharma M L, Arora M K. Prediction of seismicity cycles in the himalayas using artificial neural networks[J]. Acta Geophysica Polonica, 2005, 53(3): 299-309.
[5] Garcia S R, Romo M P, Mayoral J M. Estimation of peak ground accelerations for Mexican subduction zone earthquakes using neural networks[J]. Geofisica Internacional, 2006, 46(1): 51- 62.
[6] Kohler A, Ohrnberger M, Scherbaum F. Unsupervised pattern recognition in continuous seismic wavefield records using Self-Organizing Maps[J]. Geophysical Journal International, 2010, 182(3): 1619-1630.
[7] Riahi N, Gerstoft P. Using graph clustering to locate sources within a dense sensor array[J]. Signal Processing, 2017, 132: 110-120.
[8] Steinberg B Z, Beran M J, Chin S H, et al. A neural network approach to source localization[J]. The Journal of the Acoustical Society of America, 1991, 90(4): 2081-2090.
[9] Ozard J M, Zakarauskas P, Ko P. An artificial neural network for range and depth discrimination in matched field processing[J]. The Journal of the Acoustical Society of America, 1991, 90(5): 2658-2663.
[10] Caiti A, Parisini T. Mapping ocean sediments by RBF networks[J]. IEEE Journal of Oceanic Engineering, 1994, 19(4): 577-582.
[11] Caiti A, Jesus S. Acoustic estimation of seafloor parameters: A radial basis functions approach[J]. The Journal of the Acoustical Society of America, 1996, 100(3): 1473-1481.
[12] Michalopoulou Z H, Alexandrou D, Moustier C. Application of neural and statistical classifiers to the problem of seafloor characterization[J]. IEEE Journal of Oceanic Engineering, 1995, 20(3): 190-197.
[13] Stephan Y, Demoulin X, Sarzeaud O. Neural direct approaches for geoacoustic inversion[J]. Journal of Computational Acoustics, 1998, 6(01n02): 151-166.
[14] Benson J, Chapman N R, Antoniou A. Geoacoustic model inversion using artificial neural networks[J]. Inverse Problems, 2000, 16(6): 1627-1639.
[15] Bucker H P. Use of calculated sound fields and matched field detection to locate sound source in shallow water[J]. The Journal of the Acoustical Society of America, 1976, 59(2): 368-373.
[16] Schmidt H, Baggeroer A B, Kuperman W A, et al. Environmentally tolerant beamforming for high-resolution matched field processing: Deterministic mismatch[J]. The Journal of the Acoustical Society of America, 1990, 88(4): 1851-
1862.
[17] Westwood E K. Broadband matched-field source localization[J]. The Journal of the Acoustical Society of America, 1992, 91(5): 2777-2789.
[18] Baggeroer A B, Kuperman W A, Mikhalevsky P N. An overview of matched field methods in ocean acoustics[J]. IEEE Journal of Oceanic Engineering, 1993, 18(4): 401- 424.
[19] Michalopoulou Z H, Porter M B. Matched-field processing for broad-band source localization[J]. IEEE Journal of Oceanic Engineering, 1996, 21(4): 384-392.
[20] Gerstoft P. Inversion of seismoacoustic data using genetic algorithms and a posteriori probability distributions[J]. The Journal of the Acoustical Society of America, 1994, 95(2): 770-782.
[21] Gingras D F, Gerstoft P. Inversion for geometric and geoacoustic parameters in shallow water: Experimental results[J]. The Journal of the Acoustical Society of America, 1995, 97(6): 3589-3598.
[22] Collins M D, Kuperman W A. Focalization: Environmental focusing and source localization[J]. The Journal of the Acoustical Society of America, 1991, 90(6): 1410-1422.
[23] Dosso S E. Matched-field inversion for source localization with uncertain bathymetry[J]. The Journal of the Acoustical Society of America, 1993, 94(6): 1160-1163.
[24] Baer R N, Collins M D. Source localization in the presence of gross sediment uncertainties[J]. The Journal of the Acoustical Society of America, 2006, 120(2): 870- 874.
[25] Dosso S E, Wilmut M J. Uncertainty estimation in simultaneous Bayesian tracking and environmental inversion[J]. The Journal of the Acoustical Society of America, 2008, 124(1): 82-97.
[26] Dosso S E, Wilmut M J. Comparison of focalization and marginalization for Bayesian tracking in an uncertain ocean environment[J]. The Journal of the Acoustical Society of America, 2009, 125(1): 717-722.
[27] Lefort R, Real G, Dremeau A. Direct regression for underwater acoustic source localization in fluctuating oceans[J]. Applied Acoustics, 2017, 116: 303-310.
[28] Niu H, Reeves E, Gerstoft P. Source localization in an ocean waveguide using supervised machine learning[J]. The Journal of the Acoustical Society of America, 2017, 142(3): 1176-1188.
[29] Niu H, Ozanich E, Gerstoft P. Ship localization in Santa Barbara Channel using machine learning classifiers[J]. The Journal of the Acoustical Society of America, 2017, 142(5): EL455-EL460.
[30] Wang Y, Peng H. Underwater acoustic source localization using generalized regression neural network[J]. The Journal of the Acoustical Society of America, 2018, 143(4): 2321-2331.
[31] Huang Z, Xu J, Gong Z, et al. Source localization using deep neural networks in a shallow water environment[J]. The Journal of the Acoustical Society of America, 2018, 143(5): 2922-2932.
[32] Liu Y, Niu H, Li Z. Source ranging using ensemble convolutional networks in the direct zone of deep water[J]. Chinese Physics Letters, 2019, 36(4): 044302-1- 044302- 4.
[33] Niu H, Gong Z, Ozanich E, et al. Deep-learning source localization using multi-frequency magnitude-only data[J]. The Journal of the Acoustical Society of America, 2019, 146(1): 211-222.
[34] Li W. Machine learning in acoustic applications with wave physics models, a tutorial[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1683-1683.
[35] Gerstoft P. Graph clustering for localization within a sensor array[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1729-1729.
[36] Niu H, Gong Z, Wang H, et al. Big data based ocean acoustic source localization via deep learning[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1729-1730.
[37] Ozanich E, Gerstoft P, Purohit A, et al. Ocean acoustic range estimation in noisy environments using convolutional networks[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1743-1743.
[38] Song H. Classification of multiple source depths in a time-varying ocean environment using a convolutional neural network (CNN)[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1744-1744.
[39] Miller J H, Potty G, Tripathy A, et al. Source localization using a compact tetrahedral array[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1745-1745.
[40] Wang W, Su L, Ma L, et al. Source localization using back propagation neural network and a single vector receiver[C]∥The Journal of the Acoustical Society of America, 2018, 144(3): 1855-1855.
[41] Bishop C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: Chaps.4,5, and 7.
[42] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.
[43] Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140.
[44] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]∥IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2016: 770-778.
[45] Abadi M, Agarwal A, Barham P, et al. TensorFlow: Large-scale machine learning on heterogeneous distributed systems[CP]. Software available from tensorflow.org, 2015.
[46] Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: Machine learning in Python[J]. Journal of Machine Learning Research, 2011, 12: 2825-2830.
