1 引言
随着微波技术的发展,由通信系统、导航系统、雷达系统等电磁波收发设备的增加而导致的频谱拥挤情况已经不容忽视。采用传统波形的雷达系统容易与其他同频工作的通信、导航等民用设备产生相互干扰,特别是在HF、VHF和UHF等拥挤的频段。针对此类情况,有研究者提出了一种新型的雷达波形形式:稀疏频率波形。稀疏频率波形是一种在频带上稀疏分布着若干离散阻带的特殊波形,为在高度拥挤频谱环境下工作的波形提供了很好的选择。利用稀疏频率波形,雷达系统可以避免来自同频段其他设备的相互干扰;并且波形能通过将几个带宽较小的不相交信道合并,形成更大的带宽,从而提高频带利用率。Lindenfeld在文献[1]中首次提出稀疏频率波形的概念,提出了一种计算效率高的超宽带雷达和通信波形提取算法,该算法具有良好的频谱抑制和距离旁瓣最小化能力。文献[2]研究了具有旁瓣约束的稀疏频率波形设计方法,建立了广义积分旁瓣电平(Generalised Integrated Sidelobe Level, GISL)的边界,衡量最佳平均通带阻带功率比。Aubry等人[3- 4]提出了通过性能检测设计稀疏频率波形的方法。
模糊函数理论是研究稀疏频率雷达波形的主要工具,一种设计思路是在优化设计过程中权衡自相关函数(Auto-correlation Function, ACF)约束和功率谱密度(Power Spectral Density, PSD)约束,得到满足性能需求的稀疏频率波形。衡量ACF旁瓣特性的主要指标有峰值旁瓣电平(Peak Sidelobe Level, PSL)和积分旁瓣电平(Integrated Sidelobe Level, ISL)[5]。现阶段,稀疏频率波形设计普遍存在的问题是较窄带宽的直接组合将导致设计波形的ACF具有较高的旁瓣,因此研究的重点是如何有效的抑制旁瓣。目前,主要有两类抑制ACF旁瓣和PSD阻带功率的方法:一是发射波形和接收波形的联合设计,发射波形设计主要考虑阻带功率约束,接收波形设计主要考虑降低响应范围内的旁瓣[1];二是在单个发送波形设计中,设计出既满足阻带功率要求又满足低旁瓣性要求的波形[6-10]。
稀疏频率雷达波形设计有降低ISL/PSL的要求与难点,互补码的研究为此提供了一种新的思路。互补码又称为Golay码,最早由Marcel J.E. Golay提出,它具有良好的低副瓣特性,主瓣是码长的两倍,副瓣为零,且任意两个互补码自相关函数之和为零。互补码的良好特性在雷达和通信系统中都存在广泛应用。学者们研究了互补码在通信中的应用[12-18],如功率控制、信道估计等;文献[11]研究了互补码在地波雷达中的应用;文献[19]提出了一种改进的互补码,并分析了其在雷达中的应用。
本文重点分析雷达发射波形,首先,提出了一种应用互补码低副瓣特性设计稀疏频率波形的方法。考虑两个序列ACF之间关系,当阻带抑制增强时,能有效地抑制ACF的旁瓣电平。然后,先后分析两种约束,一种是ACF旁瓣约束优化PSD特性,另一种是PSD阻带约束优化ACF旁瓣特性,并分别分析两者的优化效果。最后,应用优化工具进行数值仿真验证本文所提方法的有效性。
2 稀疏频率波形和互补码
2.1 具有旁瓣抑制的稀疏频率波形设计
本文考虑的稀疏频率波形是一组连续基带复波的数字样本,该波形是恒模波形,模为常数(只对相位进行调制),拥有最佳的发射功率利用率。根据奈奎斯特采样定理,对连续波形进行采样,波形的带宽用B表示,脉冲持续时间为T,奈奎斯特采样频率为fs≥B,采样间隔为Ts,样本个数为N=T/Ts,则该波形经过采样后每个采样点可表示为:
xn=eφn,n=1,…,N
(1)
其中φn是第n个样本的相位值。该波形可以写成矢量离散形式:
x=[x1,x2,…,xn]T∈CN×1
(2)
其频谱即傅里叶变换为:
(3)
假设雷达波形分布在频带[fL, fH]内,其功率谱具有NS个阻带,其中第k个阻带的频带范围为[fk1, fk2]。在实际过程中,不同阻带频率内的受干扰程度不同,因此对每个阻带分别进行加权,第k个阻带的权重为wk>0。第k个频带的频谱能量通过以下公式计算
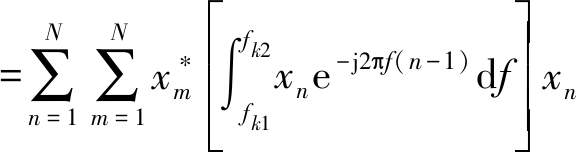
(4)
波形设计过程中,考虑PSD阻带约束,可根据文献[1]中的理论构造目标函数JPSD:
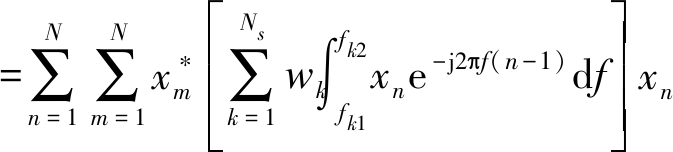
(5)
其中,上标(·)*表示共轭。定义N×N的矩阵R,R中第m行第n列元素表示为:
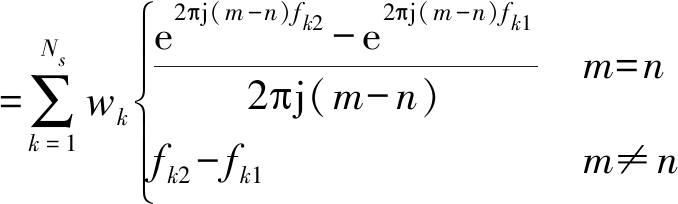
(6)
因此式(5)中目标函数JPSD可表示为离散形式:
JPSD=xHRx
(7)
其中,上标(·)H表示共轭转置。
若仅对式(7)进行优化,只是优化了波形抑制干扰的能力,设计出的波形ACF旁瓣较高,因此还需添加ACF旁瓣约束。定义序列x的自相关函数为:
(8)
本文采用ISL来衡量波形自相关函数的旁瓣性能,定义波形x自相关函数的ISL为JISL:
(9)
该目标函数表示为矩阵的形式为:
(10)

可以看出,对于一个波形优化过程,同时最小化式(7)的JPSD和式(10)的JISL是比较困难的。本文考虑对整体进行优化,加入权值λ构建如下目标函数:
J=λJPSD+(1-λ)JISL
(11)
其中0<λ<1是用来衡量PSD和ACF旁瓣的权重因子。将式(7)和式(10)代入(11)得到总目标函数为:
(12)
2.2 互补码
互补码是一个相对概念,由两个非周期序列组成,两个序列的归一化ACF旁瓣大小相等,符号相反。因此,自相关函数之和是一个δ函数,只在中心处有一个峰值。
设两个序列x和y,其中x={xn},y={yn},n=0,...,N-1,其自相关函数分别为:
(13)
当满足
(14)
时,x和y则为一对互补序列。
互补码不仅具有良好的自相关特性,在频域上还具有互补性。将互补序列映射到频域上,对公式(14)进行傅里叶变换:
Sx( f )+Sy( f )=const
(15)
其中,Sx( f )是rx(k)的傅里叶变换,Sy( f )是ry(k)的傅里叶变换。由此可知互补的两个序列在N个离散点上的PSD之和是一个常数。
3 互补码设计稀疏频率雷达波形
基于互补码的定义可以看出互补序列的自相关函数之和具有良好的旁瓣特性,自相关函数只在中心处取峰值,旁瓣均为零。本文应用了互补码进行设计并与传统的方法进行比较,得出该方法在稀疏频率波形设计中具有更好的旁瓣特性。结合两个序列的互补情况来介绍本文设计方法,其中每个稀疏频率波形都是恒模波形。为权衡阻带抑制和旁瓣抑制,本文提出两种设计约束,分别是对波形的阻带进行约束从而衡量自相关函数旁瓣电平的大小;对波形的旁瓣电平进行约束从而衡量阻带功率谱密度。
3.1 PSD阻带约束的稀疏频率波形设计
第一类设计侧重于抑制具有PSD阻带约束的旁瓣电平,可以应用于要求阻带较小的场合。利用互补码的概念,本文需衡量设计的单个稀疏频率雷达波形的ISL,用两个互补序列x和y自相关函数之和设计波形。首先,两者的自相关函数之和可表示为:
rxy(k)=rx(k)+ry(k)
(16)
为了抑制旁瓣电平,常用衡量指标为最小化ISL,将两个互补序列的ISL表述为:
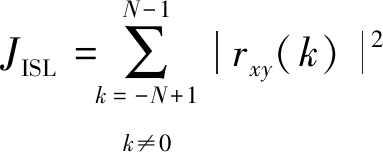
(17)
根据式(8)和式(10)的定义可将式(17)写成矩阵形式:
JISL(x,y)=(Qxx+Qyy)H(Qxx+Qyy)
(18)
第一类设计的前提是对波形PSD阻带进行约束,通常考虑约束阻带总功率,因此在设计中希望阻带总功率不超过某一固定值,此处设为Ps,则可以将问题明确表述为优化问题:
minJISL(x,y)
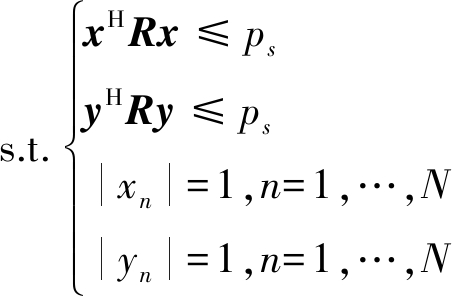
(19)
该优化问题是非凸的,不能求出闭合形式的解,属于有约束非线性优化问题,本文采用基于内点法的数值优化工具对该问题进行优化。内点法是罚函数法的一种,属于约束优化算法,只适用于不等式约束最优化问题。
3.2 ACF旁瓣约束的稀疏频率波形设计
第二类设计侧重于抑制具有ACF旁瓣约束的阻带功率,可以应用于要求ACF旁瓣较小的场合。在这种情况下,优化的目标函数是最小化阻带的总功率。将互补序列x和y的阻带总功率表示为矩阵形式:
JPSD(x,y)=xHRx+yHRy
(20)
第二类设计的前提是对波形ACF旁瓣进行约束,通常限制旁瓣电平低于某一固定值qs。约束旁瓣电平可以考虑约束PSL和ISL,本文只考虑约束ISL,同时需要考虑到两个互补序列的总能量。则可将问题明确表述为优化问题:
minJPSD(x,y)
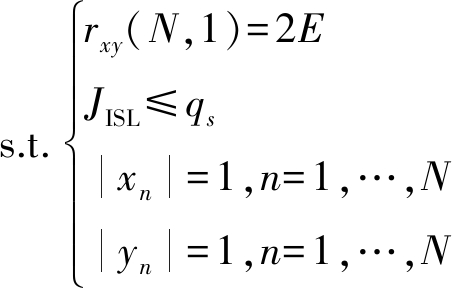
(21)
其中,E表示一个序列的总能量。该优化问题是非凸的,属于有约束非线性优化问题,本文同样采用优化工具选择内点法来对该问题进行优化。
4 仿真验证
本文进行仿真研究验证所提出用互补码方法设计稀疏频率雷达波形的有效性,本节将给出一些仿真结果。为方便和文献[10]中的方法进行对比,本文考虑相同的仿真环境,选择频率范围为[0,710]kHz的波形,设置五个阻带和六个通带,阻带范围分别为[30,150]、[160,180]、[200,260]、[280,350]、[370,400]kHz。在时域内设置信号的长度为N=143,脉冲持续时间为200 μs,奈奎斯特采样时间间隔为1.399 μs。该算法主要对优化问题(19)和(21)进行优化,本文通过使用MATLAB优化工具箱中的‘fmincon’函数来进行优化,其含义是寻找有约束的非线性规划问题的最小值,选择的优化算法是工具箱中的内点算法“inter-point”。
4.1 PSD阻带约束的稀疏频率波形设计
本小节将通过解决式(19)中的优化问题来验证所提出方法的第一个设计,对波形PSD阻带进行约束,验证用互补码方法设计稀疏频率波形是否能够降低旁瓣电平,比较波形x和y的ACF旁瓣电平JISL(x),JISL(y)与本文方法的旁瓣电平JISL(x,y),同时将该方法与文献[10]中所提方法进行比较。设置相同的比较条件,将波形的平均通带阻带功率比(APSPR)设置为相同的23.98 dB,即APSPR=20lg(Pp/Ps),其中Pp是通带平均功率,Ps是阻带平均功率。仿真得出:波形x的APSPR为23.99 dB,波形y的APSPR为23.97 dB,互补码波形的APSPR为23.98 dB,文献[10]中波形的APSPR为23.98 dB。输出波形的功率谱密度函数如图1(a)所示,对波形x和y的PSD阻带进行约束,得到本文互补码方法的稀疏频率雷达波形的PSD如图1(b)所示,与文献[10]方法相比其阻带功率较低。
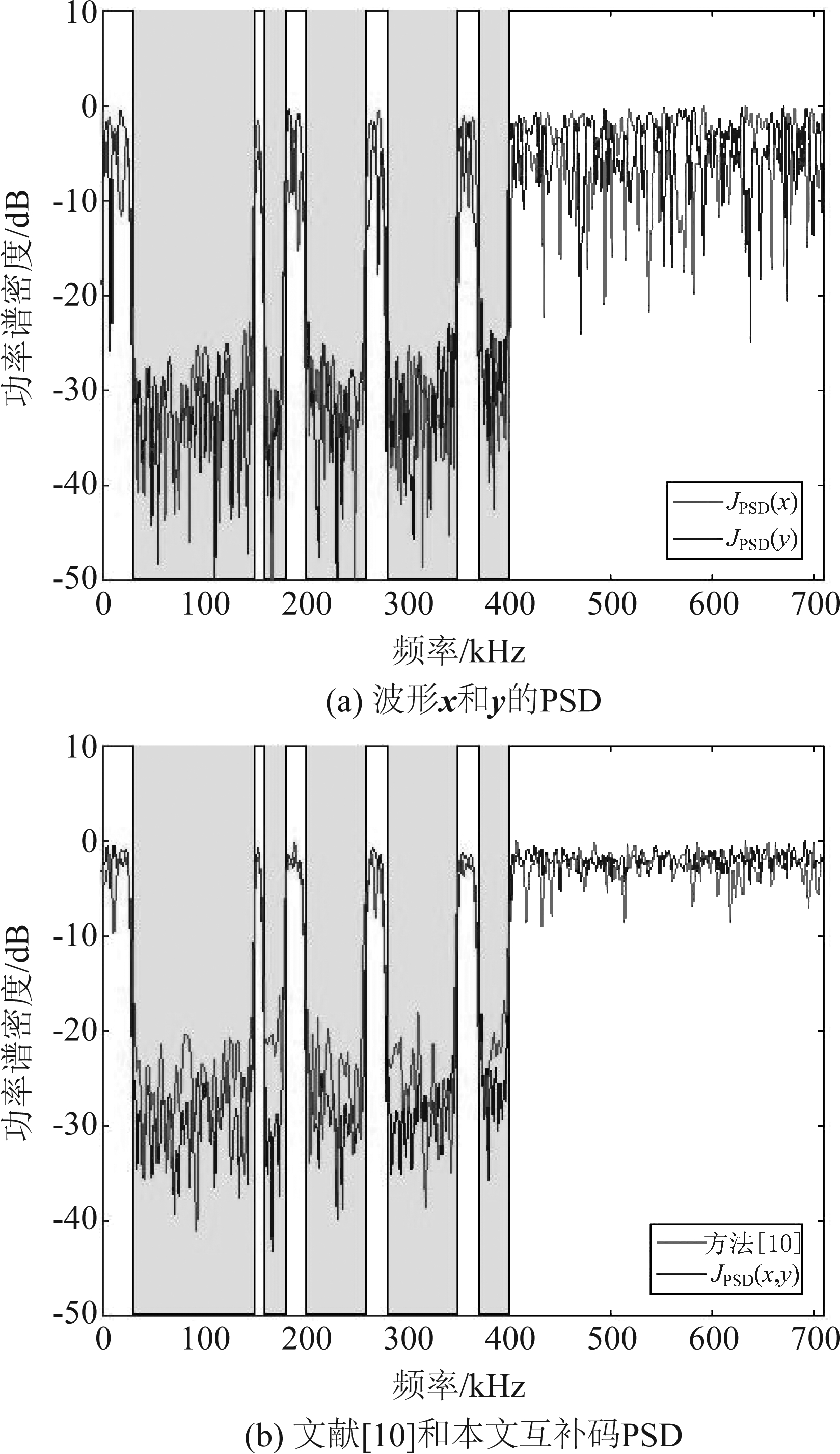
图1 阻带约束的PSD对比
Fig.1 PSD Performance Comparison of Stopband Constraint
输出波形的自相关函数如图2所示,其自相关函数的电平是以dB为单位的归一化值。图2(a)为波形x、y与本文互补码方法的ACF比较,JACF(x)、JACF(y)分别是波形x和y的自相关函数,JACF(x,y)是本文互补码方法设计的稀疏频率波形的自相关函数。通过横向比较可以看出用互补码方法设计出的稀疏频率波形比单独一个波形x或y具有更低的旁瓣电平。图2(b)为文献[10]与本文互补码方法的ACF比较,通过比较可以看出本文互补码方法比文献[10]方法具有更低的ACF旁瓣电平。
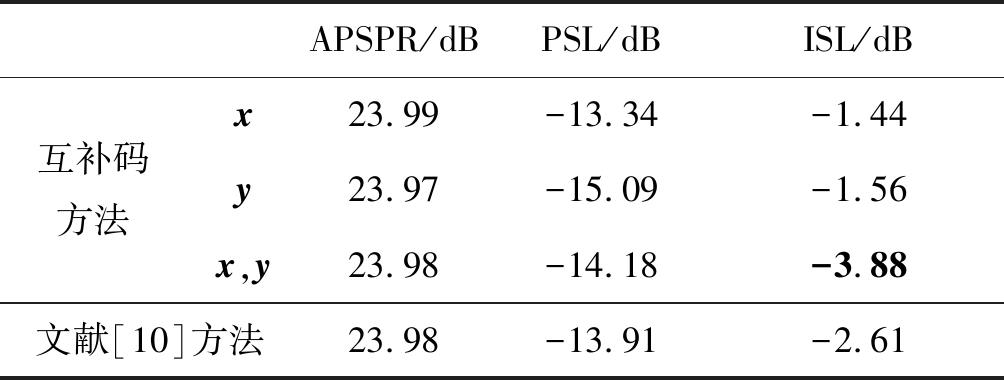
仿真得到的具体数值,波形x自相关函数的ISL为-1.44 dB,波形y自相关函数的ISL为-1.56 dB,互补码波形自相关函数的ISL为-3.88 dB,文献[10]中波形自相关函数的ISL为-2.61 dB。本文设计的方法虽不是专门抑制PSL,但此处也展示出其在本文设计中的性能,具体的数值如表1所示。由图2可以看出,本文所提出的方法抑制旁瓣的性能比文献[10]中的方法要好,其有更低的ISL和PSL,同时能够将阻带抑制到给定的水平。
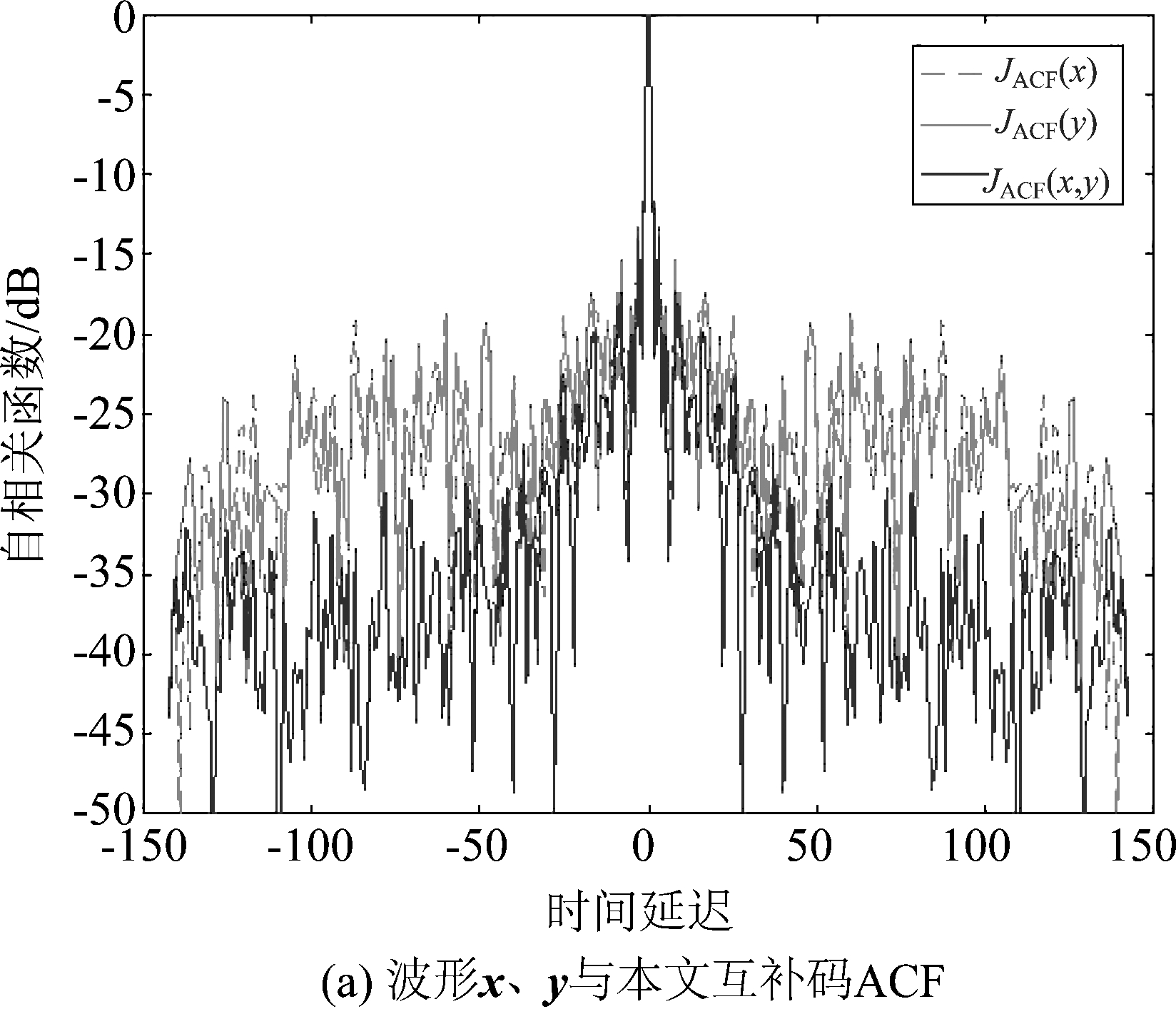
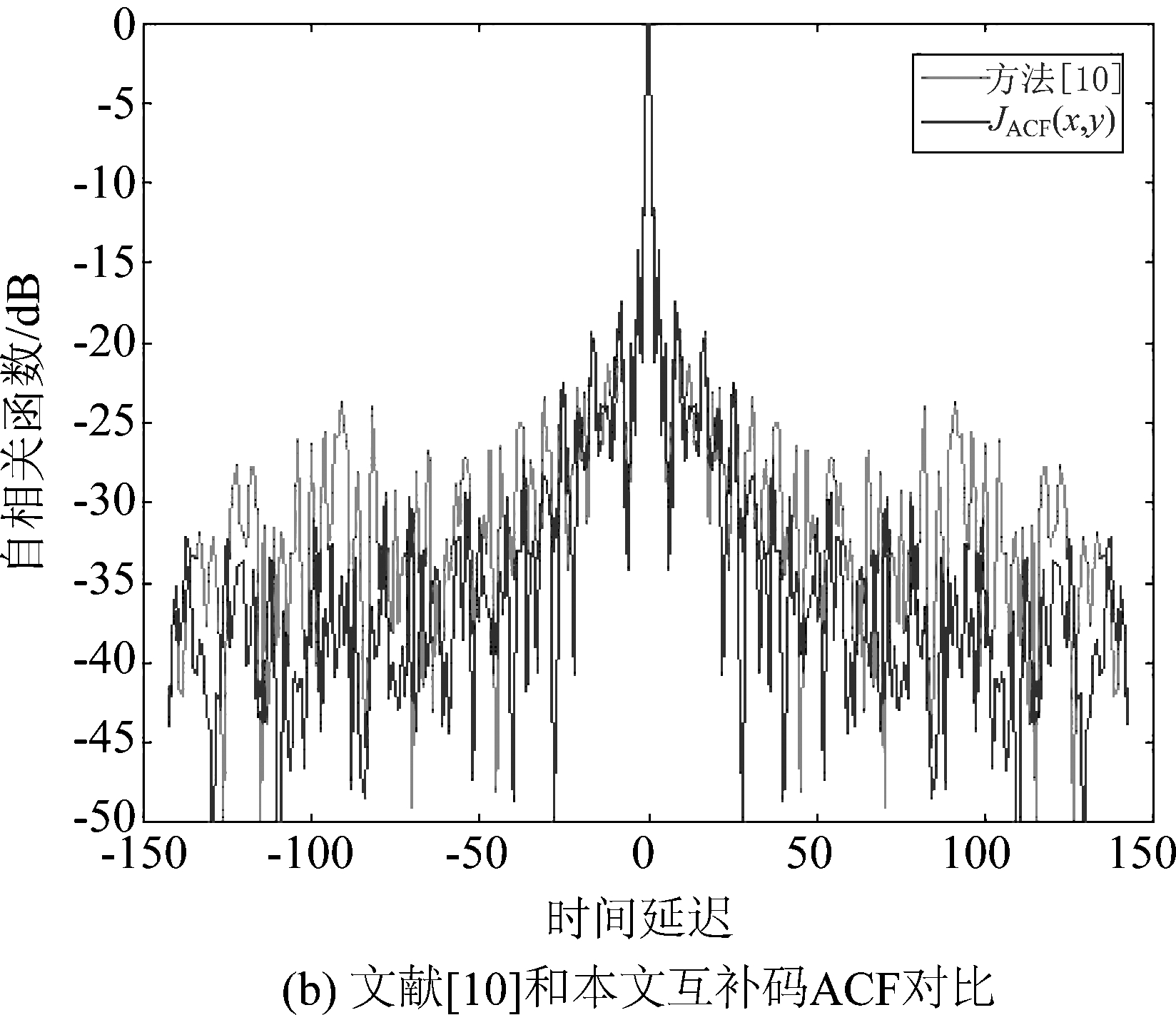
图2 阻带约束的ACF对比
Fig.2 ACF Performance Comparison of Stopband Constraint
表1 阻带约束的ACF和PSD比较
Tab.1 PSD and ACF performance comparisons of stopband Constraint
APSPR/dBPSL/dBISL/dB互补码方法xyx,y23.9923.9723.98-13.34-15.09-14.18-1.44-1.56-3.88文献[10]方法23.98-13.91-2.61
4.2 ACF旁瓣约束的稀疏频率波形设计
本小节通过解决式(21)中的优化问题来验证本文的第二个设计,对稀疏频率波形的旁瓣电平进行约束,获得具有阻带抑制的稀疏频率波形后,将本文提出的方法与文献[10]中的方法进行比较,两种方法的APSPR均设置为19.89 dB。经过仿真得到输出波形的PSD性能如图3所示。波形x的APSPR为20.45 dB,波形y的APSPR为19.39 dB,互补码波形的APSPR为19.89 dB,文献[10]中波形的APSPR为19.89 dB。

图3 旁瓣约束的PSD对比
Fig.3 PSD Performance Comparison of Sidelobe Constraint
结果波形的自相关函数如图4所示。其中,图4(a)为波形x、波形y与互补码的自相关函数;图4(b)是本文所提出方法与文献[10]中所提方法的ACF对比。由图可以看出,本文互补码方法设计的稀疏频率雷达波形具有更低的积分旁瓣电平。
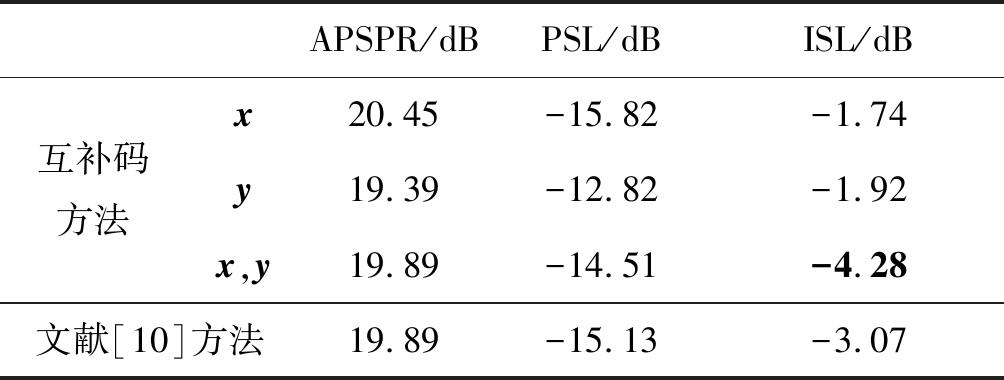
仿真得到的具体数值为:互补码波形自相关函数的ISL为-4.28 dB,文献[10]中波形自相关函数的ISL为-3.07 dB。此处也给出本文应用互补码设计稀疏频率波形的PSL性能,互补码波形自相关函数的PSL为-14.51 dB,文献[10]中波形自相关函数的PSL为-15.13 dB。表2将列出具体数值对仿真结果进行直接比较。
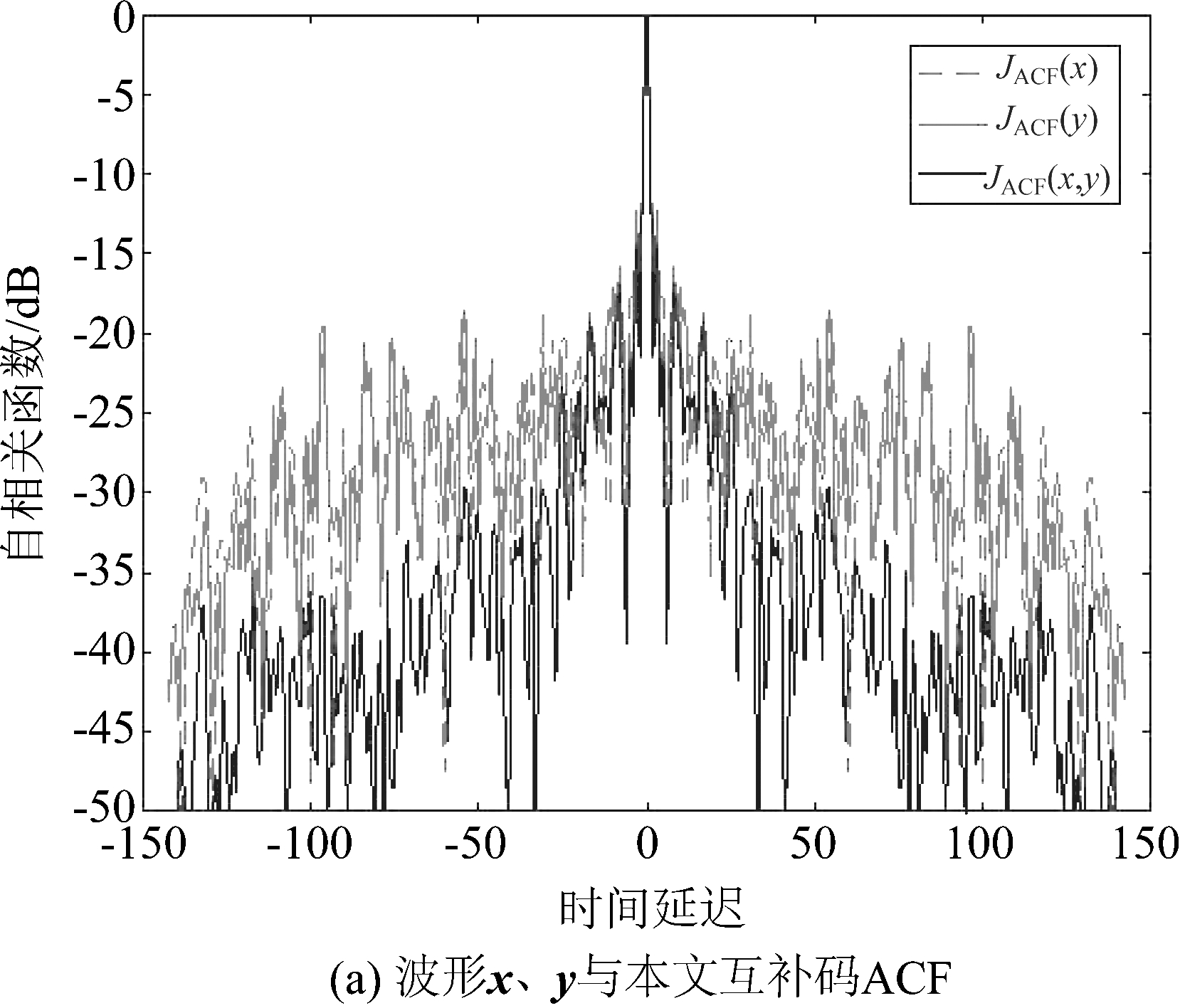
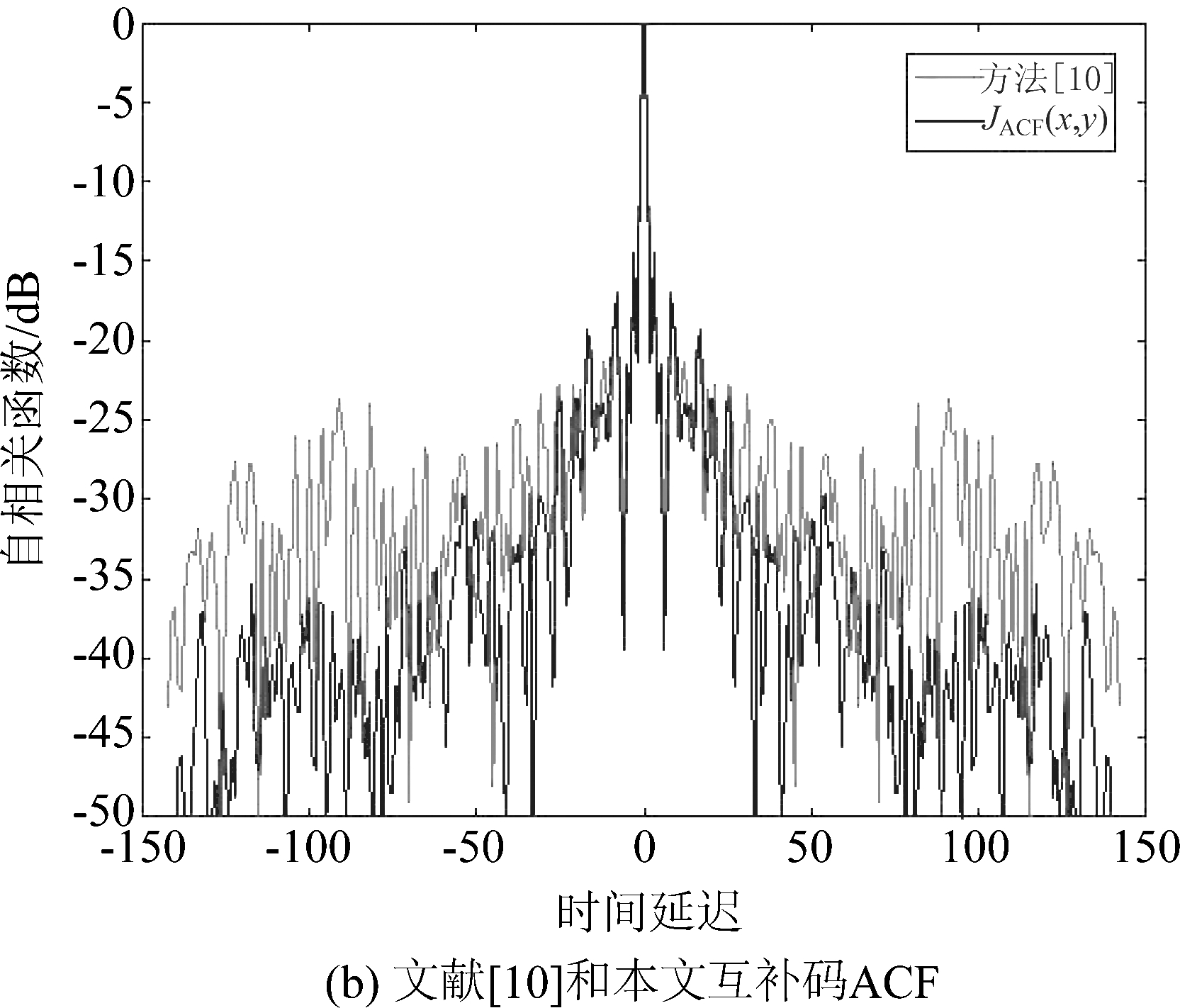
图4 旁瓣约束的ACF对比
Fig.4 ACF Performance Comparison of Sidelobe Constraint
表2 旁瓣约束的ACF和PSD性能比较
Tab.2 PSD and ACF Performance Comparisons of Sidelobe Constraint
APSPR/dBPSL/dBISL/dB互补码方法xyx,y20.4519.3919.89-15.82-12.82-14.51-1.74-1.92-4.28文献[10]方法19.89-15.13-3.07
5 结论
在频谱拥挤的情况下,稀疏频率波形是抑制同频干扰的一种解决方案。本文提出了一种互补码的稀疏频率波形设计方法。通过利用两个序列之间的互补性,可以更好地实现旁瓣抑制和阻带抑制的性能。在相同仿真环境下与其他方法对比,仿真结果验证了所提出方法的有效性。
[1] Lindenfeld M J. Sparse Frequency Transmit-and-Receive Waveform Design[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 851- 861.
[2] Wang Guohua, Lu Yilong. Bounds on Generalized Integrated Sidelobe Level in Waveforms with Stopbands[J]. Electronics Letters, 2010, 46(23): 1561-1562.
[3] Aubry A, Maio A De, Piezzo M, et al. Radar Waveform Design in a Spectrally Crowded Environment via Nonconvex Quadratic Optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1138-1152.
[4] Aubr A, Carotenuto V, Maio A De, et al. Optimization Theory-based Radar Waveform Design for Spectrally Environments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 31(12): 14-25.
[5] 麦超云, 孙进平, 周锐. MIMO 雷达方向图与稀疏频率波形联合设计[J]. 信号处理, 2016, 32(11): 1261-1268.
Mai Chaoyun, Sun Jingping, Zhou Rui. Joint Design of MIMO Radar Pattern and Sparse Frequency Waveform[J]. Journal of Signal Processing, 2016, 32(11): 1261-1268.(in Chinese)
[6] Mai Chaoyun, Lu Songtao, Sun Jingping, et al. Codesign of Beam Pattern and Sparse Frequency Waveforms for MIMO Radar[J]. International Journal of Antennas and Propagation, 2015: 1-12.
[7] Wang Guohua, Lu Yilong. Designing Single/Multiple Sparse Frequency Waveforms with Sidelobe Constraint[J]. IET Radar Sonar and Navigation, 2011, 5(1): 32-38.
[8] He Hao, Stoica P, Li Jian. Waveform Design with Stopband and Correlation Constraints for Cognitive Radio[C]∥IEEE International Workshop on Cognitive Information Processing. IEEE, 2010: 1- 4.
[9] Wang Guohua, Lu Yilong. Sparse Frequency Waveform Design Based on PSD Fitting[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2011: 22-27.
[10] Wang Guohua, Mai Chaoyun, Sun Jingping, et al. Sparse Frequency Waveform Analysis and Design Based on Ambiguity Function Thoery[J]. IET Radar Sonar and Navigation, 2016, 10(4): 707-717.
[11] 曲海山. 互补码设计及其在地波雷达中的应用[D]. 西安: 西安电子科技大学, 2010.
Qu Haishan. The Design of Complementary Codes and Its Application in Surface Wave Radar[D]. Xi’an. Xidian University, 2010.(in Chinese)
[12] Song Junxiao, Babu P, Palomar D. Sequence Set Design with Good Correlation Properties via Majorization-Minimization[J]. IEEE Transactions on Signal Processing. IEEE, 2016, 11(1): 2866-2879.
[13] Searle S, Howard S, Moran B. The Use of Complementary Sets in MIMO Radar[C]∥Conference on Signals, Systems and Computers. IEEE, 2009: 510-514.
[14] Levanon N. Noncoherent Radar Pulse Compression Based on Complementary Sequences[J]. IEEE Transactions on Aerospace and Electronic Systems. IEEE, 2009, 45(2): 742-747.
[15] Schmidt K. Complementary Sets Generalized Reed-Muller Codes and Power Control for OFDM[J]. IEEE Transactions on Information Theory. IEEE, 2007, 53(2): 808- 814.
[16] Garcia E, Garcia J, Urena J, et al. Multilevel Complementary Sets of Sequences and Their Application in UWB[C]∥International Conference on Indoor Positioning and Indoor Navigation (IPIN). IEEE, 2010: 1-5.
[17] Tseng S M, Bell M R. Asynchronous Multicarrier DS-CDMA using Mutually Orthogonal Complementary Sets of Sequences[J]. IEEE Transactions on Communications. IEEE, 2000, 48(1): 53-59.
[18] Spasojevic P, Georghiades C N. Complementary Sequences for ISI Channel Estimation[J]. IEEE Transactions on Information Theory. IEEE, 2001, 47(3): 1145-1152.
[19] 胡恒, 贺亚鹏, 庄珊娜. 高频地波雷达稀疏频率波形优化设计[J]. 电子与信息学报, 2012, 34(6): 1291-1296.
Hu Heng, He Yapeng, Zhuang Shanna. Sparse Frequency Waveform Design for High Frequency Surface Wave Radar[J]. Journal of Eleotronice and Information Technology, 2012, 34(6): 1291-1296.(in Chinese)


