1 引言
空时自适应处理(Space-Time Adaptive Processing, STAP)是用于杂波背景中动目标检测的关键技术。在STAP中,需要估计待检测距离单元的杂波协方差矩阵(Clutter Covariance Matrix, CCM)。传统的STAP方法使用待检测距离单元附近距离单元的训练样本来估计CCM。根据STAP理论[1],要准确估计CCM,训练样本须满足以下条件:(1)所有的训练样本独立同分布;(2)为使估计杂波协方差矩阵带来的杂波抑制性能损失小于3 dB,训练样本数至少为2倍系统自由度;(3)所有训练样本必须不包含目标信号。然而,实际环境中杂波分布往往是非均匀的,使得用于估计杂波协方差矩阵的训练样本数很难满足要求,从而导致估计的CCM不准确,杂波抑制性能严重下降。
作为机载雷达最有效的杂波抑制手段,STAP技术已由单输入多输出(Single-Input Multiple-Output, SIMO)雷达拓展到了多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达[2]。相比SIMO-STAP,MIMO-STAP可以实现更窄的杂波凹口,提升最小可探测速度性能,提高多普勒分辨率,并且更能降低杂波水平[3- 4]。近年来,稀疏恢复技术被应用到STAP中,与传统的STAP算法相比,稀疏恢复算法可在训练样本数较少的情况下精确地估计出杂波谱[5]。基于贝叶斯学习(SBL)的稀疏恢复算法[6]在杂波满足一定概率分布的前提下可恢复出精确的杂波谱,但如果杂波实际的概率分布模型与假设的概率分布模型存在偏差,该方法的性能就会严重下降。OMP算法[7]通过不断挑选与残差矢量相关性最大的原子进入支撑集,从而不断减小残差,直到残差小于门限值。该算法简单、高效,但因为原子间相关性较强,导致该算法恢复效果并不理想。正则化FOCUSS算法[8]也可以用于杂波谱的稀疏恢复,但是该算法需要设定恰当的超参数,才能获得较好的性能,而实际上超参数的设定往往不易把握。因此,亟需寻求一种恢复精确度高且使用方便的稀疏算法来恢复杂波谱。
为解决上述问题,本文引入一类更有效的稀疏恢复算法,即加权SPICE(Sparse Iterative Covariance-based Estimation)算法[9]。该算法不需要考虑杂波的先验分布模型,且不需要设置任何超参数,使用十分方便。仿真结果表明,加权SPICE算法能够获得较好的恢复精度,得到的空时二维滤波器能够有效地抑制杂波。
2 杂波谱稀疏恢复问题建模
2.1 MIMO雷达杂波信号模型
考虑均匀线阵体制机载MIMO雷达在正侧视条件下的杂波模型。设MIMO雷达发射的各波形满足正交关系,通过匹配滤波,可以在接收端分离出各个发射阵元信号。设线阵天线中发射阵元个数为M,接收阵元个数为N,1个相干处理间隔内发射K个脉冲,脉冲重复频率为fr,发射波长为λ,发射阵元间距和接收阵元间距分别为dt和dr(一般为避免栅瓣问题,取dr=λ /2)。
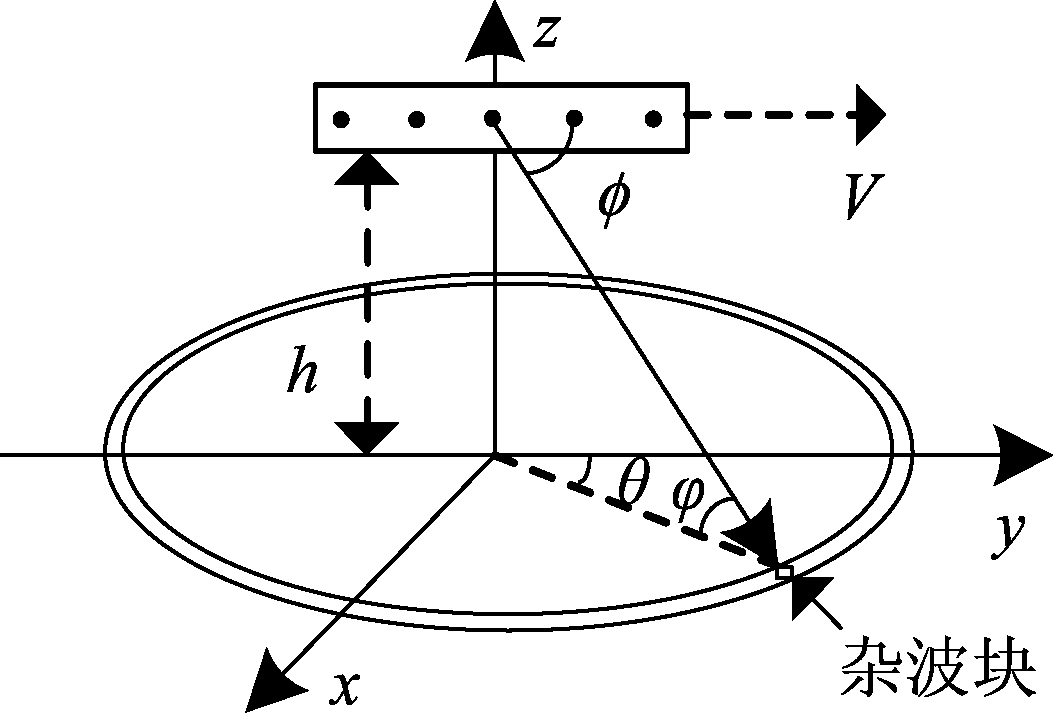
图1 机载MIMO雷达几何模型
Fig.1 Geometric model of airborne MIMO radar
如图1所示,每个距离环都可切分为多个杂波块,φ为杂波块的俯仰角,θ为杂波块的方位角,φ为线阵方向与杂波块方向所成的空间锥角。V为载机速度,h为载机距离地面的高度。
设第l个距离环俯仰角为φl,将其均匀切分为Nc个杂波块,其中第p个杂波块的方位角为θp。设fs表示杂波块对应的空间频率, fd表示杂波块对应的多普勒频率,则杂波块对应的空时导向矢量可表示为
v(fd, fs)=vd(fd)⊗vt(fs)⊗vr(fs)
(1)
其中⊗表示Kronecker积;vt为发射导向矢量,vr为接收导向矢量,vd为时域导向矢量。发射和接收导向矢量分别为
vt(fs)=[1 ej2πγfs…ej2π(M-1)γfs]T
(2)
vr(fs)=[1 ej2πfs…ej2π(N-1)fs]T
(3)
其中γ为发射阵元间距与接收阵元间距之比;第p个杂波块的空间频率与θp、φl关系式为fs(θp,φl)=drcos(θp)cos(φl)/λ。
时域导向矢量为
vd(fd)=[1 ej2πfd…ej2π(K-1)fd]T
(4)
其中第p个杂波块的多普勒频率与θp、φl关系式为fd(θp,φl)=2Vcos(θp)cos(φl)/(λfr)。
则可将第l个距离环对应的杂波表示为
(5)
其中σp为第p个杂波块的回波幅度, fs,p为第p个杂波块的空间频率, fd,p为第p个杂波块的多普勒频率。
2.2 MIMO雷达杂波谱的稀疏恢复模型
一般情况下,为得到稀疏恢复所需的字典,需将整个空时二维平面网格化,将所有网格节点对应的空时导向矢量取出组成超完备字典ψ。设Q=NM,将空时二维平面空间频率和多普勒频率分别离散为Ns格和Nd格,Ns=ρsQ,Nd=ρdK,其中ρs和ρd分别为fs和fd的离散化系数。字典ψ的大小取决于ρs和ρd,但目前ρs和ρd尚没有明确的最优值,只能结合具体问题给出经验化的取值。
杂波分布在空时二维平面上具有稀疏性[10],可由超完备字典近似表示为
(6)
其中v(fd,i, fs,j)表示空时二维平面上空间频率为fs,j,多普勒频率为fd,i时所对应的空时导向矢量;σ为待求的稀疏参数矢量。
基于稀疏恢复的STAP方法关键在于估计空时功率谱P。空时功率谱的求解可以分为两种思路[11]:(1)先使用训练样本恢复σ,再由σ估计P;(2)直接由最大似然估计的协方差矩阵估计P。数学上,前一种思路具体可表述为
(7)
(8)
其中y为不含目标信号的观测信号矢量;ε为误差范围值;
与
互为共轭。
现有的已用于STAP的稀疏恢复方法大都是第一种思路,第二种思路可表述为
(9)
其中RML为杂波样本协方差矩阵的最大似然估计;(·)*表示共轭转置。
加权SPICE算法是一种基于协方差矩阵直接求解杂波空时功率谱P的算法,其使用的就是第二种思路。
3 加权SPICE 算法
3.1 加权SPICE算法的基本框架
加权SPICE算法建立在统一的框架之上。为获得加权SPICE算法的基本框架,需先对SPICE[12]进行分析,具体如下:
机载MIMO雷达观测信号可以表示为
y=ψ σ+e
(10)
其中e表示噪声矢量。观测信号矢量y对应的协方差矩阵为:
R=E[yy*]
=E[(ψ σ+e)(ψ σ+e)*]
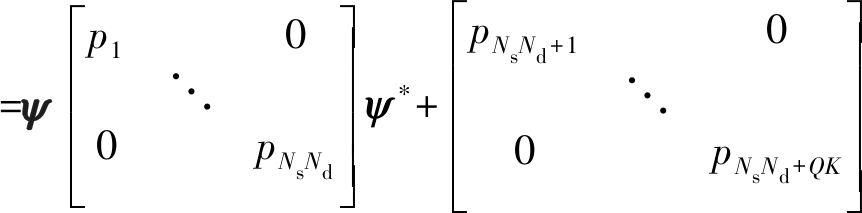
=APA*
(11)
其中A=[ψ IQK],将A以列向量的形式进行划分则可以得到A=[a1a2 … aNsNd+QK];P=diag(p),其中p=[p1,…,pNsNd+QK]T,p中第(NsNd+1)到(NsNd+QK)项表示噪声功率。
由式(11)可以看出,协方差矩阵R是关于{pk}的函数,SPICE算法可以通过最小化以下目标函数估计{pk}:
(12)
将式(12)中常数项忽略,且除以
可将目标函数转化为
(13)
令c=1/‖y‖2,则{pk}的求解转化为以下式子的求解:
(14)
对{pk}进行统一缩放,将式(14)转化为以下式子:
(15)
其中
与
关系式为
将式(15)中的
替换为p,并将其换一种表示形式,则{pk}的求解问题最终转化为:
(16)
其中第二项为控制稀疏度的惩罚项,惩罚项中{wk}为加权系数。当通过式(16)求得{pk}后,可通过统一的缩放关系求得式(12)中最起始的{pk}。
式(16)即为加权SPICE算法的基本框架,SPICE、LIKES、SLIM和IAA算法的区别可以归结为加权系数{wk}不同。当加权系数为式(13)中的加权系数时,式(16)即为SPICE算法的目标求解式。当惩罚项中加权系数为其他时,可得到此框架下LIKES[13]、SLIM和IAA算法的目标求解式。其中,LIKES算法的加权系数为
算法的加权系数为
算法的加权系数为
3.2 加权SPICE算法的求解
式(16)中的问题可以用梯度下降法进行求解,具体求解过程如下:
首先,式(16)关于pk求导可得
(17)
则第(i+1)次的迭代关系式为
(18)
其中
表示由
所求得的协方差矩阵;
为梯度下降法所取的步长,步长可取不同值。
其中第一种步长为
(19)
第二种步长为
(20)
若取第一种步长,则第(i+1)次的迭代关系式可进一步表示为:
(21)
若取第二种步长,则第(i+1)次的迭代关系式可进一步表示为:
(22)
LIKES、SLIM和IAA算法可根据步长的不同最终可分别得到两个版本的迭代关系式。
LIKES加权系数为
将其中的
用
替换,且当取第一种步长时,得迭代关系式版本a为
(23)
当取第二种步长时,得迭代关系式版本b为
(24)
LIKES算法具体迭代步骤为:(1)设定变量l起始值为0,m为一个周期内的迭代次数,确定起始值
使用相应的迭代关系式进行迭代,i在一个周期内取值变化为i=l,l+1,…,l+m-1,在此周期内
维持固定值,即加权系数维持固定值;(3)判断每次迭代结果是否满足停止条件。若满足,则停止迭代,输出
若不满足,迭代m次跳出该周期后,进入新周期,将l值更新为l+m,同时更新
返回步骤(2)。
SLIM加权系数为
当取第一种步长时,得迭代关系式版本a为
(25)
当取第二种步长时,得迭代关系式版本b为
(26)
IAA加权系数为
将其中的用替换,且当取第一种步长时,得迭代关系式版本a为
(27)
当取第二种步长时,得迭代关系式版本b为
(28)
SLIM算法和IAA算法迭代步骤一致,具体为:(1)设定迭代起始值使用相应的迭代关系式进行迭代;(3)判断是否满足停止条件。若满足,则停止迭代,输出若不满足,则更新
返回步骤(2)进入下一次迭代。
3.3 计算复杂度分析
将各加权SPICE算法和SBL算法、正则化FOCUSS算法、OMP算法的计算复杂度进行比较,计算复杂度的大小以使用单个训练样本进行求解所需复数乘法的次数作为衡量标准。
如表1所示,其中KLIKES、KIAA、KSLIM分别表示LIKES、IAA、SLIM算法的迭代次数,且设LIKES算法迭代总次数为其迭代周期的n倍;SBL采用的是EM迭代寻优算法,KSBL表示SBL算法的迭代次数;KFOC表示FOCUSS算法的迭代次数;KOMP表示OMP算法的迭代次数,rs表示OMP算法的稀疏度。
由表1可知,在各算法迭代次数相同的前提下,因为NsNd远大于MNK,故而LIKES、IAA、SLIM算法运算复杂度小于SBL和FOCUSS算法,而OMP算法因为存在稀疏度rs的限制,其运算复杂度小于各加权SPICE算法。加权SPICE算法中SLIM运算复杂度最小,其次为LIKES,最大的为IAA算法。因此,从计算复杂度这点来讲,各加权SPICE算法虽然次于OMP,但却优于SBL和FOCUSS算法,在计算复杂度方面具有一定优势。
表1 计算复杂度比较
Tab.1 Comparison of the computational complexity
算法计算复杂度LIKESO(((MNK)3+2(MNK)2NsNd+MNKNsNd)KLIKES+MNKNsNdn)IAAO(((MNK)3+2(MNK)2NsNd+2MNKNsNd)KIAA)SLIMO(((MNK)3+(MNK)2NsNd+(MNK)2+MNKNsNd)KSLIM)SBLO((MNK(NsNd)2+(MNK)3+2(MNK)2NsNd+(NsNd)2+2MNKNsNd)KSBL)FOCUSSO(((MNK)3+2(MNK)2NsNd+(NsNd)2+2MNKNsNd)KFOC) OMPO(((MNK(rs)2+(rs)3+(MNK)2rs+MNKNsNd+2MNKrs)KOMP)
4 仿真实验
LIKES、SLIM和IAA算法都有两个版本的迭代关系式,为方便后续仿真分析,全部选取a版本进行仿真实验。
仿真条件:飞机在空中匀速直线飞行,其飞行速度V为140 m/s;天线为发射阵元数为4,接收阵元数为4的均匀线阵,其发射阵元间距和接收阵元间距都为半波长,波长为0.8 m;一个相干处理间隔内脉冲数为8,脉冲重复频率为700 Hz;距离环独立杂波源个数Nc为361,杂噪比为50 dB;训练样本数为6。
仿真实验中,各算法具体参数设置如下:LIKES、SLIM、IAA迭代停止条件均为
SBL算法[6]停止条件为
算法[8]取0.8范数,设置的正则化参数为0.02,停止条件为
算法[7]稀疏度设置为36。
4.1 字典维数大小对输出SINR的影响
所有稀疏算法的恢复性能都与字典维数密切相关,加权SPICE算法也不例外。为评估字典维数大小对加权SPICE算法恢复精度的影响,采用输出信干噪比(SINR)作为衡量基准。SINR (无有源干扰时)定义为输出信号与输出杂波加噪声信号能量的比值,具体表示为
(29)
其中vt为目标信号矢量,RI为杂波协方差矩阵与噪声协方差矩阵之和。
图2中各SINR曲线均为100次蒙特卡罗实验所得。由图2可以看出,LIKES、SLIM、IAA算法随着字典维数的不断增大,其输出SINR性能不断提升,当字典维数NsNd大于8MNK后,再继续增加字典维数,输出SINR性能提升不再明显,三种算法的输出SINR性能基本达到最佳。因此,后续仿真字典维数NsNd取8MNK,即ρs取2,ρd取4。这使得在保证加权SPICE算法能够达到较好输出SINR性能的同时,尽可能地降低计算量。
4.2 杂波空时二维谱比较
理想条件下,将SLIM、IAA和LIKES与SBL、FOCUSS以及OMP估计生成的杂波谱进行比较。
由图3可以看出,SLIM、SBL算法恢复出的杂波谱均匀连续分布于杂波脊线,最接近由已知CCM得到的精确杂波谱。LIKES和IAA算法恢复出的杂波谱部分区域略有展宽,但恢复效果总体不错。FOCUSS算法恢复的杂波谱略有展宽,总体恢复效果不够理想。OMP算法恢复出的杂波谱部分区域能量分布过离散,恢复效果较差。可以看出,SLIM、IAA和LIKES算法恢复出的杂波谱精度较高,在恢复精度上比较占有优势。
4.3 输出SINR比较
考虑三种场景来模拟现实环境:(1)理想情况下,每个训练样本的杂波信号独立生成,杂波块的复振幅为满足复高斯分布的独立随机变量;(2)存在时域非理想因素,主要考虑杂波内部起伏(ICM),采用Ward提出的ICM模型[14]。模型的时间自相关函数服从以下分布:
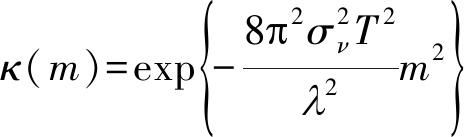
(30)
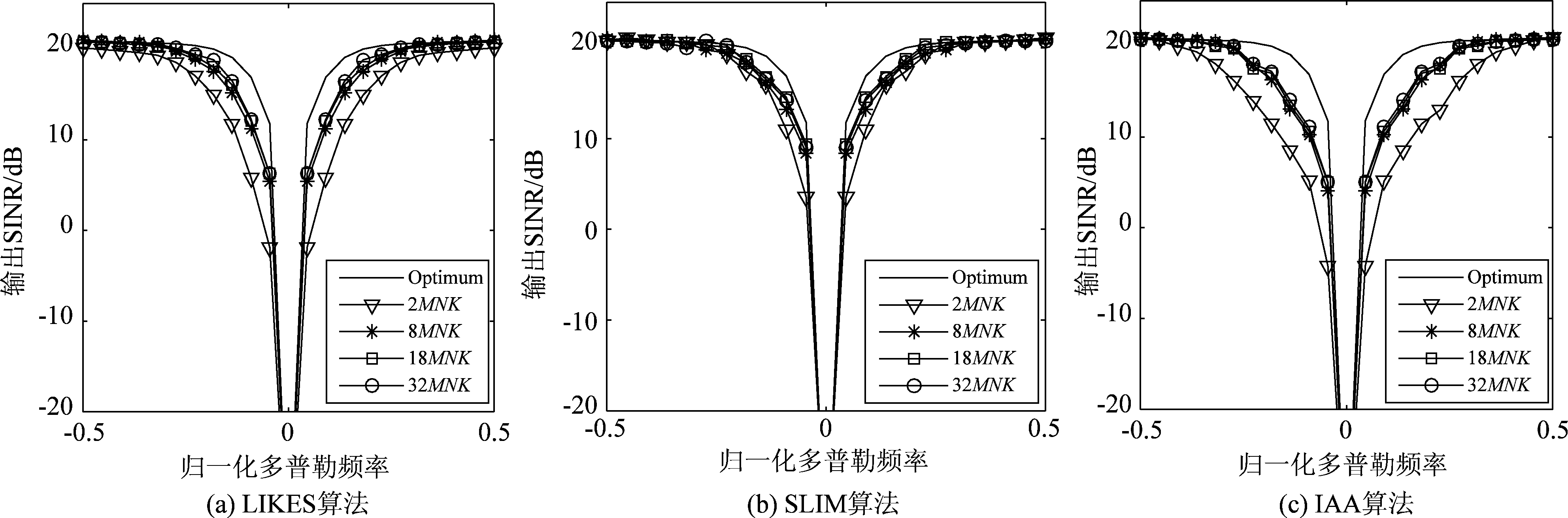
图2 不同字典维数的输出SINR曲线
Fig.2 Output SINR curves with different dictionary dimensions
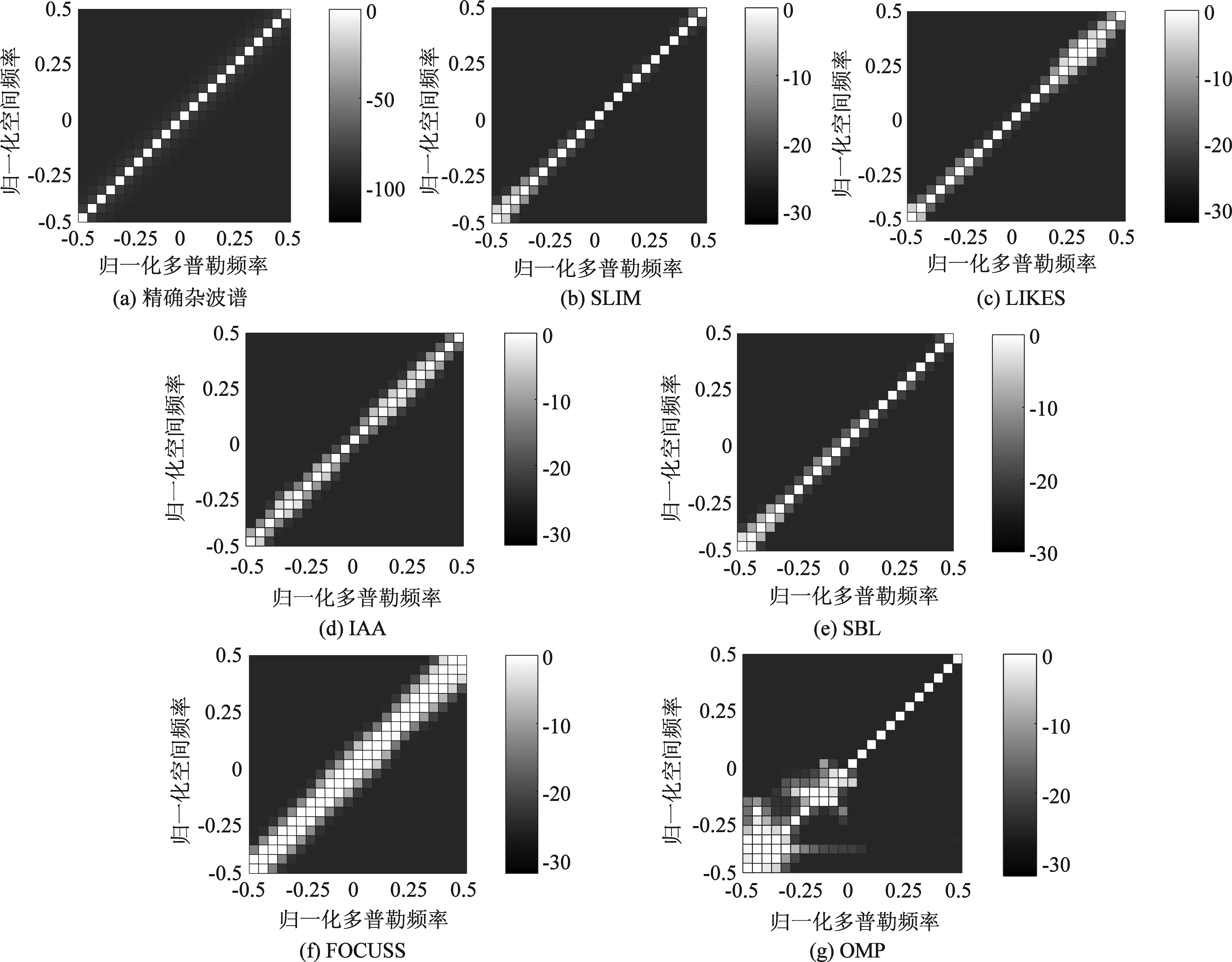
图3 各算法估计的杂波谱
Fig.3 The clutter spectrum estimated by each algorithm
其中σν为速度标准偏移量,设置为0.3。
(3)存在空域非理想因素,主要考虑角度独立的阵列误差。假设阵列误差的幅度和相位均为窄带模型[14],且幅度误差和相位误差分别服从以下均匀分布:
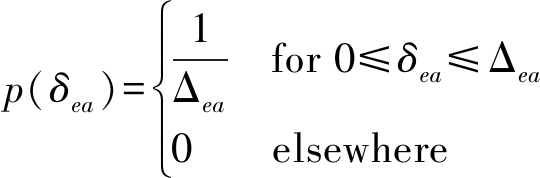
(31)
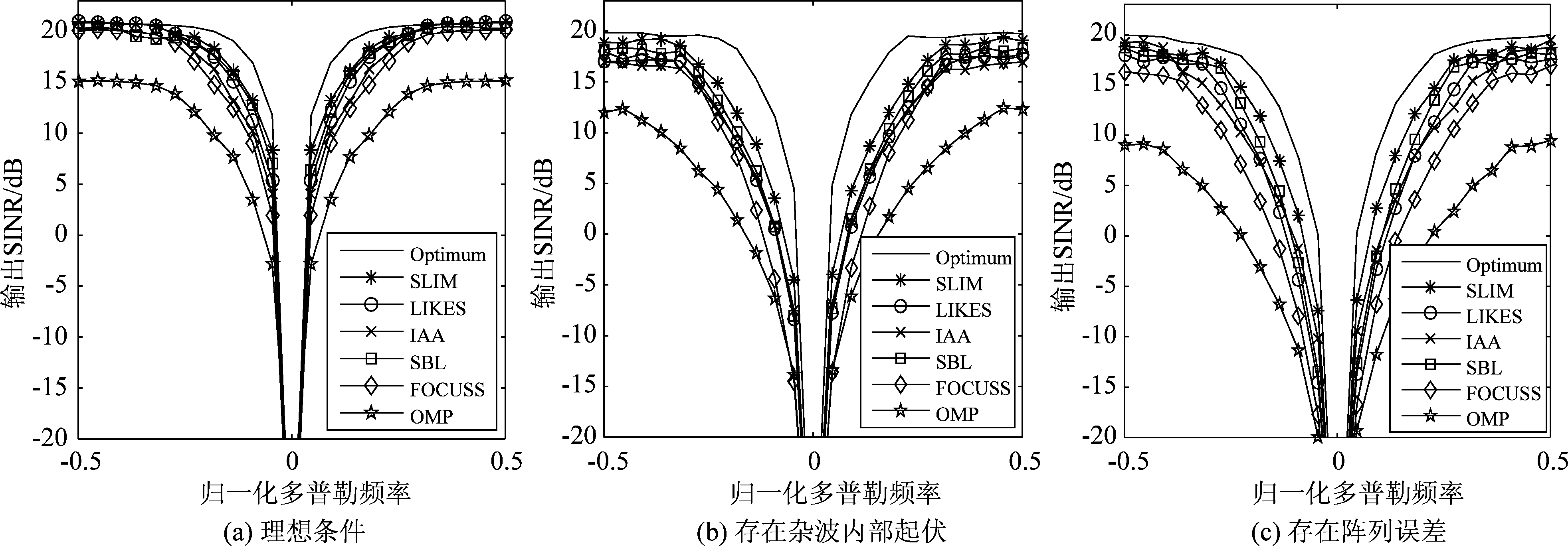
图4 输出SINR比较
Fig.4 Comparison of the output SINR
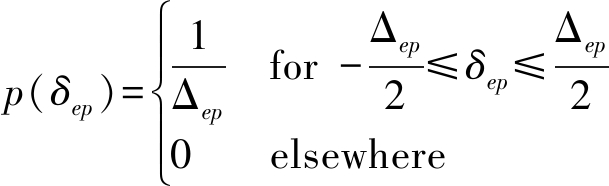
(32)
设置Δea为0.02,Δep为2°。
图4中各SINR曲线均为100次蒙特卡罗实验所得。由图4(a)可以看出,在理想条件下,SLIM算法和SBL算法的输出SINR性能最优,对应凹口展宽程度最小。LIKES算法性能略次于SLIM和SBL,IAA算法性能略次于LIKES。各加权SPICE算法输出SINR性能都优于FOCUSS算法。OMP算法相比其他所有对比算法性能最差,对应凹口展宽程度最大。由图4(b)和4(c)可以看出,在非理想条件下,杂波谱的展宽导致各算法输出SINR曲线凹口相应展宽。此时,SLIM算法性能最优,LIKES、IAA算法性能在非理想条件下与SBL算法比较接近,但却明显优于FOCUSS算法,OMP算法性能依旧最差。显然,SLIM、LIKES和IAA算法与其他稀疏算法相比有着较好的输出SINR性能,且在非理想条件下,其恢复性能依旧较好。
4.4 距离向输出功率
在存在杂波内部起伏的条件下,用各算法生成的空时滤波器对不同距离门的信号进行滤波。图5给出了各算法从第110到150距离门的输出功率曲线,其中目标处在第130距离门,其空间频率为0,归一化多普勒频率为0.15。由图5可以看出,SLIM算法最能探测到目标,其在非检测距离单元的输出功率比SBL算法低3 dB左右。LIKES、IAA以及SBL算法都能够明显检测出目标,非检测距离单元的输出功率比FOCUSS算法低2 dB左右。FOCUSS算法也能检测出目标,但检测效果相对较差。OMP算法并不能检测到目标,其目标信号完全淹没于杂波信号。由此可得,SLIM、LIKES和IAA算法的杂波恢复精度较高,得到的空时滤波器能够有效抑制杂波,从而实现动目标检测。
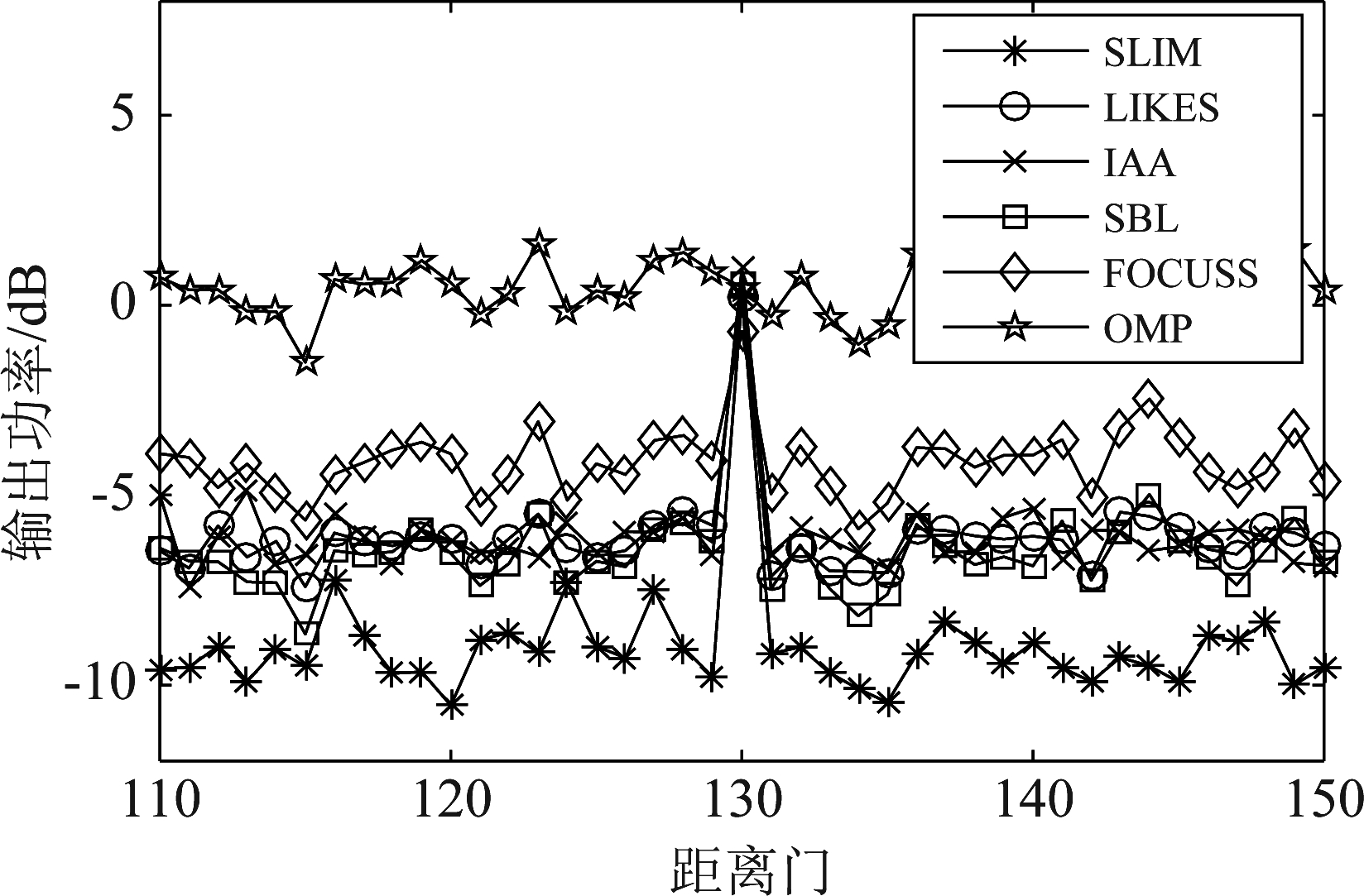
图5 距离向输出功率
Fig.5 Output power at different range cell
5 结论
本文为解决机载MIMO雷达STAP技术在非均匀杂波条件下杂波抑制性能严重下降的问题,引入了加权SPICE算法用于杂波谱的稀疏恢复。在该统一框架下的SLIM、LIKES和IAA算法不需要像SBL算法考虑杂波的先验分布模型,也不需要像FOCUSS算法考虑超参数的设置问题,实际操作十分简便,可以较好地解决MIMO-STAP杂波抑制问题。仿真实验表明,SLIM、LIKES和IAA等加权SPICE算法能够精确地恢复出杂波谱,在理想条件下和非理想条件下都有着较好的输出SINR性能,在稀疏算法中性能相对较优,得到的空时二维滤波器杂波抑制性能良好,能够较好地实现动目标检测。
[1] Reed I S, Mallett J D, Brennan L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974(6): 853- 863.
[2] 王洪雁, 裴炳南. 非完备杂波先验知识场景下MIMO-STAP稳健波形设计[J]. 信号处理, 2015, 31(11): 1418-1424.
Wang Hongyan, Pei Bingnan. Robust Waveform Design for MIMO-STAP in the Case of Imperfect Clutter Prior Knowledge[J]. Journal of Signal Processing, 2015, 31(11): 1418-1424.(in Chinese)
[3] Tang B, Li J, Zhang Y, et al. Design of MIMO radar waveform covariance matrix for clutter and jamming suppression based on space time adaptive processing[J]. Signal Processing, 2016, 121: 60- 69.
[4] Tang B, Tang J. Joint design of transmit waveforms and receive filters for MIMO radar space-time adaptive processing[J]. IEEE Transactions on Signal Processing, 2016, 64(18): 4707- 4722.
[5] Yang Z, Li X, Wang H, et al. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity[J]. Iet Signal Processing, 2016, 10(2): 150-161.
[6] Wipf D P, Rao B D. Sparse Bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164.
[7] Zhang T. Sparse recovery with orthogonal matching pursuit under RIP[J]. IEEE Transactions on Information Theory, 2011, 57(9): 6215- 6221.
[8] Rao B D, Engan K, Cotter S F, et al. Subset selection in noise based on diversity measure minimization[J]. IEEE Transactions on Signal Processing, 2003, 51(3): 760-770.
[9] Stoica P, Zachariah D, Li J. Weighted SPICE: A unifying approach for hyperparameter-free sparse estimation[J]. Digital Signal Processing, 2014, 33: 1-12.
[10] 阳召成, 黎湘, 王宏强. 基于空时功率谱稀疏性的空时自适应处理技术研究进展[J]. 电子学报, 2014, 42(6): 1194-1204.
Yang Zhaocheng, Li Xiang, Wang Hongqiang. An Overview of Space-Time Adaptive Processing Technology Based on Sparsity of Space-Time Power Spectrum[J]. Acta Electronica Sinica, 2014, 42(6): 1194-1204.(in Chinese)
[11] 阳召成. 基于稀疏性的空时自适应处理理论和方法[D]. 长沙: 国防科学技术大学, 2013.
Yang Zhaocheng. Theory and Methods of Sparsity-Based Space-Time Adaptive Processing[D]. Changsha: National University of Defense Technology, 2013.(in Chinese)
[12] Stoica P, Babu P, Li J. SPICE: A Sparse Covariance-Based Estimation Method for Array Processing[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 629- 638.
[13] Petre Stoica, Prabhu Babu. SPICE and LIKES: Two hyperparameter-free methods for sparse-parameter estimation[J]. Signal Processing, 2012, 92(7): 1580-1590.
[14] Duan K, Liu W, Duan G, et al. Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP[J]. Iet Radar Sonar & Navigation, 2018, 12(5): 557-564.
