1 引言
进一步提升5G通信系统性能的首要技术方向是提高系统频谱效率,而大规模MIMO成为最有力的关键技术之一[1]。为了更好地利用大规模阵列增益优势,基站(Base Station,BS)端需要获取准确的信道状态信息(Channel Status Information,CSI)[2]。然而CSI的获取需要消耗大量的导频开销,尤其是对于频分双工(Frequency Division Duplex,FDD)大规模MIMO系统,因此对于下行链路的信道估计方法的研究尤为重要。
在大规模MIMO系统中信道信息为高维矩阵,需进行降维处理。研究表明,传播环境中重要散射体数量有限,基站端共址天线具有固有的时间相关性,大规模MIMO系统的信道脉冲响应(Channel Impulse Response,CIR)呈现结构化稀疏性[3]。压缩感知理论(Compressive Sensing Theory,CST)能够以远低于Nyquist要求的采样速率恢复原始信号,借助CS理论和大规模MIMO信道的稀疏性,可较大幅度减少信道估计的导频开销。依据这一事实,文献[4]利用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法来估计大规模MIMO-OFDM系统中的CIR,与传统的最小二乘(Least Squares,LS)方法相比可以减少导频开销。另外,对于不同BS天线与用户之间的CIR具有共同稀疏性的情况,在[5]中将大规模MIMO系统中的信道估计问题转化为联合稀疏信号恢复问题,并分析了等效传感矩阵的块相干性,提出了块优化的正交匹配追踪(Block-optimized Orthogonal Matching Pursuit,BOOMP)算法以进一步提高信道估计性能。
针对大规模MIMO-OFDM系统中的大维数据,许多文献利用CIR的固有稀疏性来降低导频开销。文献[6]提出一种压缩感知辅助的信道估计方案,同时利用LS和CS技术,进一步减少所需的导频开销。然而,在实际通信系统中,很难获得信道的先验知识。因此文献[7]提出一种稀疏自适应的压缩感知信道算法,可以在信道稀疏性未知的情况下快速恢复信道状态信息。在文献[8]中提出块贝叶斯稀疏信道估计方法,利用信道的块稀疏相关性,比传统的稀疏频道估计方法有效,但复杂度较高。
为进一步减少频分双工大规模MIMO系统多用户的下行链路信道估计的导频开销,本文提出一种称为基于时间相关和多测量矢量模型的块贝叶斯压缩感知的信道估计算法(Block Bayesian Compressed Sensing channel estimation based on Time-dependent and Multi-measurement vector models,TMBB-CS)。因为实际信道的稀疏度是未知的,利用贝叶斯算法得到信道的先验信息,从而获得信道的稀疏信息,又因为信道矩阵的非零行存在时间相关性,信道是时间相关稀疏的,利用该特性,可以在欠采样条件下压缩感知信道的状态信息。仿真结果表明,所提出的TMBB-CS算法能够显著降低信道估计的导频开销,且具有较强的鲁棒性。
符号说明:⊗表示Kronecker积;
表示定义符;黑色粗体表示向量或矩阵;vec(·)表示向量化;diag(·)表示对角矩阵。
2 系统模型
2.1 信道模型
FDD频分双工大规模MIMO系统如图1所示,其中基站端(BS)有M(M>100)根天线,用户端(US)有K个用户且均为单天线用户。
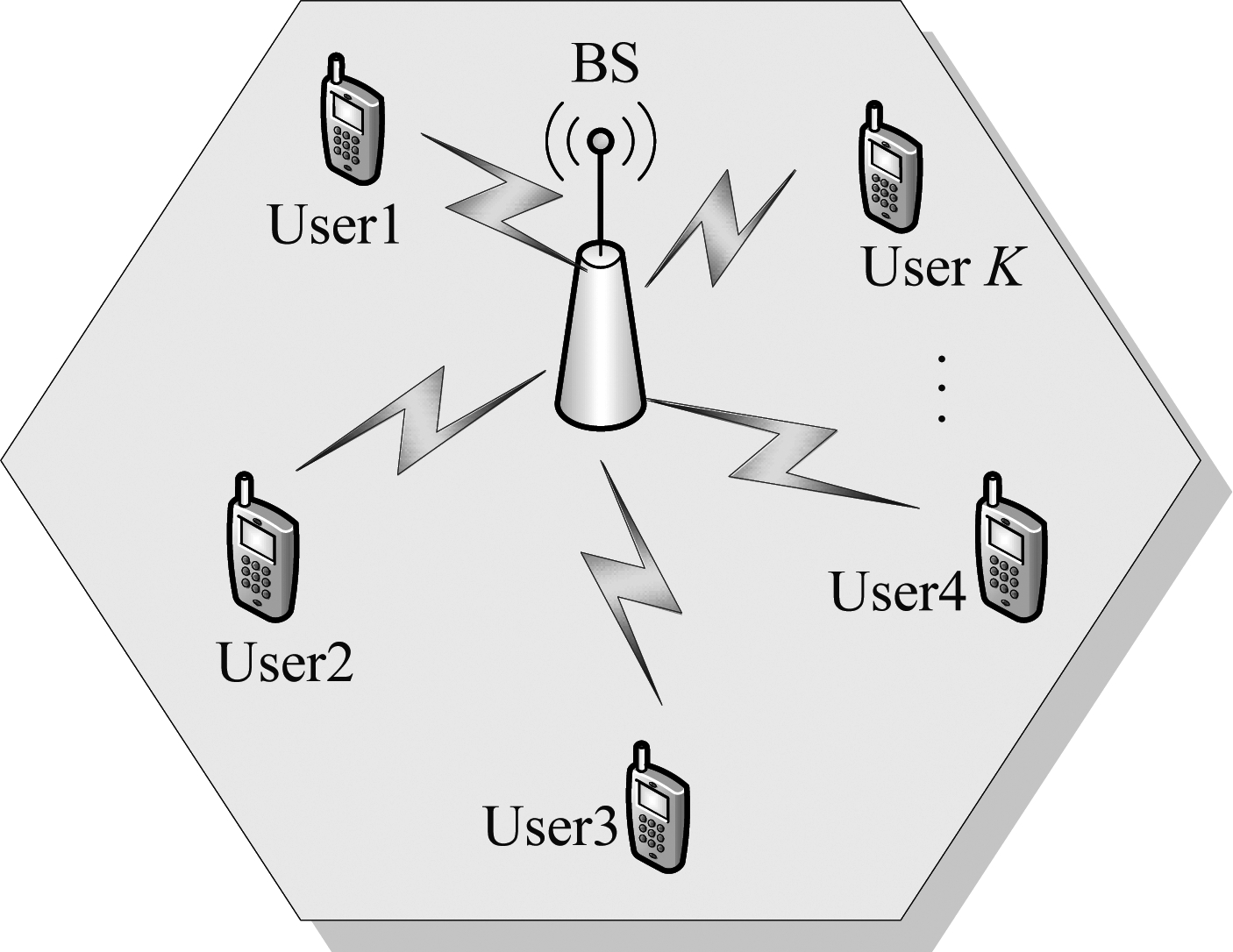
图1 多用户下行系统模型
Fig.1 Multi-user downlink system model
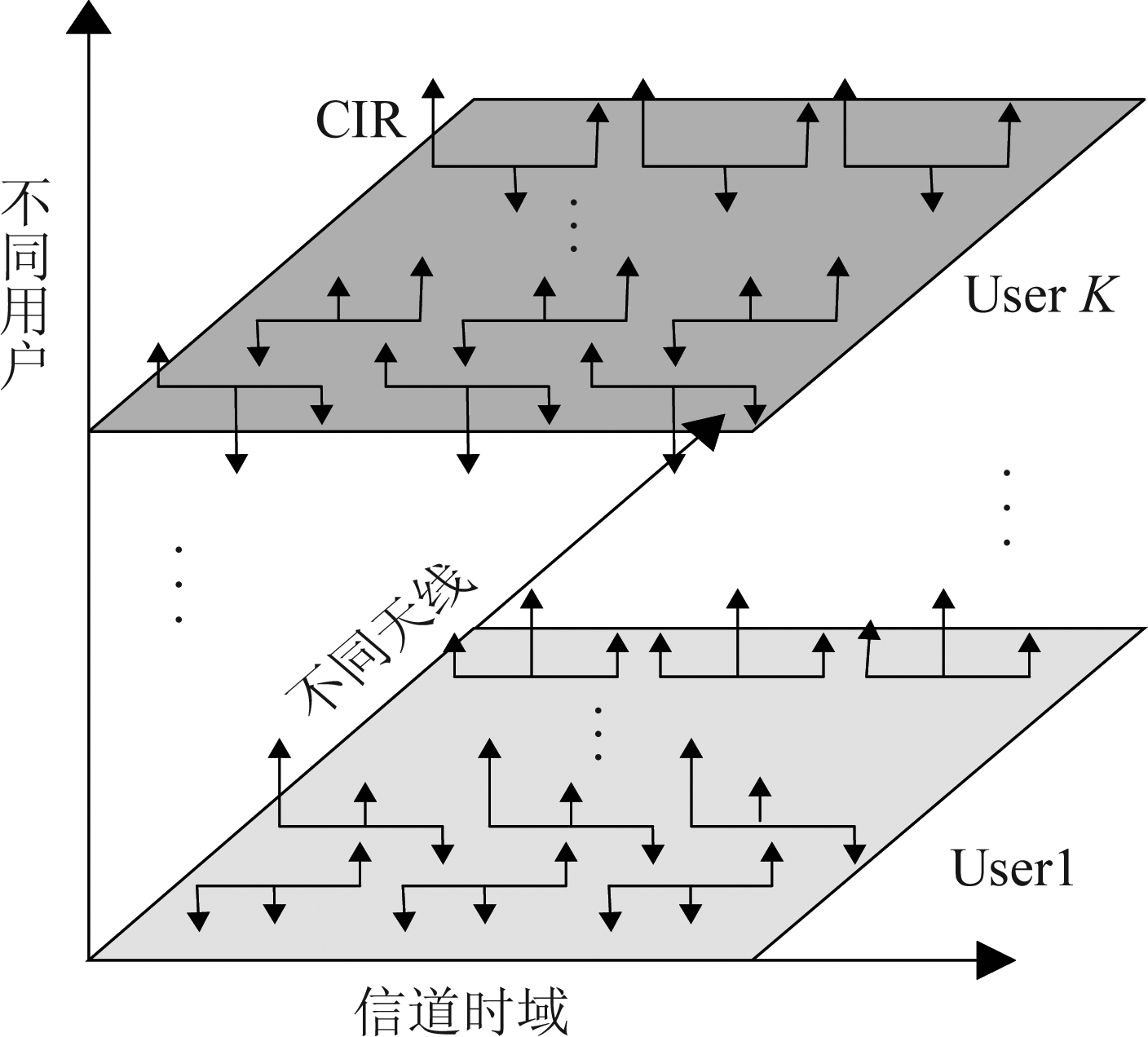
图2 信道在时域上的稀疏性
Fig.2 Sparsity of channels in time domain
对于下行链路,BS的第m个发射天线与某个用户之间的时间域信道脉冲响应(CIR)可以表示为:
hm=[hm[1],hm[2],...,hm[L]]T,1≤m≤M
(1)
其中L是CIR的信道等效长度。由于传输环境中的散射体数量有限,且只有少量的多径决定大部分能量,因而信道矢量hm具有稀疏性。假设hm相互独立,且每个hm的密度分布服从高斯分布,即:
(2)
其中γm≥0控制hm的行稀疏度,即当γm=0时,则hm=0;Bm为一正定矩阵,获取hm行内的相关结构,即为信道的时间相关性。
上述时间相关性是指,在路径增益的相干时间期间,几个连续OFDM符号中的信道可以认为是准静态的,可将一个OFDM符号的信道估计应用于相邻的几个OFDM符号,由此可进一步减少导频开销,增加可用频谱和能量资源。大规模MIMO信道的稀疏性如图2所示。
2.2 信号传输
大规模MIMO-OFDM系统中利用多测量矢量(Multiple Measurement Vector,MMV)压缩感知模型进行信道估计,将时间相关性考虑进去。
设OFDM子载波总数为N,导频子载波数为Np(Np≪M)。在用户端,在去除循环前缀(Cyclic Prefix,CP)和离散傅里叶变换(DFT)操作之后,利用单测量矢量(Single Measurement Vector,SMV)得到单用户接收的导频信号为:
(3)
其中xm∈CNp×1由第m根天线的导频信号组成,F∈CNp×Np的归一化DFT矩阵,
是F取前L列的部分DFT矩阵,n∈CNp×1为加性高斯白噪声,即
为等效传感矩阵,
为M根基站天线的CIR集合。
扩展到MMV模型,K个用户的接收信号可表示为:
Y=ΦH+N
(4)
其中Y=[y1,y2,...,ys,...,yK],Y∈CNp×K为K个用户观测矢量组成的测量矩阵;Φ∈CNp×ML为等效传感矩阵,
为K个用户的CIR矩阵;N=[n1,n2,...,nK],N∈CNp×K。
令y=vec(YT)∈CNpK×1,
=Φ⊗ΙK,h=vec(HT)∈CMLK×1,n=vec(NT),则MMV模型可转化为SMV模型,即:
y=h+n=
(5)
其中φm是Φ的第m列;hm∈CK×1是h的第m块,且
即H中的R个非零行表示h中有R个非零块,则h是块稀疏。
3 贝叶斯算法压缩感知模型
3.1 贝叶斯信道估计
文献[9]中首次由Ji Shihao等人提出贝叶斯理论在压缩感知中的应用。由贝叶斯理论可知,稀疏信号的恢复是利用信道h的块稀疏结构的先验知识以及观测矢量y,从而求出h的最大后验估计值,此值由h的高斯分布的期望给出。
根据式(5),y的高斯似然模型为:
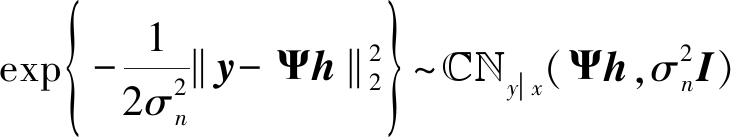
(6)
信道h的先验分布为:
(7)
其中Σ0为:
(8)
根据贝叶斯理论得h的后验分布,即:
(9)
其中均值和协方差分别为:
Ty
(10)
根据[10]中矩阵求逆引理:(A+BCD)-1=A-1-A-1B(C-1+DA-1B)-1DA-1,有以下推导式(11):
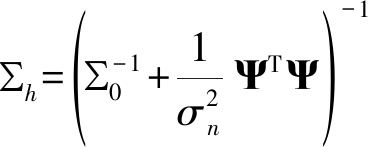
Σ0T)-1Σ0
(11)
根据以上得出的超参数
的最大后验(Maximum Posterior,MAP)估计为:
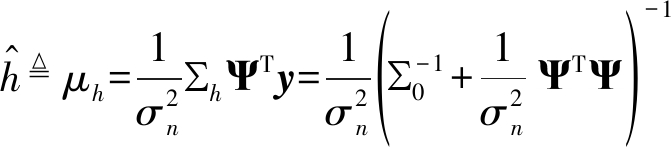
Ty
(12)
=
T)-1Ty
(13)
=TT)-1y
(14)
=Σ0T
Σ0T)-1y
(15)
其中式(12)是由式(11)得到的;(13)的理论依据是
的理论依据是(I+AB)-1A=A(I+BA)-1。
3.2 贝叶斯超参数估计
在对贝叶斯超参数估计之前,由于参数的项数多而数据有限,使得每个hm对应的矩阵Bm欠拟合,因此用一个正定矩阵来模拟所有源协方差矩阵,则式(8)变为Σ0=Γ⊗B,其中Γdiag(γ1,...,γML)。文献[11]已给出SMV模型的贝叶斯超参数的估计规则,具体如下所示:
(16)
(17)
(18)
其中
上述模型在大规模MIMO高维参数空间中运行很慢,因此需要改进。本文采用近似简化算法,使其在MMV模型的参数中可以直接执行。
文献[12]给出的MMV模型中块贝叶斯算法的估计超参数,并不会出现在更高维空间中运行较慢的情况。估计规则如下:
T)-1
(19)
ΓT)-1Y
(20)
(21)
基于式(19)～(21)给出的估计规则,本文采用以下近似来实现时间相关的MMV模型中块贝叶斯算法。
除了在一般条件下,在高信噪比(Signal to Noise Ratio,SNR)条件下和在低时间相关条件下,近似也是合理的。使用近似简化式(16)的估计规则,其中第一项采取如下近似方法:
Σ0T)-1(φm⊗IK)·B]
h)m
(22)
同理,近似第二项得到:
(23)
由式(22)和(23)简化形式,得到式(16)中γm的估计规则为:
(24)
为简化式(17)中的B,有
Σ0T)-1Σ0
Σ0T)-1·
(Φ⊗I)(Γ⊗B)≈Γ⊗B-[(ΓΦT)⊗B]
由
式的定义,可得:
则式(17)简化为:
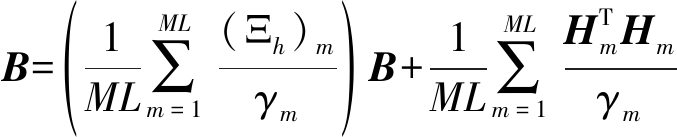
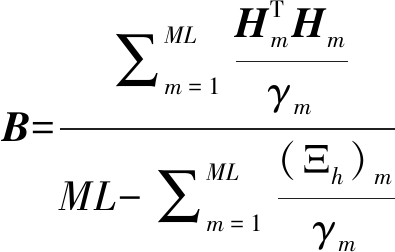
为了提高鲁棒性,使用如下B的估计规则:
(25)
式(25)估计规则仅在高SNR和无噪声情况下表现较好,而在低/中SNR情况下(如SNR≤20 dB)并不稳定,因此在
中添加一正则项,即:
(26)
其中ρ为一正标量,正则化形式可保证是正定的。
类似地,式(18)中的
可简化为:
(27)
注:若将ΦΓΦT的非对角线元素设置为0,则可进一步提高强噪声下估计规则的鲁棒性。
3.3 时间相关的块贝叶斯算法
根据2.2部分推导出的超参数估计规则,图3对所提出的TMBB-CS信道估计算法进行了归纳总结。
输入:基站天线数M,用户数K,信道长度L,迭代次数T,导频信号x,接收信号y。初始化:1.根据式(3)得到等效传感矩阵Φ。2.时间相关度β=i,i∈(0,1)。3.块索引集Λ0=⌀。4. μh=0;阈值ε=1e-3。循环:for t=1∶T1.找到非零块的索引位置:䂠t←find pos(γm>ε)。2.非零块位置设为1:γ䂠tm←1。3.更新索引集:Λt=Λt-1∪{䂠t}。4.更新传感矩阵Φt=[Φt-1,θ䂠t]。5.由式(19)计算协方差h。6.由式(27)计算噪声方差σ2n。7.由式(26)计算矩阵B。8.由式(24)更新γm。end输出:由式(20)计算μH,得信道估计值H^。
图3 时间相关的块贝叶斯信道估计算法
Fig.3 Time-correlation block Bayesian channel estimation algorithm
β表示信道的AR系数,表示其时间相关性,可设置不同的时间相关度β;在迭代过程中,当γm<ε时,将γm设为0,μH中相关的第m块变为0,其相关的传感矩阵φm⊗IK被删除。循环步骤中的第1步γm与阈值ε比较得出信道非零块位置,第5步计算估计协方差,第7步计算B得出hm各行时间相关性,第8步通过更新γm可得到信道的稀疏度。
4 复杂度分析
在这部分中,对所提出的TMBB-CS信道估计算法的复杂度进行分析。由于乘法运算要比加法运算量要大很多,因此仅考虑乘法运算量并以此作为TMBB-CS算法的复杂度。因为最开始是初始化过程,因此可以忽略前4步的复杂度。对于主循环部分,考虑第t次迭代的复杂度,并且计算集中在步骤5～8。对于步骤5,计算一次协方差h的复杂度为O((MLK)3+M2L2K3Np);对于步骤6,由式(27)可以得出计算
的复杂度为O(NpK),计算
的复杂度为
所以求解式(27)的总的复杂度为
对于步骤7,式(26)中
的计算复杂度为O(K2),其中加法运算的复杂度可忽略,最终计算步骤7的复杂度为O(K2);对于步骤8,式(24)中
的计算复杂度为O(K2+K),同样忽略加法复杂度,所以计算步骤8的复杂度为O(K2+K)。与MSBL算法的复杂度相比,唯一的不同之处是在式(24)中用替换了
因此TMBB-CS算法需要额外计算矩阵B和
但因为B的维度较小且正定对称,因此额外的计算量较低。
5 仿真结果
利用MATLAB工具对所提出的算法进行仿真,以下的每个实验均是迭代2000次。系统设置参数为:M=125,K=7,L=100,Np=25。在实验仿真中,通过判断γm是否小于一个小阈值(比如10-5)来决定h中相关块是否设置为0。用均方误差(Mean Square Error,MSE)来评估信道估计性能,MSE定义如下:
(28)
上式(28)中,
为信道估计值;H为信道实际值。
所提出的TMBB-CS算法与文献[11]中的TSBL算法、文献[12]中的MSBL算法以及文献[13]提出的MP-FOCUSS算法进行性能比较。TSBL算法是针对单测量矢量模型所提出的时间相关信道估计算法;MSBL算法仅是针对多测量矢量模型提出的算法,未涉及时间相关性;MP-FOCUSS算法是当存在多个测量向量时,用于计算线性逆问题的稀疏求解算法。
设置用户数K从1到7,通过均方误差的均值来显示各个算法的性能差异。图4各子图展示的是不同时间相关度设定(β取值不同)条件下各算法性能,这里取三个典型值作为代表,即β为0、0.5以及0.9。从而可以更清晰的看出本文所提出的TMBB-CS算法的优越性。
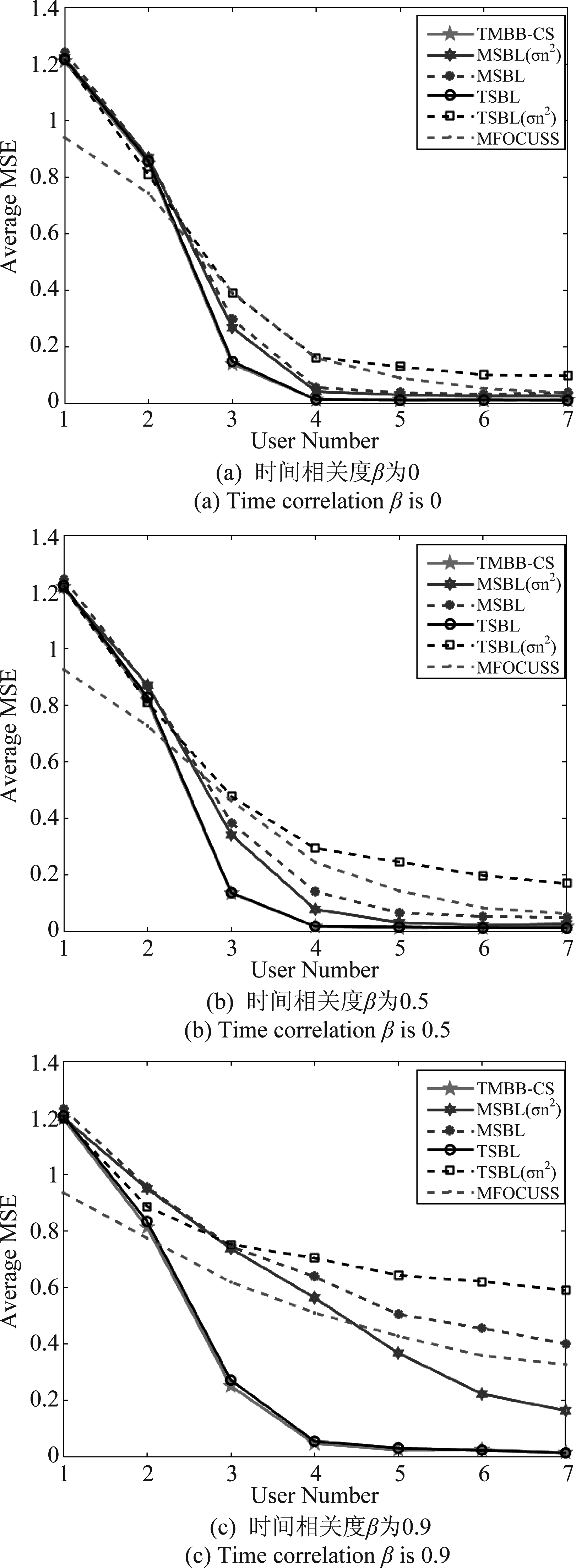
图4 不同时间相关度下的平均MSE
Fig.4 The average MSE at different time correlations
图4各子图中设置SNR=25 dB,同时保持其他实验设置不变。图中显示了随着用户数K的增加,所有算法均能体现较好的性能。但是随着|β|→1,所提出的TMBB-CS算法明显比其他文献中的算法更优,在多测量矢量模型下的优势也更明显。但是无论时间相关性如何,TMBB-CS和TSBL在不同的时间相关度下均具有优异的性能。
在图5中显示出TSBL和TMBB-CS算法在不同噪声水平上的MSE性能均优于其他算法。这意味着即使在低SNR情况下,利用信道的时间相关性进行信道估计是有益的。但需要强调的是,尽管TSBL、MFOCUSS和TMBB-CS算法的估计规则在低信噪比情况下可能不是最优的,但是与MSBL相比,提出的估计规则可以接近最优性能。
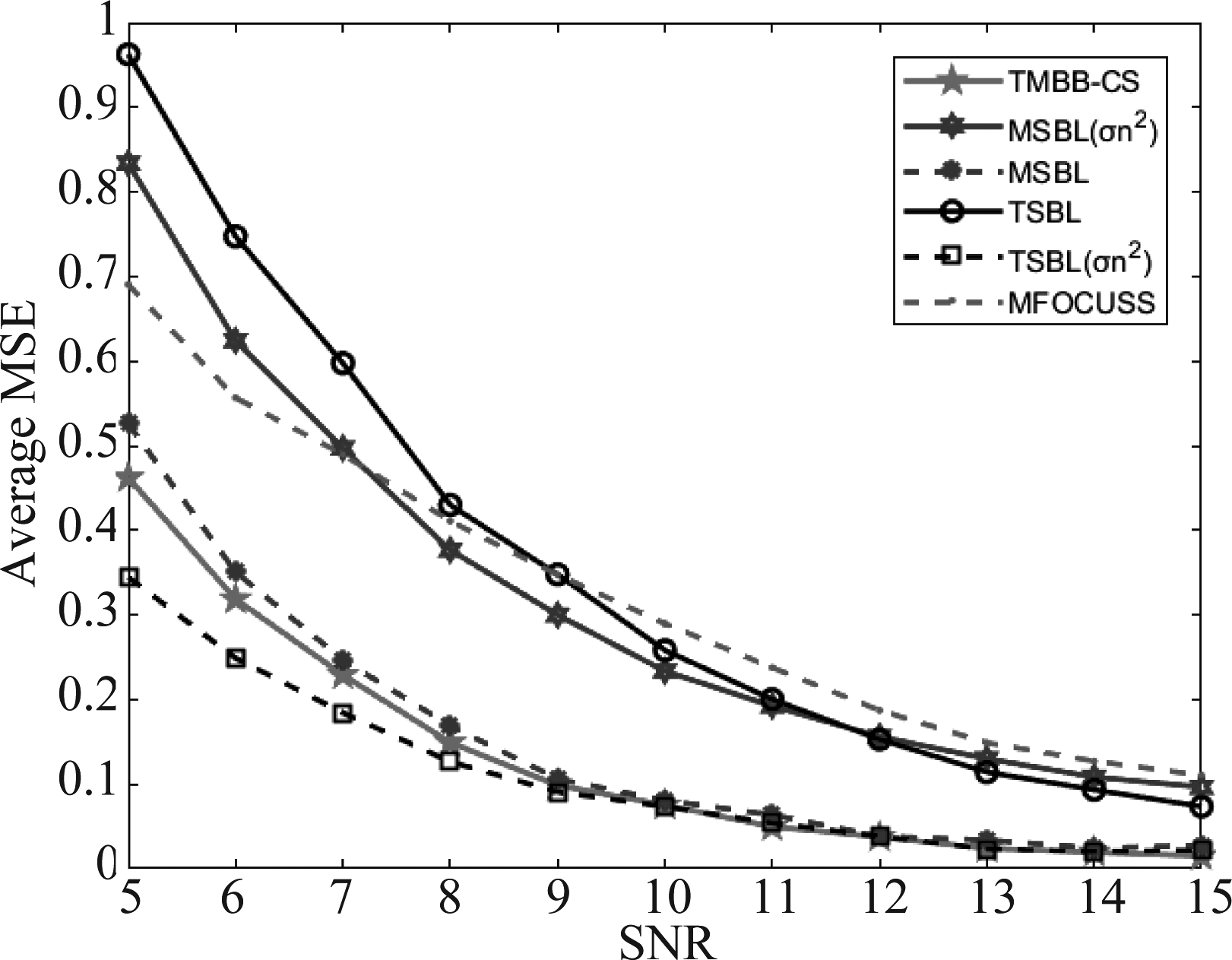
图5 不同SNR下的各算法的平均MSE
Fig.5 Average MSE of each algorithm at different SNRs
为此,在图5中,再次比较TMBB-CS和MSBL,这两种算法都使用了λ学习规则。TMSBB-CS使用估计规则式(27)的简化形式,即将ΦΓΦT的非对角线元素设置为零。图5结果表明,当使用其估计规则时,MSBL的性能非常差。在工程应用中,很难获得最佳
用估计是一种可实现的次优选择,所以在工程应用中选用TMBB-CS算法是一种接近最优的选择。
6 结论
将所提出的基于TMBB-CS信道估计方法用于FDD大规模MIMO系统信道估计中,可在信道稀疏度未知的情况下利用块贝叶斯框架估计信道。该算法利用了信道时间相关性以及块稀疏性,并利用MMV模型对下行链路中的多个用户进行信道估计。仿真结果显示,所提出的TMBB-CS算法性能优于其他文献提出的算法,鲁棒性更好。由于实际应用中存在大量不可测的未知因素,因而更稳定的信道估计方法还有待研究。
[1] Gao Zhen, Dai Linglong, Han Shuangfeng, et al. Compressive Sensing Techniques for Next-Generation Wireless Communications[J]. IEEE Wireless Communications, 2018, 25(3): 144-153.
[2] Muthu P S B, Ponnusamy K. Design of linear precoder for correlated multiuser MIMO system with imperfect CSI[J]. AEU-International Journal of Electronics and Communications, 2017, 74: 55- 62.
[3] Gao Zhen, Dai Linglong, Dai Wei, et al. Structured Compressive Sensing-Based Spatio-Temporal Joint Channel Estimation for FDD Massive MIMO[J]. IEEE Transactions on Communications, 2016, 64(2): 601- 617.
[4] Qi Chenhao, Wu Lenan. Uplink channel estimation for massive MIMO Systems exploring joint channel sparsity[J]. Electronics Letters, 2014, 50(23): 1770-1771.
[5] Qi Chenhao, Huang Yongming, Jin Shi, et al. Sparse channel estimation based on compressed sensing for massive MIMO systems[J]. IEEE International Conference on Communications (ICC), 2015: 4558- 4559.
[6] Han Y, Lee J, Love D J. Compressed Sensing-Aided Downlink Channel Training for FDD Massive MIMO Systems[J]. IEEE Transaction on Communications, 2017, 65(7): 2852-2862.
[7] Imran K, Madhusudan S, Dhananjay S. Compressive Sensing-based Sparsity Adaptive Channel Estimation for 5G Massive MIMO Systems[J]. Applied Sciences, 2018, 8(5): 754-754.
[8] Guan Gui, Li Xu, Lin Shan. Block Bayesian sparse learning algorithms with application to estimating channels in OFDM systems[C]∥International Symposium on Wireless Personal Multimedia Communications (WPMC). Sydney: IEEE, 2014: 238-242.
[9] Ji Shihao, Xue Ya, Carin L. Bayesian Compressive Sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356.
[10] Kay S M. Fundamentals of statistical signal processing[M]. Prentice Hall PTR, 1998.
[11] Zhang Zhilin, Rao B D. Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-Block Correlation[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 2009-2015.
[12] Wipf D P, Rao B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704-3716.
[13] Cotter S F, Rao B D, Engan K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477-2488.
[14] Justin Z, Philip S. Efficient High-Dimensional Inference in the Multiple Measurement Vector Problem[J]. IEEE Transactions on Signal Processing, 2013, 61(2): 340-354.
[15] Zhang Ruoyu, Zhang Jiayan, Gao Yulong, et al. Block Bayesian matching pursuit based channel estimation for FDD massive MIMO system[J]. AEU-International Journal of Electronics and Communications, 2018, 93: 296-304.
