1 引言
无人机(Unmanned Aerial Vehicle, UAV)具有成本低廉、操作简单、配置灵活、携带轻便等特点得到广泛应用[1]。伴随着对无人机通信数据带宽和传输速率要求的不断提升,利用大规模天线阵列和毫米波频段实施通信已引起学术界和工业界的广泛兴趣[2- 4]。比如,美国国防高级研究计划局正在研制一种基于“影子”无人机的毫米波通信系统,用以连接战场士兵和前线基地、战术作战中心以及情报监视侦察设施[5]。此外,利用毫米波频段实现无人机通信也是第五代(Fifth-Generation, 5G)移动通信系统的应用场景之一[6]。
无人机通信与传统陆地移动通信的传播环境不同,无人机周围基本没有散射体,散射体只存在于地面站附近。同时,无人机飞行速度快,场景变化明显,多普勒效应也更剧烈。近年来,国内外专家学者对UAV信道进行了大量研究。比如,文献[7]提出了一种基于物理几何的随机信道模型;文献[8]分别研究了UAV在城郊场景下空地信道的统计特性,包括时延扩展(Delay Spread, DS)、路径损耗以及莱斯因子等;考虑到UAV的移动性以及通信时的高度变化,文献[9]针对UAV多输入多输出(Multiple-Input-Multiple-Output, MIMO)信道提出了一种三维球形几何随机模型(Geometry Based Stochastic Model, GBSM)。需要指出的是,上述UAV信道研究均假设信号在5 GHz以下频段传输,不适用于结合毫米波技术的UAV信道。
目前已有学者对5G移动场景下的毫米波信道进行了研究,比如文献[10-11]分别基于28 GHz和73 GHz频段的信道测量数据,提出了一种基于毫米波技术的三维统计信道模型,该模型能够有效复现实测的信道冲激响应;文献[12]通过毫米波段58.5 GHz的信道测量和射线跟踪仿真,揭示了室外开放空间环境中主要的传播机制。针对UAV飞行场景的毫米波信道研究还比较少,文献[13]利用软件仿真研究了UAV毫米波信道特性,包括城市、郊区、农场和海面下不同飞行高度信道的时间相关特性;文献[14]则分析了不同高度、场景下的UAV毫米波信道的空时特性。
基于几何光学和一致性绕射理论的射线跟踪方法(Ray-tracing, RT)是一种确定性信道建模方法,并在诸多典型场景的信道建模中得到了应用。当使用毫米波进行通信时,由于毫米波传输频率高,波长短,频带宽,其信号时间分辨率高,传输几何特性明显,因此采用RT方法进行建模,然而,RT方法主要用于静态场景,不适用于动态模型,因此本文基于课题组前期UAV信道模型研究基础结合毫米波传播特性[15-16],提出了一种基于射线追踪的三维UAV毫米波通信几何信道模型,该模型采用了射线跟踪原理和传统几何随机模型架构,同时综合考虑UAV飞行过程中的空时特性。此外,文中还详细分析UAV几何场景参数与信道模型参数的计算方法,该算法通过迭代方式直观体现了信道参数的时间演进过程。
2 信道模型
典型无人机毫米波通信场景如图1所示,考虑下行链路即UAV与地面站 (Ground Station, GS)的通信信道。由于传播环境导致的反射和散射等影响,GS接收信号通常包含直射分量、地面反射分量及周围建筑物散射分量。图中,αν和βν分别表示UAV飞行速度的方位角和俯仰角,故飞行速度矢量为vUAV=νUAV[cos βνcos αν,cos βνsin αν,sin βν]T;同理,第l条传播路径的发射(接收)信号的归一化方向向量
可表示为
其中,
和
分别为发射信号的方位角与俯仰角,
和
分别为接收信号的方位角与俯仰角。
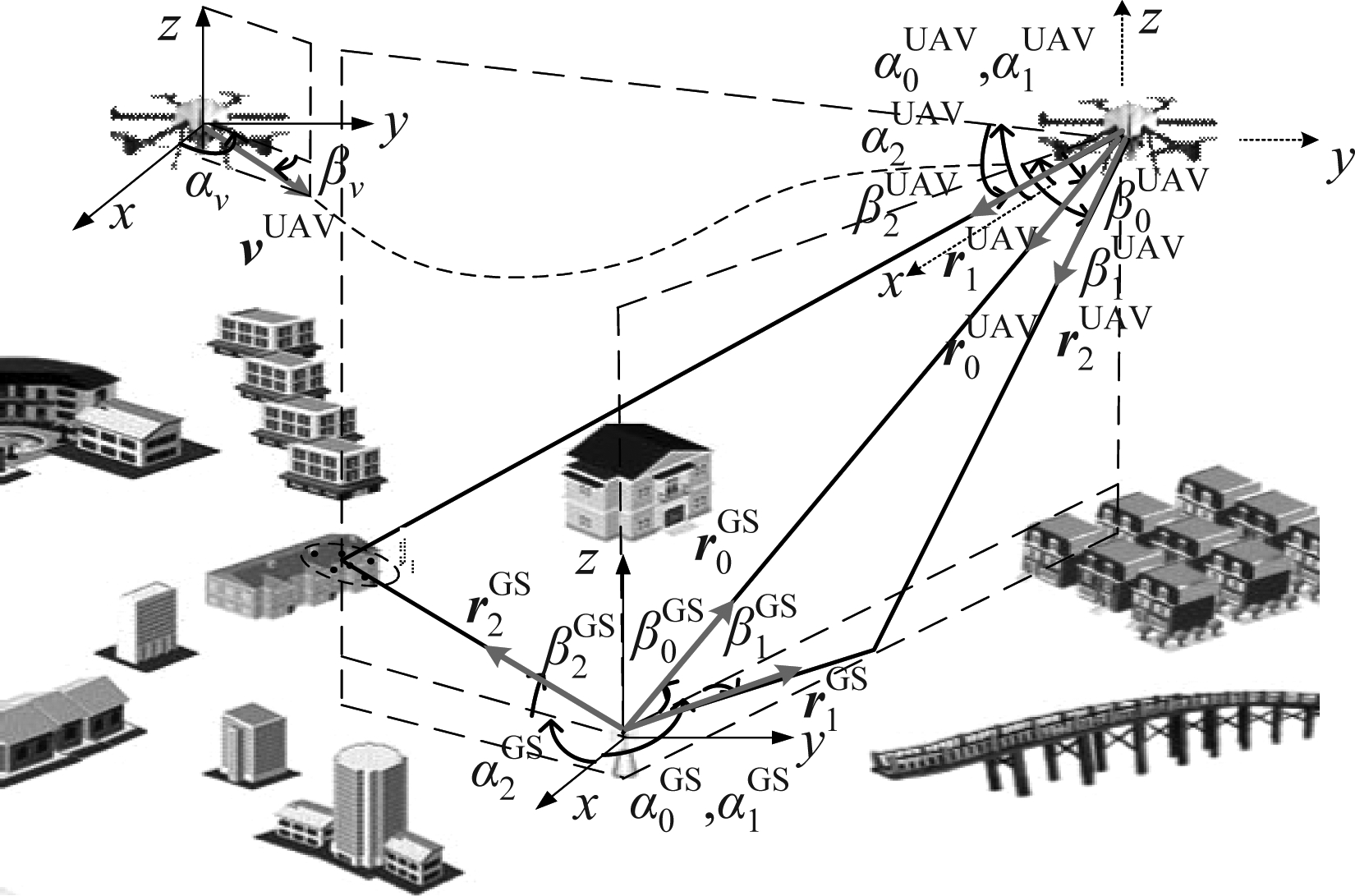
图1 无人机对地毫米波通信信道
Fig.1 The mmWave communication channel between UAV and GS
毫米波通信波长短、频带宽,使得信号时延分辨率高,几何光学传输特征更明显,因而传统的多簇延迟抽头模型不能对其进行地精确描述[17]。本文结合射线跟踪原理并考虑动态传播场景,将无人机毫米波信道表示为具有不同时延、幅度和二维角度的射线之和
(1)
其中,L(t)表示随场景和时间变化的有效传播射线数目;Pl(t),τl(t)和
l分别表示t时刻第l条射线时变的幅度,时延和随机相位;λ0表示载波波长。
3 模型参数分析与计算
3.1 几何场景参数
我们假设GS和散射体短时间内位置基本不变,以GS为系统坐标原点,则第l个散射体的位置矢量可表示为
其中
表示散射体与GS的相对距离。同理,UAV初始位置矢量表示为
其中DUAV(t0)表示初始时刻的直射距离。因此,t时刻UAV的瞬时位置矢量可用如下迭代形式表示
LUAV(t)=LUAV(t-Δt)+vUAV·Δt
(2)
在此基础上,可以证明GS和UAV、散射体和UAV之间的欧式距离分别为
DUAV(t+Δt)=‖LUAV(t+Δt)‖
(4)
令
分别表示UAV,GS以及散射体S三维坐标的x轴分量,y轴分量以及z轴分量,则第t时刻非直射路径的离开角的方位角(Azimuth Angle of Departure, AAoD)和俯仰角(Elevation Angle of Departure, EAoD)可表示为
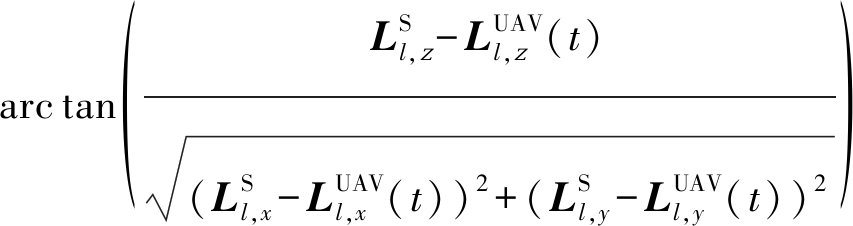
(5)
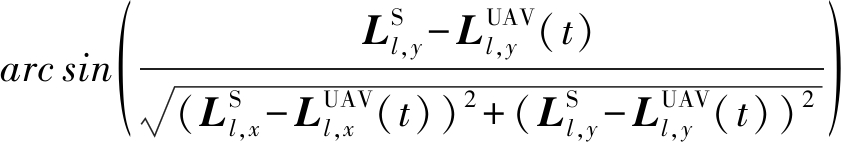
(6)
同理,此时非直射路径的到达角的方位角(Azimuth Angle of Arrival, AAoA)和俯仰角(Elevation Angle of Arrival, EAoA)可表示为
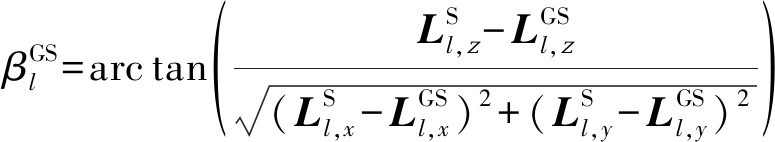
(7)
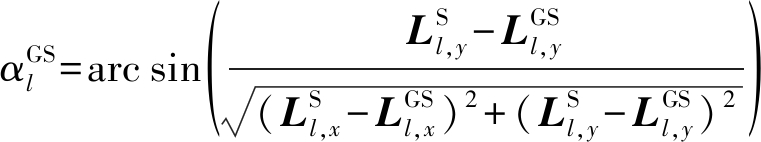
(8)
同理,可以证明第t时刻直射路径的离开角与到达角的方位角和俯仰角可分别表示为
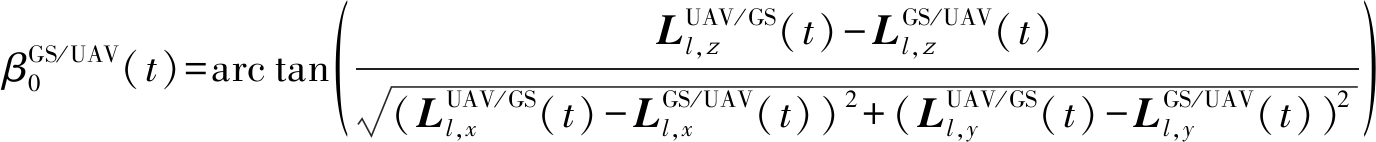
(9)
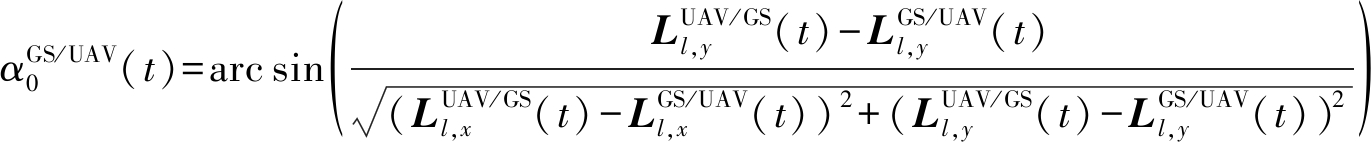
(10)
3.2 信道模型参数
考虑到直射径传播环境和自由空间环境类似,因此本文模型中直射径的信号幅度采用如下方法计算
=32.44+20 log( f )+20 log(DUAV(t))
(11)
式中,PUAV为发射端信号功率,PGS(t)为接收端信号功率, f表示信号频率,单位为MHz,DUAV(t)表示t时刻的直射路径长度,单位为km。同时,反射和散射路径的信号幅度可以在此基础上增加额外损耗获得,即
Pl(t)=P0(t)+Ll(t)
(12)
其中,Ll(t)=-10lg|RFe-jΔφ(t)|2,RF表示反射系数,Δφ(t)表示反射路径与直射路径的相位差
(13)
式中,
表示反射路径与直射路径的长度差值。
其次,第l条射线在t时刻的非直射路径的时延可表示为
(14)
式中,c为光速。同理,直射路径的时延可表示为
(15)
4 数值仿真
4.1 仿真场景及参数
本节将利用上述模型参数计算方法针对南京航空航天大学(Nanjing University of Aeronautics & Astronautics, NUAA)江宁校区传播场景进行信道建模,并分析该场景下毫米波信道特性。图2给出了江宁校区的卫星视图,有效场景区域约1.1 km×1.59 km。为简化射线跟踪运算的复杂度,我们对该传播场景进行简化,将复杂建筑物近似为规则的几何模型。实际勘测中,我们发现该有效区域包含66个建筑物,平均高度约为30 m。建筑物表面均为混凝土,校园开阔地面大部分为湿土。另外,假设UAV下行链路毫米波通信的中心频率为28 GHz,带宽为500 M。UAV和GS的天线均采用垂直极化的全向天线,GS天线高度2 m,UAV飞行高度为75 m,飞行速度10 m/s,仿真时间150 s。鉴于毫米波频段通信的传播损耗非常大,为保证UAV对GS正常通信,我们选取了三条始终存在视距路径的飞行轨迹进行建模。
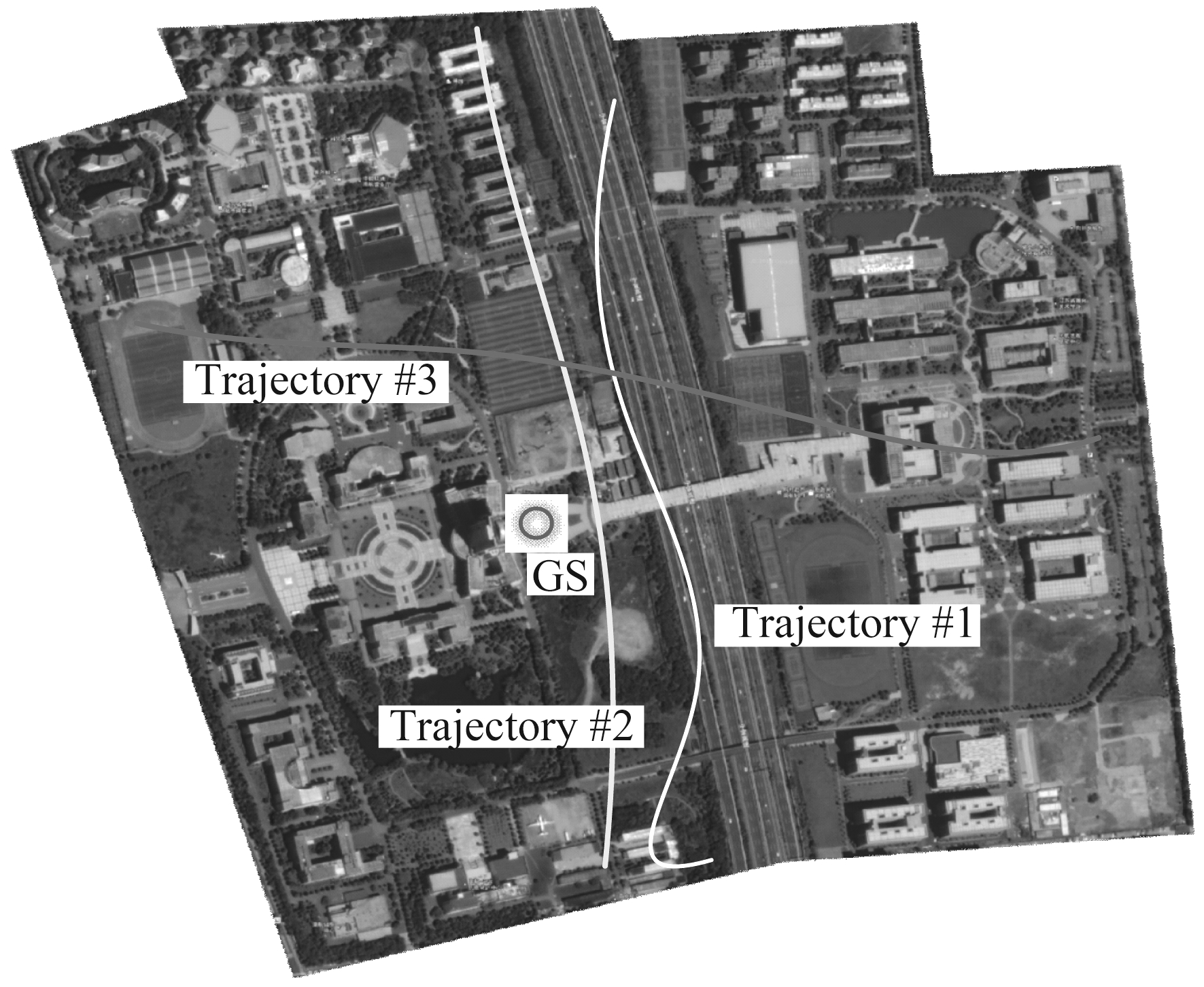
图2 南京航空航天大学江宁校区卫星视图
Fig.2 Satellite view of the Jiangning Campus, NUAA
4.2 仿真结果及分析
结合第3节模型参数计算方法,图3给出了飞行轨迹1情况下信道的时变单位冲激响应建模结果,由图可以看出:1)UAV对地始终存在视距路径,但视距路径的时延和功率存在时变性;2)地面反射路径和散射路径随着位置不同而产生随机的生灭;3)包含主要能量的传播路径约为3～4条,包括直射径、地面反射径和建筑物散射径。为了进一步观察多径信号的时延特性,我们依次对三条飞行轨迹进行建模仿真,并对所有时刻的多径时延进行统计如图4所示,其中图4(b)时延扩展表示时延的功率加权的均方根值。由图可以看出:1)地面反射路径的时延为100～200 ns,大部分时间与视距路径共存,因而也是影响接收机性能的主要因素;2)时延扩展分布在0～700 ns之间且主要集中于40～60 ns之间,这与文献[18]城市场景实测结果的最高值400 ns和平均值35 ns都比较吻合。
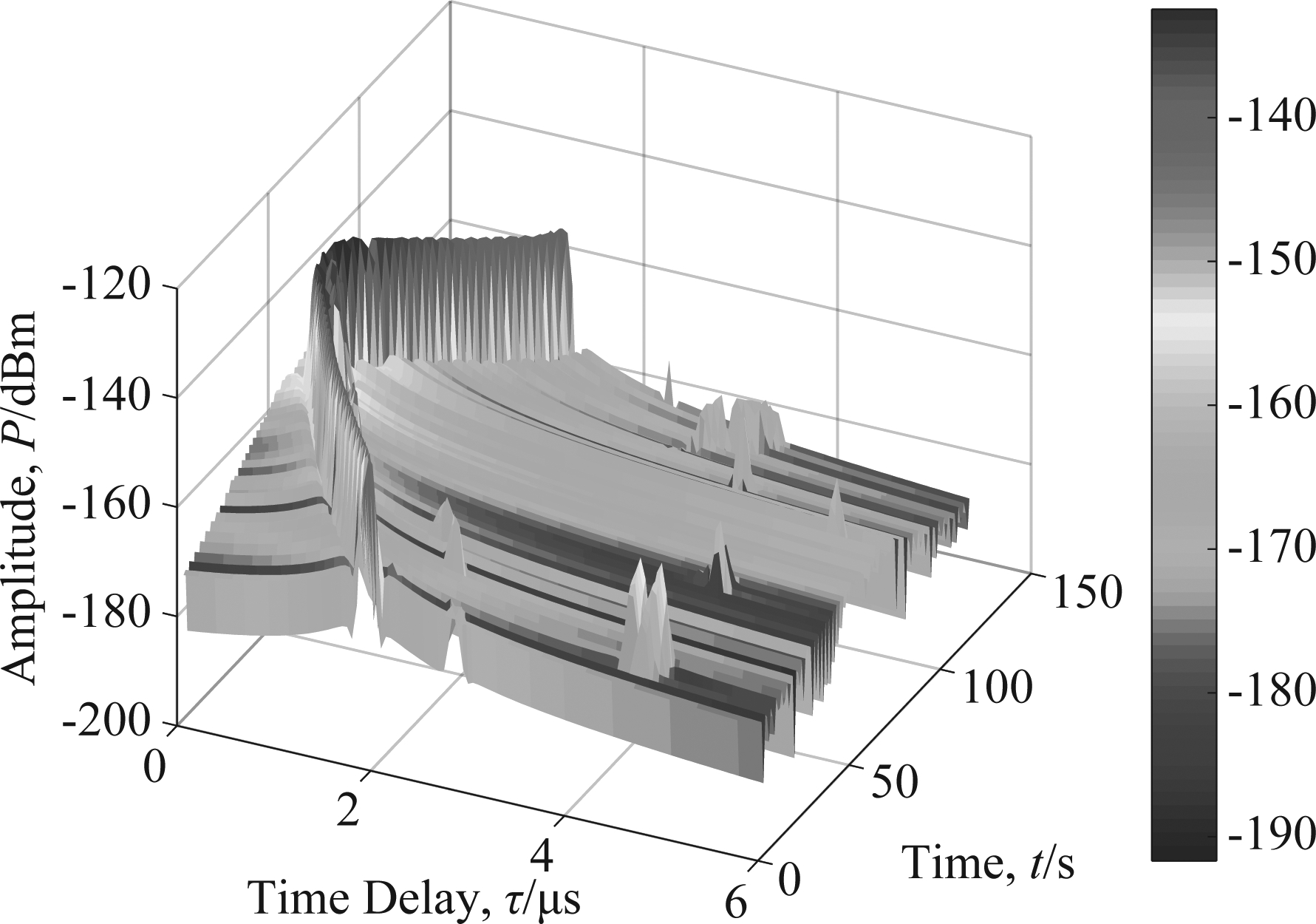
图3 信道时变冲激响应
Fig.3 Time-variant channel impulse response
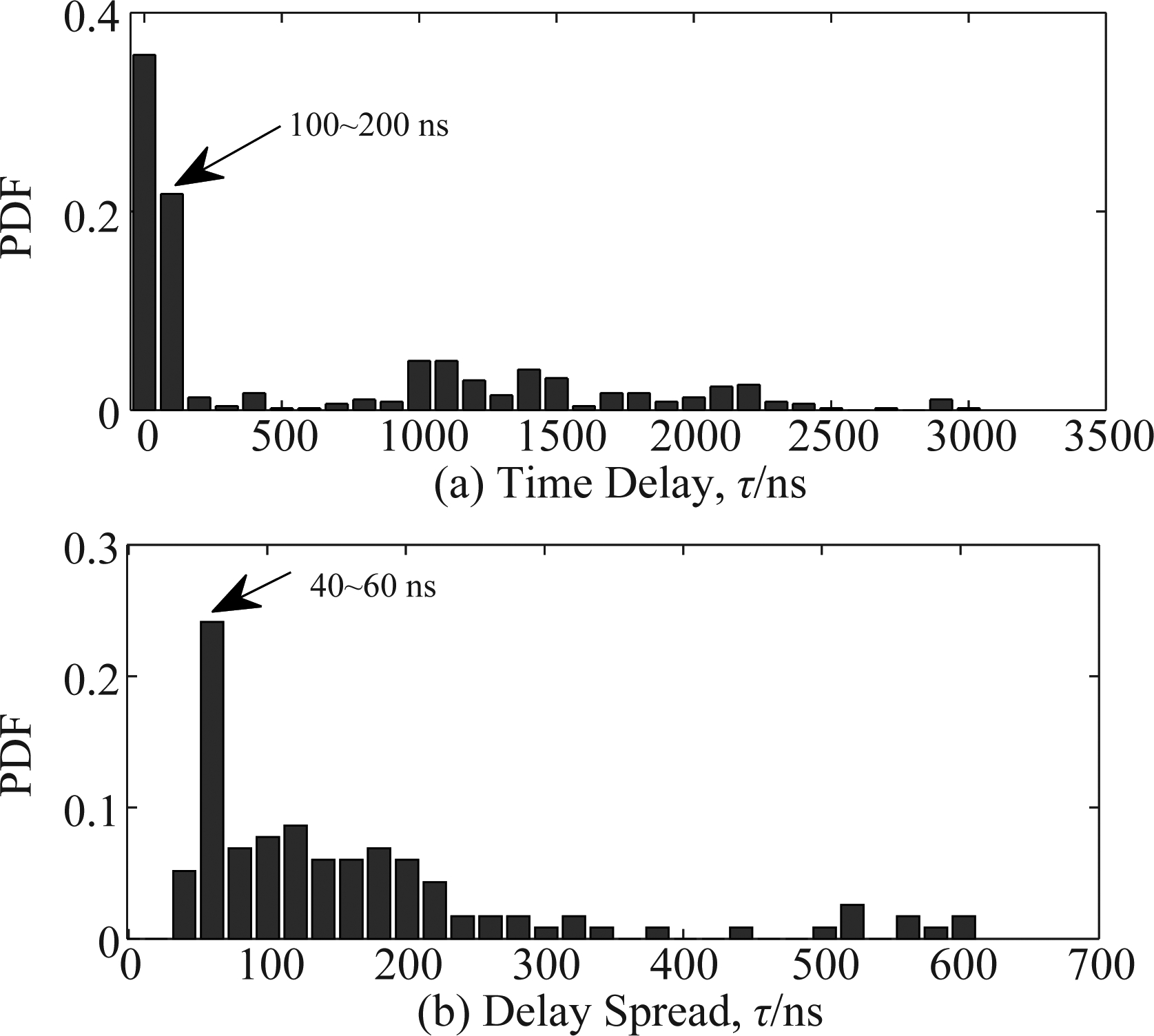
图4 时延和时延扩展的统计分布
Fig.4 Statistical distributions of time delay and DS
图5给出了飞行路径1情况下,三条主要传播路径信号的方位角与俯仰角的随时间变化情况。图中,俯仰角的变化范围相对较小,原因在于UAV在飞行过程中,飞行高度基本保持不变。然而,随着UAV空间位置的变化,方位角变化幅度很大。同时,为了观测方位角和俯仰角的分布特性,我们将不同时刻的所有路径角度值减去均值后进行统计,统计结果如图6所示。在此基础上,图7给出了角度扩展(Angle Spread, AS)的统计分布,并利用对数正态分布对其进行拟合,可以看到对数正态分布可以较好的拟合实测数据。文献[19]收集了城市环境中空地通信下800个角度扩展数据,并使用了Akaike
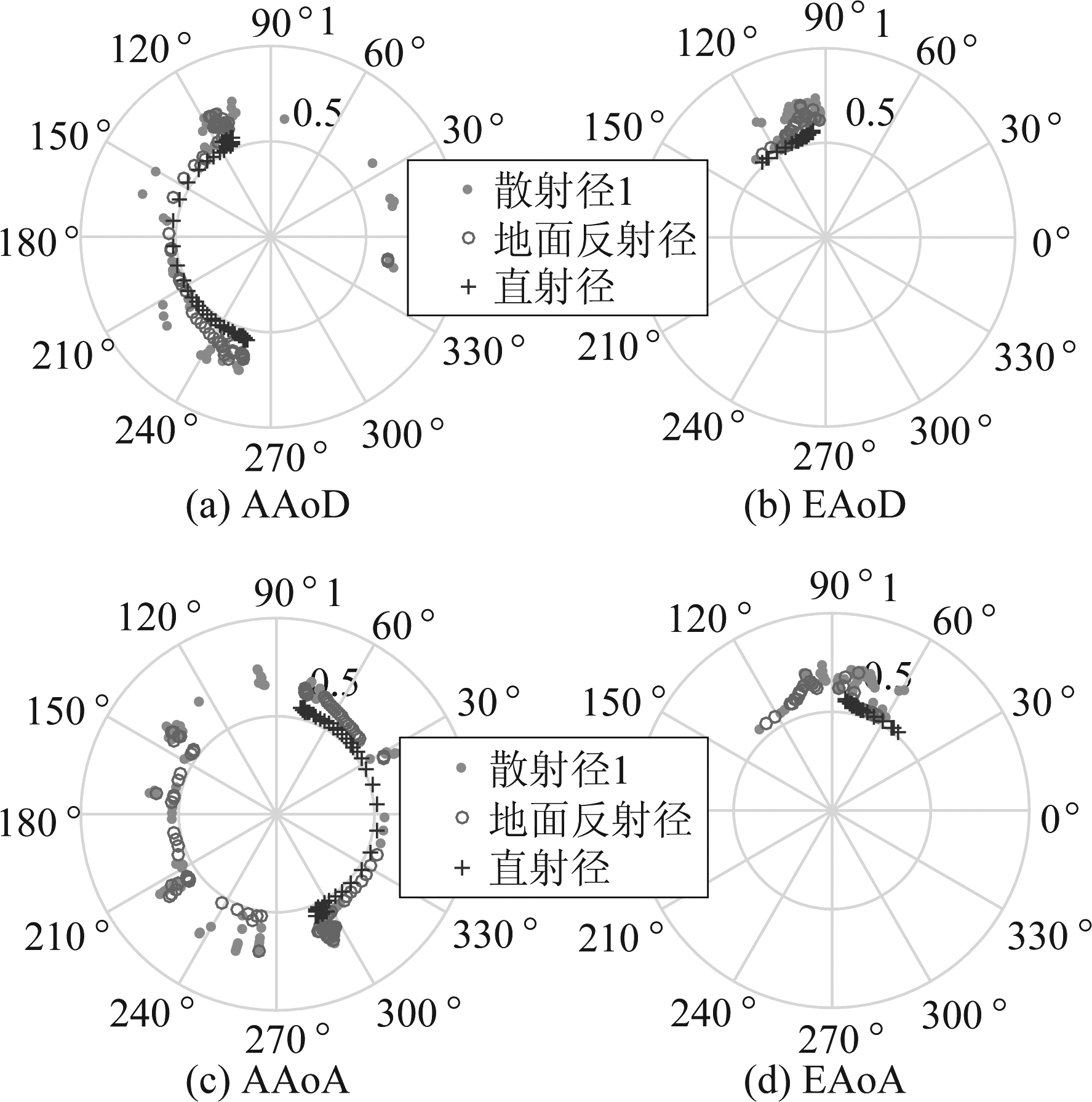
图5 不同角度的计算结果
Fig.5 Calculated results of different angles
图6 不同角度的统计分布
Fig.6 Statistical distributions of different angles
准则方法来比较多种分布函数,比较结果表明,对数正态分布是最符合该条件下的角度扩展分布,这也与本文仿真拟合结果相吻合。另外,到达角和离开角的角度均值与文献[20-21]提供的城市校园场景中的毫米波通信实测结果比较接近,该实测结果显示AAOD相比于AAOA,其分布更加集中,与图6结果相符合。
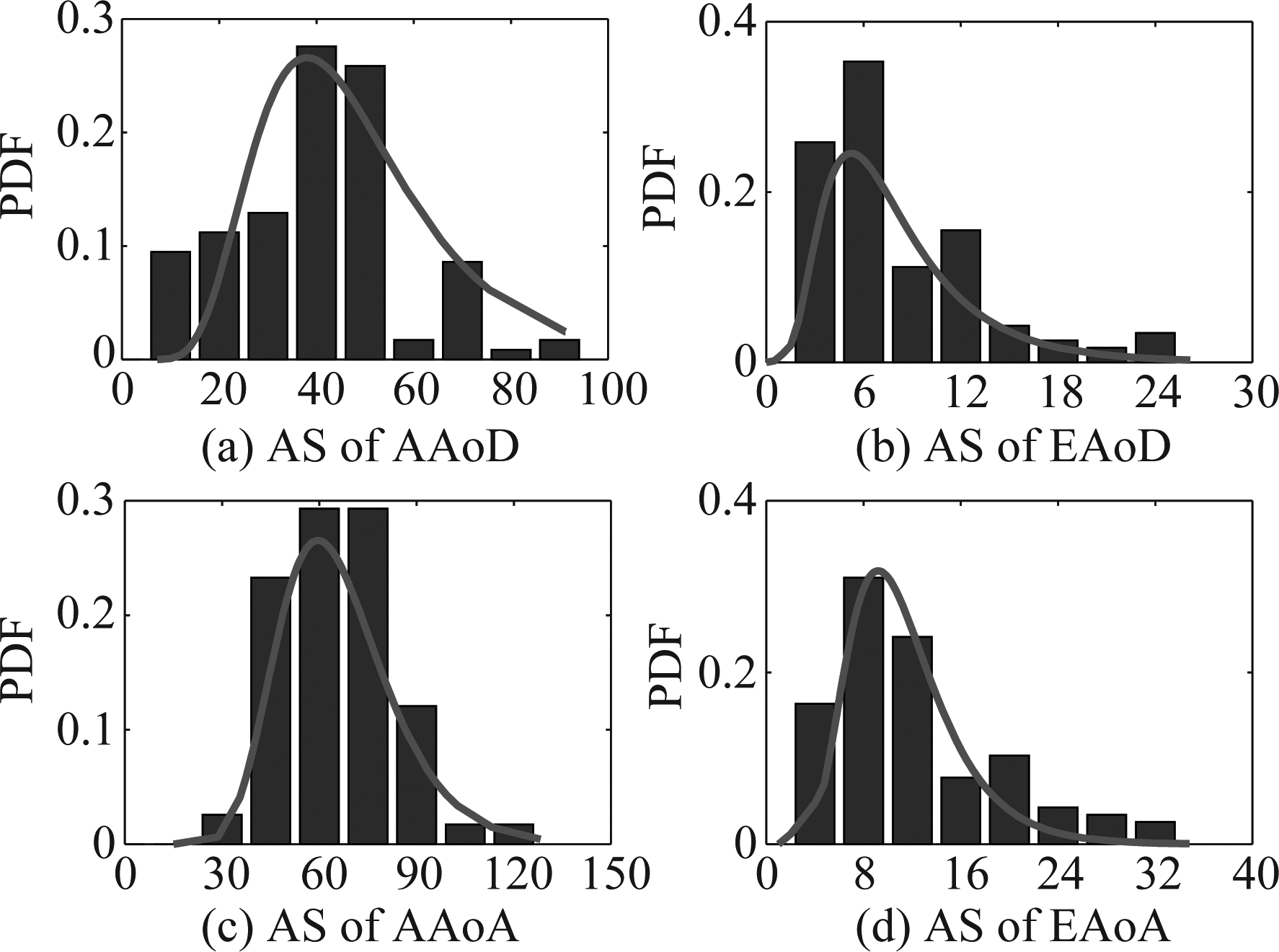
图7 不同角度扩展的统计分布
Fig.7 Statistical distributions of different ASs
5 结论
本文提出了一种三维UAV毫米波几何信道模型并推导给出了时变几何参数和模型参数的迭代计算方法。仿真结果表明,UAV的快速移动导致传播环境中散射簇的随机生灭,使得UAV毫米波信道存在非平稳特性。同时,多径时延和角度分布等信道统计特性与实测结果较吻合,有效验证了该模型的有效性。因此,该模型可用于评估和模拟无人机毫米波通信链路的状况,为优化UAV无线通信系统性能、空中基站布置以及空中巡航路线等提供理论基础。
[1] Zeng Yong, Zhang Rui, Lim T J. Wireless communications with unmanned aerial vehicles: opportunities and challenges[J]. IEEE Communications Magazine, 2016, 54(5): 36- 42.
[2] Mezzavilla M, Polese M, Zanella A, et al. Public safety communications above 6 GHz: Challenges and opportunities[J]. IEEE Access, 2018, 6: 316-329.
[3] Xiao Zhenyu, Xia Pengfei, Xia Xianggen. Enabling UAV cellular with millimeter-wave communication: Potentials and approaches[J]. IEEE Communications Magazine, 2016, 54(5): 66-73.
[4] Geise R, Weiss A, Neubauer B. Modulating Features of Field Measurements with a UAV at Millimeter Wave Frequencies[C]∥2018 IEEE Conference on Antenna Measurements & Applications (CAMA): IEEE, 2018: 1- 4.
[5] Chandler J, Steagall R W. DARPA’s mobile hotspot program drives E-band performance benchmarks[J]. Microwave Journal, 2014, 57(10): 22-32.
[6] Sharma V, Bennis M, Kumar R. UAV-assisted heterogeneous networks for capacity enhancement[J]. IEEE Communications Letters, 2016, 20(6): 1207-1210.
[7] Simunek M, Pechac P, Fontan F P. Excess loss model for low elevation links in urban areas for UAVs[J]. Radio Engineering, 2011, 20(3): 561-568.
[8] Matolak D W, Sun R. Air-Ground Channel Characterization for Unmanned Aircraft Systems—Part III: The Suburban and Near-Urban Environments[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 6607- 6618.
[9] Jin Kun, Cheng Xiang, Ge Xiaohu, et al. Three dimensional modeling and space-time correlation for UAV channels[C]∥IEEE Vehicular Technology Conference: IEEE, 2017: 1-5.
[10] Samimi M K, Rappaport T S. 3-D statistical channel model for millimeter-wave outdoor mobile broadband communications[C]∥IEEE International Conference on Communications: IEEE, 2015: 2430-2436.
[11] Samimi M K, Rappaport T S. 3-D millimeter-wave statistical channel model for 5G wireless system design[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(7): 2207-2225.
[12] Kim M, Iwata T, Umeki K, et al. Simulation based mm-wave channel model for outdoor open area access scenarios[C]∥IEEE URSI Asia-Pacific Radio Science Conference: IEEE, 2016: 1292-1295.
[13] Khawaja W, Ozdemir O, Guvenc I. UAV air-to-ground channel characterization for mmWave systems[C]∥IEEE Vehicular Technology Conference: IEEE, 2017: 1-5.
[14] Khawaja W, Ozdemir O, Guvenc I. Temporal and Spatial Characteristics of mmWave Propagation Channels for UAVs[J]. arXiv preprint arXiv: 1803.08252, 2018.
[15] 朱秋明, 周生奎, 霍帅珂, 等, 无人机中继平台覆盖区域研究[J]. 航空学报, 2014, 35(1): 223-229.
Zhu Qiuming, Zhou Shengkui, Huo Shuaike, et al. A Statistical Area Coverage Model for Unmanned Aerial Vehicles as Relay Platforms[J]. Acta Aeronautica et Astromautica Sinica, 2014, 35(1): 223-229.(in Chinese)
[16] Zhu Qiuming, Jiang Kaili, Chen Xiaomin, et al. A Novel 3D Non-Stationary UAV-MIMO Channel Model and Its Statistical Properties[J]. China Communications, 2018, 15(12): 147-158.
[17] Molisch A F, Tufvesson F. Propagation channel models for next-generation wireless communications systems[J]. IEICE Transactions on Communications, 2014, 97(10): 2022-2034.
[18] Sun R, Matolak D W. Over-harbor channel modeling with directional ground station antennas for the air-ground channel[C]∥IEEE Military Communications Conference: IEEE, 2014: 382-387.
[19] Zhang Ruonan, Lu Xiaofeng, Zhao Jianping, et al. Measurement and modeling of angular spreads of three-dimensional urban street radio channels[J]. IEEE Transactions on Vehicular Technology, 2017, 66(5): 3555-3570.
[20] Ko J, Cho Y J, Hur S, et al. Millimeter-wave channel measurements and analysis for statistical spatial channel model in in-building and urban environments at 28 GHz[J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 5853-5868.
[21] Samimi M, Wang K, Azar Y, et al. 28 GHz angle of arrival and angle of departure analysis for outdoor cellular communications using steerable beam antennas in New York City[C]∥Vehicular Technology Conference: IEEE, 2013: 1- 6.
