1 引言
最小均方(Least Mean Square,LMS)算法作为经典的自适应滤波算法,在实际中获得大量应用,但在非线性系统中,该算法的性能显著退化。Liu Weifeng等[1]人基于核方法提出核最小均方(Kernel Least Mean Square,KLMS)算法,它能够有效地处理多种非线性问题。由于KLMS算法的随机性大,金明明等[2]提出了核块最小均方(Kernel Block Least Mean, KBLMS)算法,降低了KLMS算法的稳态误差。但核自适应滤波器(KAF)是一种生长型网络,计算量和存储容量持续增加。为应对这一问题,Liu Yuqi等[3]将随机特征网络应用到KLMS算法中,提出了基于随机特征网络的核最小均方(Randomized feature networks-based kernel least mean square, KLMS-RFN)算法;Chen Badong等[4-5]将在线矢量量化应用到KLMS中,提出量化核最小均方(Quantized Kernel Least Mean Square,QKLMS)算法,其主要思想在于把“冗余”数据量化到其最近的数据上。Zheng Yufei对QKLMS算法进行改进,提出了凸组合量化的核最小均方(Convex combination of quantized kernel least mean square algorithm, CC-QKLMS)算法[6],使QKLMS算法在收敛速度较快的同时还能得到较高的滤波精度。文献[7]将迁移学习应用到KLMS和QKLMS中,提出最近实例质心估计核最小均方(The Nearest Instance Centroid-Estimation Kernel Least Mean Square, NICE-KLMS)算法和最近实例质心估计量化核最小均方(The Nearest Instance Centroid-Estimation Quantized Kernel Least Mean Square, NICE-QKLMS)算法。NICE-KLMS算法将中心点集合划分为具有局部紧支撑的子集之和,减少了每个输入数据与权值相乘的计算量,NICE-QKLMS算法继承了NICE-KLMS和QKLMS算法的优点,不仅降低了输入数据与权值相乘的计算量,还降低了存储容量。
在实际系统中,经常存在着自然环境、人造设备等产生的脉冲噪声[8-9],这些脉冲噪声可以用α稳定分布的模型很好的建模。但因为α稳定分布噪声不存在二阶以及二阶以上统计量,所以基于最小均方误差(Minimum Mean Square Error, MMSE)准则的算法都不再适用。针对上述问题,Shao Min等[10-11]人提出了基于最小分散系数(Minimum Dispersion, MD)准则的最小平均P范数(Least Mean P-norm,LMP)算法,金明明等[12]将核方法应用到LMP中,提出了核最小平均P范数(Kernel Least Mean P-norm,KLMP)算法。与其他核自适应滤波器(KAF)存在的问题一样,KLMP算法计算量和存储容量较大,在训练集较大时,训练模型时间太长。
为了降低KLMP算法的计算量,本文将迁移学习引入KLMP算法中,提出最近实例质心估计核最小平均P范数(The Nearest Instance Centroid-Estimation Kernel Least Mean P-norm, NICE-KLMP)算法,并引入在线矢量量化,提出最近实例质心估计量化核最小平均P范数(The Nearest Instance Centroid-Estimation Quantized Kernel Least Mean P-norm, NICE-QKLMP)算法。NICE-QKLMP算法不仅降低了计算量,还通过删减量化冗余的中心点降低了存储容量。
2 基础知识
2.1 再生核希尔伯特空间
希尔伯特空间(Hilbert Space, HS) H作为完备的内积空间,必定存在正交基
且HS中的任意矢量x均有以下表示形式:
(1)
其中,ak为基函数的系数。
如果在HS中加入可再生核,那么它就是再生核希尔伯特空间[13](Reproducing Kernel Hilbert Space, RKHS)。RKHS上的任意函数f均有以下表示形式:
(2)
其中,κ(u(j),·)为核函数,每个核函数分别与不同的中心点u(j)有关;aj是扩展系数。
2.2 核最小平均P范数算法
在α稳定分布噪声背景下,选择代价函数是J=E{|e(n)|p},得到LMP算法权重ω(n)的更新公式[10]为
ω(n+1)=ω(n)+μp|e(n)|(p-1)sgn(e(n))u(n)
(3)
其中,u(n)为输入矢量,e(n)为误差信号,μ为步长因子,p为范数且取值满足0<p<α<2。α是决定α稳定分布噪声脉冲性能的特征指数[10];α越小,则噪声的脉冲性能越显著;反之则越弱;当特征指数α未知时,可先利用样本分位数法[14]估计得到α,然后选取合适的范数p。经过大量仿真实验证明,样本分位数法能够很好的估计特征指数α,准确精度可达98.26%。利用核技巧可得KLMP的更新公式[12]为
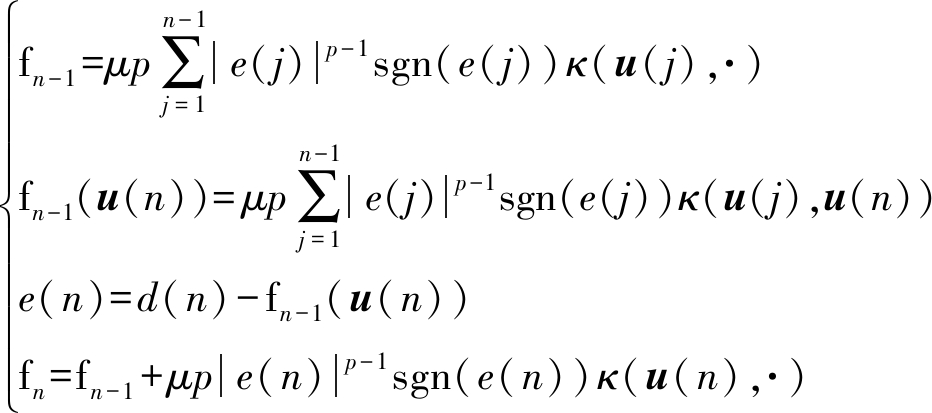
(4)
其中fn是输入为u(n)时的输出量,且核函数是高斯核函数
κ(u(j),u)=exp(-h‖u(j)-u‖)
(5)
3 最近实例质心估计的核最小平均P范数算法
由式(4)可见,在训练过程中,输入数据u(n)作为核的中心,μp|e(n)|(p-1)sgn(e(n))作为核系数,都存储在存储器中。KLMP的拓扑结构是一个生长型网络,每添加一个新的输入数据就需要扩充一个新的单元,当n增大时,计算量和存储容量持续增加。将最近实例质心估计(NICE)方法应用到KLMP[12]和QKLMP[4-5,12]算法中,分别得到NICE-KLMP算法和NICE-QKLMP算法。NICE-KLMP算法可以显著降低计算量,而NICE-QKLMP算法不仅降低了计算量,还显著降低了存储容量。
3.1 最近实例质心估计
最近实例质心估计方法是对现有稀疏化方法的优化,通过忽略特定簇之外的中心点来限制训练中心点数的增长。当式(2)的κ(u(j),·)选取高斯核函数时,则f为N个高斯核函数的总和,其中每个核函数与不同的中心点u(j)相关,且均按指数衰减形式衰减至零。NICE[7]的思想是当输入样本u(n)所在簇距离其他簇足够远时,可近似认为该输入样本与其他簇均正交。将这样的核函数划分为m个正交集合,可以得到输出数据为
(6)
其中
定义集合R*={u(j), j=1,...,N*},则对于所有u(j)∉R*, κ(u(j),u(n))=〈φ(u(j)),φ(u(n))〉=0,φ(·)是输入数据在RKHS中的映射。由于精度有限,我们将正交性约束适当放宽至〈φ(u(j)),φ(u(n))〉<ε;结合式(5),集合R*可近似等效为R*≈{u(j):‖u(j)-u(n)‖<γε};其中ε为任意正实数,γε为相应的距离值。
NICE将基于样本实例获得的中心点集合(总滤波器)划分为具有局部紧支撑结构的子集之和(子滤波器),在KAF中,每个输入样本仅在一个子滤波器中具有非零输出。因此,总滤波器可以划分为若干个独立的子滤波器,每个子滤波器分别专注于训练不同的输入,从而达到减少计算量的目的。
NICE使用最近邻搜索算法[7]搜索最近簇,该算法与K最近邻(k-NN)分类算法[15]类似。然而,在搜索最近簇时,k-NN算法是计算输入到所有存储中心距离的加权平均,NICE则是计算输入到最近簇质心的距离,且每个簇中心的数量预先并未确定,而是直接从数据中获得实例。
当更新滤波器权重时,如果输入数据与其最近簇之间的距离超过预定阈值,则以输入为质心形成新的簇。为了避免学习中出现大的不连续性,利用迁移学习的思想将该最近簇中的所有中心以及相应的系数迁移到新形成的簇中,但不用于更新质心。另一方面,如果距离低于预定义的阈值,则将输入数据添加到最近的簇中,并执行一步质心更新。
3.2 NICE-KLMP算法
在NICE-KLMP中,我们使用第一个数据样本u(1)初始化第一个簇(子滤波器),该输入数据作为簇1的质心,即c(1)=u(1),c(1)表示簇1的矢量质心,并且由式(4)初始化得到第一个扩展系数a1(1)=μp|d(1)|(p-1)sgn(d(1))[12];对于后续的所有样本数据u(n),均分别计算样本数据与每个簇矢量质心的距离r,求得最小质心距离
(7)
其中num为簇总个数,c(j)为第j个簇的矢量质心。选择最小质心距离所在第j*个子簇,计算样本数据通过该子簇的输出数据
(8)
其中,Cj*表示第j*个簇中心点集合,|Cj*|表示集合Cj*的元素个数,Cj*(i)表示第j*个簇中第i个中心点, aj*(i)表示第j*个簇中第i个扩展系数。计算得到输出误差
e(n)=d(n)-y(n)
(9)
其中d(n)为期望输出。
假设质心阈值为rc,当选择高斯核作为核函数时,可利用非标准化标准差σk 来表示质心阈值[7]
(10)
其中,h为核参数,ξ为一个正整数。根据最小质心距离与质心阈值,进行如下两种运算:
1)簇群保留:当
时,分配输入样本数据到其最近的簇中,更新最近簇中的中心数、质心以及扩展系数。
2)拆分:当
时,建立新簇,且用输入样本数据形成新簇的质心和相应扩展系数。
显然,簇群保留和拆分行为都不会改变KLMP算法,当输入新样本数据时,KLMP算法更新全局滤波器的权重,而NICE-KLMP则是将样本数据分配到最近的子滤波器中并更新该子滤波器的权重或者分离出新的簇,形成新的子滤波器。
上述方法中,当拆分形成新簇时,需要用一个样本数据从头开始进行子滤波器的初始化更新,这会导致滤波器性能在时间上不连续。从长远来看,这种跳跃微不足道,但是,对于短期更新,需要复制来自最近簇的权重和中心(虽然该簇群的质心超出质心阈值,但在空间上仍然最接近),从而实现在时间上的连续。因此得到本文所提出的NICE-KLMP算法如表1所示。
表1 NICE-KLMP算法
Tab.1 NICE-KLMP algorithm
初始化:选择合适的参数μ、p和核κa1(1)=μpd(1)(p-1)sgn(d(1)),c(1)=u(1),C1={u(1)},簇总个数num=1L(1)=1 %L(1)表示簇1中用于质心更新的有效长度s(1)=1 %s(1)表示簇1中中心点个数输入训练对{u(n),d(n)}:由式(7)得到最小质心距离rcmin和其所在簇序号j∗由式(8)计算输出数据y(n)由式(9)计算输出误差e(n)若rcmin≤rc:存储新的中心:Cj∗={Cj∗,u(n)}计算并存储第j∗个子簇的扩展系数:aj∗(s(j∗)+1)=μpe(n)(p-1)sgn(e(n));更新第j∗个子簇的质心位置、有效长度和中心点总个数:c(j∗)=L(j∗)c(j∗)+u(n)L(j∗)+1,L(j∗)=L(j∗)+1,s(j∗)=s(j∗)+1;否则,建立新簇:c(num+1)=u(n),L(num+1)=1;迁移最近簇的中心点:Cnum+1={Cj∗,u(n)}迁移并更新最近簇的扩展系数:s(num+1)=s(j∗)+1,anum+1(s(num+1))=μpe(n)(p-1)sgn(e(n)),anum+1={aj∗,anum+1(s(num+1));更新簇总个数:num=num+1。
3.3 NICE-QKLMP算法
NICE-QKLMS算法中,预定阈值包括质心阈值rc和量化阈值rq,当rq=
,NICE-QKLMP算法退化为NICE-KLMP算法。NICE-QKLMP算法除需执行NICE-KLMP算法的簇保留和拆分外,还增加了簇内合并运算。即由输入数据根据式(7)计算出最小质心距离
和最小质心距离所在簇Cj*,计算输入数据与第j*个簇中所有中心点的距离,找出最小中心距离
(11)
以及中心点所在序号m*,根据
与
与rq的大小,执行以下三种运算:
1)簇群保留:当且
时,将该样本数据分配到距离最近的簇中并保留样本数据,更新子滤波器的扩展系数和质心位置。
2)簇内合并:当
且
时,将此样本数据分配到最近的簇中并与此簇中距离最近的中心点合并,只使用子滤波器的输出误差e(n)更新该中心点u(m*)的扩展系数,簇的大小和质心位置保持不变。
3)拆分:当时,新样本用于形成新簇的质心和相应的扩展系数。为避免短期学习的不连续,将最近簇中的中心和相应权值迁移到新簇中。
因此得到本文提出的NICE-QKLMP算法如表2所示。
表2 NICE-QKLMP算法
Tab.2 NICE-QKLMP algorithm
初始化:选择合适的参数μ、p和核κa1(1)=μpd(1)(p-1)sgn(d(1)),c(1)=u(1),C1={u(1)},簇总个数num=1L(1)=1 %L(1)表示簇1中用于质心更新的有效长度s(1)=1 %s(1)表示簇1中中心点个数输入训练对{u(n),d(n)}:由式(7)得到最小质心距离rcmin和其所在簇序号j∗由式(8)计算输出数据y(n)由式(9)计算输出误差e(n)若rcmin≤rc:由式(10)求得最小中心距离rqmin和中心点所在序号m∗量化:若rqmin
3.4 NICE-KLMP和NICE-QKLMP算法的均方误差(MSE)收敛性分析
α稳定分布信号是一种更加广义化的高斯分布信号,具有与高斯信号相同的线性稳定特性[14],因此NICE-KLMP和NICE-QKLMP算法可类似于NICE-KLMS和NICE-QKLMS算法进行收敛性分析。
假设e-、e+分别为先验误差估计和后验误差估计;ω为权重矢量;ω*为最佳权重矢量;θ为权重误差矢量;
为α稳定分布噪声信号的均方差。θ、e-和e+的计算公式如下
(12)
根据文献[7]的MSE稳定性分析可推导得到,若NICE-KLMP算法的步长满足
(13)
则该算法的MSE收敛。
对于NICE-QKLMP算法,可分别对三种运算进行收敛性分析:
1)簇群保留:该运算将输入数据u(n)分配到最近的簇j*中且保留该数据,与NICE-KLMP算法相同,所以不会改变NICE-QKLMP算法的收敛性。
2)簇内合并:输入数据u(n)被分配到最近的簇j*中且用于更新最近的中心点u(m*)的权重。由NICE-QKLMS算法的收敛性分析[7]可推导得出,若NICE-QKLMP算法的步长满足
(14)
则该算法的MSE收敛。
3)拆分:该运算与NICE-KLMP算法相同,故不会影响NICE-QKLMP算法的收敛性。
由上述分析可得,NICE-KLMP和NICE-QKLMP算法在步长满足一定条件的情况下是收敛的。
4 仿真分析
本文将NICE-KLMP和NICE-QKLMP算法应用于Mackey-Glass时间序列的短期预测,分析比较NICE-KLMP、NICE-QKLMP、NICE-KLMS、LMP和KLMP算法的性能。
Mackey-Glass时间序列由下面的时间-延迟普通微分方程[16]生成:
(15)
参数设置为: b=0.2,c=0.1,τ=30。时间周期用一个6 s的采样周期进行离散。在实验中,选择自适应滤波器的阶数为12;高斯核参数为1;LMS算法的步长μ为0.005;NICE-KLMS、KLMP、NICE-KLMP和NICE-QKLMP算法的步长μ均为0.100;其中NICE-QKLMP算法的量化阈值rq为0.330。用3000个样本作为训练数据,100个样本作为测试数据,每一组均采用蒙特卡洛方法进行100次仿真,得到测试均方误差(MSE)曲线[17]和网络规模增长曲线,即训练时所需中心点的增长曲线。
4.1 参数选择
实验1 α稳定分布噪声背景下NICE-KLMP算法的质心阈值选取。α稳定分布噪声的各参数设置为对称系数β=0、位置参数a=0、特征指数α=1.4、分散系数γ=0.04,范数p=1.3。已知质心阈值是非标准差σk的线性函数,质心阈值的选择取决于正整数ξ。选取ξ分别为1、2、3、4,得到NICE-KLMP算法的测试MSE曲线和网络规模增长曲线如图1所示。
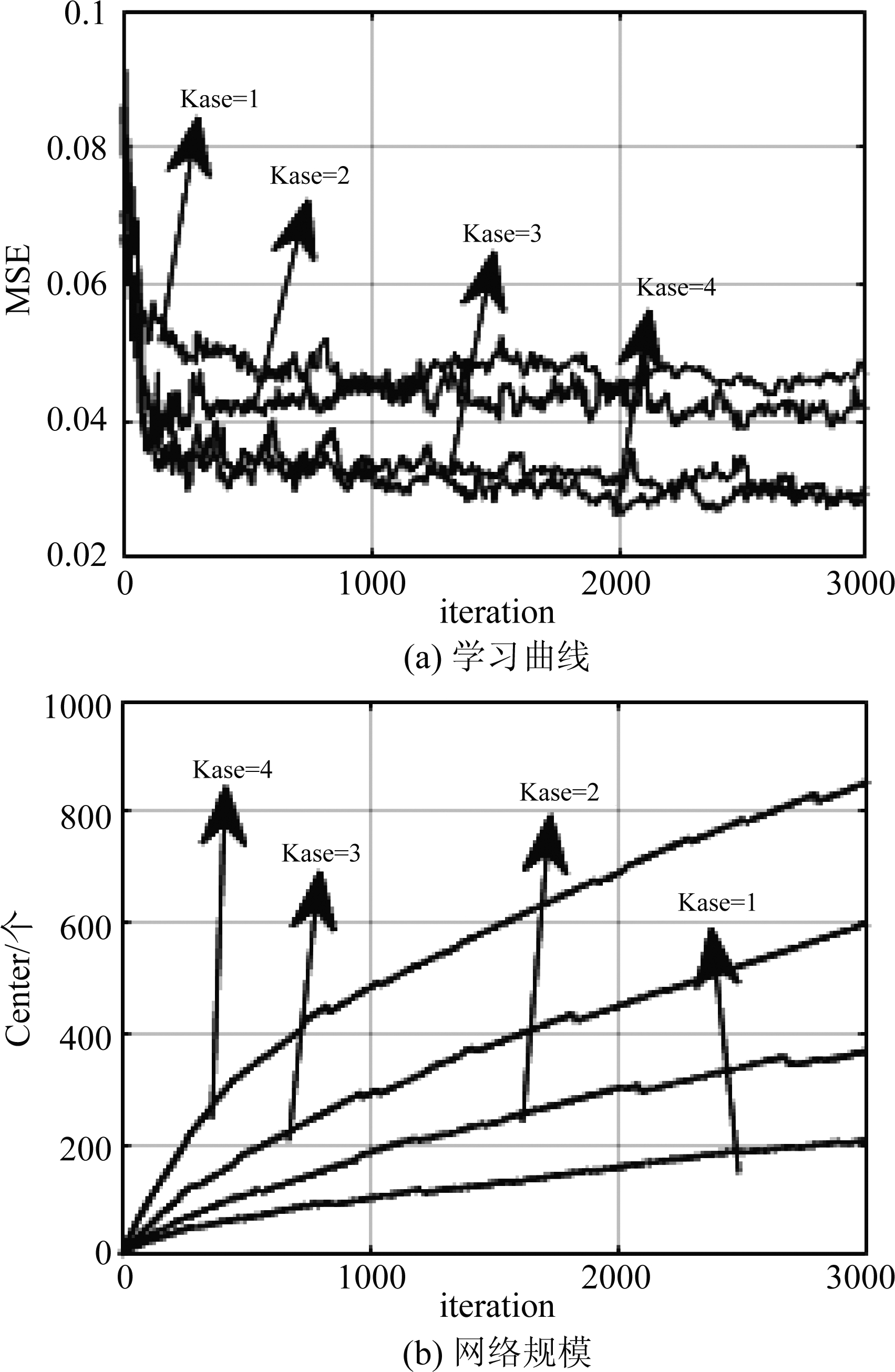
图1 不同质心阈值下NICE-KLMP算法的性能比较
Fig.1 Performance comparison of NICE-KLMP under different centroid distance threshold
由图1可得,在α稳定分布噪声背景下,随着正整数ξ减小(即质心阈值的减小),NICE-KLMP算法的网络规模逐渐减小,相应地NICE-KLMP算法的稳态均方误差逐渐增大。这是因为当质心阈值减小时,子滤波器的总个数增加,且每个子滤波器中的中心点训练数据减小,导致稳态均方误差增大。当ξ增大至3时,NICE-KLMP算法能够在网络规模较小的情况下得到较小的稳态均方误差。下文实验中取ξ=3。
实验2 α稳定分布噪声背景下NICE-KLMP算法的p值选取。质心阈值rc为2.1213,α稳定分布噪声的各参数同实验1,由于范数p需满足0<p<α<2,因此选择范数p分别为1.2、1.25、1.3、1.35,得到NICE-KLMP算法的测试MSE曲线如图2所示。
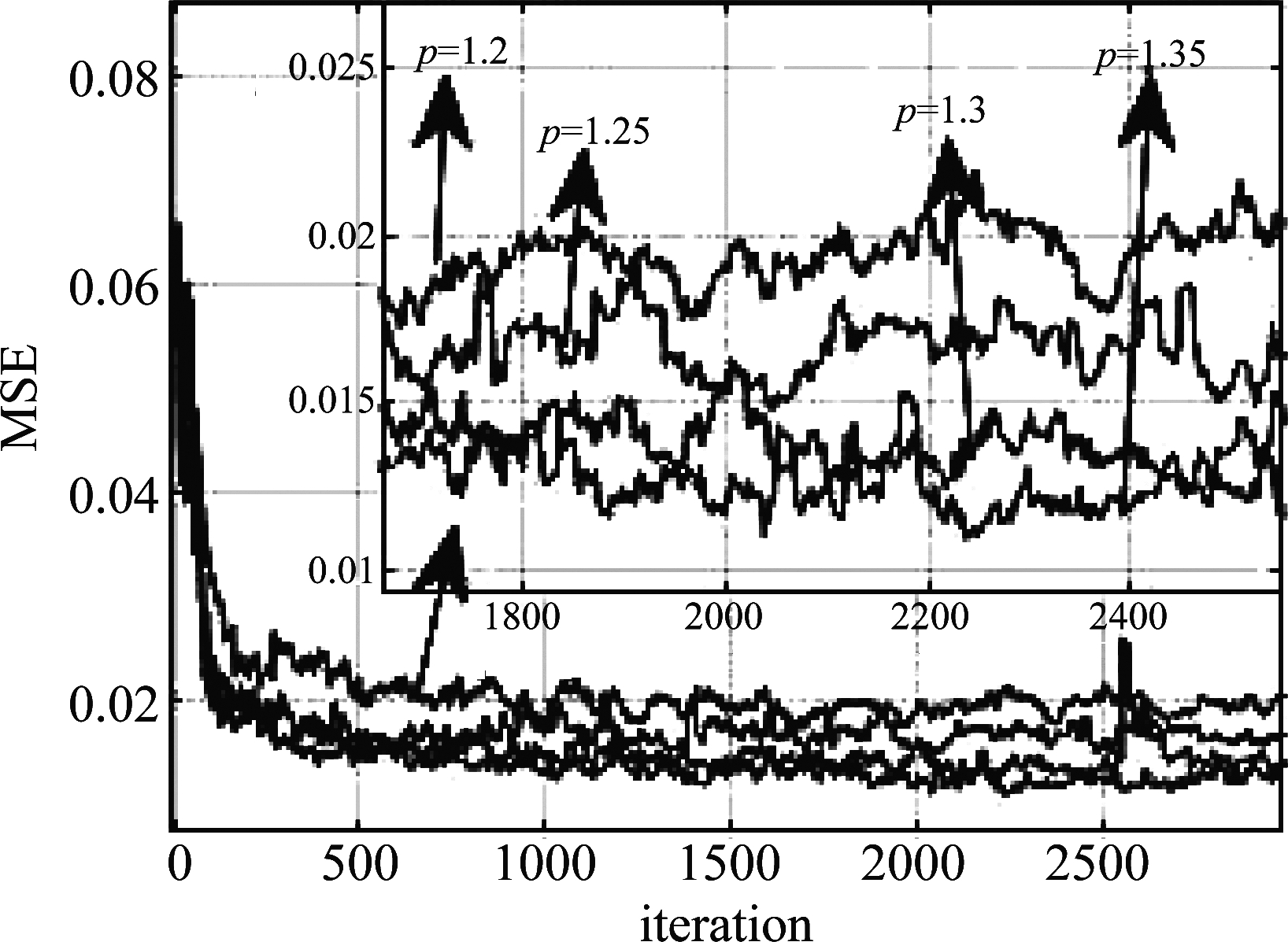
图2 特征指数为1.4时,不同范数p下NICE-KLMP算法的性能比较
Fig.2 Performance comparison of NICE-KLMP under different norm when the characteristic index is 1.4
由图2可得,当特征指数α为1.4时,随着范数p增大,NICE-KLMP算法的稳态均方误差逐渐减小;当范数p值分别为1.3、1.35时,对NICE-KLMP算法稳态均方误差的影响相差不大。
综上所述,在以下仿真实验中,选择正整数ξ为3,即质心阈值dc为2.1213;当α稳定分布噪声的特征指数α已知时,选择p=α-0.1。
4.2 算法仿真与性能分析
实验3 高斯噪声背景下NICE-KLMS、KLMP、NICE-KLMP算法的性能比较。高斯白噪声的均值和方差分别为0、0.04,得到的三种算法的测试MSE曲线和网络规模增长曲线如图3所示。
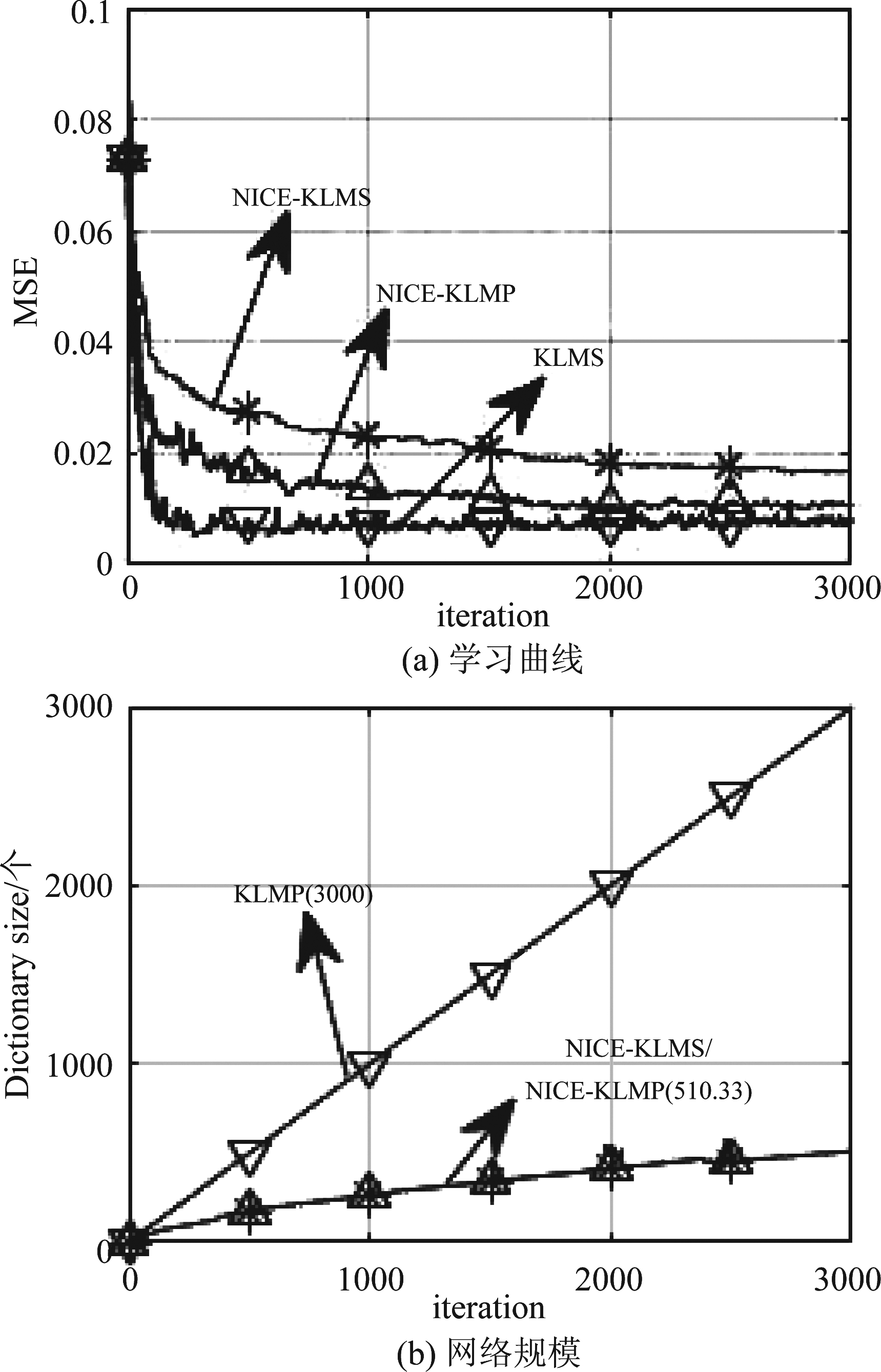
图3 高斯噪声下NICE-KLMS、KLMP、NICE-KLMP性能比较
Fig.3 Performance comparison of NICE-KLMS, KLMP and NICE-KLMP under gaussian noise
由图3(a)可得,在高斯噪声背景下,KLMP算法的收敛速度最快且稳态均方误差最小,NICE-KLMP算法的性能次之,NICE-KLMS算法的收敛速度最慢且稳态均方误差最大。由图3(b)可得,KLMP算法的网络规模随着迭代次数线性增加,而NICE-KLMS和NICE-KLMP算法的网络规模增加很缓慢,KLMP算法的网络规模明显大于NICE-KLMS和NICE-KLMP算法。NICE-KLMS和NICE-KLMP算法均将整个空间分为三个子空间,每一个子空间对应一个子滤波器,每次训练时平均仅使用510.33个中心点,比KLMP算法的3000个中心点少很多,所以NICE-KLMS和NICE-KLMP算法以牺牲收敛速度和稳态均方误差为代价减少了训练时的计算量。
实验4 α稳定分布噪声背景下NICE-KLMS、KLMP、NICE-KLMP算法的性能比较。α稳定分布噪声的各参数设置同实验1,信噪比SNR为-10 dB,得到三种算法的测试MSE曲线和网络规模增长曲线如图4所示。
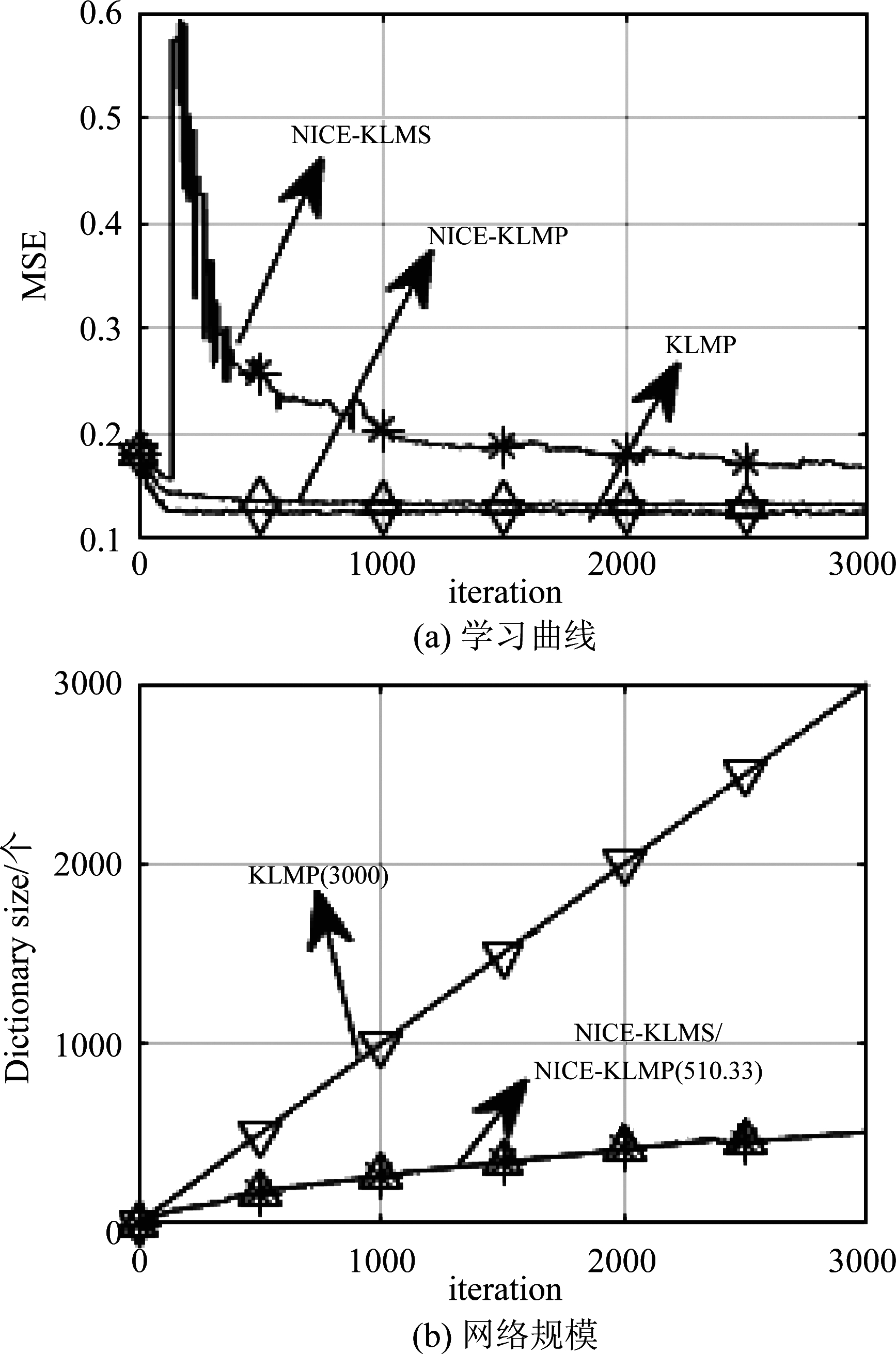
图4 α稳定分布噪声下NICE-KLMS、KLMP、NICE-KLMP性能比较
Fig.4 Performance comparison of NICE-KLMS, KLMP and NICE-KLMP under α-stable distributed noise
由图4(a)可得,在α稳定分布噪声背景下,NICE-KLMS的测试MSE曲线波动非常剧烈。而NICE-KLMP和KLMP算法没有显著的波动,有较好的稳态和抗噪声性能。图4(b)结果与图3(b)结果类同。因为在测试MSE性能相当的情况下,NICE-KLMP算法比KLMP算法的网络规模大大减少,所以在α稳定分布噪声环境下,NICE-KLMP算法优于KLMP算法。
实验5 α稳定分布噪声背景下LMP、KLMP、NICE-KLMP、NICE-QKLMP算法的性能比较。α稳定分布噪声参数同实验1,得到四种算法的测试MSE曲线和网络规模增长曲线如图5所示。
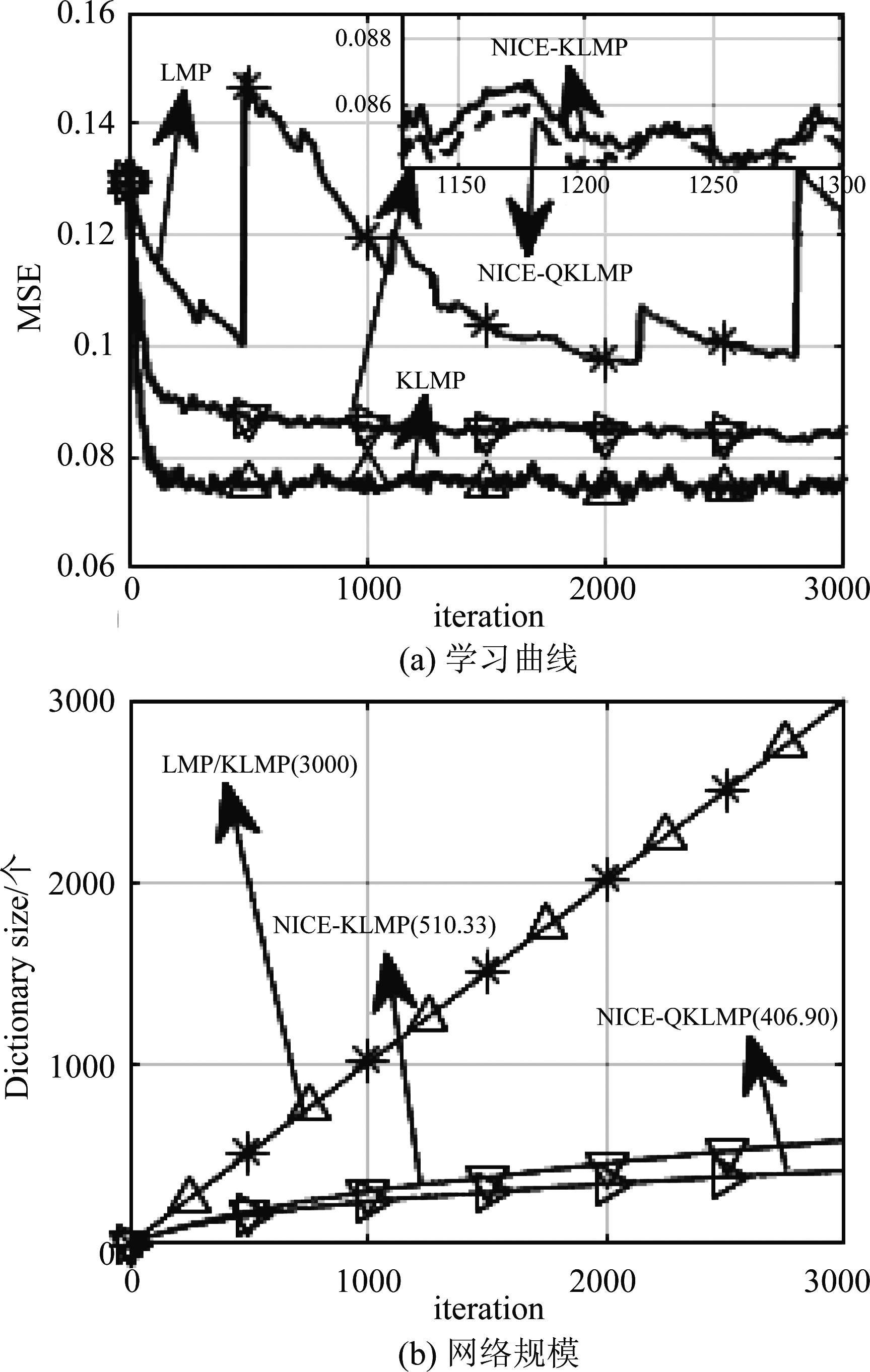
图5 α稳定分布噪声下LMP、KLMP、NICE-KLMP、NICE-QKLMP性能比较
Fig.5 Performance comparison of LMP, KLMP, NICE-KLMP and NICE-QKLMP under α-stable distributed noise
由图5(a)可得,LMP算法的测试MSE曲线波动剧烈,稳定性最差;在KLMP、NICE-KLMP和NICE-QKLMP三种算法中,KLMP算法的稳态均方误差最小,NICE-KLMP算法的稳态均方误差较NICE-QKLMP算法略小一些,但是可以认为基本相同。由图5(b)可以看出,在第3000次迭代时,KLMP算法将3000个中心点全部作为训练数据训练模型,这导致每次训练的计算量非常大;NICE-KLMP算法将整个空间分为三个子空间,它们分别表示一个子滤波器,每次训练时平均使用510.33个中心点,这使训练模型的计算量大大降低;而NICE-QKLMP算法每次训练时平均仅使用406.90个中心点,该算法引入在线矢量量化方法,不仅将整个空间分为三个子空间,而且对每个输入数据进行处理,将冗余的数据量化到距离最近的数据上,因此,该算法在降低计算量的同时还大大减少了存储容量。
实验6 α稳定分布噪声背景下不同特征指数α对NICE-KLMP、NICE-QKLMP算法的性能影响。选取α稳定分布噪声的特征指数α分别为1.4、1.6、1.8,噪声其他参数同实验1;p分别选择1.3、1.5、1.7,得到两种算法的测试MSE曲线如图6所示。
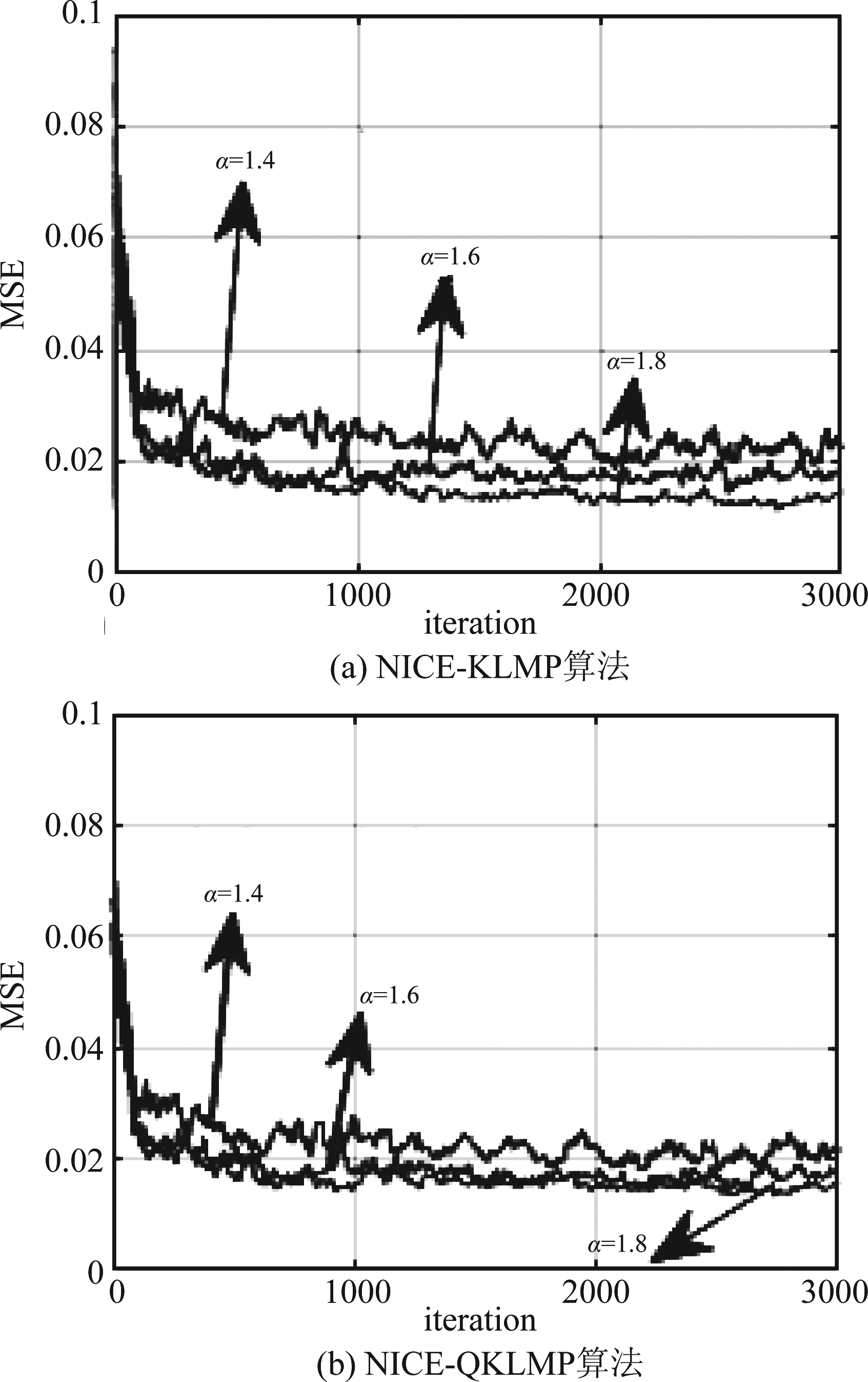
图6 不同特征指数α下NICE-KLMP、NICE-QKLMP算法性能比较
Fig.6 Performance comparison of NICE-KLMP and NICE-QKLMP under different characteristic indexes
由图6(a)、(b)可知,随着特征指数α增大,NICE-KLMP和NICE-QKLMP算法的稳态均方误差稍有减小。这是因为特征指数α决定了α稳定分布噪声的脉冲特性,特征指数α越大,噪声分布的脉冲特性越弱,对信号的影响也越小,因此随着α增大,两种算法的收敛性能稍有提高。
实验7 α稳定分布噪声背景下不同信噪比SNR时NICE-KLMP、NICE-QKLMP算法性能。信噪比SNR分别为-10 dB、-15 dB、-20 dB,其他实验参数同实验1,得到两种算法的测试MSE曲线如图7所示。
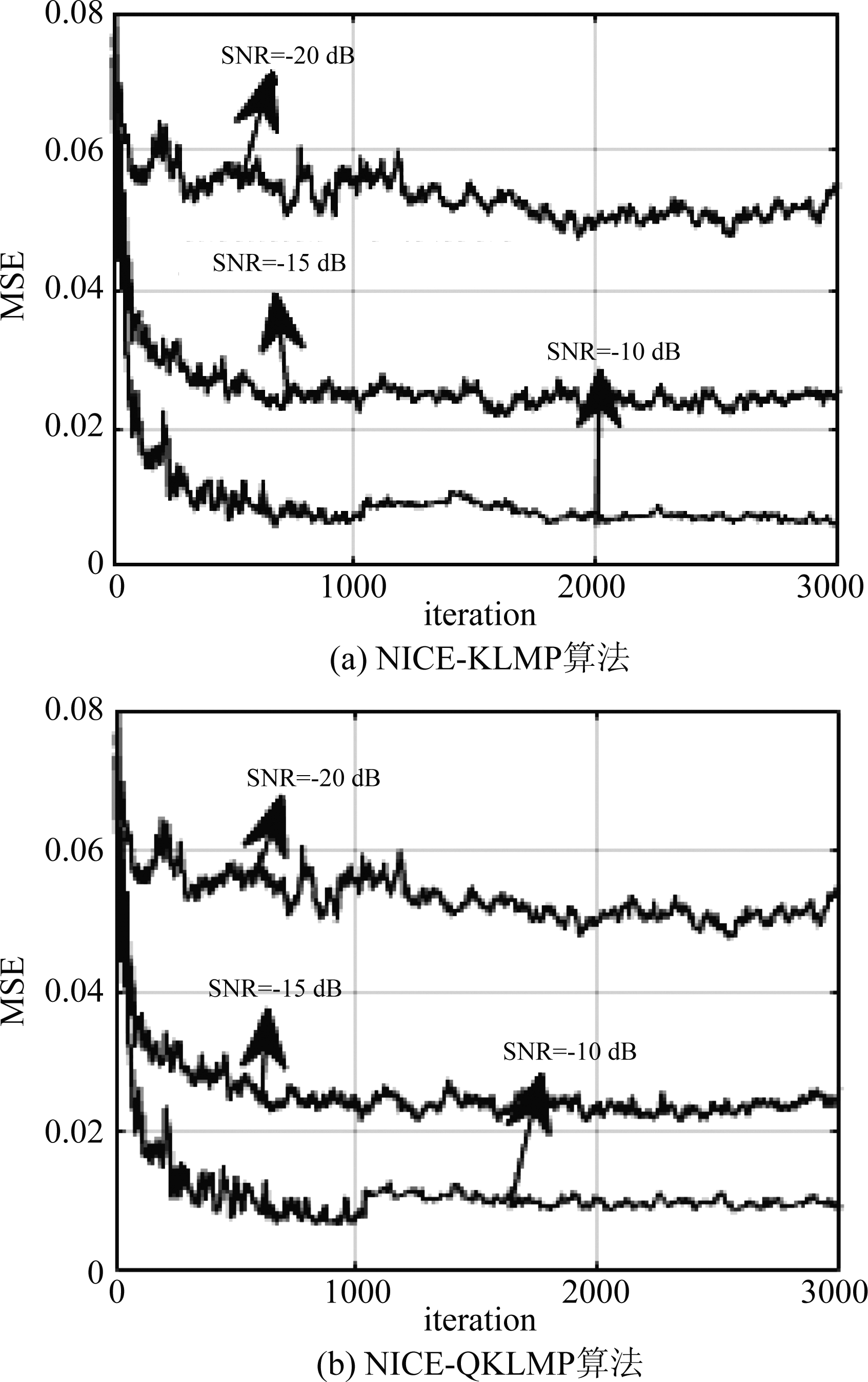
图7 不同信噪比SNR下NICE-KLMP、NICE-QKLMP算法的性能比较
Fig.7 Performance comparison of NICE-KLMP and NICE-QKLMP algorithms with different SNR
由图7(a)、(b)可知,随着信噪比SNR逐渐减小,NICE-KLMP和NICE-QKLMP算法的稳态均方误差逐渐增大。当SNR高于-15 dB时,两种算法仍具有较快的收敛速度和较低的稳态均方误差;但当SNR降低到-20 dB时,两种算法的稳态均方误差太大,波动明显。
综上实验可得, NICE-QKLMP算法的性能最好,NICE-KLMP算法次之,KLMP算法最差。NICE-KLMP和NICE-QKLMP算法在信噪比大于-15 dB时能保持较好的收敛性能,且两种算法以牺牲非常小的收敛速度和稳态均方误差为代价大大降低训练时的计算量,其中NICE-QKLMP算法还结合在线矢量量化方法减少了训练数据的存储容量。
5 结论
针对α稳定分布噪声下核最小平均P范数算法的计算复杂度高问题,本文应用最近实例质心估计和在线矢量量化方法,提出了NICE-KLMP和NICE-QKLMP算法。Mackey-Glass 时间序列预测的仿真结果表明, NICE-KLMP和NICE-QKLMP 算法的复杂度显著低于LMP、KLMP算法,且抗脉冲噪声性能显著强于LMP和NICE-KLMS算法。
[1] Liu W F, Pokharel P P, Principe J C. The kernel least mean square algorithm[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 543-554.
[2] 赵知劲, 金明明. 基于块自适应滤波的核最小均方算法[J]. 计算机工程, 2017, 43(9): 162-166.
Zhao Z J, Jin M M. Kernel least mean square algorithm based on block adaptive filtering[J]. Computer Engineering, 2017, 43(9): 162-166.(in Chinese)
[3] Liu Y, Sun C, Jiang S D. A kernel least mean square algorithm based on randomized feature networks[J]. Applied Sciences, 2018, 8(3): 458.
[4] Chen B D, Zhao S L, Zhu P P, et al. Quantized kernel least mean square algorithm[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(1): 22-32.
[5] Chen B D, Qin Z D, Sun L. Steady-state mean square performance of a sparsified kernel least mean square algorithm[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, USA, 2017: 2701-2705.
[6] Zheng Y F, Wang S Y, Feng Y L. Convex combination of quantized kernel least mean square algorithm[C]∥Sixth International Conference on Intelligent Control and Information Processing, Wuhan, China, 2016: 186-190.
[7] Li K, Principe J C. Transfer learning in adaptive filters: the nearest instance centroid-estimation kernel least mean square algorithm[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6520- 6535.
[8] Li S, Qiu T S, Zhang S F. Space-time blind equalisation in impulsive noise[J]. IET Signal Processing, 2009, 3(6): 445- 458.
[9] Kim N. Blind Signal processing based on information theoretic learning with kernel-size modification for Impulsive Noise Channel Equalization[J]. Wseas Trans on Communications, 2010, 9(7): 418- 428.
[10] Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010.
[11] 沈峰, 姜利, 单志明. 非高斯噪声环境下的信号检测与自适应滤波方法[M]. 北京: 国防工业出版社, 2014: 144-164.
Shen F, Jiang L, Shan Z M. Signal Detection and Adaptive Filtering in Non-Gauss Noise Environment[M]. Beijing: National Defence Industrial Press, 2014: 144-164.(in Chinese)
[12] 赵知劲, 金明明. α稳定分布噪声下的核最小平均P范数算法[J]. 计算机应用研究, 2017, 34(11): 3308-3310.
Zhao Z J, Jin M M. Kernel least mean P-norm algorithm in α stable distribution noise[J]. Application Research of Computers, 2017, 34(11): 3308-3310.(in Chinese)
[13] Washizawa Y, Yamashita Y. Kernel wiener filter[J]. IEICE Technical Report Neurocomputing, 2004, 103(733): 73-78.
[14] 邱天爽, 张旭秀, 李小兵. 统计信号处理: 非高斯信号处理及其应用[M]. 北京: 电子工业出版社, 2004: 140-159
Qiu T S, Zhang X X, Li X B. Statistical signal processing: non-gaussian signal processing and its applications[M]. Beijing: Publishing House of Electronics Industry, 2004: 140-159.(in Chinese)
[15] Altman N S. An introduction to kernel and nearest-neighbor nonparametric regression[J]. American Statistician, 1992, 46(3): 175-185.
[16] Liu W F, PARK II, Principe J C. An information theoretic approach of designing sparse kernel adaptive filters[J]. IEEE Trans on Neural Networks, 2009, 20(12): 1950-1961.
[17] Wu Z Z, Shi J H, Zhang X, et al. Kernel recursive maximum correntropy[J]. Signal Processing, 2015, 117: 11-16.
