1 引言
随着社会的高速发展,基于GPS的室外导航系统已得到广泛的发展和应用,近年来,室内已经成为人们工作生活的场所,室内定位技术成为了研究和发展的热门问题,但由于卫星信号容易受到障碍物的干扰造成定位精度下降,对定位目标不能达到精确的定位,已经很难满足人们的日常需求[1]。目前常用的室内定位算法有泰勒级数算法、Chan算法与Elman神经网络算法等[2- 6],Sun Jian等人提出了一种基于最小二乘法和优化算法的室内到达时间定位三维算法,通过模拟和现场测试来评估测距和定位精度[7];Liu Ying等人提出了基于CFSFDP的自适应室内定位方法[8]。Elman神经网络算法与其他定位算法相比优势显著,因此是当前国内外室内定位学者研究重点之一[9]。本文提出了DHOHF-Elman神经网络定位算法,对传统Elman神经网络拓扑结构进行改进,较好地克服了传统Elman神经网络算法的不足[10]。本文选用IEEE802.15.4a信道模型收集样本数据[11-12],并利用DHOHF-Elman神经网络的定位算法将测到的RSSI(Received Signal Strength Indication,RSSI)值作为输入对网络进行训练与测试,进而提高了定位精确度和收敛速度。
2 超宽带定位信道模型
基于超宽带定位法是新兴的一种无线电技术,与传统通信技术的定位方法有很大区别,其不需要利用传统通信系统中的载波,而是将小于1 ns极窄高斯脉冲通过发送和接收传输数据,这种脉冲具有超宽的频谱,其穿透力极强,其谱密度较低瞬时功率高,可进行高速通信,且该定位技术具有电路简单,高分辨率,定位精度高和较好的抗多径效果等优点[13-16]。利用UWB技术进行室内定位,参数不同的信道模型适用于不同的室内环境,目前常用的信道模型有Δ-K模型、S-V模型和IEEE802.15.4a模型等,相对成熟的信道模型为IEEE802.15.4a信道模型,该模型是IEEE802.15小组基于S-V模型开发设计的适用于无线传感器网络的信道模型,其频谱可在2 GHz~10 GHz之间,适用范围广泛,可用于复杂的室内环境[17-18]。因此本文选取UWB定位技术中接收信号强度法来研究室内定位问题,为了在信号覆盖不到的室内环境下实现UWB精确定位,可选用IEEE802.15.4a信道模型作为仿真的信道模型。
通过参考文献可定义天线衰减系数为![]() 基准频率fc=5 GHz,得到信号衰减值和发射信号频率与距离之间的方程为:
基准频率fc=5 GHz,得到信号衰减值和发射信号频率与距离之间的方程为:
(1)
其中:
根据美国联邦通信委员会的规定,PL0表示当距离d0为1 m时的信号衰减值,取PL0=43.9 dB;天线的实际发射功率为PTX-amp( f );发射效率为ηTX-ant( f );取天线增益Aant=3;n为路径损耗指数取1.79;t=1.12±0.12;k为频率对路径损耗影响因子。这种信道模型适用于根据距离与路径损耗关系的模型,可达到较好的超宽带信号拟合的效果,因此在采集样本数据时采用此信道模型。
3 Elman神经网络算法优化方案
Elman神经网络在90年代被Elman提出,是对人大脑的基本特性的模拟和抽象,是同时具有局部记忆单元和局部反馈连接的一种递归神经网络。传统Elman神经网络结构主要包括输入层、承接层、隐含层和输出层四个部分,其中通常被用来做延时算子的联系单元是承接层,可以通过训练学习对其连接权进行修正,承接层的反馈连接部分主要由一组结构单元组成,其作用是记忆上一时刻输入层的输出值,通过将输入神经元加权再传递给输出神经元,输出神经元通过加权的形式输出,另一边,承接层神经元将接收隐含层神经元传递的数据,等待下一时刻把数据回传至隐含层。其网络拓扑结构如图1所示。
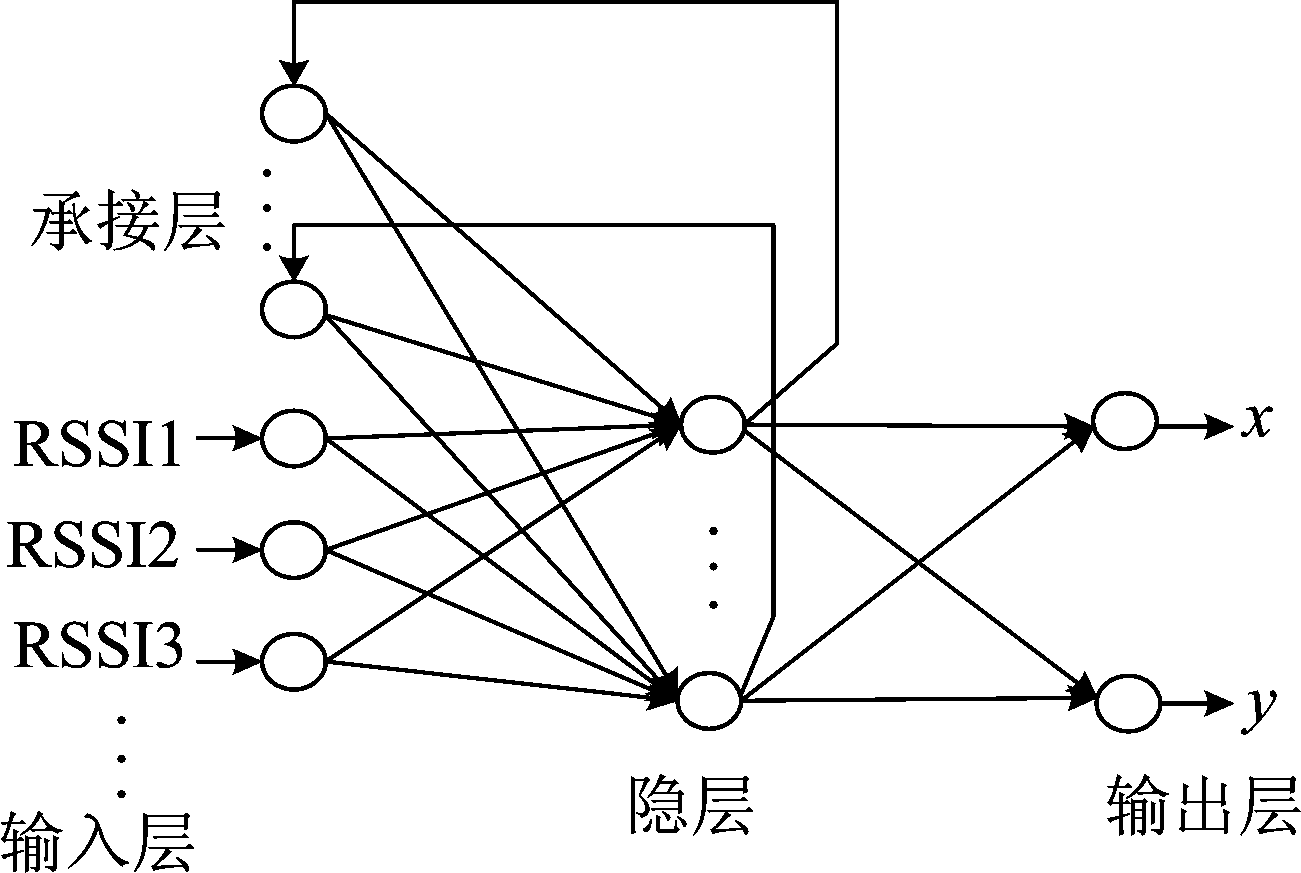
图1 传统Elman神经网络拓扑结构图
Fig.1 Topology of traditional Elman neural network
传统Elman神经网络只考虑了单个隐含层节点的反馈,但没有注意到其余层节点之间的反馈也会对网络的预测精度和信息处理功能产生影响,进而导致最终输出结果的不同,因此在处理室内定位问题上可能存在精度不达标,实时传输性差的问题,所以对传统的算法进行改进是十分必要的,由于传统Elman神经网按神经元之间复杂的连接关系可组成不同的网络结构,从而产生不同的信息处理效果,因此本文在传统Elman神经网络的基础上设计了一个含有双隐含层的神经网络结构,即同时存在内部反馈和外部反馈机制,达到了两种反馈机制相组合的可循环反馈神经网络的效果。内部反馈连接是由输入层、第一隐含层和第一承接层三部分组成的连接,外部反馈连接则是由第二隐含层、第二承接层与输出层组成的连接。也就是通过增加神经网络一层隐含层来达到提高训练精度的效果,在隐含层增加一层承接层可使系统具有适应时变特性的能力从而增强了全局网络的稳定性。将通过增加一层承接层来对输出层的网络历史信息进行存储记忆并把它作为第二隐含层的部分输入,可减少隐含层的输入负荷,从而达到了分担单一隐含层压力的目的。这种内外反馈机制相结合的网络结构比传统Elman神经网络增加了输出节点的反馈,不仅对神经网络输出的历史信息进行了充分利用,而且提高了网络对历史信息的灵敏度,当输入较多时,可有效控制函数不被溢出和加快网络的收敛速度,能够有效地改善预测精度。
4 DHOHF-Elman神经网络模型建立
传统Elman神经网络采用的是单层神经元反馈机制,其学习方法是梯度下降法,存在网络训练不稳定、收敛速度缓慢、泛化性差以及易陷入局部最优解的问题,由于在现实生活中要保证室内定位系统的高时效性和高精度性,因此针对出现的以上问题,本文将从神经网络拓扑结构和神经网络学习方法两个方面对传统Elman神经网络进行改进,在保证网络全局稳定的情况下,可进一步提高算法收敛速度和定位精度,在一定程度上解决了上述问题。
4.1 网络拓扑结构的确定
DHOHF-Elman神经网络结构包括输入层、第一隐含层、第一承接层、第二隐含层、第二承接层和输出层六个部分。其中输入层的单元仅仅起到信号的传输作用,隐含层单元不具备信息处理功能,由它传出的神经元的值将由承接层接收,用来记忆隐含层单元上一时刻的输出值,承接层的神经元经过一定信号的延迟并完成信息存储后,再回传至隐含层,这种连接方式使得建立的神经网络具有动态的记忆功能,输出层神经元采用的是线性函数用相同的节点起到加权的作用,由于目前尚未有固定的模型来设置隐含层神经元的节点个数,通常可参考经验公式:
(2)
式中l隐含层节点个数;n表示输入层节点个数;m表示输出层节点个数;q为常数,取值范围通常为[0,10]。
根据经验公式可粗略估计出隐含层节点数的取值范围,经过多次尝试,分别对初始权值、阈值和隐含层节点个数进行优化,选取误差值最小时对应的节点数作为隐含层的节点数,最终确定改进的DHOHF-Elman神经网络各层神经元节点个数为1-10-10-1,即当输入层神经元节点数为1,隐含层神经元节点数为10,输出层神经元节点数为1时误差最小具有最好的预测性能。本文输入层采用的是线性函数,第一隐含层采用的是tansig函数,第二隐含层采用logsig函数作为激活函数,输出层固定采用purelin函数的组合。其函数表达式如下:
(3)
(4)
purelin(x)=kx
(5)
DHOHF-Elman神经网络拓扑结构如图2所示。
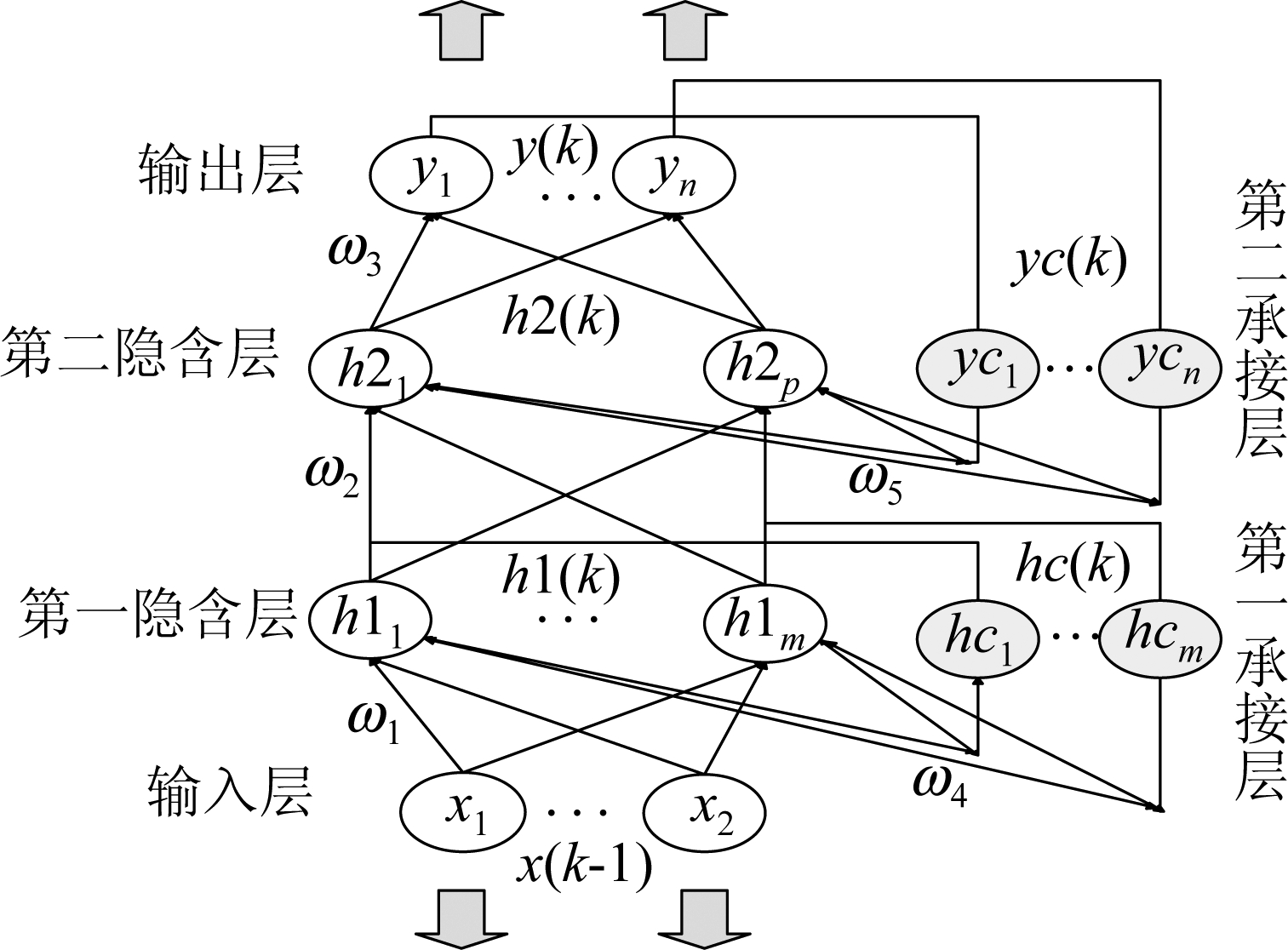
图2 DHOHF-Elman神经网络拓扑结构图
Fig.2 Topology of DHOHF-Elman neural network
如图3为仿真结构图能够更直观地表现DHOHF-Elman神经网络各层之间的连接关系。
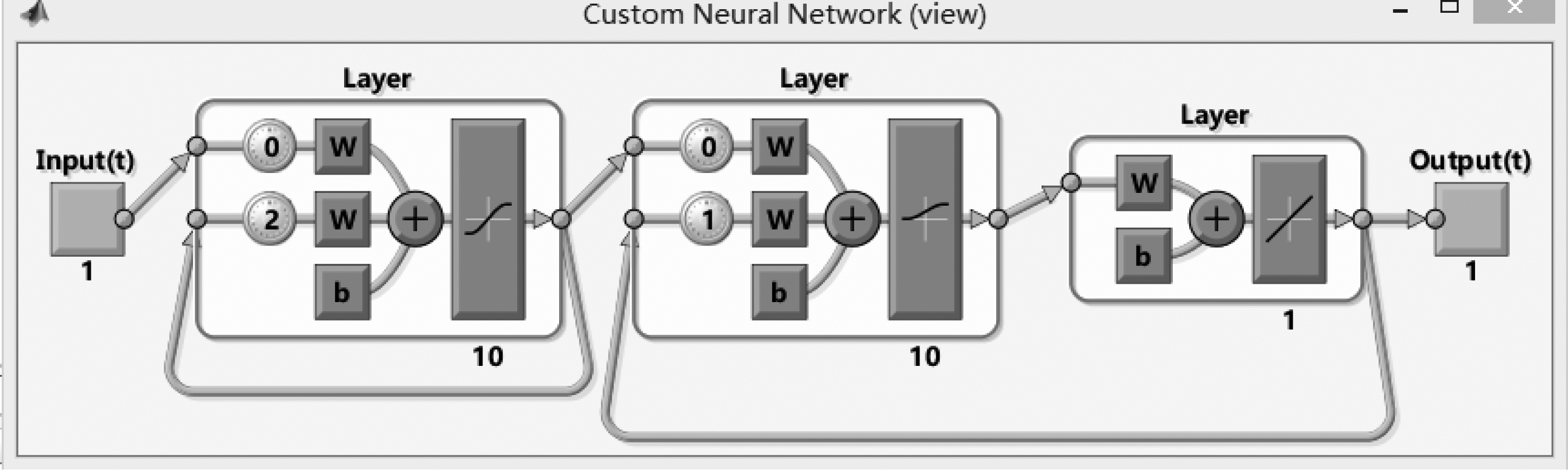
图3 DHOHF-Elman神经网络结构图
Fig.3 Structure of DHOHF-Elman neural network
设x=(x1,x2,...,xr)为第一隐含层的输入向量,改进的DHOHF-Elman神经网络数学模型如下:
h1(k)=f(ω1·x(k-1)+ω4·hc(k)-θ1)
(6)
hc(k)=h1(k-1)
(7)
h2(k)=f(ω2·h1(k)+ω5·yc(k)-θ2)
(8)
y(k)=g(ω3·h2(k)-θ3)
(9)
yc(k)=y(k-1)
(10)
其中:k-迭代时间步;h1表示第一隐含层的输出;第一隐含层神经元与第一承接层个数一致,hc表示第一承接层的输出;h2表示第二隐含层的输出;y表示输出层的输出;yc表示第二承接层的输出;函数f(·)表示隐含层神经元激活函数,即![]() 表示输出层神经元激活函数;ω1是第一隐含层到输入层连接权值;ω2是第二隐含层到第一隐含层连接权值;ω3是输出层到第一承接层连接权值;θ1表示第一隐含层阈值;θ2表示第二隐含层阈值;θ3表示输出阈值。设第k步系统的实际输出为yd(k),则输出的误差可用E表示,则函数公式为:
表示输出层神经元激活函数;ω1是第一隐含层到输入层连接权值;ω2是第二隐含层到第一隐含层连接权值;ω3是输出层到第一承接层连接权值;θ1表示第一隐含层阈值;θ2表示第二隐含层阈值;θ3表示输出阈值。设第k步系统的实际输出为yd(k),则输出的误差可用E表示,则函数公式为:
(11)
更新网络权值的公式为:
ω(t)=ω(t-1)+Δω(t)
(12)
更新阈值公式同理。
4.2 学习算法的选取
在Elman神经网络训练中学习算法的选取往往对最后的结果产生很大的影响,所以选取合适的学习算法是成功构建Elman模型的关键。通过参考大量文献发现目前Elman神经网络的学习算法通常以traingdx和trainlm为主。本文分别将选取traingdx与trainlm为学习算法的Elman神经网络进行对比试验,发现在相同条件下,trainlm作为学习算法在本次对比试验中比traingdx学习算法网络表现更好,清晰地看出选取trainlm作为改进网络的学习算法具有更高的网络性能,学习速率高,收敛效果更好,训练速度快且预测精度高,得到的均方误差相对较小,适合中等规模的网络训练。结果如图4所示。
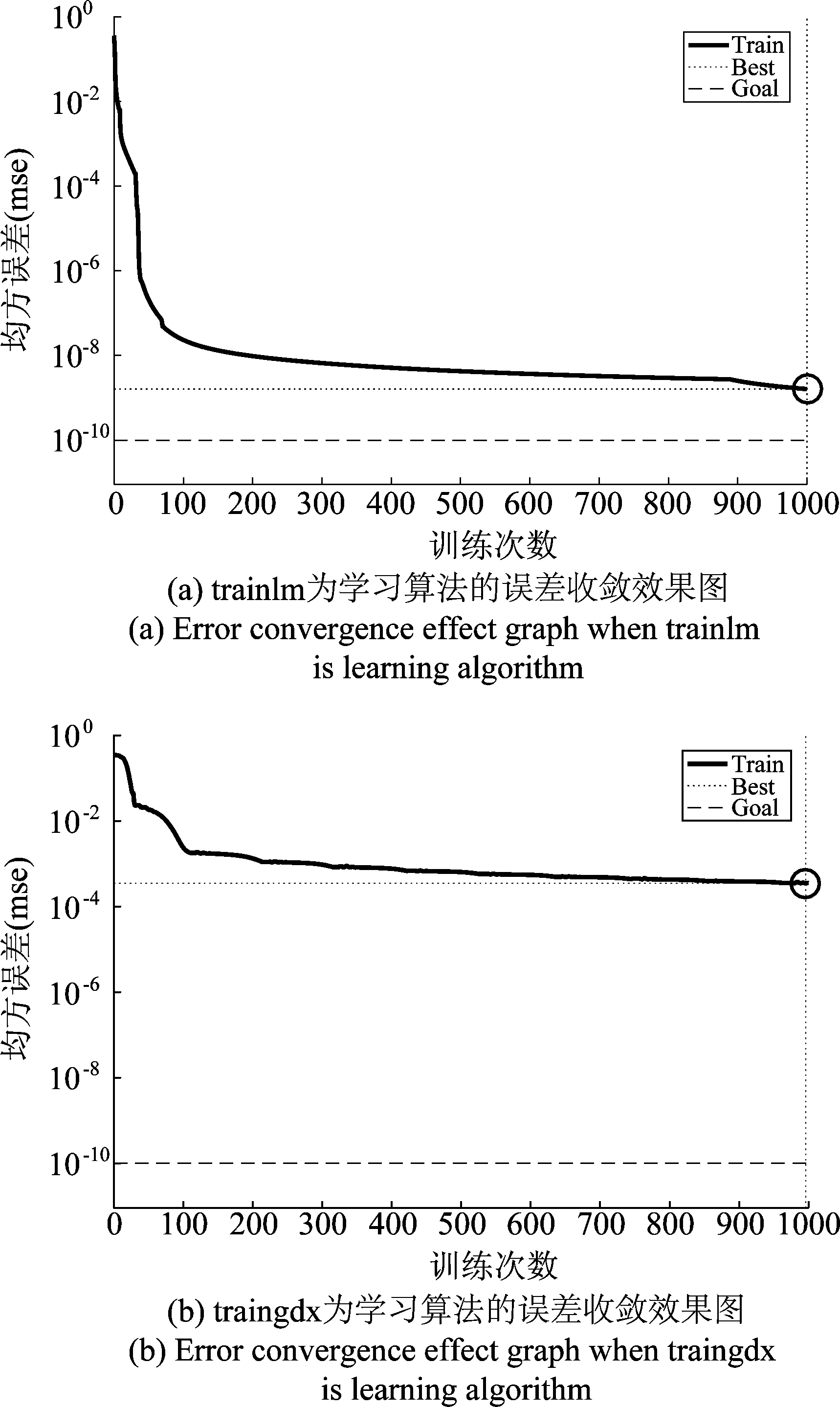
图4 不同学习算法误差收敛图
Fig.4 Error convergence effect graph of different learning algorithm
5 验证及结果分析
通过建立的信道模型产生大量实验数据,对其中的异常值进行筛选和剔除,在网络覆盖的范围内,选取合理的数据作为样本输入,对构建的Elman神经网络和优化后的DHOHF-Elman神经网络模型进行训练,设置每次实验中的最大训练次数为1000次,训练误差为0.01,学习率为0.1。再取一组实验数据作为测试样本,其中将测量得到的RSSI值归一化并代入已经训练好的网络中,得到输出,并将输出结果进行反归一化得到神经网络模型估计的测距结果,将这个结果与信道模型得到的测距结果进行仿真对比,可以确定算法的定位精度。
算法流程图如下:
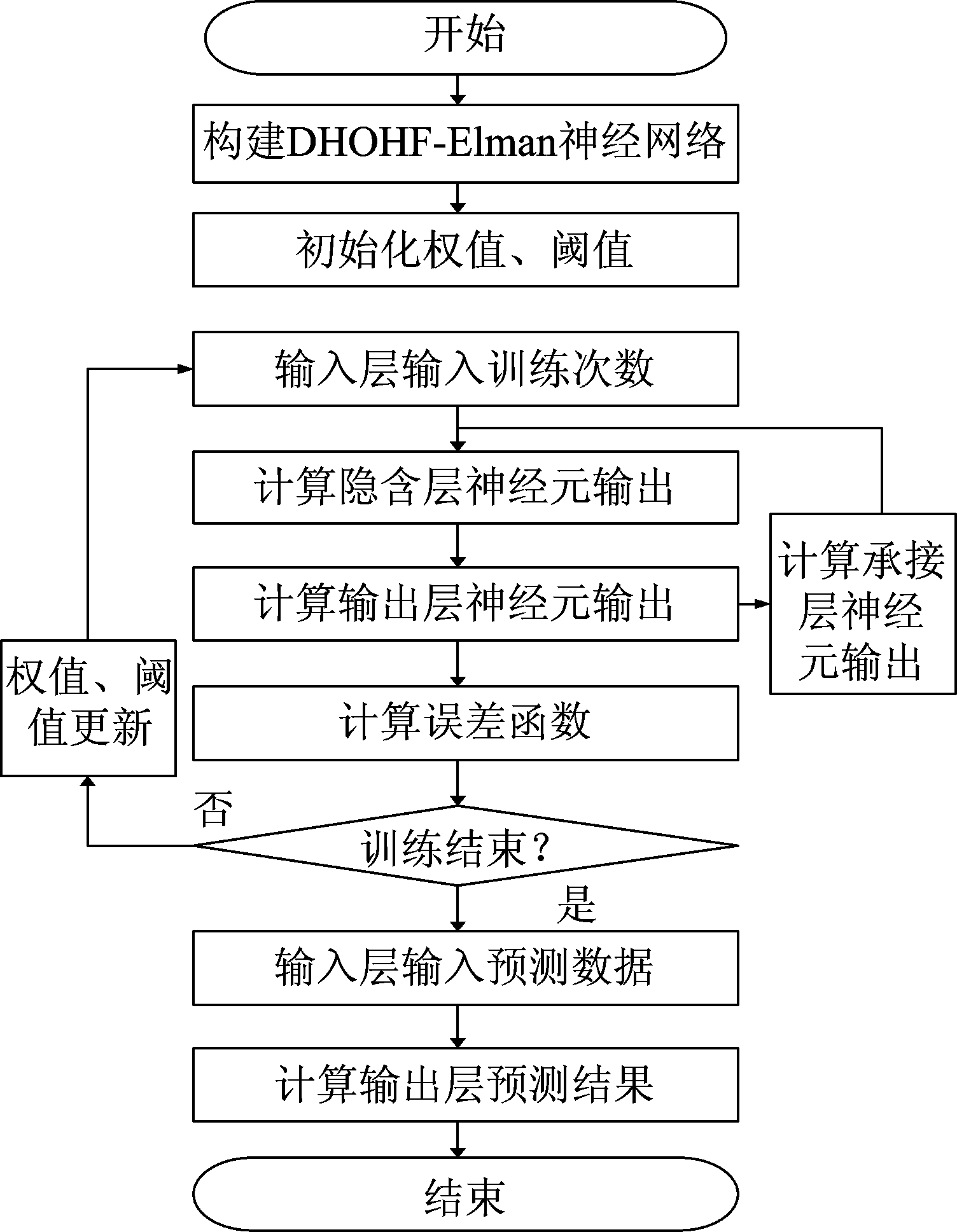
图5 算法流程图
Fig.5 Algorithm flow graph
按照如上所示的流程框图,将对传统的算法和优化后的算法应用于室内定位问题,并进行性能仿真对比,可得到如图6的结果。
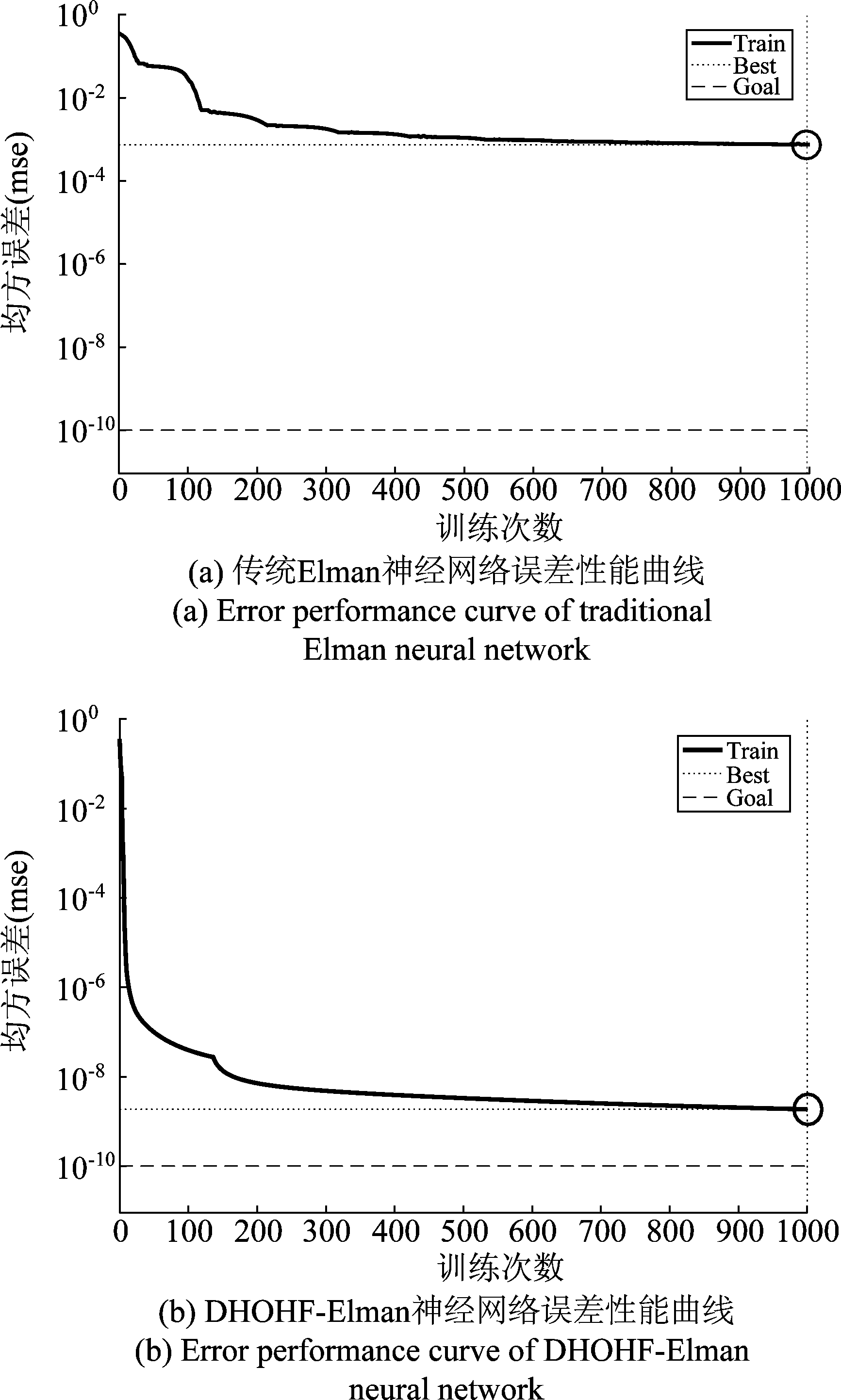
图6 2种神经网络的误差性能曲线
Fig.6 Error performance curve of two neural network
传统Elman神经网络测距模型训练得到的均方误差如图6(a)所示,可发现其收敛速度较慢,训练次数需高达100次均方误差才能下降到0.01以下。而DHOHF-Elman神经网络误差性能曲线如图6(b)所示,训练次数大概在20次时,均方误差就下降到了0.01,且收敛速度远远大于传统Elman神经网络。
为了更好的表现DHOHF-Elman神经网络与传统Elman神经网络在定位误差上的区别,网络拟合数据与真实数据的对比结果如图7所示,由实验结果可清晰地看出传统Elman神经网络训练后拟合值与真实值有较大误差,而DHOHF-Elman神经网络模型训练后拟合数据和真实数据曲线基本吻合,定位精度更高。
将传统Elman神经网络和DHOHF-Elman神经网络分别在有无高斯白噪声环境下进行仿真验证,仿真后对曲线进行平滑处理如图8(a)、(b)所示,可以清楚地看出在无高斯白噪声环境下传统Elman神经网络模型的定位误差泛化,容易造成局部最优解,而DHOHF-Elman神经网络模型定位误差与信号强度之间变化趋势明显,且不易陷入局部最优解,如在信号强度值为-30 dB时,传统的Elman神经网络定位误差大概在0.2 m,而DHOHF-Elman神经网络定位误差达到0.001 m,其定位精度远远高于传统Elman神经网络。在存在高斯白噪声环境下对两种神经网络模型进行定位误差分析如图8(c)、(d)所示,可清楚地看到传统Elman神经网络模型下定位误差泛化严重,而DHOHF-Elman神经网络模型下的定位误差明显小于传统Elman神经网络模型,且定位误差与强度之间变化趋势较为明显,定位效果更好。
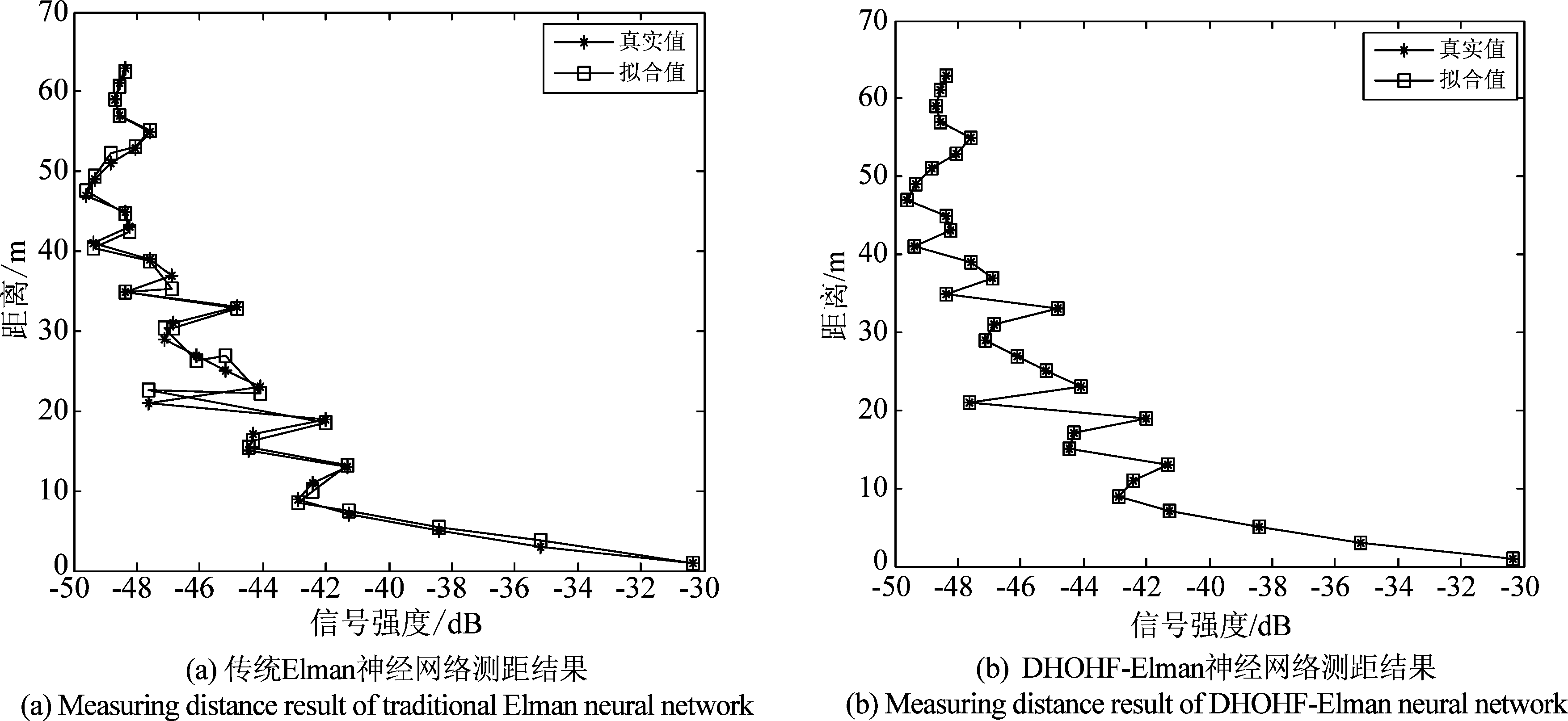
图7 2种神经网络的测距结果
Fig.7 Measuring distance result of two neural network
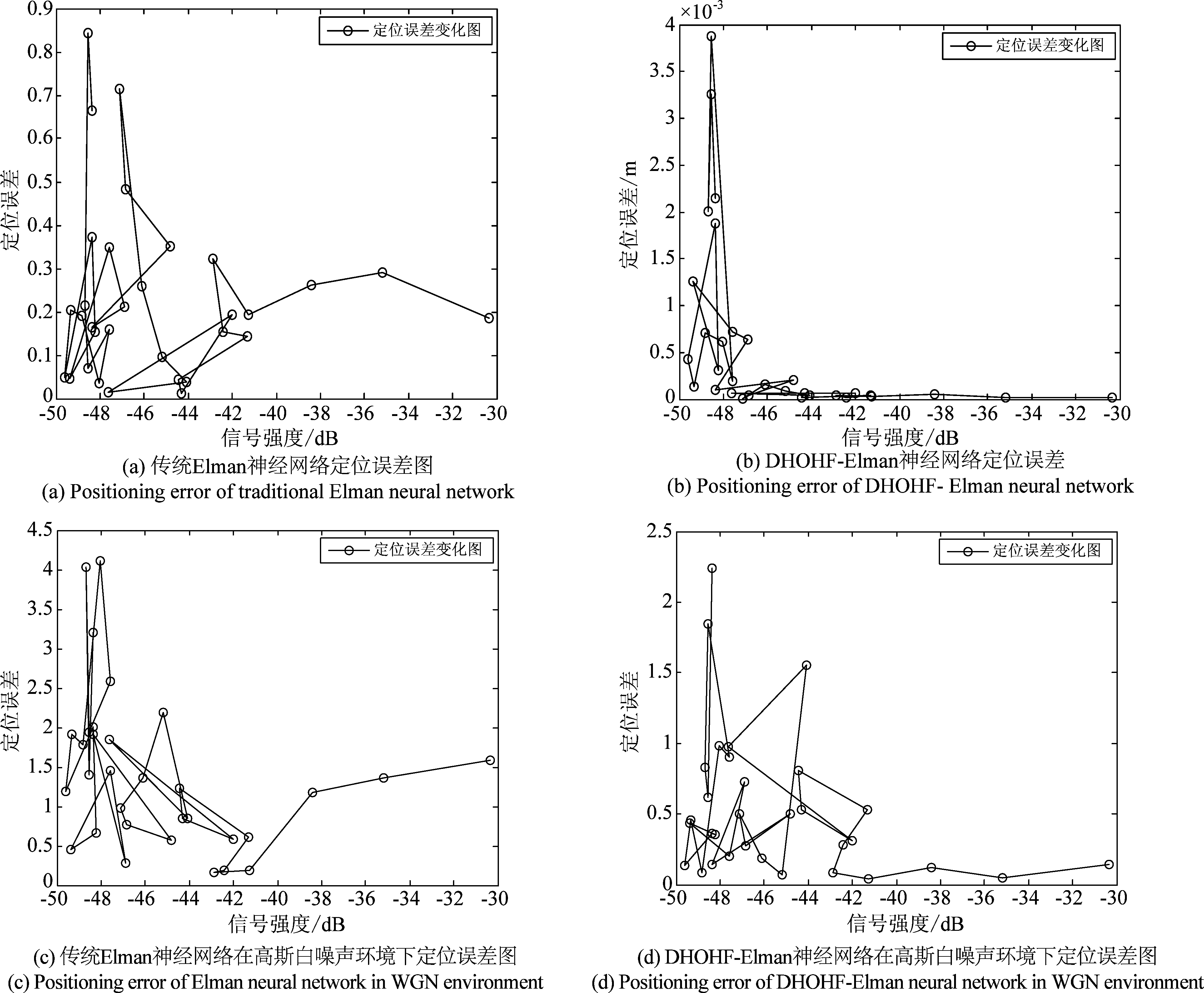
图8 2种神经网络在不同环境下的定位误差
Fig.8 Positioning error of two neural network in different environments
6 结论
经过大量仿真表明,在使用传统Elman神经网络进行测距时,会存在定位环境不稳定,定位均方误差收敛速度慢和定位精度不高等问题。本文提出了一种基于UWB的DHOHF-Elman神经网络室内定位算法,以信道模型产生的数据作为样本训练网络,利用训练好的网络模型来进行测距,使传统Elman神经网络存在的问题得到了有效的改善和优化,通过仿真验证,DHOHF-Elman神经网络使定位精度更高,收敛速度更快。
[1] 邓中亮, 尹露, 唐诗浩, 等. 室内定位关键技术综述[J]. 导航定位与授时, 2018, 5(3): 14-23.
Deng Zhongliang, Yin Lu, Tang Shihao, et al. A summary of key technologies for indoor positioning[J]. Navigation, Position and Timing, 2018, 5(3): 14-23.(in Chinese)
[2] 程俊, 周礼争, 余敏, 等. 基于RSSI滤波的改进型泰勒级数室内定位算法[J]. 计算机技术与发展, 2016, 26(5): 51-55.
Cheng Jun, Zhou Lizheng, Yu Min, et al. Indoor Localization Algorithm of Improved Taylor Series Based on RSSI Filter[J]. Computer Technology and Development, 2016, 26(5): 51-55.(in Chinese)
[3] 陆音, 王宝全, 丘觐玮. CHAN算法在LOS和NLOS环境下的定位研究[J]. 计算机技术与发展, 2015, 25(9): 61- 65.
Lu Yin, Wang Baoquan, Qiu Jinwei. Study on Localization of CHAN Algorithm in LOS and NLOS Environment[J]. Computer Technology and Development, 2015, 25(9): 61- 65.(in Chinese)
[4] Guan W, Lu B, Li B, et al. A TDOA localization Algorithm Based on Elman Neural Network for Cellular networks[J]. Information Technology Journal, 2013, 12(23): 7143-7147.
[5] 仲江涛, 秦斌, 吴健春, 等. 基于Kalman滤波的Chan室内定位算法改进[J]. 通信技术, 2017, 50(10): 2223-2228.
Zhong Jiangtao, Qin Bin, Wu Jianchun, et al. Modified Chan In-door Positioning Algorithm based on Kalman Filter[J]. Communication Technology, 2017, 50(10): 2223-2228.(in Chinese)
[6] 陈榕. 基于Elman神经网络及RSSI优化的无线传感器网络室内定位算法的研究与设计[D]. 南昌: 华东交通大学, 2016.
Chen Rong. Research and design of indoor localization algorithm for wireless sensor networks based on elman neural network and rssi optimization[D]. Nanchang: East China Jiaotong University, 2016.(in Chinese)
[7] Sun J, Fu Y, He J, et al. Nonlinear programming-based ranging optimization for three-dimensional indoor time of arrival localization[J]. International Journal of Distributed Sensor Networks, 2017, 13(10): 1-12
[8] 刘影, 贾迪, 王和章. 复杂环境下基于CFSFDP的自适应室内定位方法[J]. 信号处理, 2018, 34(4): 465- 475.
Liu Ying, Jia Di, Wang Hezhang. Adaptive Indoor Localization Algorithm of Based on CFSFDP in Complex Environment[J]. Journal of Signal Processing, 2018, 34(4): 465- 475.(in Chinese)
[9] 韩庆玉, 李媛, 宫红彩, 等. 基于Elman神经网络的无线传感器网络测距模型[J]. 山东科学, 2011, 24(6): 92-95.
Han Qingyu, Li Yuan, Gong Hongcai, et al. An Elman neural networks based ranging model for wireless sensor networks[J]. Shandong Science, 2011, 24(6): 92-95.(in Chinese)
[10] 梅贵琴. 改进的Elman神经网络和网络参数优化算法研究[D]. 重庆: 西南大学, 2017.
Mei Guiqin. The research on improved elman neural network and parameter optimization algorithm[D]. Chongqing: Southwest University, 2017.(in Chinese)
[11] 欧阳昱. 基于超宽带的室内定位算法研究[D]. 南京: 南京邮电大学, 2013.
Ouyang Yu. A study on indoor positioning algorithm based on ultra-wideband technology[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2013.(in Chinese)
[12] 邹胜男. 基于RSSI测距的室内定位算法研究与实现[D]. 南京: 南京信息工程大学, 2017.
Zou Shengnan. Research and implement of indoor positioning technology based on RSSI[D]. Nanjing: Nanjing University of Information Science and Technology, 2017.(in Chinese)
[13] Loyez C, Rolland N, Bocquet M. UWB technology applied to millimeter-wave indoor location systems[C]∥Radar Conference. IEEE, 2015: 1-5.
[14] Li H, Ren B. Wireless location for indoor based on UWB[C]∥Control Conference. IEEE, 2015: 6430- 6433.
[15] 曾庆化, 王敬贤, 孟骞, 等. 基于UWB优化配置的室内行人导航方法[J]. 中国惯性技术学报, 2017, 25(2): 186-191.
Zeng Qinghua, Wang Jingxian, Meng Qian, et al. Indoor pedestrian navigation method based on optimal allocation of UWB[J]. Journal of Chinese Inertial Technology, 2017, 25(2): 186-191.(in Chinese)
[16] 王全辉, 黄建军, 胡坚耀. 超宽带定位的AGV定位跟踪算法研究[J]. 信号处理, 2017, 33(4): 516-522.
Wang Quanhui, Huang Jianjun, Hu Jianyao. Research on AGV location tracking algorithm for ultra-wideband positioning[J]. Journal of Signal Processing, 2017, 33(4): 516-522.(in Chinese)
[17] Dong F, Shen C, Zhang J, et al. A TOF and Kalman filtering joint algorithm for IEEE802.15.4a UWB Locating[C]∥Information Technology, Networking, Electronic and Automation Control Conference, IEEE. IEEE, 2016: 948-951.
[18] 张宴龙. 室内定位关键技术研究[D]. 合肥: 中国科学技术大学, 2014.
Zhang Yanlong. Research on the key techniques of indoor localization[D]. Hefei: University of Science and Technology of China, 2014.(in Chinese)

