1 引言
随着电磁环境日益复杂,干扰设备和侦察设备的能力日益增强,为提高可靠的传输能力,认知抗干扰通信已成为现代通信的重点研究方向[1]。
认知抗干扰通信系统可以自动感知电磁环境,依据电磁环境的动态改变,智能决策出最优的抗干扰策略,实现自适应抗干扰传输,其中,智能决策为其核心。为了提升决策的性能,研究人员在智能决策中引入各类机器学习算法以完成更智能的决策推理[2]。文献中常见的智能决策算法有基于案例的推理[3]、基于规则的决策[4]、启发式算法[5]、群体智能算法[6]、神经网络[7]、深度学习[8]、强化学习[9]等。其中,基于案例的推理容易获得案例库,但只能在现存的案例中进行匹配;基于规则的决策能够处理未知的情形,但需要建立复杂的规则库;启发式算法和群体智能算法能够在知识库里进行快速搜索并找到最优策略;强化学习算法收敛慢;神经网络具有一定的容错能力和泛化能力,在网络训练好的情况下可以快速决策,而且算法简单、鲁棒性强、非线性映射能力强、自学能力好[10]。BP神经网络作为一种由误差反向传播算法训练的多层前向传播的神经网络,能够在事先不了解映射关系的情况下学习和存储大量的输入—输出模型映射,可以近似任意精度的连续函数,具有自组织、自适应和强大的非线性映射能力,这些优异的性质使其成为目前最广泛使用的神经网络模型之一[11-12]。
神经网络在解决模式分类、函数逼近、预测等问题时具有良好的性能[13]。文献[14]介绍了一种基于神经网络的干扰识别算法,在全干噪比条件下,识别效果良好;文献[15]提出了一种新的尖峰神经网络结构,减少了执行函数逼近时所需训练样本和所需神经元的数量;文献[16]提出了一种基于交叉序列分割算法和BP神经网络算法的组合预测模型算法,该算法大大提高了短期预测误差的实时性,并显著降低了预测误差率。
国内外对于将神经网络算法应用到通信抗干扰决策的研究还处于初始阶段,文献[17]设计了一种基于径向基神经网络的抗干扰系统,主要是将神经网络运用到通信波形切换以抵抗不同类型的干扰。但在认知抗干扰通信系统中,为了更好地适应复杂电磁环境的变化,通常需要决策的是满足系统最优抗干扰效能(或性能)的系统参数,不仅仅是通信模式的选择,还包括通信模式下的系统参数配置,因此本文设计了一种基于BP神经网络的认知抗干扰实时决策引擎,根据感知的电磁环境信息,决策出适应环境变化的系统参数,包括频谱资源、波形参数、功率和干扰抑制方式等,通过仿真分析,验证了采用该引擎的认知抗干扰通信系统在不同干扰环境下具有很强的抗干扰性能。
本文内容安排如下:第2节设计了基于BP神经网络算法的抗干扰实时决策引擎模型;第3节阐明了基于BP神经网络实时决策引擎原理,包括:输入输出和判别标准设计,决策实现步骤,主要参数分析;第4节仿真分析了引擎的抗干扰能力、容错能力、泛化能力,并将本文提出的决策引擎与采用遗传算法和人工蜂群算法的决策引擎进行了性能比较。
2 基于BP抗干扰实时决策引擎模型
基于BP神经网络的抗干扰实时决策引擎如图1所示,引擎分为网络搭建与实时决策两部分。网络搭建部分主要根据样本库的数据和设定的网络参数建立并训练BP神经网络,得到训练至收敛的网络。网络训练完成后,系统感知外界电磁环境后得到外界环境信息:其中环境信息包括干扰信息(干扰类型、干扰参数等)和信道信息(信道类型、信道参数等);然后将感知得到的数据进行去量纲归一化;再将处理后的数据送入训练完成的网络里得到决策结果,决策结果包括频谱资源(可用子带等)、波形参数(调制编码方式等)、功率和干扰抑制方式(频域干扰抑制、时域干扰抑制、变换域干扰抑制等)等;最后,决策引擎根据反馈的传输性能,判断决策参数是否满足当前要求,根据判断结果进行调整,丰富样本库内容。
3 基于BP神经网络的抗干扰决策原理
本文研究的认知抗干扰通信系统采用频域扩频非连续正交频分复用(Non-Contiguous Orthogonal Frequency Division Multiplexing, NC-OFDM)技术传输体制,该系统基于BP神经网络的抗干扰决策框图如图2所示,其中训练样本通过以下方式获得:设
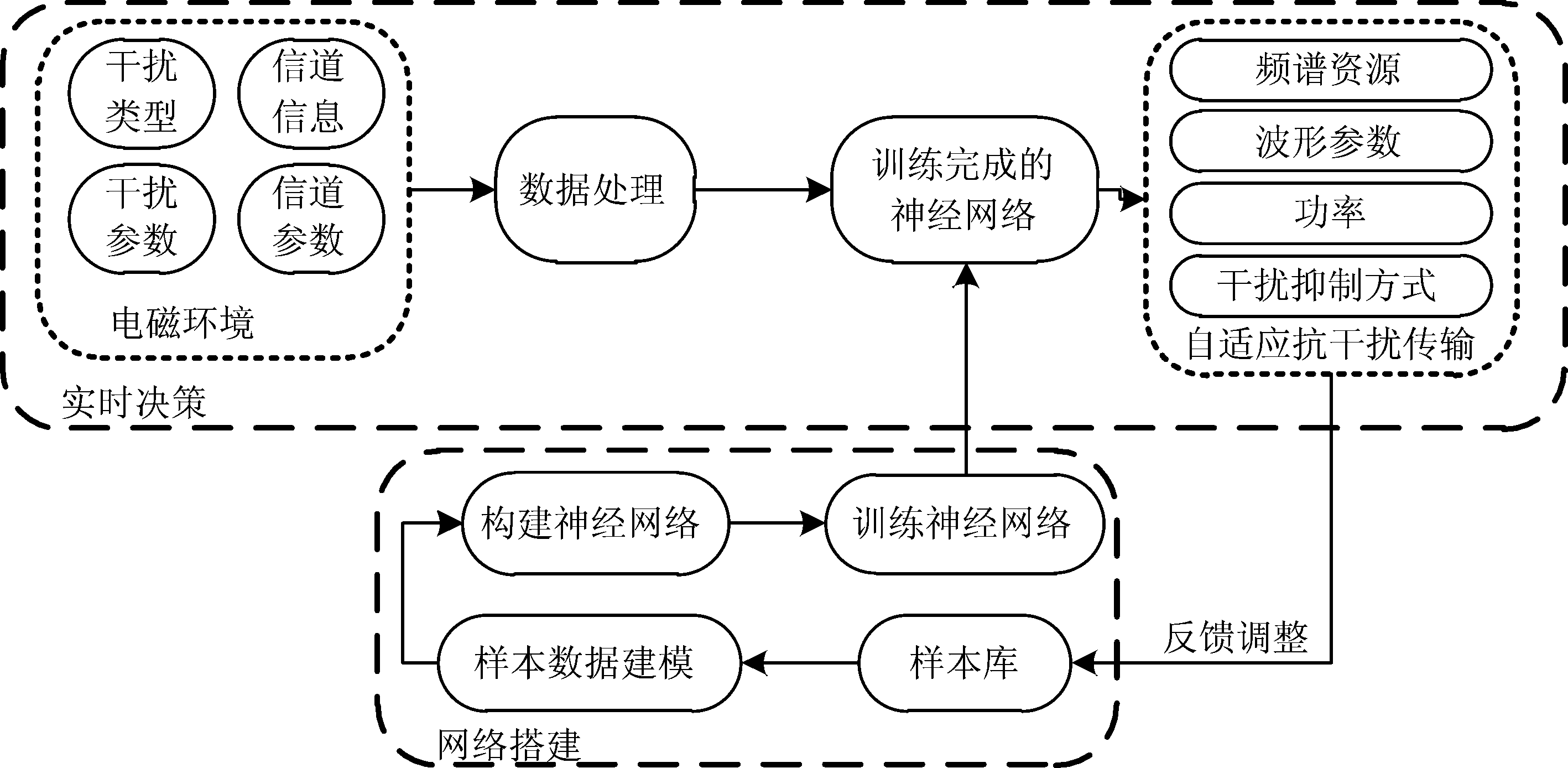
图1 基于BP神经网络算法的通信抗干扰实时决策引擎模型
Fig.1 BP Neural network based cognitive anti-jamming decision engine model
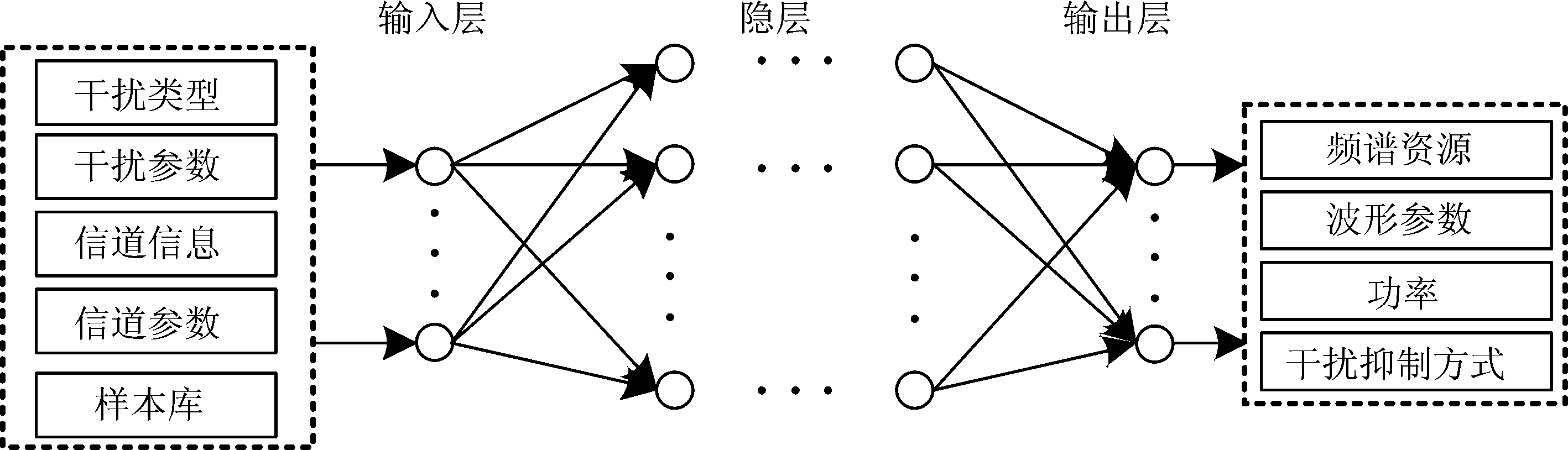
图2 基于BP神经网络的抗干扰决策框图
Fig.2 Block diagram of anti-jamming decision based on BP neural network
置不同的信道类型、干扰类型、干噪比(Jamming to Noise Ratio, JNR)、调制编码方案(Modulation and Coding Scheme,MCS)、发射功率、可用频率子带数、干扰抑制方式,仿真得到相应的系统误码率和平均信息速率,将不同信道类型、干扰类型、JNR下目标函数值最大的样本作为训练样本,目标函数值用于衡量系统性能,包括抗干扰性能、功率效率和传输效率,目标函数如式(1)所示。
E=wB fB+wR fR+wP fP
(1)
fB, fR, fP分别为最小化误包率归一化、最大化平均信息传输速率归一化、最小化发射功率归一化[5],wB、wR和wP分别表示三者的权重,wB+wR+wP=1。获得训练样本后,使用样本库对BP神经网络进行训练,网络收敛后,输入实际的外界环境信息进行决策,得到该情况下的决策结果。
3.1 输入输出和判别标准设计
基于NC-OFDM的认知抗干扰通信系统传输参数如表1所示,MCS参数如表2所示。
表1 系统传输参数
Tab.1 System transmission parameters
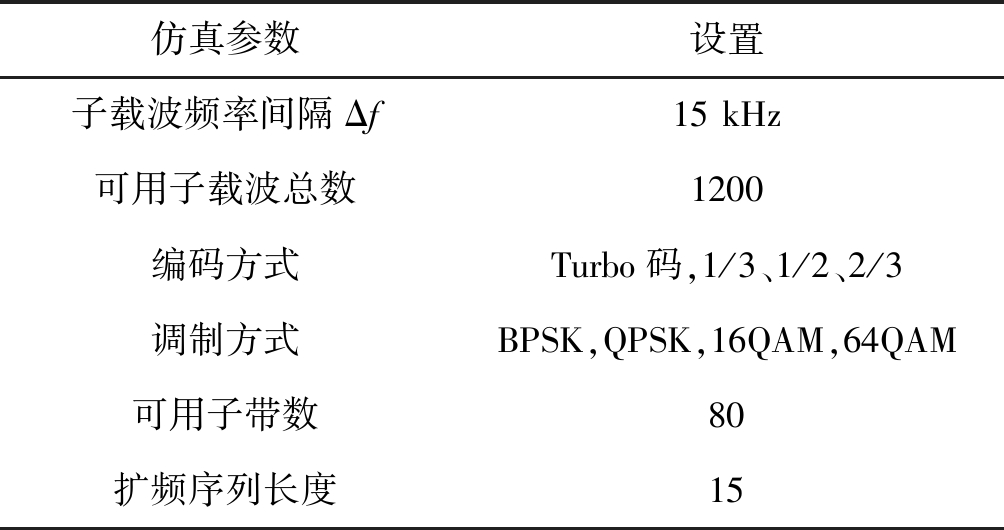
仿真参数设置子载波频率间隔Δf15 kHz可用子载波总数1200编码方式Turbo码,1/3、1/2、2/3调制方式BPSK,QPSK,16QAM,64QAM可用子带数80扩频序列长度15
3.1.1 输入输出设计
神经网络要求输入参数之间具有较小的相干性,因此,设置输入参数:信道类型(AWGN信道、各种衰落信道等)、信道参数(噪声功率、信道衰落系数等)、干扰类型(瞄准式干扰、部分带干扰、锯齿波带宽干扰等)、干扰参数(干扰功率、频率吻合度、频带因子、占空比等),其中频率吻合度的定义是干扰与信号的中心频率绝对差值同信号带宽一半之比,频带因子的定义是干扰带宽与信号带宽的比值。
表2 MCS索引
Tab.2 MCS index
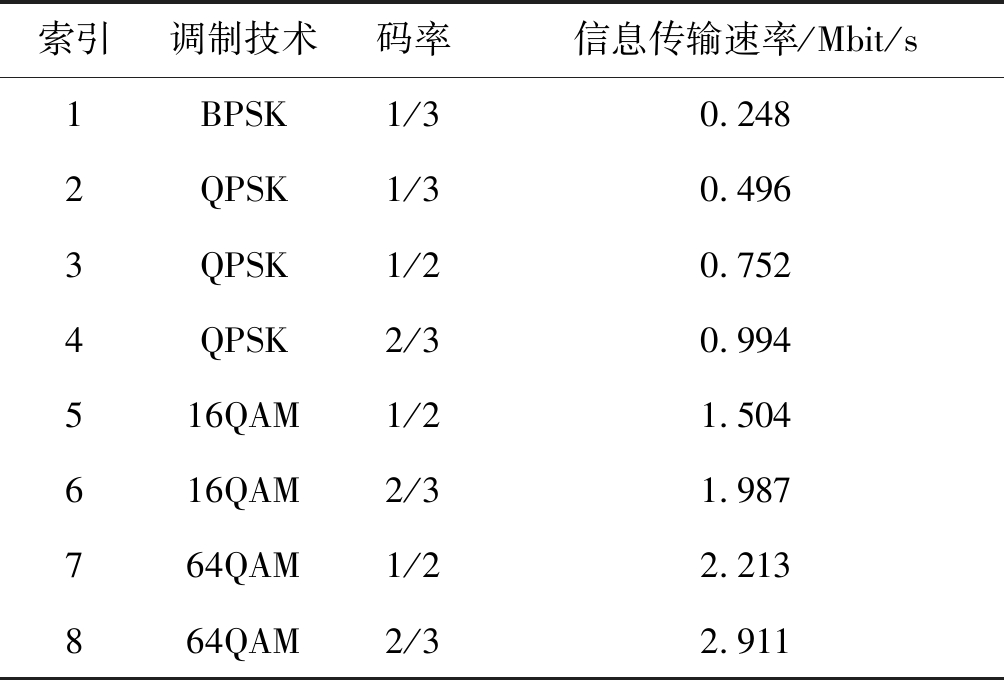
索引调制技术码率信息传输速率/Mbit/s1BPSK1/30.2482QPSK1/30.4963QPSK1/20.7524QPSK2/30.994516QAM1/21.504616QAM2/31.987764QAM1/22.213864QAM2/32.911
神经网络常用的激活函数为sigmoid函数,当输入参数的绝对值过大,将使得神经元达到饱和,反向传播能力变差甚至导致网络不收敛,所以本文对输入参数进行去量纲归一化,如式(2)所示:
(2)
根据系统性能要求,设置本文的输出参数为:MCS阶数、信号发射功率、可用频率子带数和干扰抑制方式。本文设置输出层采用一个神经元表示一种参数的一种可能取值,所以NL取值较大。
3.1.2 判别标准设计
将损失函数作为网络性能的判别准则,损失函数为神经网络输出层的均方误差,损失函数越小,网络性能越好,但该标准难以直观地反映网络性能的优劣,因此,本文将损失函数值和输出结果准确率同时作为评价实时决策性能的指标,以便更加直观地判断决策引擎的性能。
3.2 决策实现步骤
1)离线过程:
a)由训练样本集合建立的样本库。
b)训练网络至收敛。
2)在线过程:将干扰类型、干扰参数、干噪比根据式(2)去量纲尺度变换,连同信道类型一起输入到神经网络对应的输入节点,通过离线训练完成的神经网络决策输出,决策出适应当前环境的最佳系统参数设置。
3)对通信系统进行可用频率子带数、调制编码方式、发射功率和干扰抑制方式的参数配置和频谱分配。
3.3 参数分析
对于BP神经网络算法,影响决策性能的参数主要有网络大小、初始化方式、小批量数据量和学习率。
3.3.1 网络大小
神经网络的大小是通过层数与每层的节点个数共同决定的。一方面,神经元个数和层数增加能够增强网络复杂度,从而解决复杂度更高的问题,但网络太大会导致算法复杂度增加、训练时间变长、泛化能力变差及导致“过拟合”问题;另一方面,网络太小可能引起映射能力变差与“欠拟合”问题。所以,网络大小对算法性能至关重要,常用试凑法确定网络大小。
3.3.2 初始化方式
初始化过程包含对权重值w1,w2,...,wL(wl是神经网络第l层全体权重值构成的矩阵)与偏置b1,b2,...,bL(bl是神经网络第l层所有偏置构成的向量)的初始化。如果初始值接近最优值且收敛方向能快速收敛,则能加速训练。可见,初始化方式于网络收敛过程而言十分重要。激活函数在零点附近较敏感,所以常在该区间内取值。通常使用的两种初始化方式为:初始化方式1:每个权重和偏置的初始值为![]() 初始化方式2:每个权重的初始值
初始化方式2:每个权重的初始值![]() 每个偏置的初始值
每个偏置的初始值![]()
3.3.3 小批量数据量
网络常用小批量数据的平均梯度值估计整体数据的平均梯度值。若小批量数据量过小,则无法表示数据特性,网络的“估计”误差增大;若小批量数据量过大,会使得计算量增加,网络收敛变慢。因此,小批量数据量通常选取几到几百。
3.3.4 学习率
学习率η直接决定了算法的学习速率。若η过大,会导致权重和偏置调整步进过大,损失函数曲线震荡,难以完美收敛;若η过小,会导致权重和偏置调整步进过小,难以快速收敛。所以选择合适的η能加快网络收敛速度。学习率通常取值为η∈(0,1)。
4 性能仿真分析
在AWGN信道下对认知抗干扰系统基于BP神经网络的抗干扰实时决策的抗干扰能力、容错能力和泛化能力进行仿真,由于感知器对环境参数的估计结果可能存在偏差,所以本文对同种环境信息取1000个样本进行训练,共10000个样本,其中75%的样本作为训练样本,25%的样本作为测试样本。系统的目标误块率小于0.01,BP神经网络的仿真参数如表3。
表3 BP神经网络算法仿真参数
Tab.3 BP neural network algorithm simulation parameters

参数设置网络大小4×30×100×100×82初始化方式初始化方式2小批量数据量5η0.1
4.1 抗干扰能力
训练完成的神经网络在不同干扰下的决策结果如表4。
从表4可以看出,不同环境下,决策引擎均能满足误块率低于10-2,误码率低于10- 6,满足系统要求。在JNR为40 dB的部分带干扰下,频带因子越大,在保证系统误包率性能满足要求的前提下,决策出的可用子带数越少,平均信息速率较低;在相同干扰环境中(如JNR为20 dB和JNR为40 dB 下频带因子为0.5的部分带干扰),JNR越大,对系统性能影响越大,决策出的可用子带数越少,平均速率越低,因此系统在JNR为20 dB下频带因子为0.5的部分带干扰中具有更高的信息速率;JNR相同时,不同干扰对系统性能影响不同,在BPSK瞄准式干扰下的平均信息速率高于0.5频带因子部分带干扰,这是因为BPSK瞄准式干扰是窄带干扰,而0.5频带因子的部分带干扰是带宽干扰,经决策,前者可用子带数更多,所以在保证传输误包率的情况下,前者平均信息速率更高;本文中的脉冲干扰采用白噪声进行幅度调制,干扰带宽为采样带宽、脉冲周期为1 ms,从表4可以看出,在占空比为0.3和0.7的脉冲干扰下,占空比越大,在保证系统误包率性能满足要求的前提下,决策出MCS阶数更低,平均信息速率也更低。
4.2 容错能力
考虑到实际情况下感知器对SNR和干扰参数的估计会有偏差,将10%的训练数据中的SNR和干扰参数引入不同的归一化均方根误差(Normalized Root Mean Squared Error,NRMSE),如表5所示。
表4 不同干扰下的抗干扰决策结果
Tab.4 Anti-jamming decision results under different jamming environments

干扰类型干扰参数JNR/dB决策结果(MCS,SNR/dB,子带数,干扰抑制方式)误块率系统BER平均信息速率/MbpsBFSK瞄准式干扰0.1频率吻合度408,2,80,频域<10-2<10-62.91BPSK瞄准式干扰0.1频率吻合度408,2,80,频域<10-2<10-62.91部分带干扰0.1频带因子408,10,80,频域<10-2<10-62.91部分带干扰0.5频带因子408,7.5,70,频域<10-2<10-62.56部分带干扰0.5频带因子208,6.5,80,频域<10-2<10-62.91部分带干扰0.7频带因子407,6.5,60,频域<10-2<10-61.67线性调频干扰0.3频带因子扫频周期216 ms408,3,80,频域<10-2<10-62.91单音扫频0.3频带因子扫频周期216 ms408,2,80,频域<10-2<10-62.91脉冲干扰0.3占空比408,2.5,80,时域<10-2<10-62.91脉冲干扰0.7占空比405,5,80,时域<10-2<10-61.50
表5 不同误差设置
Tab.5 Different error settings
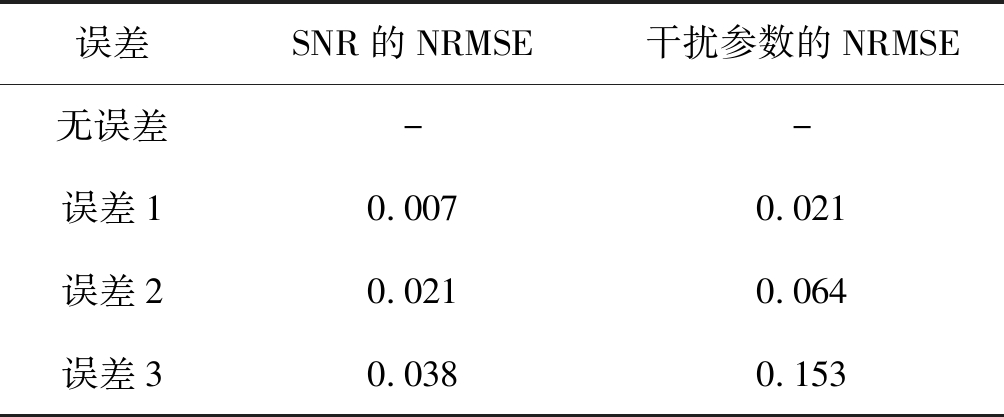
误差SNR的NRMSE干扰参数的NRMSE无误差--误差10.0070.021误差20.0210.064误差30.0380.153
为了说明不同误差下网络的容错能力,测试数据不引入误差,分析训练数据引入不同误差下网络的决策准确率和损失函数,仿真结果如图3所示。
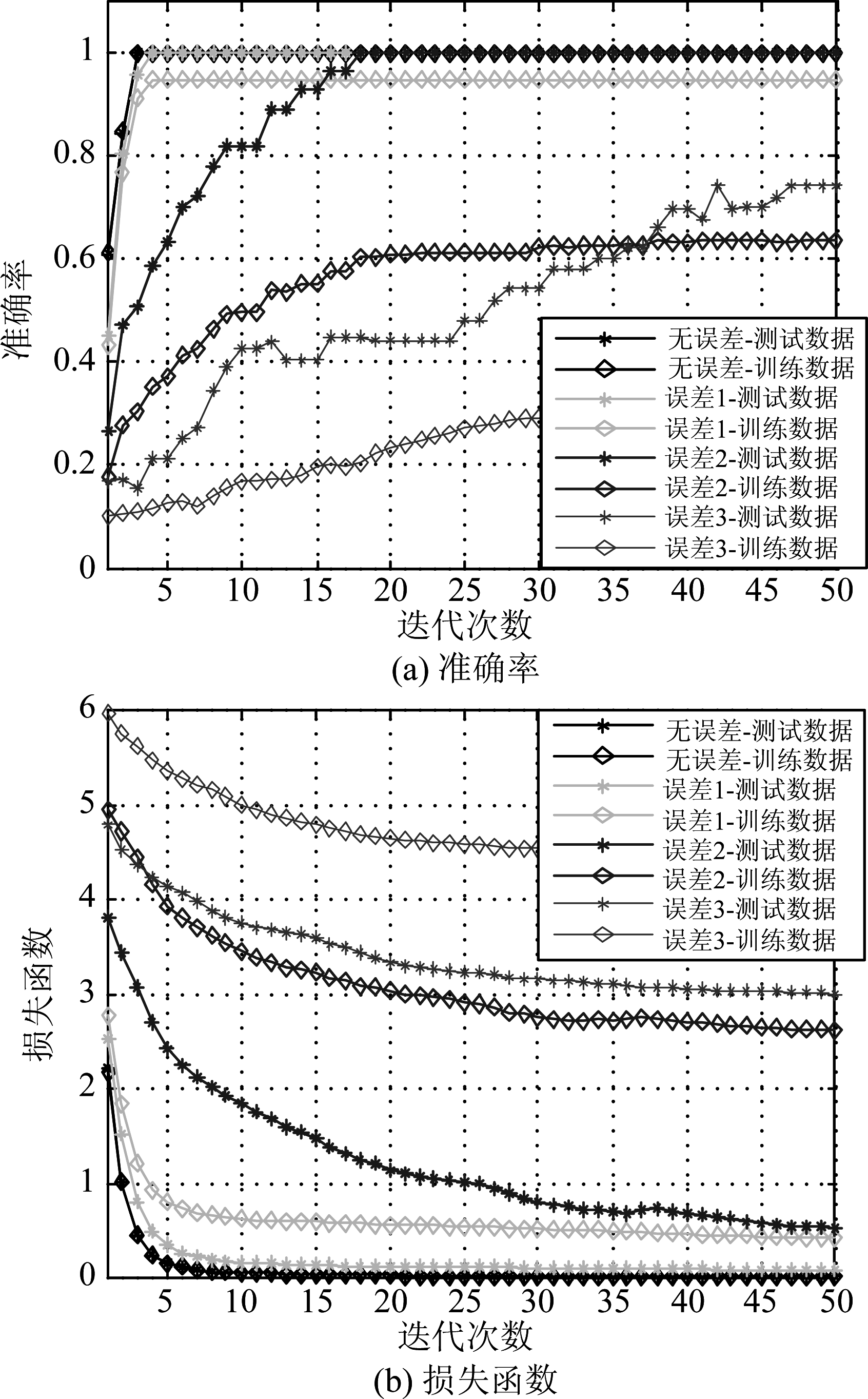
图3 BP神经网络在不同样本误差下损失函数值和准确率
Fig.3 Loss function value and accuracy of BP neural network under different sample error
通过图3可以看出,对BP神经网络而言,将训练数据引入较小误差时对网络的输入输出规律影响较小,所以在训练数据无误差、引入误差1和引入误差2的情况下,测试数据的准确率达到100%。当无误差时,网络准确率在3代左右实现收敛,损失函数收敛后趋于0;在引入误差1的情况下,损失函数值较大且训练数据的准确率低于无误差时训练数据的准确率,但测试数据准确率在4代左右也能够达到100%;在引入误差2的情况下,虽然损失函数较高且收敛缓慢,但测试数据准确率可以收敛至100%;在引入误差3的情况下,测试数据准确率只收敛至63%左右。因此,文中提出决策引擎有一定的容错能力。
4.3 泛化能力
将测试数据中不包含的同类型数据作为测试数据测试本文算法的泛化能力。训练数据中包含频带因子0.1、0.5、0.7的部分带干扰数据和占空比0.3、0.7的脉冲干扰数据,测试JNR为40 dB的20%部分带干扰数据和占空比0.5的脉冲干扰数据,测试结果如表6所示。
从表6可以看出,把20%部分带干扰数据输入到训练好的网络中,决策出MCS为8、SNR为10 dB、可用子带数为80、采用频域干扰抑制,与最优解相比,决策出的SNR较大,未能实现最小化功率的目标,但系统误块率小于0.01,BER小于10- 6,满足系统要求,且实现了最大平均信息速率。将占空比为0.5的脉冲干扰数据输入到训练好的网络中,决策出MCS为7、SNR为5.5 dB、可用子带数为70、采用时域干扰抑制,与最优决策结果相比,引擎决策出的SNR略小、MCS的阶数略低、可用的子带数略低,虽无法实现最大化平均信息速率,但系统误块率小于0.01,BER小于10- 6,满足系统要求。因此,本文中提出的基于BP神经网络的抗干扰实时决策引擎在干扰参数发生变化时,能够决策出满足系统要求的频谱资源分配、系统参数配置和干扰抑制方式,具有一定的泛化能力。
4.4 不同决策引擎性能比较
在JNR为40 dB的50%部分带干扰环境中,将基于遗传算法[5]、人工蜂群算法与BP神经网络算法的通信抗干扰决策引擎进行对比,遗传算法设置种群数为30,选择方式选用轮盘赌方式,重组比例为50%,交叉概率设置成0.7,变异概率设置为0.4;人工蜂群算法种群数设置成30,侦查蜂个数设置成3,淘汰门限设置成10。不同决策引擎下决策结果数据对比如表7所示。
表6 泛化能力测试结果
Tab.6 Generalization ability test results

干扰类型干扰参数决策结果(MCS,SNR/dB,子带数,干扰抑制方式)最优解(MCS,SNR/dB,子带数,干扰抑制方式)误块率系统BER平均信息速率/Mbps部分带干扰0.2频带因子8,10,80,频域8,8,80,频域<10-2<10-62.91脉冲干扰0.5占空比7,5.5,70,时域8,9,80,时域<10-2<10-62.21
表7 不同决策引擎的抗干扰决策结果
Tab.7 Anti-jamming decision results of different decision engine
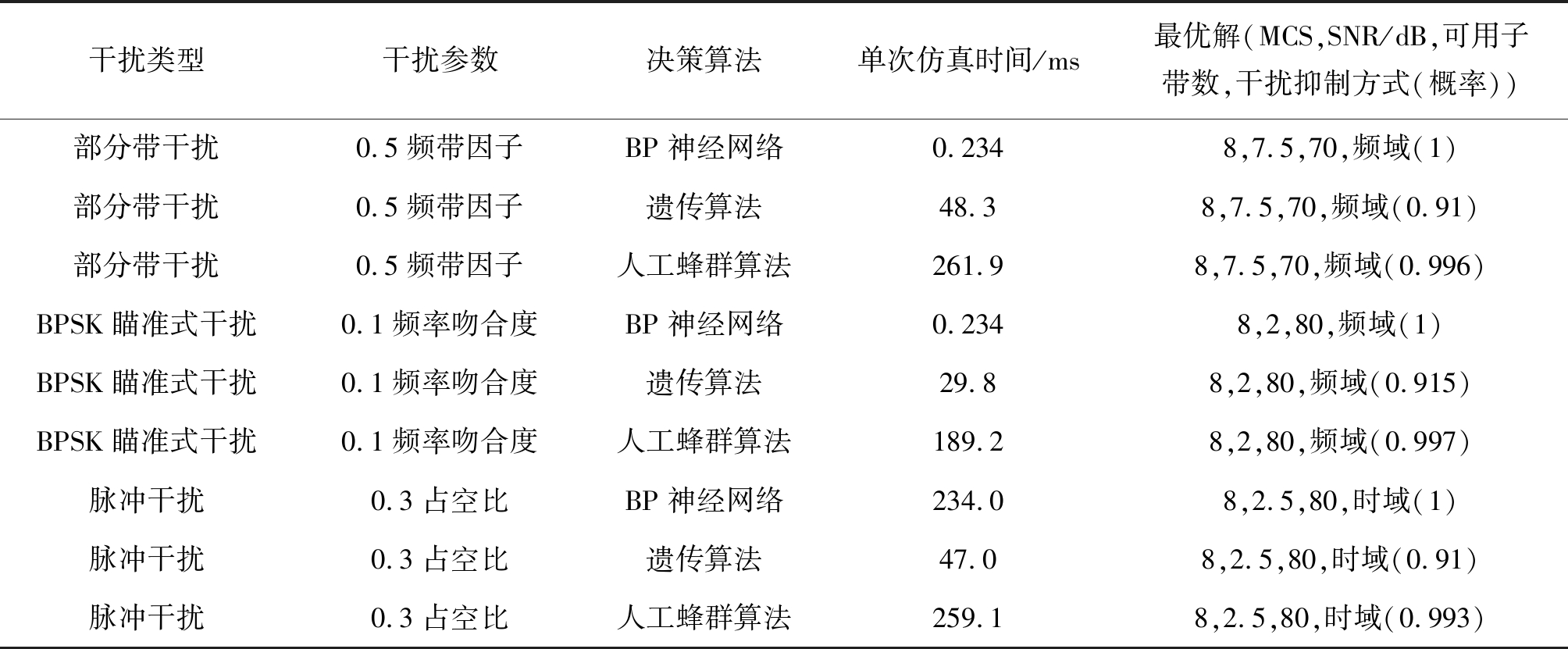
干扰类型干扰参数决策算法单次仿真时间/ms最优解(MCS,SNR/dB,可用子带数,干扰抑制方式(概率))部分带干扰0.5频带因子BP神经网络0.2348,7.5,70,频域(1)部分带干扰0.5频带因子遗传算法48.38,7.5,70,频域(0.91)部分带干扰0.5频带因子人工蜂群算法261.98,7.5,70,频域(0.996)BPSK瞄准式干扰0.1频率吻合度BP神经网络0.2348,2,80,频域(1)BPSK瞄准式干扰0.1频率吻合度遗传算法29.88,2,80,频域(0.915)BPSK瞄准式干扰0.1频率吻合度人工蜂群算法189.28,2,80,频域(0.997)脉冲干扰0.3占空比BP神经网络234.08,2.5,80,时域(1)脉冲干扰0.3占空比遗传算法47.08,2.5,80,时域(0.91)脉冲干扰0.3占空比人工蜂群算法259.18,2.5,80,时域(0.993)
训练好的基于BP神经网络算法的决策引擎的平均运行时间远小于基于遗传算法与基于人工蜂群算法的决策引擎,这是因为遗传算法和人工蜂群算法每次运行都必须通过迭代完成搜索,迭代过程时间开销大,但BP神经网络采用离线学习,训练完成的网络只需简单运算即可得到决策结果,保证通信的实时性;基于BP神经网络算法的决策引擎得到最优解的概率为1,高于其他两种决策引擎得到最优解的概率;另一方面,4.3节的仿真结果表明,BP神经网络具有一定的泛化能力,而遗传算法和人工蜂群算法只能根据已有的数据进行决策。所以,基于BP神经网络算法的抗干扰实时决策引擎的性能相比于其他两种的性能更优。
5 结论
本文设计了一种基于BP神经网络算法的抗干扰实时决策引擎,可在干扰环境中能够快速决策,并适应电磁环境变化,在干扰环境中能够达到优异的抗干扰性能;当输入训练数据的估计偏差在一定范围内时,引擎能够保证测试数据的准确率,具有一定的容错能力;当训练数据缺乏当前干扰下的数据时,该引擎能够根据已有数据决策输出满足系统要求的决策结果,具有一定的泛化能力;与采用遗传算法与人工蜂群算法相比,本文提出的抗干扰实时决策引擎性能更优。
[1] 李少谦, 程郁凡, 董彬虹, 等. 智能抗干扰通信技术研究[J]. 无线电通信技术, 2012, 38(1): 1- 4.
Li S Q, Cheng Y F, Dong B H, et al. Research on Intelligent Anti-jamming Communication Techniques[J]. Radio Communications Technology, 2012, 38(1): 1- 4.(in Chinese)
[2] Pietro R, Oligeri G. Jamming mitigation in cognitive radio networks[J]. IEEE Network, 2013, 27(3): 10-15.
[3] Minor M, Montani S, Recio-García J. Process-oriented case-based reasoning[J]. Information Systems, 2014, 40(1): 103-105.
[4] Yang Y, Fu C, Chen Y, et al. A belief rule based expert system for predicting consumer preference in new product development[J]. Knowledge-Based Systems, 2016, 94(C): 105-113.
[5] 刘小玲. NC-OFDM系统的智能抗干扰决策技术研究[D]. 成都: 电子科技大学, 2016.
Liu X L. Research on Intelligent Anti-interference Decision Technology of NC-OFDM System[D]. Chengdu: University of Electronic Science and Technology, 2016.(in Chinese)
[6] Tian D, Hu J, Sheng Z, et al. Swarm Intelligence Algorithm Inspired by Route Choice Behavior[J]. Journal of Bionic Engineering, 2016, 13(4): 669- 678.
[7] 楼奇哲, 刘乐, 姚元. 采用卷积神经网络的海面多目标检测研究[J]. 信号处理, 2018, 34(9): 1053-1059.
Lou Q Z, Liu L, Yao Y. Research on multi-target detection of sea surface using convolutional neural network[J]. Journal of Signal Processing, 2018, 34(9): 1053-1059.(in Chinese)
[8] Kwon D, Kim H, Kim J, et al. A survey of deep learning-based network anomaly detection[J]. Cluster Computing, 2017(5): 1-13.
[9] Shamaee M, Shiri M, Sabaei M. A Reinforcement Learning Based Routing in Cognitive Radio Networks for Primary Users with Multi-stage Periodicity[J]. Wireless Personal Communications, 2018, 101(1): 465- 490.
[10] Seshagiri S, Khalil H. Output feedback control of nonlinear systems using RBF neural networks[J]. IEEE Transactions on Neural Networks, 2000, 11(1): 69-79.
[11] Fang Y, Pang M, Wang B. A course control system of unmanned surface vehicle (USV) using back-propagation neural network (BPNN) and artificial bee colony (ABC) algorithm[J]. Procedia Computer Science, 2017, 111: 361-366.
[12] Lin Y, Chen X. BP Neural Network Learning Algorithm and its Software Implementation[J]. Applied Mechanics and Materials, 2014, 513-517: 738-741.
[13] Basheer I. Artificial Neural Networks: Fundamentals, Computing, Design, and Application[J]. Journal of Microbiological Methods, 2000, 43(1): 3-31.
[14] 朱清祎, 尚朝轩, 董健. 雷达干扰模式识别技术综述[J]. 飞航导弹, 2018(8): 71-75.
Zhu Q Y, Shang C X, Dong J. Overview of radar jamming pattern recognition technology[J]. Flying Missile, 2018(8): 71-75.(in Chinese)
[15] Ulbrich S, Steward T, Peric I, et al. Model-based polynomial function approximation with spiking neural networks[C]∥2017 IEEE 16th International Conference on Cognitive Informatics & Cognitive Computing (ICCI*CC). Oxfordshire: IEEE, 2017: 22-27.
[16] Yang G, Lu L. Application of a traffic flow prediction model based on neural network in intelligent vehicle management[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2019(33): 1-18.
[17] 刘猛, 戚红雨, 王荆宁, 等. 基于神经网络算法的智能抗干扰系统设计[J]. 计算机测量与控制, 2018, 26(10): 155-159, 169.
Liu M, Qi H Y, Wang J N, et al. Design of Intelligent Anti-jamming System Based on Neural Network Algorithm[J]. Computer Measurement & Control, 2018, 26(10): 155-159, 169.(in Chinese)



