1 引言
压缩感知(CS, Compressed Sensing)是一种抽样和压缩同时进行的技术,其过程是将高维信号投影在一个低维空间上并通过优化算法从投影中高概率重构原始信号[1]。在一些使用相干检测的无线通信系统中,信道估计的优劣对于接收机重建信号质量的好坏至关重要[2]。由于宽带无线通信系统中多径信道会呈现稀疏特性,压缩感知理论中稀疏信号恢复算法可应用在稀疏信道估计中[3]。既然CS可以利用少量观测值重构出高维信号,基于压缩感知的稀疏信道估计可以比传统最小二乘法(LS, Least Square)和最小均方误差(MMSE, Minimum Mean Squared Error)算法具有更少的导频开销[4]。
基于CS的导频辅助信道估计目前已经被广泛研究,并且许多稀疏信号恢复算法已经应用于信道估计,例如,正交匹配追踪算法(OMP, Orthogonal Matching Pursuit)[5]、同时正交匹配追踪算法[6]、和稀疏度自适应匹配追踪算法[7]等。稀疏信道估计的另一个研究焦点是导频的设计。导频位置和符号取值的设计在一定程度上会影响基于CS的稀疏信道估计的性能。正交频分复用(OFDM,Orthogonal Frequency Division Multiplexing)技术在无线通信系统中得到了广泛的应用[8],对于基于LS和MMSE方法的信道估计,它的最优导频放置模式是导频子载波等间隔分布[9]。但对于基于CS重建算法的稀疏信道估计,等间隔放置导频生成的导频图案用于信道估计效果并不好,因此需要进一步研究最佳导频放置模式。CS的研究已经证明,恢复矩阵互相关值越小[1],稀疏信号的重建质量越高。在基于压缩感知的信道估计中,恢复矩阵由导频位置决定,因此可以将最小化恢复矩阵的互相关值作为选取最佳导频位置的准则。
为了获得OFDM系统中最佳导频放置模式,我们可以利用穷举法列出所有可能的导频图案,即搜索
种组合来获取全局最优解,N表示OFDM子载波数,Np表示导频个数,但由于其极高的计算量,使用穷举法设计导频是不切实际的。为了减小搜索空间和算法复杂度,文献[10]采用了两种随机搜索算法,即随机序列搜索(SSS, Stochastic Search Schemes)和随机并行搜索算法来优化导频图案。这两种方案都是由两层循环组成。在外循环中,随机生成导频图案作为内循环的初始化的导频图案。在内循环中,以贪婪迭代的方式更新得到导频图案,两种方案的区别在于内循环的更新搜索方式不同。SSS算法在内循环中顺序更新初始导频图案的每个位置,而SPS算法是采用对每个位置更新后从中选出具有最小互相关值的导频图案作为内循环的最终优化结果,文献[10]已经证明SSS算法性能略优于SPS算法。该算法每次只考虑一个分支的情况,即只在该分支寻求最优解,只得到一个范围内的最优解,但并不是全局最优解。文献[11]提出一种迭代组缩减(IGS,Iterative Group Shrinkage)的搜索方式获得导频分配方案,该方案不是直接从所有可能的导频子集中搜索最佳导频图案,而是以后向方式迭代地从所有OFDM子载波中移除子载波。在每次通过删除这些子载波后计算所得矩阵的互相关值,保留具有最小相干值的矩阵直到得到具有需要导频图案个数的子载波。但该算法复杂度较高,且优化后的互相关值仍然过大,将生成导频图案应用于信道估计效果不佳。在文献[12]中,同时考虑优化导频位置与导频符号功率,采用二阶圆锥规划方法获得导频图案。实际系统中不同子载波上导频符号的功率通常相同,导频功率的优化不具有实际意义。因此,本文与文献[10]和[11]一样,假设所有导频符号功率相同,仅考虑优化导频位置。
本文提出一种树状随机搜索方法来解决OFDM系统中导频图案的优化问题。该方案是从一个根节点下产生若干个分支节点,搜索得到其中最小的M2个节点,再将本次迭代产生的M2个分支节点作为下一次迭代的M2个父节点,最终多次循环迭代后产生一个接近最优的导频放置模式。相比文献[10]本文算法引入树状结构,由于树状结构在每一层综合考虑各个分支的特性,同时对多个分支进行优化,避免了优化过程中陷入某一个分支的局部最优问题,使其能搜索到具有更小互相关值的导频图案,与文献[11]的IGS算法相比,本文算法用从根节点出发搜索导频子集代替后向搜索,能够搜索到更小的互相关值。
2 系统模型
2.1 压缩感知理论模型
压缩感知理论是通过一组特定波形去感知信号,得到一组压缩数据。通过信号的稀疏特性,在接收端利用非线性重建算法从压缩的数据中估计出原始信号。
X是在稀疏基
=[
1,2,…,N]上的N维采样的信号,即:
n 或 X=Θ
(1)
其中Θ是投影系数θn构成的N×1维向量,当Θ中大多数值为0,只有K个较大的非零值时,可以称信号X对于基是K稀疏的。可以通过X在一个M×N维测量矩阵Φ上的线性投影获得M个观测值,接收端就可以通过这些观测值重构出原始信号。这M个观测值是通过下式获得:
y=ΦX=ΦΘ=TΘ
(2)
信号重建任务是通过测量向量y精确重建或者逼近信号X。其中测量向量y为M×1维列向量,测量矩阵和基矩阵的乘积为恢复矩阵T。压缩感知观测部分的设计是围绕测量矩阵的设计展开的,在基矩阵一定的情况下,则是要设计恢复矩阵T。
2.2 OFDM系统模型
考虑有N个子载波的OFDM系统,其中使用Np个梳状导频子载波(表示为P1,P2,...,PNp,1≤P1,P2,...,PNp≤N)传输导频信号用于频率选择性衰落信道的估计,则接收端接收信号可以表示为:
y=XH+n=XWh+n
(3)
其中发送信号矩阵X=diag(X(0)…X(N-1))∈CN×N,信道频域采样值H∈CN×1,加性高斯白噪声向量n∈CN×1,离散傅里叶变换矩阵W∈CN×L是标准N×N维傅里叶变换阵的前L列,L为信号长度。
(4)
其中
从N×N维单位矩阵中抽取对应导频位置的Np行得到Np×N维选择矩阵S,导频子载波上的接收信号如下式所示:
yp=XpWph+np
(5)
发送导频符号为Xp=SXST=diag(X(P1),X(P2),...,X(PNp))∈CNp×Np;接收导频符号的频域表示为yp=Sy=[Y(P1),Y(P2),...,Y(PNp)]T∈CNp×1;np=Sn∈CNp×1为独立同分布的加性高斯白噪声;Wp=SW∈CNp×L为离散傅里叶变换阵(DFT),由W矩阵中对应的索引为导频位置集合的Np行构成。
在接收端yp、Xp、Wp均为已知信号。将A=XpWp定义为恢复矩阵,我们的任务是保证稀疏矩阵h可以从观测值yp中较为准确的恢复出来。通过对式(2)和式(5)的观察,OFDM系统信道估计模型与压缩感知所描述的问题十分相似,那么可以将上述信道估计问题转换为压缩感知问题求解。而恢复矩阵由导频的设计决定,所以可以根据压缩感知中恢复矩阵的设计原则来解决导频的优化问题。
3 导频优化算法
CS的最新研究进展表明,如果恢复矩阵A满足限制等距特性(RIP),则可以使用yp和恢复矩阵A来重建稀疏矩阵h,然而由于RIP准则的复杂性,在实际中采用它优化导频的可能性很小。因此,通常采用复杂度较低的互相关最小准则(MIP)作为恢复矩阵优劣的衡量标准。MIP条件比RIP强,因为MIP意味着RIP,但反之则不然。 此外,MIP比RIP更直观,更实用。 因此,在本文中,我们将MIP视为恢复矩阵A的设计准则,从而解决导频的设计问题。将矩阵的相关性定义为两个不同列之间的最大绝对相关性,表示为:
(6)
〈A(m),A(n)〉表示恢复矩阵A第m列和第n列的内积。其中Pi表示的导频子载波位置,即我们的研究目标可以转换为设计恢复矩阵A使其具有最小的μ,当我们只考虑导频位置而导频符号取值相同时,上式可简化为:
(7)
在基于CS的稀疏信道估计中,导频图案决定了恢复矩阵,因此可以根据对恢复矩阵的设计确定导频图案。我们的任务就是如何在N个总子载波中选取Np个作为导频子载波,即寻找最优的导频图案P,使得恢复矩阵的μ值最小,将该最优导频图案记为Popt。
本文采用树状结构代替文献[10]算法的内循环过程,当分支数为1时相当于没有内循环的SSS算法,当分支数大于1时,本文算法可以同时考虑每一层各个分支的特性,避免SSS算法仅在某一个分支中寻找局部的最小互相关值,而陷入局部最优问题。相比较SSS算法,本文算法往往能搜索到更小的μ值。
本文采用一种新的树状搜索算法直接从所有可能的个导频图案集合中搜索最佳导频图案Popt。图1为二分支树算法的结构,不同的节点代表着不同的导频图案,层数代表了父节点待替换导频在导频集合中的序号,阴影部分表示为存活节点,它代表着该层替换后留下的μ值较小的导频图案,每个父节点产生的子节点总个数对应着导频候选集F的大小。假定根节点个数Nroot=1,每层存活节点数Nsuv=2,每个父节点产生子节点总个数Nall=4。如图所示,1号为根节点,对应着随机产生的初始导频图案,对根节点的第一根导频进行替换,共产生4种新的导频图案,选取μ值较小的两个结果1.2,1.4作为对第二根导频替换的父节点,再对两个父节点的第二根导频进行替换一共产生八个子节点,同样选取μ值较小的两个节点(2.3,2.8)作为第三根导频替换的父节点,因此,在接下来的步骤中,我们总是需要从八个子节点选择精炼两个,以此规律替换剩余导频,最终选择出具有最小互相关值的节点。具体实现算法如下所示:
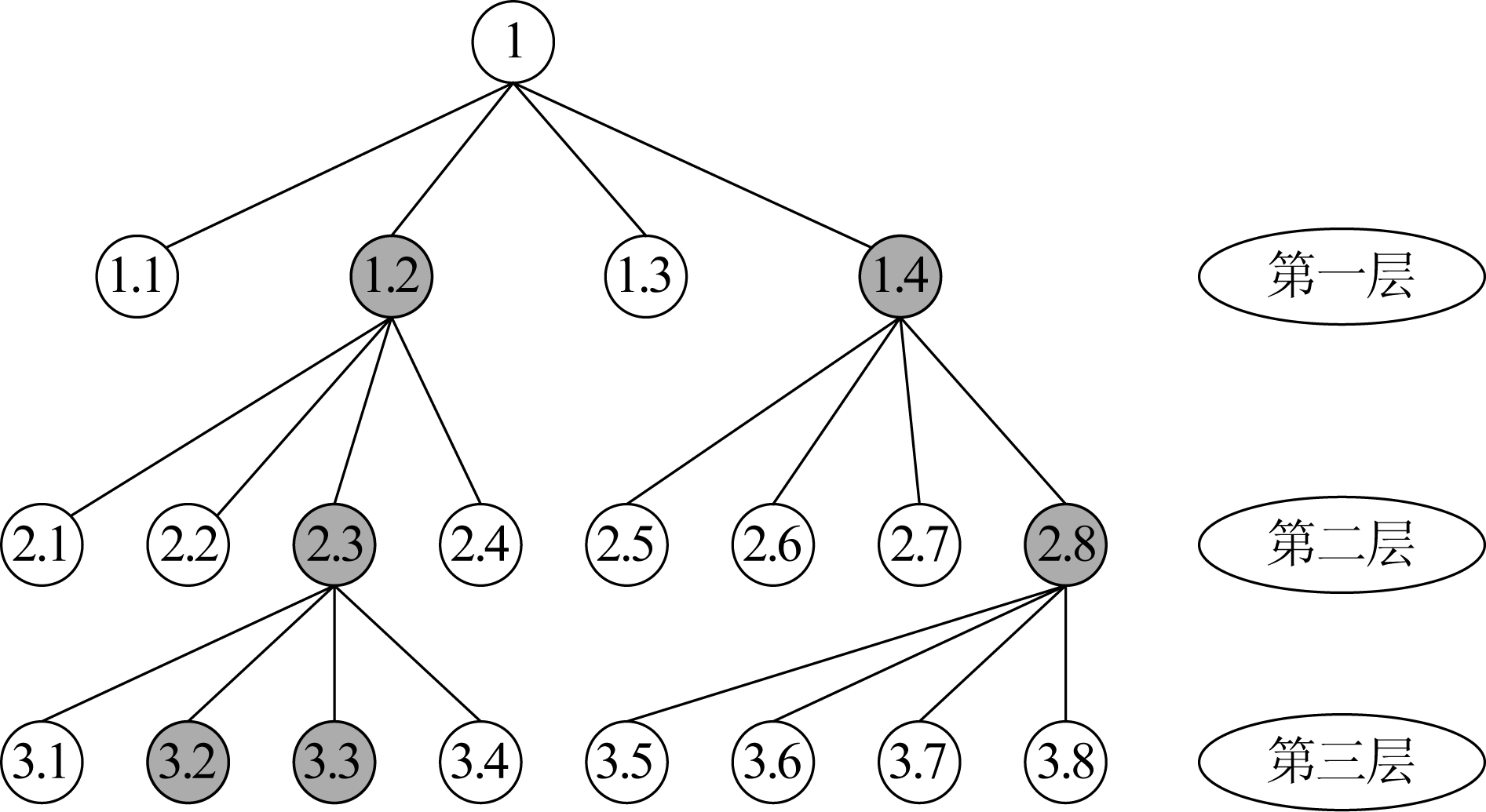
图1 分支树
Fig.1 Branching tree
TSS导频优化算法 初始化:设置根节点个数Nroot=M1和存活分支个数Nsuv=M2;导频数Np,OFDM子载波数N,根节点序号l=1。步骤1 根节点序号为l。从N个子载波中随机抽取Np个导频子载波,生成导频图案P作为根节点。步骤2 令待调整导频符号的导频序号m=1。集合Fl,m为根节点序号为l时生成的导频图案P中除了第m根导频a之外的其余Np-1根导频,即Fl,m=a\P,候选集Cl,m为总子载波构成的集合C和Fl,m的差集,即Cl,m=C-Fl,m。每次按顺序从集合Cl,m中取出一根导频,替换P中的第m根导频,一共可以产生N-Np+1个新的导频图案。步骤3 产生存活子节点。从新的N-Np+1个导频图案中计算μ值并选取最小的M2个导频图案作为存活子节点,使得存活子节点序号j=1并且使m=m+1。步骤4 由上一轮迭代产生的第j个存活子节点作为本次迭代的父节点。Fjl,m为第j个父节点除了本轮需要替换的第m根导频之外的其余Np-1根导频构成的集合,候选集Cjl,m=C-Fjl,m。再按顺序从集合Cjl,m中取出一根导频,替换第j个父节点中的第m根导频。步骤5 判断j是否为M2,若为真则一共可以产生M2×(N-Np+1)个新的导频图案,并继续执行步骤6;若为假,则使得j=j+1,并跳转至步骤4。步骤6 从新的M2×(N-Np+1)个导频图案中计算μ值并选取最小的M2个导频图案作为存活子节点。步骤7 判断m是否为Np,若为Np,则分别记录最小的μ值及其对应的导频图案在v向量与Z矩阵的第l列中,并跳转至步骤8;若m不为Np则使j=1且m=m+1并跳转至步骤4继续迭代。步骤8 判断l是否等于M1,若为假,则执行l=l+1并跳转至步骤1;若为真,则跳转至步骤9。步骤9 结果输出。若v向量中μ值绝对值最小的是第i列,对应选择Z矩阵中第i列中的导频图案Popt即作为优化好的导频图案。
在得到优化好的导频图案之后,我们将生成的导频图案应用于信道估计中,采用运算量较低的OMP算法完成信道估计。
4 复杂度分析
本文的算法复杂度主要来源于μ值的计算次数,在每一次迭代过程中μ值计算N-Np+1次。假设TSS算法根节点个数和SSS算法外循环次数同为M1,TSS算法分支个数和SSS算法内循环个数为M2,导频数Np,OFDM子载波数N。SSS算法的μ值计算次数最大为M1×M2×Np×(N-Np+1),本文采用的TSS算法的μ值计算次数为M1×(M2×(Np-1)×(N-Np+1)+(N-Np+1))。表1列出了三种不同参数取值情况下的μ值计算次数,可以看出本文算法较文献[10]的SSS算法复杂度更低。
表1 TSS和SSS算法复杂度分析
Tab.1 The computing complexity analysis of the algorithm of SSS and TSS
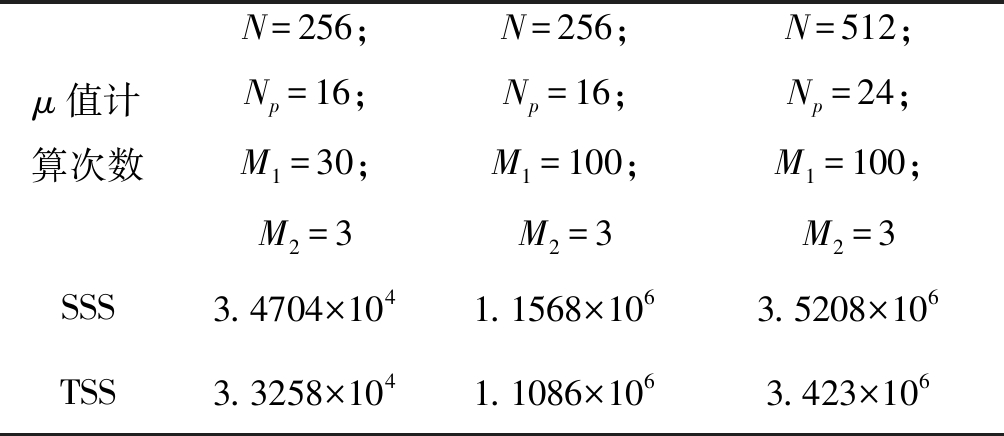
μ值计算次数N=256;Np=16;M1=30;M2=3N=256;Np=16;M1=100;M2=3N=512;Np=24;M1=100;M2=3SSS3.4704×1041.1568×1063.5208×106TSS3.3258×1041.1086×1063.423×106
5 仿真结果
为验证算法的有效性,将本文的TSS算法和文献[10]的SSS算法,文献[11]的IGS算法进行比较,主要性能指标为使用对应算法获得的导频图案后的信道估计均方误差(MSE, Mean-Square Error)和系统的误比特率曲线(BER, Bit Error Ratio)。在具有2.8 GHz的Intel Core i7-7700HQ CPU和8GB内存的宏碁笔记本电脑上运行的MATLAB R2017a。具体仿真参数设置如下:OFDM子载波数目N=256,最大时延对应的抽样时间倍数L=50,发射天线的导频数Np=16,将生成的导频图案应用于系统并使用OMP算法进行信道估计。
5.1 不同算法迭代过程中所获μ值比较
图2给出了N=256,Np=16,未优化的初始导频图案均为[146,120,4,86,41,200,78,132,42,149,65,161,169,182,110,21]的单次外循环下两种算法的μ值下降曲线。从图中可以看出按顺序替换16根导频,两种算法在替换导频位置序号较小时, μ值下降趋势较快,随着替换导频位置序号的增大,本文算法仍旧能维持较大的μ值下降趋势。相比于SSS算法,本算法能够以更快的速度收敛于更小的μ值。
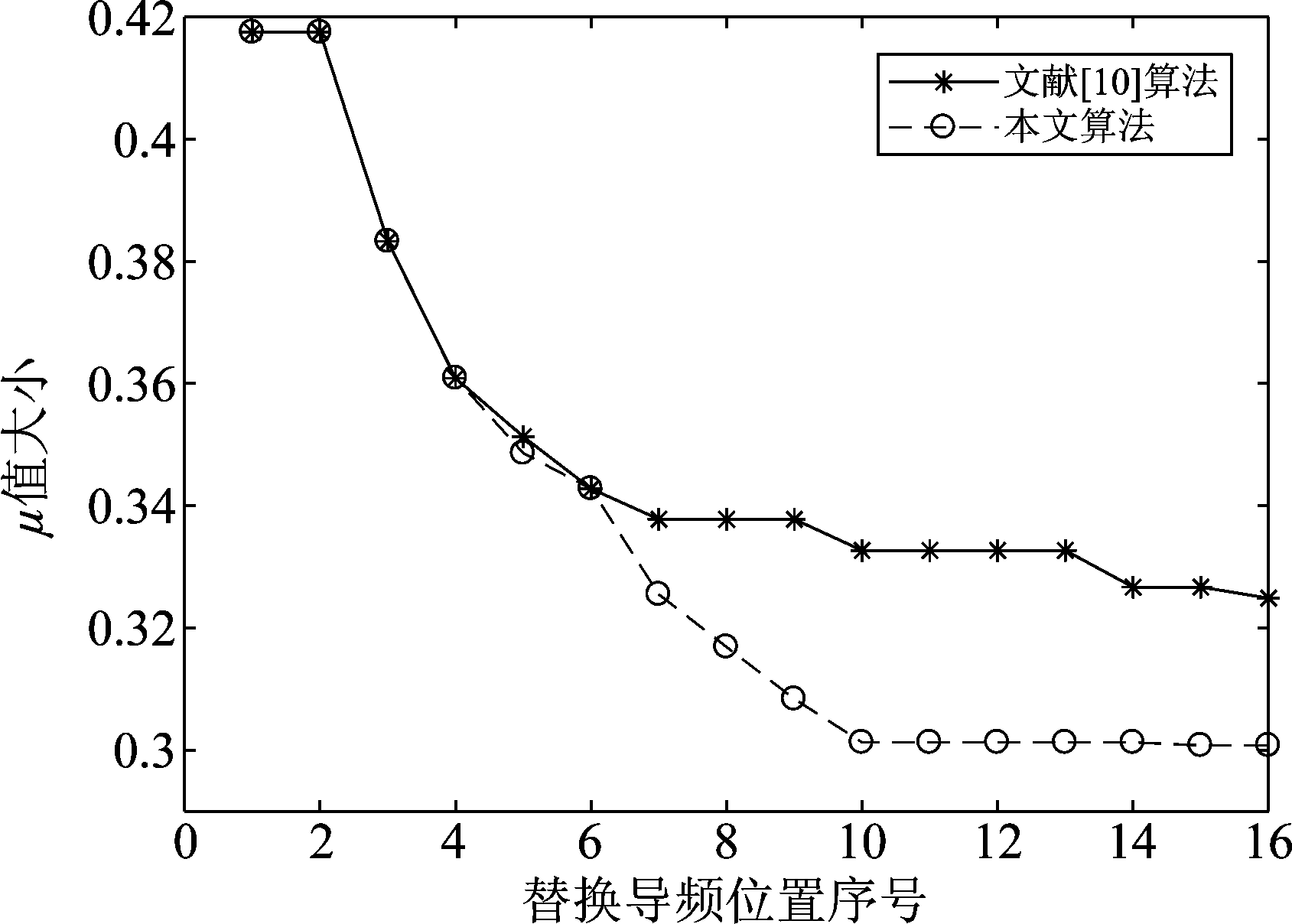
图2 各方案μ值下降曲线
Fig.2 Decline curves of μ-value in different algorithms
5.2 信道估计MSE比较
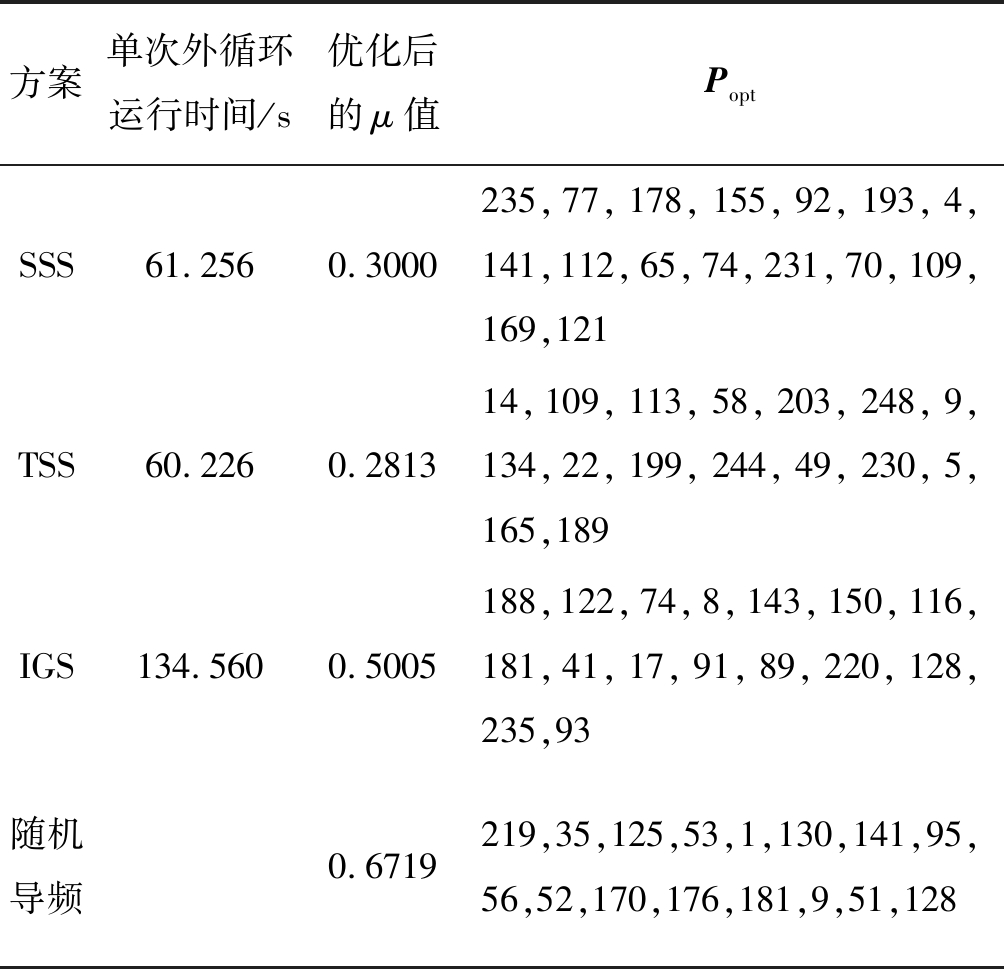
表2给出了当N=256,Np=16,SSS算法外循环次数U=100,内循环次数I=3;IGS算法每次减少子载波数为7;TSS算法根节点个数U=100,分支个数I=3时,各种方案优化后的导频图案及其μ值。从该表可以看出,本文算法运行时间略低于SSS算法,明显优于IGS算法,且比传统优化算法能搜索到更小的μ值。
图3比较表2中不同算法优化出的导频图案应用于系统信道估计时的均方误差(MSE)曲线。我们在这里采用的CS重建算法是正交匹配追踪从图中可以看出,本文方案生成的导频子集明显优于随机生成的导频图案和IGS算法优化的导频图案,而且在高信噪比时较文献[10]的SSS算法性能更优。
表2 各方案优化后的μ值及导频图案
Tab.2 μ-value and pilot pattern optimized by different pilot design schemes
方案单次外循环运行时间/s优化后的μ值PoptSSS61.2560.3000235,77,178,155,92,193,4,141,112,65,74,231,70,109,169,121TSS60.2260.281314,109,113,58,203,248,9,134,22,199,244,49,230,5,165,189IGS134.5600.5005188,122,74,8,143,150,116,181,41,17,91,89,220,128,235,93随机导频0.6719219,35,125,53,1,130,141,95,56,52,170,176,181,9,51,128
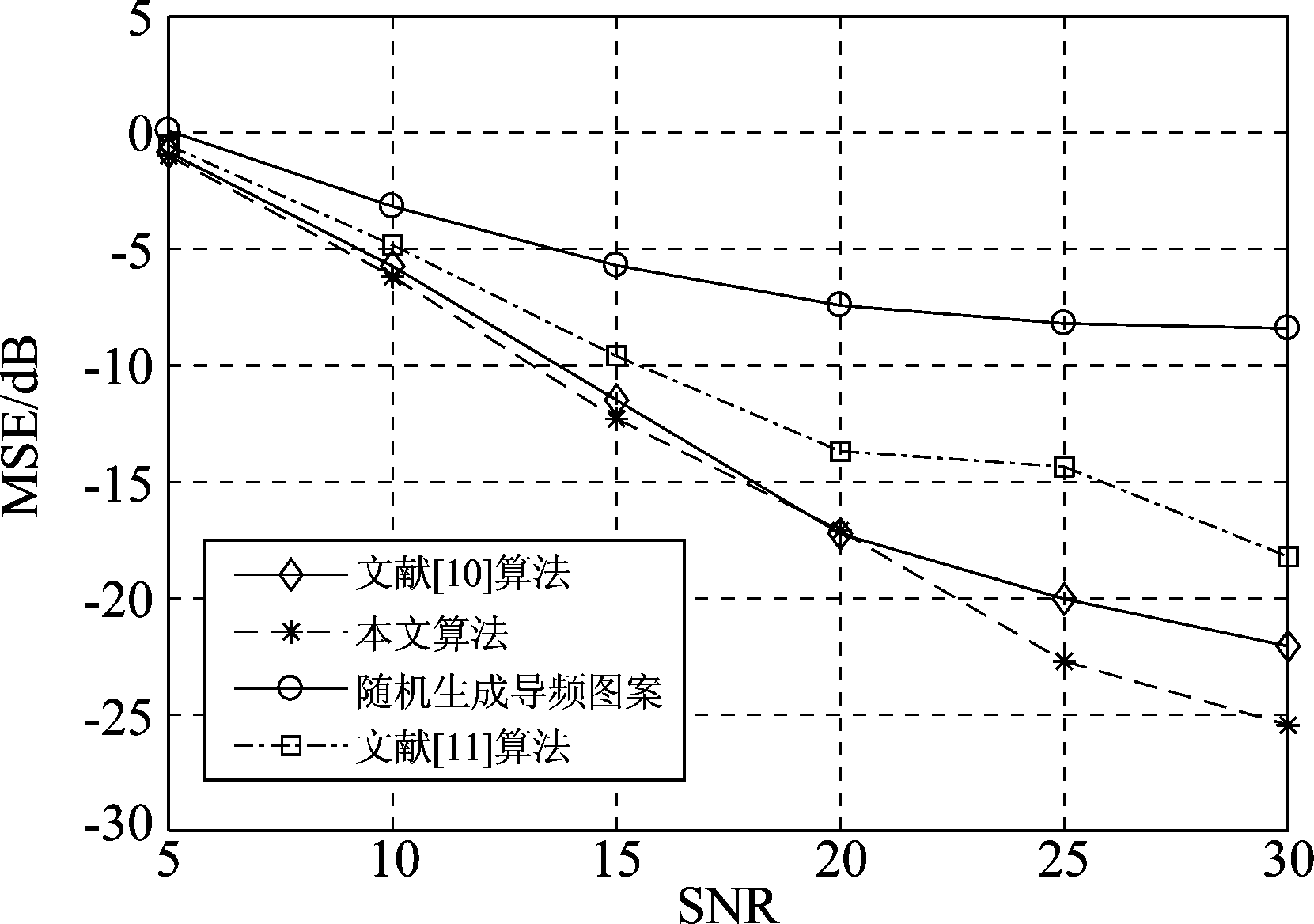
图3 各算法的MSE性能比较
Fig.3 MSE performance comparisons for different pilot design schemes
5.3 BER比较
将两种算法获得的表2中的导频图案应用于信道估计,并且基于信道估计的结果进行信号的解调,采用16QAM调制,每次仿真循环次数为5000次,取平均结果。图4比较了采用不同导频图案时的误码率(BER)随信噪比的变化关系。由图可见,使用本文提出的TSS算法得到的导频图案能够使得系统的误码率明显低于使用其他导频图案时的误码率,说明本文提出的导频优化方法可以有效改进系统的误码率。
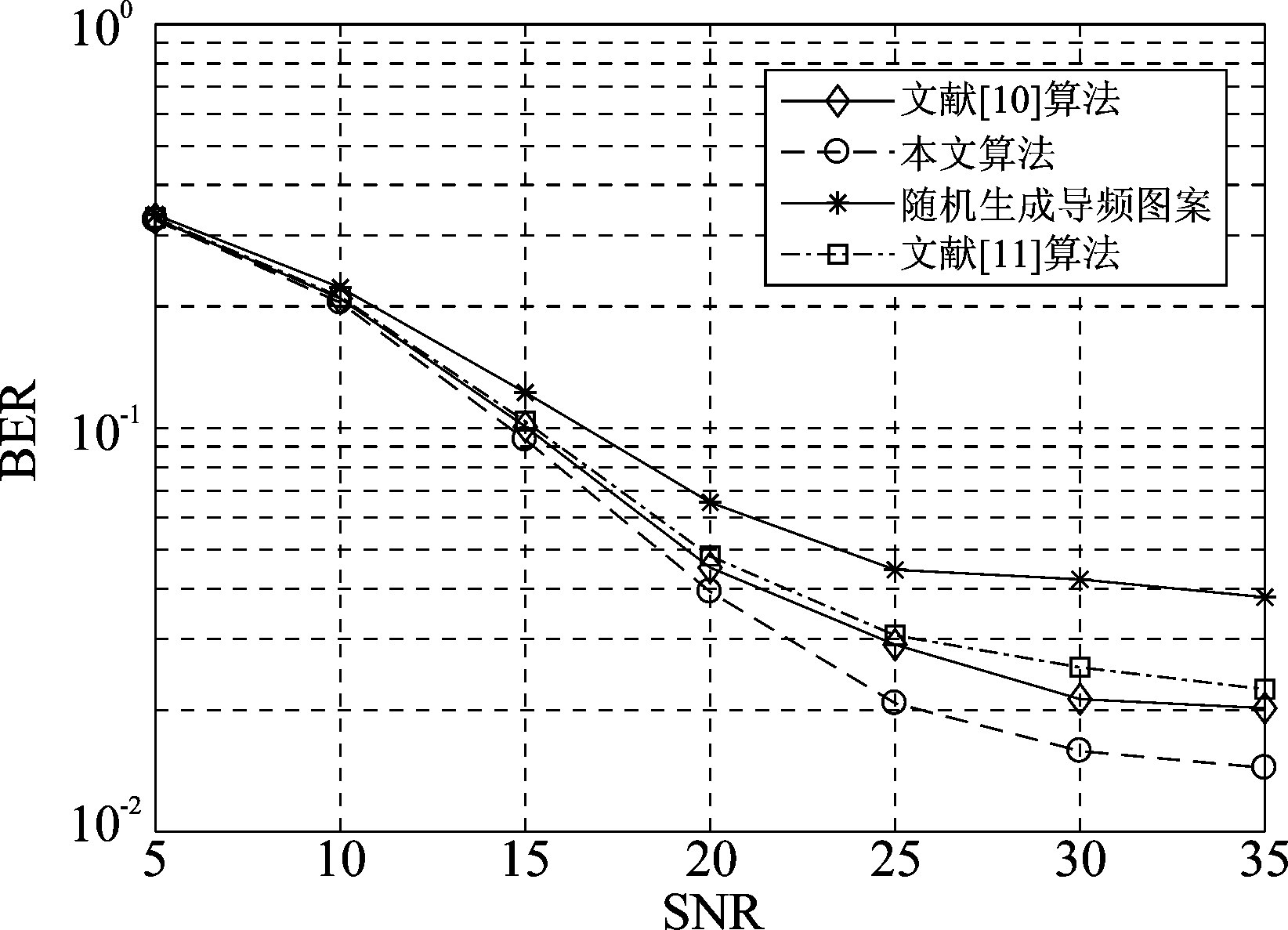
图4 各算法的BER性能比较
Fig.4 BER performance comparisons for different pilot design schemes
6 结论
本文针对OFDM系统中的稀疏信道估计问题,提出了一种新的导频优化方法TSS算法。该算法通过对μ值下降幅度大的分支更加关注,在每条分支线中采用随机搜索的方案,并综合考虑导频替换时各分支的μ值变化。仿真结果表明,本文提出的算法较传统优化算法能使获得的导频图案具有更小的恢复矩阵互相关值,算法复杂度较传统优化算法低。另外,与SSS算法获得的导频图案相比,本文提出的TSS算法获得的导频图案能使得系统的MSE和BER性能更优。
[1] 何雪云, 潘林, 彭伟刚. 压缩感知在稀疏信道估计中的应用[J]. 通信技术, 2011, 44(9): 27-29.
He Xueyun, Pan Lin, Peng Weigang. Application of Compressive Sensing Theory in Sparse Channel Estimation[J]. Communications Technology, 2011, 44(9): 27-29.(in Chinese)
[2] Pejoski S, Kafedziski V. Improved Asymptotic Capacity Lower Bound for OFDM System with Compressed Sensing Channel Estimation for Bernoulli Gaussian Channel[J]. Radioengineering, 2016, 25(2): 283-288.
[3] Hu Die, Wang Xiaodong, He Lianghua. A New Sparse Channel Estimation and Tracking Method for Time-Varying OFDM Systems[J]. IEEE Transactions on Vehicular Technology, 2013, 62(9): 4648- 4653.
[4] Berger C R, Wang Z, Huang J, et al. Application of compressive sensing to sparse channel estimation[J]. IEEE Communications Magazine, 2010, 48(11): 164-174.
[5] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655- 4666.
[6] Tropp J A, Gilbert A C, Strauss M J. Simultaneous sparse approximation via greedy pursuit[C]∥IEEE International Conference on ICASSP, 2005: 721-724.
[7] Do T T, Gan L, Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]∥42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove. IEEE, 2008: 581-587.
[8] Uwaechia A N, Mahyuddin N M. Improved Time-Domain Threshold Determination for Sparse Channel Estimation in OFDM System[M]. 9th International Conference on Robotic, Vision, Signal Processing and Power Applications. Springer Singapore, 2017: 175-183.
[9] Tong L, Sadler B M, Dong M. Pilot-assisted wireless transmissions: general model, design criteria, and signal processing[J]. Signal Processing Magazine IEEE, 2004, 21(6): 12-25.
[10] Qi Chenhao, Yue Guosen, Wu Lenan, et al. Pilot Design Schemes for Sparse Channel Estimation in OFDM Systems[J]. Vehicular Technology IEEE Transactions on, 2015, 64(4): 1493-1505.
[11] Qi Chenhao, Wu Lenan. Tree-based backward pilot generation for sparse channel estimation[J]. Electronics Letters, 2012, 48(9): 501.
[12] Mohammadian R, Amini A, Khalaj B H. Compressive Sensing-Based Pilot Design for Sparse Channel Estimation in OFDM Systems[J]. IEEE Communications Letters, 2017, 21(1): 4-7.
