1 引言
在现代电子战中,由于欺骗式电子干扰能以较小的投入获得较好的干扰效果,因此一直备受青睐[1]。尤其是近几年数字射频储存器(DRFM: Digital Radio Frequency Memory)的高速发展为欺骗式干扰提供了有力的技术支持[2- 4]。通过对雷达信号的截获与储存,DRFM不仅能快速复制转发在时域和频域上与目标回波高度相似的干扰信号,还能通过对RCS调制来模拟目标的散射[5]等多种信息,使干扰信号极具欺骗性,从而迷惑敌方雷达的检测和跟踪系统,达到掩护目标突防的作战目的。因此,对欺骗假目标的识别是电子对抗中亟待解决的重要问题,这对提高雷达在复杂电磁干扰环境下的目标探测和定位跟踪能力具有十分重要的军事价值。
针对欺骗式电子干扰,单基地雷达可通过频率捷变、发射信号优化[6]、极化特性差异[7]、运动学信息[8]和DRFM量化误差[9]等多种方式进行对抗。然而,受制于探测视角单一,所获得目标信息有限的问题,单基地雷达的抗干扰能力受到了严重制约。而多基地组网雷达系统具有多视角,配置灵活,信息冗余等优良特性,在“四抗”性上带来了天然优势[10],已成为提升雷达抗干扰能力的重要发展趋势[11]。文献[12]提出了在集中式组网雷达下的将多目标跟踪和自适应同源门限检测相结合的抗虚假距离目标方法;文献[13]基于真假目标空间分布差异,提出了在分布式组网雷达下,通过航迹关联检验的方法对抗距离假目标干扰;文献[14]充分利用了真目标在空间位置和速度上的相关性,增强了组网雷达对假目标的鉴别能力;文献[15]提出了对目标径向速度进行检验的干扰识别方法,解决了假目标密集度增大而导致鉴别效果恶化的问题;文献[16]提出了联合最近邻-角度信息的多重判别方法,在保证识别率的同时有效降低了关联判别时间;为充分发挥组网雷达的“集群”优势,文献[17-18]研究了在异地配置下,基于角度和距离量测的主/被动雷达抗欺骗干扰技术;针对密集假目标干扰造成检测概率降低的问题,文献[19]采用主/被动雷达体制,巧妙利用量测预处理和融合技术,在提高抗干扰能力的同时实现了对目标的稳定跟踪。然而,上述抗干扰方法仅仅只在雷达量测数据层面,舍弃了回波信号上的有用信息,譬如幅度和相位,未能充分发挥多基地雷达的抗干扰能力。鉴于此,根据目标回波和干扰信号在空间散射特性上的差异,文献[20]提出了一种通过幅度相关性检验来识别欺骗假目标的方法,但是由于只利用了信号的幅度信息,当脉冲数目较少,信噪比较低时,雷达被欺骗率仍然较高。
为解决此问题,本文在目标回波与干扰信号幅度相关性差异的基础上,充分利用了两者在多普勒维和距离维上的差异,提出了一种多维信息联合的欺骗干扰抑制算法。第2部分介绍了多基地雷达信号模型,第3部分详细说明了该干扰抑制算法,第4部分通过数字仿真验证了该算法的有效性,第5部分是对本文的总结。
2 信号模型
如图1所示为1个发射站和N个接收站组成的多基地雷达系统,其中发射站位于(xt,yt),各接收站位于(xr,1,yr,1),(xr,2,yr,2),...,(xr,N,yr,N)。假设系统已完成时间和空间同步,此时一搭载了干扰设备的突防飞机正处在雷达探测威力区内,其位置为(x,y),则第n个接收站的基带目标信号为:
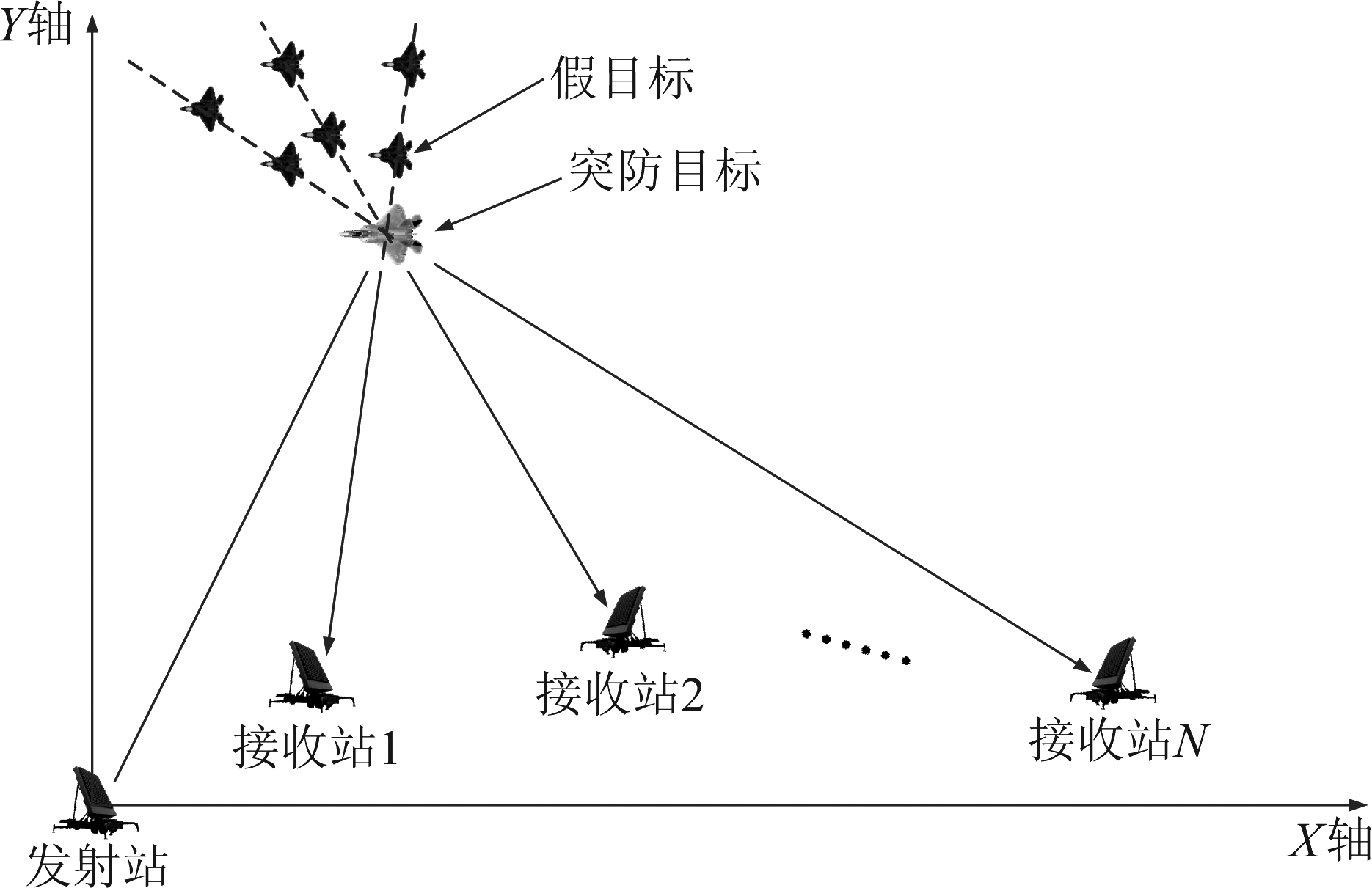
图1 多基地雷达系统探测场景
Fig.1 Detection scenario of multi-static radar system
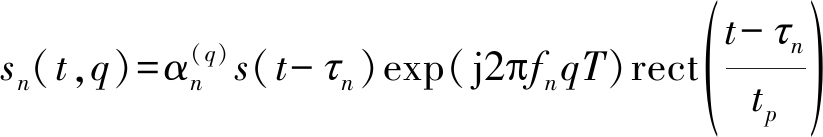
q=1,2,...,Q
(1)
其中,t表示快时间,q表示慢时间,Q表示在一个相参处理间隔(CPI: Coherent Processing Interval)内的相参脉冲数目,s(t)是基带发射波形,T是脉冲重复间隔(PRI: Pulse Repetition Interval),tp为脉冲宽度,
表示第n个接收站中第q个脉冲散射系数,τn为第n个接收站中的目标时延, fn为第n个接收站中的目标多普勒频率[21]:
(2)
式中,λ是波长,ν(t)表示速度在目标与发射站连线上的分量,ν(n)表示速度在目标和第n个接收站连线上的分量。
假设信号参数与雷达布站满足回波独立条件[22-23]:
(3)
式中,L是基线长度,R是目标相对节点雷达的径向距离,D目标尺寸。
为实现突防,干扰机利用截获到的雷达信号实施干扰(自卫干扰),产生K个距离-速度复合欺骗假目标。假设各接收站中已完成了对干扰信号的时延校准[29],则第n个接收站的基带干扰信号为:
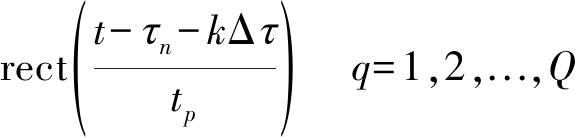
(4)
其中,
表示第n个接收站中第k个假目标的第q个脉冲散射系数,Δτ是干扰机调制的假目标时延间隔(对应的假目标距离为假目标密集度), fk是干扰机直接调制的第k个假目标多普勒频率。
考虑到雷达内部噪声,第n个接收站的基带接收信号为:
yn(t,q)=sn(t,q)+sn,F(t,q)+wn(t,q)
q=1,2,...,Q
(5)
其中wn(t,q)是接收机噪声,且有
是噪声功率。
各接收站对信号进行脉冲压缩,慢时间积累和恒虚警检测(假设检测概率为1)后,提取检测到目标的距离和,多普勒频率以及由一个CPI内所有脉冲散射系数构成的慢时间复包络序列(SCES:Slow-time Complex Envelope Sequence)[20],组成多维信息矩阵In:
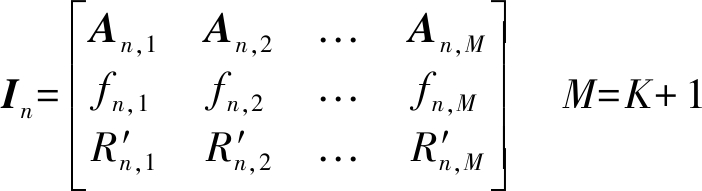
(6)
式中fn,m,Rn,m和An,m分别表示第n个接收站中第m个目标的多普勒频率,时延对应的距离和以及SCES:
An,m=Bn,m+Wn
(7)
其中,
为噪声序列,Bn,m为信号复幅度构成的慢时间复幅度序列,且有以下关系:
(1)若第m个目标是真目标,则:
(8)
其中,由于满足回波独立条件,
为真目标回波功率。
(2)若第m个目标是假目标,则:
(9)
其中,Bn,m为未知的随机矢量。
3 多维信息联合干扰抑制算法
从信号模型中可以发现,在幅度维上,目标回波各向异性[20];在多普勒维上,目标多普勒具有多样性[28];在距离维上,目标空间位置具有“同源”性[12]。基于以上特性,在融合中心将多维信息矩阵In,n=1,2,...,N依次通过幅度维和多普勒维的干扰识别,最后在距离维对虚假目标的定位结果作进一步识别抑制,并同时实现对真目标的定位,如图2所示。
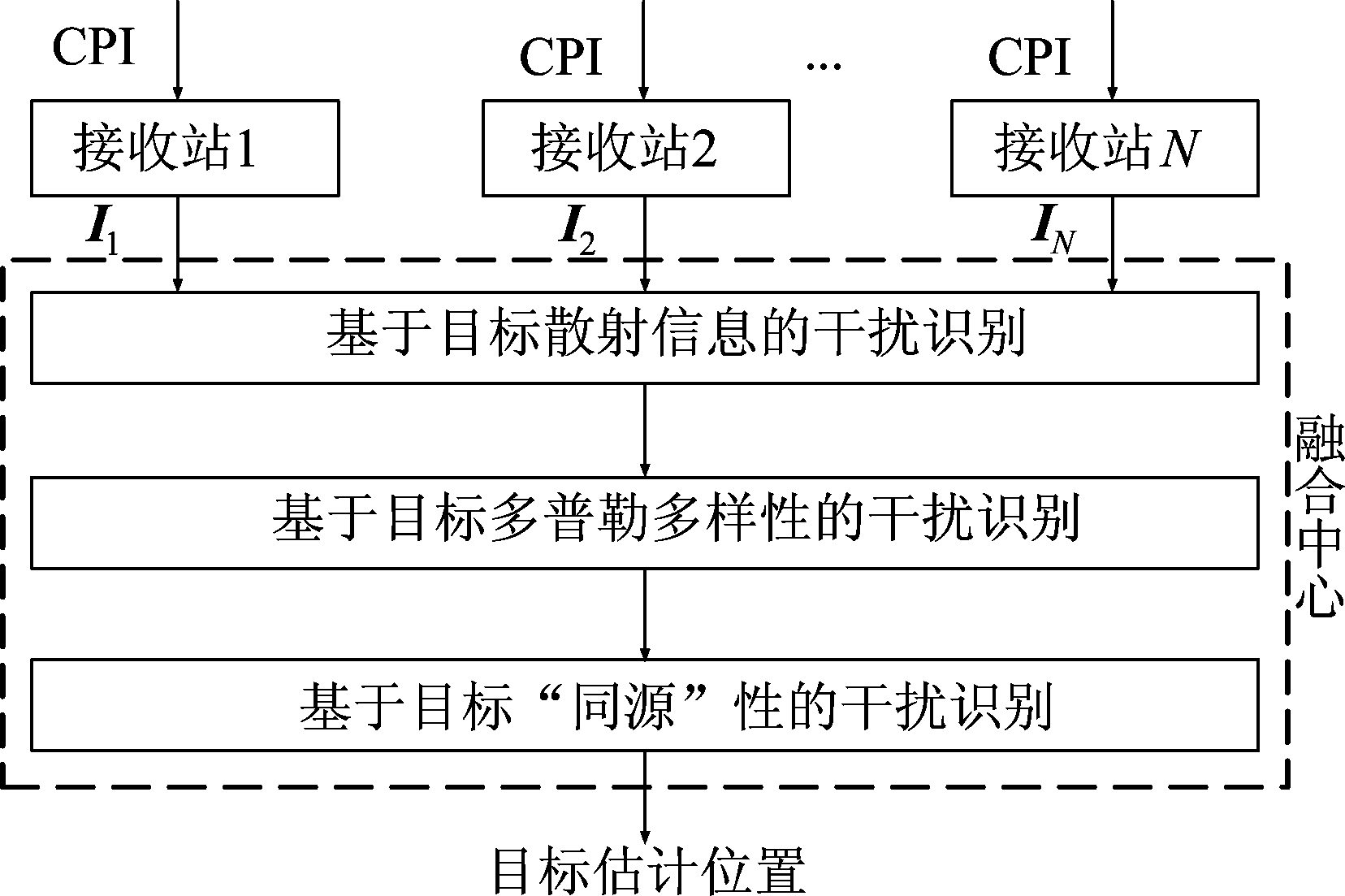
图2 多维信息联合干扰抑制算法流程图
Fig.2 Flow diagram of the suppression algorithm based on multi-dimensional information association
3.1 基于目标散射信息的干扰识别
考虑接收站1中第m个目标的SCES A1,m和接收站2中第m′个目标的SCES A2,m′。由文献[22-23]可知,站点间真假目标回波具有明显的相关性差异:真目标回波复包络相互独立,而干扰信号复包络具有相关性,据此可建立如下假设检验:
(10)
从文献[20]中分析可知,干扰信号在各站点中的复幅度序列是完全相关的,即满足B2,m′=k·B1,m,且
故当H0假设成立时,A1,m和A2,m′相关性系数为:
(11)
式中,J1,m和J2,m′分别为H0成立下A1,m和A2,m′的干噪比。
从式(11)可以看出,H0条件下的相关性系数与干噪比有关,且在J1,m和J2,m′足够大时,相关性系数ρm,m′|H0几乎为1。然而在H1假设下,无论是不同假目标的组合,不同真目标的组合还是真目标和假目标的组合情况,由于其复幅度间的独立性[20],相关性系数ρm,m′|H1均为0。因此,可利用CPI内目标幅度的时间样本A1,m和A2,m′作为式(11)所示的相关性系数估计,即:
(12)
鉴于相参脉冲个数Q一般不多,相关性系数估计
是一个虚部较小的复数,因此取其实部作为检验统计量μm,m′:
(13)
考虑到欺骗干扰效果并不依赖功率,故将真实目标信噪比(SNR:Signal Noise Ratio)和虚假目标干噪比(JNR: Jammer Noise Ratio)统一定义为目标噪声比(TNR:Target Noise Ratio),计算检验门限ζm,m′[20,24]:
(14)
其中,
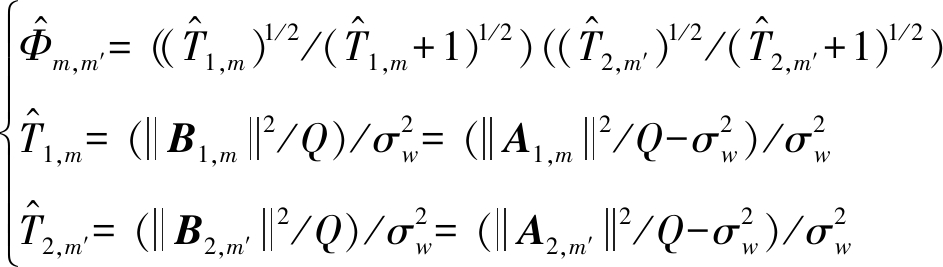
(15)
式中,
分别为A1,m和A2,m′的目标噪声比TNR的估计值。
从而式(10)可转化为:
(16)
对两站点中任意两个目标均进行式(16)检验,一旦被检验为H0,则剔除该目标,并进行式(17)所示的相参积累,以此提高干噪比,用于甄别其余站点中的欺骗干扰。
J=A1,m+A2,m′
(17)
3.2 基于目标多普勒多样性的干扰识别
以两个站点为例进行说明,设f1,m为接收站1中第m个目标的多普勒频率, f2,m′为接收站2中第m′个目标的多普勒频率。在多基地雷达系统中,由于目标的多普勒频率与各站点的空间布置紧密相关[21],如式(2)所示,因此其具有多样性[28]。然而,由于虚假目标是由同一部干扰机产生,因此其多普勒频率在不同站点间是相同的。故,据此可建立如下假设检验:
(18)
因为
其中
和
分别为没有雷达量测误差下f1,m和f2,m′的真实值,df1和df2分别为两雷达的多普勒测量误差,且均服从均值为零,方差为
的正态分布。故,计算两站点间的目标多普勒频率差Δf12=f1,m-f2,m′。在H0假设成立时,多普勒频率差Δf12=df1-df2满足正态分布,即
由此,可建立如式(19)所示的检验统计量ζ1,用于表征目标间的多普勒频率差。当H0成立时,ζ1则服从自由度为1的卡方分布。
(19)
这样,式(18)所示的原假设检验问题即可转化为:
(20)
式中,
为满足显著性水平为α的χ2(1)分布上侧分位数。
至此,对任意两个目标均进行上述多普勒检验,一旦被检验为H0,则剔除该目标,以此遍历所有站点。
3.3 基于目标“同源”性的干扰识别
为防止遗漏假目标对雷达系统造成欺骗,这里首先对剩余目标进行TOA定位[25-26],接着将定位结果通过“同源”性检验,进一步识别并剔除假目标,最后融合定位结果,实现对真目标定位。
3.3.1 多基地雷达TOA定位
在图1所示的多基地雷达系统中,设
为待估计目标位置,Rt是目标到发射站距离,Rn是目标到第n部接收站的距离,
是发射站-目标-第n部接收站的距离和。以接收站1,2组合的TOA定位为例,从图中几何关系可得:
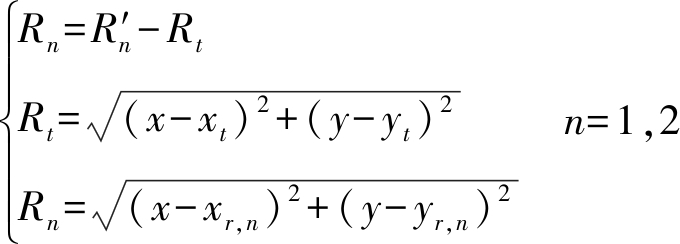
(21)
定义
对式(21)中
两边同时平方并化简可得:
Ax=b
(22)
式中,
(23)
(24)
(25)
当接收站不在一条直线上时,满足rank(A)=2,则估计目标位置
为:
(26)
其中x=x0+dx,x0=[x0,y0]T表示目标真实位置,
表示定位误差,且服从正态分布dx～N(0,
2)。
令
则式(26)可表示为:
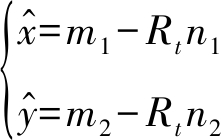
(27)
其中,
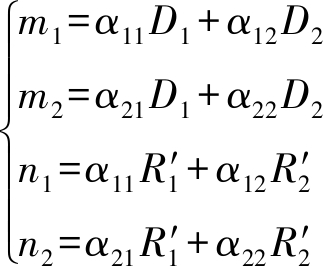
(28)
将式(27)带入(Rt)2=(x-xt)2+(y-yt)2可得:
(m1-xt)2+(m2-yt)2=0
(29)
故,Rt即为(29)所示方程的解,带入(27)中计算出待估计目标位置
3.3.2 TOA定位精度
对
两边同时微分并化简可得:
(30)
其中,
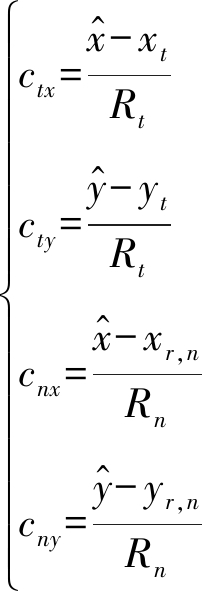
(31)
定义
则(30)可化简为:
dx=(CTC)-1CTdR′=BdR′
(32)
其中
为距离和量测误差向量,且服从正态分布
为雷达距离和量测误差精度。
从而计算出定位误差dx的协方差矩阵2为:
2=E[dx(dx)T]=
(33)
3.3.3 目标“同源”性检验
考虑到虚假目标数目较多时,容易出现组合爆炸的问题,因此在进行“同源”性检验之前,首先对所有的定位结果做“最近邻关联”的匹配处理[12,14]:将任意两接收站的组合作为参考组合,计算参考组合的每个目标定位结果与其余组合的所有定位结果的欧氏距离,并将其中最小距离对应的定位结果作为参考组合中该目标的关联目标,从而形成对参考组合的每一个目标定位结果的关联序列。
然而,由于受到干扰的影响,关联序列中可能全是真目标的定位结果,也可能存在部分虚假目标的定位结果,甚至可能全是虚假目标的定位结果。因此,需要对关联序列做下面的“同源”性检验。
不失一般性,考虑三个接收站的定位结果关联序列AZ={x12,x13,x23},其相应的定位误差协方矩阵序列为
由于真目标具有“同源”性[12],不同站点组合的真目标定位结果必然在空间上汇聚,而虚假目标的定位结果在空间上是离散的,因此可对接收站1,2组合的定位结果x12和接收站1,3组合的定位结果构建如下的假设检验:
(34)
计算不同定位结果间的距离V=x12-x13。当H0假设成立时,V=dx12-dx13服从均值为零,协方差矩阵为3的正态分布,即V～N(0,3),其中:
3=E[V·(V)T]=E[dx12(dx12)T]+
E[dx13(dx13)T]-E[dx12(dx13)T]-E[dx13(dx12)T]
(35)
由于不同站点间彼此独立,有:
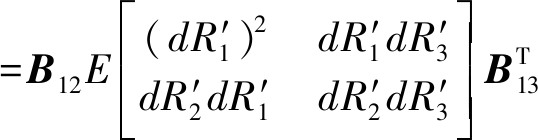
(36)
同理可得
由此,可建立如式(37)所示的检验统计量ζ2,用于表征目标定位结果之间的离散程度。当H0成立时,ζ2则服从自由度为2的卡方分布。
ξ2=VT(3)-1V
(37)
这样,式(34)所示的原假设检验问题即可转化为:
(38)
式中,
为满足显著性水平为α的χ2(2)分布上侧分位数。
最后,对关联序列中AZ中的任意两个定位结果均进行上述的“同源”性检验,当所有的检验结果均为H0,融合其定位结果[27]:
(39)
(40)
4 仿真验证
不失一般性,这里以1发3收的多基地雷达系统为例进行仿真验证。各雷达站坐标如表1所示,目标位于(5 km,7 km),速度380 m/s。在实验1中,通过对比识别前后的定位结果验证了该算法的有效性;在实验2中,通过与文献[20]对比,验证了在相同条件下,该算法能有效提高系统抗干扰能力;在实验3中,详细分析了雷达和干扰参数对系统抗干扰能力的影响情况。
表1 雷达站点位置
Tab.1 The positions of radar stations
站点名称发射站接收站1接收站2接收站3坐标/km:(x,y)(0,0)(0,1)(1,0)(4,0)
4.1 实验1:有效性验证
设定相参脉冲个数Q=8,目标噪声比TNR=3 dB,雷达测距精度σR′=100 m,多普勒测量精度σf=10 Hz,假目标数目6个,假目标密集度为500 m,多普勒欺骗间隔为1.5 kHz,仿真结果如图3所示。
可以看到,若没有进行干扰辨识而直接定位,将产生大量假目标,以至于目标真实位置被完全掩盖,如图3(a);反之,经过干扰抑制后,输出的目标估计位置只有一个,且与目标真实位置几乎重合。
4.2 实验2:抗干扰性能提升验证
以真目标识别率(识别结果中只有真目标)和雷达被欺骗率(识别结果中存在假目标)为标准验证该算法的性能提升情况。设定假目标个数为1,相参脉冲个数Q从4均匀变化到64,TNR分别为0 dB,3 dB,6 dB,9 dB,12 dB,蒙特卡洛次数1万次,仿真结果如图4所示。接着,为分析多假目标干扰对算法性能的影响,保持其他条件不变,设定TNR=3 dB,脉冲个数Q分别为8,14,20,假目标数目从3均匀变化到11,仿真结果如图5所示。
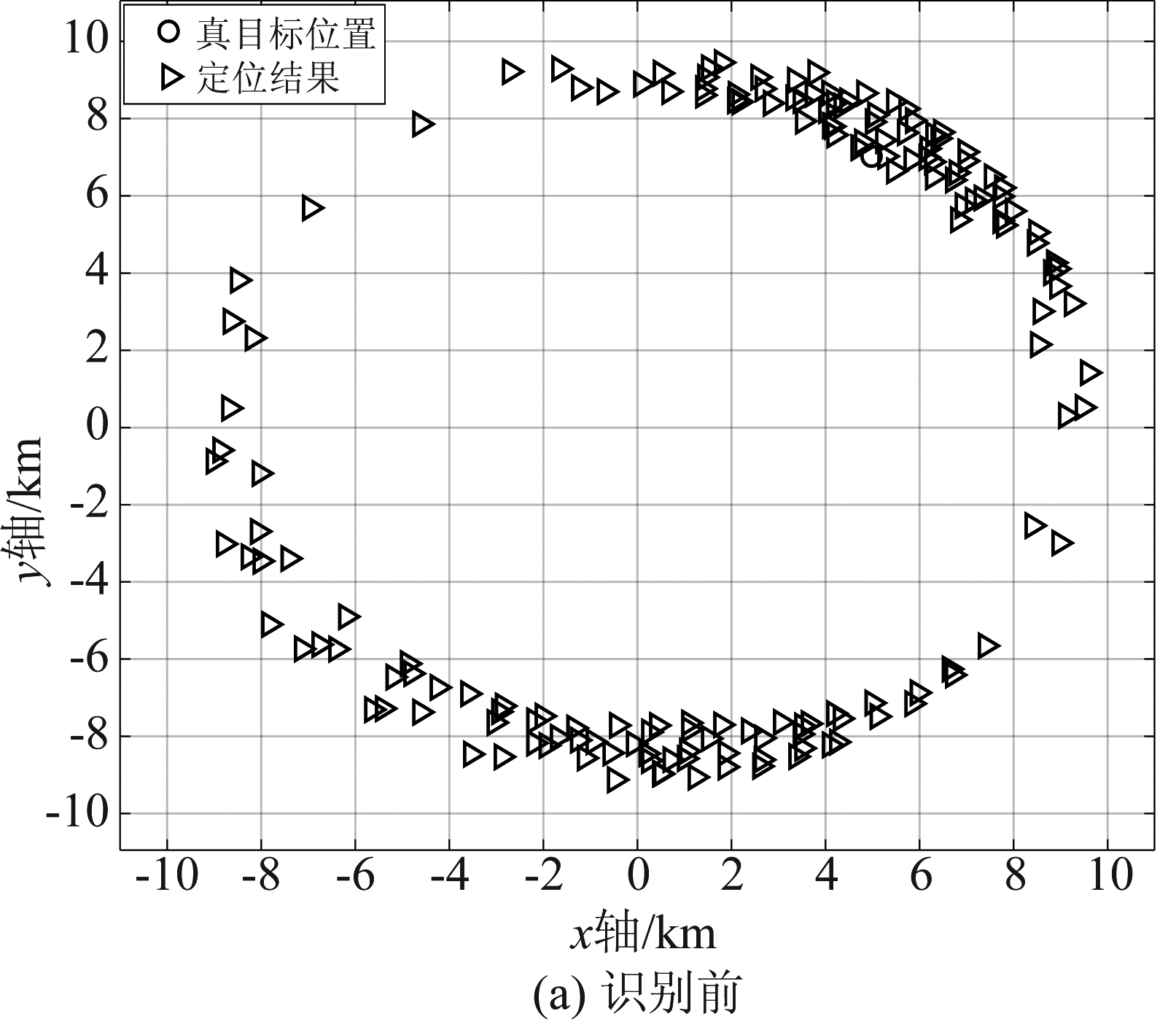
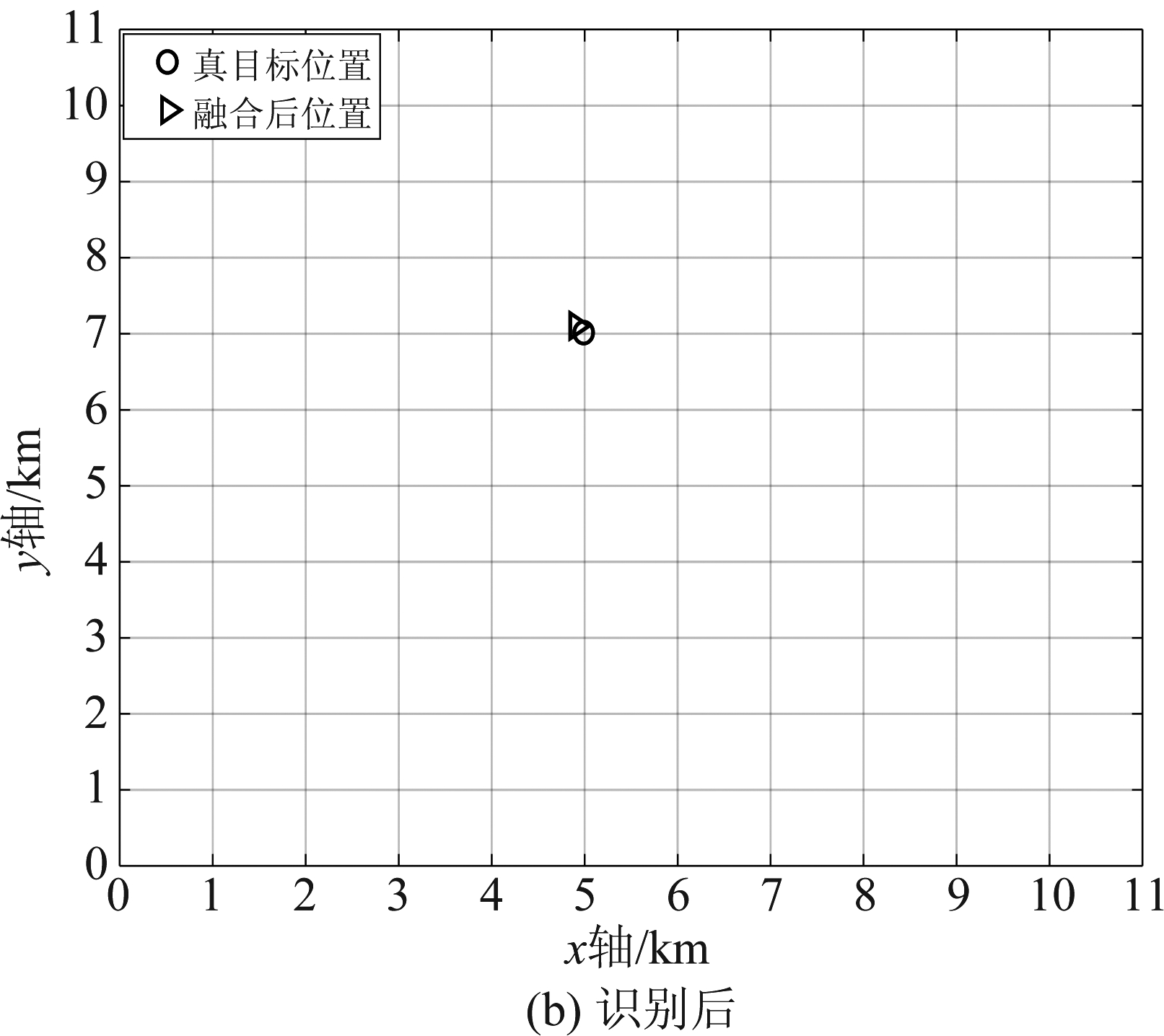
图3 识别前后定位结果
Fig.3 The localization results before and after the identification
如图4(a)所示,随着TNR和Q的增大,真目标识别概率会不断提高,并最终收敛于90%左右。但由于幅度,多普勒以及距离信息之间相互独立,其对应的干扰识别过程也是彼此独立,因此真目标识别率是各维度识别率的乘积,故相比于文献[20]只采用了幅度信息,该算法的真目标识别率会有所下降(依旧处在可接受范围内)。然而,在脉冲个数Q较少,TNR较低的情况下(如TNR=0,Q=4),相比于文献[20],该算法却能极大地降低雷达被欺骗率,如图4(b)所示。
图4 脉冲个数和TNR对抗干扰性能影响
Fig.4 The influence of pulse number and TNR on anti-jamming performance
图5 假目标数目和脉冲个数对抗干扰性能影响
Fig.5 The influence of false target number and pulse number on anti-jamming performance
从图5(a)中可以发现,真目标识别率与相参脉冲个数成正比,而与假目标个数成反比。同时与图4类似,其识别率相比于文献[20]略有下降,然而当脉冲个数较少,假目标个数较多时(如Q=8,假目标个数为11),相比于文献[20]高达60%以上的被欺骗率,该算法却能保证雷达被欺骗率几乎为零,如图5(b)所示。综上所述,该算法是以降低一定的真目标识别率为代价,极大地降低了雷达被欺骗率。
4.3 实验3:雷达和干扰参数对抗干扰性能的影响分析
图6 雷达参数对抗干扰性能影响
Fig.6 The influence of radar parameters on anti-jamming performance
为分析雷达和干扰相关参数对算法抗干扰性能的影响情况。设定假目标数目为1,相参脉冲个数为12,TNR为12 dB,雷达测距精度从50 m均匀增大到300 m,多普勒测量精度分别为5 Hz,10 Hz和15 Hz,蒙特卡洛次数1万次,仿真结果如图6所示。接着,保持其他条件不变,假目标密集度从0.1 km均匀增加到1.6 km,假目标多普勒频率分别为1 kHz,2 kHz和3 kHz,仿真结果如图7所示。
如图6所示,真目标识别率几乎不受雷达相关参数的影响,基本维持在85%左右的较高水平;而雷达被欺骗率只受测距精度影响,随测距精度的恶化逐渐升高,但依然保持在较低水平(低于1.4%)。
从图7中可以发现,真目标识别率同样不受干扰相关参数的影响,依然维持在85%左右,而雷达被欺骗率只受假目标密集度影响,随密集度的降低逐渐降低,最终几乎收敛于零。
图7 干扰参数对抗干扰性能影响
Fig.7 The influence of jamming parameters on anti-jamming performance
5 结论
针对目标突防过程中实施的距离-速度复合欺骗干扰,本文充分利用了目标回波与干扰在幅度,多普勒和距离维上的差异,提出了多维信息联合的干扰抑制算法。从数字仿真结果可知,该算法是以牺牲一定真目标识别率为代价,有效地解决了在脉冲个数较少,信噪比较低时雷达被欺骗率较高的问题,并能实现对真目标定位。同时可以发现,雷达和干扰相关参数对算法的抗干扰性能影响很小,始终保持了较高的真目标识别率和较低的雷达被欺骗率,对实际工程应用具有一定的参考价值。
[1] Schleher D C. Electronic Warfare in the Information Age[M]. Boston, MA: Artech House, 2000.
[2] Berger S D. Digital radio frequency memory linear range gate stealer spectrum[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 725-735.
[3] Ozdil O, Serin M, Ispir M, et al. Channelizer structure in DRFM systems for real signals[C]∥IEEE International Conference on Signal Processing and Communications Application, Haspolat, Turkey, June 2013: 1- 4.
[4] Olivier K, Cilliers J E, Du Plessis M. Design and performance of wideband DRFM for radar test and evaluation[J]. Electronics Letters, 2011, 47(14): 824- 825.
[5] Tian X. Radar deceptive jamming detection based on goodness-of-fit testing[J]. Journal of Information & Computational Science, 2012, 9(13): 3839-3847.
[6] Zhang J D, Zhu D Y, Zhang G. New Antivelocity Deception Jamming Technique Using Pulses with Adaptive Initial Phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290-1300.
[7] 李永祯, 胡万秋, 陈思伟, 等. 有源转发式干扰的全极化单脉冲雷达抑制方法研究[J]. 电子与信息学报, 2015, 37(2): 276-282.
Li Yongzhen, Hu Wanqiu, Chen Siwei, et al. Active Repeater Jamming Suppression Using Polarimetric Monopulse Radar[J]. Journal of Electronics & Information Technology, 2015, 37(2): 276-282.(in Chinese)
[8] Rao B, Xiao S P, Wang X S, et al. Maximum Likelihood Approach to the Estimation and Discrimination of Exoatmospheric Active Phantom Tracks Using Motion Features[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 794- 818.
[9] Greco M, Gini F, Farina A. Radar Detection and Classification of Jamming Signals Belonging to a Cone Class[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1984-1993.
[10] 王欢, 焦光龙, 谢军伟. 基于雷达组网中新技术的研究[J]. 现代雷达, 2007(1): 9-11, 22.
Wang Huan, Jiao Guanglong, Xie Junwei. Study on New Technologies Applied in Radar Network[J]. Modern Radar, 2007(1): 9-11, 22.(in Chinese)
[11] 张林让, 赵珊珊, 周宇, 等. 网络化雷达协同抗欺骗式干扰技术研究进展[J]. 数据采集与处理, 2014, 29(4): 516-525.
Zhang Linrang, Zhao Shanshan, Zhou Yu, et al. Research Advance on Cooperative Anti-Deception Jamming in Netted Radar[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 516-525.(in Chinese)
[12] 赵艳丽, 王雪松, 王国玉, 等. 多假目标欺骗干扰下的组网雷达跟踪技术[J]. 电子学报, 2007(3): 454- 458.
Zhao Yanli, Wang Xuesong, Wang Guoyu, et al. Tracking Technique for Radar Network in the Presence of Multi-Range-False-Target Deception Jamming[J]. Acta Electronic Sinica, 2007(3): 454- 458.(in Chinese)
[13] 赵艳丽, 陈永光, 蒙洁, 等. 分布式组网雷达抗多假目标欺骗干扰处理方法[J]. 电光与控制, 2011, 18(3): 25-30.
Zhao Yanli, Chen Yongguang, Meng Jie, et al. A Data Processing Method against Multi-False-Target Deception Jamming for Distributed Radar Network[J]. Electronics Optics & Control, 2011, 18(3): 25-30.(in Chinese)
[14] 赵珊珊, 张林让, 周宇, 等. 组网雷达点迹信息融合抗假目标干扰方法[J]. 电子科技大学学报, 2014, 43(2): 207-211.
Zhao Shanshan, Zhang Linrang, Zhou Yu, et al. Measurement Fusion Method against False-Target Jamming for Radar Network[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(2): 207-211.(in Chinese)
[15] 吉喆, 王国宏, 张翔宇. 基于径向速度检验的雷达网距离多假目标鉴别[J]. 电光与控制, 2017, 24(7): 17-22, 27.
Ji Zhe, Wang Guohong, Zhang Xiangyu. Discrimination of Multi-Range-False-Target Jamming for Radar Network Based on Radial Velocity Testing[J]. Electronics Optics & Control, 2017, 24(7): 17-22, 27.(in Chinese)
[16] 王国宏, 吉喆. 基于多重判别的雷达网距离向多干扰目标鉴别[J]. 系统工程与电子技术, 2017, 39(1): 40- 48.
Wang Guohong, Ji Zhe. Multi-range-false-target jamming for radar network based on multiple discriminations[J]. Systems Engineering and Electronics, 2017, 39(1): 40- 48.(in Chinese)
[17] 李世忠, 王国宏, 徐海全, 等. 异地配置的主/被动雷达抗多假目标干扰[J]. 火力与指挥控制, 2013, 38(5): 10-13.
Li Shizhong, Wang Guohong, Xu Haiquan, et al. Study on Algorithm Against Multi-false-Target Deception Jamming for Active/Passive Radar at Different Sites[J]. Fire Control & Command Control, 2013, 38(5): 10-13.(in Chinese)
[18] 李世忠, 王国宏, 徐海全, 等. 三维空间主/被动雷达抗多假目标干扰研究[J]. 现代防御技术, 2012, 40(6): 118-124.
Li Shizhong, Wang Guohong, Xu Haiquan, et al. Algorithm Against Multi-False-Target Deception Jamming for Three-Dimensional Active/Passive Radar at Different Sites[J]. Modern Defence Technology, 2012, 40(6): 118-124.(in Chinese)
[19] 李迎春, 王国宏, 孙殿星, 等. 基于主被动雷达数据融合的抗密集假目标干扰技术[J]. 电光与控制, 2015, 22(8): 12-17, 32.
Li Yingchun, Wang Guohong, Sun Dianxing, et al. Technique Against Dense False-Target Jamming Based on Data Fusion of Active and Passive radars[J]. Electronics Optics & Control, 2015, 22(8): 12-17, 32.(in Chinese)
[20] 赵珊珊, 张林让, 周宇, 等. 利用空间散射特性差异进行有源假目标鉴别[J]. 西安电子科技大学学报, 2015, 42(2): 20-27.
Zhao Shanshan, Zhang Linrang, Zhou Yu, et al. Active false-target discrimination method based on the difference in spatial scattering characteristic[J]. Journal of Xidian University, 2015, 42(2): 20-27.(in Chinese)
[21] Chernyak V S. Fundamentals of Multisite Radar Systems: Multistatic Radars and Multi Radar Systems[M]. London, U.K: CRC Press, 1998.
[22] Fishler E, Haimovich A, Blum R, et al. MIMO radar: An idea whose time has come[C]∥Radar Conference, 2004. Proceedings of the IEEE. IEEE, Philadelphia, PA, USA, July 2004: 71-78.
[23] Zhou S H, Liu H W, Zhao Y B, et al. Target spatial and frequency scattering diversity property for diversity MIMO radar[J]. Signal Processing, 2011, 91(2): 269-276.
[24] Rober M K, Tülay A, Fukumizu K, et al. Special Issue on Advances in Kernel-based Learning for Signal Processing[J]. IEEE Signal Processing Magazine, 2013, 30(14): 14-15.
[25] Rui L, Ho K C. Elliptic localization: Performance study and optimum receiver placement[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4673- 4688.
[26] Hanebeck U D, Schmidt G. Closed-form elliptic location with an arbitrary array topology[C]∥Acoustics, Speech, and Signal Processing, 1996. ICASSP-96. Conference Proceedings. 1996 IEEE International Conference on. IEEE, Atlanta, GA, USA, May 1996, 6: 3069-3072.
[27] 何友, 修建娟, 张晶炜, 等. 雷达数据处理及应用[M]. 3版. 北京: 电子工业出版社, 2013.
He You, Xiu Jianjuan, Zhang Jingwei, et al. Radar data processing with applications[M]. 3rd edn. Beijing: Publishing House of Electronics Industry, 2013.(in Chinese)
[28] Bo L, Yao S, Chang-you Z. Study of multistatic radar against velocity-deception jamming[C]∥International Conference on Electronics, Communications and Control(ICECC), Ningbo, 2011: 1044-1047.
[29] 葛萌萌, 崔国龙, 孔令讲, 等. 分布式雷达盲源分离干扰抑制算法[J]. 信号处理, 2017, 33(12): 1562-1570.
Ge Mengmeng, Cui Guolong, Kong Lingjiang, et al. Jamming Suppression Based on Blind Source Separation in Distributed Radars[J]. Journal of Signal Processing, 2017, 33(12): 1562-1570.(in Chinese)
