1 引言
盲源分离(Blind Source Separation,BSS)在只有混合信号的情况下,利用信号的统计特性等信息对源信号进行分离。盲源分离典型的应用是解决“鸡尾酒会问题”,即分离室内传声器接收到的来自多个声源的卷积混合语音信号,其在医学核磁共振信号分离[1]和振动故障检测[2]等方面也有重要应用。
盲源分离算法可分为时域算法和频域算法。针对卷积混合的语音信号,时域算法计算量较大,通常将信号转换到频域进行处理。独立分量分析(Independent Component Analysis, ICA)是一种应用广泛的盲源分离算法,主要基于信号的高阶统计特性,通常对瞬时混合的非高斯信号有较好的分离性能[3- 4]。在频域分离卷积混合信号时,ICA算法假设每个频点信号满足独立性,在每个频点中单独进行信号分离。然而频域ICA算法会因频点间的排序不确定性导致算法性能下降,因此需要在信号反变换回时域前解决排序不确定问题。
独立向量分析(Independent Vector Analysis, IVA)是ICA算法的扩展,仍然在每个频点中单独更新分离矩阵,但该算法在每个频点的更新中都利用了各频点之间的高阶相关性,从原理上能有效解决频域盲源分离算法中的排序不确定问题,因而是近年来的研究热点[1,5-9]。不同频点之间的高阶相关性的强弱并不相同,相邻频点之间的相关性较强,距离较远的频点之间的相关性较弱。基于这个特点,Lee等提出了基于clique划分的自然梯度IVA算法[10],Na等提出了重叠子带的快速IVA算法[11],二者的区别主要是在重叠部分频点的更新迭代。但是采用重叠的方式依然不能有效避免clique或子带间的排序问题。
传统IVA算法采用多变量拉普拉斯分布(multivariate Laplace Distribution)作为源信号的统计假设来构建代价函数,记为L-IVA(Laplace IVA)[5]。基于牛顿迭代的快速IVA算法收敛速度快于基于自然梯度的算法,且无需设置步长,该方法记为F-L-IVA(Fast Laplace IVA)算法[6]。在IVA算法中采用多变量广义高斯分布(multivariate Generalized Gaussian Distribution, GGD)[8,12],或采用多变量t分布(multivariate Student t Distribution)[13-14]源信号的统计假设的算法分别记为GGD-IVA算法和t-IVA算法,已有研究表明,二者比L-IVA算法性能更好,因为多变量广义高斯分布和多变量t分布更符合语音分布模型。
为了提高算法模型的灵活性以及声源的分离性能,本文首先将GGD和t分布用于快速IVA算法中,采用clique重叠划分方法,分别得到FOC-GGD-IVA(Fast Overlap Clique GGD-IVA)算法和FOC-t-IVA(Fast Overlap Clique t-IVA)算法,这两种算法相比于基于拉普拉斯分布的FOC-L-IVA(Fast Overlap Clique L-IVA)算法,具有更好的分离性能。然后将GGD和t分布用于重叠子带快速IVA算法中,得到FOS-GGD-IVA(Fast Overlap Subband GGD-IVA)算法和FOS-t-IVA(Fast Overlap Subband t-IVA)算法。此外,进一步对子带划分方式进行了改进,不同于前面两类算法,本文采用无重叠子带划分,同时在子带之间采用功率比相关的方法[15]解决子带之间的排序问题,结合GGD和t分布,分别得到FNS-GGD-IVA(Fast Non-overlap Subband GGD-IVA)算法和FNS-t-IVA(Fast Non-overlap Subband t-IVA)算法,实验结果表明,FNS类算法的性能整体上优于FOC类和FOS类算法,考虑语音频带特性差异,采用非均匀子带划分可进一步提高算法性能。本文对FNS类算法在实际录音环境下进行了实验分析,验证了算法在实际环境中的可行性。
2 盲源分离模型
设声源信号sm(n),m=1,2,...,M通过一个线性多输入多输出(Multi-Input Multi-Output, MIMO)系统后,被传声器接收得到卷积混合信号xj(n), j=1,2,...,J,其中,M为声源个数,J为传声器个数。用房间冲激响应(Room Impulse Response,RIR)模型描述MIMO系统,在无噪情况下,卷积混合过程可表示为:
(1)
其中hmj(τ),τ=0,1,...,F-1表示房间冲激响应的系数,F为混合滤波器的长度。进一步假设M=J,即只考虑适定的情况。盲源分离的分离过程表示为:
(2)
其中wjm(κ),κ=0,1,...,Q-1表示分离滤波器的系数,Q为分离滤波器的长度。混合过程和分离过程可用图1表示。
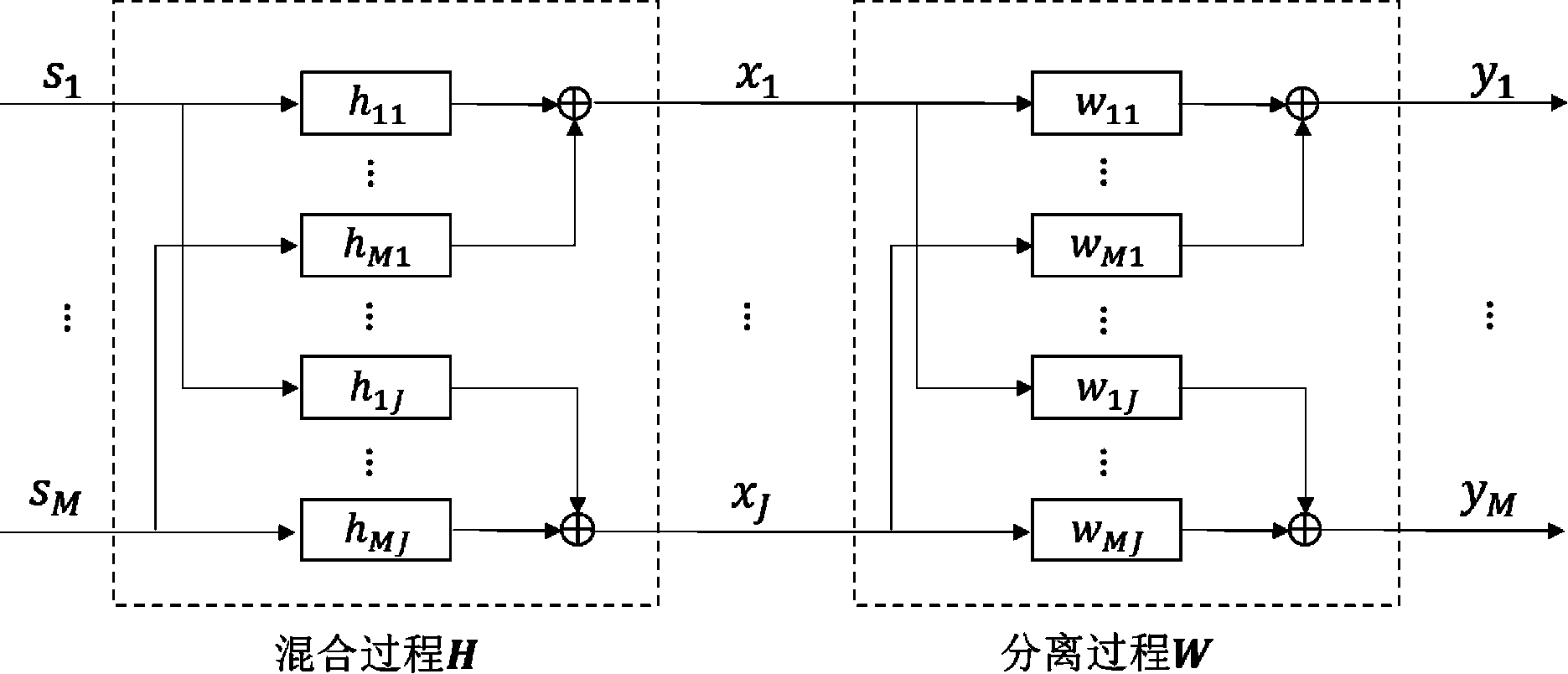
图1 盲源分离过程示意图
Fig.1 Process diagram of blind source separation
时域的卷积可以转化为频域的乘积,语音是非平稳信号,仅具有短期平稳性,因此需要采用短时傅里叶变换(Short-Time Fourier Transform, STFT)将信号转换到时频域,此时混合和分离过程可表示为:
(3)
(4)
其中,![]() 是第m个声源信号的第(k,l)个时频点的频谱,可看成随机变量
是第m个声源信号的第(k,l)个时频点的频谱,可看成随机变量![]() 的第l个样本值;
的第l个样本值;![]() 是第j个传声器的混合信号的第(k,l)个时频点的频谱;
是第j个传声器的混合信号的第(k,l)个时频点的频谱;![]() 是估计得到的第m个信号的第(k,l)个时频点的频谱;
是估计得到的第m个信号的第(k,l)个时频点的频谱;![]() 表示第k个频点的混合矩阵H(k)中第j行第m列元素,
表示第k个频点的混合矩阵H(k)中第j行第m列元素,![]() 表示第k个频点的分离矩阵W(k)中的第m行第j列元素,(·)T表示转置,k=1,2,...,K表示频点索引,l=1,2,...,L表示帧索引。仅在频域中对每个频点单独进行瞬时混合的分离会有排序问题,从而导致算法失效,估计的声源信号在变换回时域前需要解决排序不确定问题。
表示第k个频点的分离矩阵W(k)中的第m行第j列元素,(·)T表示转置,k=1,2,...,K表示频点索引,l=1,2,...,L表示帧索引。仅在频域中对每个频点单独进行瞬时混合的分离会有排序问题,从而导致算法失效,估计的声源信号在变换回时域前需要解决排序不确定问题。
3 IVA算法
3.1 传统快速IVA算法
IVA算法利用频点之间的高阶相关性解决频域排序问题。基于自然梯度的传统IVA算法下降速度和分离效果受步长影响明显。Lee等[6]用牛顿迭代方法推导得到基于拉普拉斯分布的快速IVA(F-L-IVA)算法,在保持算法性能的同时能加快收敛速度,且无需设置步长,避免了因步长不当引起的性能下降或运行时间过长。
F-L-IVA算法的代价函数为:
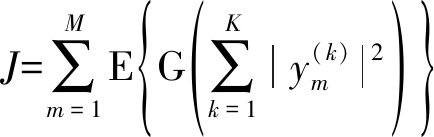
(5)
其中E(·)表示数学期望,G(·)是非线性函数,根据文献[6],其具体表达式为:
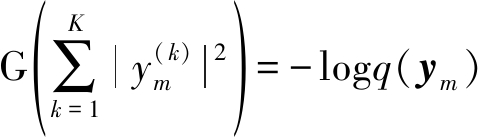
(6)
其中![]() 表示声源分布,在F-L-IVA算法中为多变量拉普拉斯分布。利用牛顿迭代,推导得到的分离矩阵更新公式为:
表示声源分布,在F-L-IVA算法中为多变量拉普拉斯分布。利用牛顿迭代,推导得到的分离矩阵更新公式为:
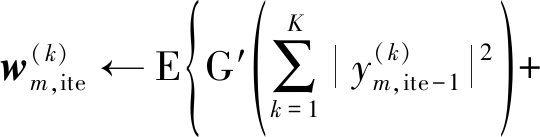
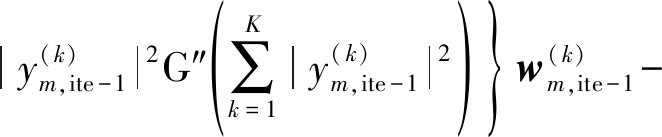
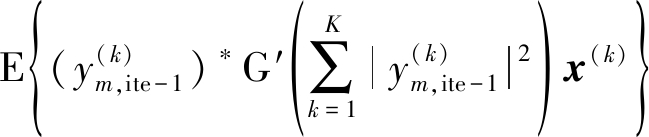
(7)
其中G′(·)和G″(·)分别表示G(·)的一阶导数和二阶导数,ite表示当前迭代次数,![]() 是
是![]() 的第m列元素,(·)*表示共轭,
的第m列元素,(·)*表示共轭,![]()
3.2 基于GGD和t分布的快速IVA算法
多变量拉普拉斯分布的表达式为:
(8)
由于傅里叶变换的正交性,Σm是对角矩阵。并且算法在迭代结束后会进行幅度调整,因此不失一般性Σm可取为单位阵。本文中的概率分布均采用单位阵代替Σm。进一步考虑信号在分离前进行了零均值处理,因此式(8)可退化为:
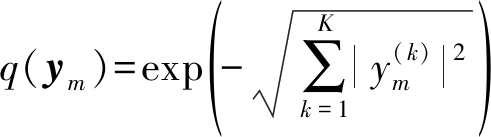
(9)
一些学者采用多变量GGD来代替多变量拉普拉斯分布[8,12],多变量GGD表达式为:
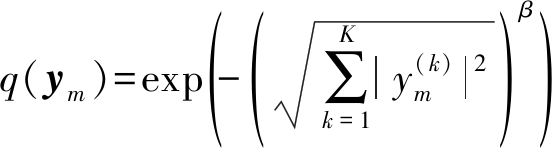
(10)
其中β是形状参数(shape parameter)。由该表达式可知,当β=1时,GGD是拉普拉斯分布;当β=2时,GGD是高斯分布;0< β<2时,GGD表示超高斯分布。
t分布包含了柯西分布和高斯分布两种特殊分布,是具有稳定特性的α-stable分布族的一部分,因此t分布也具有一定的稳定特性[16-17]。并且t分布引入的t-copula模型能更好地对频点之间的相关性建模[13]。多变量t分布的表达式为:
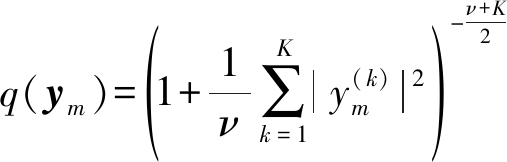
(11)
其中ν表示自由度。ν越小,则t分布的尾部更重,ν=1时,t分布即为柯西分布,ν→ 时,t分布趋于高斯分布。
时,t分布趋于高斯分布。
拉普拉斯分布、GGD、t分布均可用于快速IVA算法的实现。令![]() 通过式(6)可求得各分布对应的非线性函数以及其导数,见表1。
通过式(6)可求得各分布对应的非线性函数以及其导数,见表1。
表1 各分布对应的非线性函数
Tab.1 Nonlinear contrast functions of different distributions

G(z)G′(z)G″(z)拉普拉斯分布z12z-14z3GGD(z)ββ2zβ2-1β2 β2-1()zβ2-2t分布ν+K2log 1+zν()ν+K2ν11+zν-ν+K2ν21 1+zν()2
4 基于子带划分的快速IVA算法
相邻频点之间的统计相关性远大于相隔较远的频点之间的相关性,对TIMIT数据库中的一段男声一段女声语音进行Spearman相关程度分析,从图2中可见,相隔很远的频点之间的相关性几乎为0。因此,利用IVA算法在每个频点中进行分离矩阵的更新时,可考虑只用其邻近频点进行更新计算。
为避免频段之间的排序问题,Lee等采用重叠方式来划分clique[10],见图3(a),Na等采用重叠子带方式[11],见图3(b)。但是仅在相邻clique或者子带之间保留重叠部分仍然有可能发生排序问题。不同于上述划分方式,本文采用无重叠子带划分,为了保证相邻子带之间的排序连续性,本文提出采用功率比相关的方法连接子带,见图3(c)。对估计的分离矩阵求逆可得估计的混合矩阵:
(12)
其中N×1的向量![]() 表示估计得到的第m个声源到N个传声器之间的第k个频点的传递函数。第m个声源在时频点(k,l)处的功率比定义为:
表示估计得到的第m个声源到N个传声器之间的第k个频点的传递函数。第m个声源在时频点(k,l)处的功率比定义为:
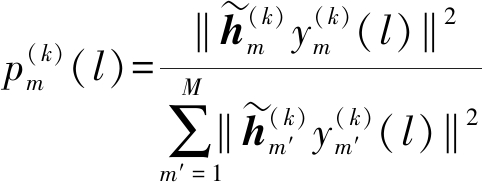
(13)
其中‖·‖2表示向量的2范数。式(13)定义了在时频点(k,l)处第m个声源在某一通道的混合信号中所占的比重,![]() 越接近1说明第m个声源占主导成分,越接近0则说明其他声源占主导成分。
越接近1说明第m个声源占主导成分,越接近0则说明其他声源占主导成分。![]()
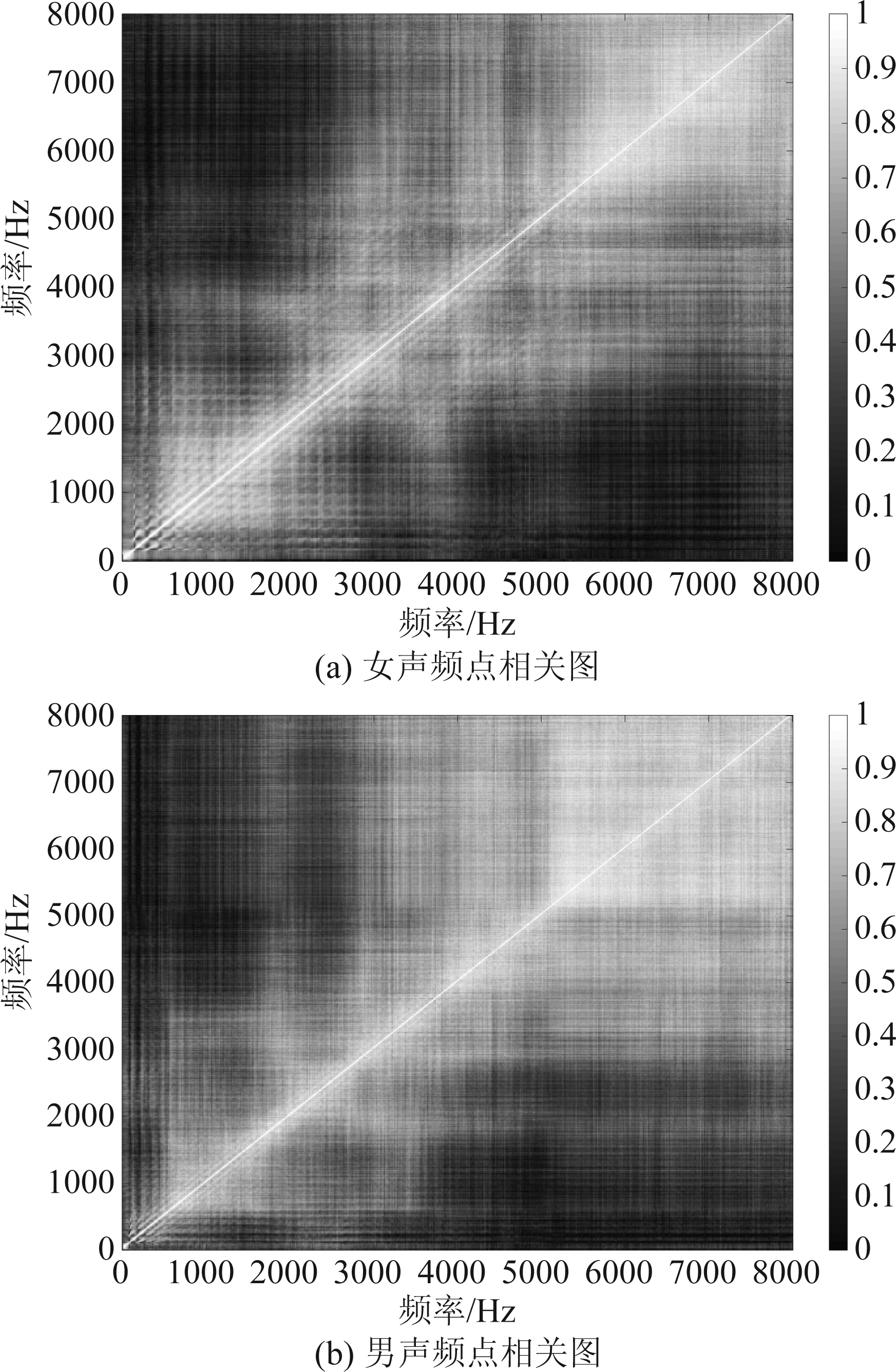
图2 两段语音的频点相关图
Fig.2 Frequency bins correlation of two speech signals
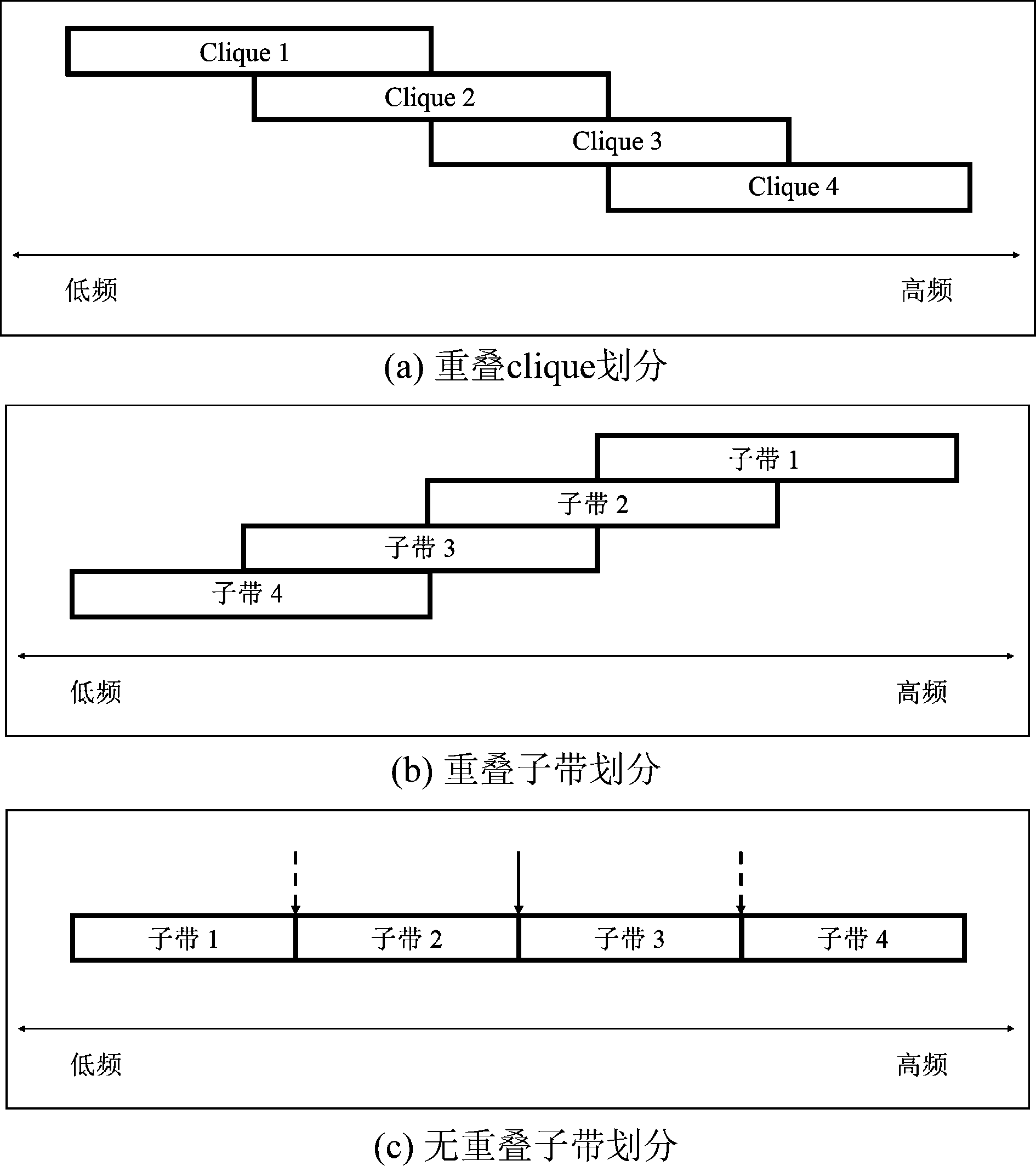
图3 频率划分示意图
Fig.3 Diagram of frequency bands division
则表示![]() 随着时间变化的序列。假设在某个子带中所有频点的排序是∏k,对第m个声源求质心gm:
随着时间变化的序列。假设在某个子带中所有频点的排序是∏k,对第m个声源求质心gm:
(14)
其中,id表示第m个声源在当前排序∏k中排在第id位,NK表示当前子带的频点数。式(14)得到两段子带的质心后,计算使得两段子带相应质心的Pearson相关系数最大的排序即为正确的排序:
(15)
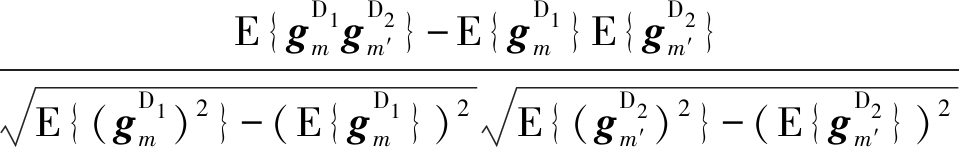
(16)
其中D1和D2分别表示要排序的两段子带。与通常的逐频点排序后处理不同,在IVA算法保证子带内的排序后,再采用功率比相关保证子带之间的排序,增加的运行时间较少,可以与因重叠子带而增加的运算时间抵消。无重叠子带划分示意图见图3(c),排序时先分别将虚箭头处连接起来,然后连接实箭头处,最终得到全频带的正确排序。
基于上述子带划分和排序纠正,本文先将GGD与t分布与重叠的clique划分相结合用于快速IVA中,得到FOC-GGD-IVA算法和FOC-t-IVA算法,合称FOC类算法。再将GGD与t分布用于重叠子带快速IVA算法中,得到FOS-GGD-IVA算法和FOS-t-IVA算法,合称FOS类算法。最后对子带划分进行改进,采用无重叠的子带划分方式,在算法收敛后采用功率比相关进行子带排序,得到FNS-GGD-IVA算法和FNS-t-IVA算法,合称FNS类算法。
4.1 FNS-GGD-IVA算法
将多变量GGD写成子带划分形式:
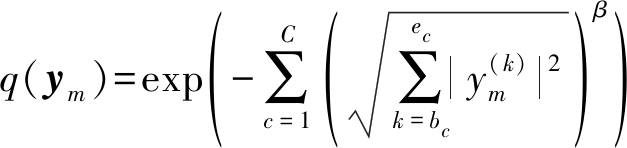
(17)
其中,C是总的子带数,bc和ec分别是第c个子带的第一个和最后一个频点索引,将式(7)代入式(6),令![]() 则非线性函数及其一二阶导数可以写成:
则非线性函数及其一二阶导数可以写成:
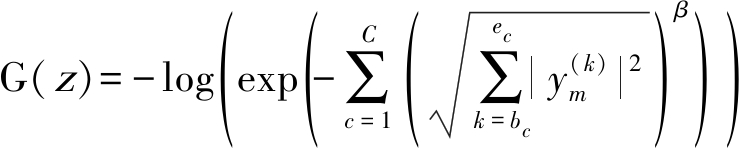
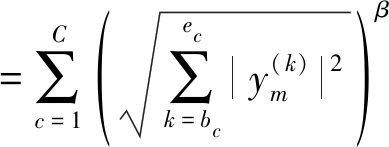
(18)
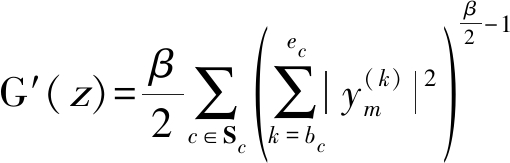
(19)
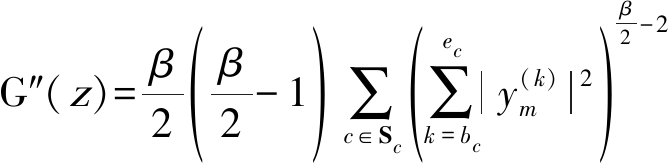
(20)
其中Sc是包含有当前更新频点k的子带集合。将以上非线性函数代入式(7)迭代更新分离矩阵直至代价函数收敛或者达到最大迭代次数。FOC-GGD-IVA算法的非线性函数推导过程与上述过程一致,不同之处在于C是表示总的clique数,并且FOC-GGD-IVA算法中的Sc在更新clique重叠区域的频点时包含两个clique,而FNS-GGD-IVA算法中的集合Sc一直只有一个子带,因此在FNS-GGD-IVA算法中关于Sc的求和符号是可以忽略的。
FOS-GGD-IVA算法则是在各子带中单独运行基于GGD的快速IVA算法,且子带和子带内的频点是从高频向低频逐渐迭代,当一个频点达到以下条件:
(21)
即表明该频点已经收敛,直接进入下一个频点的迭代,因此FOS-GGD-IVA算法中重叠的部分只更新在上个子带中未收敛的频点。其中tr(·)表示求迹,根据文献[11]门限ε值取为1×10-10。
4.2 FNS-t-IVA算法
将多变量t分布写成子带划分形式:
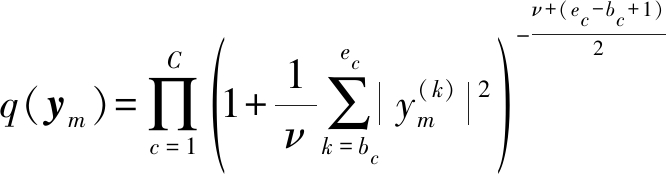
(22)
基于自然梯度的t-IVA算法对于步长的选择较为敏感,步长设置较大极易导致算法无法收敛,因此将t分布用于快速IVA算法可增强其稳定性。在快速IVA算法中,将式(22)代入非线性函数G(z)及其一二阶导数的表达式,得:
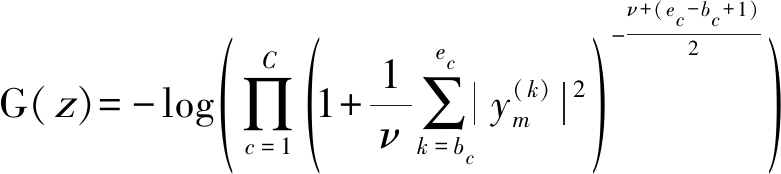
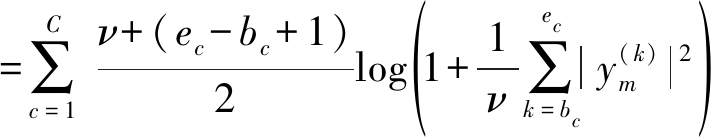
(23)
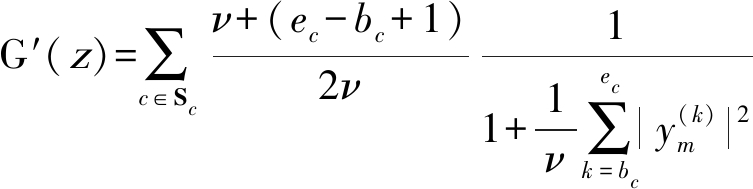
(24)
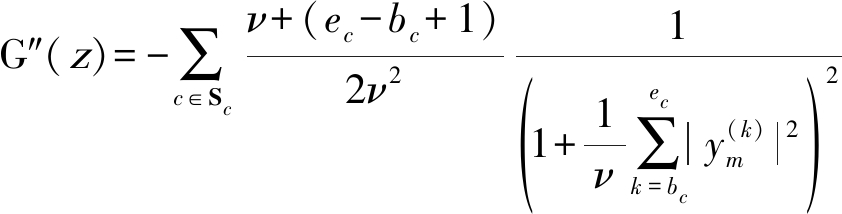
(25)
将以上非线性函数代入式(7)迭代更新分离矩阵。三种t-IVA算法(FOC类,FOS类,FNS类)的区别则与4.1节中提到的类似。
4.3 算法步骤
结合以上推导以及分析,FNS类IVA算法的具体步骤见表2。FOC类IVA算法没有功率比相关的子带排序后处理,不需要进行第6步,其余均与表2一致。
表2 FNS类IVA算法步骤
Tab.2 Steps of FNS IVA algorithm

Step1 对混合信号进行STFT变换;Step2 对信号进行中心化和白化处理;Step3 划分子带;Step4 迭代更新过程:根据式(4)计算更新的ym;判断每个频点属于的子带;根据式(6)、(7)结合相应的分布表达式更新分离矩阵;计算代价函数;判断是否达到停止条件(收敛或者达到最大迭代次数),若没达到,继续迭代;Step5 用MDP(Minimal Distortion Principle)准则解决幅度不确定问题[18];Step6 根据式(12)~(16)纠正子带排序;Step7 根据式(4)计算更新的ym;Step8 将估计的信号变换回时域信号,得到最终的分离信号。
5 算法测试与分析
为了验证算法的有效性,本文通过仿真实验和实际录音实验对各算法进行性能对比。仿真实验中的混合信号由实际录取的房间传递函数与纯净语音卷积混合而成。采样率为16 kHz,STFT帧长和汉宁窗长度为2048点,帧移1024点。实际录取的房间传递函数选自RWCP数据库(1) RWCP数据库:http:∥research.nii.ac.jp/src/en/RWCP-SSD.html,选取混响时间0.3 s的房间E2A的传递函数。采用BSS_Eval工具箱[19]对算法进行性能衡量,主要选用的客观指标为信扰比SIR(Signal-to-Interference-Ratio)和信号失真比SDR(Signal-to-Distortion-Ratio)。
随机选取长度10 s的纯净语音作为声源。实验示意图见图4,2×2(2个声源2个传声器)情况下使用扬声器S1和S3,传声器X1和X3进行实验,3×3(3个声源3个传声器)情况下则使用扬声器S1、S2和S3,传声器X1、X2和X3进行实验。
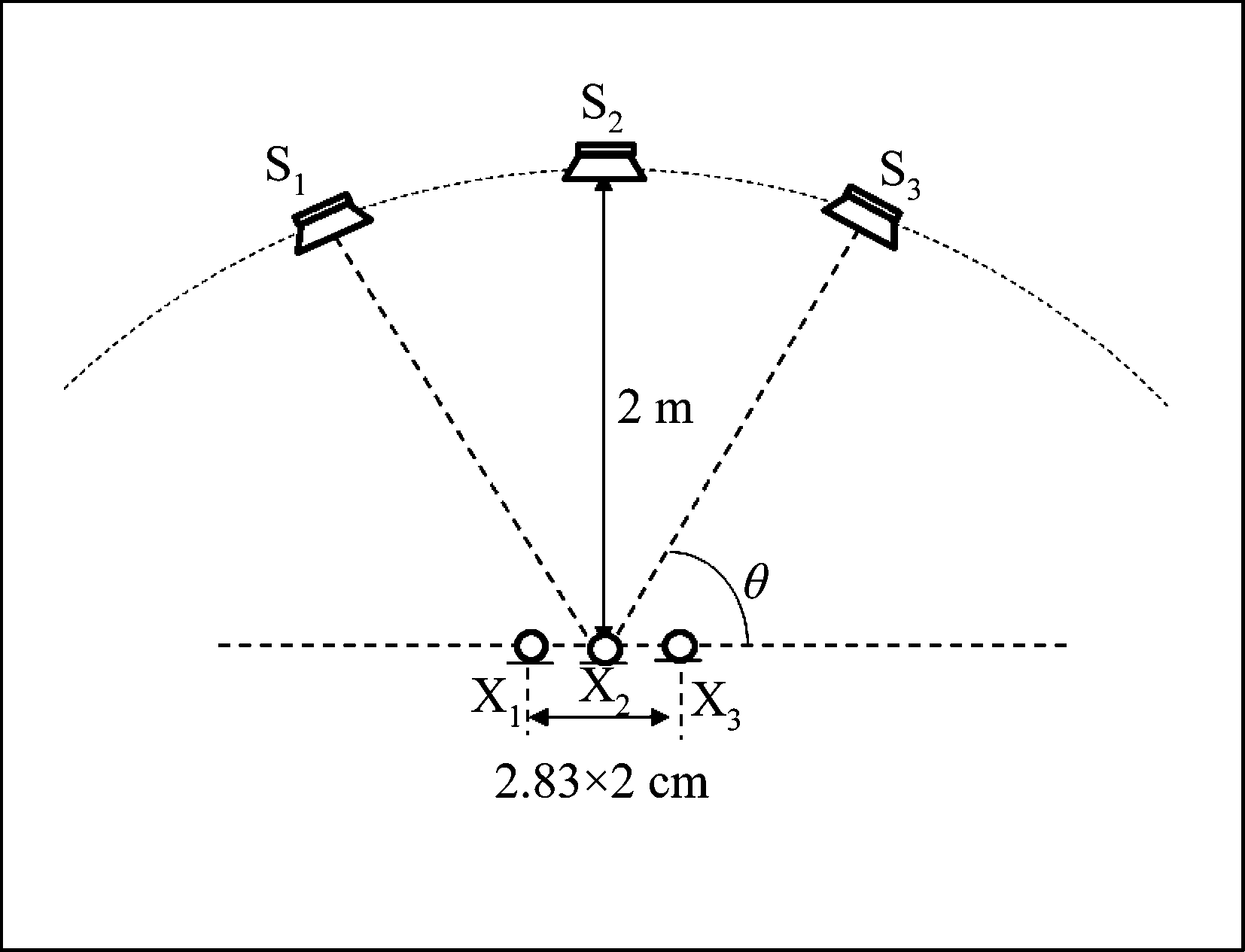
图4 实验示意图
Fig.4 Schematic diagram of experimental set-up
5.1 均匀划分子带实验仿真
均匀划分实验中的clique和子带划分见图3,将频率点均匀划分为4段,FOC算法中clique之间的重叠率为50%,具体频带划分为[0, 3200]、[1600, 4800]、[3200, 6400]、[4800, 8000]Hz。FOS算法中子带划分中也重叠50%,具体子带划分将上述FOC类算法中的划分从高频到低频进行调整即可。FNS算法中子带划分没有重叠,具体子带划分为[0, 2000]、[2000, 4000]、[4000, 6000]、[6000, 8000]Hz。2×2情况下随机选取5对声源,每组声源4对角度:声源S3固定在50°方向,声源S1依次在70°、90°、110°、
130°方向,将20组实验的性能指标提升的平均值进行对比。3×3情况下同样随机选取5对声源,每组实验仍有4组角度:声源S3固定在50°方向,声源S1固定在130°方向,声源S3依次在70°、90°、110°方向,以及声源S1、S2、S3分别在90°、70°、50°方向,将20组实验的性能指标提升的平均值进行对比。对比结果见表3~表6。前面已经提到,传统的快速IVA算法中采用的多变量拉普拉斯分布可在多变量GGD中令β=1得到,因此表3、表4中F-GGD-IVA算法参数β=1所在的列就是F-L-IVA算法。
表3 基于多变量GGD的IVA算法SIR(dB)提升值对比
Tab.3 Comparison of SIR(dB) improvement among IVA algorithms based on multivariate GGD
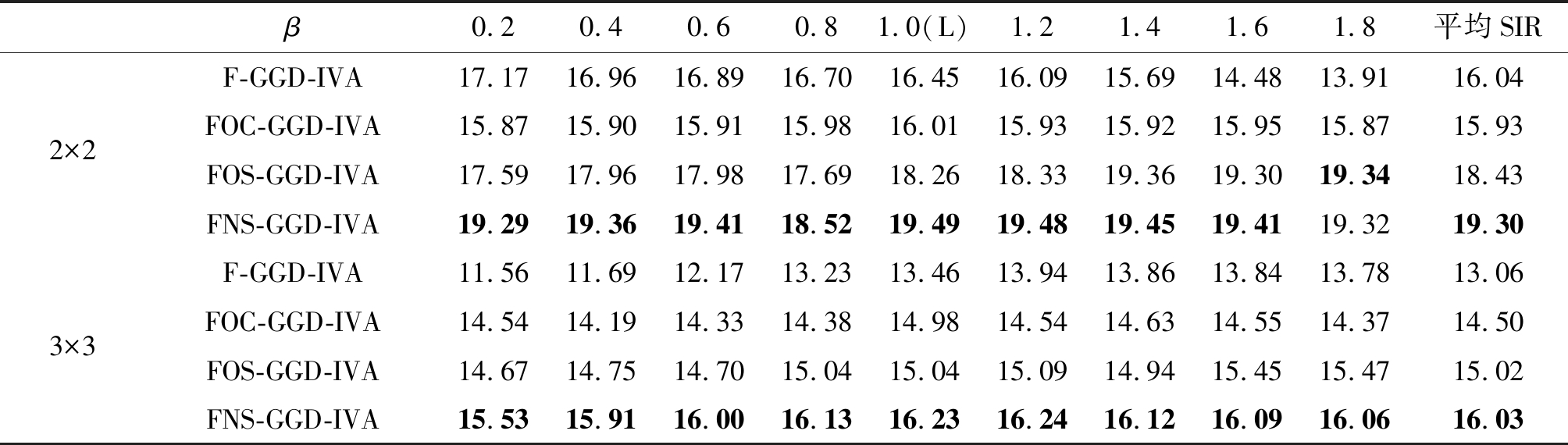
β0.20.40.60.81.0(L)1.21.41.61.8平均SIR2×2F-GGD-IVA17.1716.9616.8916.7016.4516.0915.6914.4813.9116.04FOC-GGD-IVA15.8715.9015.9115.9816.0115.9315.9215.9515.8715.93FOS-GGD-IVA17.5917.9617.9817.6918.2618.3319.3619.3019.3418.43FNS-GGD-IVA19.2919.3619.4118.5219.4919.4819.4519.4119.3219.303×3F-GGD-IVA11.5611.6912.1713.2313.4613.9413.8613.8413.7813.06FOC-GGD-IVA14.5414.1914.3314.3814.9814.5414.6314.5514.3714.50FOS-GGD-IVA14.6714.7514.7015.0415.0415.0914.9415.4515.4715.02FNS-GGD-IVA15.5315.9116.0016.1316.2316.2416.1216.0916.0616.03
表4 基于多变量GGD的IVA算法SDR(dB)提升值对比
Tab.4 Comparison of SDR(dB) improvement among IVA algorithms based on multivariate GGD
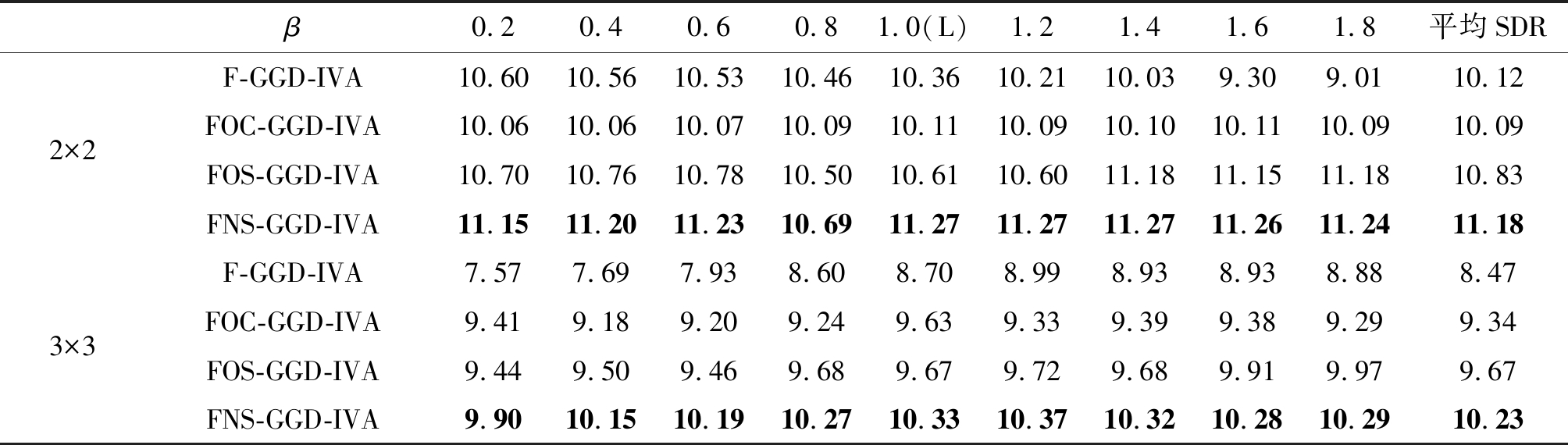
β0.20.40.60.81.0(L)1.21.41.61.8平均SDR2×2F-GGD-IVA10.6010.5610.5310.4610.3610.2110.039.309.0110.12FOC-GGD-IVA10.0610.0610.0710.0910.1110.0910.1010.1110.0910.09FOS-GGD-IVA10.7010.7610.7810.5010.6110.6011.1811.1511.1810.83FNS-GGD-IVA11.1511.2011.2310.6911.2711.2711.2711.2611.2411.183×3F-GGD-IVA7.577.697.938.608.708.998.938.938.888.47FOC-GGD-IVA9.419.189.209.249.639.339.399.389.299.34FOS-GGD-IVA9.449.509.469.689.679.729.689.919.979.67FNS-GGD-IVA9.9010.1510.1910.2710.3310.3710.3210.2810.2910.23
表5 基于多变量t分布的IVA算法SIR(dB)提升值对比
Tab.5 Comparison of SIR(dB) improvement among IVA algorithms based on multivariate t distribution
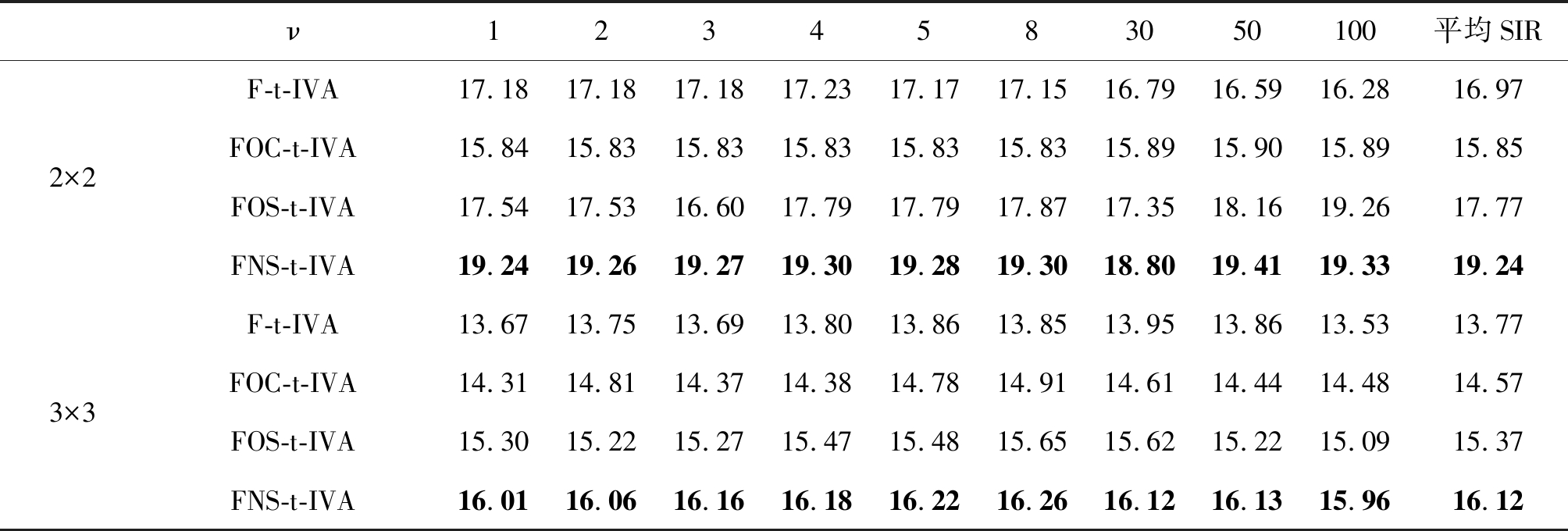
ν1234583050100平均SIR2×2F-t-IVA17.1817.1817.1817.2317.1717.1516.7916.5916.2816.97FOC-t-IVA15.8415.8315.8315.8315.8315.8315.8915.9015.8915.85FOS-t-IVA17.5417.5316.6017.7917.7917.8717.3518.1619.2617.77FNS-t-IVA19.2419.2619.2719.3019.2819.3018.8019.4119.3319.243×3F-t-IVA13.6713.7513.6913.8013.8613.8513.9513.8613.5313.77FOC-t-IVA14.3114.8114.3714.3814.7814.9114.6114.4414.4814.57FOS-t-IVA15.3015.2215.2715.4715.4815.6515.6215.2215.0915.37FNS-t-IVA16.0116.0616.1616.1816.2216.2616.1216.1315.9616.12
表6 基于多变量t分布的IVA算法SDR(dB)提升值对比
Tab.6 Comparison of SDR(dB) improvement among IVA algorithms based on multivariate t distribution
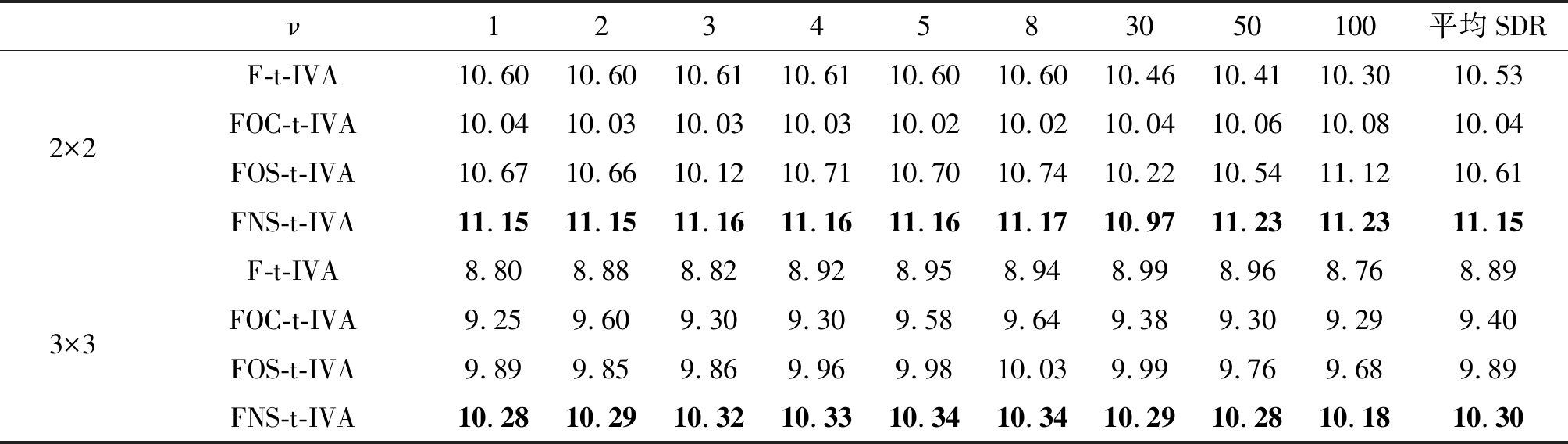
ν1234583050100平均SDR2×2F-t-IVA10.6010.6010.6110.6110.6010.6010.4610.4110.3010.53FOC-t-IVA10.0410.0310.0310.0310.0210.0210.0410.0610.0810.04FOS-t-IVA10.6710.6610.1210.7110.7010.7410.2210.5411.1210.61FNS-t-IVA11.1511.1511.1611.1611.1611.1710.9711.2311.2311.153×3F-t-IVA8.808.888.828.928.958.948.998.968.768.89FOC-t-IVA9.259.609.309.309.589.649.389.309.299.40FOS-t-IVA9.899.859.869.969.9810.039.999.769.689.89FNS-t-IVA10.2810.2910.3210.3310.3410.3410.2910.2810.1810.30
从表中数据可见, FOC-GGD-IVA算法和FOC-t-IVA算法相比于全频带的F-GGD-IVA算法和F-t-IVA算法,在3声源情况下性能有明显提升。FOS类算法的重叠部分的频点有第二次迭代来提高频点的收敛概率,比FOC类算法的性能更优,但是从表中也可以看出FOS类算法在混响环境下对声源分布参数较为敏感,不同参数之间性能差异较大。本文提出的FNS-GGD-IVA算法和FNS-t-IVA算法的性能在FOC类和FOS类算法的基础上有进一步的提高,验证了FNS类算法能更好地利用相邻频点之间的高阶相关性,同时可避免子带之间的排序问题。
5.2 非均匀划分子带实验仿真
从图2中可见,低频段相邻频点之间的相关性较弱,而高频段相邻频点之间则有很强的相关性[10]。这是由语音频谱特性决定的,语音中低频时具有线谱特征,而高频是宽带。因此在低频段可采用较宽的子带来保证高阶相关性强弱不一的频点之间的排序一致性,而在高频段只需要采用较窄的子带就可以保证频点之间的强相关性[10]。
因此,本文对FNS类算法中子带的均匀划分和非均匀划分进行对比实验分析。实验设置与5.1节中的2×2情况一致,均匀划分引用5.1节中的数据,非均匀划分时,将4段子带划分为:[0,3000]、[3000,5000]、[5000,7200]、[7200,8000]Hz。不失一般性,实验分别选取GGD中的三个β值以及t分布中的三个ν值进行对比,结果见图5,每个子图中左边是FNS-GGD-IVA算法,右边是FNS-t-IVA算法。从图中可见,非均匀划分子带可以在一定程度上提升算法的SIR性能,但是SDR性能没有提高。
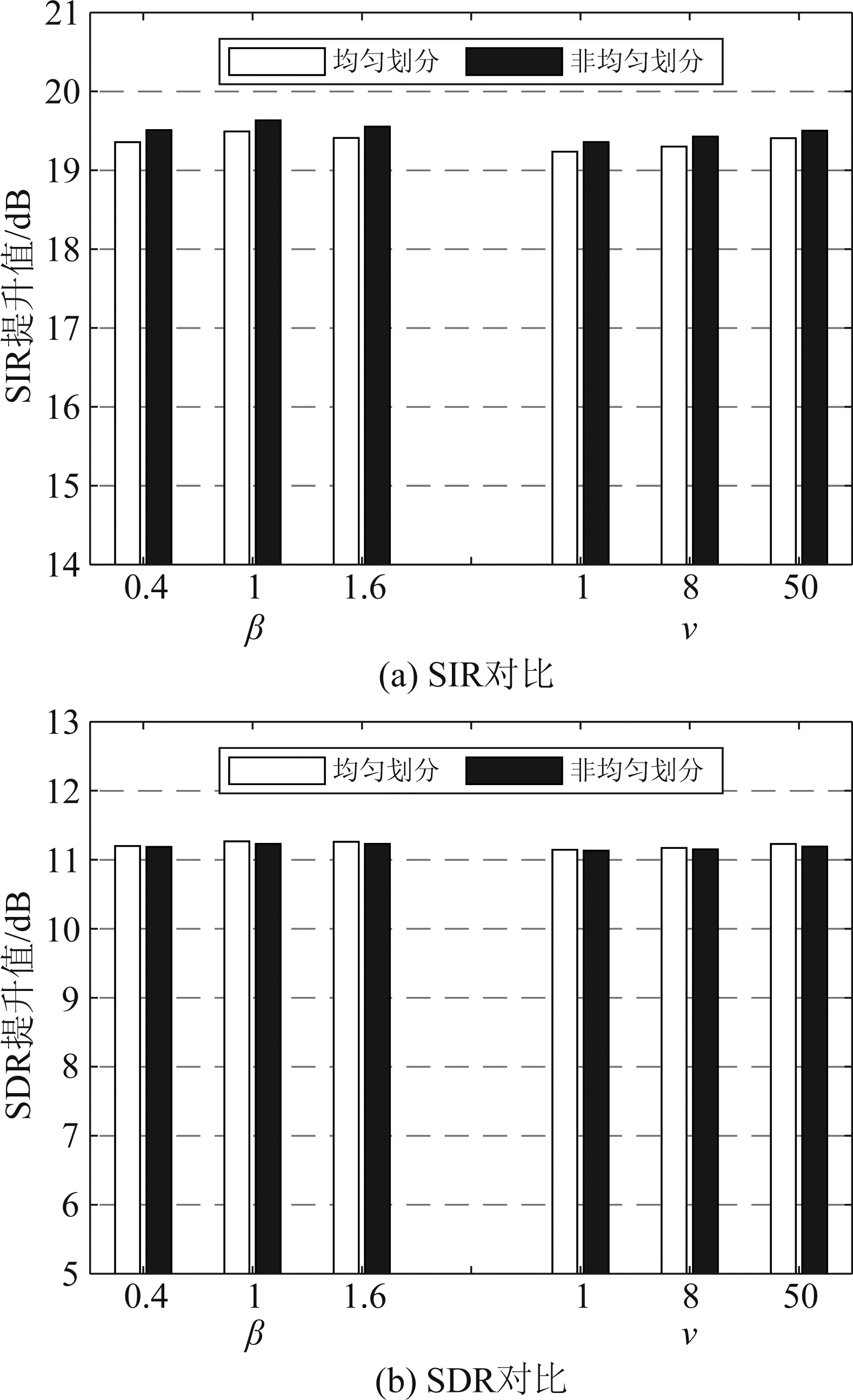
图5 FNS类算法的不同划分方式性能对比图
Fig.5 Comparison of FNS algorithm performance with different subbands division
5.3 实际录取语音的分离实验
实际录音环境中除了混响以外还可能存在传声器自噪声等,为了检验算法在实际录音环境中的语音分离性能,本文采用SiSEC2011的dev1数据库(2) SiSEC2011:http:∥sisec2011.wiki.irisa.fr/tiki-indexbfd7.html?page=Underdetermined+speech+and+music+mixtures对各算法进行分离性能对比。在2×2实验情况下,传声器之间距离为5 cm,混响时间为0.25 s。声源位置共有3对角度:140°和100°,100°和75°,140°和45°,每对角度都有一组男声混合语音和一组女声混合语音,语音长度10 s,采样率16 kHz。将以上6组实验结果取平均值进行对比,实验结果如图6所示。从图中可见,在实际录音环境中,不同参数的FOC类和FOS类算法性能不稳定,而FNS类算法的分离性能在绝大多数情况下都是优于其他算法的。
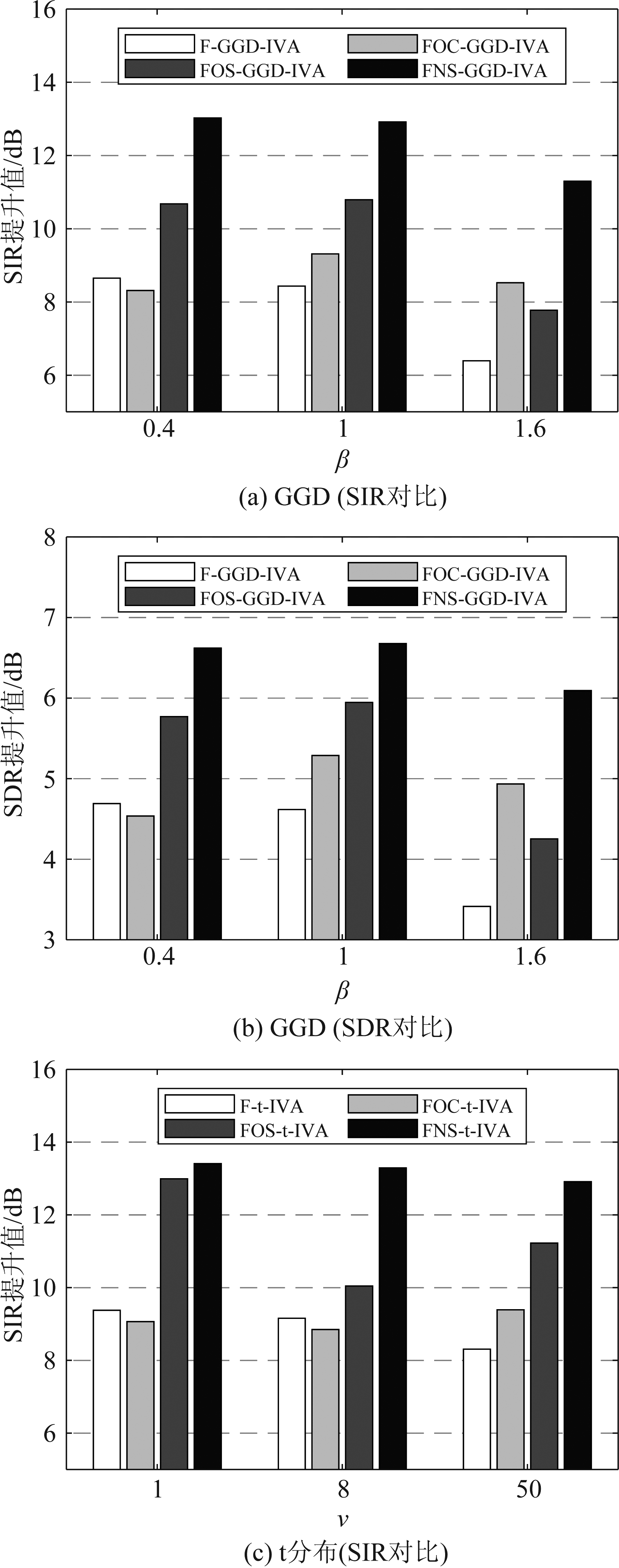
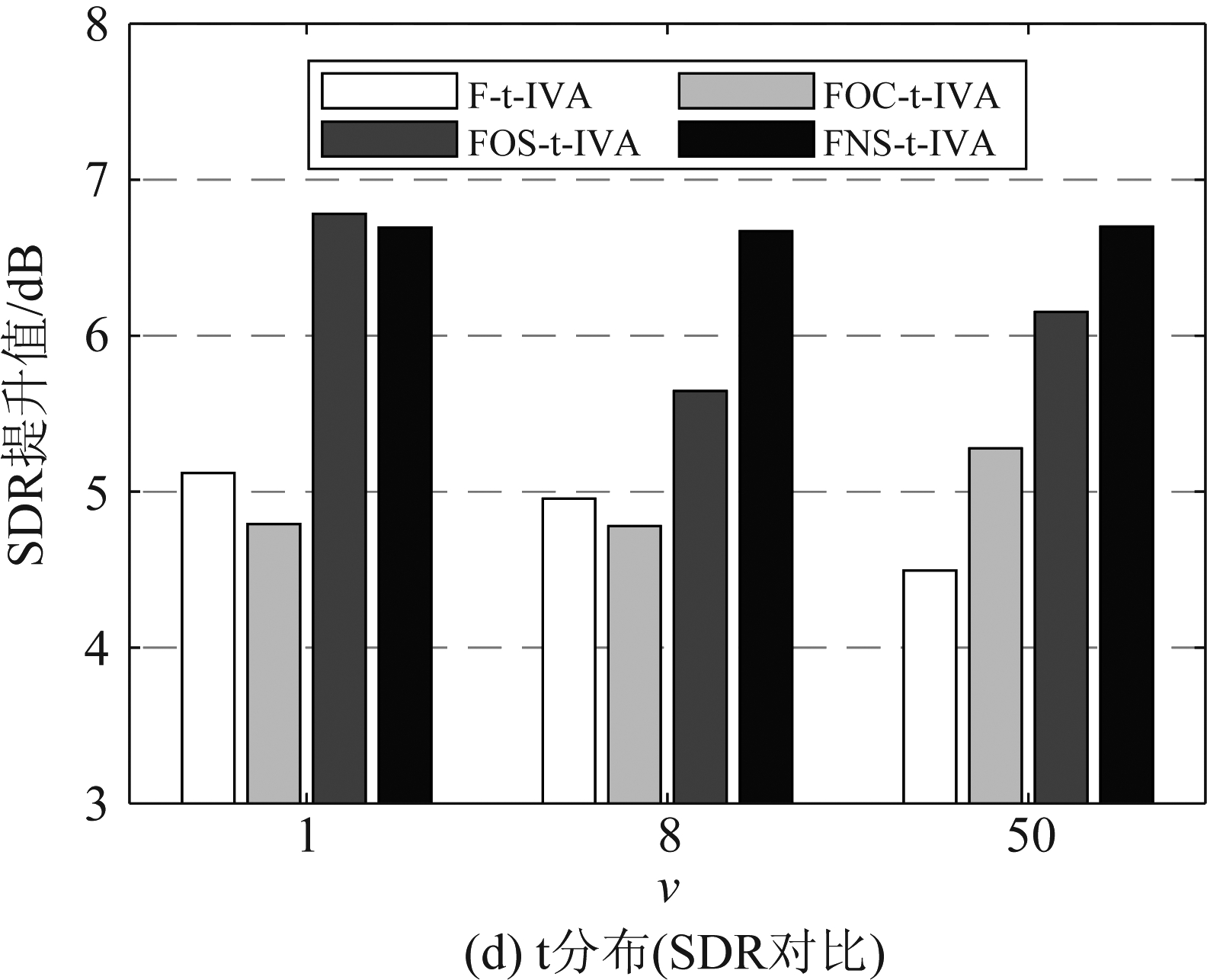
图6 实际录音情况下的算法性能对比
Fig.6 Comparison of algorithms performance with live recordings
6 结论
本文研究了快速IVA算法,提出将多变量广义高斯分布和多变量t分布与子带划分相结合提高其算法性能,采用无重叠子带划分以及功率比相关进行子带排序后处理。算法利用了相邻频点之间高阶相关性更强以及语音分布模型更符合尾部更重的概率密度分布的特点,针对不同声源数量的卷积混合信号进行了实验分析,对提出算法的不同分布参数的算法性能进行了对比。实验结果表明,本文提出的算法具有更优的盲分离性能,根据语音特性进行非均匀子带划分也进一步提高了信扰比等性能。
[1] Kuang L-D, Lin Q-H, Gong X-F, et al. Adaptive independent vector analysis for multi-subject complex-valued fMRI data[J]. Journal of Neuroscience Methods, 2017, 281: 49- 63.
[2] Haile M A, Dykas B. Blind source separation for vibration-based diagnostics of rotorcraft bearings[J]. Journal of Vibration and Control, 2016, 22(18): 3807-3820.
[3] Comon P. Independent component analysis, a new concept?[J]. Signal Processing, 1994, 36(3): 287-314.
[4] Nordhausen K, Oja H. Independent component analysis: A statistical perspective[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2018, 10(5): e1440.
[5] Kim T, Attias H T, Lee S-Y, et al. Blind source separation exploiting higher-order frequency dependencies[J]. IEEE Transactions on Audio, Speech and Language Processing, 2007, 15(1): 70-79.
[6] Lee I, Kim T, Lee T-W. Fast fixed-point independent vector analysis algorithms for convolutive blind source separation[J]. Signal Processing, 2007, 87(8): 1859-1871.
[7] 顾凡, 王惠刚, 李虎雄. 一种强混响环境下的盲语音分离算法[J]. 信号处理, 2011, 27(4): 534-540.
Gu Fan, Wang Huigang, Li Huxiong. A blind speech separation algorithm with strong reverberation[J]. Signal Processing, 2011, 27(4): 534-540.(in Chinese)
[8] Zhao Q, Guo F, Zu X, et al. An Acoustic Signal Enhancement Method Based on Independent Vector Analysis for Moving Target Classification in the Wild[J]. Sensors, 2017, 17(10): 2224.
[9] 付卫红, 张琮. 基于步长自适应的独立向量分析卷积盲分离算法[J]. 电子与信息学报, 2018, 40(9): 2158-2164.
Fu Weihong, Zhang Cong. Independent Vector Analysis Convolutive Blind Separation Algorithm Based on Step-size Adaptive[J]. Journal of Electronics & Information Technology, 2018, 40(9): 2158-2164.(in Chinese)
[10] Lee I, Jang G-J. Independent vector analysis based on overlapped cliques of variable width for frequency-domain blind signal separation[J]. EURASIP Journal on Advances in Signal Processing, 2012, 2012(1): 113.
[11] Na Y, Yu J, Chai B. Independent vector analysis using subband and subspace nonlinearity[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013(1): 74.
[12] Liang Y, Harris J, Naqvi S M, et al. Independent vector analysis with a generalized multivariate Gaussian source prior for frequency domain blind source separation[J]. Signal Processing, 2014, 105: 175-184.
[13] Liang Y, Chen G, Naqvi S, et al. Independent vector analysis with multivariate student’s t-distribution source prior for speech separation[J]. Electronics Letters, 2013, 49(16): 1035-1036.
[14] Mogami S, Kitamura D, Mitsui Y, et al. Independent low-rank matrix analysis based on complex student’s t-distribution for blind audio source separation[C]∥2017 IEEE 27th International Workshop on Machine Learning for Signal Processing (MLSP), 2017: 1- 6.
[15] Wang L, Ding H, Yin F. A region-growing permutation alignment approach in frequency-domain blind source separation of speech mixtures[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(3): 549-557.
[16] Keriven N, Deleforge A, Liutkus A. Blind Source Separation Using Mixtures of Alpha-Stable Distributions[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018: 771-775.
[17] Samorodnitsky G, Taqqu M. Stable non-gaussian random processes: stochastic models with infinite variance[M]. New York: Chapman Hall, 1994: 1-111.
[18] Matsuoka K. Minimal distortion principle for blind source separation[C]∥Proceedings of the 41st SICE Annual Conference SICE 2002. IEEE, 2002: 2138-2143.
[19] Vincent E, Gribonval R, Févotte C. Performance measurement in blind audio source separation[J]. IEEE Transactions on Audio, Speech and Language Processing, 2006, 14(4): 1462-1469.


