1 引 言
时差参数估计是时差定位与测距系统的关键,在雷达、声呐、导航等领域得到广泛应用,成为近年来的研究热点[1]。多载波通信具有良好的抗干扰与抗截获性能,在通信领域中得到广泛的应用[2-3],利用多载波信号进行测距定位相关的研究也一直在进行[4- 6]。无源时差定位是目标定位的重要手段,也一直是定位领域的研究热点[7-10],而其定位精度的关键在于准确的时差参数估计。时差参数估计精度主要受限于信号带宽[11],因此如何提高利用信号的有效带宽成为研究的热点。当前这方面的研究主要集中在外辐射源雷达领域。
外辐射源雷达也是无源定位系统的一种,利用多个外辐射源信号来提高外辐射源雷达的性能已有部分研究,主要是通过利用多个信号来提高作用距离、定位精度和检测性能。现有外辐射源雷达系统多采用单照射源信号,可利用的信号功率、带宽都有限,作用距离、定位精度和检测性能等均受到限制。为此,拓展照射源种类和个数,增加系统可利用的信号功率,成为外辐射源雷达的一个重要发展方向,不少文献做了此方面的研究[12-15]。Mendi等人提出利用多个GSM发射站的信号来提高目标参数估计精度[12],Tasdelen等人通过利用多个频道的FM广播信号作为外辐射源,得到了比单个FM频道信号更高的测距精度[13],Bongioanni建立了基于多频FM信号的外辐射源雷达试验系统[14],利用多信号非相参合成改善目标检测的稳健性。李军等人以应用最为广泛的广播电视信号外辐射源雷达为背景,研究了基于多个FM电台信号的多频外辐射源雷达相参处理技术,提出了多信号相参合成的原理和方法,分析了其相对于传统单频外辐射源雷达在检测性能上获得的巨大改善[15]。这些研究都利用多个照射源的信号来改善外辐射源雷达的性能。
上述研究虽然已在多频段信号综合利用提高系统性能方面做了很多工作,但并未对时差定位参数估计领域开展研究。文献[16]研究了多载波信号的TDOA估计,但其出发点是降低时差计算的数据传输量,而不是利用多载波信号提升TDOA估计的精度,且针对的是已知信号场景,并不适用于无源定位场景。
在多载波信号的接收过程中,受限于采集带宽、传输速率和存储容量等条件,经常利用多通道接收的方式分别对各个载波信号进行窄带接收采集。而在这类辐射源的检测与定位参数估计中,只利用单通道信号的检测概率低、定位参数估计精度不高。为提高多载波信号辐射源的定位性能,研究多载波信号相干积累的时差估计算法显得尤为必要。本文根据多载波信号频域信息丰富的特点,基于单载波信号互相关函数分析,从理论上分析了多载波信号不同载波互相关函数的相位关系,提出了多载波信号的相参积累时差估计算法,推导了多载波信号的时差估计理论界,揭示了时差估计精度与多载波信号各参数的影响关系,并比较分析了时差估计精度相对于单载波信号的性能提升情况。
2 单载波基带信号互相关函数分析
一个载频为Fc,带宽为B,时宽为T,能量为E的平坦谱信号,两路含时差的接收信号可建模为
(1)
其自相关函数为
Rxx(Δτ)=![]() s(t)s*(t-Δτ)dt
s(t)s*(t-Δτ)dt
=Esin c(BΔτ)ej2πFcΔτ
(2)
对应的互相关函数为:
Rxy(Δτ)=Esin c(B(Δτ-τd))ej2πFc(Δτ-τd)
(3)
在真实位置τd处具有峰值E,该处的相位为0。
在实际工程应用中,处理的信号一般为变频后的基带信号,即载频变到0,此时信号模型变为:
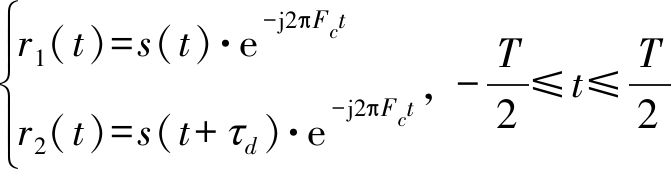
(4)
互相关函数变为
=Esin c(B(Δτ-τd))e-j2πFcτd
(5)
可见,变频到基带即中心频率变到0后,互相关函数缺少了乘积项ej2πFcΔτ,在真实位置τd处的相位不再为0。
3 多载波基带信号相参时差估计算法
当信号为多载波信号时,其频域分布是分段的。假设各载波信号载频的最小间隔为B0,第一个载频为f1,多载波的数量为M,则各载波信号对应的载频分别为f1+mB0(m∈[0,1,…,M-1])。假设各载波信号带宽均为B,能量均为E,则第m个载波信号的互相关函数为
Rm,xy(Δτ)=Esin c(B(Δτ-τd))ej2π(f1+mB0)(Δτ-τd)
(6)
当各载波信号都变到基带时,第m个载波信号的互相关函数变为
Rmb,xy(Δτ)=Esin c(B(Δτ-τd))e-j2π(f1+mB0)τd
(7)
从上式可以看出,不同载波信号的互相关函数具有不同的相位-2π(f1+mB0)τd,多个载波信号的互相关函数要实现相参积累,必须使各载波信号的互相关函数在真实时差位置τd处的相位一致,使各载波信号的能量能够相参积累。
实际情况下,真实的时差值τd未知,因此,各载波信号互相关函数的相位-2π(f1+mB0)τd是一个非0的未知数。相位一致必须通过相位补偿来实现,在搜索不同的时差Δτ时,可以对各载波信号的互相关函数乘上ej2πΔτ(f1+mB0),则各载波信号的互相关函数在真实时差值τd处,相位都为0,可以实现相参积累。
因此,多载波信号相参积累的互相关函数可表示为
(8)
而
(9)
因此有
=Eejπ(Δτ-τd)[2f1+(M-1)B0]sin c(B(Δτ-τd))
(10)
当|B0(Δτ-τd)-n|趋近于零时(其中n为整数),不难证明
(11)
此时有
RMb,xy(Δτ)≈MEejπ(Δτ-τd)[2f1+(M-1)B0]
·sin c(B(Δτ-τd))sin c(MB0(Δτ-τd))
(12)
可以看出,当B0(Δτ-τd)=0,±1,±2,…±N时,即Δτ=τd±n/B0时,RMb,xy(Δτ)会出现周期性的峰值。文献[17]已对互相关函数周期性峰值对时差参数估计的影响进行过分析,本文不再深入讨论。
4 性能分析
胡来招在文献[18]中从信号空间与能量的角度分析了时差估计精度,结果如下:
(13)
这个结果与Stein在文献[10]中给的时差估计克拉美劳界(CRB:Cramer-Rao Bound)是一致的。其中Ws为信号能量,ΔΩ为信号角频的二阶中心矩或者均方根带宽
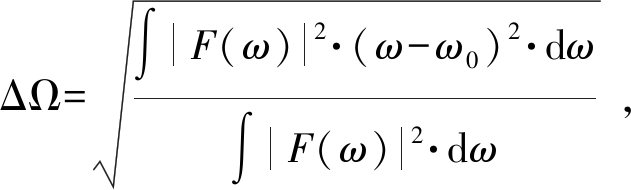

(14)
多载波有M个载波信号,每个载波信号的带宽为B,且为平坦矩形谱,则多载波信号的总能量为Ws=M·B·T·S0,其中S0为功率谱密度。各载波载频可以表示为
fm=f1+(m-1)B0,m=1,2,…,M
(15)
根据式(12),有
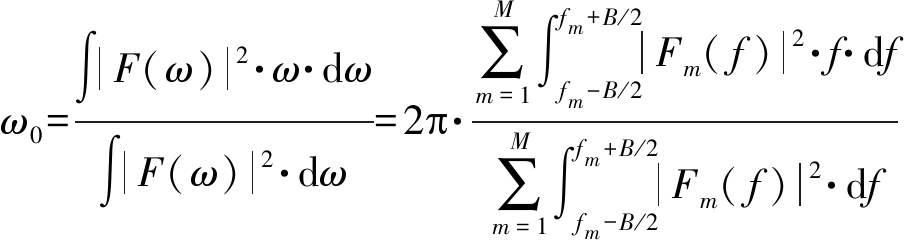
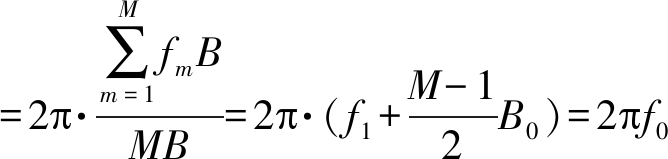
(16)
即多载波信号频率的一阶矩为信号载波的均值。
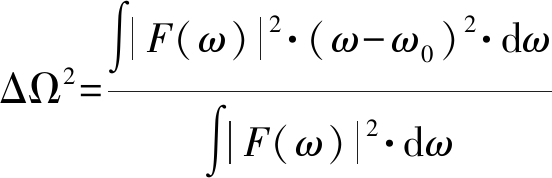
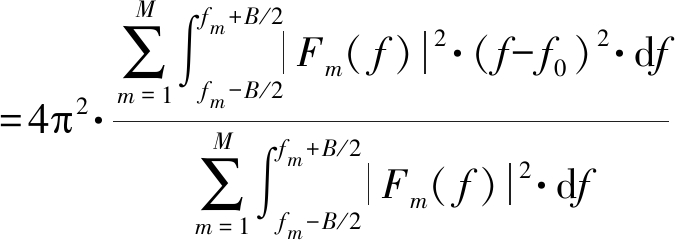
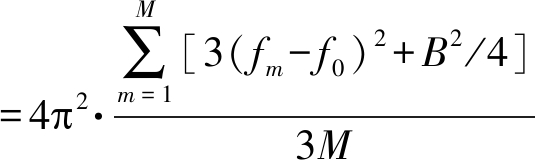
(17)
其中Bs=MB0可定义为多载波信号的频率覆盖范围。因此
(18)
上式中MB·T·SNR=Ws/N0。从上式可以看出,多载波信号的时差估计精度与多载波信号的频率覆盖范围、信号能量和噪声谱密度相关,但主要受多载波信号频率覆盖范围影响。多载波信号相对单载波信号均方根带宽提高了MB0/B倍,信号总能量提高了M倍,故时差估计精度能提高![]() 倍。
倍。
5 仿真分析
为验证提出算法和理论性能分析的有效性和正确性,通过仿真与单载波处理结果和CRB进行了比较。仿真场景设置如下:多载波信号的载波个数为4,各载波信号带宽12.5 kHz,调制方式均为BPSK,各载波信号中心频率分别间隔100 kHz,信号持续时间200 ms,多通道同步采集,各通道复采样的采样率为20 kHz,蒙特卡洛仿真次数200次。仿真得到的时差与估计性能如图1所示。其中,SingleSig表示单载波信号单独处理的时估计仿真性能;CA表示四个载波信号相参积累处理的时差估计仿真性能;CRB1表示单载波信号处理的参数估计CRB;CRB2表示四个载波信号相参积累处理的参数估计CRB。
从图1的仿真结果可以看出:(1)提出的多载波相参积累算法的时差估计精度远远高于单载波处理的时差估计精度,验证了多载波相参积累方法对于提高时差估计精度的有效性;(2)当信噪比高于6 dB时,两种处理方法的时差估计仿真性能与对应的时差估计CRB贴近,验证了理论性能分析的正确性。
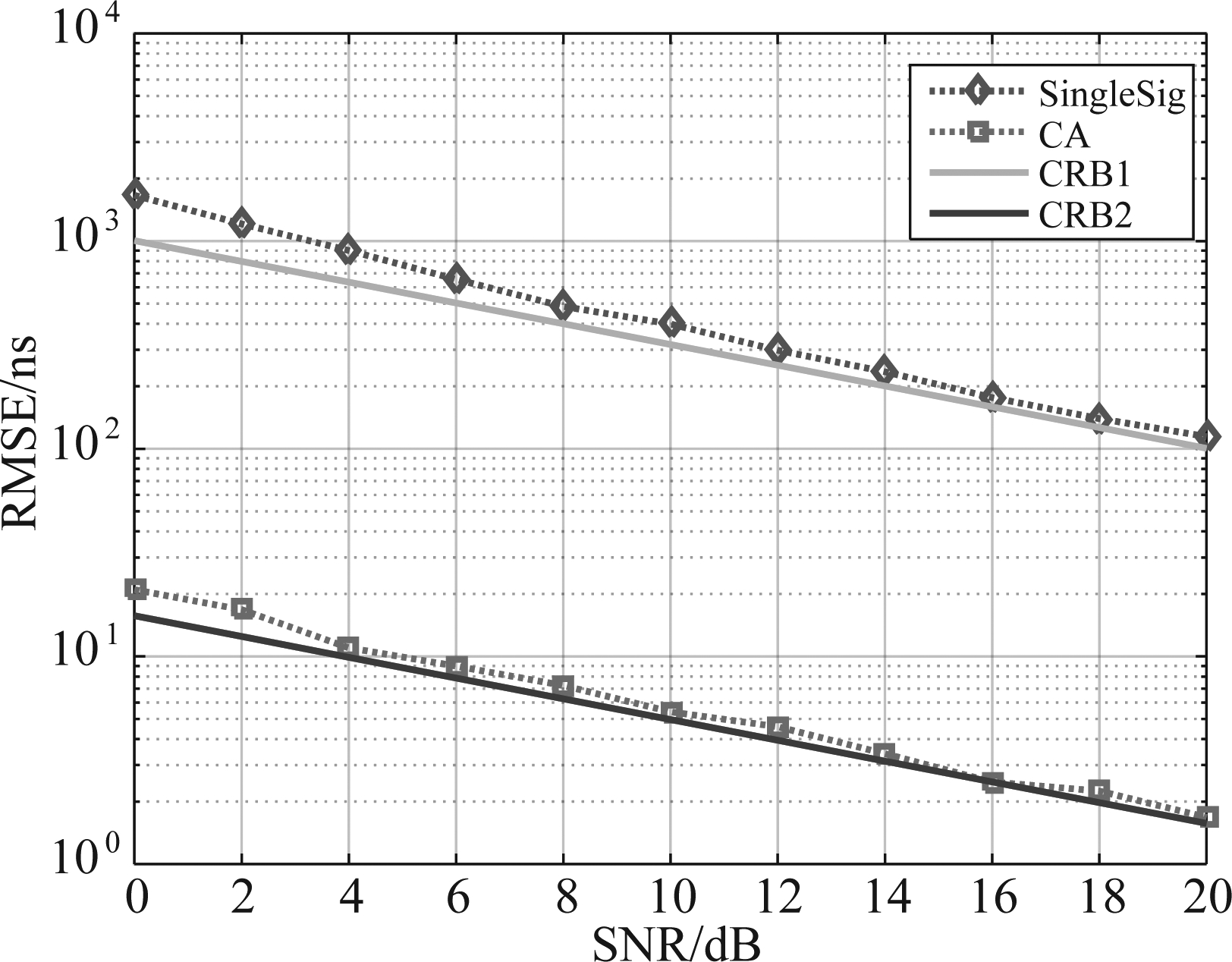
图1 各算法时差估计仿真结果与CRB对比图
Fig.1 Comparison of simulation results and CRB
图2与图3给出了多载波相参积累互相关函数与单载波处理的互相关函数图。可以看出,多载波相参积累互相关函数呈梳齿状,梳齿之间的间隔为1/100 kHz=10 us,梳齿的形状由函数sin c(MB0(Δτ-τd))决定,每个梳齿的宽度取决于多载波信号的频率覆盖范围MB0,载波数越多,梳齿越窄,整个互相关函数的包络由函数sin c(B(Δτ-τd))决定,单个载波信号的带宽越窄,互相关函数越宽。因此,相比单载波处理,多载波相参积累后,主瓣宽度即中间的梳齿宽度相比单载波的互相关函数主瓣变窄了很多,所以时差估计精度能够获得很大的提升。
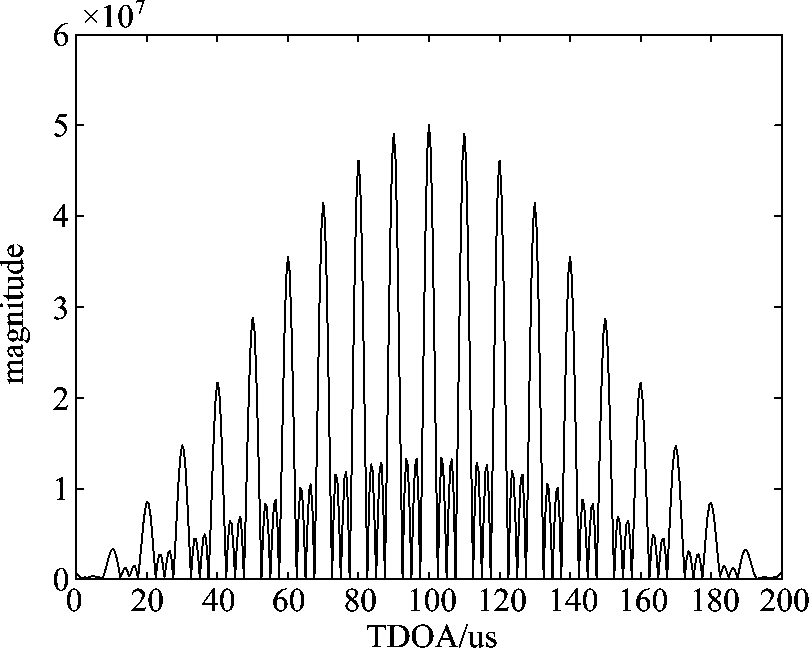
图2 多载波相参积累互相关函数图
Fig.2 Illustration of coherent integration CCF

图3 单载波信号互相关函数图
Fig.3 Illustration of CCF for single carrier signal
6 结论
多载波相参积累能够显著提升多载波信号的时差估计性能,在多载波信号的无源时差定位中具有很高的应用价值。本文基于多载波信号多通道窄带接收采集模型,在单载波信号互相关函数分析的基础上,研究了多载波信号互相关函数相参积累的时差参数估计算法,通过各载波信号互相关函数的相位差补偿实现相参积累,获得了时差参数估计性能的提升。该算法除了时差参数估计性能的提升外,还可提升基于相关检测方法的目标检测概率,这对于微弱信号目标的检测具有重要的参考意义。本文的研究虽然是只针对多载波信号,但其研究成果也可推广应用于同一目标同时辐射多个信号的无源定位场景,对于多元信号联合的时频差参数估计也具有重要的借鉴意义。
[1] 李晶, 赵拥军, 李东海. 基于马尔科夫链蒙特卡罗的时延估计算法[J]. 物理学报, 2014, 63(13): 130701-1-7.
Li Jing, Zhao Yongjun, Li Donghai. Time delay estimation using Markov Chain Monte Carlo method[J]. Acta Physical Sinica, 2014, 63(13): 130701-1-7.(in Chinese)
[2] Ruhallah A and Shahram S. Sum-Rate Optimal Network Beamforming and Subcarrier Power Allocation for Multi-Carrier Asynchronous Two-Way Relay Networks[J]. IEEE Transactions on Signal Processing, 2015, 63(15): 4129- 4143.
[3] 魏红鑫, 王燕敏, 李云洲, 等. 密集小区多载波系统中基于业务排队的能效优化[J]. 清华大学学报, 2017, 57(8): 867- 871.
Wei Hongxin, Wang Yanmin, Li Yunzhou, et al. Queue-aware energy savings in multi-carrier small-cell networks[J]. Journal of Tsinghua University, 2017, 57(8): 867- 871.(in Chinese)
[4] Zhang Y M, Li X, Moeness G A. Array Processing for RFID Tag Localization Exploiting Multi-Frequency Signals[C]∥Proceedings of SPIE, 2009, Orlando, FL, USA, April 16, 7349(734907): 1-11.
[5] Abdo G, Abbas O. Utilization of Multiple-Antenna Multicarrier Systems and NLOS Mitigation for Accurate Wireless Indoor Positioning[J]. IEEE Transactions on Wireless Communications, 2016, 15(10): 6570- 6584.
[6] 贺磊南, 卢虎, 姬正洲. 采用多载波相位测距的Wi-Fi精密定位方法[J]. 西安交通大学学报, 2017, 51(8): 65-71.
He Leinan, Lu Hu, Ji Zhengzhou. A Precise Positioning Method of Wi-Fi Using Multi-Carrier Phase Ranging[J]. Journal of Xi’an Jiaotong University, 2017, 51(8): 65-71.(in Chinese)
[7] Griffiths H D, Baker C J. Passive coherent location radar system-Part I: performance prediction[J]. IEE Proc-Radar Sonar Navig., 2005, 152(3): 153-159.
[8] Cheung K W, So H C, Ma W K, et al. A constrained least squares approach to mobile positioning: algorithms and optimality[J]. EURASIP Journal on Applied Signal Processing, 2006, 2006: 1-23.
[9] Torrieri D J. Statistical theory of passive location system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, 20(2): 183-197.
[10] 杨宇翔, 夏畅雄, 同武勤. 高低轨双星定位中的时变时频差参数估计[J]. 信号处理, 2012, 28(10): 1465-1471.
Yang Yuxiang, Xia Changxiong, Tong Wuqin. Estimation of the time varying TDOA and FDOA in GEO-LEO dual-satellites location system[J]. Signal Processing, 2012, 28(10): 1465-1471.(in Chinese)
[11] Stein S. Algorithms for ambiguity function processing[J]. IEEE Trans. on Acoustics, Speech, and Signal Processing, 1981, 29(3): 588-599.
[12] Mendi U M D, Sarkar B K. Passive radar using multiple GSM transmitting stations[C]∥International Radar Symposium, 2006, Krakow, Poland, 2006: 1- 4.
[13] Tasdelen A S, Koymen H. Range Resolution Improvement in Passive Coherent Location Radar Systems Using Multiple FM Radio Channels[C]∥Proceedings of the Institution of Engineering and Technology Forum on Waveform Diversity and Design in Communications, Radar and Sonar, London, 2006: 23-31.
[14] Bongioanni C, Colone F, Lombardo P. Performance analysis of a multi-frequency FM based passive bistatic radar[C]∥2008 IEEE Radar Conference, Rome, 2008: 1- 6.
[15] 李军, 刘红明, 何子述, 等. 一种多频外辐射源雷达信号相参处理方法[J]. 电子学报, 2011, 39(12): 2890-2894.
Li Jun, Liu Hongming, He Zishu, et al. Coherent Processing Technique of Passive Radar Based on Multi-Frequency Signal[J]. Acta Electronica Sinica, 2011, 39(12): 2890-2894.(in Chinese)
[16] Richard K M, Jamie S V, John F R. Bandwidth Efficient Cooperative TDOA Computation for Multicarrier Signals of Opportunity[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2311-2322.
[17] 欧阳鑫信. 跳频信号时差估计与直接定位方法研究[D]. 成都: 电子科技大学, 2017.
Ouyang Xinxin. Reseach on Time Difference of Arrival Estimation and Direct Position Determination for Frequency-Hopping Signals[D]. Chengdu: University of Electronic Science and Technology of China, 2017.(in Chinese)
[18] 胡来招. 信号的协同[M]. 北京: 国防工业出版社, 2015: 10-14.
Hu Laizhao. Collaboration Upon the Signal[M]. Beijing: National Defense Industry Press, 2015: 10-14.(in Chinese)
