1 引言
随着智能移动终端的普及,人们越来越期待能在移动终端上运行更多的计算密集型应用[1]。这些计算密集型应用所需的强大计算能力以及对于时延的严格要求和设备的有限资源产生了巨大的矛盾,这也成为了提高用户体验满意度的瓶颈[2-3]。
为了加强无线终端设备的计算能力,移动边缘计算(Mobile Edge Computing, MEC)被提出[4-5]。相比于将计算任务迁移到远端云上进行计算,移动边缘计算可以看做是“更靠近地面的云”。移动边缘服务器位于无线网络边缘,更靠近用户,可以高效地为周围的用户提供服务。移动边缘计算允许移动终端迁移计算任务至附近的移动边缘服务器上,比如小区基站和WiFi接入点等[6]。相比于云计算,移动边缘计算能够在网络的边缘处理和减少数据量。同时,移动边缘计算具有低延迟、位置感知的特点,并可以改进服务质量(Quality of Service, QoS),用于流媒体和实时应用程序[7]。移动边缘计算可以完成实时大数据分析,支持密集的分布式数据收集点,并在娱乐、广告、个人计算和其他应用中持有优势[8]。
针对移动边缘的迁移计算,近年来许多学者都展开了研究,也取得了很多的研究成果。文献[9]以减少系统损耗为目的,联合优化迁移决策、计算资源配置、发射功率配置以及带宽分配。在文献[10-11]中,将边缘服务器的文件存储策略考虑进来,通过联合优化资源分配,提升系统性能及收益。文献[12-16]以减少延迟、节约能源、提高服务质量为目的,利用凸优化算法,对资源进行优化分配。文献[17-21]研究了正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)上行无线通信系统,基于移动边缘计算技术的任务迁移问题,其中[17]采用斯塔克尔伯格模型法,优化用户迁移量和基站定价,最大化基站盈利。[18]提出一个基于宏云无线接入网(Cloud Radio Access Network, C-RAN)的多用户多远端射频头(Remote Radio Head, RRH)系统中,用户和RRH的关联、无线资源和功率分配联合优化问题,采用一种基于拍卖的分布式资源分配方法,最小化RRH的平均反应时间。[17-18]没有优化子载波的选择。[19-20]联合优化迁移策略和资源分配,使得在时延约束下最小化系统总能耗。[21]研究了基于正交频分多址的MEC系统的联合子载波和功率分配问题,以最小化各移动设备的最大时延。[19-21]对于01变量是放缩到[0,1]范围,没有保持优化过程中二元变量的特性。
本文重点研究了基于OFDM的单用户,多移动边缘服务器(Mobile Edge Server,MES)的边缘计算系统,用户将计算任务分块迁移到各个MES(下文简称基站)进行计算。从基站之间公平协作的角度出发,提出用户的迁移计算时延最小—最大化问题,保证基站协作计算的最长时延最短。联合优化用户的子载波选择、在各个子载波上的发射功率分配和到各个基站的迁移量。为了解决提出的非线性规划问题,将最小—最大化(minimize-maximum, min-max)问题转化为最小化(minimize, min)问题,提出一个基于泰勒展开的次优化解法。不同于[17-21]中不优化分配子载波或将子载波的二元变量放缩到[0,1]范围,本文不仅优化了子载波的选择还保证了原始二元变量的特性。
2 系统模型
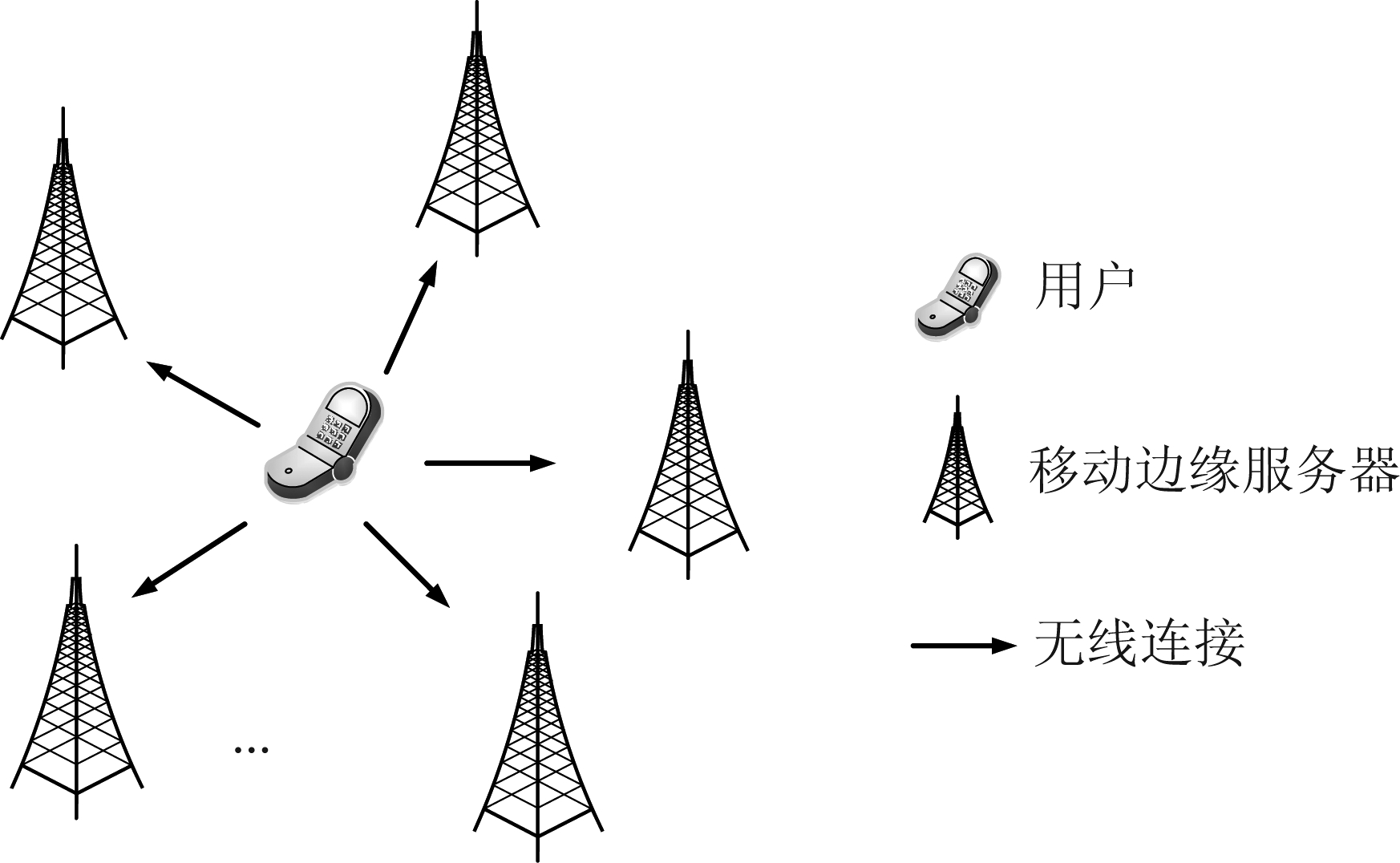
图1 系统模型
Fig.1 System model
如图1所示,系统有1个单天线用户,K个单天线基站,基站集合记为![]() 用户有D bits的数据需要计算,数据可分割迁移到基站进行计算,定义迁移到基站k的比特数为βk。迁移量向量表示为[β1β2...βK],记为β。用户采用OFDM进行数据的发送,有Nc个子载波,子载波集合记为
用户有D bits的数据需要计算,数据可分割迁移到基站进行计算,定义迁移到基站k的比特数为βk。迁移量向量表示为[β1β2...βK],记为β。用户采用OFDM进行数据的发送,有Nc个子载波,子载波集合记为![]() 一个子载波只能分配给一个基站,一个基站可以分配多个子载波,总的带宽为B。νk,n表示是否子载波指示变量,当子载波n分配给用户与基站k之间的连接时νk,n=1,反之νk,n=0。载波指示向量表示为[ν1,1ν1,2...ν1,Ncν2,1...ν2,Nc...νK,Nc],记为v。pk,n表示用户与基站k在第n个子载波上的发射功率。发射功率向量表示为[p1,1p1,2...p1,Ncp2,1...p2,Nc...pK,Nc],记为p。用户和基站k在子载波n上的无线接入信道因子为hk,n=|hk,n|e∠hk,n,则发射信号信噪比表示为
一个子载波只能分配给一个基站,一个基站可以分配多个子载波,总的带宽为B。νk,n表示是否子载波指示变量,当子载波n分配给用户与基站k之间的连接时νk,n=1,反之νk,n=0。载波指示向量表示为[ν1,1ν1,2...ν1,Ncν2,1...ν2,Nc...νK,Nc],记为v。pk,n表示用户与基站k在第n个子载波上的发射功率。发射功率向量表示为[p1,1p1,2...p1,Ncp2,1...p2,Nc...pK,Nc],记为p。用户和基站k在子载波n上的无线接入信道因子为hk,n=|hk,n|e∠hk,n,则发射信号信噪比表示为![]() 能达到的每秒最大传输速率(bits per second, bps)为
能达到的每秒最大传输速率(bits per second, bps)为![]() 用户和基站k的总传输速率表示为
用户和基站k的总传输速率表示为
(1)
则用户与基站k之间传输时间为
(2)
3 问题描述
移动边缘迁移计算中,多基站之间的协作有利于缩短计算时延,节约用户的计算资源与耗能。为了缩短用户和基站之间的计算时延,采用min-max公平性原则并提出一个min-max问题。问题最小化了用户与基站之间的最长时延,提高了协作的公平性。考虑到相比于上行迁移量,回传的数据量很小,回传时间忽略不计,同时基站的计算资源丰富,忽略计算时间[22-23]。
C2: νk,npk,n≥0,∀n,∀k
C4: βk≥0,∀k
C6: νk,n∈{0,1},∀n,∀k
(3)
其中,P表示用户总的最大发射功率,D表示用户计算任务的大小,RC表示用户到各个基站的最大前传容量。约束1表示各个子载波上总的发送功率在最大发射功率范围内,约束2限制各个子载波上的发射功率非负。约束3保证迁移到各个基站的文件比特数之和为需要计算的任务量,约束4保证到各个基站的迁移数据量非负。约束5和约束6表示OFDM中每个子载波只能分配给一个基站,分配因子取值为0或者1,约束7表示前传容量约束,防止迁移计算堵塞和过大计算压力。
其中,子载波选择因子νk,n是二元变量,问题Q1是个混合整数非线性规划问题,最优解可以通过穷举法获得,计算的复杂度随着子载波、分割精度的增加呈指数增加,计算量过于庞大。本文提出的算法,根据用户设备的不同、所处环境不同,分低信噪比特殊情况和普适情况提出次优算法,降低计算复杂度,且收敛较快。
4 优化算法
在此章节中,首先利用分式规划和引入放松变量,将min-max分式问题转化为min问题,再根据高低信噪比情况提出不同求解方法。
Q1中,约束C6是一个二元变量,因此用等价形式重写约束,形式为
C6a:0≤νk,n≤1,∀n,∀k
(4)
(5)
相比于放缩νk,n到[0,1]范围比,这种重写方式保证了C6的二元变量特性,再结合泰勒展开式[24],可以转化为:
(6)
问题中目标函数是分数形式,根据参考文献[25],给出下述定理。
定理1 问题Q1的最优解{p*,β*,v*}和用户到基站k的最短时延![]() 当且仅当下式满足时达到:
当且仅当下式满足时达到:
(7)
其中, p*, β*,v*分别表示问题Q1中,各个子载波上发射功率分配向量p,各个基站的数据分配向量β和子载波选择向量v的最优解。
为解决min-max问题,引进一个新的变量uk,n=νk,npk,n,再引入一个松弛变量ξ。结合上述定理,令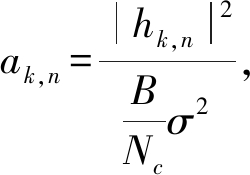 问题Q1转化为
问题Q1转化为
C2′:uk,n≥0,∀n,∀k
C3-C5
C6a:0≤νk,n≤1,∀n,∀k
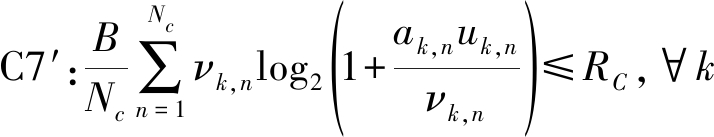
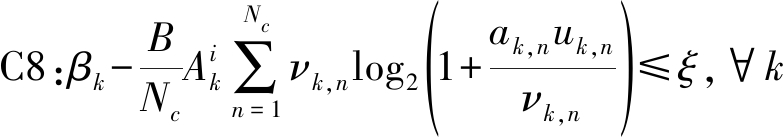
(8)
4.1 特殊情况(低信噪比通信)
在特殊应用场景下,比如手机的发射功率低,或信道环境较差,即低信噪比的通信环境下,由于![]() 问题简化为以下形式:
问题简化为以下形式:
C1′,C2′,C3-C5,C6a,C6b′
(9)
低信噪比情况中,目标函数和约束都转化为凸函数,可以用凸优化工具包求解。提出的算法在每一次迭代过程中,主要使用凸优化算法,因此,整体的计算复杂度是多项式形式的,表示为O(κ1·N),其中κ1表示凸优化求解迭代次数,N代表凸优化算法的复杂度,该复杂度是以多项式的形式,多项式的表达式和基站个数K和子载波个数Nc有关。
4.2 普适情况
当用户为有高发射功率的设备或信道环境较好,即在高信噪比环境下进行通信时,为解决问题Q2,对于C7′非凸条件的转换最为关键。约束C7′利用对数特性可重写为:
(10)
此时等价形式仍然是非凸形式,结合二元函数在点(xk,yk)处的泰勒展开式为:
(11)
对C7′进行泰勒展开得到一个近似的线性约束,表达式为:
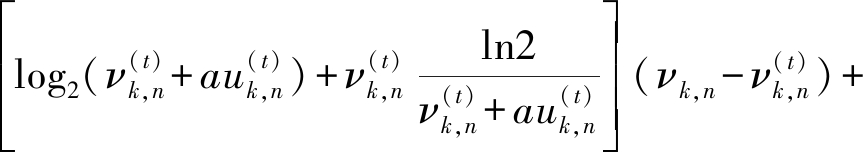
(12)
此时问题变成:
C1′,C2′,C3-C5,C6a,C6b′
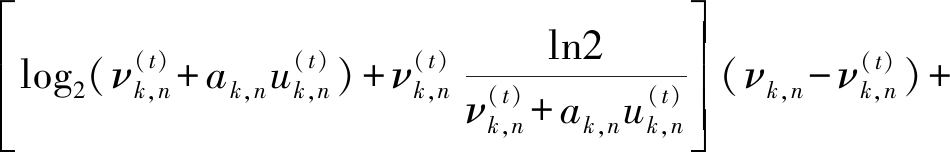
(13)
其中约束C8′存在分母可能为0的情况,在现实生活中,νk,n=0意味着子载波n没有被分配到用户与基站k之间的通信中,因此设置当νk,n=0时,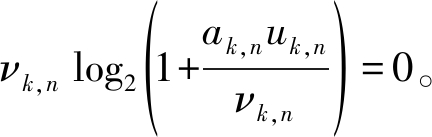 同时,约束C8′中存在变量的相乘相除形式,引用定理2[26],约束C8是关于变量u,β,v,ξ的凸函数。
同时,约束C8′中存在变量的相乘相除形式,引用定理2[26],约束C8是关于变量u,β,v,ξ的凸函数。
定理2 当f(b)是凹函数时,af(b/a)对于(b,a)也是凹函数。
结合定理2,问题就变成凸问题可以用拉格朗日乘子法求解法求解,其拉格朗日函数为
L(u,β,v,ξ,α,ω,δ,ε,![]() ,φ,η,κ,λ,σ)
,φ,η,κ,λ,σ)
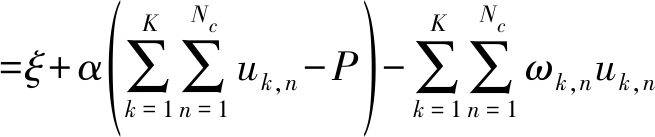
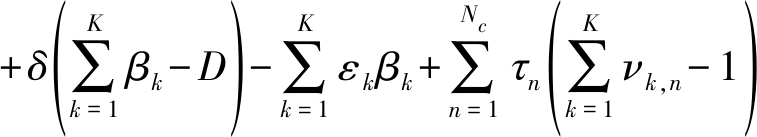
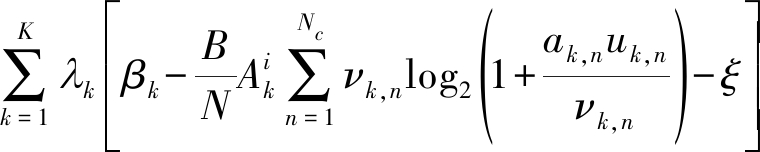
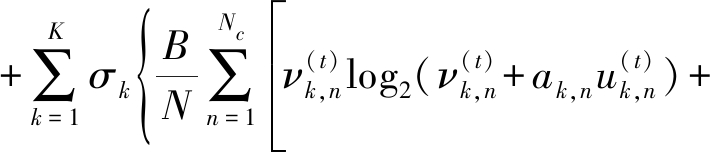
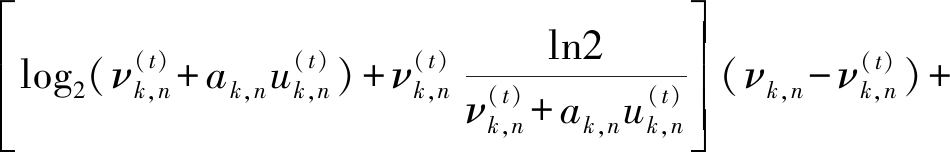
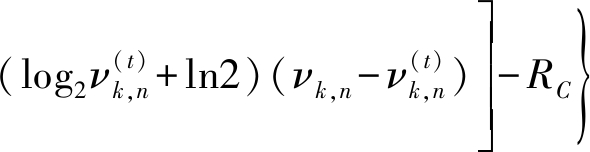
(14)
其中,![]() 为分别对应约束C1′,C2′,C3-C5,C6a,C6b′,C8和C9的拉格朗日乘子,Q4的对偶问题为
为分别对应约束C1′,C2′,C3-C5,C6a,C6b′,C8和C9的拉格朗日乘子,Q4的对偶问题为
α,ω,δ,ε,![]() ,φ,η,κ,λ,σ)
,φ,η,κ,λ,σ)
C10:α,δ≥0
ω,ε,![]() ,φ,η,κ,λ,σ
,φ,η,κ,λ,σ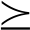 0
0
(15)
求解对偶问题时,先给定拉格朗日乘子初始值,变量u,β,v,ξ可由KKT条件获得。再将拉格朗日乘子利用梯度下降法更新。分别L(u,β,v,ξ,α,ω,δ,ε,![]() ,φ,η,κ,λ,σ)对uk,n求导得到
,φ,η,κ,λ,σ)对uk,n求导得到
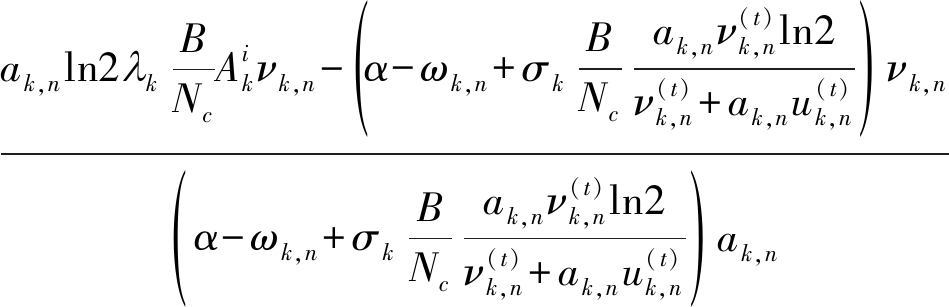
(16)
其中,![]() 为变量uk,n的最优值,可以得到各个子载波分配的发射功率pk,n最优值为
为变量uk,n的最优值,可以得到各个子载波分配的发射功率pk,n最优值为
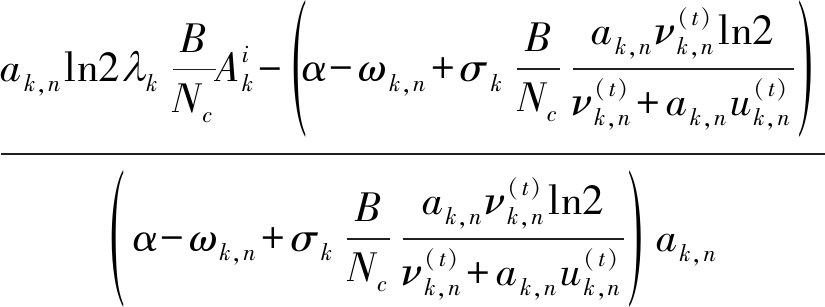
(17)
同理,通过对νk,n求导得到
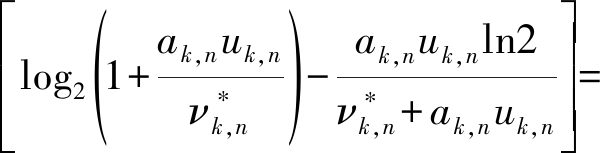
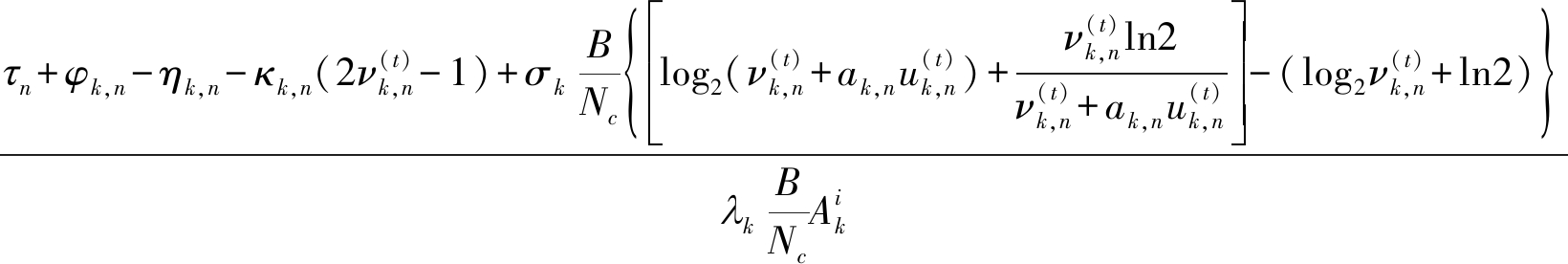
(18)
因为uk,n=νk,npk,n,所以![]()
得到变量最优解后,根据梯度下降法更新拉格朗日乘子,依次求导各乘子的倒数,因篇幅此处省略各表达式。拉格朗日乘子更新式为:
Ω(j+1)=[Ω(j)-ΔΩ(j) Ω(j)]+
Ω(j)]+
(19)
其中Ω∈{α,ω,δ,ε,![]() ,φ,η,κ,λ,σ},[x]+=max{0,x}。j是迭代计数,ΔΩ(j)是更新的步长。
,φ,η,κ,λ,σ},[x]+=max{0,x}。j是迭代计数,ΔΩ(j)是更新的步长。
提出的算法在每一次迭代过程中,主要包括泰勒一阶展开近似迭代优化和凸优化,因此,整体的计算复杂度是多项式形式的,表示为O(κ1N·κ2M),其中κ1表示凸优化求解迭代次数,κ2表示泰勒一阶展开近似迭代次数,N代表凸优化算法的复杂度,M代表泰勒一阶展开近似算法的复杂度,两者的复杂度是以多项式的形式,多项式的表达式皆和基站个数K和子载波个数Nc有关。具体的优化算法算法步骤如算法1所示。
算法1

1.初始化:给定P,Nc,K的值,最大迭代次数I和误差量ε。初始化参数i=1,j=1,t=0用户到基站k的传输时间Aik=0。2.当i
5 仿真分析
本章节中,对本文对提出的算法采用MATLAB进行仿真,并对结果进行分析。假设基站个数K=4,子载波个数Nc=64个,用户需要计算的任务大小为D=100 bits。4个基站和用户均匀独立地分布在边长为1 km的正方形区域内,基站z和用户之间的距离为dz,之间的信道向量表示为![]() 其中PaLoz是距离dz的路径损耗,
其中PaLoz是距离dz的路径损耗,![]() 是发射天线增益,ζz是对数正态阴影衰落系数,gz是小规模衰落系数。采用3GPP LTE标准预测信道,
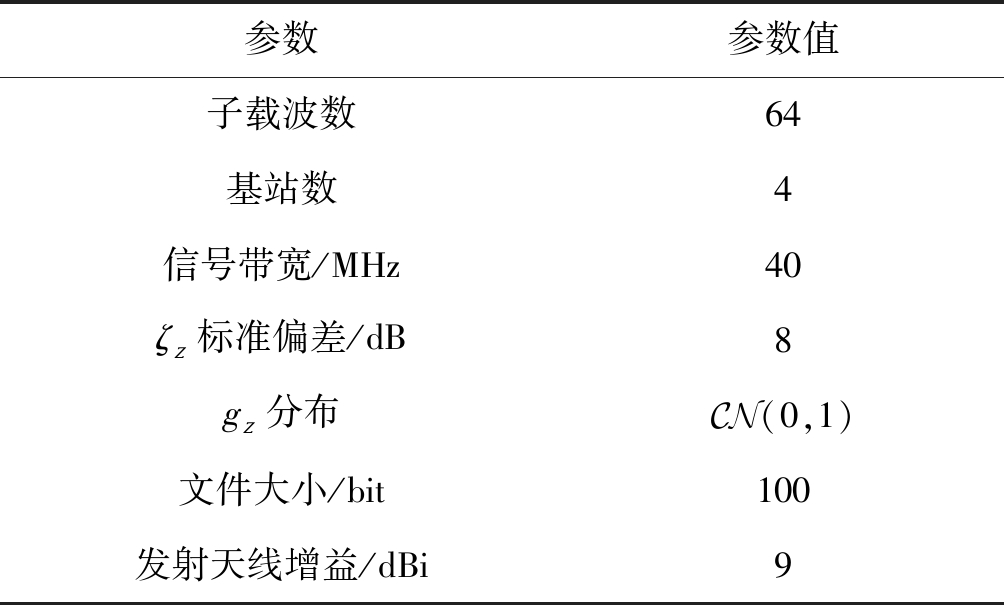
是发射天线增益,ζz是对数正态阴影衰落系数,gz是小规模衰落系数。采用3GPP LTE标准预测信道,![]() 参数值由表1所示。
参数值由表1所示。
根据用户的不同发射功率,可以选择合适的算法求解。当前传容量约束为Rc=1e5 bps时,画出两个算法在不同的用户总发射功率约束下的收敛及延迟仿真图。从仿真图2中可以看出,用户的总发射功率越大,计算的延迟就越小,这有赖于发射功率增大则传输速率增大。低信噪比时的简化算法不仅计算量少,且收敛速度远远快于普适算法,但优化效果有所损失。当P=0.01 W时,简便算法收敛速度比普适算法要快,结果介于普适算法P=0.01~0.001 W之间,计算复杂度相比于普适算法而言要小很多,适用于对于精度要求不高但需要快速出结果的低信噪比情况。
表1 仿真参数
Tab.1 Simulation parameters
参数参数值子载波数64基站数4信号带宽/MHz40ζz标准偏差/dB8gz分布 (0,1)文件大小/bit100发射天线增益/dBi9
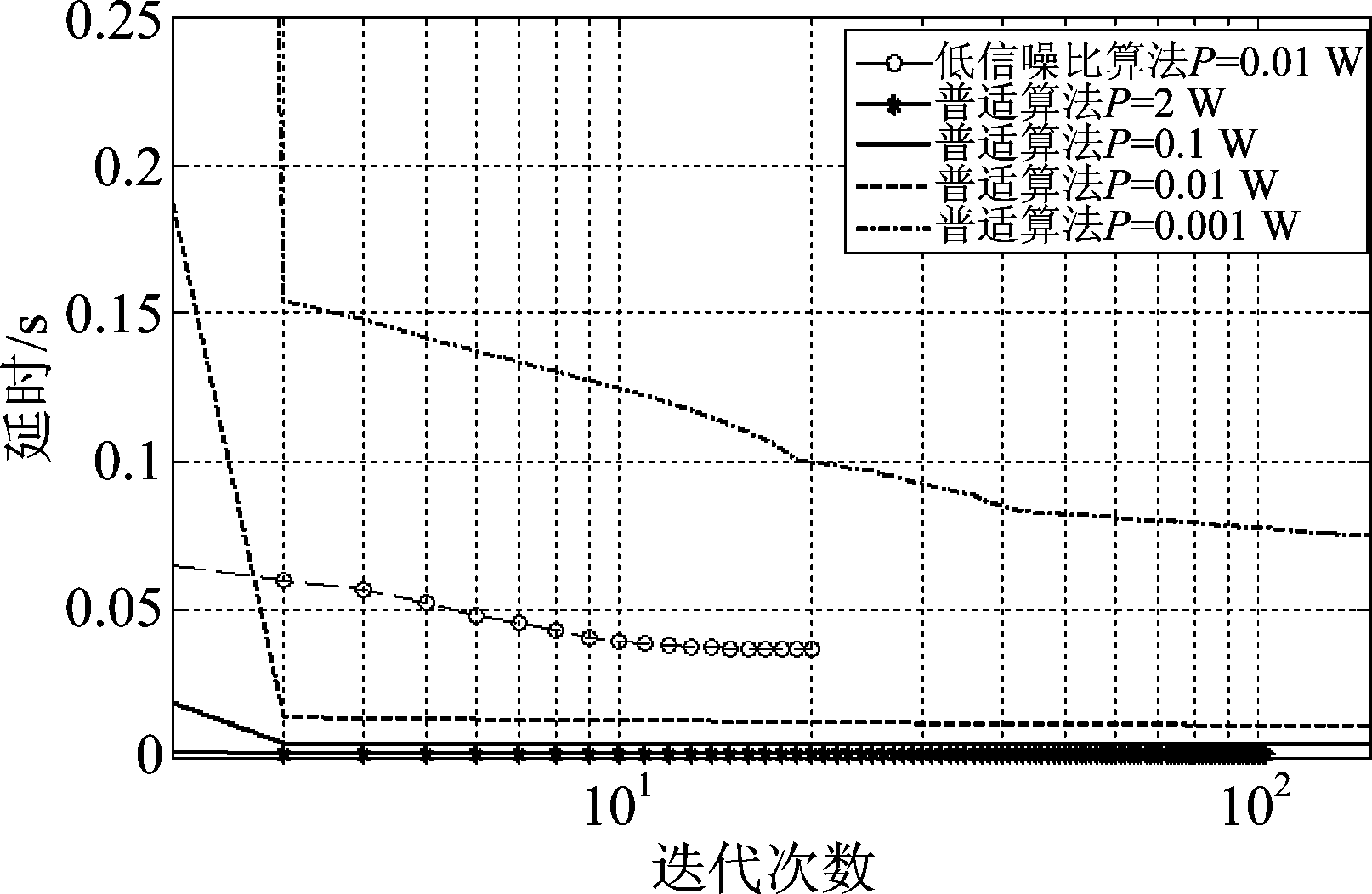
图2 不同算法在不同发射功率下的收敛效果和迁移延迟
Fig.2 The convergence and delay of different algorithms under different transmit Power
当用户的总发射功率不变时,前传约束的变化对于计算时延的影响如图3所示,此时采用普适算法,且P=2 W。从图中可以看出,前传容量大小与时延成反相关,说明当前传容量约束放宽时,传输速率的限制逐渐衰弱,更多的计算量会被迁移至信道条件良好的基站进行计算,因而降低计算时延。随着约束放宽,前传容量约束对问题影响逐渐削弱。
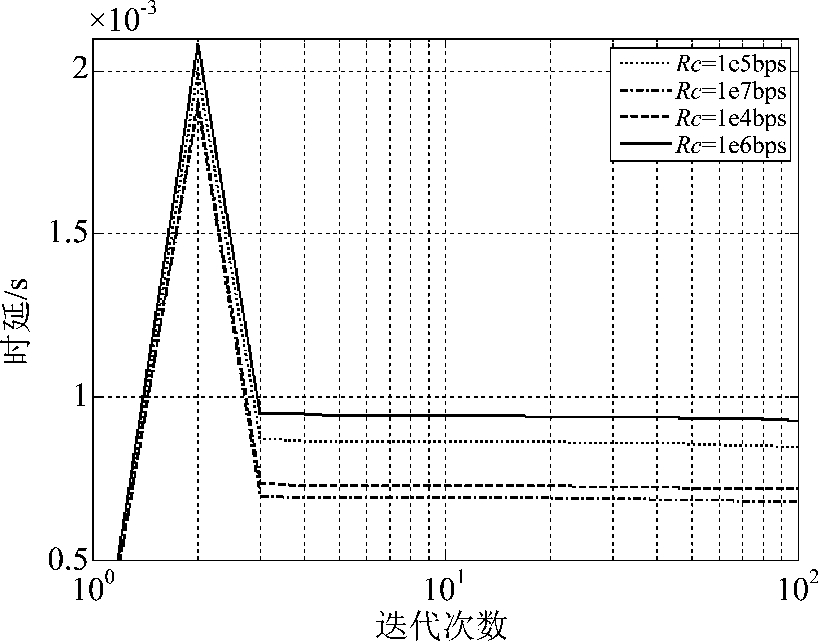
图3 不同前传容量约束下的收敛效果和迁移延迟
Fig.3 The convergence and delay of different algorithms under different capacity constraints
为体现优化算法对系统的性能提升,将优化算法下的系统时延与平均分配数据量、发射功率、子载波到各个基站情况下的情况,以及任务作为一个整体并选择信道条件最好的基站进行迁移的情况进行对比。此时,发射功率P=2 W,前传容量约束为Rc=5e6 bps,D=100 bits。相比于平均分配数据量、发射功率、子载波到各个基站情况下的迁移,本文提出的优化算法缩短迁移时延约31.8%;相较于将任务作为一个整体并选择信道条件最好的基站进行迁移的情况,时延约减少25%。这不仅说明本文提出的优化算法能有效的提升系统性能,也说明了在迁移决策的制定过程中,不合理的迁移策略甚至可能降低系统性能,在本次仿真环境中,平均分配策略比整体迁移策略的时延要多10%。
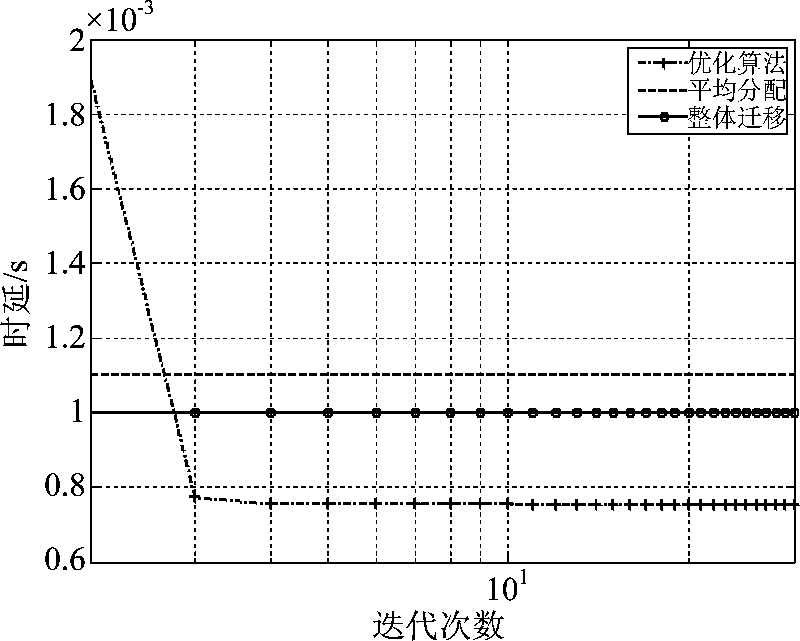
图4 优化迁移与非优化迁移性能对比
Fig.4 Performance comparison between optimized offloading and non-optimized offloading
6 结论
本文提出一个基于OFDM边缘迁移计算的多基站协作模型,通过优化子载波选择,分配各个子载波上的发射功率和迁移到各个基站的迁移量,实现资源的调度,达到前传容量约束下的最大计算时延最小化的优化目标。在基站计算能力强且回传结果小的基础上,计算时延为用户到基站的传输时延。依据信噪比大小,除了普适算法之外还提出一个适用于低信噪比的简化算法。通过仿真,两个算法都能很快收敛,且计算复杂度远远低于穷举法,实用性强。下一步的研究方向是在此基础上,结合机器学习,通过对情况的分集,达到快速分配的效果。
[1] Kwak J, Kim Y, Lee J, et al. DREAM: Dynamic Resource and Task Allocation for Energy Minimization in Mobile Cloud Systems[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2510-2523.
[2] 孙远, 李春国, 黄永明, 等. 基于云接入网络的多目标资源分配算法设计[J]. 信号处理, 2017, 33(3): 294-303.
Sun Y, Li C G, Huang Y M, et al. Multi-Objective Resource Allocation Design Algorithm in Cloud Radio Access Network[J]. Journal of Signal Processing, 2017, 33(3): 294-303.(in Chinese)
[3] Cuervo E, Balasubramanian A, Cho D K, et al. MAUI: making smartphones last longer with code offload[C]∥International Conference on Mobile Systems, Applications, and Services. DBLP, 2010: 49- 62.
[4] Chiang M, Zhang T. Fog and IoT: An Overview of Research Opportunities[J]. IEEE Internet of Things Journal, 2017, 3(6): 854- 864.
[5] Mao Y, You C, Zhang J, et al. A Survey on Mobile Edge Computing: The Communication Perspective[J]. IEEE Communications Surveys & Tutorials, 2017, PP(99): 1-1.
[6] Bi S, Zhang Y J. Computation Rate Maximization for Wireless Powered Mobile-Edge Computing with Binary Computation Offloading[J]. IEEE Transactions on Wireless Communications, 2018, 17(6): 4177- 4190.
[7] Tran T X, Hajisami A, Pandey P, et al. Collaborative Mobile Edge Computing in 5G Networks: New Paradigms, Scenarios, and Challenges[J]. IEEE Communications Magazine, 2017, 55(4): 54- 61.
[8] Stojmenovic I, Wen S. The Fog computing paradigm Scenarios and security issues[C]∥Computer Science and Information Systems. IEEE, 2014: 1- 8.
[9] Chen X. Decentralized Computation Offloading Game for Mobile Cloud Computing[J]. Parallel & Distributed Systems IEEE Transactions on, 2014, 26(4): 974-983.
[10] Sardellitti S, Scutari G, Barbarossa S. Joint Optimization of Radio and Computational Resources for Multicell Mobile-Edge Computing[J]. IEEE Transactions on Signal & Information Processing Over Networks, 2014, 1(2): 89-103.
[11] Wang C, Liang C, Yu F R, et al. Computation Offloading and Resource Allocation in Wireless Cellular Networks With Mobile Edge Computing[J]. IEEE Transactions on Wireless Communications, 2017, 16(8): 4924- 4938.
[12] Lin Y D, Chu T H, Lai Y C, et al. Time-and-Energy-Aware Computation Offloading in Handheld Devices to Coprocessors and Clouds[J]. IEEE Systems Journal, 2017, 9(2): 393- 405.
[13] Mu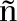 oz O, Pascual-Iserte A, Vidal J. Optimization of Radio and Computational Resources for Energy Efficiency in Latency-Constrained Application Offloading[J]. IEEE Transactions on Vehicular Technology, 2015, 64(10): 4738- 4755.
oz O, Pascual-Iserte A, Vidal J. Optimization of Radio and Computational Resources for Energy Efficiency in Latency-Constrained Application Offloading[J]. IEEE Transactions on Vehicular Technology, 2015, 64(10): 4738- 4755.
[14] Chen X. Decentralized Computation Offloading Game for Mobile Cloud Computing[J]. Parallel & Distributed Systems IEEE Transactions on, 2014, 26(4): 974-983.
[15] He Y, Yu F R, Zhao N, et al. Big Data Analytics in Mobile Cellular Networks[J]. IEEE Access, 2017, 4: 1985-1996.
[16] Deng S, Huang L, Taheri J, et al. Computation Offloading for Service Workflow in Mobile Cloud Computing[J]. IEEE Transactions on Parallel & Distributed Systems, 2015, 26(12): 3317-3329.
[17] Seong-Hwan K, Sangdon P, Min C, et al. An Optimal Pricing Scheme for the Energy Efficient Mobile Edge Computation Offloading with OFDMA[J]. IEEE Communications Letters, 2018: 1-1.
[18] Ferdouse L, Das O, Anpalagan A. Auction Based Distributed Resource Allocation for Delay Aware OFDM Based Cloud-RAN System. GLOBECOM 2017-2017 IEEE Global Communications Conference, Singapore, 2017: 1- 6.
[19] Cheng K, Teng Y, Sun W, et al. Energy-Efficient Joint Offloading and Wireless Resource Allocation Strategy in Multi-MEC Server Systems[C]∥2018 IEEE International Conference on Communications (ICC), Kansas City, MO, 2018:1- 6.
[20] You C, Huang K, Chae H, et al. Energy-Efficient Resource Allocation for Mobile-Edge Computation Offloading[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1397-1411.
[21] Li M, Yang S, Zhang Z, et al. Joint subcarrier and power allocation for OFDMA based mobile edge computing system[C]∥2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE, 2017.
[22] Ko S, Huang K, Kim S, et al. Live Prefetching for Mobile Computation Offloading[J]. IEEE Transactions on Wireless Communications, 2017, 16(5): 3057-3071.
[23] Guo H, Liu J. Collaborative computation offloading for multi-access edge computing over fiber-wireless networks. IEEE Transactions on Vihicular Technology, 2018: 1-1.
[24] Ng D W K, Wu Y, Schober R. Power Efficient Resource Allocation for Full-Duplex Radio Distributed Antenna Networks[J]. IEEE Transactions on Wireless Communications, 2015, 15(4): 2896-2911.
[25] 张敏, 侯琪, 何世文, 等. 一种分布式天线系统的最大化能源效率传输优化算法[J]. 信号处理, 2018, 34(4): 400- 408.
Zhang M, Hou Q, He S W, et al. Energy Efficient Optimization Algorithm for Distributed Antenna Systems[J]. Journal of Signal Processing, 2018, 34(4): 400- 408.(in Chinese)
[26] Guo S, Zhou X, Xiao S, et al. Fairness-Aware Energy-Efficient Resource Allocation in D2D Communication Networks[J]. IEEE Systems Journal, 2019, 13(2): 1273-1284.



