1 引言
宽带信号DOA估计是阵列信号处理领域中的研究热点,其被广泛应用在雷达、通信、声呐中。宽带信号DOA估计问题已经经历了一段很长的研究历程,在此期间出现了大量的方法[1-3]。然而,这些方法大多适用于平稳信号,当待处理信号为非平稳的chirp信号时,以上方法的DOA估计性能就会急剧下降。
已经有学者针对宽带chirp信号的DOA估计问题进行了相关研究,例如Gershman等人[4]基于最大似然(ML)原理,采取多维搜索的方法实现宽带chirp信号的DOA估计,但是该方法计算复杂度过高。Wang等人[5]利用一种迭代方法,结合MUSIC算法进行DOA估计,该方法存在两个问题,一方面其估计结果对初始参数的选择十分敏感,另一方面该方法需要进行多次的迭代来提高估计精度。
时频分布是处理宽带chirp信号的有力工具,它将时间信号变换到时频域,揭示了各频率分量随时间的变化趋势[6- 8],不同的chirp信号分量可以在时频域中被区分出来。同时,空间时频分布(STFD)与阵列信号处理相结合也有助于改善DOA估计的性能并增强算法对噪声的鲁棒性。Gershman和Amin[9]首次将STFD的概念拓展到了宽带DOA估计中,将时频分布与CSM算法相结合来处理宽带chirp信号,拓宽了STFD的应用范围。然而该方法估计结果易受聚焦误差的影响。之后,Cirillo等人[10]在此基础上又提出了一系列改进算法,但这些方法只有在大快拍数的情况下才能取得较好的结果。文献[11]通过计算对称阵元间的时频分布来构建时频域的信号模型,该方法要求阵元间隔小于等于信号最高频率所对应波长的四分之一,这一限制条件减小了阵列的有效孔径。文献[12]将短时傅里叶变换(STFT)结合STFD矩阵来分离各信号的时频点,该方法在处理多分量信号时具有良好效果,但其在信号角度间隔小的情况下分辨能力不佳。
在实际应用场景中,如雷达低空目标测角、声呐系统水下目标探测、室内定位等,由于多径效应的存在,信号经由多条路径射入阵列,阵列接收信号为相干信号,导致现有常规DOA估计方法失效。部分学者针对这一问题进行过分析研究,文献[13]利用相干信号的导向矢量与阵列流形之间的关系重构出噪声子空间。文献[14]将阵列中心阵元选为参考阵元来构造一个Toeplitz矩阵,该矩阵的秩不受相干信号影响。但这些方法效果并不理想,且会损失阵列孔径。
针对以上问题,本文提出了一种多径传播条件下宽带线性调频信号DOA估计的新方法。该方法将导向有效投影技术与宽带线性调频信号的时频特性相结合,通过时频分析,区分出不同的信号分量并逐个处理。此外,该方法在时域实现DOA估计,无需进行聚焦操作,理论上避免了聚焦误差对估计结果的影响。仿真部分验证了所提方法的有效性,并与传统的宽带DOA估计方法进行了性能对比。结果表明,与现有方法相比,所提方法性能提升显著。
2 信号模型
L元均匀线阵(ULA)接收M(M<L)个宽带线性调频信号,信号入射角度为![]() 宽带信号阵列接收模型可表示为
宽带信号阵列接收模型可表示为
x(t)=A(t)s(t)+n(t)
(1)
其中A(t)=[a(θ1,t),…,a(θM,t)]为时变的导向矢量矩阵,s(t)和n(t)分别为信号矩阵和噪声矩阵,a(θm,t)=[1,exp{j 2πfm(t)dsin θm/c},…,exp{j 2πfm(t)d(M-1)sin θm/c}]T, fm(t)为第m个信号的瞬时频率,d为阵元间距。
第l个阵元的输出
(2)
式中τl,θm是第m个信号在第l个阵元和参考阵元之间的传播时延,nl(t)是第l个阵元处的白噪声,sm(t)是接收的宽带线性调频信号,其形式为
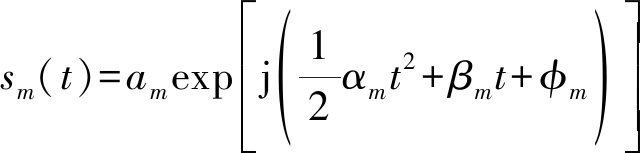
(3)
其中am表示信号的振幅,αm表示调频率,βm表示初始频率,φm表示初始相位。
多径传播条件下,宽带线性调频信号阵列接收模型可表示为
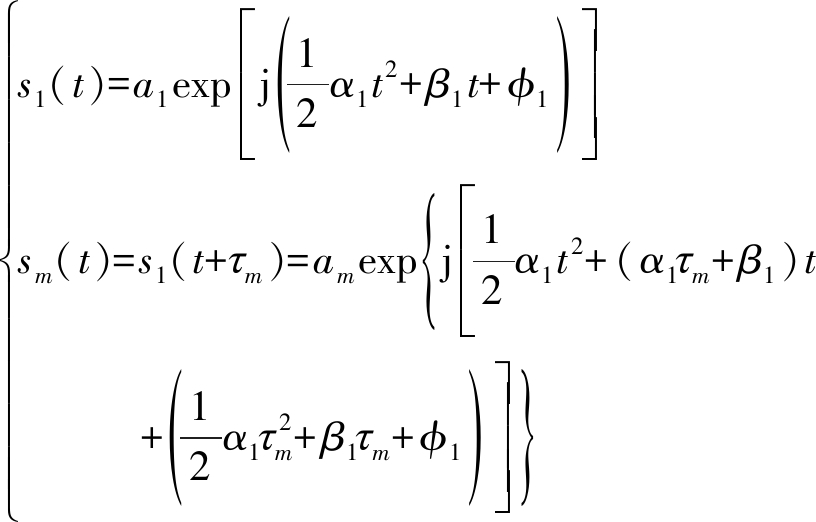
(4)
式中τm为第m个信号的多径传播时延。
接收的多径信号频率可表示为
(5)
3 DOA估计方法
观察式(4)和(5)可以发现,由于不同信号之间多径传播时延的存在,阵列所接收到的不同信号分量的频率范围是不同的。借助时频分布可以在时频图中清晰地看到各信号分量的频率范围。
平滑伪Wigner-Ville分布(SPWVD)的离散形式表示如下[9]
(6)
式中N为窗长。
SPWVD体现了信号频率和时间的联合分布信息,以及信号频率随时间的变化关系。计算阵元输出信号的SPWVD可以得到信号的时频图,在时频图中,不同的多径信号分量表现为不同的曲线,当多径传播时延足够大时,代表不同信号的曲线能够被清晰地区分。理论上,由于信号在不同阵元间的传播也存在一定时延,不同阵元输出信号的时频图也会略有不同。然而,实际情况中,信号在阵元间的传播时延一般很短,所以不同阵元输出信号的时频图几乎相同。
图1分别展示了第1、2、8个阵元输出信号的SPWVD时频图,可见,不同阵元输出信号的分布之间没有显著差异。因此,在接下来的方法中,计算第一个阵元输出信号的SPWVD来获得时频图。信号在不同阵元间传播的时延以及信号多径传播时延对算法性能的影响将在后面的仿真环节进行讨论。
在宽带阵列信号接收模型中,导向矢量为时变量,即与某一时刻接收信号的瞬时频率有关。在传统的DOA估计方法中需要进行频域的聚焦操作,将不同频点处的信号聚焦到同一参考频点,然而在聚焦过程中对来波角度的预估计误差会对最终结果有较大影响。利用导向有效投影技术[15]的思想,对接收信号在扫描角度范围内进行时域上的延时处理,构造有效噪声子空间,当扫描角度恰为信号真实的来波方向时,特征矢量与全一矢量相正交,据此可判断信号的来波方向。该操作无需进行聚焦,理论上避免了聚焦误差的影响。
在导向有效投影技术中,定义有如下对应于不同扫描角度θ的延时操作[15]
xθ(t)=[x1(t-τ1,θ),x2(t-τ2,θ),…,xL(t-τL,θ)]T
(7)
其中τl,θ是波达方向为θ的某一信号从第l个阵元到参考阵元的传播时延。在此基础上构建对应于扫描角度θ的SPWVD
(8)
不同的信号分量在时频图中表示为不同的曲线,如图1所示,据此,可区分出不同的信号分量,然后分别估计其波达方向。
在时频图中将不同的信号分量分离之后,对于N个时间点tn,在每个时间点选出属于第m个信号分量的F个频点,在这NF个时频点处分别计算式(8)
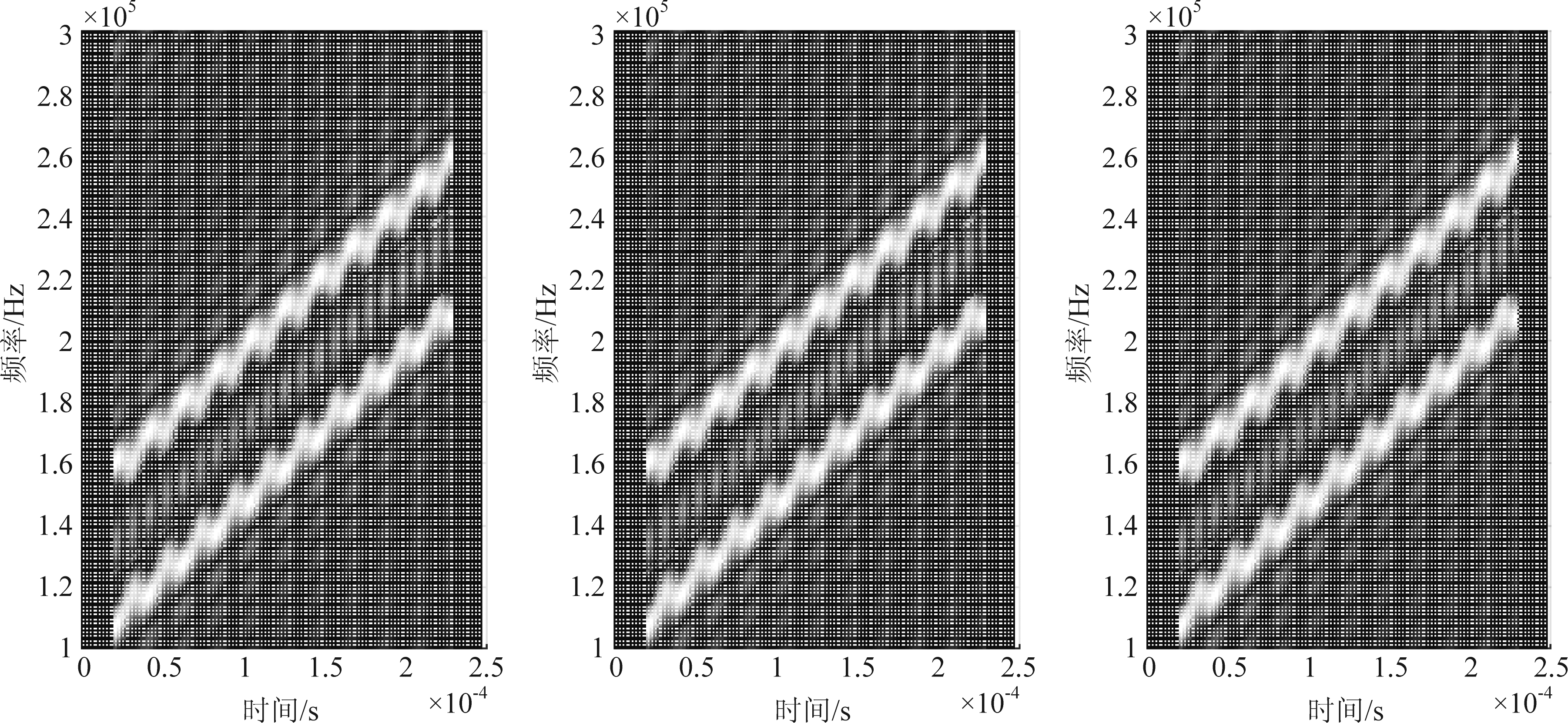
图1 第1、2、8个传感器输出信号的SPWVD
Fig.1 Pseudo-Wigner-Ville distribution of the signal in the first, second and eighth sensor
并取平均,可得平均SPWVD矩阵
(9)
其中
(10)
xm,θ(t)=[sm(t+τ1,θm-τ1,θ),sm(t+τ2,θm-τ2,θ),…,
sm(t+τL,θm-τL,θ)]T+nθ(t)
(11)
当扫描角度θ恰好等于第m个信号的波达方向θm,即τl,θm=τl,θ时,根据式(11),有
xm,θm(t)=[sm(t),sm(t),…,sm(t)]T+nθm(t)
(12)
据此可得
Dxm,θm(t, f)=γm(t, f)11H+σ2I
(13)
其中1是一个L×1维全一矢量,σ2为噪声功率,
(14)
故当扫描角度为θm时,平均SPWVD矩阵为
(15)
对平均SPWVD矩阵进行特征分解
(16)
由式(15)和式(16)有
(17)
由于Rx,m(θm)是正定的Hermitian矩阵,![]() 可得
可得
(18)
当l≠1时,![]() 因此
因此
1Hul(θm)=0, l=2,3,…,L
(19)
根据式(19),我们可以搜索以下空间谱来确定各信号分量的波达方向:
(20)
上述宽带线性调频信号DOA估计算法可概括为以下步骤:
1)计算第一个阵元输出信号的SPWVD,得到接收信号的时频图。
2)在时频图中区分出不同的信号分量,对每一个信号分量,分别选出NF个时频点。
3)对接收信号进行式(7)的延时操作并计算式(9),之后对式(9)进行特征分解。
4)对式(20)进行谱峰搜索,确定各信号分量的波达方向。
4 仿真结果
考虑2个宽带线性调频信号入射到8个阵元的均匀线阵,其中一个信号为另一个信号的多径传播信号,时延Δτ为0.01 ms。两个宽带线性调频信号的调频率均为α=4.8×109,它们的初始频率分别为β1=100 kHz,β2=148 kHz,入射角度分别为θ1=10°和θ2=15°。采样频率设定为400 kHz。
图2为通过所提方法得到的空间谱,可以看到,谱峰对应的角度恰为信号的来波方向。
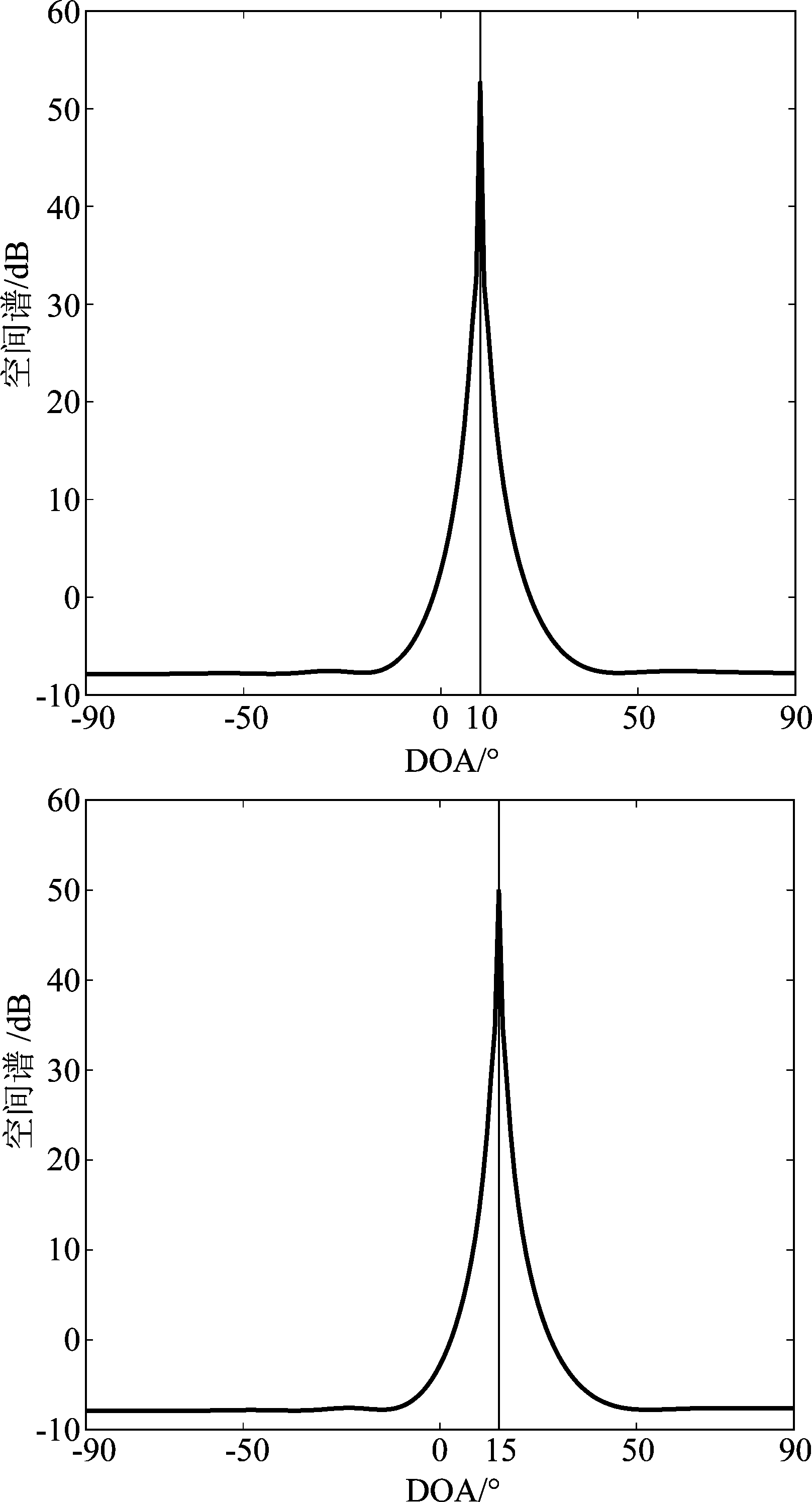
图2 两个信号源的DOA估计结果
Fig.2 DOA estimation of two sources
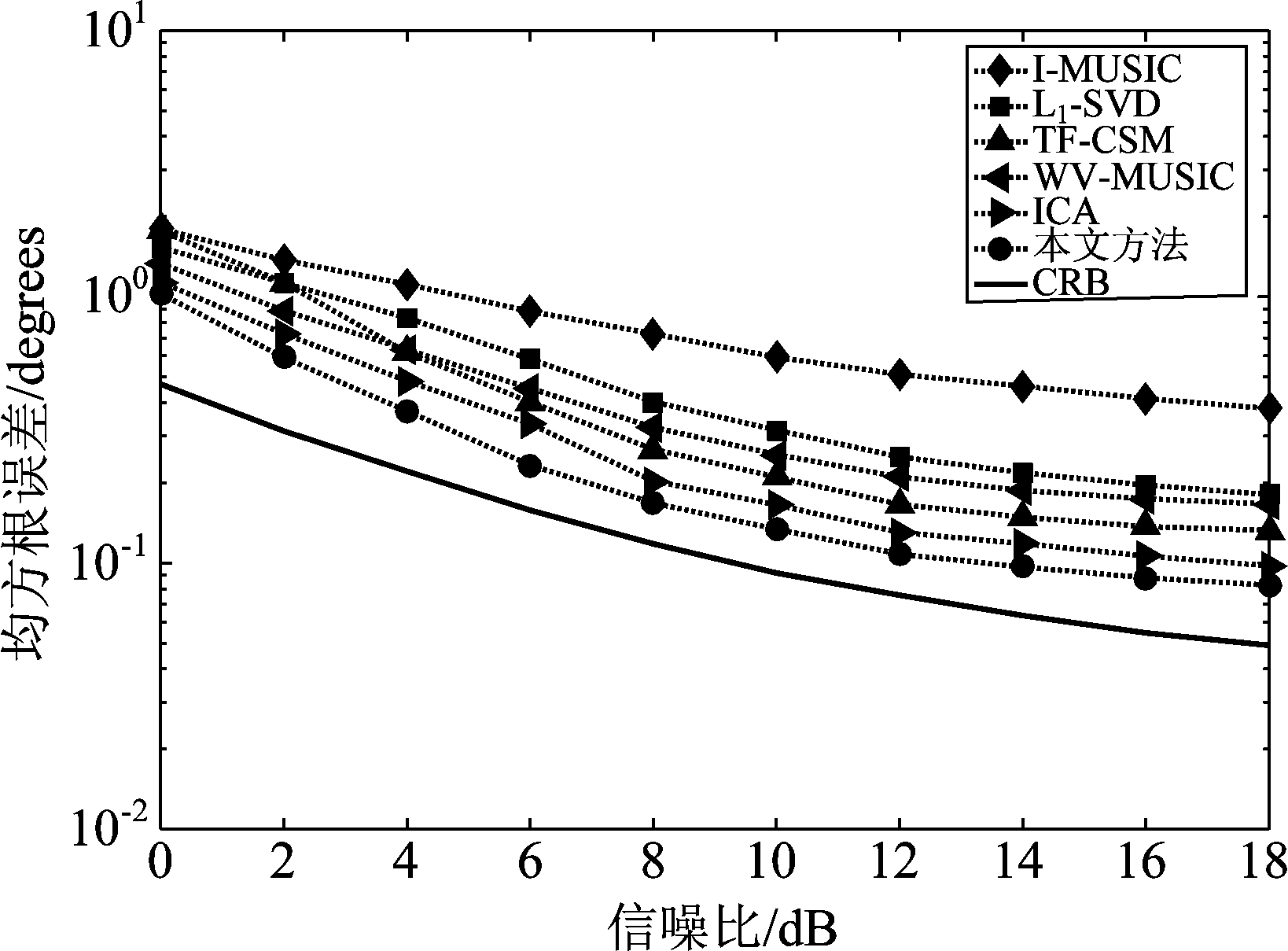
图3 不同信噪比下估计结果的均方根误差(快拍数为100次)
Fig.3 DOA estimation RMSE versus SNR (the number of snapshots is 100)
将所提方法与I-MUSIC方法[5]、TF-CSM方法[9]、L1-SVD方法[16]、WV-MUSIC方法[11]和ICA方法[17]进行比较,所有方法均进行了500次独立的蒙特卡洛实验。图3和图4分别展示了不同信噪比(SNR)和快拍数下所有方法DOA估计均方根误差(RMSE)的变化。从图中可看出,本文所提方法性能优于其他方法。
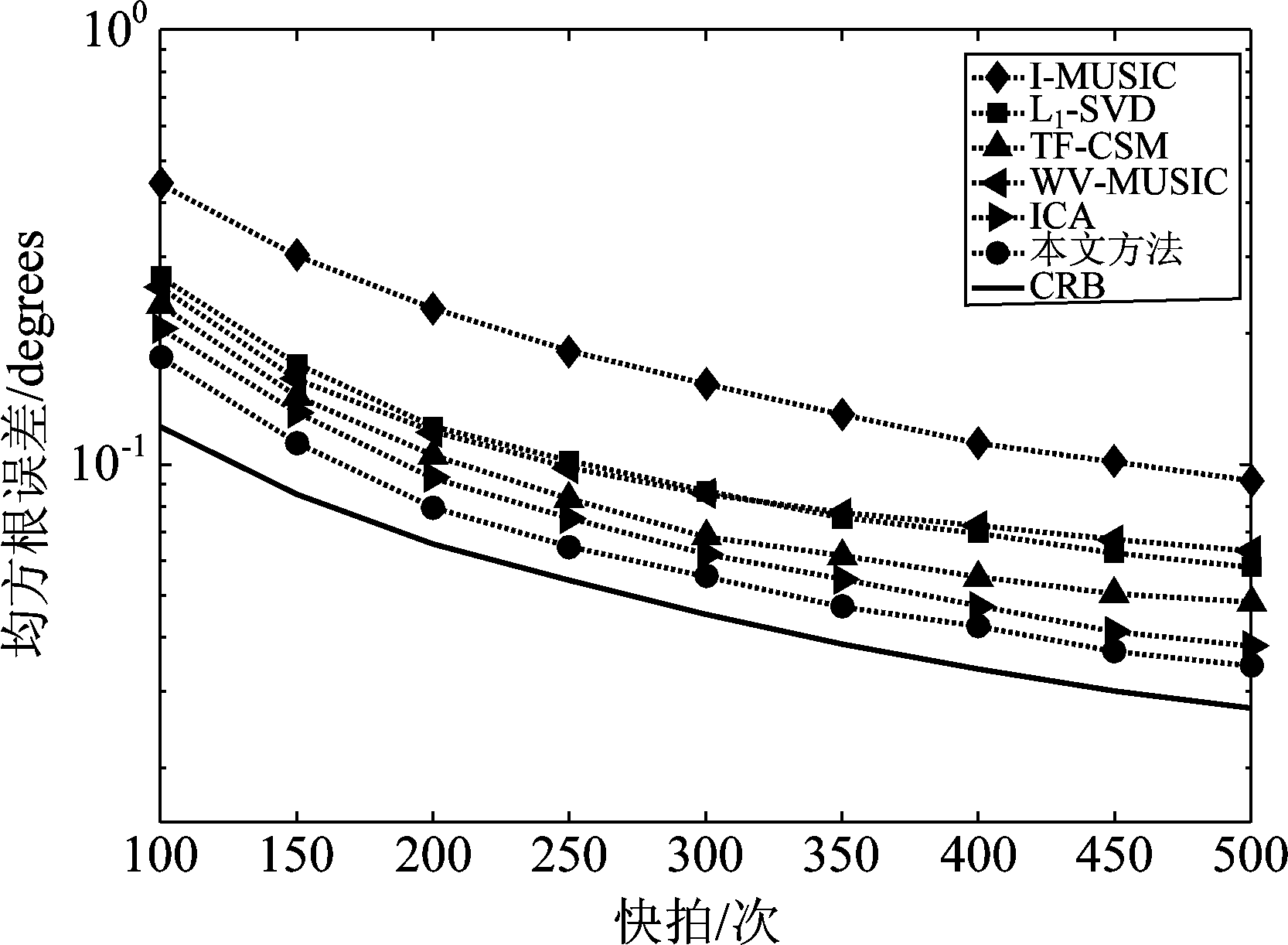
图4 不同快拍数下估计结果的均方根误差(信噪比为10 dB)
Fig.4 DOA estimation RMSE versus snapshots (SNR is 10 dB)
测试所提方法在角度分辨概率上的性能表现,同时与其他方法进行比较。将误差角度设为1°,若估计结果与真实角度相差在1°以内则视为估计成功,反之则视为失败。设函数
(21)
则角度分辨概率的数学形式可表示为
(22)
角度分辨失败概率的数学形式可表示为
PF=1-PS
(23)
图5展示了在不同SNR下各方法估计结果的失败概率,图6展示了在不同快拍数下各方法估计结果的分辨概率。可以看到,同对比方法相比,本文所提方法在低信噪比和小快拍情况下分辨概率更优。
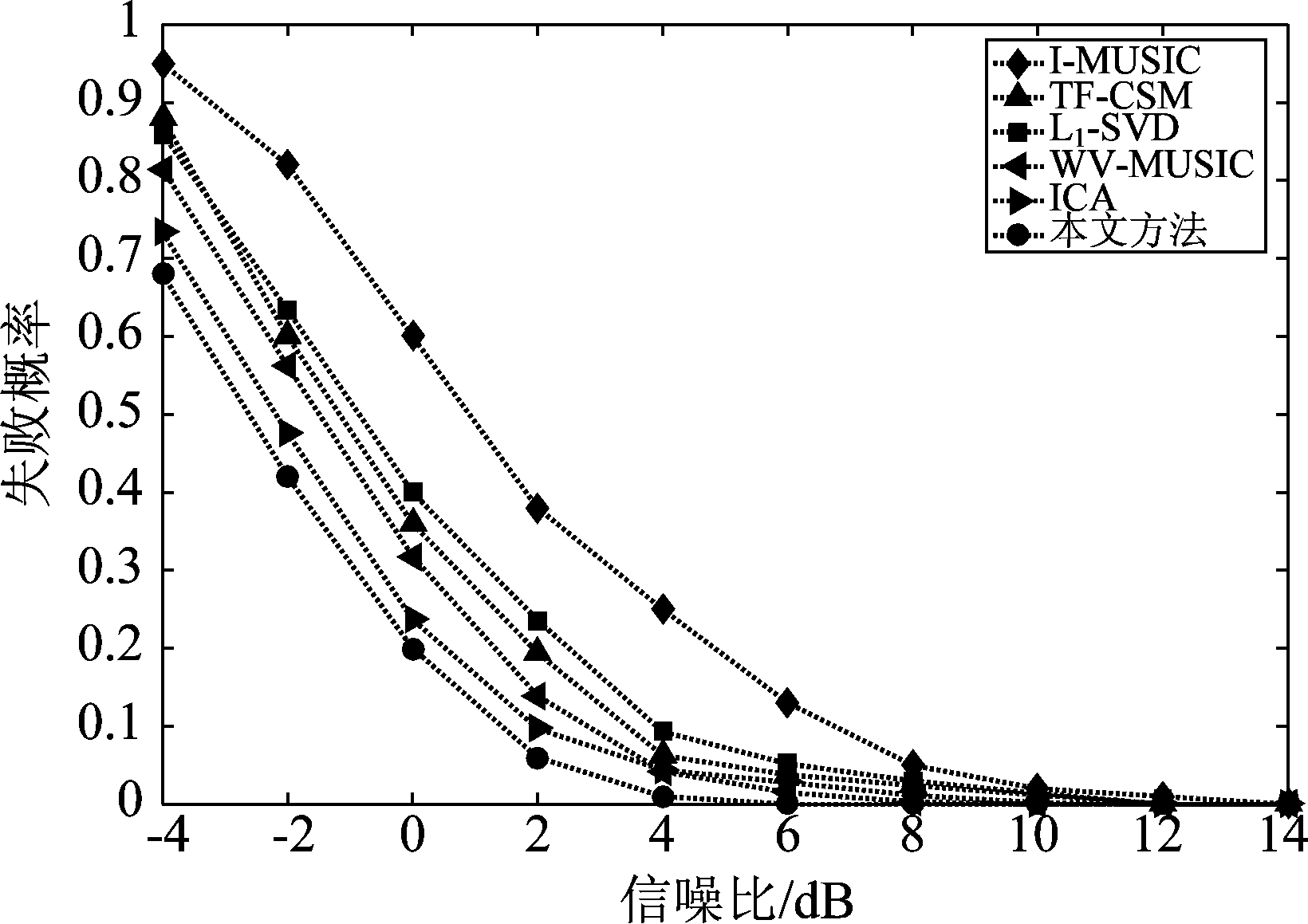
图5 不同信噪比下各方法的失败概率(快拍数为800次)
Fig.5 Failure probability versus SNR (the number of snapshots is 800)
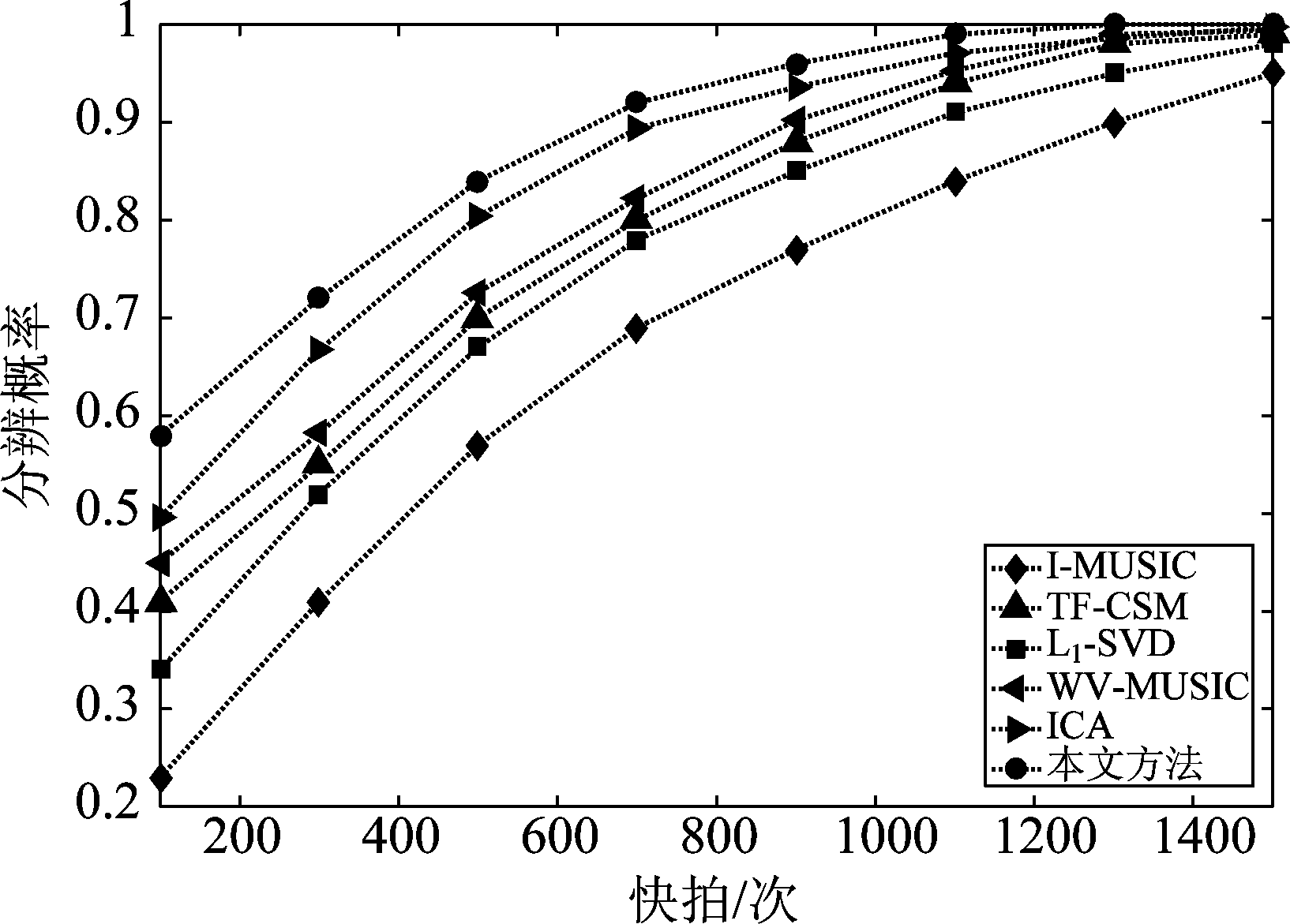
图6 不同快拍数下各方法的分辨概率(信噪比为5 dB)
Fig.6 Resolution probability versus snapshots (SNR is 5 dB)
最后,探究信号在不同阵元之间传播的时延对算法性能的影响,即选取不同阵元的输出信号计算SPWVD时频图对算法性能的影响,以及信号多径传播时延对算法性能的影响。图7为所选阵元不同时所提算法估计结果RMSE随信噪比和快拍数的变化,可以看出,使用以第一个阵元输出信号计算的SPWVD时频图会带来一定的误差,但这种误差在可接受的范围内。图8展示了在不同多径传播时延下所提算法估计结果的RMSE随信噪比和快拍数的变化,我们发现,多径传播时延的不同对算法的性能有较大影响。当不同信号分量之间多径传播时延较小时,不同信号分量的频率变化范围差别不大,即在时频图中表示各信号分量的曲线非常靠近,区分不同的信号分量以及选取分属不同信号分量的时频点将变得很困难。
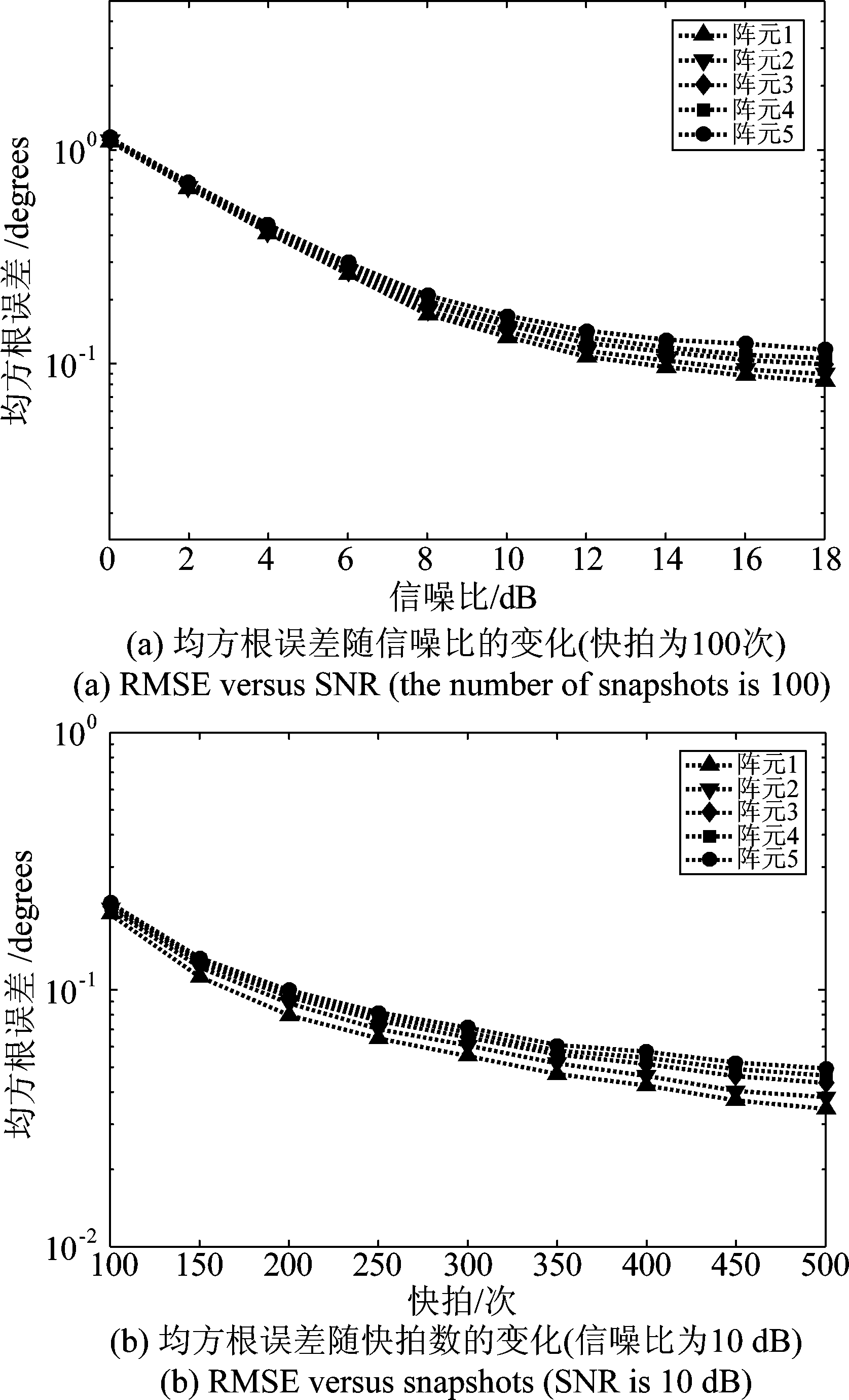
图7 选取的阵元不同时估计结果均方根误差的变化
Fig.7 RMSE versus different sensor we select
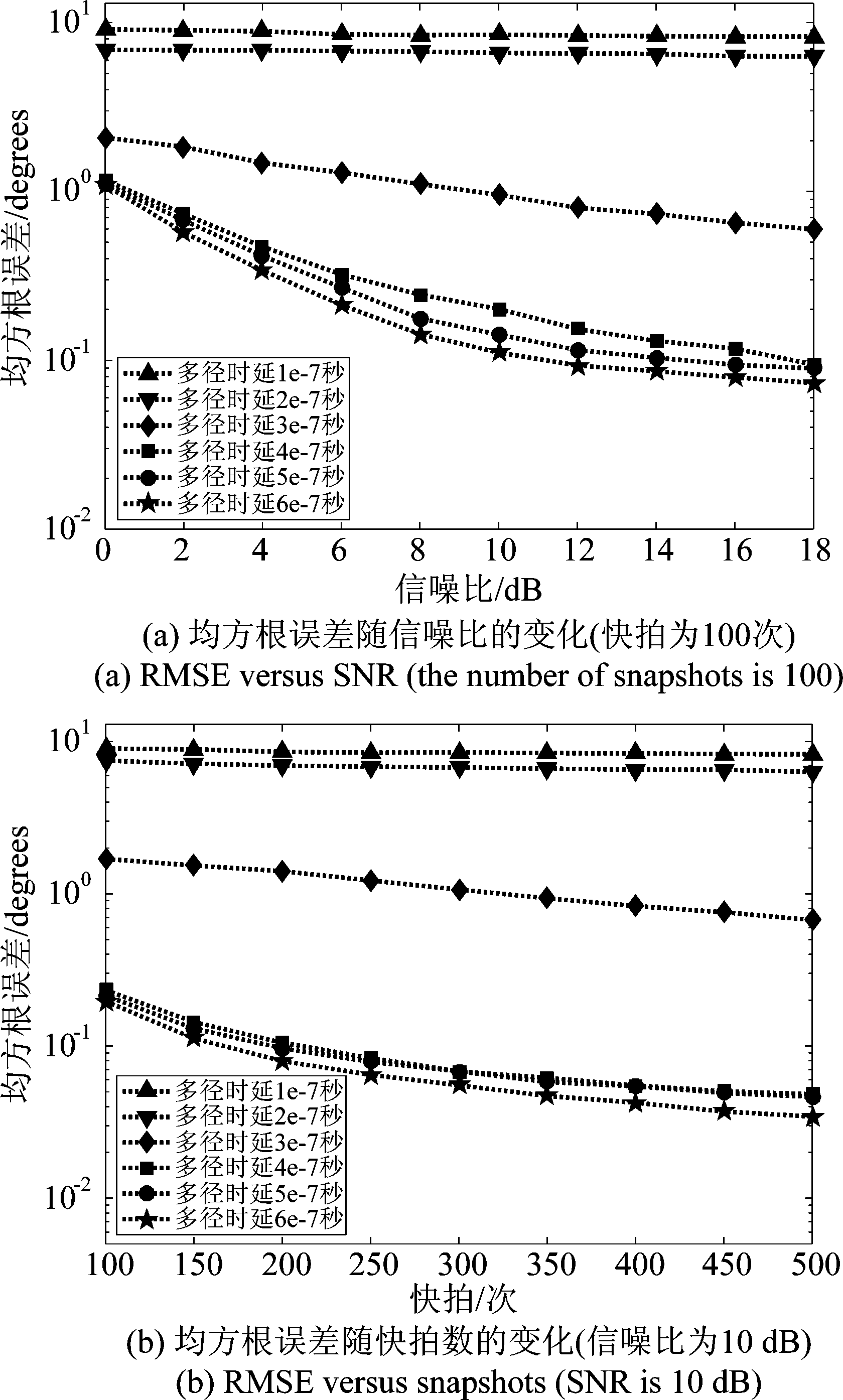
图8 信号分量多径传播时延不同时估计结果均方根误差的变化
Fig.8 RMSE versus multipath propagation delay
5 结论
本文提出了一种多径传播条件下宽带线性调频信号DOA估计的方法。该方法基于信号空间时频分布的概念,以时频分布矩阵代替传统的协方差矩阵,对不同时频特性的信号进行分离,单独估计其波达方向。所提方法无需进行聚焦操作,理论上避免了聚焦误差的影响。仿真结果验证了所提方法的有效性。
[1] Liu Wei, Weiss S. Wideband Beamforming: Concepts and Techniques[M]. Chichester, U.K.: Wiley, 2010.
[2] 蔡进, 刘春生, 陈明建, 等. 聚焦的子空间正交性测试宽带DOA估计方法[J]. 信号处理, 2018, 34(2): 221-228.
Cai Jin, Liu Chunsheng, Chen Mingjian, et al. Focused test of orthogonality of projected subspaces for wideband DOA estimation[J]. Journal of Signal Processing, 2018, 34(2): 221-228.(in Chinese)
[3] Claudio E D, Parisi R. Space Time MUSIC: Consistent signal subspace estimation for wideband sensor arrays[J]. IEEE Transactions on Signal Processing, 2018, 66(15): 2685-2699.
[4] Gershman A B, Pesavento M, Amin M G. Estimating parameters of multiple wideband polynomial-phase sources in sensor arrays[J]. IEEE Transactions on Signal Processing, 2001, 49(12): 2924-2934.
[5] Wang G, Xia X G. Iterative algorithm for direction of arrival estimation with wideband chirp signals[J]. IEE Proceedings Radar, Sonar and Navigation, 2000, 147(5): 233-238.
[6] 王勇, 姜义成. 一种新的LFM信号参数估计算法[J]. 信号处理, 2008, 24(1): 132-134.
Wang Yong, Jiang Yicheng. A new algorithm for parameter estimation of LFM signals[J]. Signal Processing, 2008, 24(1): 132-134.(in Chinese)
[7] 李军, 林秋华, 杨秀庭, 等. 近场宽带LFM信号被动测向和测距方法[J]. 系统工程与电子技术, 2016(8): 1737-1743.
Li Jun, Lin Qiuhua, Yang Xiuting, et al. Passive DOA and range estimation method for near-field broadband LFM signals[J]. Systems Engineering and Electronics, 2016(8): 1737-1743.(in Chinese)
[8] Zhang Ling, Zhang Haijian, Sun Hong. DOA estimation of closely-spaced and spectrally-overlapped sources based on time-frequency sparse representation[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, 2016: 3266-3270.
[9] Gershman A B, Amin M G. Wideband direction-of-arrival estimation of multiple chirp signals using spatial time-frequency distributions[J]. IEEE Signal Processing Letters, 2000, 7(6): 152-155.
[10] Cirillo L A, Zoubir A M, Amin M G. Direction finding of nonstationary signals using a time-frequency hough transform[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, 2005: 501-504.
[11] 田达, 黄克骥, 陈天麒. 一种小运算量的宽带线性调频信号DOA估计算法[J]. 信号处理, 2003, 19(1): 48-50.
Tian Da, Huang Keji, Chen Tianqi. A new method for DOA estimation of wideband LFM sources with low computational load[J]. Signal Processing, 2003, 19(1): 48-50.(in Chinese)
[12] Zhang Haijian, Bi Guoan, Cai Yunlong. DOA estimation of closely-spaced and spectrally-overlapped sources using STFT based MUSIC algorithm[J]. Digital Signal Processing, 2016, 52: 25-34.
[13] Gan Lu, Luo Xiaoyu. Direction-of-arrival estimation for uncorrelated and coherent signals in the presence of multipath propagation[J]. IET Microwaves, Antennas & Propagation, 2013, 7(9): 746-753.
[14] Ye Zhongfu, Xu Xu. DOA estimation by exploiting the symmetric configuration of uniform linear array[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(12): 3716-3720.
[15] Yin Bingjie, Xu Yougen, Huang Yulin, et al. Direction finding for wideband source signals via steered effective projection[J]. IEEE Sensors Journal, 2018, 18(2): 741-751.
[16] Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor array[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022.
[17] Sawada H, Mukai R, Makino S. Direction of arrival estimation for multiple source signals using independent component analysis[C]∥IEEE Seventh International Symposium on Signal Processing and Its Applications, 2003: 411- 414.


