1 引言
在短相干积累时间(Coherent Integration Time, CIT)条件下实现对低可探测大中型舰船目标的检测,尽管可大幅节省系统资源,使空、海同时探测成为可能[1-3],但短CIT也限制了对舰船目标信号的相干积累处理增益,同时多普勒频率分辨力的下降使检测域(多普勒频率域)中的海杂波展宽,导致本就处于海杂波区内的低可探测大中型舰船目标更易被强海杂波多普勒频率分量遮蔽。因此,短CIT条件下的OTHR舰船目标检测十分具有挑战性。
针对该难题,已有的方法可分为两大类,一类通过超分辨谱估计方法使舰船目标显现[4],然而,该类方法得到的多普勒谱是伪谱,各谱峰的幅度所代表的物理含义(功率或能量)的可信度有所损失,因此由该多普勒谱得到的检测结果可信度较低;另一类通过准确的海杂波抑制提高舰船目标的信杂噪比(Signal-to-Clutter-plus-Noise Ratio, SCNR),从而改善检测性能,因此,该类方法更受关注。
现有的海杂波抑制方法按原理可分为3类:1)基于参数估计的时域对消方法[5- 6];2)基于最优滤波的方法[7- 8];3)基于子空间分解的方法[9-16]。第1类方法以Root法[5]为代表,通过准确估计各海杂波多普勒频率分量的幅度、多普勒频率和初相,然后在时域中重构,最后用原信号减去这些海杂波分量,该类方法的不足在于海杂波分量与舰船目标信号分量之间缺少可信有效的区别准则,从而易造成海杂波对消不充分导致虚警,或海杂波对消过分导致漏警的情况。第2类方法需以海杂波和舰船目标信号为先验信息,虽然前者通过已有数据可估计得到,但后者在实际情况下很难获得。第3类方法以奇异值分解(Singular Value Decomposition, SVD)算法[9]、特征值分解(Eigen Value Decomposition, EVD)算法[10-11](文献[10]和[11]提出的两种方法有所不同,为方便区分,本文中分别将其称为EVD1算法和EVD2算法)、改进的EVD(Modified EVD, MEVD)算法[12]、高阶奇异值分解(High-Order SVD, HOSVD)算法[13-14]和通过相关性估计杂波(Estimate Clutter Via Correlation, ECVC)算法[15]为代表,该类方法不需要任何先验知识,利用海杂波与舰船目标信号在空间相关性上的差异,实现海杂波抑制,其中HOSVD算法对舰船目标的SCNR增益(Improvement of SCNR, ISCNR)最大[16],而EVD2算法和ECVC算法虽然有自适应机制,但它们对舰船目标的ISCNR往往不能令人满意。
针对以上方法的不足,本文提出一种OTHR短CIT条件下的自适应舰船目标检测方案,即综合峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)-HOSVD算法和改进的正交匹配追踪(Modified Orthogonal Matching Pursuit, MOMP)算法的PHM方案,该方案采取先海杂波抑制然后检测舰船目标的两步策略。本文章节安排如下:第2节分析OTHR海面回波信号模型与特性;第3节提出PHM自适应舰船目标检测方案;第4节对PHM方案的性能进行理论与仿真分析和实测数据验证;第5节总结全文。
2 OTHR海面回波信号模型与特性
在OTHR单个海面分辨单元的回波信号中,主要含有海杂波分量、可能存在的舰船目标信号分量和噪声[17]。其中,海杂波主要包括一阶分量和高阶分量,而高阶分量中对舰船目标有影响的主要是二阶分量,舰船目标则主要考虑大中型舰船目标。通常,一阶海杂波在多普勒频域中表现为两个尖峰,它们的多普勒频率为
(1)
其中fR和λR分别表示OTHR工作频率和波长, fB的单位为Hz, fR的单位为MHz,β表示入射电磁波与海面间的夹角,νc表示海面洋流的径向速度。二阶海杂波在多普勒频域表现为一阶海杂波附近的带状分布。舰船目标则表现为单个尖峰,其多普勒频率与其径向速度成线性关系。在能量方面,通常一阶海杂波最强,大中型舰船目标与二阶海杂波相当。
OTHR接收信号在经波束形成、脉冲压缩处理后,可获得大量不同方位(通道)和距离分辨单元的回波信号,任意距离分辨单元的回波信号可表示为
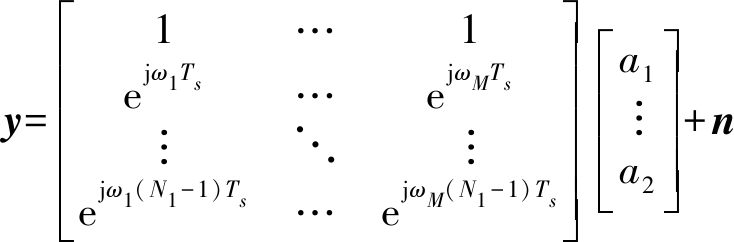
=Φa+n=c+s+n
(2)
其中{ω1,ω2,…,ωM}和{a1,a2,…,aM}分别表示M个多普勒频率分量(包括舰船目标多普勒频率分量和海杂波多普勒频率分量)的多普勒频率和幅度,Ts和N1分别表示慢时间采样间隔和采样点数,c、s和n分别表示海杂波分量、舰船目标信号分量和噪声分量。
在一段CIT内,通常电离层状态和海面检测子区内的海态均保持平稳,且海面检测子区内不同海面分辨单元处的海态是相近的。因此,一次相干积累处理后,OTHR接收到的同一检测子区内不同海面分辨单元信号中的海杂波的相关性较强,文献[18]的研究指出相邻海面分辨单元回波信号间的相关系数可达0.8～0.9。而舰船目标仅存在于某一个或若干个相邻的海面分辨单元中,因此舰船目标信号分量的空间相关性较差。舰船目标信号分量和海杂波分量之间空间相关性的差异,是子空间分解类海杂波抑制算法能够有效地利用多个海面分辨单元信号抑制海杂波的理论依据。
3 PHM自适应舰船目标检测方案
3.1 PHM方案概述
PHM自适应舰船目标检测方案的原理框图如图1所示,主要分为基于PSNR-HOSVD算法的海杂波抑制和基于MOMP算法的舰船目标检测两个部分。在海杂波抑制过程中,PSNR-HOSVD算法在有效保留舰船目标信号分量的前提下,将输入信号中的海杂波分量自适应地抑制掉,使输出结果中仅包含舰船目标信号、噪声和能量较小的剩余海杂波方位-距离-多普勒频率(Range-Doppler, RD)分量。此时海杂波抑制输出信号在方位-RD域中严格稀疏,因此在舰船目标检测时,PHM方案采用本质上为贪婪类稀疏重构算法的MOMP算法对舰船目标信号分量(即稀疏信号分量)进行重构。由于贪婪算法的机制特点,将迭代截止条件设置为重构信号分量的SCNR超过CFAR检测阈值,舰船目标信号分量的重构和检测在本质上成为同一过程,迭代停止后的重构结果即检测结果。
3.2 PSNR-HOSVD自适应海杂波抑制算法
设OTHR当前检测子区的回波信号经脉冲压缩和波束形成后,包含Θ个方位、每个方位中包含R个距离分辨单元,相干积累点数为N1,则该子区的回波信号可用3阶张量
表示。HOSVD可表示为
(3)
其中
表示核张量,
表示张量与矩阵的模式z乘积,如
表示Y(z)的左奇异向量矩阵,Y(z)为
的第z等效模式展开矩阵。张量和其第3等效模式展开矩阵Y(3)∈CN1×ΘR的结构如图2所示。
由图2(b)可见,第3等效模式展开矩阵Y(3)的各列为各个海面分辨单元的回波信号,结合式(3)可知,Y(3)的左奇异向量矩阵U3为各个海面分辨单元回波信号的一个标准正交基,与式(2)中的Φ相似。U3中的各列,即左奇异向量u3,i,(1≤i≤N1),按照其对应奇异值的大小降序排列,而奇异值的大小正是整个接收数据中各分量能量的正平方根。根据第1节中海杂波特性的分析,由于海杂波在整个检测子区内是强相关的,而舰船目标信号分量则相反,所以可利用下式进行海杂波抑制
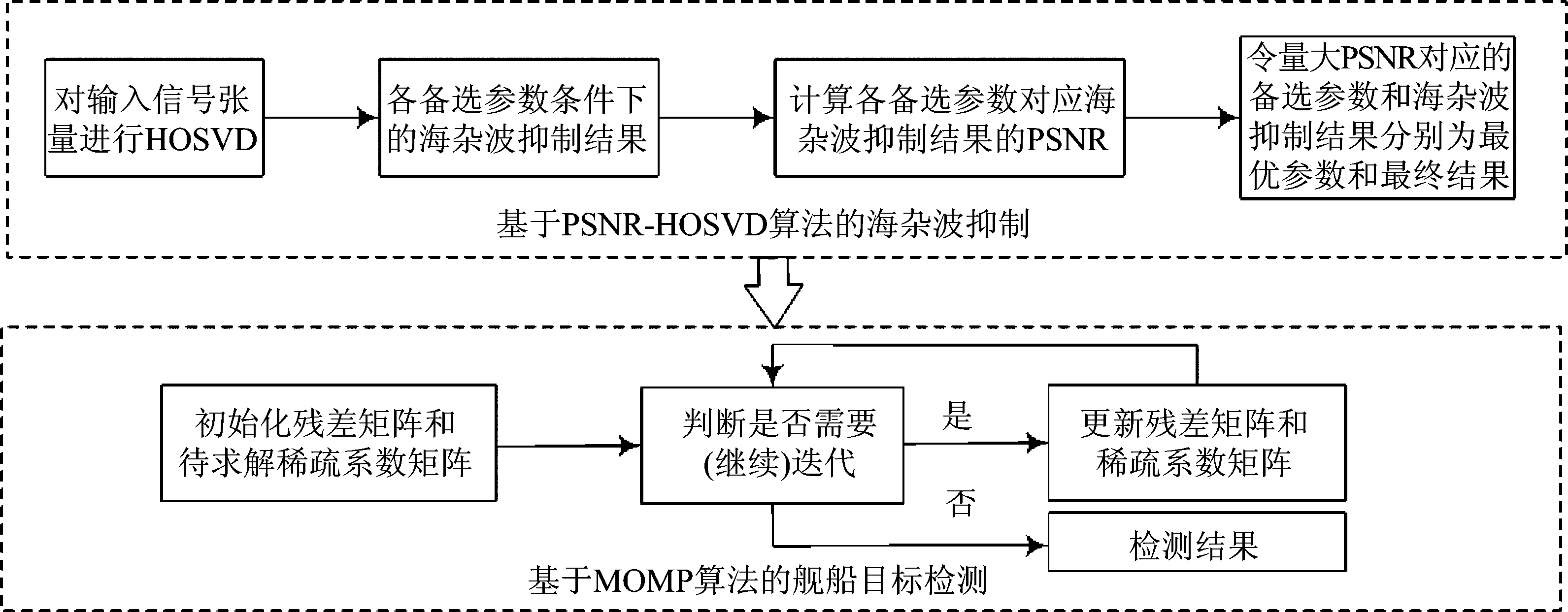
图1 PHM自适应舰船目标检测方案原理框图
Fig.1 The principle diagram of the PHM adaptive ship target detection scheme
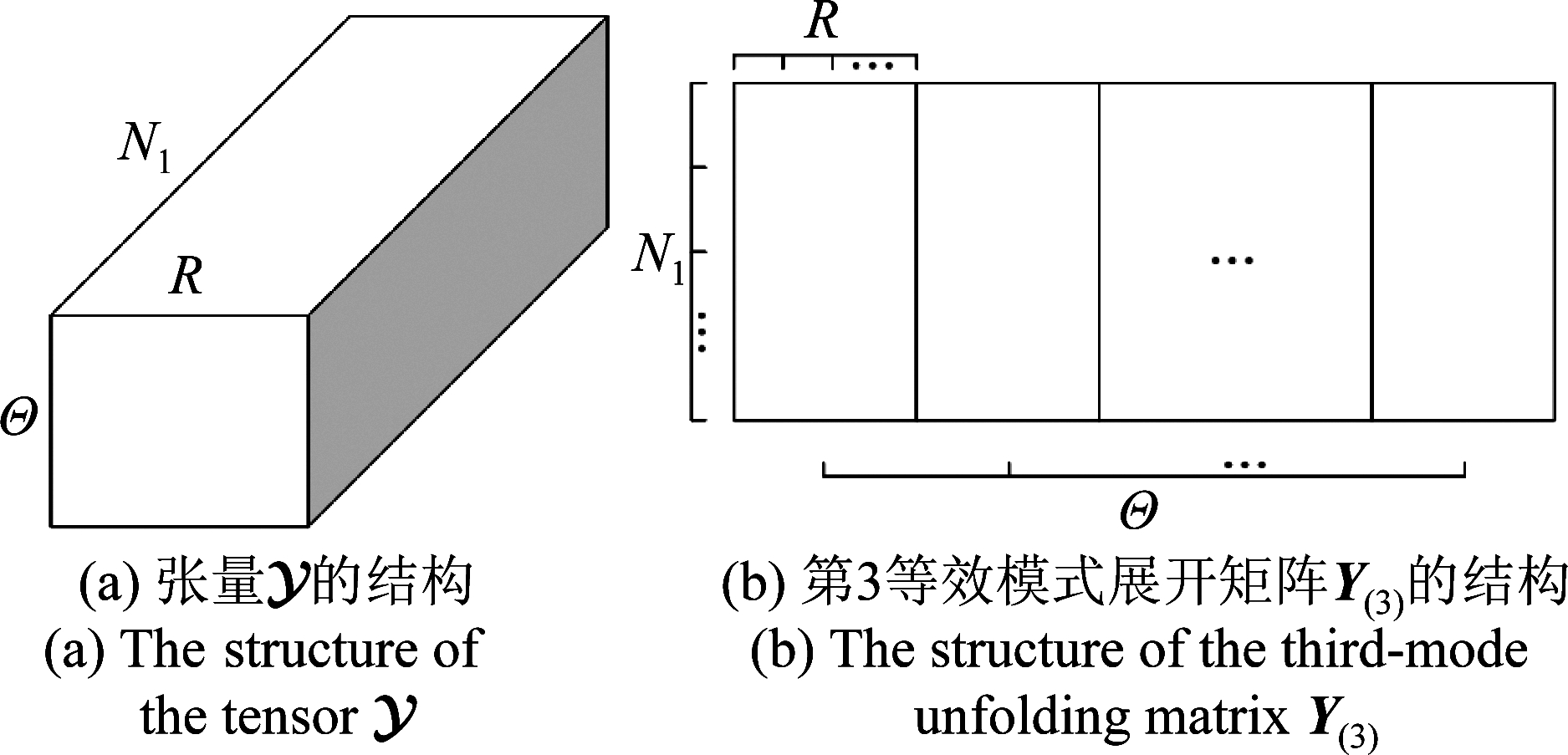
图2 张量
和其第3等效模式展开矩阵Y(3)的结构
Fig.2 The structures of the tensor and the third-mode unfolding matrix Y(3)
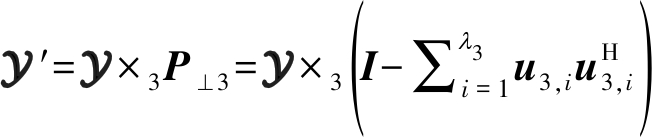
(4)
其中P⊥3表示投影矩阵,
表示海杂波抑制后的数据张量,λ3表示张成海杂波子空间的对应较大奇异值的左奇异向量个数。
PSNR-HOSVD算法仅利用第三等效模式展开矩阵的左奇异向量构造投影矩阵,区别于文献[13-14]中基于HOSVD的海杂波抑制算法中利用三个等效模式展开矩阵的左奇异向量分别构造三个投影矩阵。事实上,海杂波分量在另外两个等效模式展开矩阵的列空间中并不具有聚集特性,依据文献[9]的理论分析,将各等效模式展开矩阵与SVD方法中的Hankel矩阵相比较可知,仅第3等效模式展开矩阵Y(3)的左奇异向量矩阵可与式(2)中的Φ对应,因此由另外的两个等效模式展开矩阵的左奇异向量构造的投影矩阵不能够对海杂波进行针对性的抑制。
由式(4)可见,如何选取参数λ3,将直接影响海杂波抑制的结果。为了获取最优参数λ3,引入常应用于图像处理中描述处理前后两幅图像相似程度的PSNR[19],其定义为
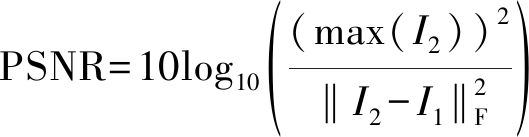
(5)
其中I1和I2分别表示处理前和处理后的两帧图像,“max(·)”表示求最大值运算,“‖·‖F”表示矩阵的Frobenius范数运算。
然后构造备选参数集,计算每个备选参数对应海杂波抑制结果及其PSNR,挑选各PSNR中的最大值对应的备选参数为最优参数,同时与其对应的海杂波抑制结果即为最终的海杂波抑制结果。
在本文应用环境中,计算不同备选参数下海杂波抑制结果的PSNR时,为减小计算复杂度,根据矩阵奇异值特性,式(5)可改写为
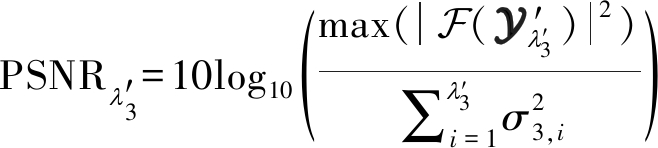
(6)
其中
表示备选参数,σ3,i为第3等效模式展开矩阵Y(3)的第i个奇异值,
表示与备选参数对应的海杂波抑制结果,“|·|”表示取绝对值运算,“F(·)”表示傅里叶变换。需要说明的是,由于张成海杂波的左奇异向量数量较少,所以备选参数只从1选取到int(N1/2),以减少不必要的计算复杂度。
通过令PSNR最大选取最优参数λ3的合理性在于,在备选参数逐渐增大的过程中,张量中被抑制的主分量逐渐从强海杂波分量过度到包括舰船目标信号分量在内的弱噪声分量。在强海杂波分量抑制阶段,式(6)等号右边取对数项中分子的减小速度远小于分母的减小速度,因此PSNR具有增大的趋势,而随着备选参数的继续增大,当舰船目标信号分量也被抑制后,张量中仅剩噪声,此时式(6)中取对数项中分子大幅下降,此后PSNR明显减小。因此,随着备选参数的逐渐增大,PSNR有先增大后减小的趋势,而令PSNR最大的备选参数,即能够使海杂波被充分抑制、同时舰船目标被尽量保留的最优参数。需要说明和指出的是,在PSNR达到最大值之前和之后,均可能不具有单调性,因此选取其最大值不能采取找拐点的方式。另外,在整个处理过程中,由于是对整个数据张量进行子空间分解,所以第3等效模式展开矩阵Y(3)的各奇异值代表的是整个矩阵Y(3)中各多普勒频率分量能量的平方根。同时由于舰船目标仅存在于某一个或较少个连续的距离分辨单元中,而海杂波多普勒频率分量则是高度空间相关的,即海杂波多普勒频率分量存在于多通道、多距离分辨单元中,所以许多比舰船目标信号能量低的海杂波通道-RD分量对应的奇异值大于舰船目标信号分量对应的奇异值,进而在PSNR-HOSVD处理结果的RD谱中,大量的比舰船目标能量低的海杂波谱峰已被抑制,而舰船目标仍能得以保留。
PSNR-HOSVD自适应海杂波抑制算法步骤可归纳如下:
1)构造备选参数集
并将其中的各个参数分别代入式(4),计算出与各个备选参数相对应的海杂波抑制后的数据张量
2)利用傅里叶变换将各个
变换到多普勒频域,得到
3)按式(6)计算各个备选参数
对应的
4)在所有的
中选出最大值,并选取其对应的
和分别作为最优参数λ3和最终的海杂波抑制后的数据张量
3.3 MOMP舰船目标检测算法
理论上,PSNR-HOSVD算法处理后得到的在RD域中严格稀疏,仅含有舰船目标信号和极少量的海杂波剩余谱峰。因此,可利用稀疏重构算法提高舰船目标的多普勒频率准确度,同时改善舰船目标的检测量SCNRD。需要说明的是,本文中使用的SCNR和SCNRD是两个不同的量,图3为它们在实测数据的中的示意图,它们分别定义如下
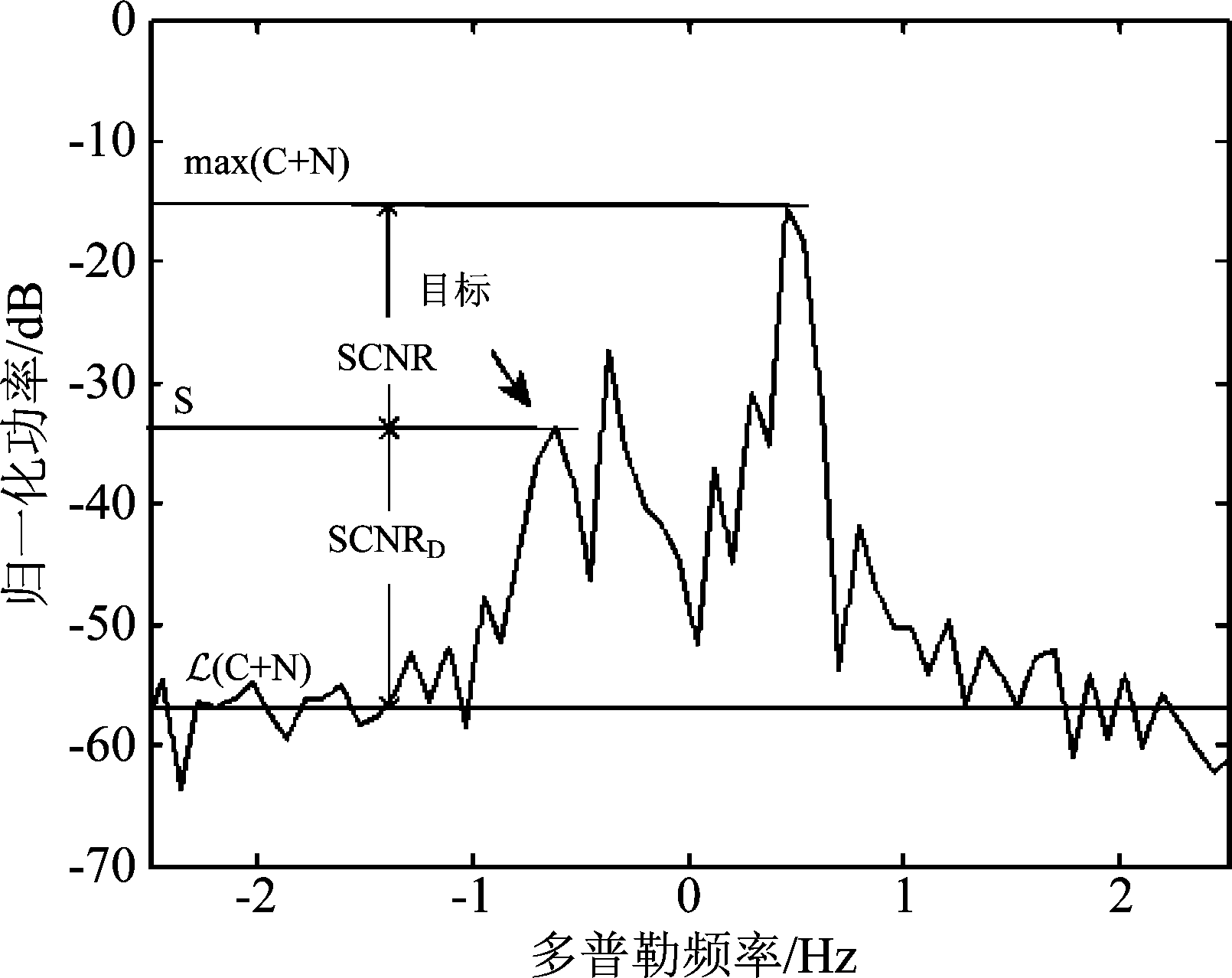
图3 SCNR和SCNRD
Fig.3 The SCNR and SCNRD
SCNR=S-max(C+N)
(7)
(8)
其中S表示RD谱中(对数尺度上)舰船目标的幅度,max(C+N)表示RD谱中除舰船目标外的最大幅度,
表示RD谱中杂波加噪声(即检测背景)基底,用排序统计的方式求取。SCNR描述的是RD谱中舰船目标与最强杂波加噪声之间的强弱关系(在海杂波抑制前主要刻画舰船目标与杂波之间的关系,而在海杂波抑制之后,刻画的可能是舰船目标与噪声之间的关系),而SCNRD描述的则是最终舰船目标被成功检测的难易程度。
考虑到矩阵在RD域中的稀疏度未知,且最终舰船目标检测以SCNRD为检测量,因此提出一种MOMP算法进行稀疏重构,同时完成舰船目标检测任务。
由于MOMP算法的处理对象是某一通道内多个连续的距离分辨单元回波信号,所以在本节中将三阶张量拆分为Θ个代表各个通道接收信号的矩阵Y′θ,(1≤θ≤Θ)分别进行处理,同时为方便表示,本节后文中所有符号均省去下标“θ”。
在MOMP算法中,首先构造超完备(冗余)字典Φ′∈CN1×N2,(N1<N2)如下
(9)
其中t1=[0,Ts,2Ts,…,(N1-1)Ts]表示采样时间序列,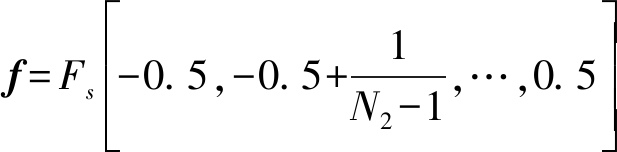
表示多普勒频率序列,系数
使字典Φ′中的各列(基向量)的l-2范数为1。
按照稀疏重构理论框架[20],Y′可表示为如下形式
Y′=[y′1,y′2,…,y′R]=
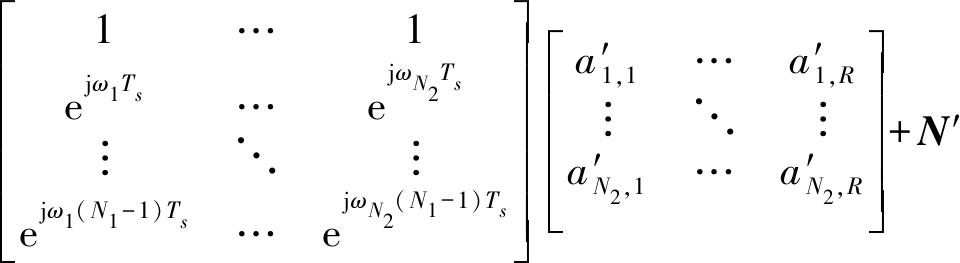
=Φ′Α′+Ν′
(10)
其中Α′∈CN2×R表示待求解的稀疏矩阵,其中的大部分元素为零,
表示杂波加噪声。
然后采取贪婪迭代的方式计算Α′,每次迭代更新Α′中一个元素,初始残差矩阵Re0=Y′,初始
其中[0]表示零矩阵。在第j次迭代中,令
(11)
然后单独更新其中的某一个元素
(12)
其中“Max”表示对矩阵中所有元素取最大值并提取其索引,需要说明的是,采用式(12)更新元素与传统的OMP算法中更新元素的方式在形式上有所区别,但本质上相同,均为采用最小二乘方法使残差最小,而式(12)之所以暗含这一原理,是因为MOMP算法中超完备字典Φ′中各列的l-2范数为1。
残差矩阵仅需更新第r列,即
Rej=Rej-1
(13)
(14)
其中“vec(·)”表示取列(或行)运算,例如vec(Re·,l)表示矩阵Re的第l列。然后判断迭代终止条件是否满足,若不满足,进入下一次迭代。
由于最终进行检测的RD谱可表示为
=20 log10(|(Φ′)H(Φ′Α′+Ν′)|)=20 log10(|Α′+(Φ′)HΝ′|)
(15)
所以MOMP算法在迭代更新稀疏矩阵Α′过程中,只需更新出SCNRD大于检测阈值Tr的元素即可。那么,迭代停止条件可设置为
(16)
其中Nnoise表示对数尺度上的杂波加噪声(基底)电平,由于式(9)定义的字典相比傅里叶变换矩阵多了系数
因此Nnoise的求取可以先利用排序统计的方式计算Y′θ在RD谱中的杂波加噪声基底,然后减去20log10(N1)获得。
MOMP舰船目标检测算法步骤可归纳如下:
1)初始化:按式(9)构建超完备字典Φ′,Re0=Y′θ,计算Y′θ的杂波加噪声电平
2)进入迭代计算:按照式(12)计算
判断不等式(16)是否成立,如果成立,停止迭代,否则继续;
3)在第j次迭代中,按照式(11)和式(12)更新
4)按照式(13)和式(14)更新Rej,返回步骤2)。
3.4 PHM计算复杂度分析
基于PSNR-HOSVD的海杂波抑制算法在子空间分解过程中仅对第3等效模式展开矩阵Y(3)进行SVD,其计算复杂度为
而在确定最优参数λ3的过程中,需要多计算int(N1/2)个PSNR,即对式(4)和式(6)重复计算int(N1/2)次,其中由于式(6)的计算相对简单,所以计算复杂度集中在式(4)上,计算复杂度约为
可见,由自适应挑选最优参数λ3多引入的计算复杂度相比HOSVD分解的计算复杂度,在数量级上低一级,其可以并入到O(R6)项中,因此,基于PSNR-HOSVD的海杂波抑制算法的计算复杂度为
算法的计算采用贪婪类迭代的方式,单次迭代计算复杂度约为N1N2R,由于通常情况下每个通道中仅有较少个RD分量被重构,因此MOMP的计算复杂度为
即使多个通道均考虑在内,MOMP算法的计算复杂度在数量级上仍远低于PSNR-HOSVD算法,因此PHM算法的计算复杂度为
4 仿真分析与实测数据验证
本节中,分别基于一帧仿真数据和一帧实测数据,对PHM方案的性能进行分析和验证。采用3个指标反映PHM方案的性能,它们分别为反映海杂波抑制性能的ISCNR,反映舰船目标检测性能改善的ISCNRD,以及反映重构舰船目标信号多普勒频率准确度的多普勒频率误差ef,它们的定义式分别如下
ISCNR=SCNRout-SCNRin
(17)
ISCNRD=SCNRD_out-SCNRD_in
(18)
ef=fd_sout-fd_sin
(19)
其中下标“out”和“in”分别表示输出和输入, fd_s表示舰船目标在多普勒谱中的多普勒频率。
4.1 仿真分析
考虑一帧仿真数据,分析不同相干积累点数对PHM方案性能的影响。首先构建维度为Θ×R×N1=5×40×128的海杂波数据,每个距离分辨单元中用两个单频信号分别表示正负一阶海杂波,加入噪声,CNR为64.6 dB,同时随机挑选一个距离分辨单元,在非海杂波区随机加入一个用单频信号表示的舰船目标,舰船目标的输入SCNR和SCNRD分别为-35.8 dB和28.8 dB,多普勒频率为-0.89 Hz。然后进行时域截取,所得数据的相干积累点数为N1∈{32,34,…,96}。最后采用PHM方案对这些数据分别进行处理(MOMP算法中采用的检测阈值Tr略小于舰船目标的输入SCNRD,为28.0 dB)。处理结果表明,舰船目标均能被成功检测,PSNR-HOSVD海杂波抑制算法处理后的ISCNR、MOMP检测算法处理后ISCNRD和多普勒频率误差ef如图4所示。由图可见,PSNR-HOSVD海杂波抑制算法处理后的ISCNR均保持在40.0 dB以上,均值为54.1 dB;海杂波抑制结果经MOMP算法处理后的ISCNRD均值为4.0 dB;ef始终为0 Hz。3个指标表明PHM方案的性能较为理想。
4.2 实测数据验证
本节考虑一帧实测数据进行PHM方案的性能验证,采用同样具有自适应机制的EVD2和ECVC两种同类算法分别加CFAR检测器构成方案1与方案2,作对比分析。采用的实测数据原本的维度为Θ×R×N1=5×40×128,对应的CIT为13.0 s,为长CIT,通道1中第31个距离分辨单元中存在一个舰船目标,其多普勒频率为-0.68 Hz,输入SCNR和SCNRD分别为-12.4 dB和38.6 dB,然后对该数据在时域中进行截取,获得的短CIT数据的维度为Θ×R×N1=5×40×64。对应CIT为6.5 s,舰船目标的多普勒频率变为-0.62 Hz,输入SCNR和SCNRD分别变为-13.9 dB和29.3 dB,可见短CIT导致舰船目标的多普勒频率发生偏差,且SCNR和SCNRD均由于相干积累增益的降低而有所降低。长、短CIT条件下通道1的RD谱和舰船目标所在距离分辨单元的多普勒谱如图5所示。分别应用方案1、方案2和PHM方案对该短CIT数据进行处理,海杂波抑制结果如图6所示。由图可见,EVD2算法的处理结果中海杂波剩余较多,ECVC算法的处理结果中海杂波和舰船目标信号均被抑制,而PSNR-HOSVD算法的海杂波抑制较为彻底,同时舰船目标信号也得到了保留,三种算法的输出SCNR分别为-6.9 dB、-6.5 dB和11.1 dB,ISCNR分别为7.0、7.4和25.0 dB。令舰船目标检测阈值Tr为28.0 dB,三种方案经舰船目标检测后的结果如图7所示,方案1和方案2中的舰船目标都未被成功检测,且方案1结果中出现较多虚警;而PHM方案则能够成功检测出舰船目标,无虚警,舰船目标的多普勒频率为-0.68 Hz,与原长CIT条件下舰船目标的多普勒频率一致,重构出的舰船目标信号的输出SCNRD(由于海杂波已经被抑制的较为彻底,所以在MOMP算法处理中无海杂波分量被重构)为36.7 dB,ISCNRD达7.4 dB。可见,PHM在实测数据条件下具有较为理想的性能。
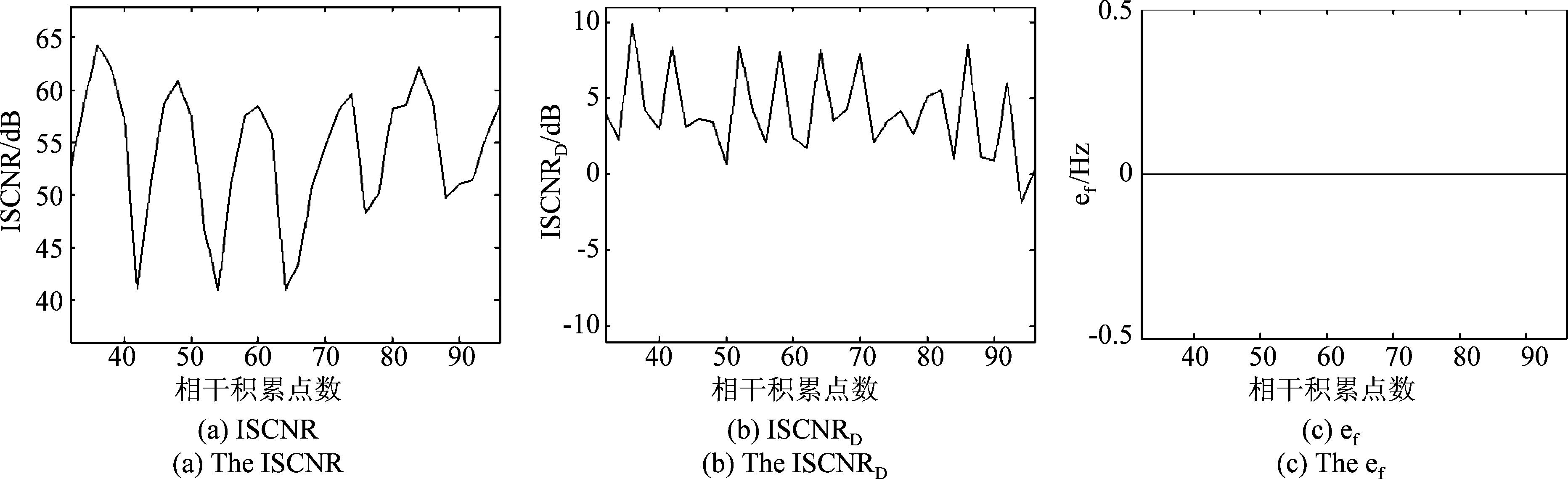
图4 仿真实验结果
Fig.4 The results of simulation experiments
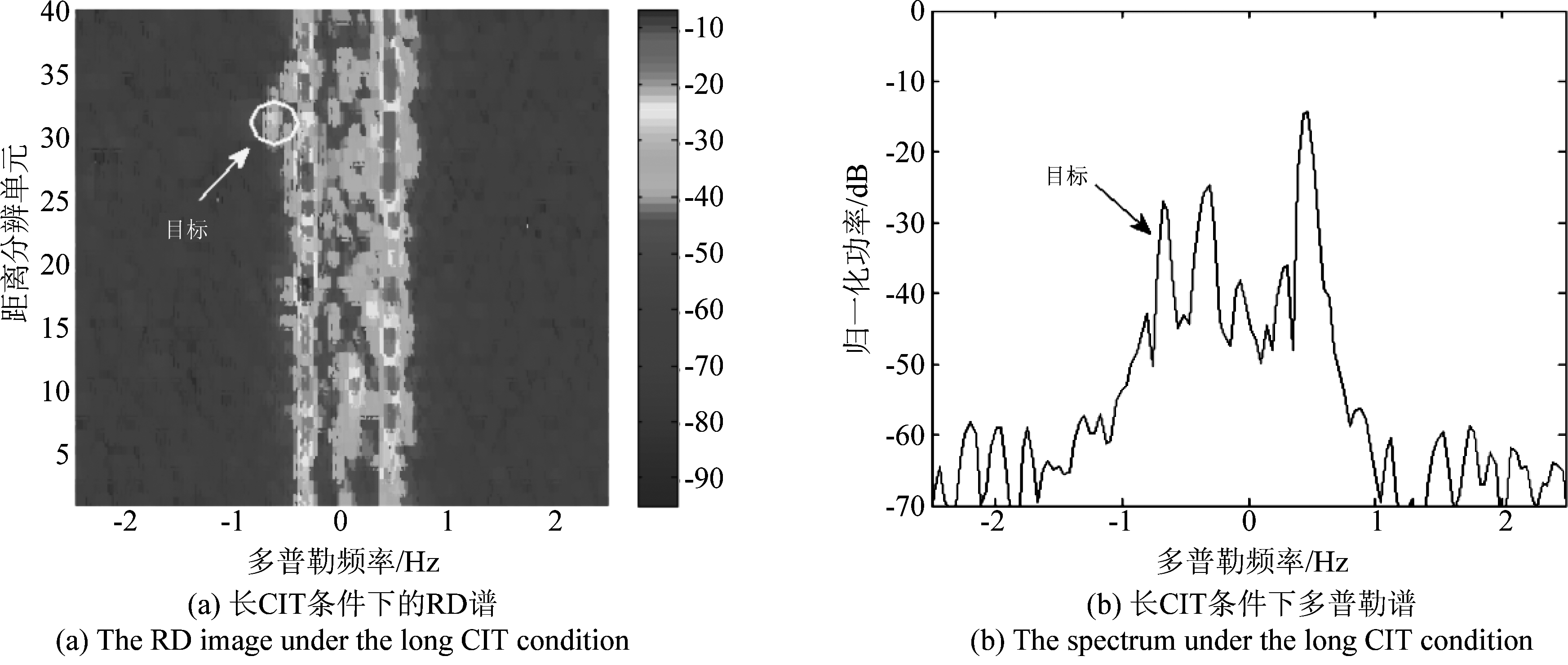
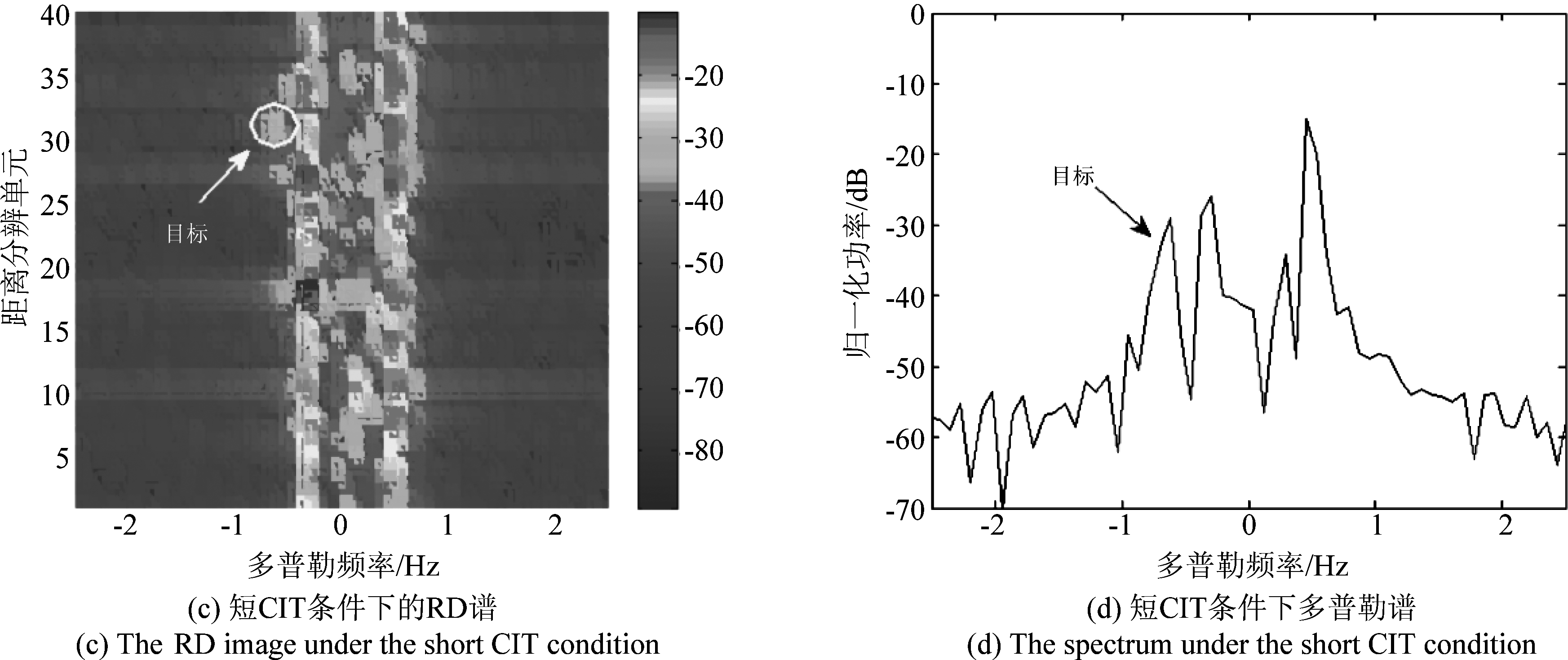
图5 长、短CIT条件下通道1的RD谱和舰船目标所在距离分辨单元的多普勒谱
Fig.5 The RD images and the spectra of the range cell within ship target under the long and short CIT condition respectively
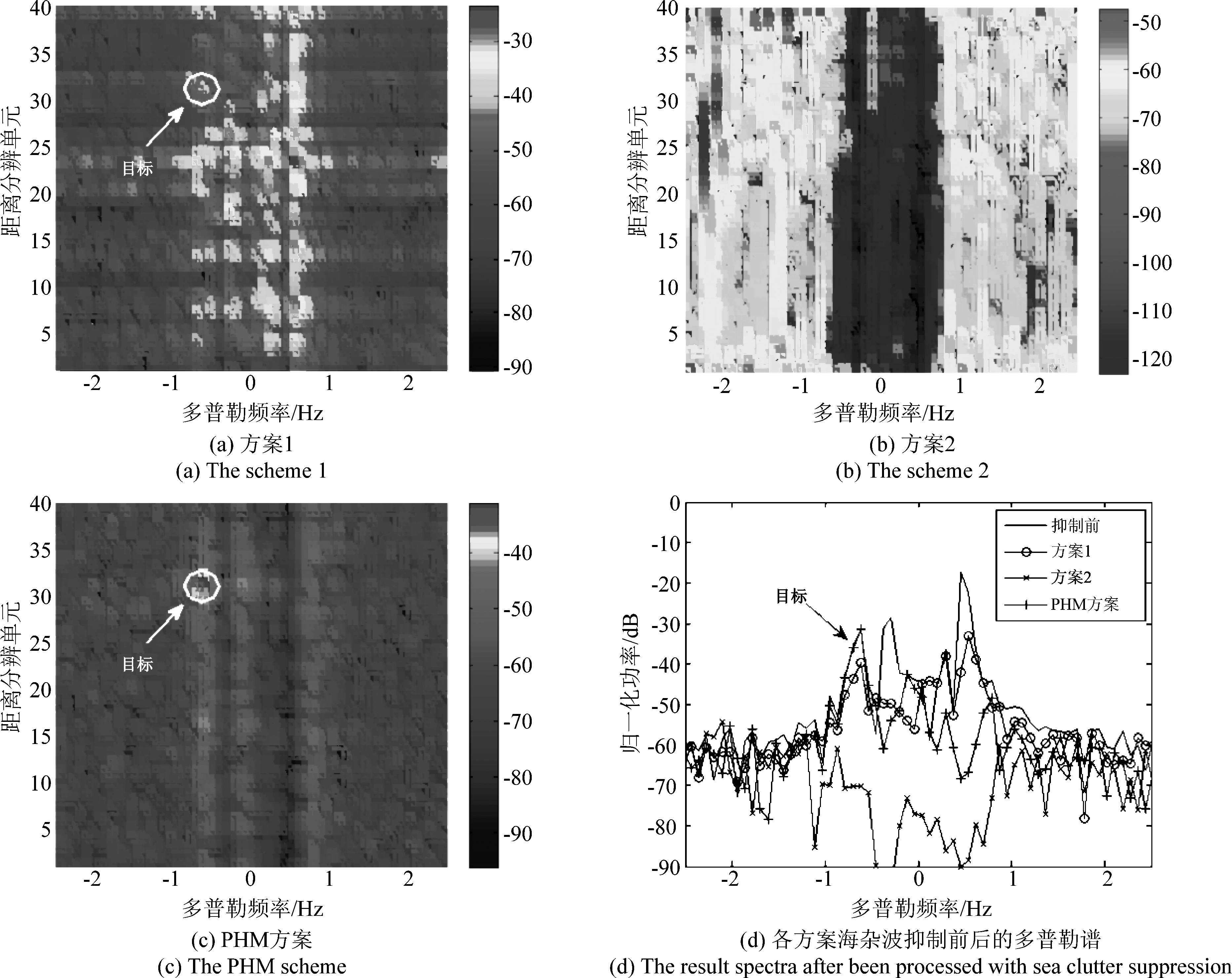
图6 各方案海杂波抑制后的RD谱和抑制前后的多普勒谱
Fig.6 The RD images and the spectra of the range cell within ship target after been processed with sea clutter suppression of the schemes
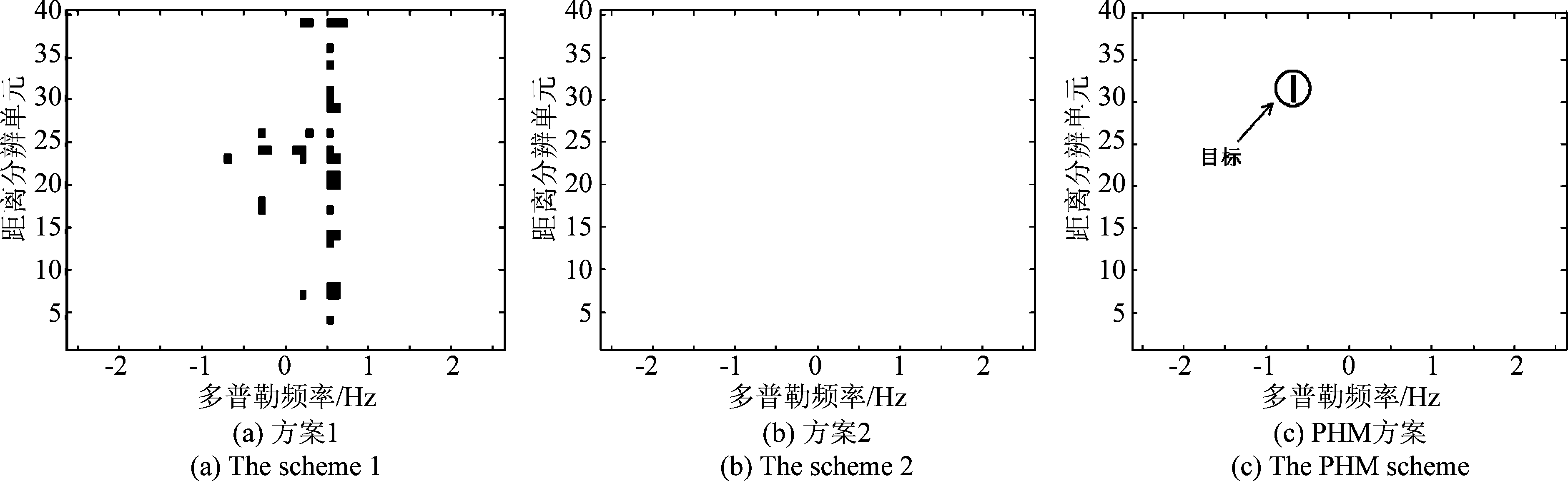
图7 各方案舰船目标检测结果
Fig.7 The detection results of the schemes
5 结论
针对OTHR短CIT条件下舰船目标检测的难题,本文提出一种PHM自适应方案,该方案采取了先抑制海杂波,然后同时重构和检测舰船目标信号的方式。在PHM方案中,PSNR-HOSVD算法是在HOSVD算法的基础上,通过引入PSNR参量并改进其计算方式,在引入较小计算复杂度的基础上实现最优预设参数的自适应确定,从而达到海杂波自适应抑制的目的;舰船目标检测则通过MOMP算法,同步完成舰船目标信号的稀疏重构与检测两个任务,从而提升舰船目标信号的输出SCNRD和多普勒频率准确度。本质上,PHM首先利用PSNR-HOSVD减少最终检测的虚警率,然后利用MOMP算法改善舰船目标的检测概率,同时改善舰船目标检测结果的多普勒频率准确度。仿真分析和实测数据处理结果表明,PHM方案可有效地改善在短CIT条件下OTHR对舰船目标的检测性能。
[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 6-10.
Zhou Wenyu, Jiao Peinan. Over-the-horizon radar technology[M]. Beijing: Publishing House of Electronics Industry, 2008: 6-10.(in Chinese)
[2] 罗欢, 陈建文, 鲍拯. 电离层和海态对天波雷达多普勒谱的影响[J]. 信号处理, 2014, 30(5): 489- 497.
Luo Huan, Chen Jianwen, Bao Zheng. Effect of ionosphere and oceanic state on Doppler spectrum of over the horizon radar[J]. Journal of Signal Processing, 2014, 30(5): 489- 497.(in Chinese)
[3] Fabrizio G A. High Frequency over-the-horizon radar[M]. New York: McGraw-Hill, 2013: 279-290.
[4] Martin R J, Kearney M J. Remote sea current sensing using HF radar: an autoregressive approach[J]. IEEE Journal of Oceanic Engineering, 1997, 1.22(1): 151-155.
[5] Root B. HF-over-the-horizon radar ship detection with short dwells using clutter cancellation[J]. Radio Science, 1998, 33(4): 1095-1111.
[6] 严韬, 陈建文, 鲍拯. 一种基于压缩感知的天波超视距雷达短时海杂波抑制方法[J]. 电子与信息学报, 2017, 39(4): 945-952.
Yan Tao, Chen Jianwen, Bao Zheng. Sea clutter suppression method for over-the-horizon radar with short coherent integration time based on compressed sensing[J]. Journal of Electronics and Information Technology, 2017, 39(4): 945-952.(in Chinese)
[7] 曹健, 王兆祎, 胡进峰, 等. 基于知识辅助的天波雷达海杂波抑制方法[J]. 系统工程与电子技术, 2018, 40(3): 533-537.
Cao Jian, Wang Zhaoyi, Hu Jinfeng, et al. Knowledge-aided ocean clutter suppression for sky-wave radar[J]. Systems Engineering and Electronics, 2018, 40(3): 533-537.(in Chinese)
[8] Hu Jinfeng, Jian Cao, Zhuo Chen, et al. Knowledge-aided ocean clutter suppression method for sky-wave over-the-horizon radar[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(3): 355-358.
[9] Poon M W Y, Khan R H, Le-Ngoc S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE Transactions on Signal Processing, 1993, 41(3): 1421-1425.
[10] 蔚娜, 李雪, 李铁成. 基于特征分解的多模杂波抑制方法[J]. 电波科学学报, 2016, 31(1): 85-90.
Wei Na, Li Xue, Li Tiecheng. An eigenvalue decomposition based method for suppressing multi-mode clutter[J]. Chinese Journal of Radio Science, 2016, 31(1): 85-90.(in Chinese)
[11] Wang G, Xia X, Root B T, et al. Maneuvering target detection in over-the-horizon radar using adaptive clutter rejection and adaptive chirplet transform[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 292-298.
[12] 赵志国, 陈建文, 鲍拯. 一种改进的OTHR自适应海杂波抑制方法[J]. 系统工程与电子技术, 2012, 34(5): 909-914.
Zhao Zhiguo, Chen Jianwen, Bao Zheng. Modified adaptive ocean clutter suppression approach in OTHR[J]. Systems Engineering and Electronics, 2012, 34(5): 909-914.(in Chinese)
[13] 薄超, 顾红, 苏卫民, 等. 基于高阶奇异值分解的天波雷达海杂波抑制算法[J]. 电波科学学报, 2014, 29(4): 715-722.
Bo Chao, Gu Hong, Su Weimin, et al. Over-the-horizon radar sea clutter suppression algorithm based on higher order singular value decomposition[J]. Chinese Journal of Radio Science, 2014, 29(4): 715-722.(in Chinese)
[14] 薄超, 顾红, 苏卫民. 基于高阶奇异值分解的OTHR海杂波抑制算法[J]. 系统工程与电子技术, 2014, 36(5): 872- 878.
Bo Chao, Gu Hong, Su Weimin. OTHR sea clutter suppression algorithm based on higher order singular value decomposition[J]. Systems Engineering and Electronics, 2014, 36(5): 872- 878.(in Chinese)
[15] Luo Huan, Xiao Hui, Yuan Jun, et al. Detection of slow radial velocity ship by OTHR[J]. Procedia Computer Science, 2018, 131(1): 551-555.
[16] 关泽文, 陈建文, 鲍拯. 天波雷达子空间分解类海杂波抑制方法评估[J]. 华中科技大学学报: 自然科学版, 2018, 46(9): 15-20.
Guan Zewen, Chen Jianwen, Bao Zheng. Performance evaluation of ocean clutter suppression methods based subspace decomposition for over-the-horizon radar[J]. Journal of Huazhong University of Science & Technology: Natural Science Edition, 2018, 46(9): 15-20.(in Chinese)
[17] 关泽文, 陈建文, 鲍拯. 天波超视距雷达海杂波模型修正与特性分析[J]. 电子与信息学报, 2017, 39(12): 2881-2888.
Guan Zewen, Chen Jianwen, Bao Zheng. Model modifying and characteristics analyzing of ocean clutter in skywave over-the-horizon radar[J]. Journal of Electronics and Information Technology, 2017, 39(12): 2881-2888.(in Chinese)
[18] 严韬, 陈建文, 鲍拯. 基于WLS的OTHR短时自适应海杂波抑制方法[J]. 华中科技大学学报: 自然科学版, 2017, 45(8): 20-25.
Yan Tao, Chen Jianwen, Bao Zheng. Adaptive sea clutter suppression method for OTHR with short coherent integration time based on weighted least square[J]. Journal of Huazhong University of Science & Technology: Natural Science Edition, 2017, 45(8): 20-25.(in Chinese)
[19] Li Qingzhong, Zhang Wandong, Li Ming, et al. Automatic Detection of Ship Targets Based on Wavelet Transform for HF Surface Wavelet Radar[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 714-718.
[20] Blanchard J, Cermak M, Hanle D, et al. Greedy algorithms for joint sparse recovery[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1694-1704.
