1 引言
波达方向(Direction Of Arrival, DOA)估计是阵列信号处理中的一个重点研究内容,其广泛应用于雷达、无线通信、声呐、电磁场等诸多军事以及民用领域[1]。随着人们不断探索,窄带信号阵列DOA估计方法有很多,其经典的几个高分辨算法有:空间分解的多重信号分类法(MUSIC)[2],旋转子空间不变法(ESPRIT)[3],最大似然估计(ML)算法[4]。 现代科技不断发展的今天,宽带雷达、宽带通信系统在实际生活中应用更加普遍,宽带信号阵列DOA估计技术的需求逐步增加,并且成为一个热门且迅速发展的研究方向。
处理宽带阵列信号的基本思想:一般是把宽带信号分割为一组不同频率的窄带信号,然后再对分割后的窄带信号进行处理并估计角度。由于不同频率使得其信号子空间也会有所不同,窄带信号DOA估计技术不能直接处理宽带信号。继而产生两类基本的宽带信号DOA估计方法:一类是非相干信号子空间算法(ISM)[5],此类算法利用各分割后窄带信号频率估计角度,而不是用宽带信号所有信息估计角度,导致分辨率不够高,且不可以处理相干信号;另一类是相干信号子空间法(CSM)[6],此算法提出“聚焦”(focusing)概念,利用聚焦矩阵把不同频率的信号空间聚焦到某一参考频率的子空间,再用窄带方法估计角度。此外,还有一些利用稀疏矩阵(sparse matrix)特性进行宽带信号DOA估计的方法[7-10],以上几类方法都需要估计协方差矩阵。
粒子滤波(Particle Filter)算法[11]是一种基于蒙特卡洛方法的顺序重要性采样法,其核心思想是通过从后验概率中抽取随机状态粒子来表达其分布。文献[12]提出了一种基于粒子滤波的宽带信号波达方向估计法,该方法利用一组随机生成的粒子对阵列流形矩阵跟踪从而进行宽带信号DOA估计,虽然解决了传统宽带DOA估计的解相干和免去求矩阵误差的问题,但是重要性权重随时间而随机递增,粒子权重集中在少数粒子上,多次迭代之后有效粒子数迅速减少,导致较大的估计误差。为解决这一问题,本文在粒子滤波时添加辅助粒子变量,通过两次重采样步骤选取粒子,使得粒子在真实状态附近分布均匀,增加了粒子多样性的同时,引导粒子向高似然区域移动,提高波达方向估计的精度。
2 宽带阵列信号模型
现有一组由M个阵元构成的均匀直线阵列,阵元之间间隔设为d,d为入射信号的最高频率对应的波长一半。 此空间内阵列接收宽带信号个数记为I,各信号入射角度记为θ1,θ2,…,θI。第m个阵元信号表示成
(1)
上式中,si(t)表示宽带信源信号,τmi是第i个源信号到达第m个阵元时相应于参考阵元的延时,表示为
(2)
c为空间中电磁波速,um(t)表示该阵元所接收的噪声,宽带信号因为存在包络延时,对式(1)采用傅里叶变换将其转化为频率域上的多个窄带信号形式
m=1,2,…,M,r=1,2,…,R
(3)
Si(fr)表示si(t)在频率fr处傅里叶系数,Um(fr)是um(t)在频率fr处的傅里叶系数。R表示宽带在频率域上分割得到的窄带个数,Xm(fr)是对第m个阵元接收到的R个快拍信号进行离散傅里叶变换后得到的频谱。下面将式(3)表示为矩阵形式
X(fr)=A(fr,θ)S(fr)+U(fr) r=1,2,…,R
(4)
其中X(fr)=[X1(fr),…,XM(fr)]T为接收数据矢量,S(fr)=[S1(fr),…,SI(fr)]T为信号矢量,V(fr)=[V1(fr),…,VM(fr)]T为噪声信号矢量,这里噪声作高斯白噪声处理,A(fr,θ)是信号方向矩阵,维数M×I,表示整个宽带的阵列流形。 其由I个形如式(5)的列矢量表示
a(fr,θi)=[e-j2πfrτ1i,e-j2πfrτ2i,…,e-j2πfrτMi]T
(5)
3 辅助粒子滤波算法
粒子滤波算法[11]是一种处理非线性非高斯状态空间模型的滤波算法,式(4)接收数据模型是随频率和波达方向而变化的非线性函数,利用粒子滤波算法处理和跟踪式(4)中目标在不同频率处阵列流形变化情况从而实现DOA估计。虽然其简单易求,在理想情况下该算法可以取得较好的性能,但是在实际中,因为粒子多样性丢失会导致算法性能较差,而辅助粒子滤波算法可以很好的解决这个问题。
辅助粒子滤波算法在粒子滤波算法基础上通过添加一个粒子选择的步骤,利用一次加权筛选得到新的粒子,使得滤波器中增加了高权值粒子,然后再进行一次加权,使得权值变化稳定。
在辅助粒子滤波算法中定义如下参数:
为参数向量,里面Sr是表示频率信号幅度,
是噪声方差,k为所估计信元个数。其观测数据似然函数表示为
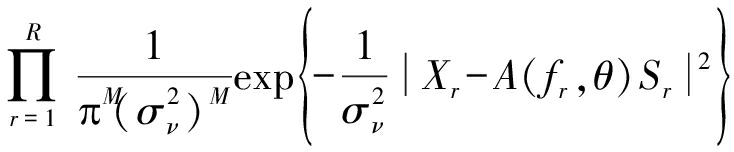
(6)
在这里当θ为已知波达角,信号的幅度Sr和噪声的方差可以由最大后验估计求
(7)
(8)
根据式(7)和(8)重新定义估计参数向量为
ψ1:R
{θ,k}
(9)
3.1 重采样
辅助粒子滤波算法需以重采样为基础,初始状态ψ0分布为p(ψ0),已知观测数据X1:R,估计后验概率密度p(ψr|X1:R),以估计参数向量ψ1:R。 若定义后验概率密度p(ψr|X1:R)由粒子集
近似表示,满足下式
(10)
其中δ是Dirac delta函数,
是频率r时的第n个粒子,
是该粒子的权值,此时频率r时的状态估计成
粒子采样最理想的方式是从后验概率密度函数中采样,但是直接从后验概率密度函数中采样非常困难,通常利用贝叶斯重要性采样法,在概率密度函数q(ψ1:r|X1:r)中进行采样,重要性密度函数可以简化为q(ψr|ψr-1,Xr),它仅与r-1处的状态ψr-1和r处的观测Xr有关。如果将频率r-1时的后验概率p(ψr-1|X1:r-1)用粒子集
表示。已知频率r时的状态采样
根据贝叶斯准则得到权重更新为
(11)
虽然重采样很好的抑制了权重退化的问题,但是多数情况下还是会受低权值粒子影响,使得DOA估计中高权值粒子较少,得到结果与实际有较大偏差,而使得整体估计效果不理想,影响滤波器整体性能。为解决这一问题,引入了辅助粒子滤波算法,辅助粒子滤波算法对原粒子集中的各权值依据似然大小进行修正,使得重采样后的粒子向似然函数高值区间移动,使更接近于状态的真实值,权值方差也更小[13]。
3.2 辅助粒子算法的融合
为了获取高似然粒子进行滤波和重采样,此算法增加一个辅助变量ip,利用辅助变量标记高似然值粒子,根据频率r-1时p(ψr-1|X1:r-1)已知,则ψr-1的后验概率密度为
(12)
利用辅助变量ip定义联合密度分布函数
(13)
因为ip的加入而需要重新定义重要性采样密度函数为
(14)
式中
其中E[·]为向量求平均值函数[13]。首先计算辅助变量权重
(15)
然后进行采样步骤产生指数
再根据符合指数的采样粒子计算最终权重,最后得到最终权值
辅助粒子滤波算法的优势是2次加权重采样,使粒子权值比1次重采样的粒子权值变化更稳定。而重采样会引起粒子塌陷在某一块小区域上,由于宽带信号DOA观测期间未发生变化,因此各频率点处粒子状态是相同的,因此粒子集中在一个区域而产生的粒子枯竭对下一频率点处的估计影响较小,所以采用重采样的方式选择粒子对宽带DOA估计性能影响较小。本文基于辅助粒子滤波的宽带波达方向估计算法流程如表1。
表1 算法流程
Tab.1 Algorithm processes
上述算法利用了两次重采样,第一次重采样后将采样所得的高权值粒子标记出来,再利用高权值粒子更新粒子状态,然后再一次重采样步骤选择粒子,最后得到最终的角度估计。
4 仿真实验
仿真实验中假设有一个由10个阵元组成的均匀线阵,阵元间距设置为中心频率对应的半波长,平面内有2个角度分别为10°和14°相干的信号入射到此线阵上。仿真中粒子数N=200,假设已知信源个数,粒子的角度初始分量是从0°～20°内随机产生的,进行 100次蒙特卡洛实验。
图1是固定信噪比时两种算法随快拍数变化时均方根误差和检测概率的变化情况。
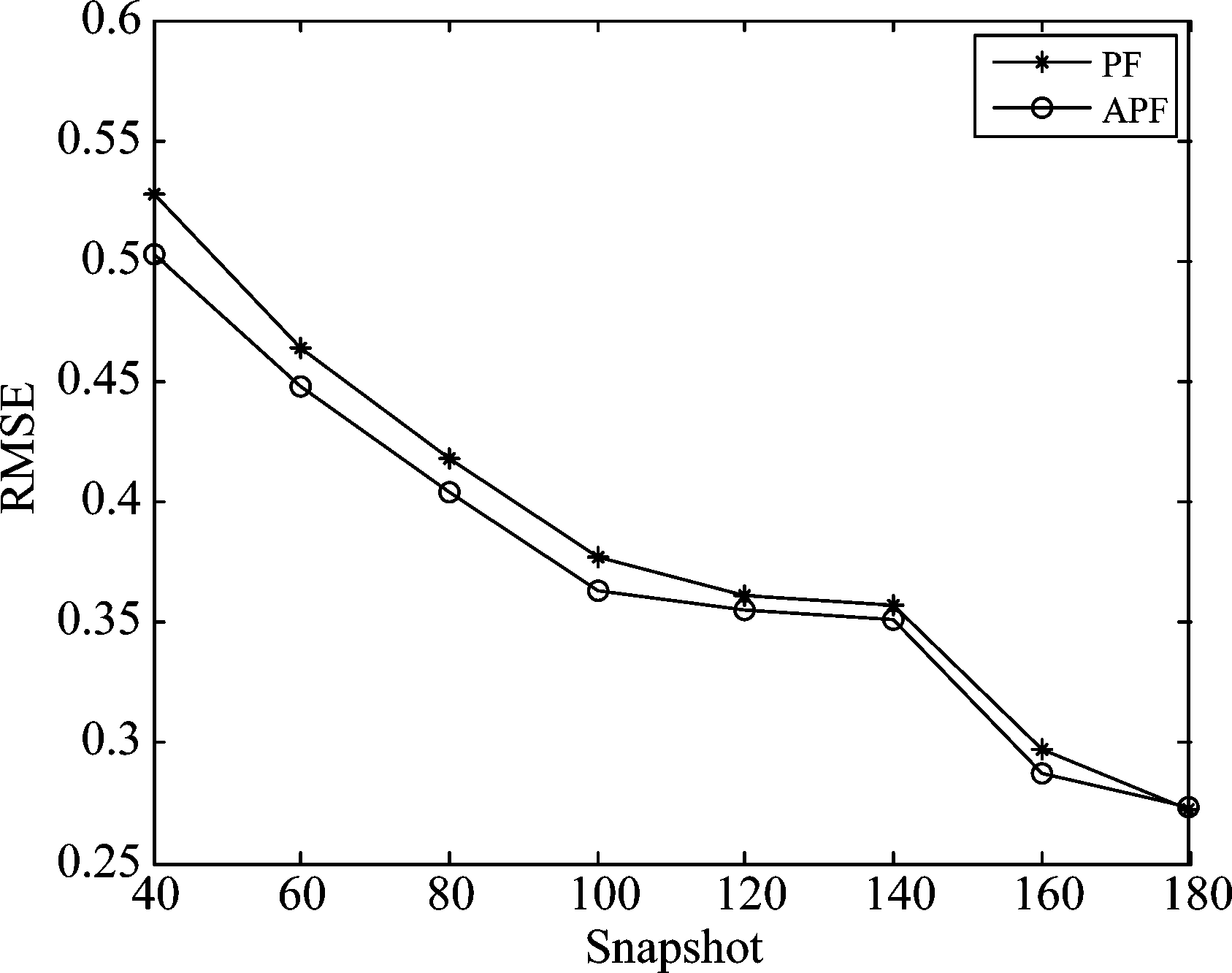
图1 RMSE随快拍数变化曲线
Fig.1 RMSE versus the snapshot
图1是固定信噪比SNR=8 dB时,均方根误差随快拍数增加而逐渐变化的仿真效果图,从图中可以看出当快拍数逐渐增加时,粒子滤波算法和辅助粒子滤波算法的均方根误差都在快速降低,可见在追求精度上两种算法都有较好的效果,但是因为辅助粒子滤波算法添加辅助变量之后使得粒子权值更加均匀,而且粒子都均匀在真实状态附近,保留更多的高权值粒子,所以均方根误差会比粒子滤波算法的均方根误差更低,精度得到进一步提高。
图2是在仿真中固定信噪比SNR=8 dB时,辅助粒子滤波算法和粒子滤波算法随着快拍数的增加检测概率的变化情况。图2反映了检测两信号的概率(若角度估计值在各自真实值1°范围内,则认为是检测到了),从图中可以看出检测概率随快拍数增加而逐步升高,而在快拍数40～80和100～180时辅助粒子滤波算法的检测概率高于粒子滤波算法。
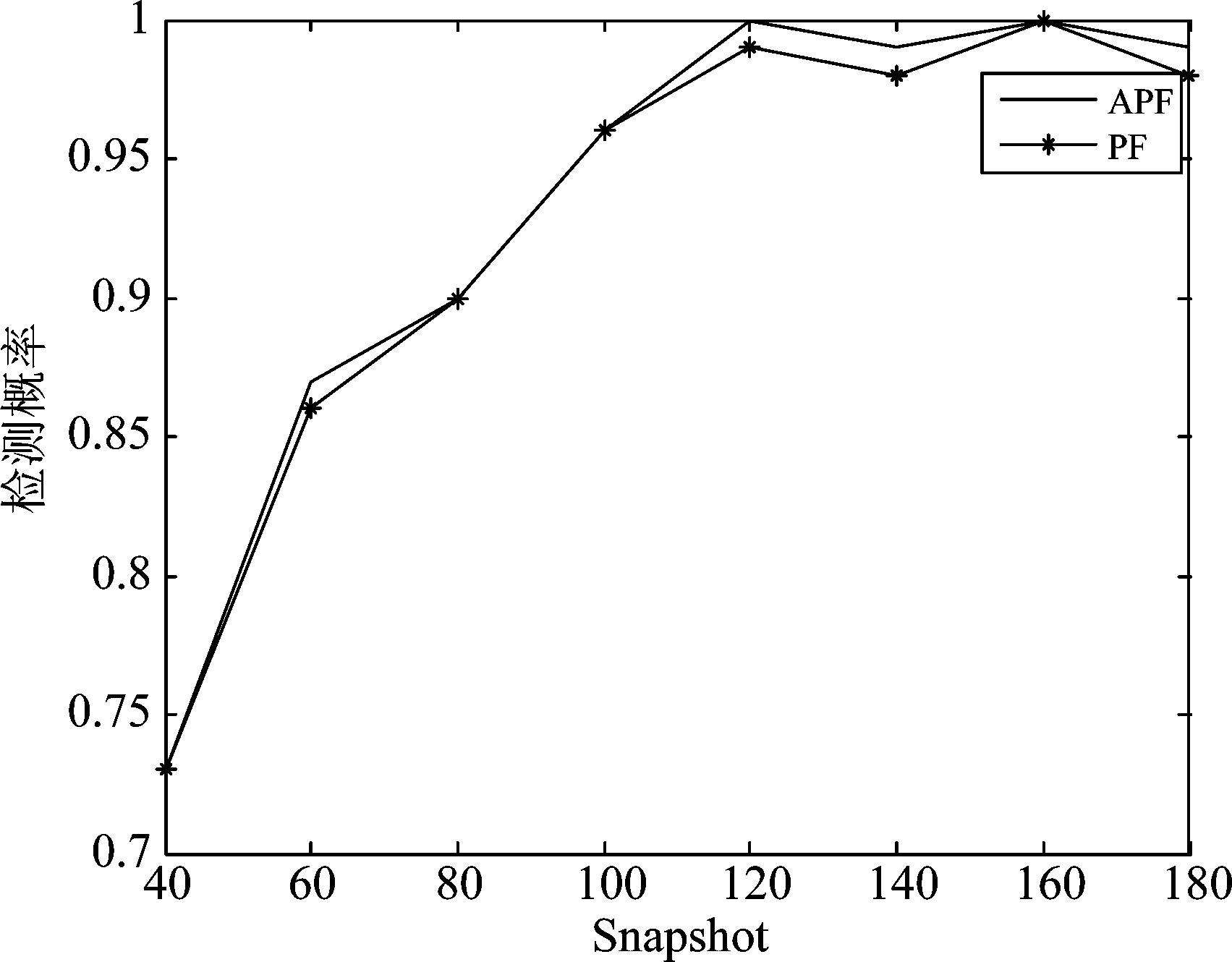
图2 检测概率随快拍数变化曲线
Fig.2 Detection probability versus the snapshot
结合图1和图2的效果,辅助粒子滤波算法在固定信噪比同时改变快拍数的情况下,均方根误差和检测概率都有比粒子滤波算法更好的表现。
下面是固定快拍数时两种算法随信噪比变化时均方根误差和检测概率变化的情况。
图3是固定快拍数为320时,均方根误差随信噪比增加而变化的仿真效果图。在信噪比为3 dB时,辅助粒子滤波算法的均方根误差比粒子滤波算法均方根误差低,由于粒子滤波算法会引起粒子衰竭,随信噪比逐渐增大辅助粒子滤波算法的均方根误差比粒子滤波算法的降低的更迅速,这是因为直接采样使得粒子滤波算法中粒子多样性消失造成的,可见辅助粒子滤波误差的控制更好。
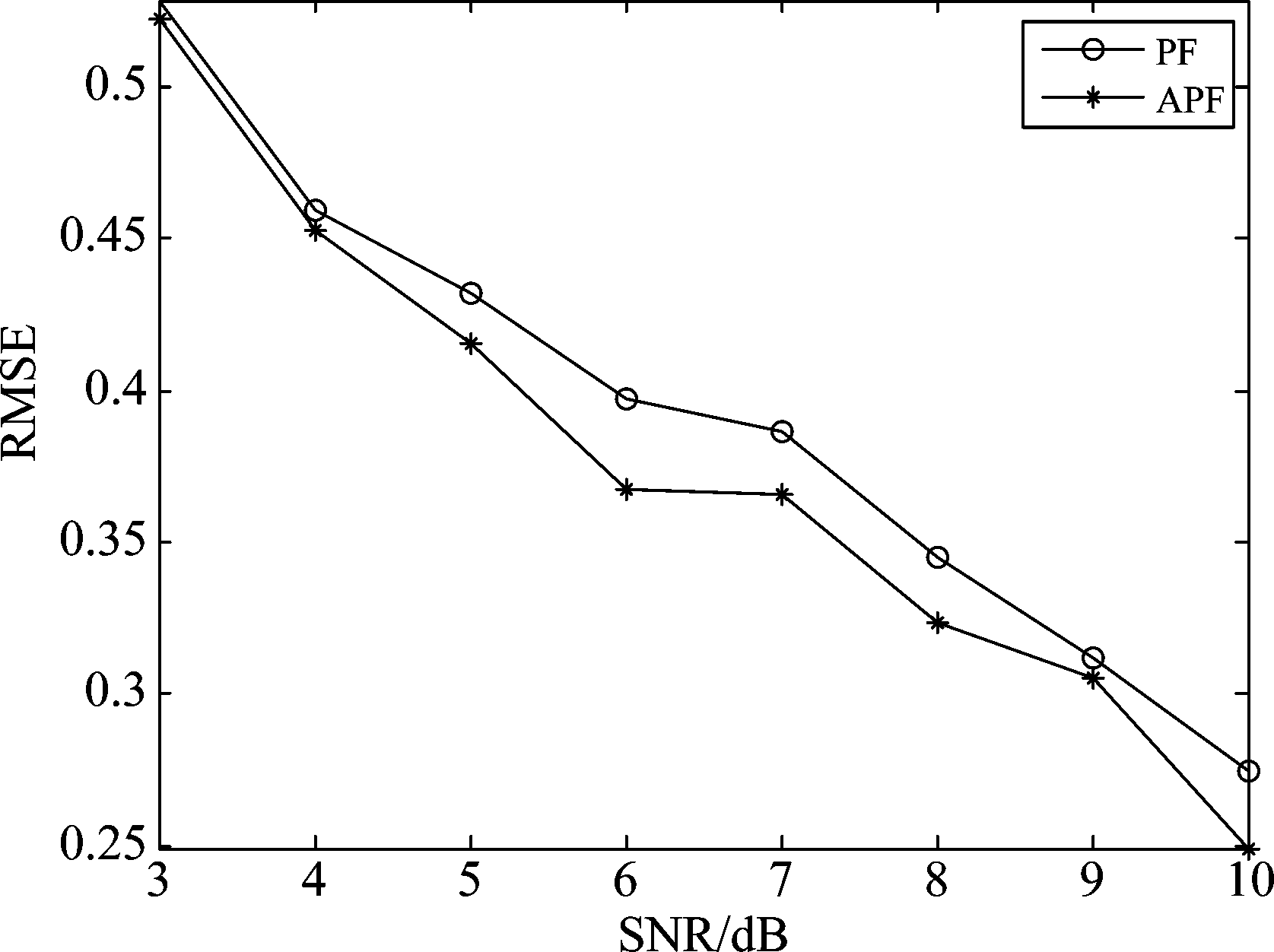
图3 RMSE随信噪比变化曲线
Fig.3 RMSE versus the SNR
图4是固定快拍数为320时,辅助粒子滤波算法和粒子滤波算法随信噪比增加检测概率的变化情况。随着信噪比的增加两种算法检测概率都逐步升高。但是辅助粒子滤波算法的检测概率更加优秀,始终高于粒子滤波算法。由此可见整体上辅助粒子滤波算法检测概率优于粒子滤波算法的检测概率。
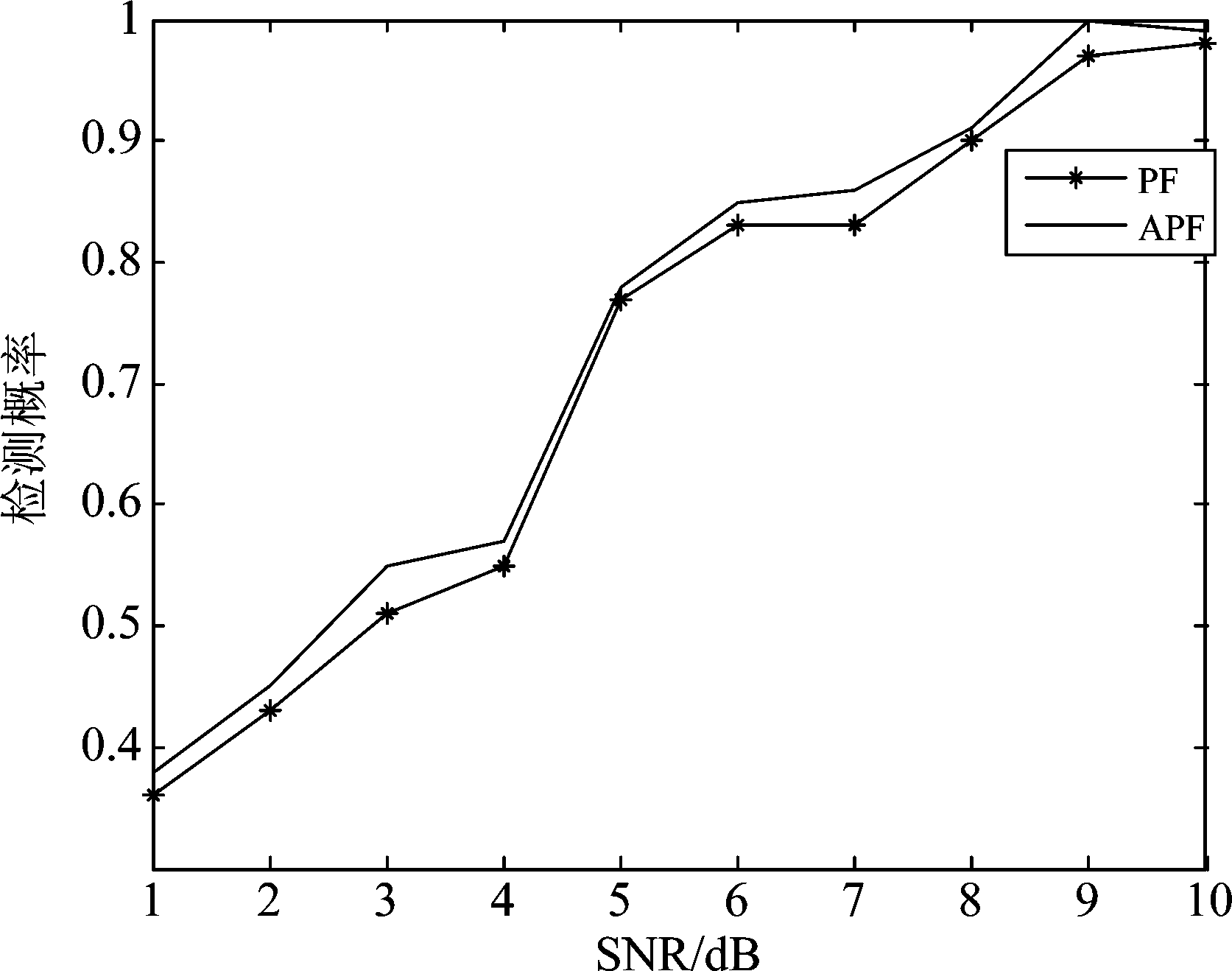
图4 检测概率随信噪比变化曲线
Fig.4 Detection probability versus the SNR
结合图3和图4的效果,辅助粒子滤波算法在固定快拍数同时改变信噪比的情况下,均方根误差和检测概率都有比粒子滤波算法更好的表现。
由上述仿真结果可以看出因加入了辅助变量而使得辅助粒子滤波算法在检测概率方面比粒子滤波优秀,在均方根误差上显示的结果,不论信噪比固定还是快拍数固定,辅助粒子滤波算法在各节点都有较好的表现,综合各实验结果辅助粒子滤波算法会有比粒子滤波算法更好的表现,本文的算法比粒子滤波算法精度更高,性能更好。
5 结论
本文提出了一种基于辅助粒子滤波算法的宽带波达方向估计的方法,对接收到的信号在频率域上分割,然后再分别用辅助粒子滤波算法处理,并估计其后验概率密度,最后得到估计的波达方向。实验结果表明在相同采样粒子数的状况下此算法比粒子滤波方法精度提高,检测概率更高,性能更优良。
[1] Liang Tianwan, Han Guangjie, Jiang Jinfang, et al. Distributed DOA Estimation Based on Manifold Separation Technique in Mobile Wireless Sensor Networks[C]∥The Workshop on Mobile Sensing. ACM, 2015: 1- 6.
[2] Li Weixing, Zhang Yue, Lin Jianzhi, et al. Wideband Direction of Arrival Estimation in the Presence of Unknown Mutual Coupling[J]. Sensors, 2017, 17(2): 230-242.
[3] Wu Yuntao, Leshem A, Jensen J R, et al. Joint Pitch and DOA Estimation Using the ESPRIT Method[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2015, 23(1): 32- 45.
[4] 艾名舜, 马红光. 基于网格爬山法的最大似然DOA估计算法[J]. 信号处理, 2011, 27(6): 890- 895.
Ai Mingshun, Ma Hongguang. Maximum Likelihood DOA Estimator based on Grid Hill Climbing Method[J]. Signal Processing, 2011, 27(6): 890- 895.(in Chinese)
[5] Zhang Jin, Dai Jisheng, Ye Zhongfu. An extended TOPS algorithm based on incoherent signal subspace method[J]. Signal Processing, 2010, 90(12): 3317-3324.
[6] Li Jun, Lin Qiuhua, Kang Chunyu, et al. DOA Estimation for Underwater Wideband Weak Targets Based on Coherent Signal Subspace and Compressed Sensing[J]. Sensors, 2018, 18(3): 902-918.
[7] Malek-Mohammadi M, Jansson M, Owrang A, et al. DOA estimation in partially correlated noise using low-rank/sparse matrix decomposition[C]∥Sensor Array and Multichannel Signal Processing Workshop. IEEE, 2014: 373-376.
[8] Tong Qian, Jin Zhixiang, Wei Cui. Fast covariance matrix sparse representation for DOA estimation based on dynamic dictionary[C]∥IEEE, International Conference on Signal Processing. IEEE, 2017: 138-143.
[9] 赵永红, 张林让, 刘楠, 等. 采用协方差矩阵稀疏表示的DOA估计方法[J]. 西安电子科技大学学报:自然科学版, 2016, 43(2): 58- 63, 101.
Zhao Yonghong, Zhang Linrang, Liu Nan, et al. DOA estimation method based on the covariance matrix sparse representation[J]. Journal of Xidian University: Natural Science, 2016, 43(2): 58- 63, 101.(in Chinese)
[10] Zhou Chengwei, Shi Zhiguo, Gu Yujie, et al. DOA estimation by covariance matrix sparse reconstruction of coprime array[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2015: 2369-2373.
[11] Fredrik Gustafsson. Particle filter theory and practice with positioning applications[J]. Aerospace & Electronic Systems Magazine IEEE, 2010, 25(7):53- 82.
[12] 吴孙勇, 廖桂生, 杨志伟. 基于粒子滤波的宽带信号波达方向估计[J]. 电子学报, 2011, 39(6): 1353-1357.
Wu Sunyong, Liao Guisheng, Yang Zhiwei. Direction of Arrival Estimation of Wideband Signal Based on Particle Filters[J]. Acta Electronica Sinica, 2011, 39(6): 1353-1357.(in Chinese)
[13] 王洪有. 基于辅助粒子滤波算法的红外目标跟踪[J]. 应用光学, 2010, 31(1): 132-135.
Wang Hongyou. Infrared target tracking base on auxiliary particle filtering algorithm[J]. Journal of Applied Optics, 2010, 31(1): 132-135.(in Chinese)
