1 引言
变换域通信系统是一种新型的认知无线通信系统。通过频点置零和扩频技术变换域通信系统 (Transform domain communication system, TDCS)可以主动规避干扰信号,提升在复杂电磁环境下的抗干扰能力[1-3]。然而在实际应用中,特别是在远距离航空通信条件下,收发端电磁频谱环境往往差异较大,会造成基函数的频谱感知失配(Spectrum sensing mismatch, SSM),导致系统抗干扰能力下降,误码率升高,严重影响收发双方的通信质量[4-5]。因此研究分析收发端不同的电磁频谱环境,设计频谱失配条件下的TDCS基函数,对提升远距离TDCS通信质量有重要意义。
目前,国内外学者对频谱失配条件下的TDCS通信性能已经有一定的研究,其中文献[6]分析了收发端基函数不一致的情况,推导了不同调制方式下其对误码率的影响,文献[7]采用类似等增益合并的方式设计接收端基函数,但其适用范围有限,在失配率较低时反而会增加误码率,是一种次优解决方案。文献[8]通过建立信令信道实现收发端的基函数频谱交换,选择收发端均未被干扰的信道传递信息,但其在动态、广域等实际中应用受限,存在频谱利用率低的问题。文献[9]依据收发端基函数0,1幅度谱对信道进行联合编码,在不同失配率下增加可用信道,从而提升系统的通信质量,但其未考虑干扰强度对信道质量的影响,可能会引入较强干扰,存在抗干扰能力差的问题。
针对以上问题, 本文提出了一种TDCS基函数优化设计方案,通过推导频谱失配条件下TDCS误码率表达式,定量分析干扰及频带利用率对误码率的影响,构建误码率的最优化模型,动态设计基函数的可用频点,达到系统频带利用率和抗干扰性能的最优化权衡。仿真结果表明该方法能够提升频谱失配条件下TDCS的误码率性能,适用于远距离条件下的变换域通信系统。
2 远距离通信分析
2.1 远距离环境频谱分析
在远距离变换域通信中,收发端电磁频谱感知结果往往存在差异,根据干扰源的相对位置,可将频谱感知结果分为以下几类[10],如图1所示。
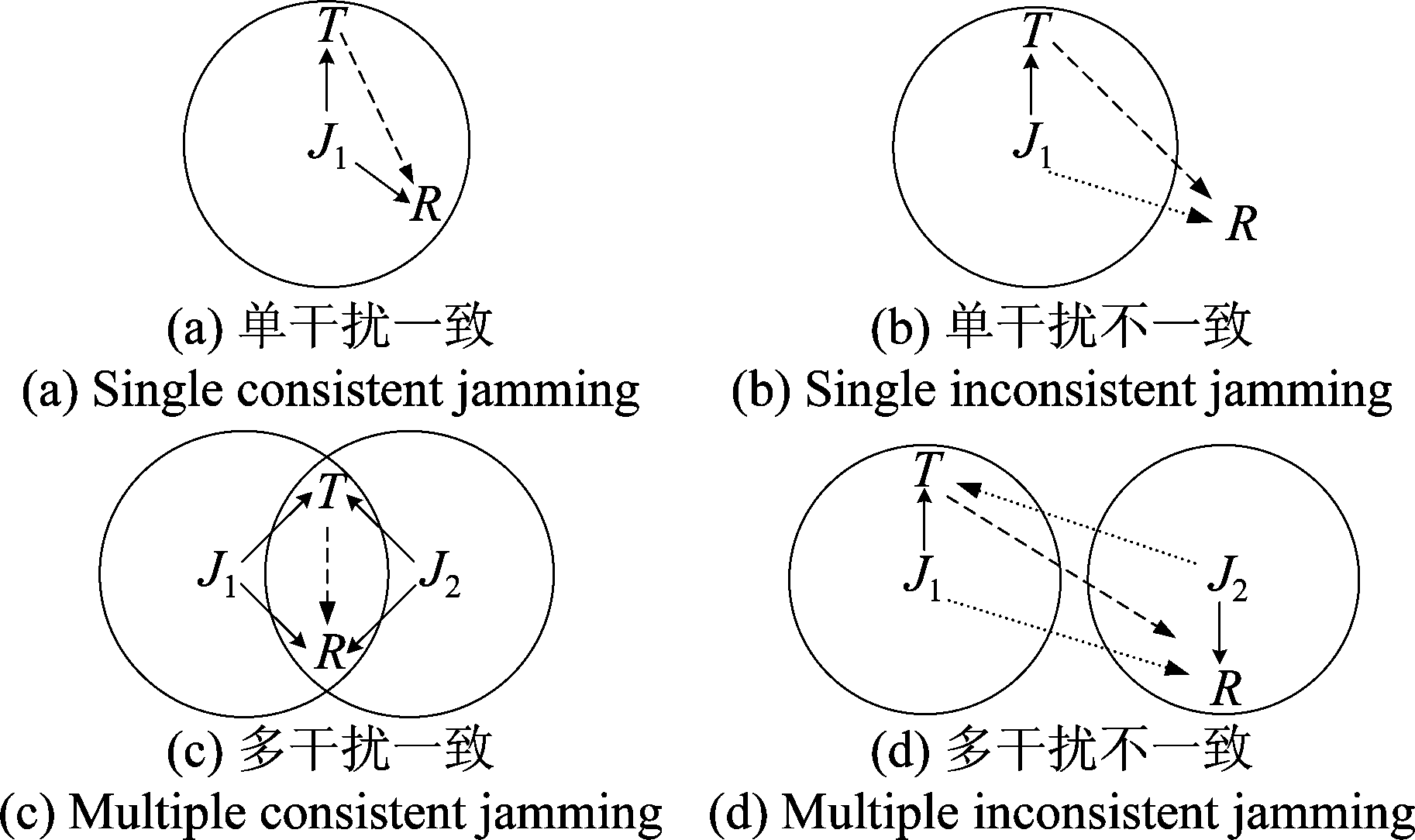
图1 频谱感知结果分类
Fig.1 Spectrum sensing type
在干扰一致的情况下,收发端可实现干扰剔除,完成质量较好的通信,在不一致的情况下,收发端基函数存在频谱失配,导致抗干扰能力下降,需要设计性能较优的基函数来提升系统通信质量。
远距离通信中人为干扰主要包括单音、多音、部分频带、线性调频和梳状谱干扰,在实际频谱失配中以梳状谱干扰为主,本文主要研究梳状谱干扰特性及在此干扰下变换域通信系统性能。梳状谱干扰是由多个窄带干扰构成的干扰信号,每个干扰中心精确瞄准通信信道中的某一工作频点[11-12]。梳状谱干扰模型可表示为:
(1)
其中ARi(t)服从瑞利分布,相位函数φRi(t)服从[0,2π]的均匀分布, fRi为第i个窄带干扰的中频频率。远距离收发端梳状谱干扰仿真如图2所示。
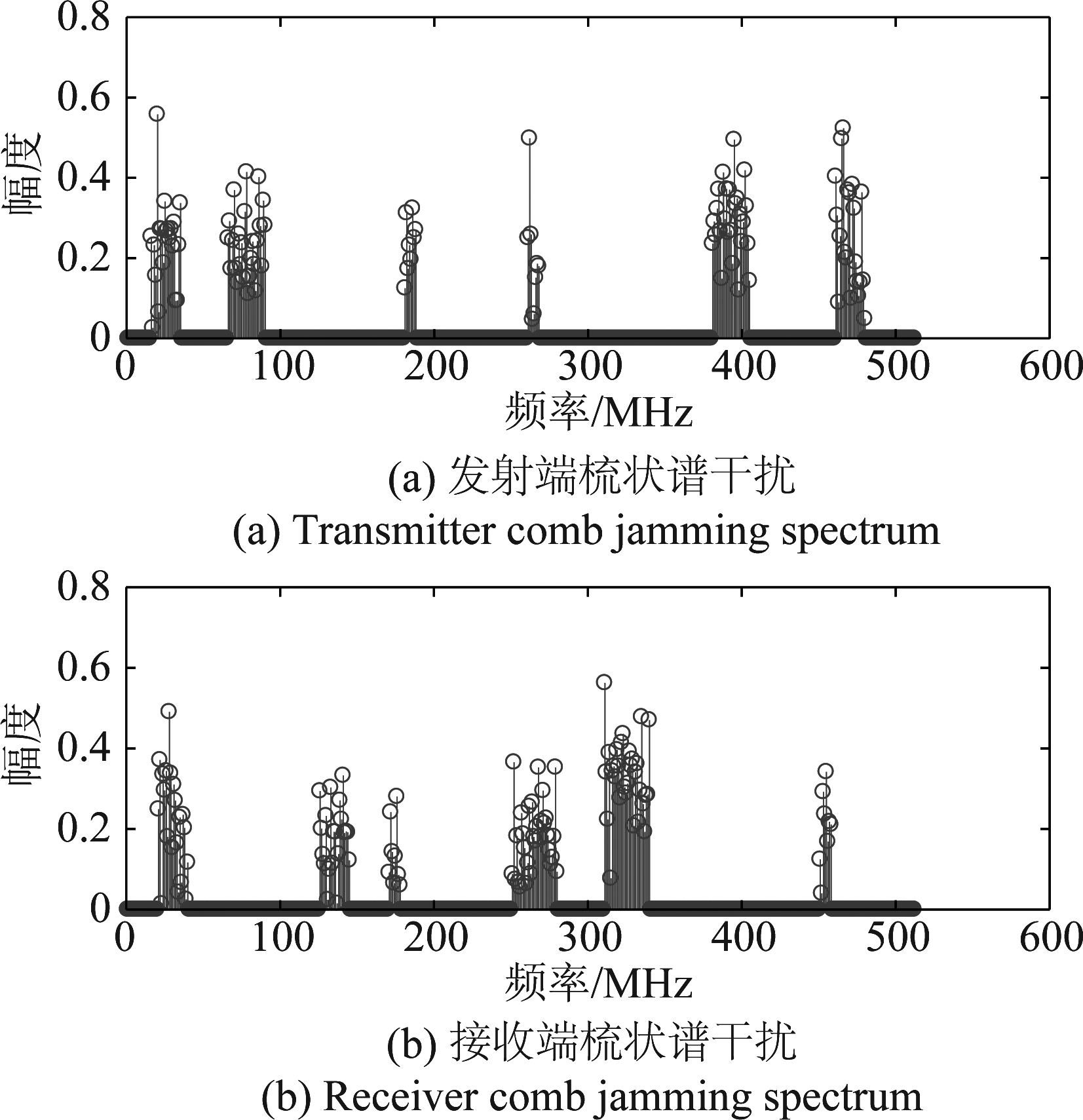
图2 梳状干扰频谱
Fig.2 Comb jamming spectrum
从图2可知,由于所处电磁干扰环境不同,收发端频谱感知结果存在部分差异。
2.2 远距离TDCS模型
在远距离频谱失配情况下,需要收发端交互电磁频谱信息,以确定频谱失配情况,调整基函数来改善通信质量,需要在原有TDCS模型中添加可靠、低速的信令信道。通信过程分为信令信道建立、频谱交互、基函数调整、数据通信四个阶段,收发端需要工作在全双工模式下。具体步骤为:
(1)收发方依据频谱监测经验数据,预置频谱信息库,从中选出一组频谱信息生成基函数并建立TDCS信令信道。对信令信道的通信质量进行检测,选择满足要求的信令信道。考虑到预置的频谱信息与所处环境干扰非正交,需要降低通信速率来提高抗干扰能力。
(2)收发方感知本地频谱信息,根据建立的低速的信令信道,进行频谱感知信息交互。
(3)收发方依据交互结果对本地基函数进行动态调整。
(4)收发方利用重构的基函数,建立TDCS信道,以正常速率进入TDCS通信状态。
远距离TDCS模型如图3所示。
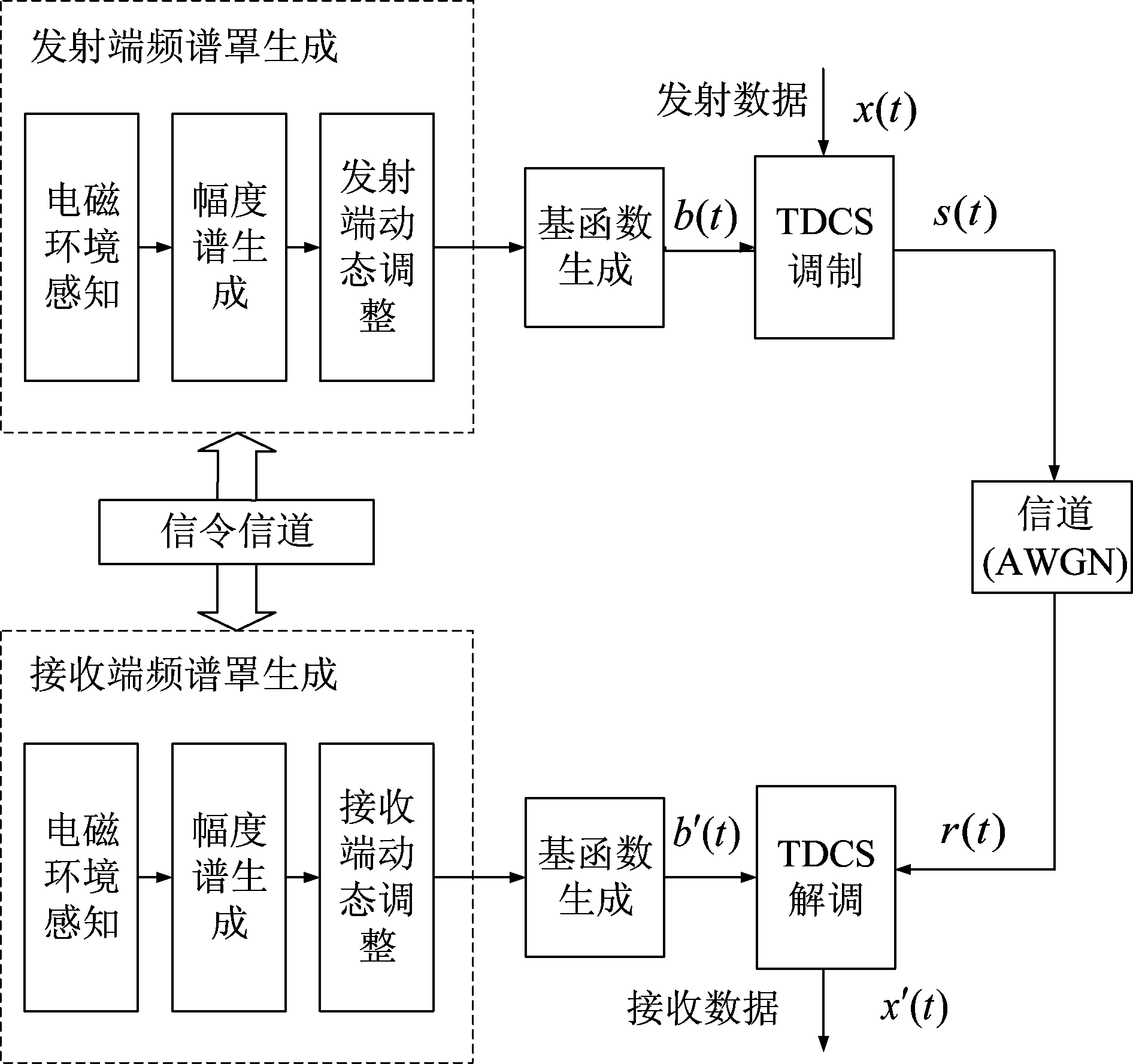
图3 远距离TDCS框图
Fig.3 Long-distance TDCS diagram
发射端通过谱估计技术,对环境电磁频谱进行采样,得到谱估计结果。将其与预先设定的干扰门限进行对比,将大于门限的干扰频点幅值置0,可用频点置1,得到幅度谱向量A={A0,A1,...,AN-1},记基函数频点集合为Ω。将Ak与随机相位ejθk相乘得到基函数的频域表达式,经过能量调整后用IDFT变换得到基函数的时域形式bn:
(2)
其中功率调整因子
为基函数幅度谱为1的点数。
TDCS常采用M阶循环码移键控(Cyclic Code Shift Keying, CCSK)进行数据调制,其发射信号可表示为:
(3)
其中,mi为第i个发送数据。
发射信号经高斯信道后传递到接收端,接收信号可表示为:
rn=sn+jn+zn
(4)
其中, jn为接收端干扰,zn是均值为0、方差为
的高斯随机变量。接收端根据本地电磁环境产生基函数与接收信号进行相关解调,解调信号可表示为:
(5)
其中(·)*代表复共轭运算,〈m〉N代表
为接收端基函数。在理想条件下,收发端基函数一致,本地基函数与干扰信号正交其相关结果为零,接收信号与本地基函数的周期循环形式解调将会呈现一个冲激响应[6]:
(6)
其中:
(7)
yz为噪声分量,通过检测冲激响应的最大值,对比周期循环函数矩阵,即可解调出发送数据[13-14]。
3 频谱失配分析
在实际无线通信环境中,收发机往往距离较远,其面对的干扰种类,强度,噪声影响各不相同,产生的基函数也不相同。由于伪随机相位依靠随机序列产生,发生错误的可能性很小,本文只考虑基函数幅度谱Ak发生错误的情况。在图2电磁环境下生成基函数幅度谱如图4所示,收发端感知的基函数幅度在某些频点上存在差异。
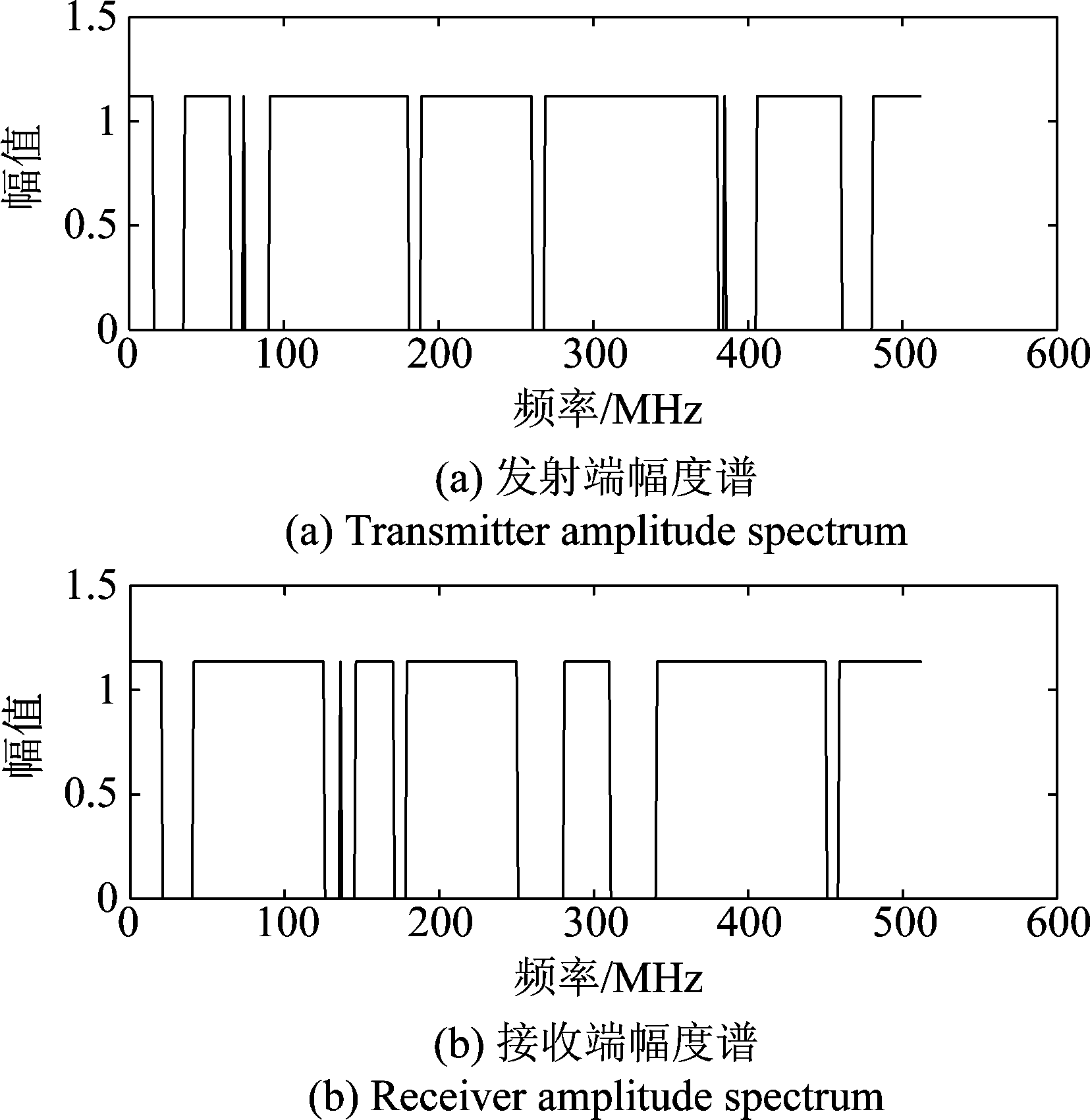
图4 频谱失配分析
Fig.4 Analysis of SSM
设
的频点集合分别为
定义基函数失配率α为:
(8)
其中,Ne为收发端不一致频点数。接收端基函数可表示为:
(9)
计算接收端基函数与发射端基函数互相关值:
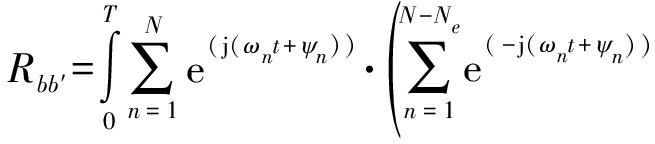
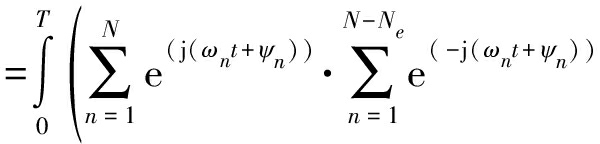
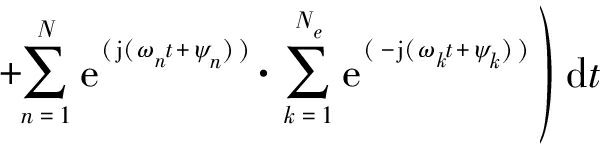
(10)
其中N∩为集合
的数量,当基函数符号间相关性较弱时,等式的第二项可以近似为0,由此可得:
(11)
其中NtT=Rbb为发射端基函数自相关值。 式(11)说明解调后信号能量下降为
当N∩降低时,相关函数的主瓣会发生不同程度的展宽,副瓣增大,自相关特性变差,将会影响系统的解调性能[4]。
在频谱失配情况下,基函数与干扰信号无法做到完全正交,即式(5)中
此时TDCS误码率与信干噪比 (signal-to-interference and noise ratio, SINR)有关, SINR可表示为[15]:
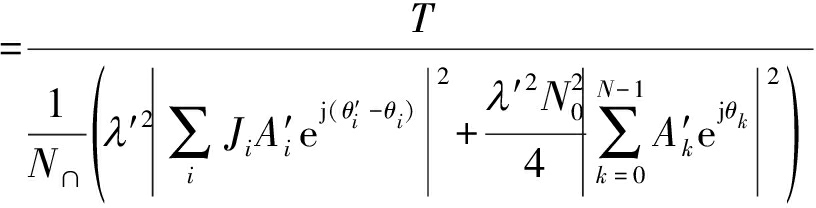
(12)
其中,N0为解调后的噪声功率,Ji为进入系统内部的干扰幅值,i取
的值。依据多元CCSK调制误码率公式可得频谱失配条件下的系统误码率为:
(13)
Q为互补误差函数。结合公式(12)和(13)知,当调制阶数确定后,收发端基函数可用频点数、进入系统内部的干扰强度均会对误码率产生影响。
4 基函数优化设计
从宏观分析可知,若保证系统的抗干扰性能不变,当频谱失配率较高时,N∩过少,导致误码率升高;若保证N∩数量,将会牺牲部分抗干扰性能。因此在不同的失配率下,频谱利用率和抗干扰性能是一种动态平衡。为此,本文提出一种频谱失配下的基函数优化设计方案,综合接收端干扰强度,失配率,噪声等因素,最优化基函数可用频点位置和数量,确保在低失配率下尽可能的将干扰剔除,在高失配率下提升基函数可用频点数,使得通信系统的抗干扰性能和频谱利用率达到最优化的权衡。
4.1 模型建立
结合式(12)、(13)可知,当基函数调制阶数选定后,收发端基函数幅度谱设计完成,其对应的误码率也确定下来。在对基函数进行设计时,应使式(12)中的表达式
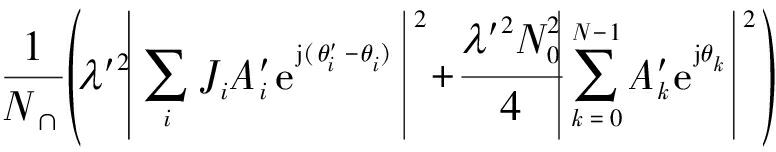
最小,从而系统误码率性能达到最优。令
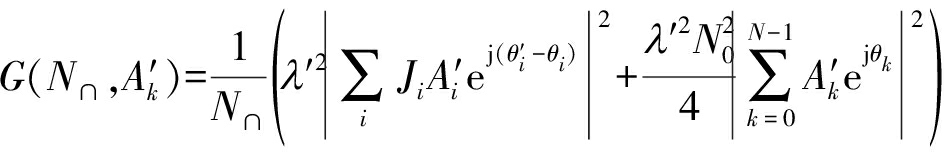
(14)
其中N∩与收发端基函数幅度谱有关。该优化问题涉及两个变量
同时优化求解的计算复杂度较高。由式(10)知影响接收端信号能量的变量是N∩,即存在0点的收发端基函数频谱不分配信号能量,并且接收端基函数实际影响进入系统内部的干扰能量。于是我们可以设定
此时式(14)可重写为:
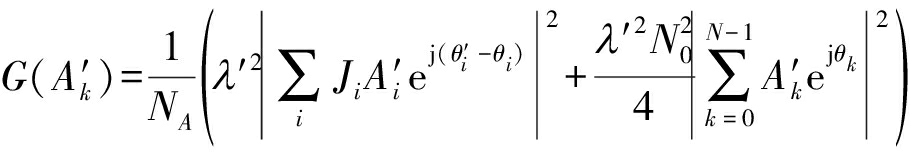
(15)
其中,NA为集合
的个数,频谱失配条件下误码率的最优化模型可建立为:
(16)
当NA过小时,CCSK调整误码率会急剧恶化,需保持其一定的数量,该数量由维度定理给出:NA≥M。给根据上述优化问题,最佳基函数幅度谱为:
(17)
4.2 搜索算法
对基函数幅度谱进行设计,即确定幅值为1的子载波索引位置集合
最速下降法通常用来求解局部最小值问题,该算法沿着最速下降梯度方向搜索,可有效降低搜索最小值的次数。采取用最速下降法搜索最佳kl的算法步骤如下:
Step 1 初始化
(1)对接收端干扰进行功率谱估计得到Jk,将每个采样点按功率从小到大排列得到
令x(0)=1;(3)选取λ为一逐渐递减序列[λ1,λ2,...,λN]。
Step 2 在可行集内,通过L次迭代求解最优化kl。
for i=1,2,...,L
初始化:x1=x(i-1)。
(1)令
其中
为取干扰
对应的子载波索引位置,依据kl分配0,1幅值点位置,得到
(2)求解G(x1)的梯度δ,计算下一步位置:x2=x1-λiδ。
(3)若G(x2)>G(x1),令x2=(x1+x2)/2,更新G(x2)的值,再次进行比较。
若G(x2)<G(x1)。令x1=x2。
(4) 令x(i)=x1,进入下一次循环。
Step 3 循环结束,得到最优解xL,根据
设计得到基函数幅度谱的最优解。
合理的步长选择能有效提升最速下降法的计算效率,保证算法的收敛性。在初始搜索时,存在大量干扰强度较低的频点,应选用较大步长,当搜索点接近极值点时,应该减小搜索步长。由于实际干扰功率大小的不确定行,求解的过程中不一定沿下降方向,因此每次循环进行一次判定,若不是下降方向,退回前一点和当前点的中点,再进行判定,确保算法沿最速方向进行。
4.3 时间复杂度分析
文献[8]算法选用收发端基函数幅度谱值均为1的频点生成新的基函数,对于子载波个数为n的基函数来说其须在接收端进行n次基函数幅度谱值对比并对n点的幅度谱值调整,运算次数为2n。算法的执行次数随n的改变而变化,故其时间复杂度为O(n)。文献[9]算法须在接收端进行n次基函数幅度谱值对比并计算失配率,之后对照规则表进行基函数幅度谱值的调整,其运算次数为2n+1,时间复杂度为O(n)。本文算法中最速下降法的迭代次数为L,每一次迭代需要进行n点基函数幅度谱值调整,1次步长计算和1次误码率对比,其运算次数为L(n+2),时间复杂度为O(Ln),若采用穷搜索算法其时间复杂度为 O(n2)。综上所述,本文所采用的最速下降法能大幅降低搜索最优解的计算量。虽较已有算法时间复杂度有所增加,但当发送数据量增大时它们之间的运算效率会逐渐接近,因此,通过理论分析可知,本文算法具有可行性和有效性。
5 仿真对比分析
为验证本文算法有效性,将其与已有算法进行仿真对比分析。
仿真条件:TDCS基函数周期长度为N=512,复随机相位由m序列映射产生,系统采用二阶CCSK调制,信道为高斯白噪声信道,发送数据独立同分布等概产生。为对比基函数在不同频谱失配率下的系统性能,选取4个不同参数的接收端干扰达到不同的失配率。收发端梳状谱干扰仿真参数设定如表1所示。
首先对推导的频谱失配条件下系统误码率表达式进行仿真验证,仿真失配率选取α=0.42,信噪比和干信比的取值范围分别0～10 dB,10～40 dB,噪声功率由信噪比计算得到,依据失配条件和干信比计算出进入系统内部的干扰功率,其结果如图5所示。可以看出,在不同干信比和信噪比下系统误码率的仿真值与理论推导结果相一致。
图6是在α=0.42时基函数幅度谱的仿真图,其中接收端干扰采用归一化的幅度谱图。从图中可以看出,本文的设计算法合理的分配了基函数的0,1幅度谱,例如在185至209采样点范围内干扰功率较小,将基函数幅度谱置1,而文献[8]算法为保证与发射端基函数一致将其置0;在264至312采样点范围内干扰功率较大,本文算法将基函数幅度谱置0,而文献[9]算法则视其为可用频点将幅度谱置1。由此可见,文献[8]算法存在频带利用率较低的问题,文献[9]算法虽然提高了频带利用率,但会引入存在较强干扰功率的频点,这两种算法不能针对干扰环境合理调整基函数幅度谱,而本文算法在保证频带利用率的同时能最大化减小干扰对系统的影响,更加合理的设计基函数幅度谱。
表1 收发端干扰参数
Tab.1 Transceiver interference parameters
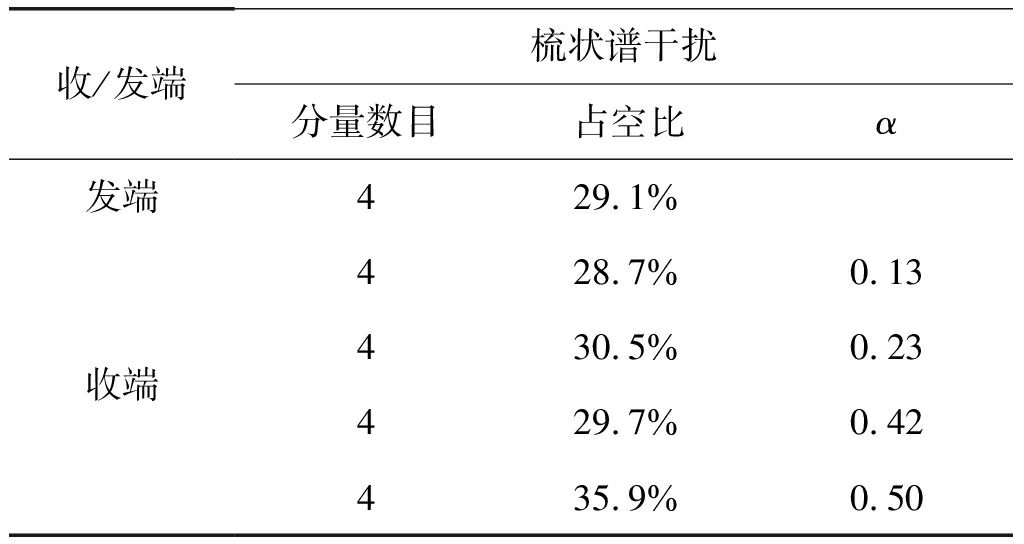
收/发端梳状谱干扰分量数目占空比α发端429.1%收端428.7%0.13430.5%0.23429.7%0.42435.9%0.50
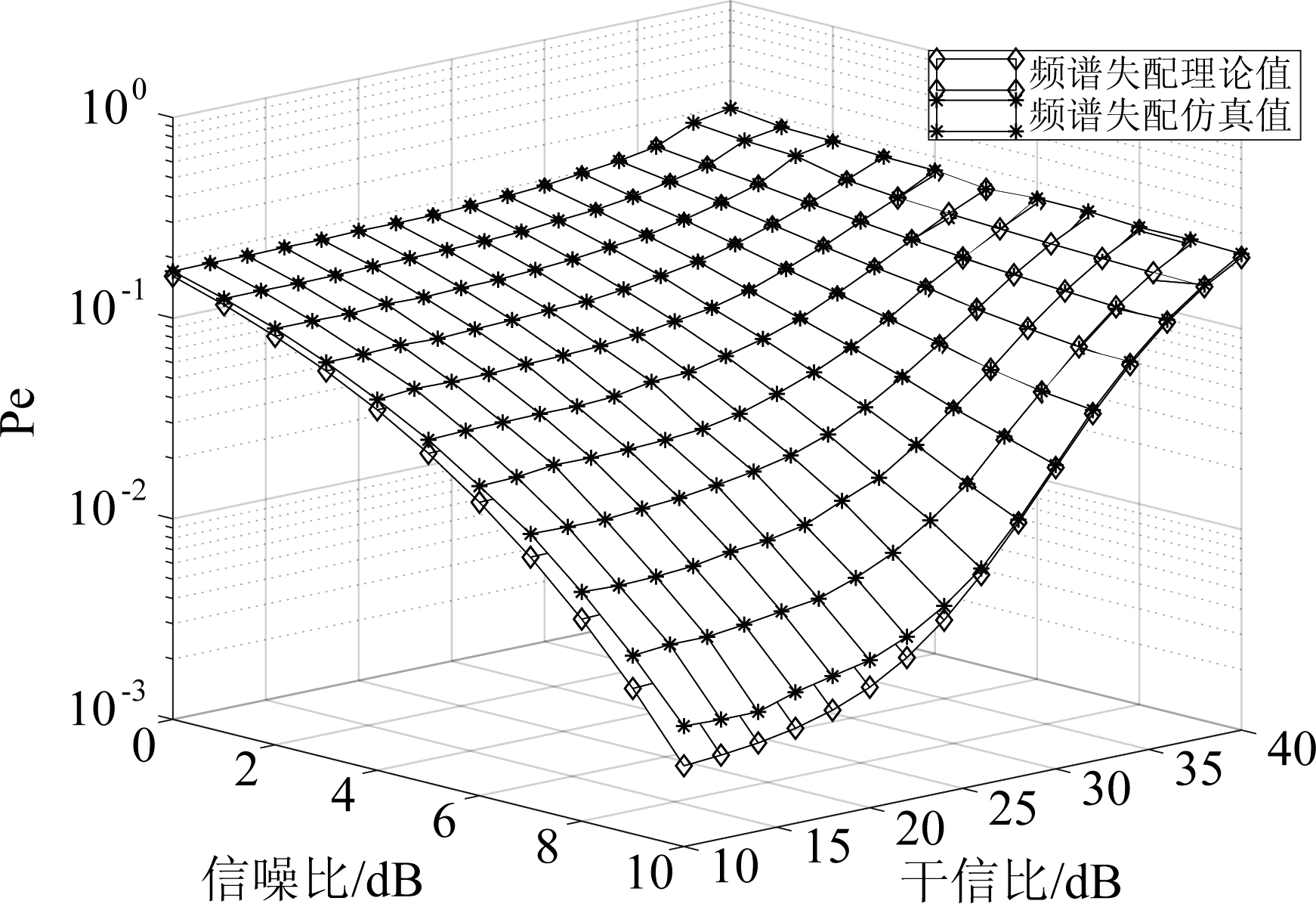
图5 频谱失配误码性能
Fig.5 BER performance of Spectrum sensing mismatch
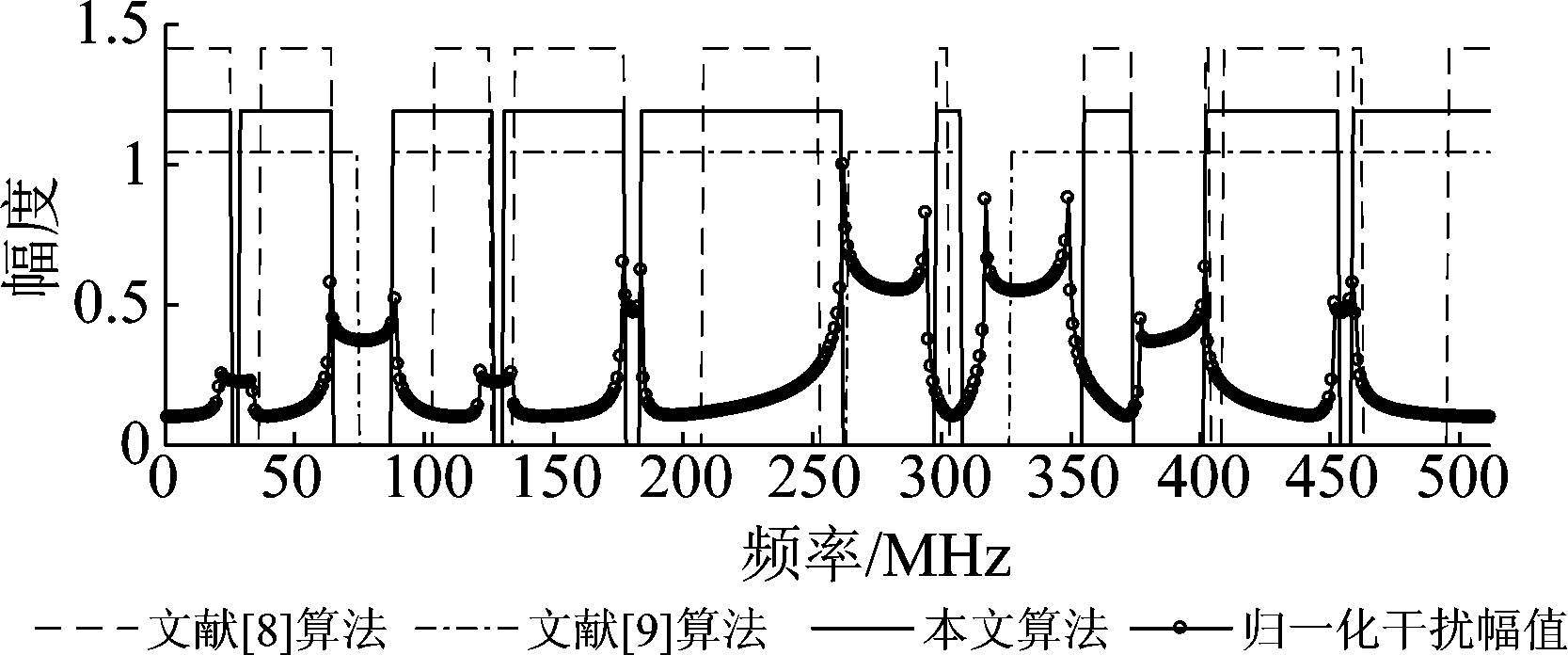
图6 干扰信号及基函数幅度谱值
Fig.6 Spectrum magnitude of interference and basic function
图7中(a)、(b)、(c)分别为在α=0.42时,本文算法、文献[8]算法、文献[9]算法设计的基函数与干扰信号的合成向量模值图,采用多次运算求平均归一化后得到。结合式(12)可知,向量和模值越小,进入系统内部的干扰能量越少。从图中可看出, 文献[8]算法采用收发端均无干扰存在的频点,进入系统内部干扰能量最少,本文算法向量和模值接近文献[8]所提算法,优于文献[9]所提算法。
为了验证本文算法的抗干扰性能,考虑在失配率α为0.13,0.23,0.42,0.50的条件下对几种算法的干信比误码性能进行对比实验,信噪比固定为5 dB,其结果如图8所示。可以看出在3种算法中,本文所提算法的抗干扰能力最好,而未经调整的原始基函数性能最差。在失配率较低时,本文算法可以剔除大部分干扰较强频点,保证良好的抗干扰能力,而随着频谱失配率增大,本文算法仍具有一定的误码率优势。而在α=0.5,干信比低于25 dB时本文算法可获得较为理想的误码率,在干信比大于25 dB时几种算法的抗干扰性能趋于一致,这说明了TDCS在大失配率下的干扰承载能力是有限的。
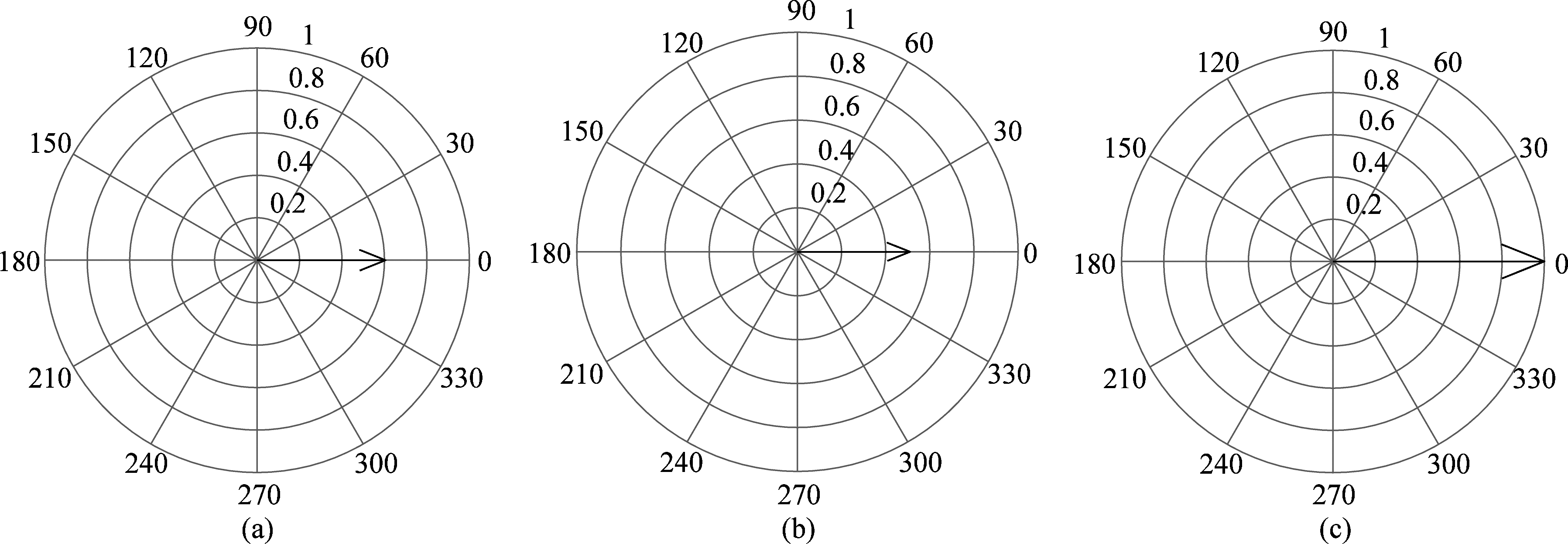
图7 干扰与基函数向量图
Fig.7 Synthetic magnitude of interference and basic function
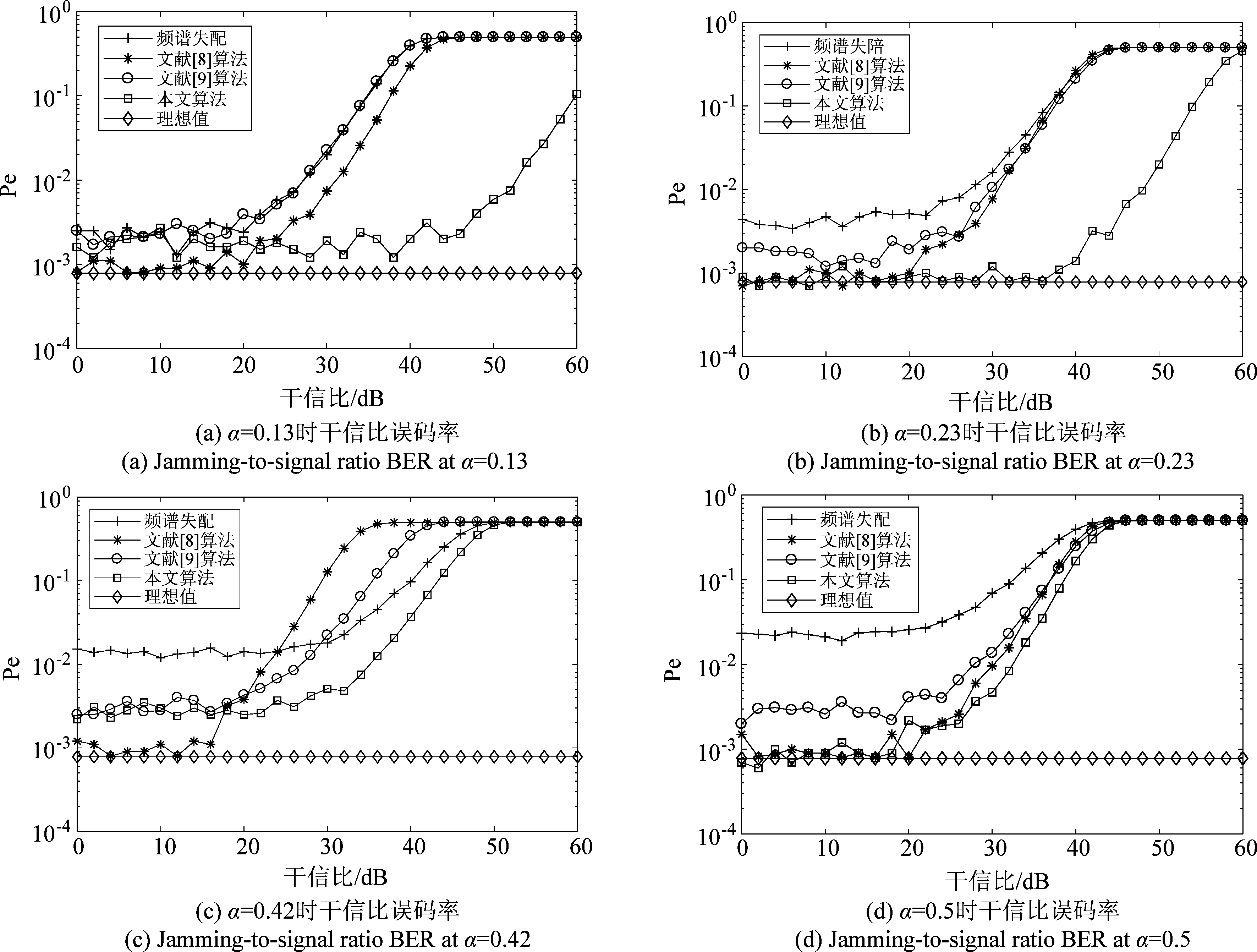
图8 3种算法在不同失配率下的干信比误码率结果
Fig.8 Jamming-to-signal ratio BER of three algorithms with different mismatch rate
令干信比取值为10 dB,对比文献[8]、文献[9]与本文所提算法设计的基函数信噪比误码率性能,仿真结果如图9所示。当失配率较低时,三种算法设计的基函数信号能量相近,因此误码率较为接近,这与图8的仿真结果相一致。当失配率增大时,采用未做调整的基函数系统误码率逐渐恶化,文献[8]、[9]所提方法在失配率α≤0.23时能不同程度的降低系统误码率,但在大失配率下效果并不理想。而本文算法综合抗干扰性能和频谱利用率,在低干信比条件下可灵活调整基函数幅度谱,选取最优的可用频点数量和位置,获得更高接收端的信干噪比。从仿真结果来看,本文算法较文献[8]算法在误码率为0.015,α=0.5时有0.7 dB左右的信噪比增益,较文献[9]算法在误码率为0.04,α=0.5时有2.6 dB左右的信噪比增益。
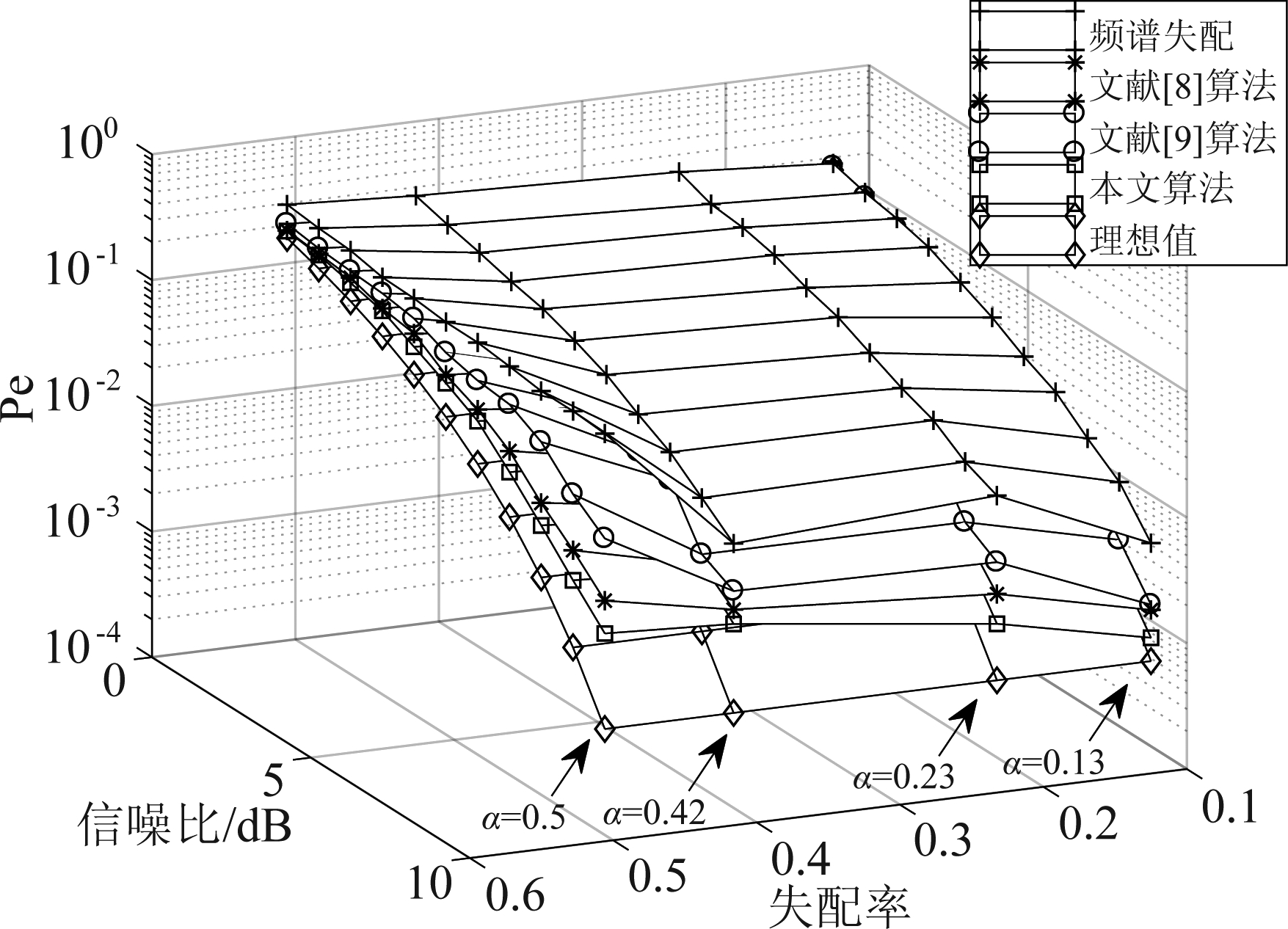
图9 3种算法在不同失配率下的信噪比误码率结果
Fig.9 Signal-to-noise ratio ratio BER of three algorithms with different mismatch rate
6 结论
在分析频谱失配条件下TDCS基函数与系统误码率关系的基础上,提出了一种基函数优化设计方案,通过构建误码率最优化模型,搜索最佳基函数幅度谱,达到系统的抗干扰性能和频谱利用率最优化的权衡,解决了远距离TDCS由于频谱失配产生的通信质量急剧下降的问题。仿真结果表明本文算法能有效提升接收端信干噪比,具有优良的抗干扰性能。这对提升TDCS在远距离通信下的通信能力,扩展TDCS应用领域具有重要意义。
[1] Hu Su, Li Fan, Guo Huiting, et al. TDCS-IDMA System for Cognitive Radio Networks With Cloud[J]. IEEE Access, 2018, 6(99): 20520-20530.
[2] Chang Cheng, Huan Hao, Guo Jianmin, et al. Complementary Peak Reducing Signals for TDCS PAPR Reduction[J]. Iet Communications, 2017, 11(6): 961-967.
[3] 梁源, 达新宇, 安卫国, 等. 变换域通信系统双门限基函数优化设计[J]. 系统工程与电子技术, 2017, 39(3): 634- 640.
Liang Yuan, Da Xinyu, An Weiguo, et al. Optimal Design of Double-threshold Basic Function in Transform Domain Communication System[J]. Systems Engineering and Electronics, 2017, 39(3): 634- 640.(in Chinese)
[4] 王柔溪. 变换域通信系统的关键技术研究与仿真分析[D]. 北京: 北京理工大学, 2016.
Wang Rouxi. Study and Simulation on Transform Domain Communication System and Related Key Technologies[D]. Beijing: Beijing Institute of Technology, 2016.(in Chinese)
[5] Liu Jenyang, Su Yu T. Performance Analysis of Transform Domain Communication Systems in the Presence of Spectral Mismatches[C]∥Military Communications Conference, 2007. Milcom. IEEE, 2007: 1-5.
[6] Jin Chuanxue, Hu Su, Huang Yixuan, et al. On Transform Domain Communication Systems under Spectrum Sensing Mismatch: A Deterministic Analysis[J]. Sensors, 2017, 17(7): 1594.
[7] 谢铁城, 达新宇, 褚振勇, 等. 收发频谱不一致条件下的变换域通信系统基函数设计[J]. 吉林大学学报: 工学版, 2014, 44(6): 1825-1830.
Xie Tiecheng, Da Xinyu, Chu Zhenyong, et al. Basis Function Design for Transform Domain Communication System in the presence of Spectral Mismatches[J]. Journal of Jilin University: Engineering and Technology Edition, 2014, 44(6): 1825-1830.(in Chinese)
[8] Han C, Wang J, Li S. A Spectrum Exchange Mechanism in Cognitive Radio Contexts[C]∥IEEE, International Symposium on Personal, Indoor and Mobile Radio Communications. IEEE, 2006: 1-5.
[9] 赵玮, 刘立, 张衡阳, 等. 联合信道状态编码的基函数生成算法[J]. 空军工程大学学报: 自然科学版, 2017(6): 89-94.
Zhao Wei, Liu Li, Zhang Hengyang, et al. A Function Generation Algorithm Based on Joint Channel Status Coding[J]. Journal of Air Force Engineering University: Natural Science Edition, 2017(6): 89-94.(in Chinese)
[10] 王桂胜, 任清华, 徐兵政, 等. 远距航空通信变换域通信系统设计[J]. 计算机应用, 2018, 38(2): 522-527.
Wang Guisheng, Ren Qinghua, Xu Bingzheng, et al. Design of Transform Domain Communication System for Long Distance Aeronautical Communication[J]. Journal of Computer Applications, 2018, 38(2): 522-527.(in Chinese)
[11] 梁金弟, 程郁凡, 杜越, 等. 联合多维特征的干扰识别技术研究[J]. 信号处理, 2017, 33(12): 1609-1615.
Liang Jindi, Cheng Yufan, Du Yue, et al. The Research of Interference Recognition Technology Based on the Joint Multi-dimensional Features[J]. Journal of Signal Processing, 2017, 33(12): 1609-1615.(in Chinese)
[12] 王桂胜, 任清华, 姜志刚, 等. 基于信号特征空间的TDCS干扰分类识别[J]. 系统工程与电子技术, 2017, 39(9): 1950-1958.
Wang Guisheng, Ren Qinghua, Jiang Zhigang, et al. Jamming Classification and Recognition in Transform Domain Communication System Based on Signal Feature Space[J]. Systems Engineering and Electronics, 2017, 39(9): 1950-1958.(in Chinese)
[13] 徐兵政, 任清华, 孟庆微, 等. 小波变换域通信系统中连续均值剔除算法研究[J]. 空军工程大学学报: 自然科学版, 2018, 19(4): 93-98.
Xu Bingzheng, Ren Qinghua, Meng Qingwei, et al. Research on Consecutive Mean Excision Algorithm in Wavelet Domain Communication System[J]. Journal of Air Force Engineering University: Natural Science Edition, 2018, 19(5): 32-39.(in Chinese)
[14] Hu Su, Wu Gang, Xiong Wenhui, et al. TDCS Waveform Design for MUI-Free Cognitive Radio Networks[C]∥Vehicular Technology Conference. IEEE, 2013: 1-5.
[15] 梁源, 达新宇, 张喆, 等. 隐蔽通信中变换域通信系统双门限基函数设计[J]. 华中科技大学学报: 自然科学版, 2017, 45(11): 11-16.
Liang Yuan, Da Xinyu, Zhang Zhe, et al. Design of Double-threshold Basic Function in Transform Domain Communication System for Covert Communication[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2017, 45(11): 11-16.(in Chinese)
