1 引言
随着移动用户的快速增长和城市化进程的加快,无线蜂窝网络已经经历了几次重大演变,从1G模拟网络到现在基于长期演进(Long Term Evolution,LTE)的4G蜂窝网络[1]以及未来5G蜂窝网络[2]。为了满足各类通信网络消费者的需求同时降低网络能耗,诸如微小区,微微小区等小基站的概念应运而生[3],无线蜂窝网络的架构也由传统的同构模型发展为如今的异构模型[4]。因此,建立异构蜂窝网络空间结构模型以及估算相关网络平均性能指标成为无线通信领域的一个热点课题。
对无线蜂窝网络的建模分析可以大致分为三种。第一种是基于传统信息理论的维纳模型(Wyner model)[5-7]。在该模型里,干扰被简化为一常数或服从简单的一维随机变量。然而,对于信干噪比(signal to interference plus noise ratio,SINR)剧烈变化的蜂窝网络(如基于LTE的4G网络),维纳模型以及与之相关的均值模型是不合适的。第二种方法假设基站呈格形分布,其覆盖区域为正六边形。但是,这类模型缺乏可扩展性,得到的结果并不精确,假设与实际也不太吻合,对于多种类型基站共存的异构网络而言同样不适用[8]。
第三种方法,也是近年来的热点方法,是利用随机几何理论及相关模型[9],分别假定基站和移动用户位置服从某个随机点过程,最常见的是泊松点过程(Poison Point Process,PPP)[10]。泊松点过程一方面能够比较客观地描述基站的分布情况,另一方面又易于分析处理,因此在异构蜂窝网络的建模方面有着广泛应用。在文献[10]中,将基站的位置描述成服从强度为λ的齐次PPP。与传统的二维平面模型不同,文献[11]首次提出了更适合小基站网络的3-D PPP模型,并基于此模型分析了小基站网络的下行覆盖概率,推导了一定条件下覆盖概率的闭合表达式。
与下行干扰分析不同,上行分析由于其自身特点将更具挑战性[12]。一方面,上行链路中的干扰是由分布在整个网络中的移动用户产生的,而不是来自基站的下行链路[13]。另一方面,上行链路普遍采用开环或闭环功率控制来克服路径损耗,其发射功率受移动台与其通信基站之间距离的影响在一定范围内不断变化[14]。这也将在干扰统计方面与下行分析有显著不同。文献[15]研究了由宏基站和小基站组成的两层网络组成在全开放接入场景下的上行链路的性能。接下来,文献[16]提出了一种两层家庭基站网络架构模型,并分析了开放/封闭接入准则下网络性能的不同。文献[15-16]中采用的功率控制模型都是完全功率控制,即路径损耗完全抵消的理想状况。文献[12]在传统的完全功率模型中引入了功率控制因子,使得功率控制具有动态性。然而,以上文献都将移动台和基站构建为二维平面模型,即2-D PPP,该模型对于闹市区呈立体分布的小基站网络并不适用,对上行信道容量也未作分析。
本文将新型3-D PPP模型应用于小基站蜂窝网络上行链路分析,推导了动态功率控制准则下的上行覆盖概率和上行信道容量的一般闭合表达式。覆盖概率和信道容量都可以通过几次数值积分直接计算得到。以实际小基站分布为参照,将本文的3-D PPP模型与传统的2-D 模型进行仿真比较。结果表明,本文提出了3-D PPP模型更适用于市区环境下的小基站网络,为小基站网络上行覆盖和上行容量提供了更准确的数值依据。
2 系统模型
2.1 信道衰落与功率控制模型
由于小基站通常分布在写字楼、商贸区等城市密集区域,因此采用适用于室内传输的Devasirvatham室内路径损耗模型[17]。为了简化问题,假设发送天线和接收天线增益均为1,无线信号频率为2.4 GHz。路径损耗可表示为
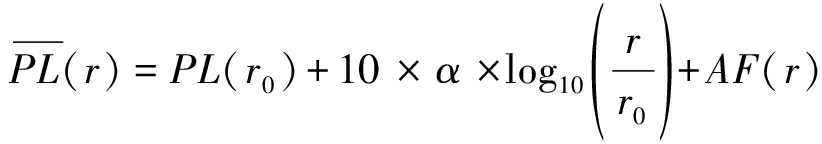
(1)
其中,r以m为单位,PL(r0)(第1 m损耗)在信号频率2.4 GHz时为40 dB,AF(r)为墙壁楼层损耗因子,以 dB为单位的表达式为AF(r)=10log10(μr)[18],参数μ是单位路径长度衰减常数。一般而言,路径损耗因子α∈(2,5),μ取0.5 dB/m。因此,路径损耗的数值表达式为Kr-(α+1),其中K为常数,
无线传输信道中除了路径损耗外,还存在阴影效应。本文采用瑞利衰落信道将用来建模移动台与基站间的阴影效应。为了简化问题,我们定义用户发射功率的基准为1,即归一化的发射功率。因此,目标基站接收到与其距离为r的移动台信号功率为gKr-(α+1),其中g综合考虑了瑞利信道和移动台发射功率的随机变量,它服从参数为1的指数分布,g～exp(1)。假设所有的移动台都采用与距离成正比的分数功率控制模型(K-1rα+1)ε以补偿路径损耗和墙壁的穿透损耗,其功率控制因子ε∈[0,1][12]。系统噪声为加性高斯白噪声,功率为σ2。
2.2 网络模型
本文考虑由同一类基站所组成小基站蜂窝网络,即网络中只有小基站这一种基站。根据PPP的掌心概率特性(Palm Probability)[19],本文着眼网络中任意选取的一个点的接收SINR,对于上行系统而言,这个点就是任意选取的一个小基站。假设小基站和移动台分别服从强度为λc和λu的齐次PPP,Φc和Φu。由于网络内用户的位置存在彼此间的独立性,这种独立性恰好与三维PPP的特性吻合(点的空间分布是独立的)。在这种情况下,假设移动台服从齐次PPP分布时完全合理的。小基站建模为服从一定参数的齐次PPP的合理性在文献[11]中已经阐述,本文不再赘述。由于TD-LTE场景中采用正交频分多址接入(Orthogonal Frequency Division Multiple Access,OFDMA)[1],网络中仅存在小区间干扰而没有小区内干扰。假设小基站的最大接入用户数为N(即,每个小基站最多提供N个正交子载波),则在基站满负荷情况下,小基站密度λc与占用相同子载波的用户密度λ相同,即,λ=λc=λu/N。假设用户通信基站的选取遵循最大接收功率原则,即每个用户选择与距离其最近的基站通信。下图1给出了小基站网络模型的示意图。图中小区0是目标小区,小区1、2是干扰小区。实线代表有用信号,虚线则是干扰信号。不失一般性,本文考虑目标基站位于坐标原点。
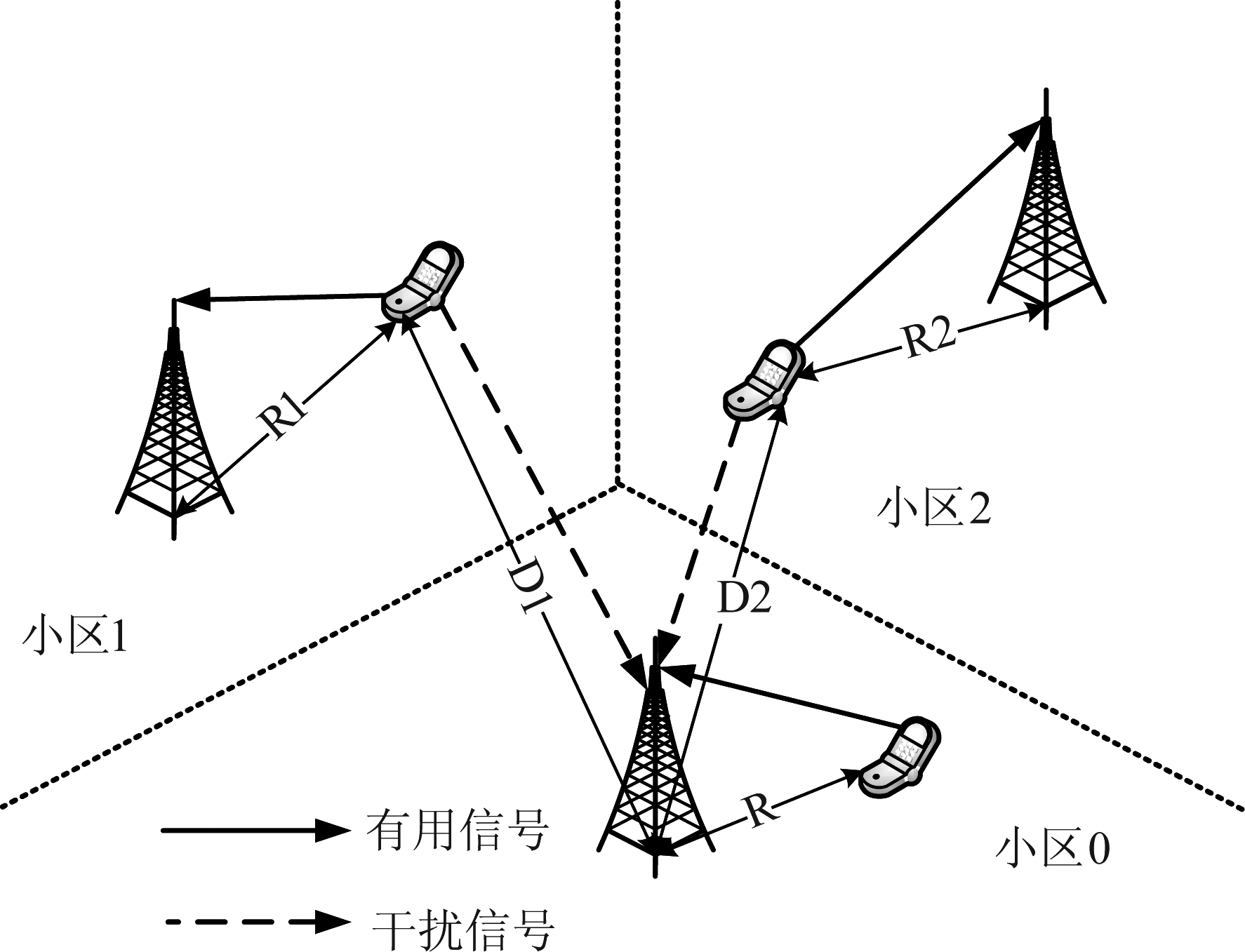
图1 小基站上行网络模型
Fig.1 Uplink network model of small cell networks
在小基站网络中,记干扰用户的集合为Z,干扰用户到目标基站和其通信基站距离的集合分别为Dz,Rz。
综合以上系统模型,在小基站蜂窝网络中,目标基站的接收SINR为
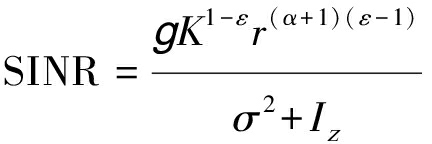
(2)
其中,
为累计干扰(相邻小区占用相同子载波的所有用户的干扰之和),gz为独立同分布随机变量,且g～exp(1),σ2为归一化的加性噪声功率。当ε=1时,公式(2)的分子变为随机变量g,意味着通过功率控制将路径损耗和墙壁的穿透损耗完全抵消,当ε=0时,意味着不做任何功率控制,所有移动台以相同的功率发射信号。
根据3-D PPP理论,目标基站到距其最近的移动台之间的距离r服从分布:
即在以目标基站为球心,R为半径的球体内没有任何移动台[19],其概率密度函数为
(3)
3 上行覆盖概率与信道容量
本节首先推导基于3-D PPP模型的小基站蜂窝网络上行覆盖概率的数学表达式,然后进一步讨论上行信道容量。
覆盖概率定义为pc(T,λ,α,ε)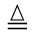
P{SINR>T},即基站的上行SINR大于信干噪比门限T的概率。
定理1 三维小基站网络上行覆盖概率为:
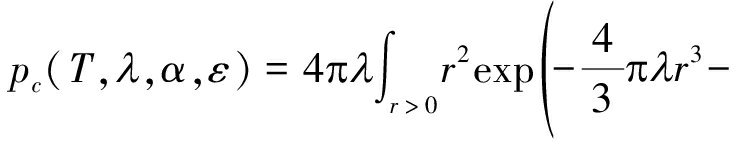
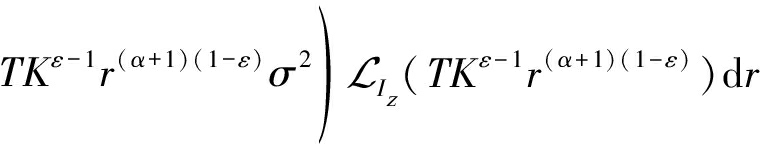
(4)
其中,
为随机变量Iz的拉氏变换
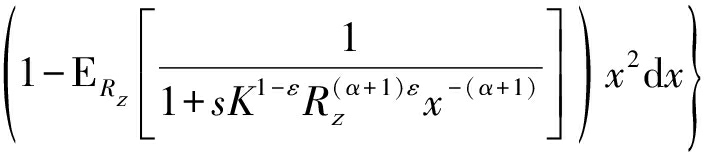
(5)
证明 根据覆盖概率的定义,3-D泊松分布特性以及瑞丽衰落特性,可得
pc(T,λ,α,ε)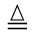Er[P{SINR>T|r}]
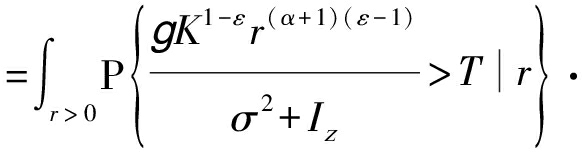
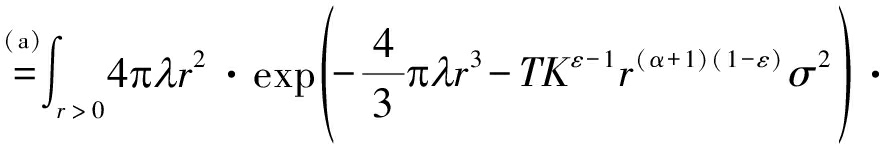
(6)
其中,步骤(a)依据g～exp(1)以及拉氏变换的定义
接下来,
可以进一步表示为
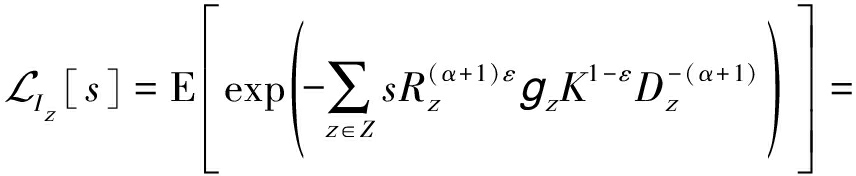
(7)
根据gz的独立性,公式(7)可改写为
(8)
Rz为所有干扰用户到各自通信基站间的距离,为独立同分布随机变量,结合gz～exp(1),公式(8)可表示为
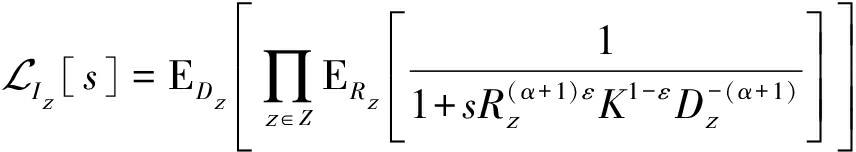
(9)
根据PPP的概率生成函数(probability generating functional,PGFL)[19],拉氏变换可进一步表示为
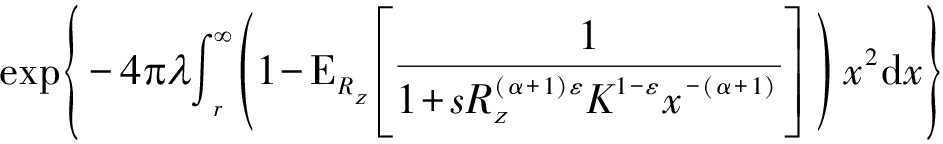
(10)
由于Rz和R为独立同分布随机变量,且具有相同的分布特性(由公式(3)给出),因此,公式(10)中的期望表达式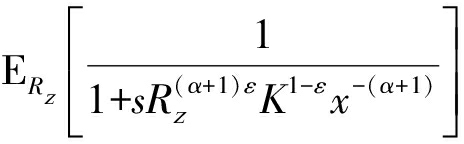
可化简为
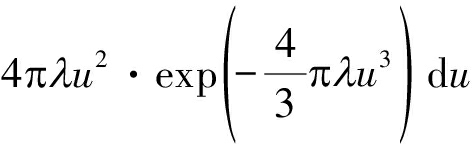
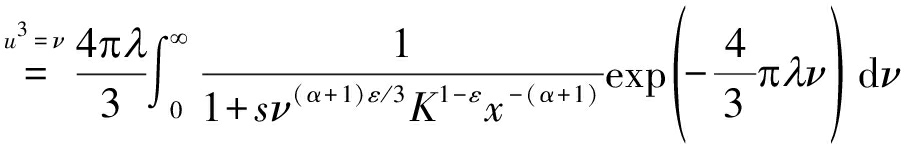
(11)
结合公式(6),则上行覆盖概率可表示为
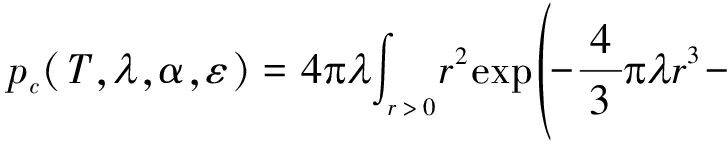
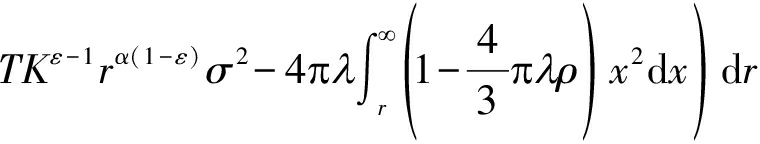
(12)
其中,
而常数K在化简过程中抵消了。
我们注意到,覆盖概率的计算涉及到三个积分,可以通过数值计算的方法计算得到。在下一节中,我们将通过仿真的手段验证该上行链路的覆盖概率的表达式的准确性。
接下来,我们将目光转向小基站网络上行信道容量的研究。首先,根据香农定理,推导目标小区单位带宽下的上行信道容量(即频谱效率,单位:bps/Hz),然后,给出在实际系统带宽和多用户连接场景下单个用户上行信道容量的数学表达式。
定理2 三维小基站网络单位带宽上行信道容量为:
C0(λ,α,ε)=
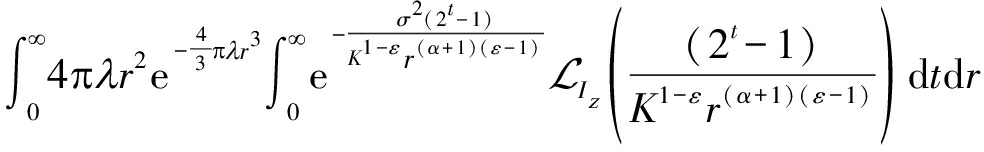
(13)
其中,拉氏变换
由公式(10)确定。
证明 根据香农定理,
C0(λ,α,ε)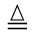E[log2(1+SINR)]
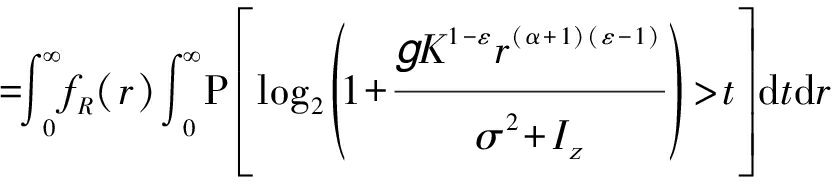
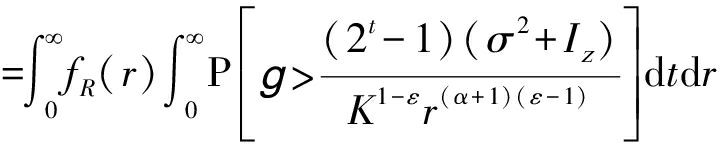
其中,
且
在实际系统带宽和基站满负荷连接场景下,目标小区及其用户间上行链路信道容量则为
(14)
其中,W表示系统带宽,N为基站连接的用户数,C0(λ,α,ε)由公式(13)确定。
4 仿真结果及分析
4.1 仿真环境
考虑一个分布有大量小基站的城市中心球形区域,其半径R=50 m。根据移动运营商提供的数据,小基站密度设置为5×10-3/m3,则在基站满负荷情况下占用相同子载波的用户密度也为5×10-3/m3。用户到目标基站的距离
其中用户坐标(x,y,z)满足x,y,z在[-R,R]间随机分布。对于传统的2-D模型,则需将所有用户投影到以R为半径的平面圆形区域,所有用户到目标基站(位于圆心)的距离需重新计算。除特殊说明外,其他仿真参数设置如下:路径损耗指数α=3.8,功率控制因子ε=0.8,用户最大发射功率23 dBm。
4.2 仿真环境
图2和图3将本文提出的3-D模型与传统的2-D模型进行仿真比较,以实际分布为参照。横坐标SINR门限,纵坐标为覆盖概率。图2为有噪声情况下的仿真比较,噪声功率σ2=-104 dBm,图3为无噪声情况下的仿真比较。
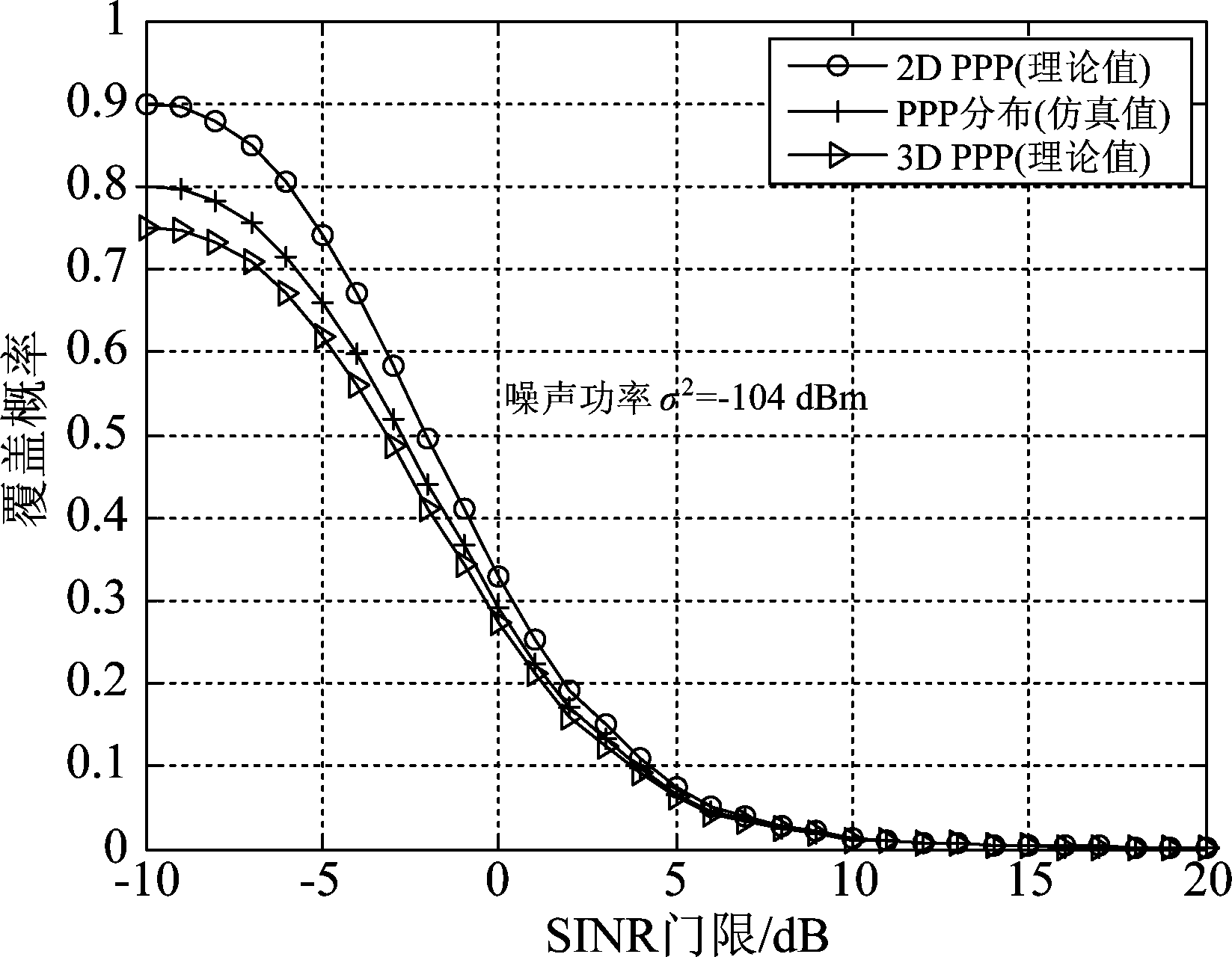
图2 噪声环境下上行覆盖概率比较
Fig.2 Comparison of the uplink coverage
probability (σ2=-104 dBm)
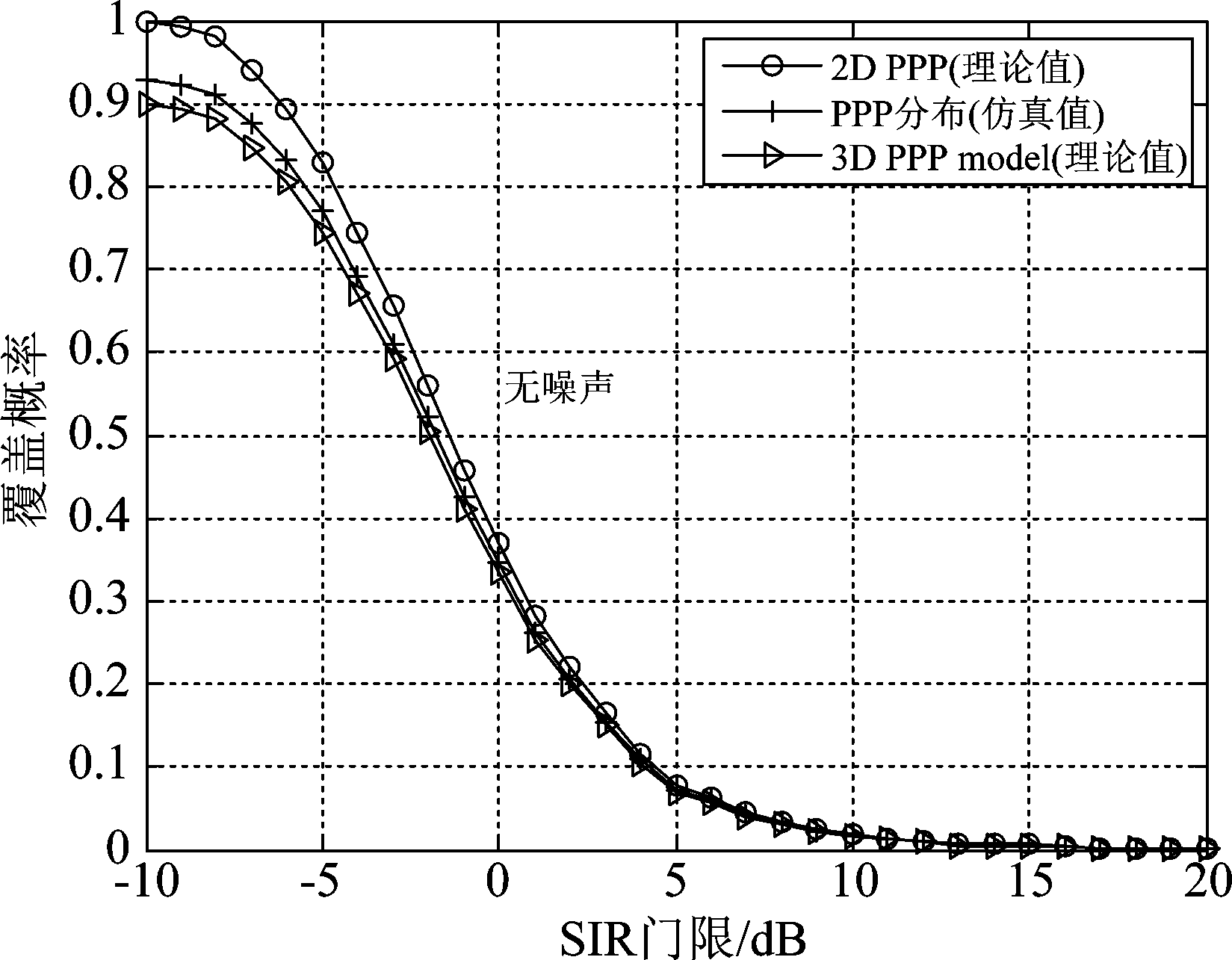
图3 无噪声环境下上行覆盖概率比较
Fig.3 Comparison of the uplink coverage probability (no noise)
从图2和图3中可以看出,相比较传统的2-D模型,在3-D模型下得到的覆盖概率更接近实际环境下的仿真和实验值。很明显,3-D模型能够更准确地描述小基站蜂窝网络的上行覆盖情况。造成这一现象的主要原因是2-D模型中用户到基站的距离是实际距离的投影,这显然不适合SINR的计算。例如,如果标记基站正好位于某用户的正上方,一旦它们被投影到一个平面上,它们之间的距离将为零。然而,本文提出的3-D模型不存在这样的问题。除此之外,对比本文上行覆盖概率和文献[11]下行覆盖概率曲线可以发现:对于上行链路,本文提出的3-D PPP方法只在低SIR/SINR门限上有一定优势;而对于下行链路,3-PPP分析方法比2-D PPP更具优势。其原因在于,蜂窝网络中移动台的发射功率要远小于基站,从而上行链路的SIR/SINR值要明显低于下行链路(尤其是SINR值),随着门限值的增大,覆盖概率的仿真值和各种模型下的理论值都会快速收敛到0。因此,在高信噪比时本文的3-D PPP分析方法对于下行链路就体现不出优势了。实际上,对于下行链路而言,当SIR/SINR门限值达到30 dB时,仿真值和理论值也都收敛到0,3-D PPP分析方法同样体现不出优势。
由于上述仿真结果已经表明,3-D PPP模型优于传统的2-D 模型,接下来的仿真我们不再将本文的3-D PPP模型与传统2-D模型做比较。
4.3 相关参数对覆盖概率的影响
图4展示了相同子载波用户密度的变化对覆盖概率的影响。在仿真过程中,SINR门限设置为-5 dB,同一子载波用户密度在1×10-3/m3至10×10-3/m3间变化。从该图中可以看出,网络上行覆盖概率随相同子载波中用户密度的增加而减小。这主要是由于同一子载波中移动用户的增加造成了较高的干扰和较低的SINR。与此同时,目标小区的上行信道容量也随之减小。然而,关注单个小区的覆盖和传输容量是不全面的,应该把着眼于整个区域所有小区传输容量的变化上,这将是我们后续研究的一部分。
图5展示了路径损耗因子对覆盖概率的影响。在仿真过程中,SINR门限设置为-5 dB和0 dB,路径损耗因子在2至5之间变化。从该图中可以看出,网络上行覆盖概率随路径损耗因子的增大而增大。其原因为:对于接收端而言,路径损耗因子的增大则意味着接收功率下降(信号功率和干扰功率均下降);而干扰为所有相邻小区干扰信号的累加,下降幅度较信号而言更为明显,导致SIR/SINR反而增大,上行覆盖概率也随之增大。但这并不意味着路径损耗越大越好,因为随着路径损耗的增大,接收信号功率下降,一旦达不到解调设备的接收灵敏度,信号将无法解调。
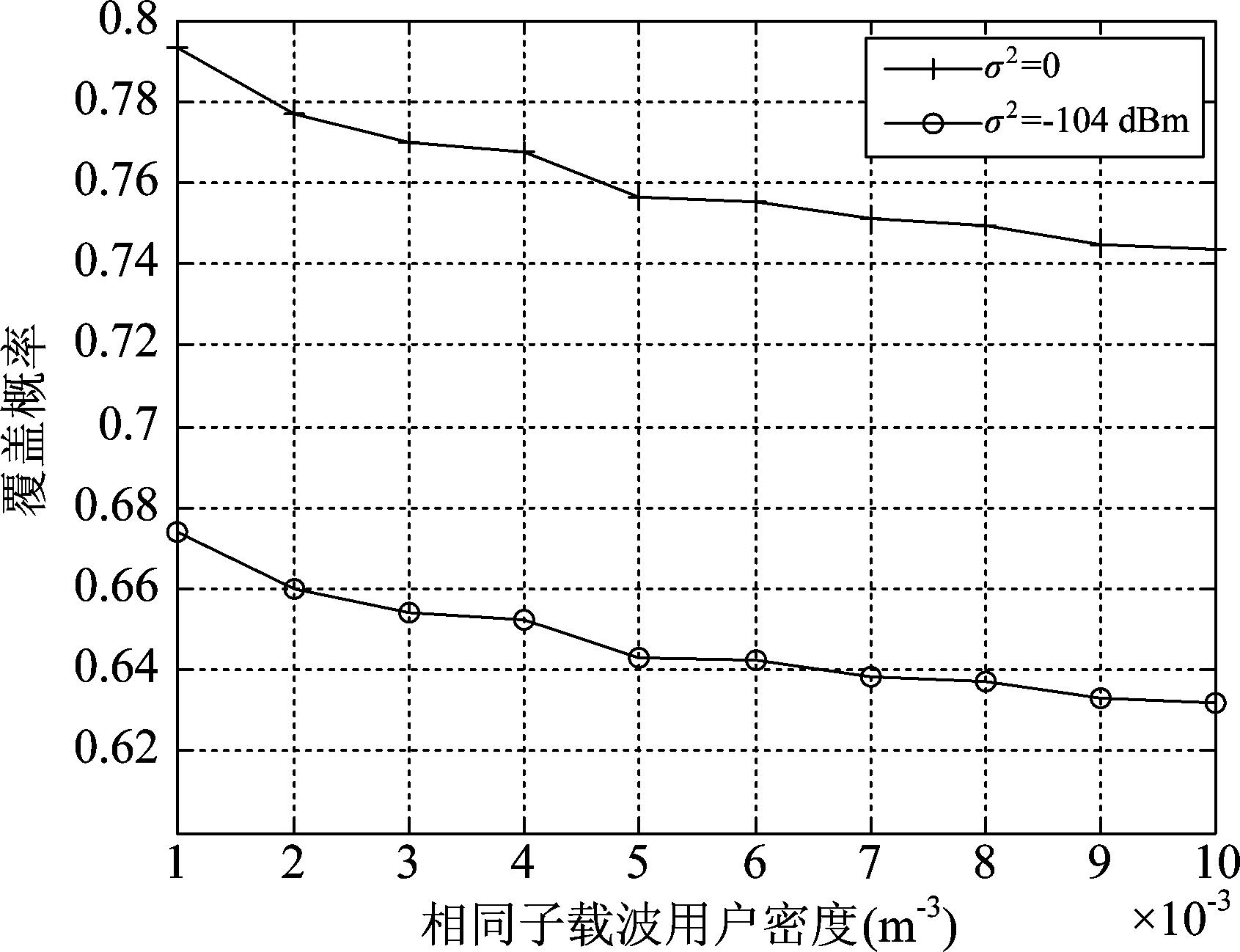
图4 相同子载波用户密度与覆盖概率的关系
Fig.4 Relationship between coverage and user density in the same sub carrier
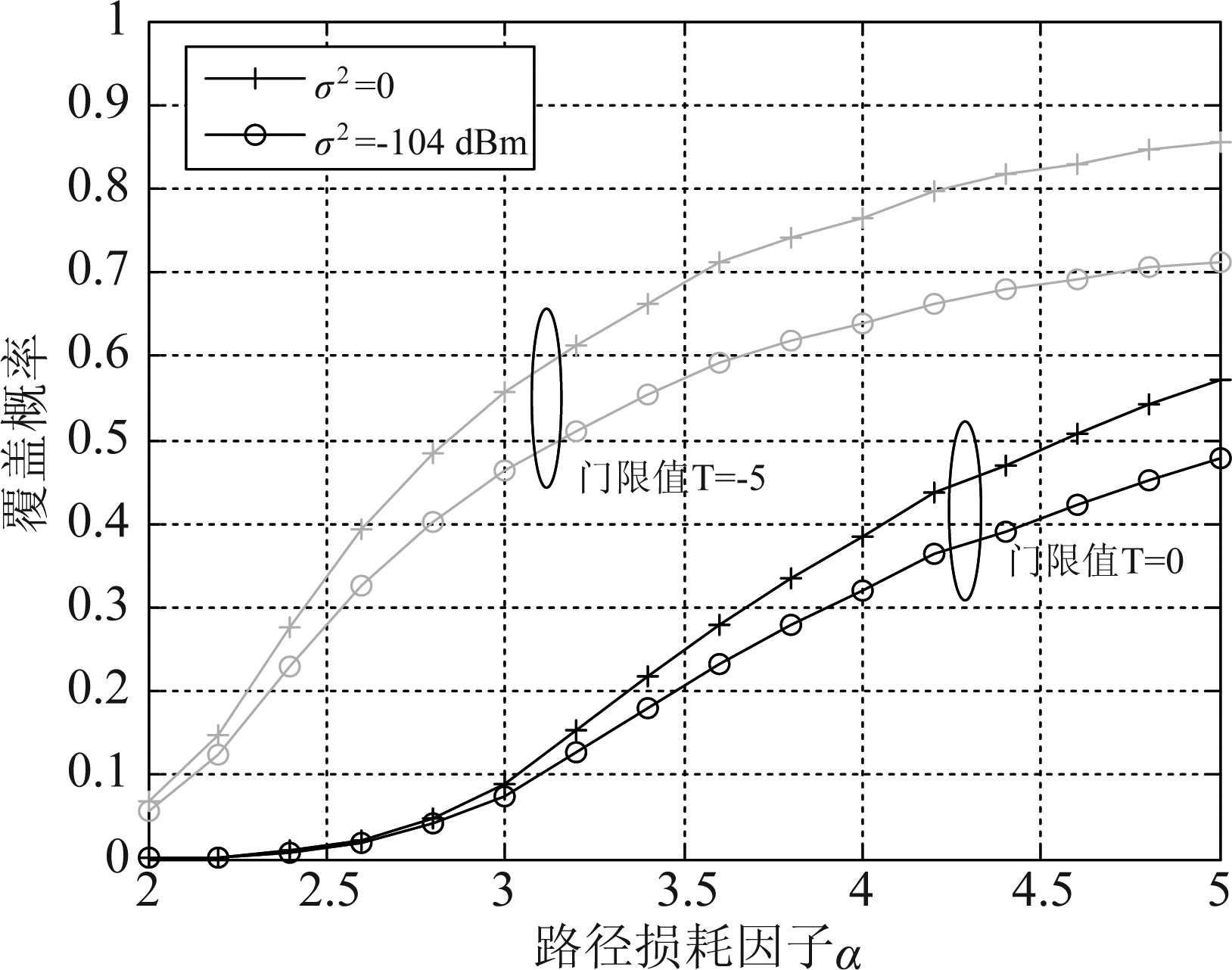
图5 路径损耗因子α与覆盖概率的关系
Fig.5 Relationship between coverage and path loss factor α
4.4 上行平均信道容量
图6和图7分别展示了不同路径损耗因子下(α=2.5、3.25和 4)上行信道容量与功率控制因子ε 和基站连接用户数N之间的关系,以实际环境的仿真值为参照。这两幅图表明,本文推导的信道容量表达式(理论值)非常接近实际环境下的仿真值。从图6中可以看出,信道容量随着ε的增大而减小。其原因在于,功率控制因子ε越大,对路径损耗的补偿越充分,干扰也就随之增大,因此SINR和信道容量自然会随之减小。从图7中我们可以发现,随着基站连接用户数N的增大,信道容量也逐渐减小。其原因在于,随着N的增加,小基站将连接更多的用户,每个用户分配的系统带宽将减小,信道容量也随之下降。
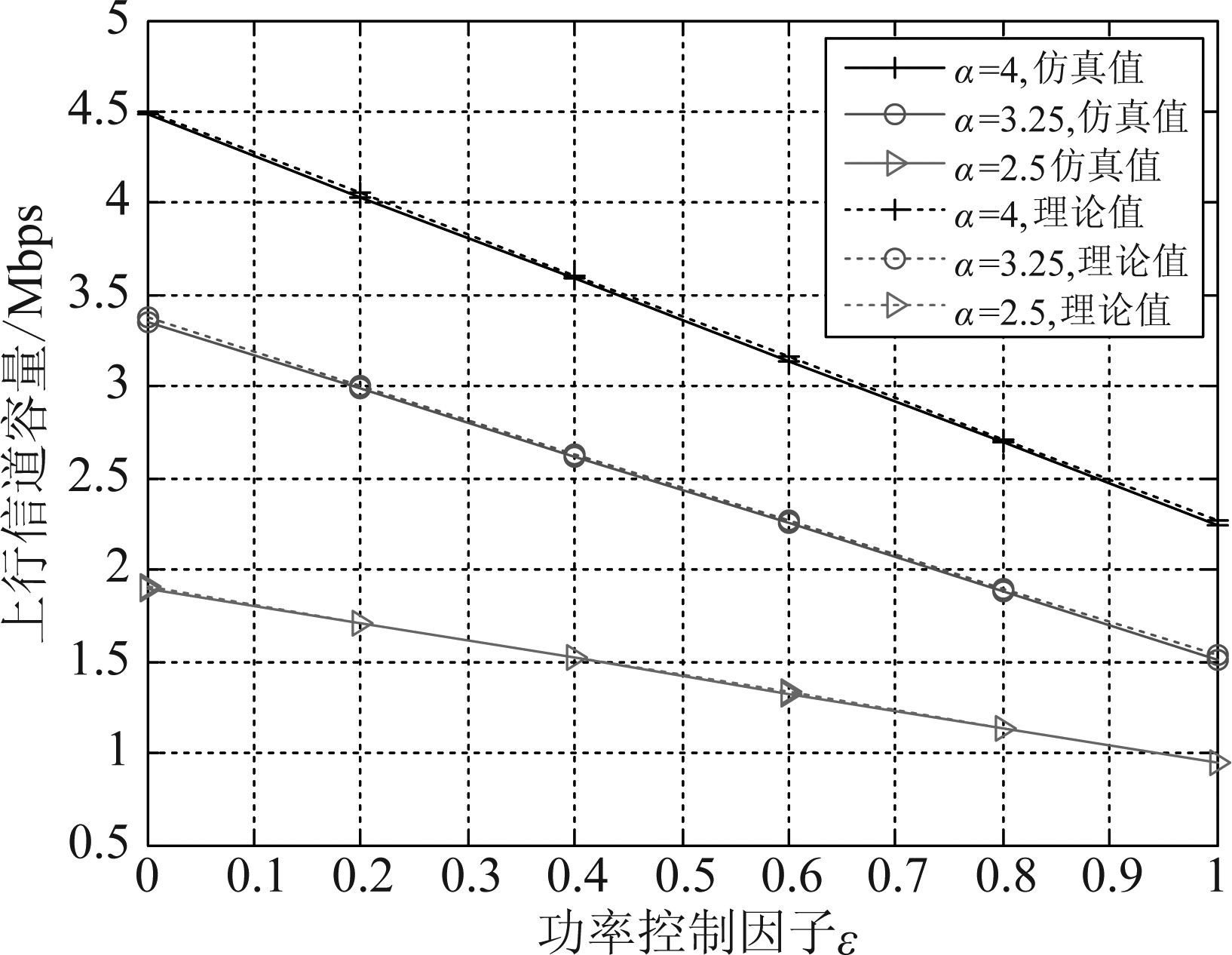
图6 信道容量与功率控制因子ε的关系
Fig.6 Average rate as a function of power control parameter ε
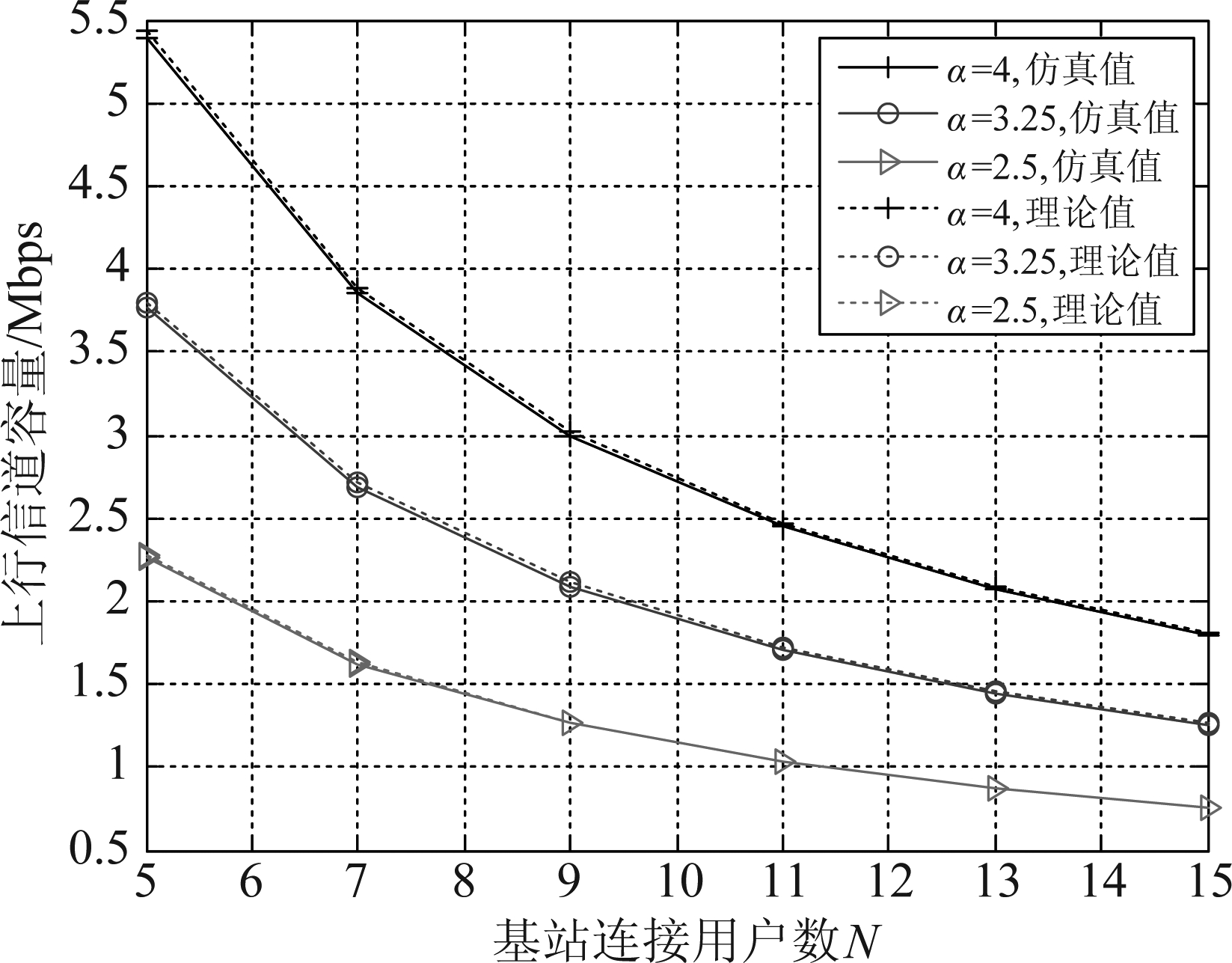
图7 信道容量与基站连接用户数N的关系
Fig.7 Average rate as a function of the connection number of small cell N
5 结论
本文提出了一种新的上行小基站网络模型,将一定区域内用户的分布建模为3-D PPP,利用点过程理论和随机几何方法推导了上行覆盖概率和信道容量的简化表达式。仿真结果表明,本文所提出的3-D PPP模型在精度上比传统的2-D模型更接近实际情况。对信道容量的仿真进一步提供了对其他上行链路性能的分析。未来的工作重点将是对异构蜂窝网络进行建模和分析。
[1] Labib M, Marojevic V, Reed J H, et al. Enhancing the Robustness of LTE Systems: Analysis and Evolution of the Cell Selection Process[J]. IEEE Communications Magazine, 2017, 55(2): 208-215.
[2] Shafi M, Molisch A F, Smith P J, et al. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment and Practice[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1201-1221.
[3] Xiao S, Zhou X, Yi Y W, et al. Robust Resource Allocation in Full-Duplex-Enabled OFDMA Femtocell Networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(10): 6382- 6394.
[4] Lin P, Zhang J, Chen Y, et al. Macro-femto heterogeneous network deployment and management: from business models to technical solutions[J]. IEEE Wireless Communications, 2011, 18(3): 64-70.
[5] Shamai S, Wyner A D. Information-theoretic considerations for symmetric, cellular, multiple-access fading channels. I[J]. IEEE Transactions on Information Theory, 1997, 43(6): 1877-1894.
[6] Shamai S, Wyner A D. Information-theoretic considerations for symmetric, cellular, multiple-access fading channels. II[J]. IEEE Transactions on Information Theory, 1997, 43(6): 1895-1911.
[7] Somekh O, Shamai S. Shannon-theoretic approach to a Gaussian cellular multiple-access channel with fading[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1401-1425.
[8] Dhillon H S, Ganti R K, Baccelli F, et al. Modeling and Analysis of K-Tier Downlink Heterogeneous Cellular Networks[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(3): 550-560.
[9] Haenggi M. Stochastic geometry for wireless networks[M] Cambridge: Cambridge University Press, 2012.
[10] Andrews J G, Baccelli F, Ganti R K. A Tractable Approach to Coverage and Rate in Cellular Networks[J]. IEEE Transactions on Communications, 2011, 59(11): 3122-3134.
[11] Pan Z, Zhu Q. Modeling and Analysis of Coverage in 3-D Cellular Networks[J]. IEEE Communications Letters, 2015, 19(5): 831- 834.
[12] Novlan T D, Dhillon H S, Andrews J G. Analytical Modeling of Uplink Cellular Networks[J]. IEEE Transactions on Wireless Communications, 2012, 12(6): 2669-2679.
[13] Mondal W U, Das G. Uplink User Process in Poisson Cellular Network[J]. IEEE Communications Letters, 2017, 21(9): 2013-2016.
[14] Tang Q, 
ngel M. Groba, Ju
rez E, et al. Closed-loop power-control governor for multimedia mobile devices[J]. IEEE Transactions on Consumer Electronics, 2017, 63(2): 153-161.
[15] Bayat S, Louie R H Y, Zhu H, et al. Distributed User Association and Femtocell Allocation in Heterogeneous Wireless Networks[J]. IEEE Transactions on Communications, 2014, 62(8): 3027-3043.
[16] Bao W, Liang B. Stochastic Analysis of Uplink Interference in Two-Tier Femtocell Networks: Open Versus Closed Access[J]. IEEE Transactions on Wireless Communications, 2015, 14(11): 6200- 6215.
[17] Omri A, Hasna M O. Modelling and performance analysis of 3-D heterogeneous cellular networks[A]. Proceedings of the 2016 IEEE International Conference on Communications(ICC’16)[C]. Kuala Lumpur, 2016: 1-5.
[18] Ma Y, Wang X, Wang H H, et al. A Joint Feedback Bit and Power Allocation Strategy for Multi-cell Systems over Composite Fading Channels[J]. Chinese Journal of Electronics, 2016, 25(3): 541-550.
[19] Sung N C, Dietrich S, Wilfrid S K, et al. Stochastic Geometry and Its Applications[M]. 3rd Edition. U.S.: John Wiley & Sons Inc., 2013.
