1 引言
卫星通信系统运营中的载波管理和RFI(Radio Frequency Interference,无线频率干扰)一直是影响卫星通信服务质量的主要问题。在某些经常变更终端位置和配置的特殊应用场合,由于不当操作或错误配置等原因,导致其他各卫星通信运营方经常面临大量“流氓载波”干扰信号。载波标签[1] (CID, Carrier Identification)技术则是近年来提出的从技术与标准上根本解决卫星通信RFI问题的创新技术。该技术在不影响原通信模式和不增加额外频带资源的前提下,通过在原通信信号上叠加高倍扩频信号[2]的方式来发送随路信息,以便发生RFI问题时能快速提取干扰载波的相关用户属性及包括设备唯一识别码在内的设备信息。从而通过应用CID技术,使得能快速识别干扰载波、快速响应RFI问题、缩短RFI事件处理周期、降低RFI事件处理成本、提升卫星通信服务质量。
DVB-CID信号为卫星通信信号(主载波)上叠加了一个高倍常规短码直扩调制信号(CID信号),由于主载波信号功率谱密度比CID信号的功率谱密度值最大高出27.5 dB,其属于一种幅度差异很大的混合信号。2005年,Nguyen等利用强信号[3]的幅度、载频等参数估计结果对强信号进行波形重构,通过抵消获得弱信号实现解调。2007年,付迪等[4]在非对称PCMA卫星信号的截获中利用同频带信号信噪比大于5 dB时,可实现盲解调。2010年廖灿辉等[5]对功率较强、带宽较宽调制信号掩盖下是否隐藏有功率较弱、带宽小于主载波4倍以上调制信号的检测问题进行研究提出了一种根据调制信号的星座特性抵消强信号的干扰的算法。2017年黄强等[6]在非对称PCMA 信号盲分离中引入非线性滤波的方法对弱信号的波形进行预测,从混合信号中减去预测的弱信号波形来降低强信号解调误码率。2018年谢岸宏等[7] 采用具有循环平稳特性的大信号掩盖不具有循环平稳特性的弱信号,在大信号和弱信号的功率比高于7 dB时,盲检测不到弱信号的存在,今年以来张乾[8]、余昆[9]等人对扩频信号在不同条件下的检测性能进行分析。由于实际接收信号发射端载波不稳定使得波形重构解调运算复杂,不利于工程实现,并考虑到主载波对CID 信号解扩的干扰影响,且DVB-CID信号属于文献[5]所提到的混合信号类型,因此本文采用星座特性抵消强信号的干扰的思路进行信号预处理,其运算量小,易于工程实现。
本文针对DVB-CID信号进行解调,有效解决了载波管理和RFI影响的问题。在主载波抵消采用文献[5]星座图抵消方式的情况下,本文提出了一种针对常规短码直扩调制信号(CID信号)解调的抗频偏算法,算法采用了样点级的伪码序列匹配解调方法,即直接对定时同步模块之前的采样数据进行伪码序列匹配解调。仿真主要研究了主载波信噪比在0 dB到6 dB下CID信号的解调误码率。
2 信号模型
DVB-CID体制中,接收信号是由一个MPSK、QAM或APSK调制的主载波信号和一个高倍扩频短码信号(CID信号)混合组成的调制信号,信号模型如下式:
y(t)=xA(t)+xC(t)+n(t)
(1)
xA(t)表示主载波信号,其符号速率为RA;xC(t)表示CID信号,其采用4096倍短码m序列扩频方式,扩频后符号速率为RC,调制方式为BPSK,成型函数为滚降系数为α=0.35的根升余弦函数,频偏相对主载波频偏为220 Hz;n(t)为高斯白噪声。主载波与CID信号符号速率和功率谱密度相对值PSDCID(dB)设置如表1所示。
表1 CID信号相对主载波信号功率谱密度值
Tab.1 Relative PSD levels for the DVB CID signal
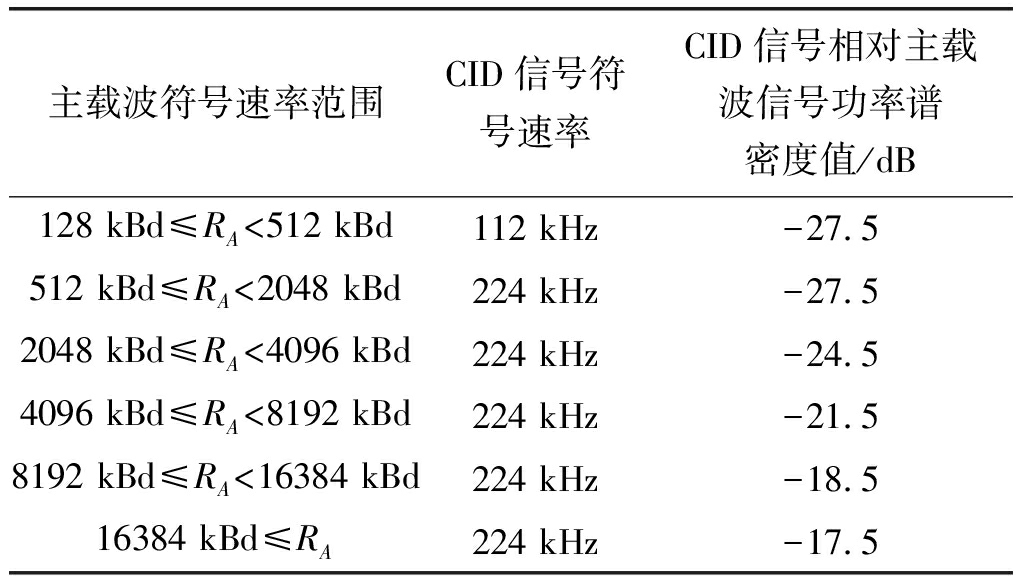
主载波符号速率范围CID信号符号速率CID信号相对主载波信号功率谱密度值/dB128 kBd≤RA<512 kBd112 kHz-27.5512 kBd≤RA<2048 kBd224 kHz-27.52048 kBd≤RA<4096 kBd224 kHz-24.54096 kBd≤RA<8192 kBd224 kHz-21.58192 kBd≤RA<16384 kBd224 kHz-18.516384 kBd≤RA224 kHz-17.5
CID信号符号速率固定为112 kHz和224 kHz为了使得其带宽窄于主载波且充分被主载波覆盖。CID信号的叠加对主载波信号的影响非常微小,可以用主载波信噪比的降低量来度量该影响。记SNIRA(dB)为主载波带内信噪比、pA(dB)为主载波功率谱密度,pC(dB)为CID功率谱密度,pN(dB)噪声功率谱密度,则pC=pA·10PSDCID/10(dB),且主载波功率为PA=pARA(dB)、CID信号功率为PC=pCRC(dB)、主载波带内噪声功率为PN=pNRC(dB),且PA/PN=10SNIRA/10,由于CID信号带宽窄于主载波且完全被主载波覆盖,则主载波信噪比降低量为DegA(dB),如下式:
DegA=10log10((PA/PN)/(PA/(PN+PC)))
=10log10(1+PC/PN)
=10log10(1+RC/RA10(SNIRA+PSDCID)/10)
(2)
由式(2)结合表1可知, SNIRA相同的情况下,随着RA成倍数增加,PSDCID增大3 dB基本不改变DegA的大小,如图1所示,当RA等于4 MHz和8 MHz时,DegA曲线基本重合,DegA的值基本不变;SNIRA相同的情况下,随着RA的增大,DegA的值处于减小趋势;当RA等于2 MHz和4 MHz时(RC和PSDCID保持不变),DegA的值在减小。如图2所示,随着RA的增大,DegA在减小;虽然随着SNIRA增大,DegA的值在增大,但是DegA值基本处于一个很小的范围内;当SNIRA取6 dB、14 dB和18 dB时,虽然DegA值在增大但其取值很小。综上所述,由于主载波信噪比降低量DegA处于一个较小值区间内变化,所以CID信号的叠加基本不影响原主载波通信模式。
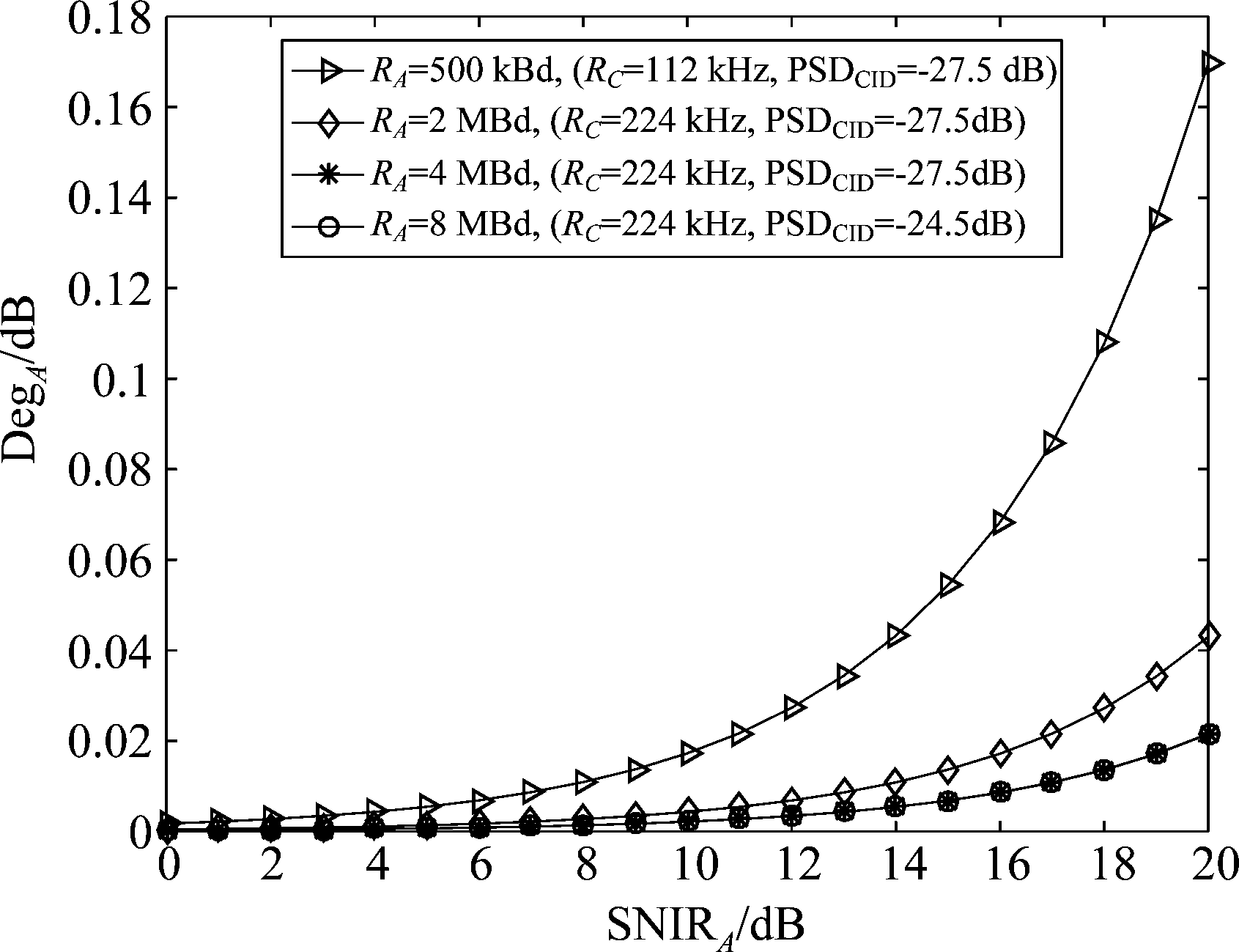
图1 主载波信噪比降低量曲线
Fig.1 Degradation of the SNR of the main carrier
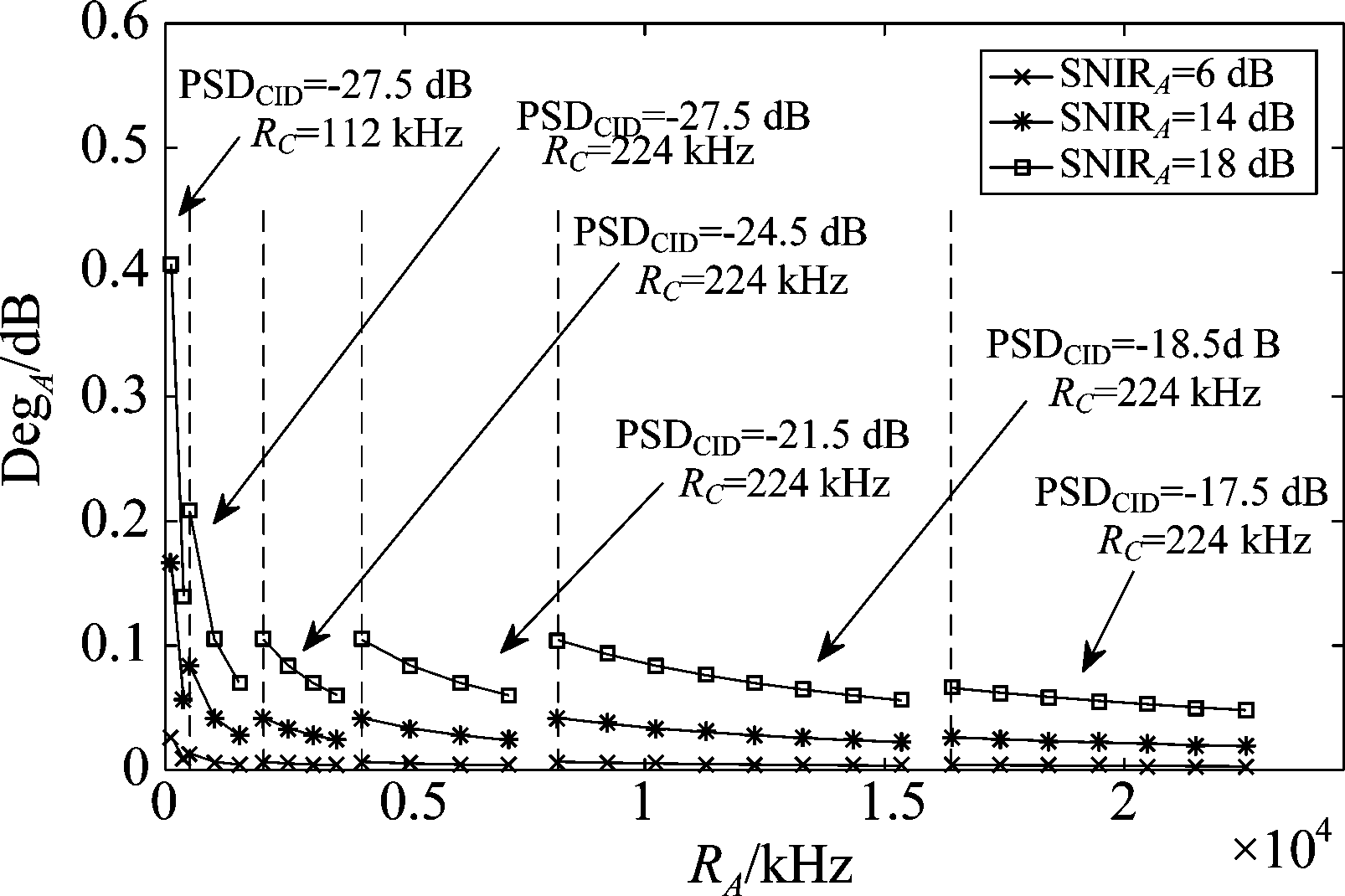
图2 主载波信噪比降低量曲线
Fig.2 Degradation of the SNR of the main carrier
3 DVB-CID解调算法
3.1 解扩条件分析
接收信号由三部分组成,分别为主载波信号、CID信号和噪声,为了解调CID信号,可以先重构消除主载波信号。当不抵消主载波信号时,将主载波视为干扰噪声,则CID信号的带内信噪比为SNIRC(dB),如下式:
SNIRC=10log10(pCRC/(pNRC+pARC))
=PSDCID+SNIRA+10log10(1/(1+10SNIRA/10))
≈PSDCID
(3)
当主载波完全抵消时,CID信号的带内信噪比为![]() 如下式:
如下式:
=PSDCID+SNIRA
(4)
由式(3)和式(4)可知,主载波完全抵消时比主载波不抵消时的CID信号的带内信噪比大SNIRA。由于CID信号的扩频增益为G=10log104096≈36 dB,在主载波完全抵消和完全不抵消下CID信号的解调性能分别与BPSK调制信号带内信噪比为(G+SNIRA+PSDCID)和(G+PSDCID)下的解调性能一致,由此可知,当SNIRA=10 dB时,主载波完全抵消比不完全抵消高出10 dB的信噪比,因此主载波抵消对于CID信号解调会带来更好的效果。
3.2 基于星座图的主载波消除算法
为了消除主载波,可以采取重构抵消方式,文献[3- 4]已给出相应的算法实现,也可以从主载波解调星座中对其进行消除[5]。因为基于星座图消除主载波方式在工程实践上运算量远小于重构抵消方式,易于工程实现,所以本文采用基于星座图方式消除主载波。
由于恒模调制的主载波信号在理想的定时判决点处不存在符号串扰,则接收信号经匹配滤波后在定时判决点处的幅度抖动完全由噪声和CID信号引起。从频域上分析,主载波星座序列xA(i)与以主载波信号符号速率为采样时钟对CID信号进行采样后的信号xC(i)频谱示意图如下:
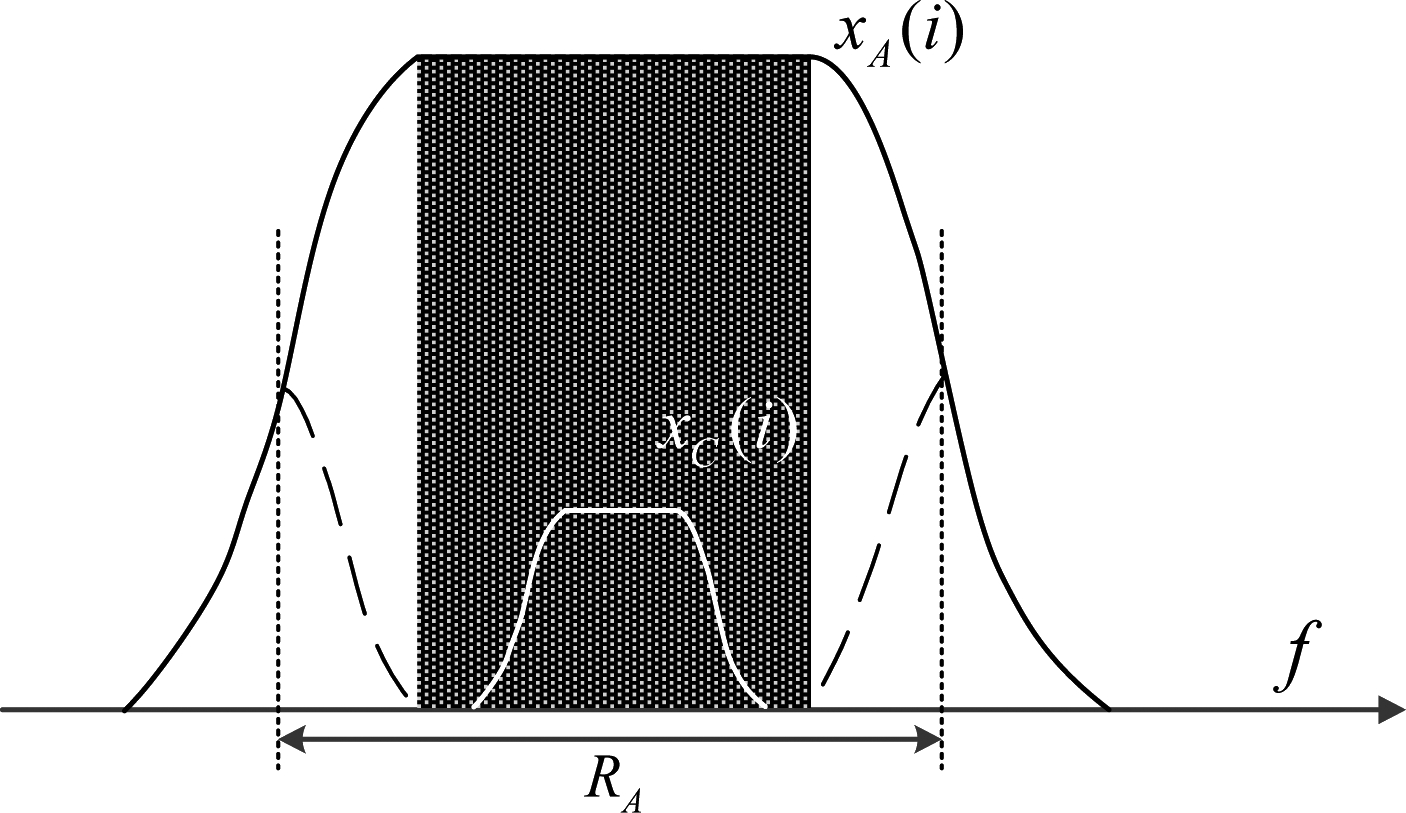
图3 主载波幅度谱示意图
Fig.3 Amplitude spectrum of the main carrier
上图中曲虚线表示主载波信号经过定时判决后周期性的频谱重叠部分,由于CID信号带宽窄于主载波带宽4倍以上且充分被主载波覆盖,根据奈奎斯特采样定理可知阴影区域中的CID信号频谱信息无损失且完全被保留,因此星座图抵消主载波的方式是可行的。
DVB-CID信号解调时经过匹配滤波、定时同步[10]和载波同步后,存在CID信号时的复基带混合信号在主载波信号定时判决点处的值简化为:
y(i)=xA(i)+n(i)
(5)
n(i)为CID信号与噪声的和信号。由于噪声和CID功率相对主载波很低,式(5)中y(i)实部与虚部的大小及正负号将由xA(i)实部与虚部的大小及正负号决定。设Uq(q=1,2,3…)代表主载波解调后的第q个星座, mq为第q个星座的中心位置, Nq为第q个星座的点数,有:
(6)
对y(i)作如下映射,用以消除主载波信号的影响。当y(i)∈U1时,对y(i)的映射示意如图5所示。
y1(i)=y(i)-mq y(i)∈Uq
(7)
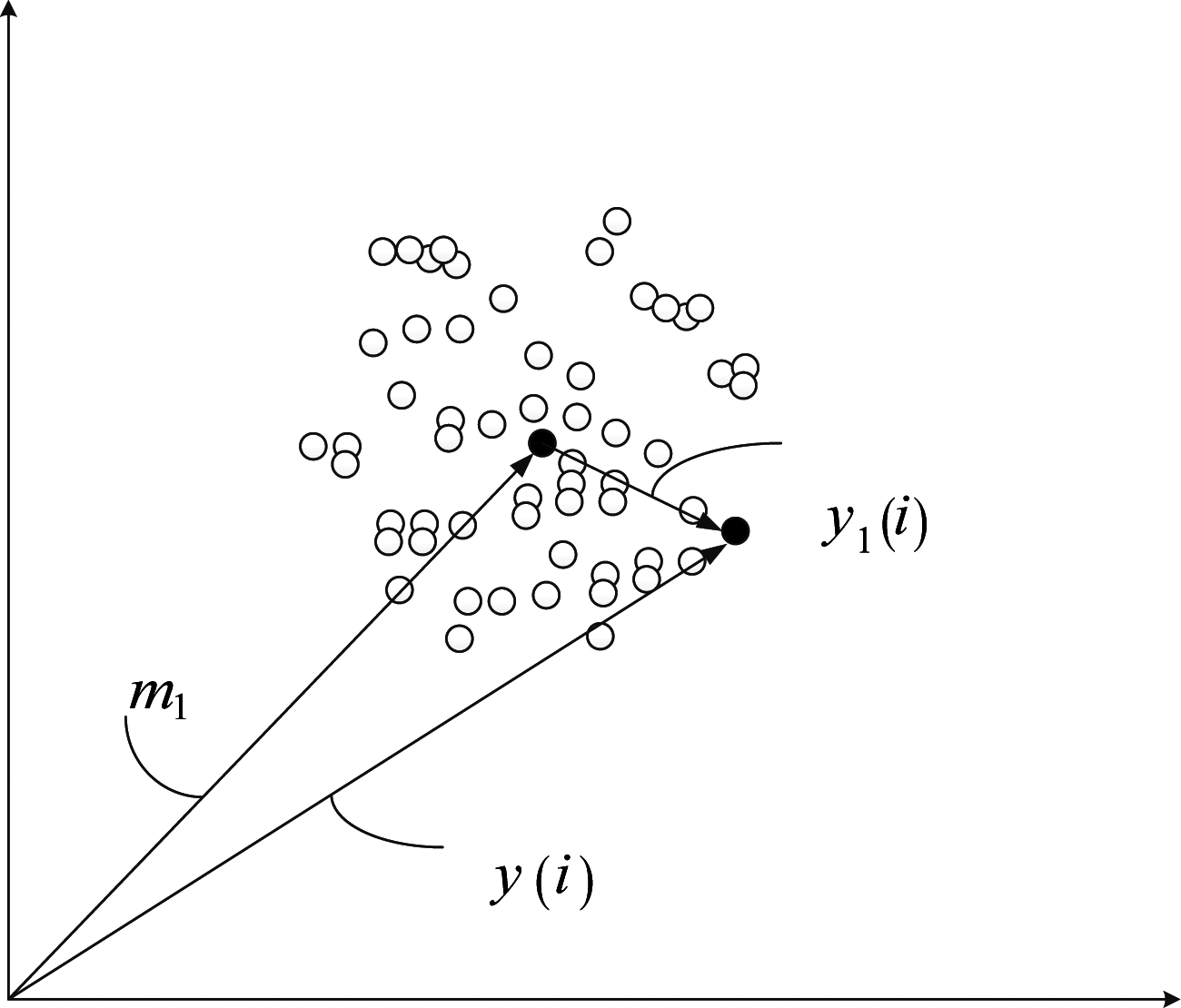
图4 y(i)的映射示意图
Fig.4 Mapping diagram of y(i)
CID信号的解调性能除了信道噪声外主要受到其他3个干扰因素影响:一是主载波叠加高斯噪声,如图3所示,由于主载波信号经过定时判决后,主载波频域波形曲虚线部分互补叠加,当主载波符号速率相对CID信号基带带宽较小使得CID信号的频谱位于主载波信号频谱滚降区域时,主载波叠加噪声对CID信号产生影响;二是上述主载波抵消过程中星座点中心值估计不准,导致主载波抵消残留项对CID信号造成干扰,如图4所示,由于星座图中心位置mq是由定时判决值y(i)取中心值得到,当mq并不是准确中心位置,会带来主载波残留信号干扰影响;三是主载波解调有误码率导致对CID信号造成干扰。虽然主载波消除也会带来以上抵消不完全因素的影响,但是相对于主载波不抵消的情况这些影响因素都是非常微弱的,主载波抵消大幅度提升了CID信号的解调性能。基于星座的主载波抵消流程框图如图5所示:
图5 主载波抵消流程框图
Fig.5 Cancellation diagram of the main carrier
3.3 基于波形的抗频偏解扩
一般解扩包括载波同步、扩频码捕获和扩频码跟踪过程[11],其均为反馈方式,但本文DVB-CID信号处理中利用星座图抵消的方式消除主载波的过程中利用反馈方式解调主载波信号已经对不稳定的载频锁定跟踪,又因为DVB信号载频与CID信号载频固定差为220 Hz,则主载波消除后的CID信号的载频可认为保持不变,则保证了CID信号利用本文抗频偏解扩时相关系数峰值幅度位置按照相隔固定的伪码周期重复出现,可利用此周期特性对进行解扩,则CID信号解扩时避免了传统扩频信号解调时需要载波提取环节,无需设计复杂的反馈网络。
本文解扩算法是基于相关方式下的,即利用扩频码与接收信号在匹配峰值位置的相关系数的幅度来实现解扩的初始同步,利用信源数据是以扩频码为周期的调制信号的特性进行解扩跟踪,根据相关系数的相位进行符号判决来解扩得到基带信号。由于DVB-CID信号经过主载波消除后得到的CID信号相对主载波载频有220 Hz的固定频偏,取CID信号符号速率为224 kHz,在一个扩频码周期内扩频码的相位变化最大为8π,由此可知扩频码对频偏特别敏感,CID的解扩必需是抗频偏的,以下在相关方式解扩的基础上提出了一种基于波形的抗频偏解扩算法,其无需定时同步和载波同步便可解扩,极大有利于工程实践。
零中频直接扩频复基带信号经过匹配滤波、d倍符号速率采样率变换后与已知的扩频伪码调制星座波形做相关运算进行解扩,算法框图如下:
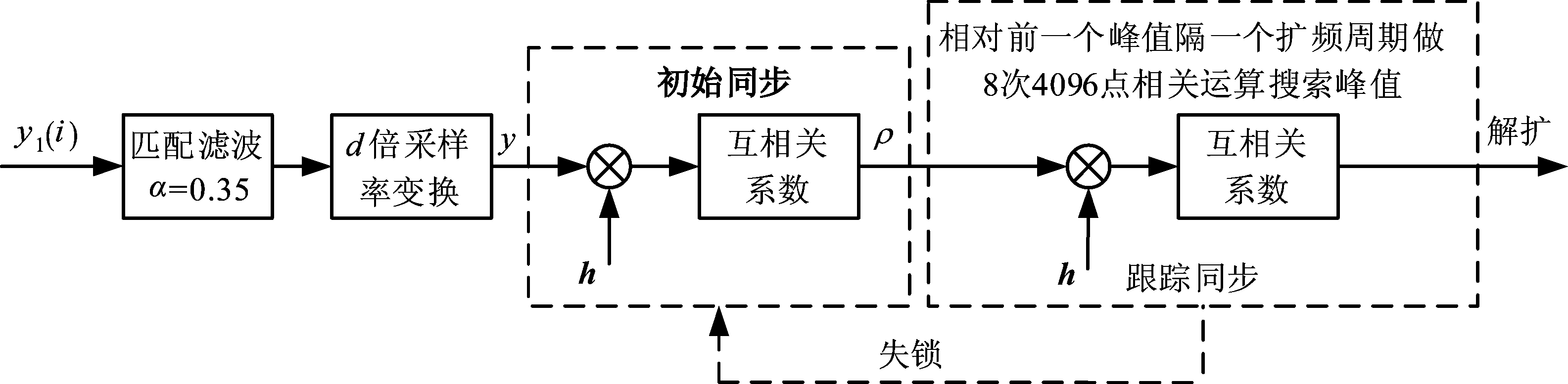
图6 相关解扩框图
Fig.6 Diagram of Correlation Despreading
图6中序列h=[h(0),h(1)…h(N-1)](h(i)=±1,i=0,1,2…N-1,N=4096)为CID信号中的扩频码m序列经过BPSK调制后的星座波形,y为采样率为CID信号符号速率d倍的待处理的基带波形信号,令y=[y(0),y(d)…y(i·d)…y((N-1)·d)](i=0,1,2…N-1,N=4096),基于波形的互相关系数表示如下式:
(8)
(·)*表示1×4096维行向量的共轭。ρ的大小表示d倍过采的基带波形信号与星座序列的相关性,当d≥4时,式(8)基于波形的解扩性能接近于对信号y定时同步后的解扩性能[12],则信号y在与星座波形h做互相关系数运算在匹配峰值位置可近似为序列h与高斯噪声向量n的和,当不考虑噪声与信号的相关性时y=h,则互相关系数ρ大小取到最大值1,当信号y在与星座波形h做互相关系数运算在不匹配的位置时,互相关系数ρ非常小,利用此峰值特性可进行解扩的初始同步,又因为待处理信号y中含有BPSK调制的连续周期的伪码序列信息,可利用此周期性在每隔一个扩频码周期附近进行相关系数峰值幅度搜索实现解扩跟踪,最后取出各峰值对应的相关系数值后便完成了解扩。
对于星座图抵消主载波后的CID信号y1(i),由于频偏影响,式(8)中分子部分中信号y匹配位置可表达为E[h·h*ej(2πf/RCi+θ)+n·h*], f、θ分别为CID信号频偏和相偏,由于噪声与信号相关性小则仅考虑信号部分,由于h·h*为一个大小恒为1的1×4096维行向量,则h·h*ej(2πf/RCi+θ)在极坐标上表示不同的大小恒为1的1×4096维行向量,导致E[h·h*ej(2πf/RCi+θ)]的值很小,峰值消失。从频域角度分析,式E[h·h*ej(2πf/RCi+θ)+n·h*]可等效为一个单频信号与噪声和的形式[13-16],由于噪声部分h*·n相关值很小,则对式E[h·h*ej(2πf/RCi+θ)+n·h*]做傅里叶变换后其在频偏2πf/RC位置会存在一个单频峰值,取出峰值位置对应的值![]() 即可解扩,具体推导如式(9)、(10)所示,改进解扩框图如图7所示。
即可解扩,具体推导如式(9)、(10)所示,改进解扩框图如图7所示。
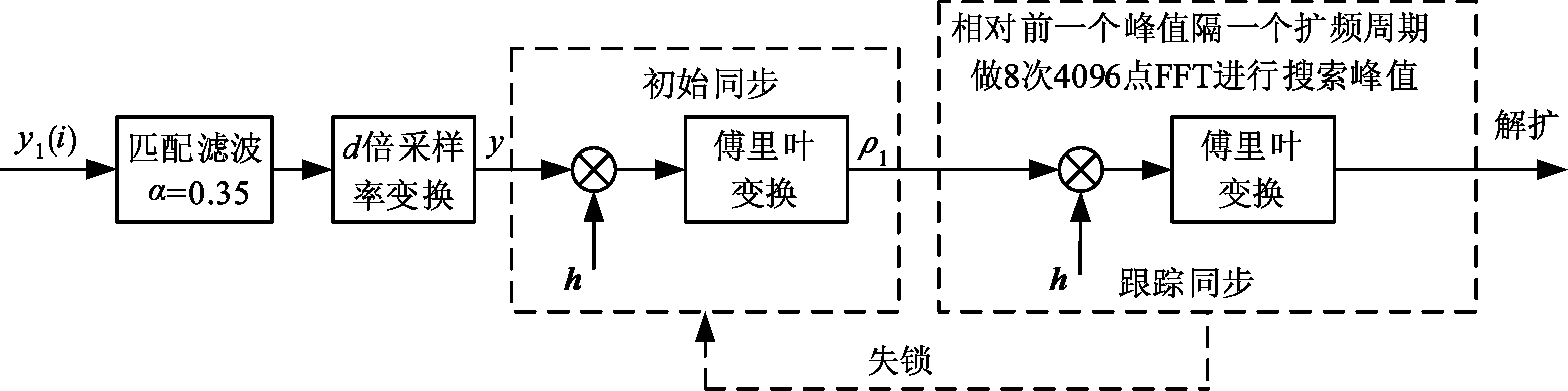
图7 抗频偏相关解扩算法框图
Fig.7 Diagram of frequency anti-offset Correlation Despreading
ρ1表达式如下:
(9)
仅考虑y中信号部分,上式可化简为:
ρ1=max(|FT[hej(2πf/RCi+θ)·h*]|/
=max(|ejθ|·|FT[hej2πf/RCi·h*]|/(N·E[h·h*]))
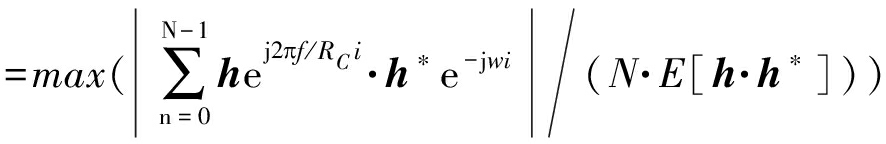
(10)
FT(·)表示傅里叶变换,max(·)表示取最大值,仅考虑y中信号部分,当w=2πf/RC时,在信号匹配位置式(10)等价于式(8)。得到峰值后,取出对应峰值位置的值ρ0进行解扩,如下式:
(11)
解扩后得到一串含固定频偏的星座序列,对此基带信号进行去频偏,纠相偏和判决后得到信息序列。
3.4 DVB-CID信号解调算法步骤
根据图5和图7算法框图,可得到抗频偏解调CID信号的流程如下:
Step 1 接收信号解调。接收信号经过下变频和匹配滤波后进行解调。
Step 2 星座图抵消。对解调完成的接收信号估计星座中心位置后进行主载波消除。
Step 3 初始同步。星座图主载波抵消后的数据经过匹配滤波和采样率变换后,利用式(9)对其进行初始同步。初始同步利用已知星座波形h与波形y做步进为1的遍历搜索,找到峰值位置时便可同步数据。
Step 4 跟踪同步。跟踪同步利用扩频短码信号的码片周期性,在初始同步的基础上,步进一个扩频周期进行第二个扩频峰值搜索,此时仅需在预判峰值位置附近进行搜索,确定峰值位置,此后峰值搜索依据前一个峰值位置延时一个扩频周期搜索下一个峰值位置,以此来跟踪同步,失锁后进而重新进行初始同步。
Step 5 解扩。得到峰值位置后取出峰值处对应的值ρ0得到数字基带信号,然后对其去频偏相偏判决后可得到CID解调信息序列。
4 仿真实验及分析
仿真条件:本文算法在MATLAB环境下对仿真信号进行测试,信号均为基带信号,主载波信号为QPSK调制信号,符号速率为RA;CID其采用4096倍短码m序列扩频方式,扩频后符号速率为RC,调制方式为BPSK,成型函数为滚降系数为α=0.35的根升余弦函数;高斯白噪声由awgn函数生成,主载波信号和CID信号信息序列为随机数,主载波信号、CID信号和噪声三者互相独立,SNR为单位符号强信号能量与噪声功率谱密度比值。本仿真主要研究特定条件下CID信号的解调性能,对实际信号解调有一定的指导意义。
4.1 算法有效性验证4.1.1 实验1:抗频偏算法有效性验证
不考虑主载波影响的前提下,CID信号仿真参数如下:数据长度为4个伪码周期片段,信噪比为SNR=-10 dB,RC=112 kHz,采样频率Fs=448 kHz;星座波形h为已知的1×4096维m序列,符号速率为112 kHz。抗频偏算法CID信号快速傅里叶变换(fft)取4096点。CID信号的相关系数幅度和抗频偏系数示意图。
如图8和图9分别为CID信号在频偏为220 Hz下使用相关系数算法和抗频偏算法相关系数示意图,其中相关系数算法无峰值出现,此方法不适用于含频偏的情况。
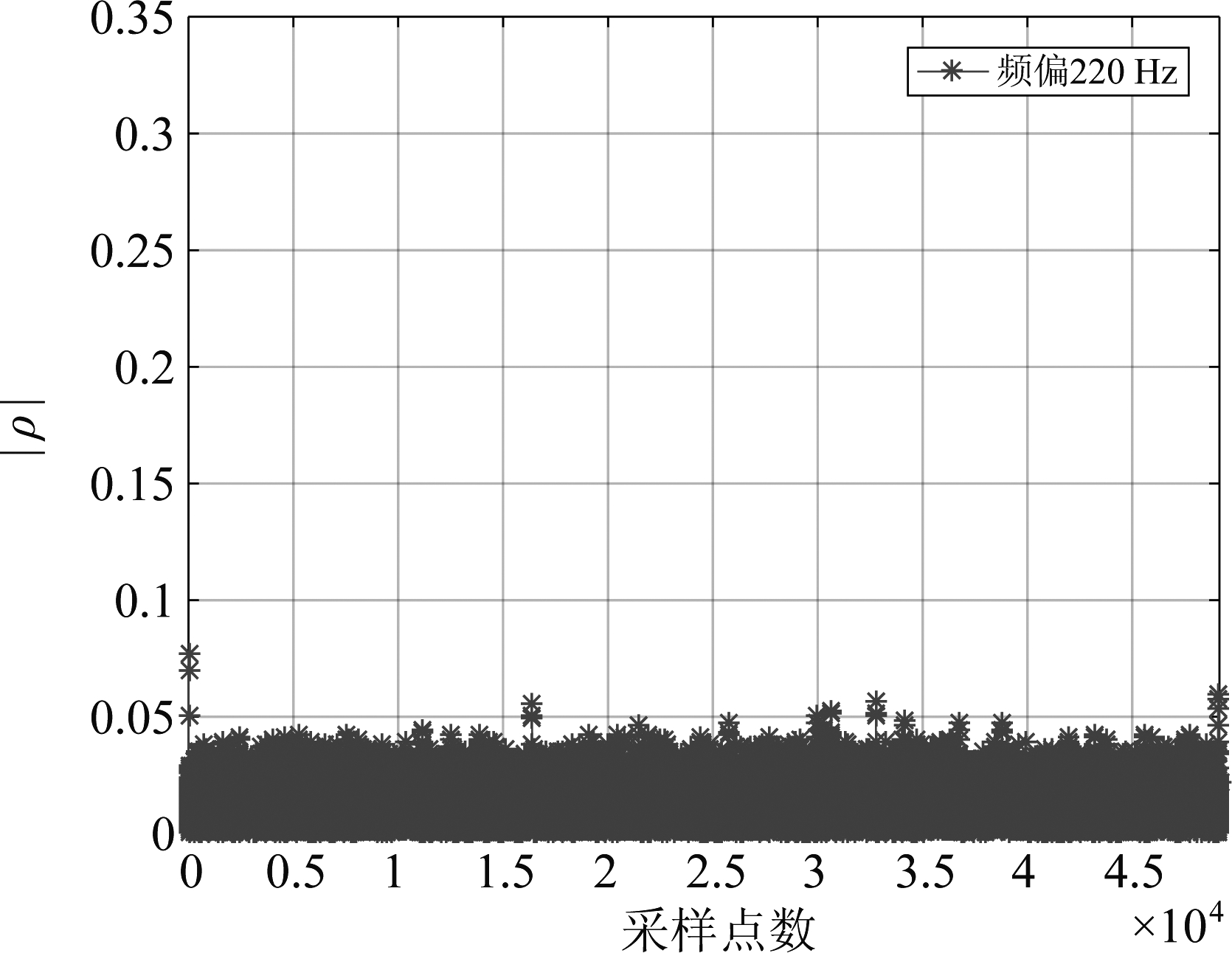
图8 CID信号的相关系数的幅度
Fig.8 The magnitude of correlation coefficient of the CID signal
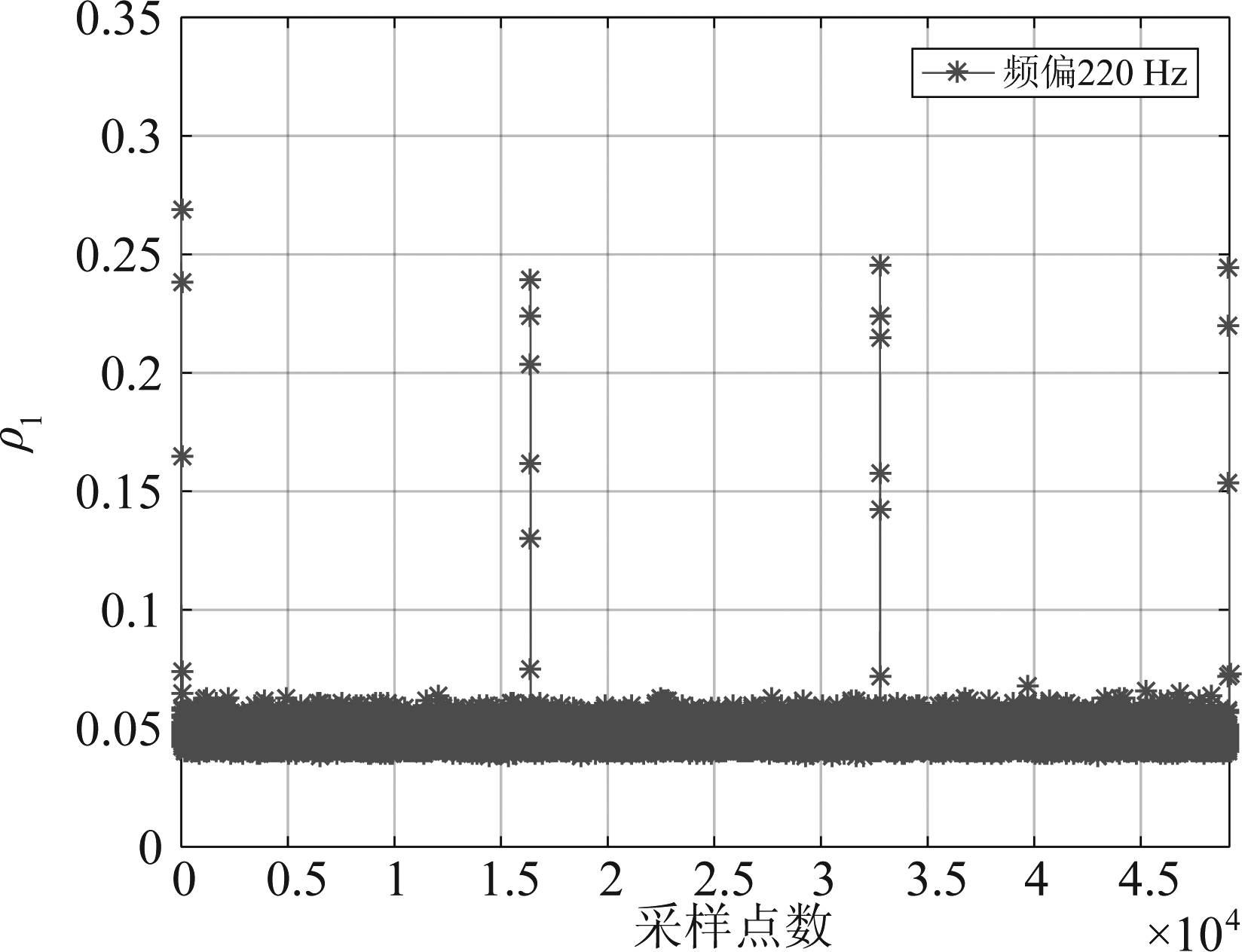
图9 CID信号的抗频偏系数
Fig.9 Frequency anti-offset coefficient of the CID signal
如图10、图11分别为CID信号在无频偏情况下使用相关系数算法和抗频偏算法相关系数示意图,两种算法峰值相等,例如在第二个峰值位置峰值均为0.309;抗频偏算法比相关系数算法的底噪高,在低信噪比下峰值被淹没时,在CID信号无频偏时相关系数算法比抗频偏算法解扩同步方法好。
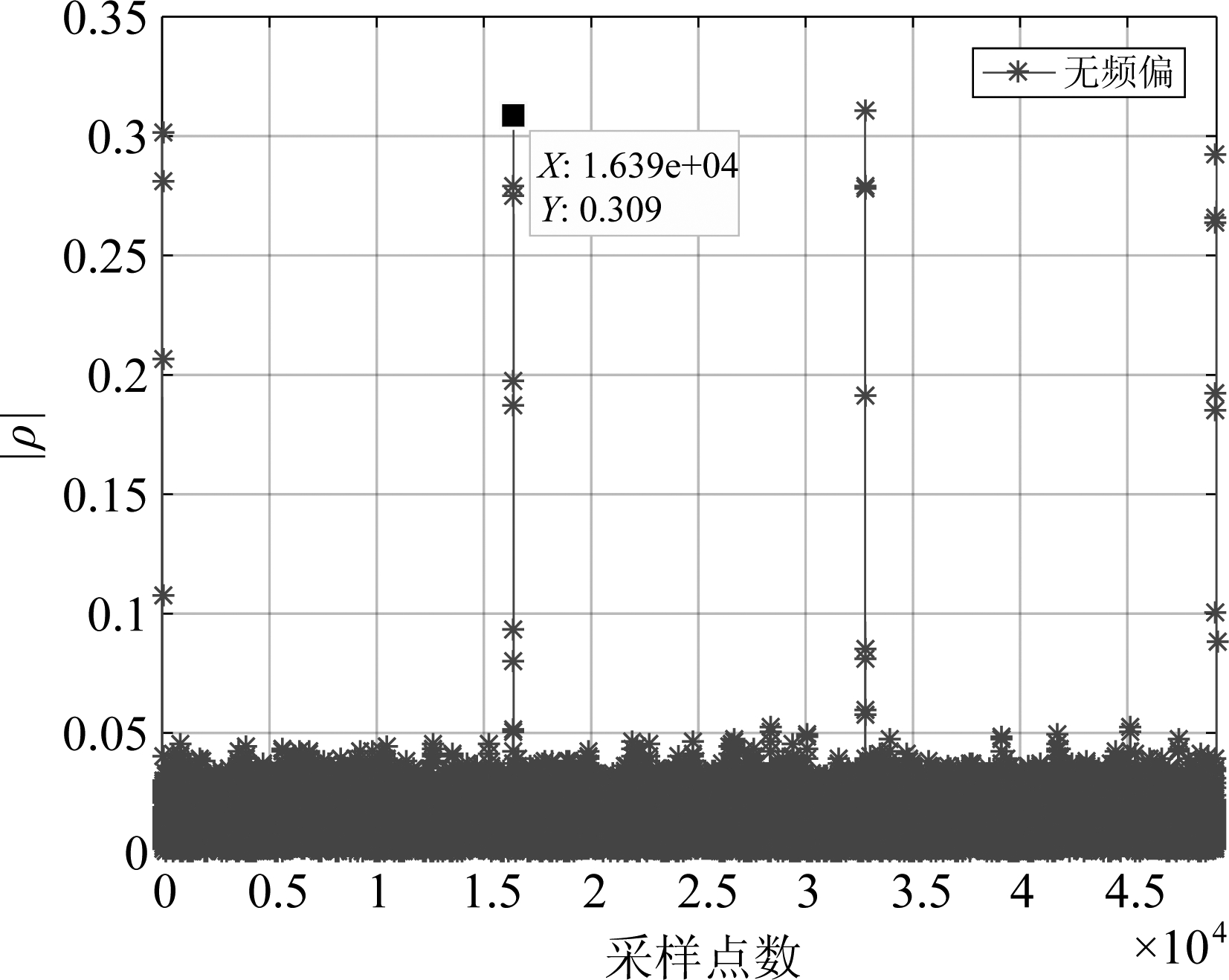
图10 相关系数的幅度
Fig.10 The magnitude of correlation coefficient
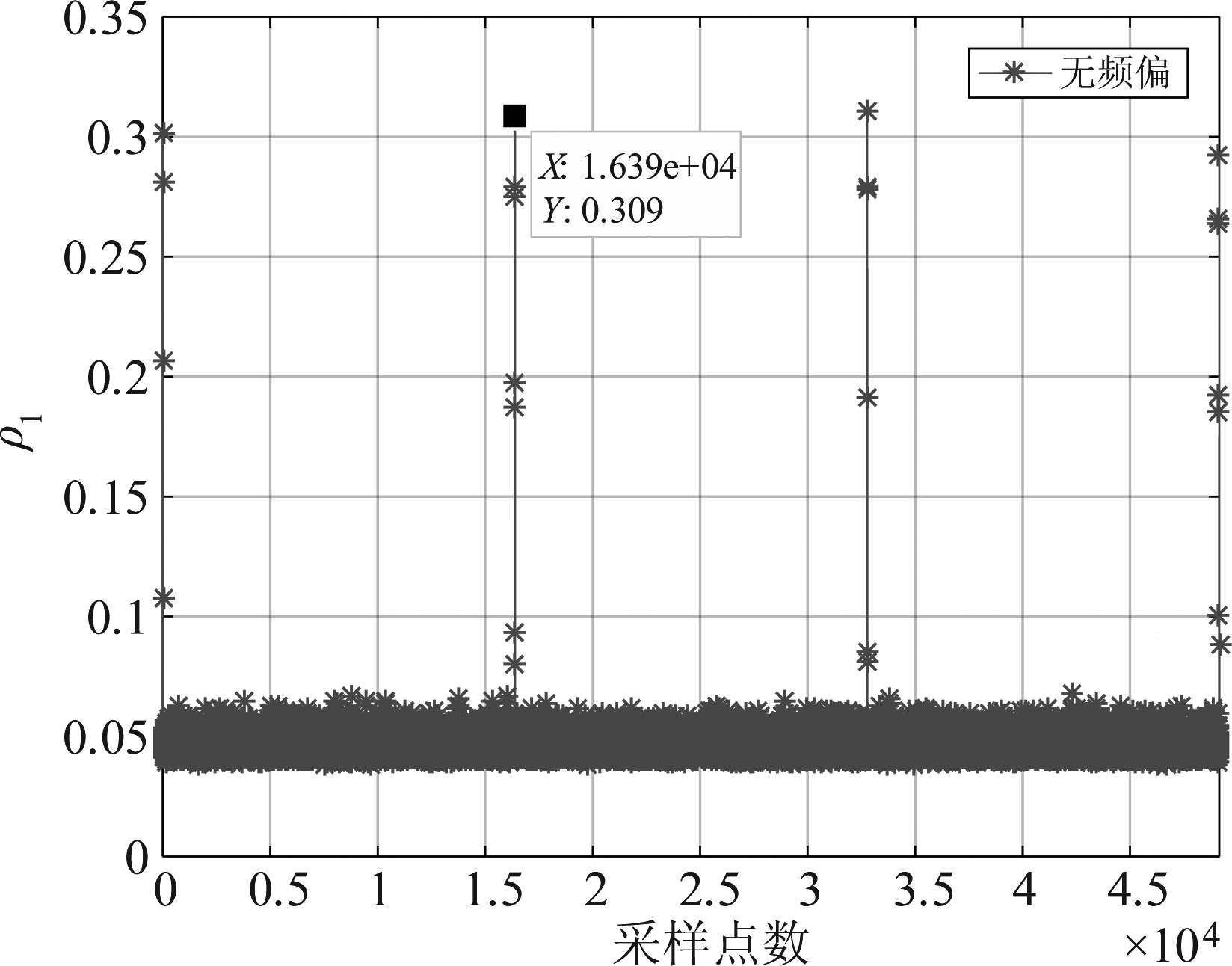
图11 抗频偏系数
Fig.11 Frequency anti-offset coefficient
如图12为图11的第二个峰值放大部分,可以看到相关系数大小在峰值两侧递减,注意峰值两侧值不对称, 这是因为基于波形的相关解扩算法有采样偏移,在符号同步之前,每个符号对应的4个采样点中不一定对应有该符号的最佳抽样时刻,即各符号的最佳抽样时刻位于两个相邻样点所对应的采样时刻之间,离最佳抽样时刻最近的样点也存在一定的采样偏移。
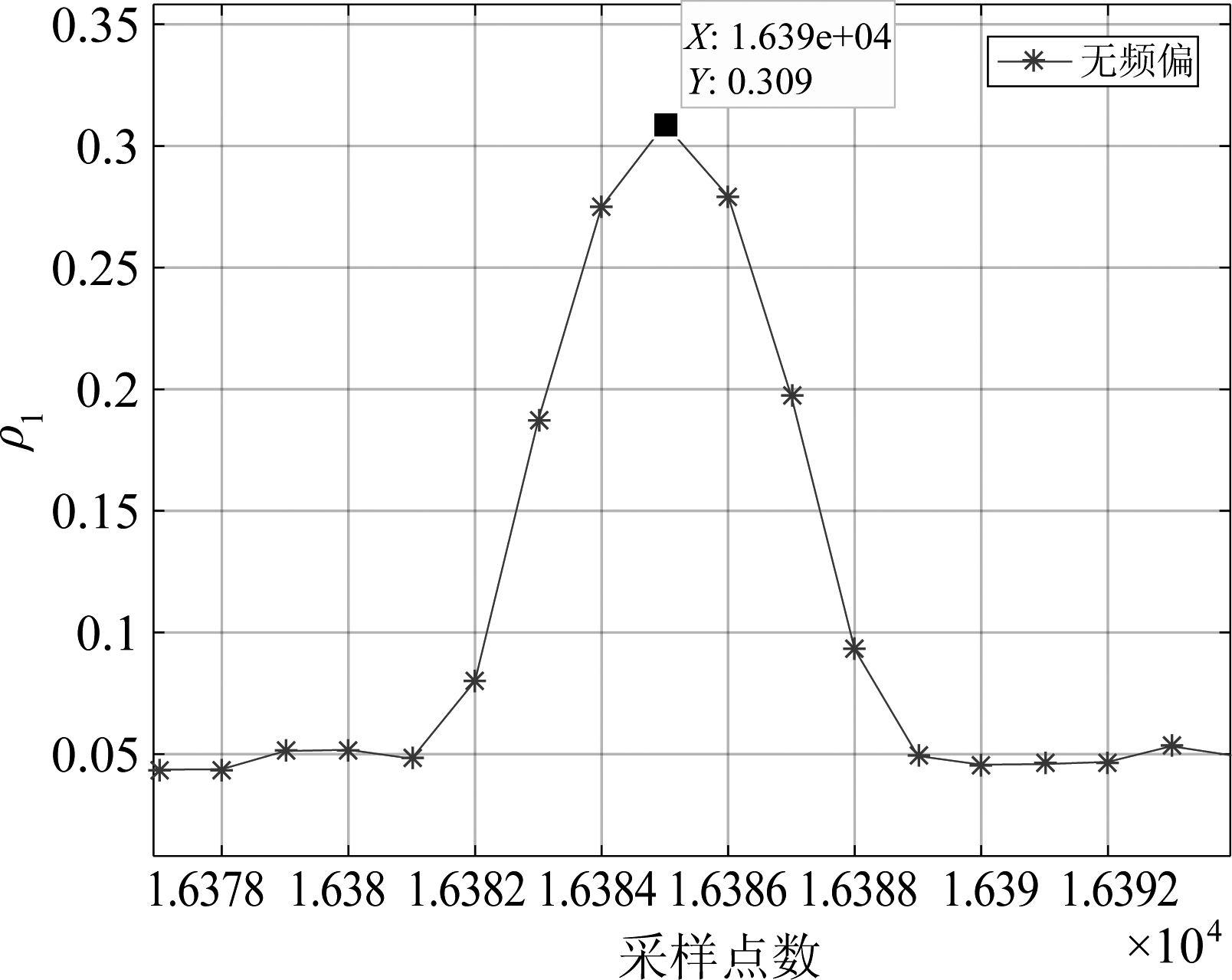
图12 抗频偏系数
Fig.12 Frequency anti-offset coefficient
4.1.2 实验2:不同信噪比下峰值获取性能
在低信噪比下相关系数峰值幅度无法出现,本文采取峰值门限获取主要依靠叠加的方式进行处理,由于信源数据是以扩频码为周期的调制信号,其相关系数峰值以扩频码周期重复出现,可利用相邻峰值叠加的方式得到当前位置的相关系数峰值,叠加过程可以理解为一种降噪过程,其增高了峰值出现的幅度。
在低信噪比下,利用相关解扩时相关系数峰值幅度被噪声淹没,导致CID信号的伪码序列无法捕获和同步,以下对相关系数峰值位置相邻多个位置峰值幅度进行叠加来获取当前峰值,当峰值归一化幅度值比次高峰值大0.1时取到最大峰值,下图为CID信号不同信噪比下叠加次数的关系。不考虑主载波影响的前提下,CID信号仿真参数如下:数据长度为1000个伪码周期片段,RC=112 kHz,采样频率为Fs=448 kHz,星座波形h为已知的1×4096维m序列,符号速率为112 kHz。抗频偏算法CID信号fft取4096点。
如图13所示,无频偏的CID信号采用相关系数算法捕获峰值,频偏为220 Hz的CID信号采用抗频偏算法捕获峰值。随着信噪比的降低,获得峰值需要的相关系数幅度叠加次数在增加,当信噪比SNR>-21 dB时,相关系数峰值捕获需要通过无需叠加方式进行;随着信噪比降低,抗频偏算法比相关系数方法叠加次数多,由图10、图11可知,虽然抗频偏算法和相关系数算法在匹配位置峰值相同,但是抗频偏算法比相关系数算法底噪高,导致在低信噪比下,抗频偏算法需要的叠加次数更多。
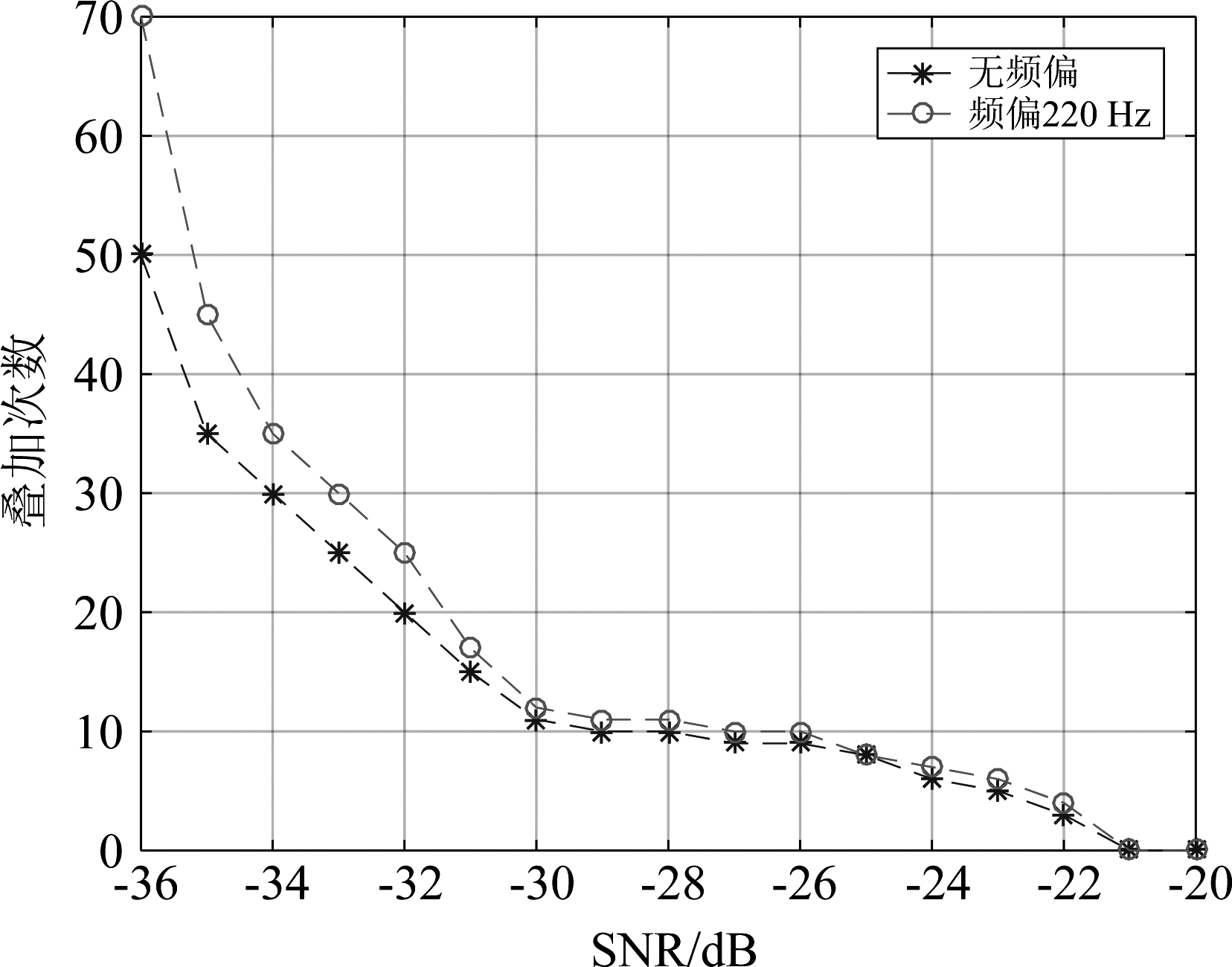
图13 叠加次数
Fig.13 Number of overlays
4.2 不同条件下CID解调算法性能测试
4.2.1 实验3:相关解扩算法和抗频偏解扩算法性能对比
不考虑主载波影响,对比抗频偏解扩算法、相关解扩算法和理论限误码率曲线分析。 根据BPSK信号的解调误码率理论限[17]可知CID信号解扩误码率理论表达式如下:
(12)
CID信号仿真参数如下:数据长度为1000000个伪码周期片段, RC=112 kHz,采样频率Fs=448 kHz;星座波形h为已知的1×4096维m序列,符号速率为112 kHz。抗频偏算法CID信号fft取4096点。
由图14可知,CID信号相关解扩算法解调性能接近理论限,由此可知基于波形的相关解扩算法中待处理信号采样率取符号速率的4倍的解调性能已经非常接近理论限,但还是性能稍差,因为基于波形的相关解扩算法有采样偏移,在符号同步之前,每个符号对应的4个采样点中不一定对应有该符号的最佳抽样时刻,即各符号的最佳抽样时刻位于两个相邻样点所对应的采样时刻之间,离最佳抽样时刻最近的样点也存在一定的采样偏移。

图14 CID信号解调误符号率曲线示意图
Fig.14 The SER curve of CID signal demodulation
在CID信号信噪比取-25 dB时,抗频偏算法误码率为1.366e-6,虽然在-25 dB已经满足工程实践要求但是抗频偏解扩算法相比相关解扩算法性能稍差,因为在抗频偏系数计算中应用快速傅里叶变换,由于栅栏效应导致峰值位置精度不准导致解扩性能变差。
如图15所示,当CID信号长度为4096点时, fft点数为8192点和2048点的CID信号解调误符号率均低于4096点的CID信号解调误码率,当数据长度不变时, fft计算过程中通过补零和取短数据数据长度不能提高算法的性能。
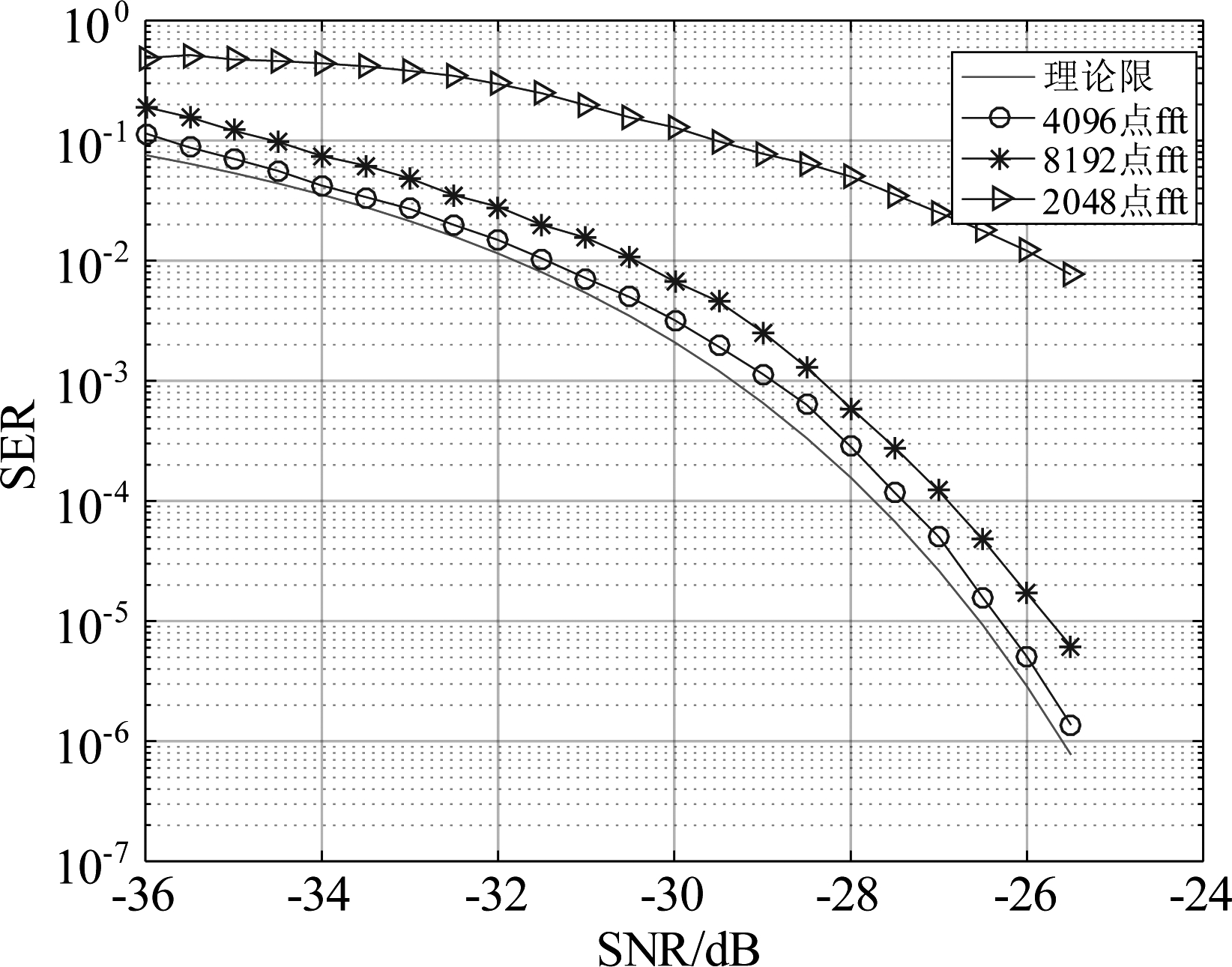
图15 CID信号解调误符号率曲线示意图
Fig.15 The SER curve of CID signal demodulation
4.2.2 实验4:星座图主载波抵消方式下主载波误码率对抗频偏解扩算法性能分析
利用星座图抵消方式对CID信号解调时,在此主要讨论当主载波信噪比在0 dB到6 dB主载波解调误码率对CID 信号的解调性能影响。
主载波信号仿真参数如下:数据长度与CID信号一致,取RA=448 kBd;CID信号仿真参数如下:数据长度为1000000个伪码周期片段, RC=112 kHz,采样频率Fs=448 kHz;PSD=-27.5 dB,抗频偏算法CID信号傅里叶变换取4096点。
在主载波不同信噪比SNR下得到误码率性能曲线如下:
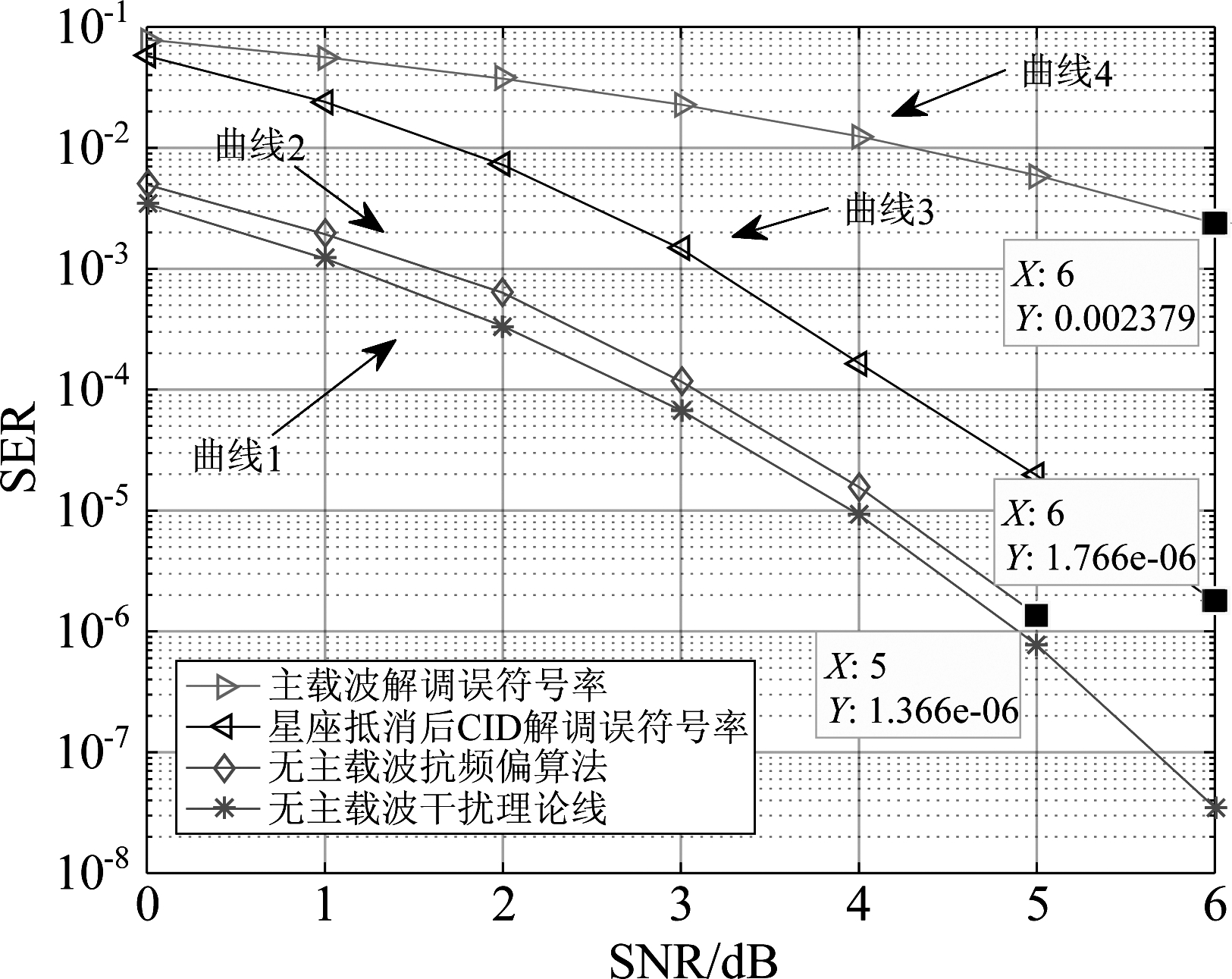
图16 信号误符号率曲线示意图
Fig.16 The SER curve of signal demodulation
如图16所示,在主载波不同信噪比SNR下,曲线4为主载波解调误码率,曲线3为星座图方式主载波消除后CID信号解调误码率,曲线1和曲线2分别表示在无主载波条件下CID信号解调理论限以及抗频偏算法下CID信号的解调误码率。
由曲线2和曲线3可知,主载波解调误码率对CID信号的解调误码率有影响。在主载波信噪比SNR为5 dB时,无主载波情况下对应信噪比下CID 信号的解调误码率达到1.366e-6,此时曲线2主载波抵消后CID信号的解调误码率为1.766e-6。
由曲线3和曲线4可知随着主载波信噪比SNR的增大,主载波BER在减小,CID信号的解调误码率也在减小,当主载波信噪比SNR为6 dB时,CID信号的解调误码率为1.766e-6,由此可知在主载波信噪比达到6 dB以上时,基于星座图抵消的方式可以满足CID信号的工程实践需求。
5 结论
本文基于对卫星通信信号上叠加CID信号的DVB-CID信号进行解调,在以星座图抵消方式消除主载波基础上,提出了一种CID信号的抗频偏解调算法,有效解决了CID信号的解调问题,应用于CID信号的解调接收工程实践可获得良好效果。此抗频偏解扩算法亦可用于低信噪比下扩频信号的解扩,其性能接近理论限,避免了传统扩频信号解调时需要载波提取环节,无需设计复杂的反馈网络,此算法相比传统的扩频解调算法运算量小,有益于工程实践。
[1] ETSI TS 103 129 V1.1.2(2014- 03).
[2] 张天骐, 李立忠, 张刚, 等. 直扩信号的盲处理[M]. 北京: 国防工业出版社, 2012.
Zhang T Q, Li L Z, Zhang G, et al. Blind Processing for Signal of Direct Sequence Spread Spectrum[M]. Beijing: National Defense Industry Press, 2012.(in Chinese)
[3] Nguyen M A, Zaghloul A I. Interference cancellation receiver for heavy-traffic aeronautical mobile environment[C]∥Digital Avionics Systems Conference, 2005. Dasc 2005. the IEEE, 2005: 1.C.4-1.1- 8 Vol.1.
[4] 付迪, 高勇. 非对称PCMA卫星信号的截获方法[J]. 现代电子技术, 2007, 30(7): 28-30.
Fu D, Gao Y. Signal Interception Method for Asymmetric PCMA Satellite Communication Systems[J]. Modern Electronics Technique, 2007, 30(7): 28-30.(in Chinese)
[5] 廖灿辉, 周世东, 朱中梁. 从强信号掩盖中检出弱信号的一种新检测算法[J]. 系统仿真学报, 2010, 22(4): 986-990.
Liao C H, Zhou S D, Zhu Z L. Novel Algorithm for Activity Detection of Weak Signals Covered by Strong Signal[J]. Journal of System Simulation, 2010, 22(4): 986-990.(in Chinese)
[6] 黄强, 彭华. 基于非线性滤波的非对称PCMA信号盲分离[J]. 信号处理, 2017, 33(5): 676- 686.
Huang Q, Peng H. Blind Separation of Asymmetric PCMA Signal Based on Nonlinear Filtering[J]. Journal of Signal Processing, 2017, 33(5): 676- 686.(in Chinese)
[7] 谢岸宏, 朱立东, 翟继强, 等. 卫星通信抗截获信号波形设计[J]. 电讯技术, 2018(3).
Xie A H, Zhu L D, Zhai J Q, et al. Waveform Design for Satellite Communication Signals with Anti-interception Capability[J]. Telecommunication Engineering, 2018(3).(in Chinese)
[8] 张乾. 基于时变滤波器的调频扩频混合信号分离的研究[D]. 北京: 北京邮电大学, 2018.
Zhang Q. Research on Separation of FM Spread Spectrum Mixed Signal Based on Time Varying Filter[D]. Beijing: Beijing University of Posts and Telecommunications, 2018.(in Chinese)
[9] 余昆. 机载超短波抗窄带干扰技术研究[D]. 郑州: 郑州大学, 2018.
Yu K. Research on Airborne Ultrashort Wave Resistant Narrowband Interference[D]. Zhengzhou: Zhengzhou University, 2018.(in Chinese)
[10] Erup L, Gardner F M, Harris R A. Interpolation in digital modems. II. Implementation and performance[J]. IEEE Transactions on Communications, 1993, 41(6): 998-1008.
[11] 易诗. 高速直扩通信系统中调制解调技术研究[D]. 成都: 电子科技大学, 2009.
Yi S. Research on Modulation and Demodulation Technology in High Speed Direct Spread Communication System[D]. Chengdu: University of Electronic Science and Technology of China, 2009.(in Chinese)
[12] Kim I K, Sung W, PIMRC. CFAR TMDA burst detection schemes for constant modulus signals[C]∥IEEE International Symposium on Personal. IEEE, 1998.
[13] 彭华. 软件无线电中的盲接收技术研究[D]. 郑州: 中国人民解放军信息工程大学, 2002.
Peng H. Blind Receiver Technologies for Software Radio[D]. Zhengzhou: Information Engineering University, 2002.(in Chinese)
[14] 熊竹林, 安建平. 一种低复杂度的低信噪比非相干直扩信号捕获算法[J]. 电子学报, 2016, 44(4): 753-760.
Xiong Z L, An J P. A Low Complexity Acquisition Algorithm for DSSS Signal with Low SNR and Non-Coherent Data Modulation[J]. Acta Electronica Sinica, 2016, 44(4): 753-760.(in Chinese)
[15] 侯骁宇, 李天昀, 杨司韩. 分布式独特码TDMA信号的检测和频率估计[J]. 信号处理, 2018, 34(10): 1211-1220.
Hou X Y, Li T Y, Yang S H. Detection and Frequency Estimation of Distributed Unique Word TDMA Signal[J]. Journal of Signal Processing, 2018, 34(10): 1211-1220.(in Chinese)
[16] 张政, 马金全, 王学成. 基于随机共振的微弱OFDM子载波数估计改进算法[J]. 信号处理, 2018, 34(9): 1086-1093.
Zhang Z, Ma J Q, Wang X C. An Improved Algorithm for Estimating the Number of Weak OFDM Subcarriers Based on Stochastic Resonance[J]. Journal of Signal Processing, 2018, 34(9): 1086-1093.(in Chinese)
[17] 曹志刚, 钱亚生. 现代通信原理[M]. 北京: 清华大学出版社, 1994.
Cao Z G, Qian Y S. Modern communication principle[M]. Beijing: Tsinghua University Press, 1994.(in Chinese)


