1 引言
现代战场上,主要的通信设备仍然是电台,如果能够实现对通信电台个体[1-2]的识别,对掌控战场态势、实现重要目标监控和打击具有重要意义。通信电台个体识别是现代信息战中取得制信息权的重要手段之一,其主要是根据各个通信设备硬件的差异在发射的信号上所表现出来与其他设备不同的特征,判断信号来自哪部设备,实现对电台的追踪,从而实现有针对性的对敌重要通信电台、载体的追踪、监视、电子干扰和军事打击。该技术的实现既可以准确获悉通信电台个体的属性信息,又可以跟踪敌电台,进而推断敌军兵力部署、分析敌通信网组成,为我军把握战场态势提供重要、及时的情报支援。
现代通信电台个体识别的研究主要分两个方向:(1)利用电台信号的暂态特征[3- 4];(2)利用电台信号的稳态特征[3- 4]。发射机处于暂态工作过程中产生的信号被称作暂态信号,暂态信号的细微特征被称为暂态特征。暂态特征的性能非常依赖于暂态信号的完整性与一致性。虽然有特征明显、易于识别这样的优点,但有对截获信号质量要求高、对噪声抵抗能力差、只能区分通信电台的类型等缺点,不能应用在通信电台个体识别上。发射机处在稳定工作状态上产生的信号称为稳态信号,稳态信号的细微特征称为稳态特征。稳态特征体现在通信电台内部各部件相互作用、本振不稳定所带来的杂散成分上,频率源的随机起伏引起的载频偏差上,以及调制器所采用的物理器件和电路参数的差异所带来的调制参数的偏差上。与暂态特征相比,稳态特征显得更加“细微”,提取更加困难,但稳态特征具有隐蔽度高、环境适应性强、不易被噪声干扰的优点。稳态特征形成机理复杂,无法用单一模型进行描述,因此提取难度大,识别性能依赖于有标签样本在样本中所占有的比例。以稳态特征为基础的电台个体识别方法,现今主要对包络特征、谱特征、参数特征等方面进行的研究。例如徐书华[5]于2007年提出基于信号杂散特征识别电台的方法,可以识别同类型的电台个体,但在低信噪比条件下识别率不高。唐智灵[6]在2013年对杂散特征进行研究,在实际信号的数据集上验证了算法性能的可靠性。梁江海[7]利用经验模态分解模型,从时域和频域分析电台信号进行识别。韩洁[8]在2017年提出将信号转换成3D-Hibert能量谱,在一定程度上实现了基于少量样本对通信电台个体的识别。以上方法在进行通信电台个体识别时,都需要有标签的样本,识别的准确度依赖于有标签的样本的数量,有标签的样本的数量制约着算法的识别性能。在军事行动中,是很难实时得到足够的有标签的样本,对敌方的电台的信号进行实时的分析,从而进一步实现对敌方通信电台的个体识别。然而最近发展火热的机器学习中的聚类方法可以实现在不需要有标签样本的情况下实现实时对通信电台个体的识别。
机器学习[9]是实现人工智能的一个重要的研究分支。其研究的主要内容是模拟人脑,利用计算机程序让带有处理器或计算功能的机器可以在“经验”中学习以提高处理问题的性能。聚类[10-12]是机器学习中无监督学习中的一种自分类方法。聚类,就是利用数据集中的特征,将数据划分到不同类或簇的过程,使得同一个簇中的数据具有较高的相似性,属于不同簇之间的数据具有较大的差异性。目前,已经有很多的聚类算法被研究人员提出,例如基于划分的K-means、K-medoids、EM算法、FCM算法,基于层次的BIRCH、Chameleon 等聚类算法,基于密度的DBSCAN、OPTICS、DENCLUE 等聚类算法,基于网格的CLIQUE 等聚类算法,基于模型的GMM等聚类方法。以上这些传统的聚类算法对凸形样本空间有较好的聚类效果,但对于非凸形结构的数据集,聚类效果不是很理想。近些年来,谱聚类算法[13-15]逐渐发展成为重要的聚类算法之一,该算法是基于谱图理论的一种新型聚类分析方法。在复杂的样本空间聚类中,谱聚类算法会表现出更好的聚类性能。
2014年,Alex Rodriguez和Alessandro Laio在Science上发表了一篇关于密度的新的聚类方法:《Clustering by fast search and find of density peaks》(基于密度峰值聚类快速搜索分类方法)。这篇文章是基于密度峰值聚类(Density Peaks Clustering,DPC)的算法。该算法提出一种新的选取聚类中心的方法。作者提出作为聚类中心的点本身具有较大局部密度,与其他密度更大的点之间的相对距离更大。基于以上两点聚类中心点的特征,DPC算法计算点的局部密度和点之间的相对距离,画出决策图(以局部密度为X轴,以相对距离为Y轴),根据决策图选取聚类中心,再对其他非中心点进行相似特征点的合并,最终达到聚类的目的[16]。DPC算法原理简单,效率更高,最为关键的是不需要先验信息,不依赖于有标签的样本。在传统通信电台个体识别方法中,最关键的问题是识别效果依赖于有标签的样本,而在实际作战中,有标签样本的获取难度非常大,是很难解决的问题。DPC算法应用在通信电台个体识别上,它所具有的优点能够很好地解决样本的问题,真正地做到无监督学习。
2 基于DPC的通信电台个体识别方法
基于DPC算法的通信电台个体识别具体流程如图1所示。本算法的核心关键就是寻找到聚类中心,这关乎到整个算法的性能。计算密度ρ和寻找聚类中心都涉及到一个超参数dc,而现在超参数dc的寻找都是根据经验在一定范围内选取,用不同的值进行计算选取最佳dc,增加了计算的复杂度。
2.1 通信电台个体识别方法具体步骤
基于DPC算法的通信电台识别方法主要的优点是直接对接收到的信号进行识别,且不需要有标签的样本,这在实际应用上有巨大的优势,识别方法是基于通信电台的“指纹特征”。其具体步骤如下所示:

图1 算法基本流程
Fig.1 Algorithm basic flow
Step 1 通信电台电台信号经过矩形积分双谱变换成为1×L维特征数据,然后进行批量归一化处理。
Step 2 利用特征数据计算各个数据的距离、寻找超参数、计算密度,利用密度和距离找到数据的聚类中心。
Step 3 将不是聚类中心的数据进行分配,实现通信电台的个体识别(部分数据聚类效果如图2所示)。

图2 部分数据聚类结果
Fig.2 Partial data clustering results
2.2 DPC算法步骤
DPC算法模型的对象是即将进行分类的点集,它以每一个节点的密度为模型基础,将待分类的点集进行聚类,具体步骤如下所示:
(1)计算所有节点之间的距离dij。本文采用的是欧氏距离,即常说的L-2范式;
d[(x1,x2,…,xn),(y1,y2,…,yn)]=
![]() 本文中r=2)
本文中r=2)
(1)
(2)寻找截断距离即超参数dc。由人工输入一个超参数dc(是一个百分比的值,一般在0.5%~5%之间)。对所有的dij进行升序排列(假如样本集有N个点,那么一共有M=N(N-1)/2个dij),截断距离为dij升序排列上第M*dc 个的值(为了叙述更加方便,本文后面直接称截断距离为dc)。
(3)计算每一个节点的密度ρi:
(2)
(χ(x) 是0-1函数,当X≥0时, χ(x)=0;当X<0时, χ(x)=1。)
ρi(密度)的意义是指与节点i距离小于dc的节点的个数。但是由于采用了0-1函数,导致密度计算会出现离散值,为避免出现这种情况,影响算法效果,所以本文采用了高斯核(实验证明高斯核效果更好):
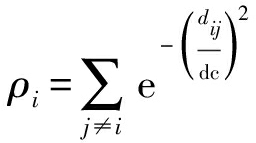
(3)
这样计算出来的密度不会出现离散值。
(4)计算相对距离δi:对于每一个节点i都能找到比节点i密度大的节点j,选取其中最小的dij;如果节点i有最的大密度,则δi为该点到其他点的最大距离。
(4)
其中节点i, j都是数据集内的点。
(5)选取聚类中心:以密度ρ 为横坐标和距离δ 为纵坐标画二维图。相对距离δ较大和拥有较高密度的点是聚类的中心点,一般而言聚类中心分布在在决策图的右上方。
图3是《Clustering by fast search and find of density peaks》一文中提供的数据,图4是基于此数据画出的密度ρ和相对距离δ的二维坐标图。从图4中可以明显看出节点1和节点10是聚类中心,而节点28虽然有较大的相对距离,但其密度偏小,不能够作为聚类中心。
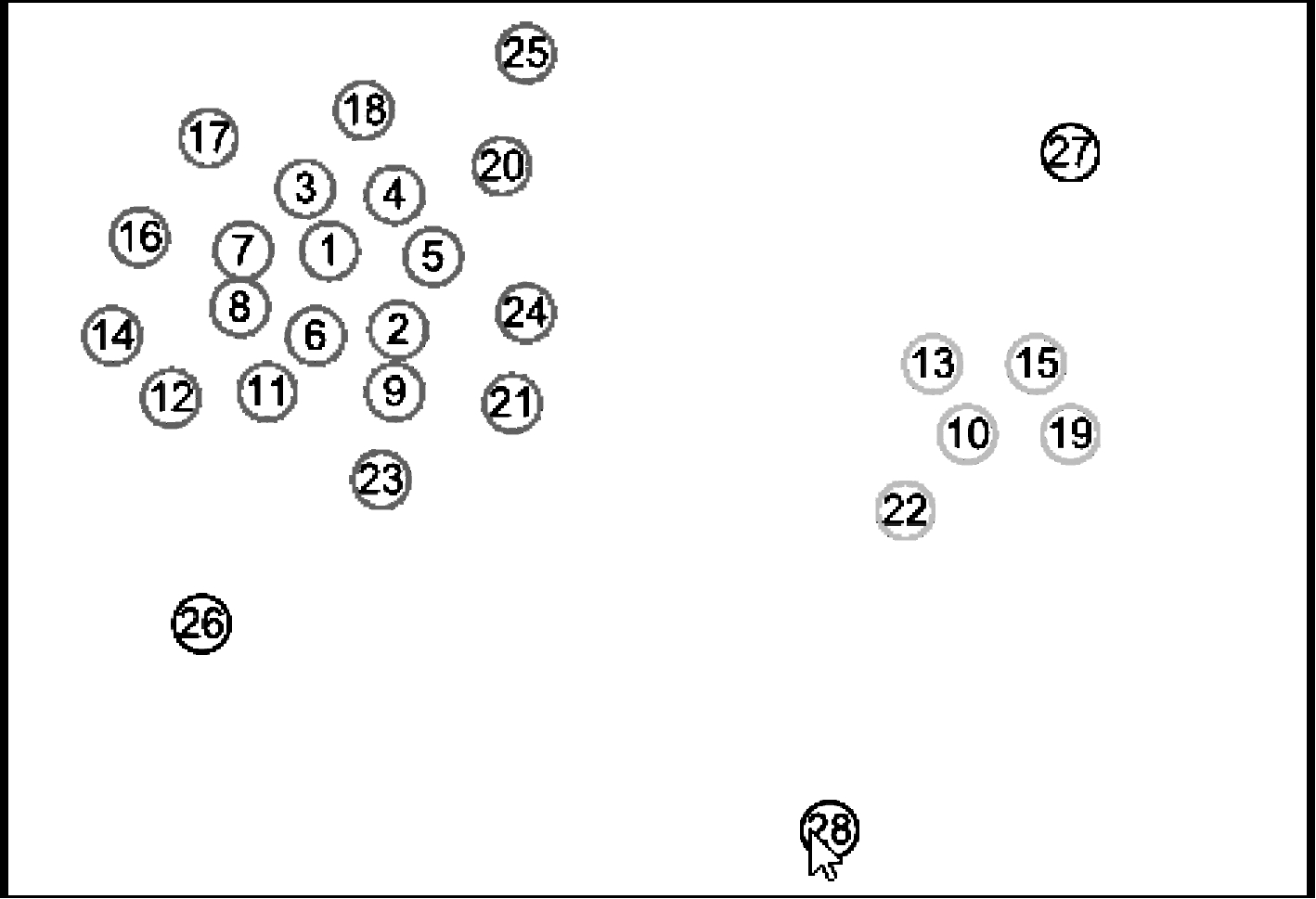
图3 原文提供的示例数据
Fig.3 Sample data provided in the original text
(6)对非聚类中心的点进行分配:
①对于每一个剩余点,其所属的聚类是其最临近且密度比其大的节点的聚类;
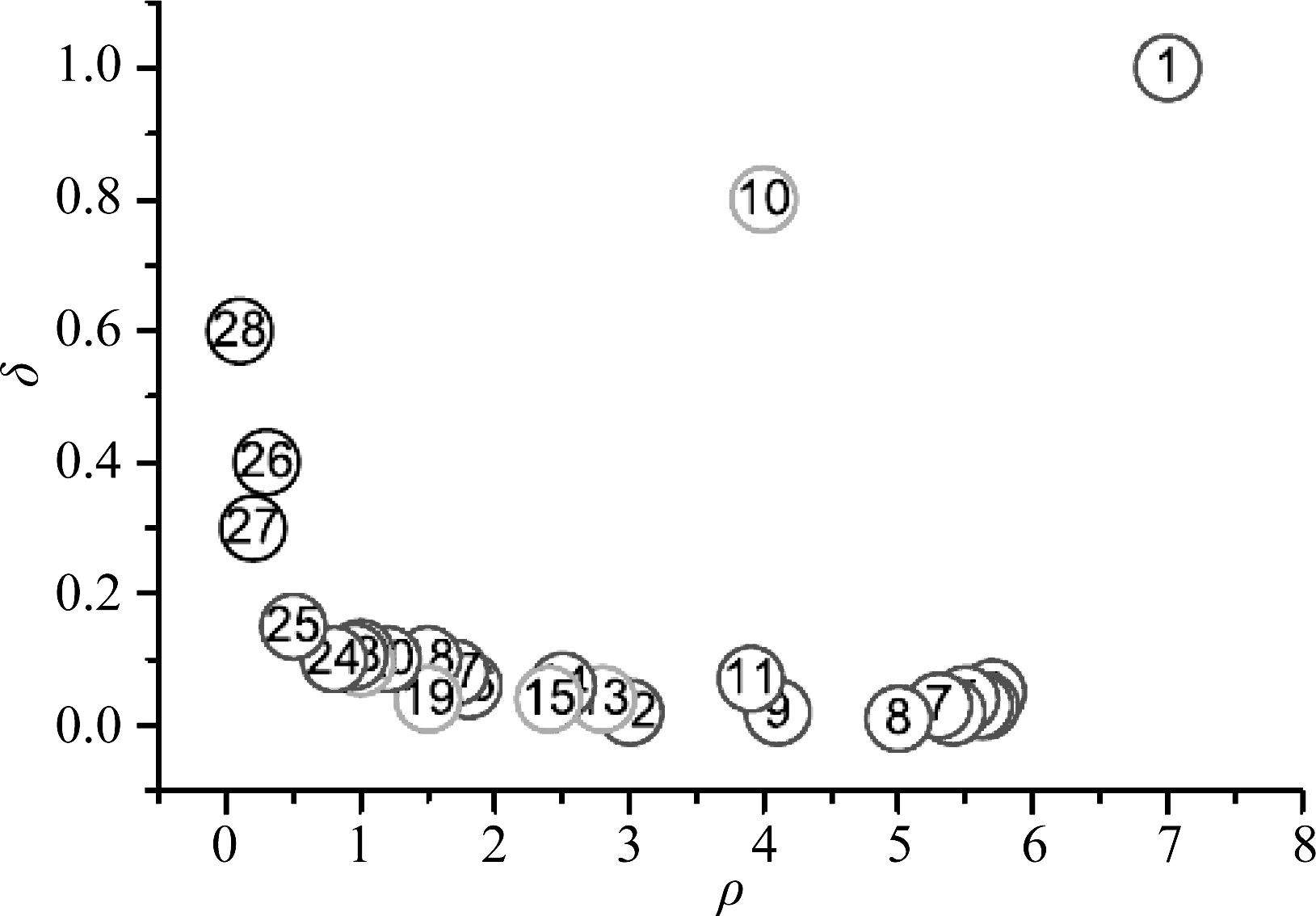
图4 基于示例数据画出的二维图
Fig.4 Two-dimensional drawing based on sample data
②不断迭代,直到没有剩余点。
(7)对孤立点的判断和删除
通过对数据进行追踪,发现在聚类过程中,会出现一些特殊的节点(称之为孤立点),它们的存在影响了步骤(6)的迭代收敛性,同时也影响了算法的识别效果。
每一个簇有一个边界区域,定义一个属于该簇的数据点集合,距离为dc。但同时该数据簇存在与其他簇中心点距离小于dc的数据点,这些数据点的总数即为该数据簇的边界密度,对于每一个簇,定义这个密度为ρb(这意味着每个簇都有属于自己的ρb)。然后对属于这个簇的数据点进行判断,其中密度大于ρb被视为部分簇核心(鲁棒性分配),其他的则视为簇光晕(可以看做噪声)。
3 实验与分析
3.1 实验数据
为了验证识别方法的可行性,实验采用了来自软件无线电(SDR)仿真的电台数据。实验数据是模拟5部电台发出的信号,总共用了2000个样本信号,具体参数如表1。
表1 实验所采用信号源
Tab.1 Signal source used in the experiment

序号发射频率/MHz工作模式样本数量/个电台135FM400电台235FM400电台355FM400电台465FM400电台575FM400
这个数据集模拟的是超短波信号,为了更加贴近实际应用场景(信号在传播过程中会受到周围环境噪声的影响),在信号上叠加了随机噪声。为了排除其他因素的影响,每个模拟电台都采集了400个样本信号,每个样本信号的长度为500 ms。在实验中,使用的样本都是从电台采集的样本信号中随机选取的且每个电台选取样本的数量都是一样的。电台1某一样本信号的功率谱如图5所示。
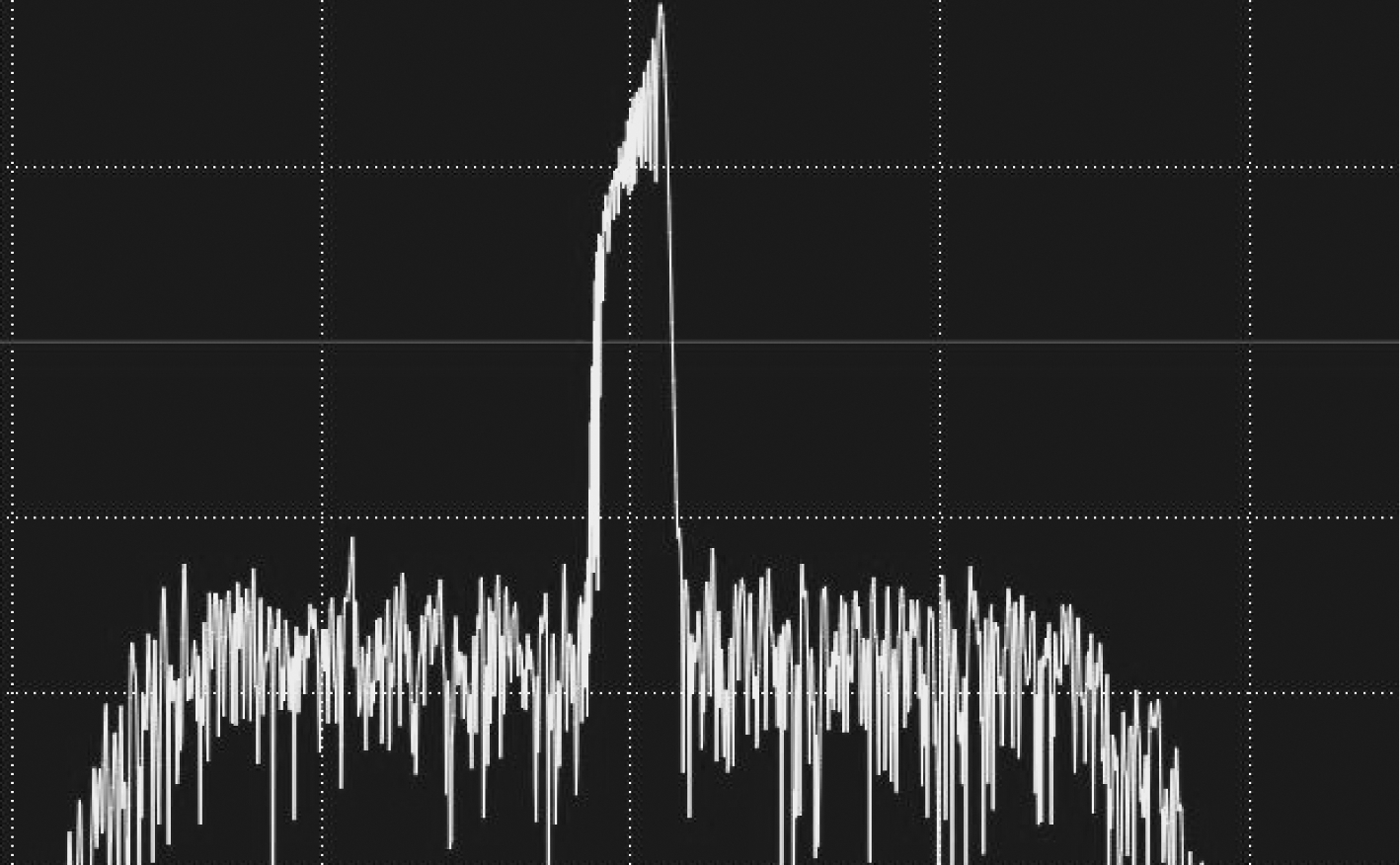
图5 电台1某一样本信号功率谱
Fig.5 Radio 1 power signal spectrum of a sample
3.2 实验准备
利用软件无线电SDR生成5个模拟电台的信号,然后叠加上随机噪声。对叠加噪声后的信号进行矩形积分双谱(SIB)变换,用来去除样本信号中高斯信号带来的影响。因为输入数据的维度对DPC算法的精度有一定的影响,所以在进行矩形积分双谱变换时输出的特征有64维、128维、256维这三种维度的数据。对于每一段信号在进行矩形积分双谱变换的同时,也经过了降维处理,得到的是1×L维的数据。在Matlab中一段信号形成的双谱特征用矩阵表示是1×L列的行向量。不同维度特征的表现形式如图6所示:
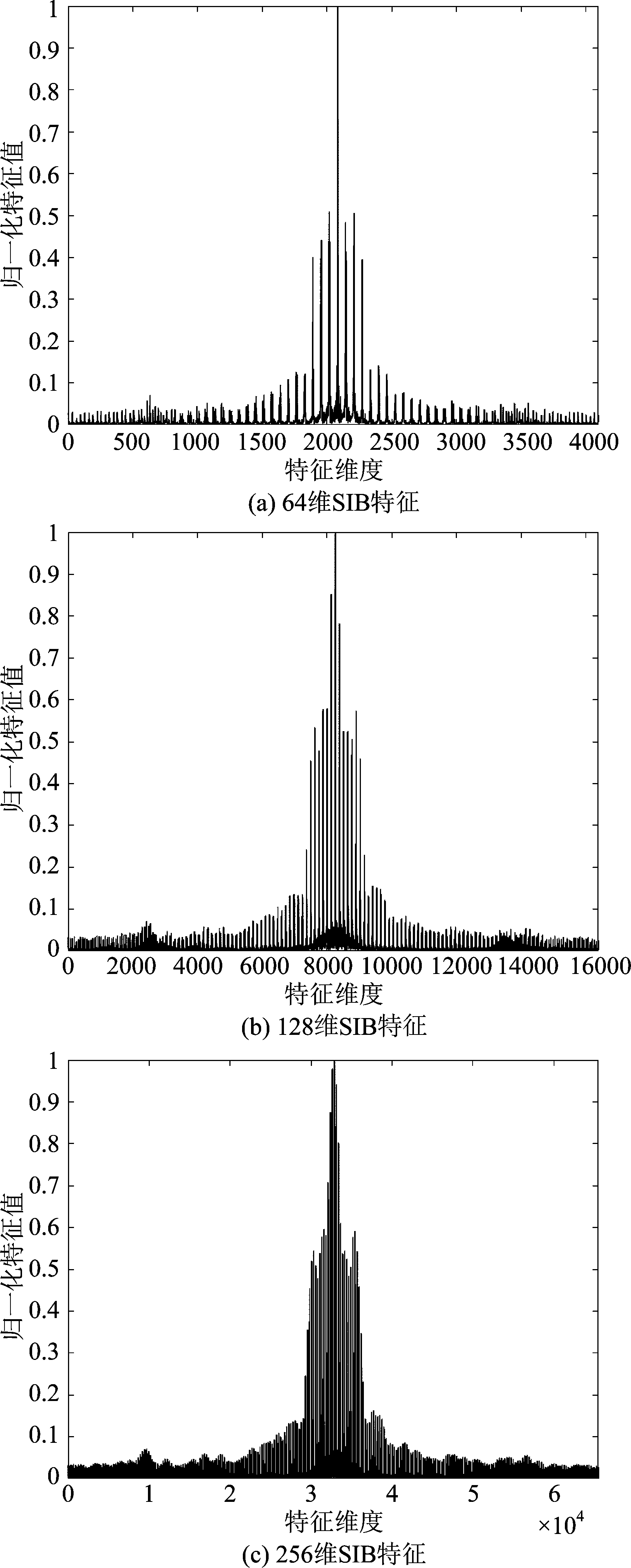
图6 不同维度SIB特征的表现形式
Fig.6 The manifestation of SIB features in different dimensions
因为现有的通信电台识别方法都是需要样本信号,暂时没有做无监督的方法进行识别,所以本文用使用了传统半监督算法(PCA)[5,17]与DPC算法进行比较。PCA半监督在进行聚类时是需要一定量的带标签的样本,才能有较好的识别效果,而DPC算法是完全不需要任何先验信息的。在这方面,基于DPC算法的通信电台识别更加具有优势。
本文在进行实验时,除了应用矩形积分双谱特征(SIB)[4],同时采用了径向积分双谱(RIB)[18]特征、轴向积分双谱(AIB)[19]特征、圆周积分双谱(CIB)[20]特征。在文献[4]中已经详细阐述过,对于通信辐射源个体识别,SIB特征相对于其他双谱特征,更能够多的保留信号的“指纹”特征,在辐射源识别上应用性更好。
3.3 实验结果分析
(1)图7显示了在不同信号样本数量时(每个电台信号样本数量一致,横坐标轴是5部电台样本信号数量之和,纵坐标是识别率),采用不同的双谱特征,输出数据在同一维度(64维)时,基于DPC算法通信电台识别情况。由图可以看出基于SIB双谱特征上的识别率明显优于其他的双谱特征。当样本的数量增加时,SIB双谱特征识别率上升地更加明显,只要样本的数量不超过DPC算法的极限,出现过拟合现象,SIB双谱特征是优于其他双谱特征的,所以本文采用的是SIB双谱特征。
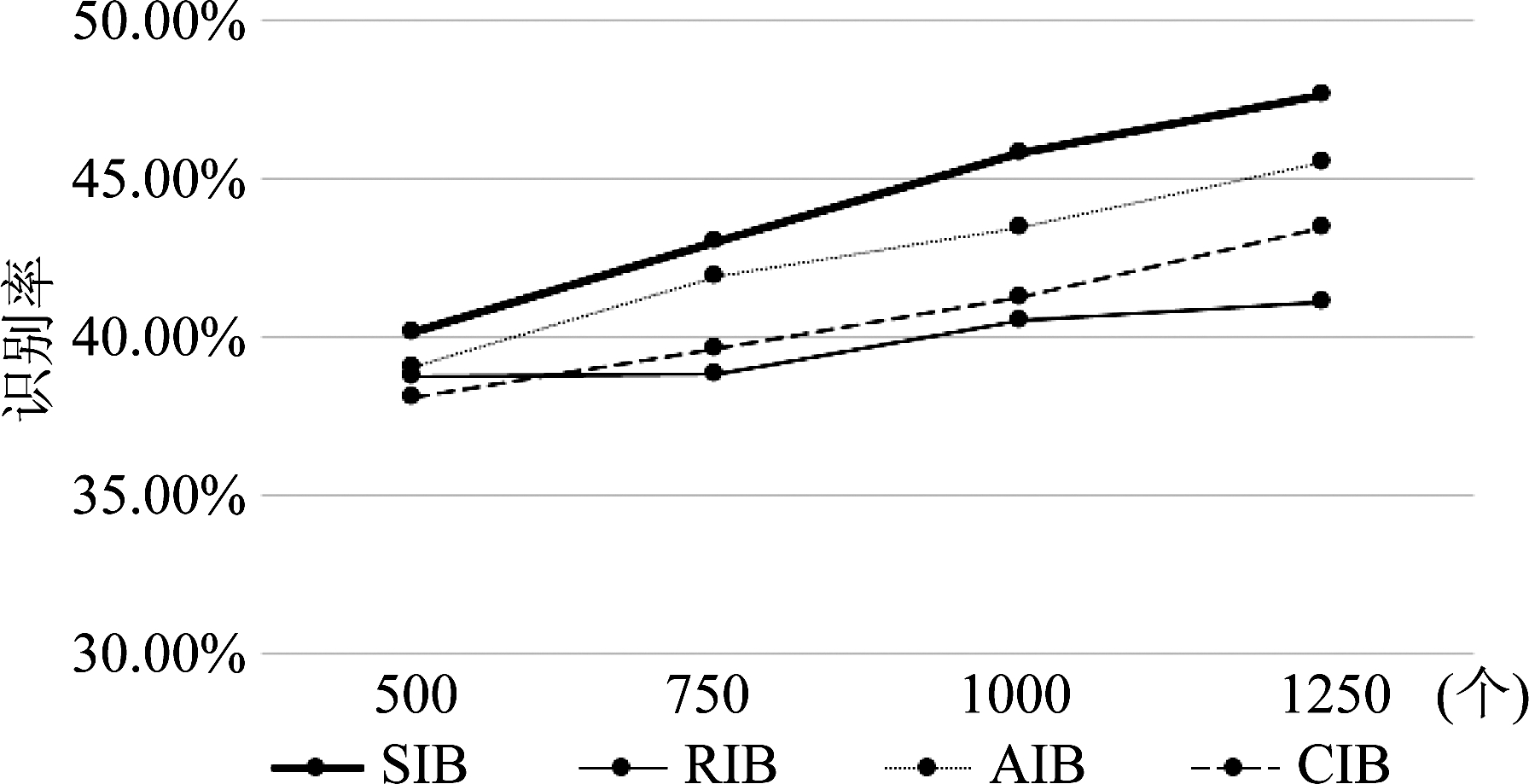
图7 采用不同双谱特征的识别率
Fig.7 Recognition rate using different bispectral features
(2)在《Clustering by fast search and find of density peaks》一文中,作者就做出了说明,数据的维度对DPC算法的识别精度是有一定的影响的。为了获得更好的识别率,本文基于64维、128维、256维特征数据分别进行了实验,实验结果如图8所示(实验中每部电台的样本数量是一致的,横坐标轴是5部电台样本信号数量之和,纵坐标是识别率)。由图可知,采用三种不同维度的特征进行时,识别率的差距并不是很大。虽然在使用128维特征时,识别的效果较好,但是随着维度的增大,算法的复杂性也随之增大,实验需要的时间也变长。所以本文采用的是64维的特征,识别性能较好,计算量较小。
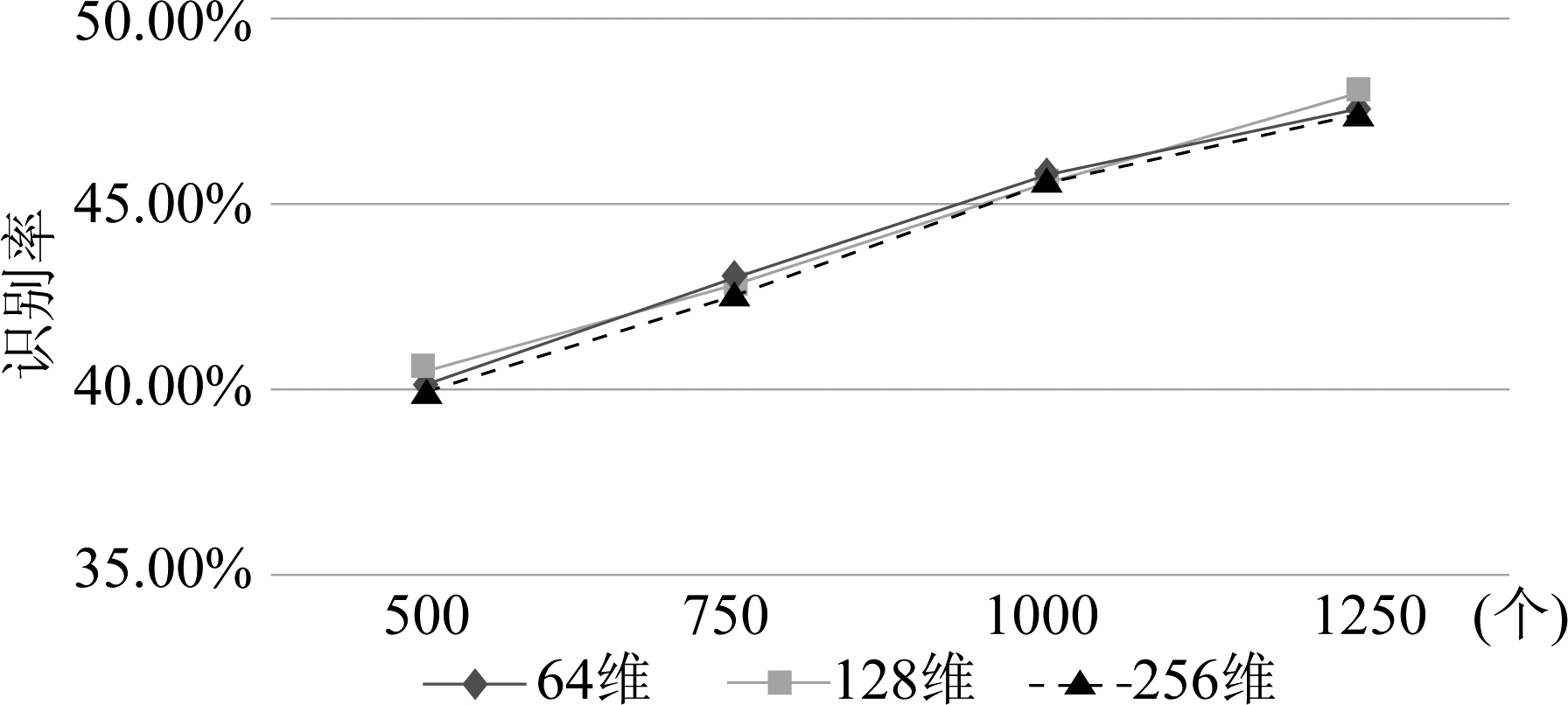
图8 采用不同维度特征的识别率
Fig.8 Recognition rate using different dimensional features
(3)为了更好地说明基于DPC算法的通信电台个体识别方法的优越性,本文用传统识别方法中的PCA法来作比较。在实验中使用了5部电台的样本信号,每次实验中每部电台样本的数量一致,都是先经过SIB双谱变换为64维的特征,然后输入到算法中进行计算和分类识别。由于PCA法需要一定量的带标签的样本,所以给予了1%的带标签的样本。PCA法并不是使用数据的密度,而是基于深度学习和分类器的方法。两种算法的具体情况如表2所示。由下表可知,在样本信号数量较少时,DPC法的识别率比PCA法低,但是差距并不大。随着信号样本数量的增加,DPC法的识别率的增加幅度比PCA 法的大,在样本信号数量达到2000时,DPC法的识别率明显比PCA法高。以上说明DPC法的识别性能是优于PCA法的。
(4)关于电台信号的实验, 信噪比对实验是有一定影响的。为了研究不同信噪比对算法识别效果的影响,本文进行了在信噪比为-10 dB,0 dB,10 dB三种情况下的实验。实验具体条件如下:信号特征为64维的矩形积分双谱特征,来自5部电台的信号,每次实验中每部电台信号数量一致。具体实验结果如表3所示,从表3中我们可以知道,信噪比对实验的结果确实是有影响,信噪比越高,实验效果越好。
基于以上实验,对实验结果进行分析,是可以得到以下四个结论:
(1)使用矩形积分双谱特征,确实能够表现通信电台的个体特征,因此矩形积分双谱特征在通信电台个体识别上具有很好的应用性。同其他特征相比,矩形积分双谱特征更加适合DPC算法,使其能应用在通信电台识别领域上。
(2)特征的维度对DPC法的性能有一定的影响,但不能简单地认为维度越高或者越低,识别的效果就越好。在实验中可以看到,特征维度造成的识别率差异并不是很明显,说明维度不是影响识别效果的一个重要因素。维度的增加也增大了计算量,完成一次实验的时间也相应地延长了,影响了工作效率。基于以上因素,选择了64维的矩形积分双谱特征来表征通信电台的个体信息。
表2 不同样本信号数量时两种方法的识别效果
Tab.2 Recognition rate of two methods when the number of different samples is different

样本数量/个识别率识别方法10001250150017502000DPC45.80%47.60%48.90%50.20%51.90%PCA46.10%47.80%48.90%49.60%50.70%
表3 不同信噪比时DPC算法的识别效果
Tab.3 Recognition effect of DPC algorithm with different SNR
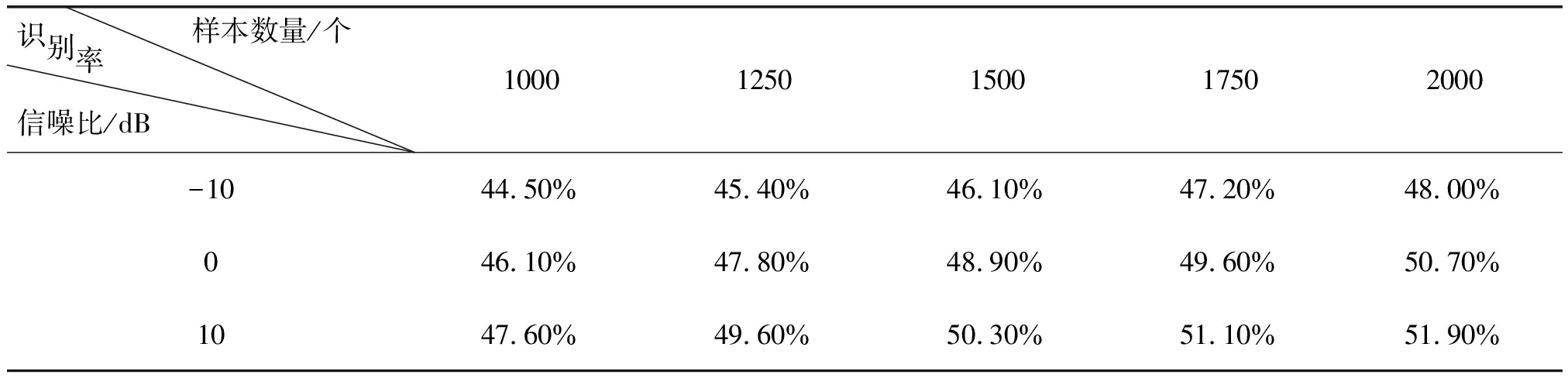
样本数量/个识别率信噪比/dB10001250150017502000-1044.50%45.40%46.10%47.20%48.00%046.10%47.80%48.90%49.60%50.70%1047.60%49.60%50.30%51.10%51.90%
(3)基于DPC算法的通信电台个体识别方法最重要的优点在于其在进行分类识别时不需要先验信息和带标签的信号样本,这在实际运用中具有重大的意义,使通信电台个体识别摆脱了需要带标签样本信号的制约。同深度学习[21-22]方法相比,DPC法不需要“学习”这一步骤,也不需要通过多层“神经层”来处理数据,在实验时具有运算量小,复杂度低的优点,在处理即时数据领域上有更好的应用前景。
(4)超参数dc的选取对DPC法的识别性也有一定的影响,对于不同的数据集,最佳的超参数是不一样的。而现在超参dc的选取只是根据经验法则在0.5%~5%里随机选取,在实际运用中是很难得到最佳的识别效果。
4 结论
本文针对现阶段通信电台个体识别的方法都依赖带标签的样本的问题,而在军事行动中又很难实时地获取带标签的样本信号,提出了基于机器学习中密度峰值聚类的通信电台个体识别方法,使其摆脱了带标签样本的制约。该算法与传统的通信电台识别方法中的PCA法进行比较,识别性能略优,且完成一次实验的时间更短,具有很好的实践性。但DPC法对聚类中心的选取是根据经验法则,这对识别性能影响较大,后面需要在这方面进行研究,提高DPC的识别效果。
[1] 任春辉. 通信电台个体特征分析[D]. 成都: 电子科技大学, 2006.
Ren Chunhui. Analysis of individual characteristics of communication station[D]. Chengdu: University of Electronic Science and Technology, 2006.(in Chinese)
[2] 许丹, 柳征, 姜文利, 等. 窄带信号中的放大器“指纹”特征提取: 原理分析及FM广播实测实验[J]. 电子学报, 2008, 36(5): 917-932.
Xu Dan, Liu Zheng, Jiang Wenli, et al. Feature extraction of “fingerprint” of amplifier in narrowband signal: principle analysis and practical experiment of FM broadcasting[J]. Acta Electronica Sinica, 2008, 36(5): 917-932.(in Chinese)
[3] 梁江海, 黄光泉, 王丰华, 等. 通信辐射源个体识别研究现状及发展趋势[J]. 电子对抗, 2014(1): 42- 48.
Liang Jianghai, Huang Guangquan, Wang Fenghua, et al. Research status and development trend of communication radiation source identification[J]. Electronic Eountermeasures, 2014(1): 42- 48.(in Chinese)
[4] 徐书华.基于信号指纹的通信辐射源个体识别技术研究[D].武汉: 华中科技大学, 2007.
Xu Shuhua. Study on identification technology of communication radiation source based on signal fingerprint[D]. Wuhan: Huazhong University of Science and Technology, 2007.(in Chinese)
[5] Xu S H. Radio transmitter classification using a new method of stray features analysis combined with PCA[A]. Military Communication Conference[C]. Orlando, FL, USA: IEEE, 2007: 1-5.
[6] 唐智灵. 通信辐射源非线性个体识别方法研究[D]. 西安: 西安电子科技大学, 2013.
Tang Zhiling. Study on nonlinear individual identification method of communication radiation source[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2013.(in Chinese)
[7] 梁江海. 一种基于经验模态分解的通信辐射源个体识别方法[J]. 中国电子科学研究院学报, 2013, 8(4): 393-397.
Liang Jianghai. An individual recognition method of communication radiation source based on empirical mode decomposition[J]. Journal of China Academy of Electronics and Information Technology, 2013, 8(4): 393-397.(in Chinese)
[8] 韩洁, 张涛, 王欢欢, 等. 基于3D-Hibert能量谱和多尺度分形特征的通信辐射源个体识别[J]. 通信学报, 2017, 38(4): 99-109.
Han Jie, Zhang Tao, Wang Huanhuan, et al. Identification of communication radiation source individuals based on 3d-hibert energy spectrum and multiscale fractal features[J]. Journal of Communication, 2017, 38(4): 99-109.(in Chinese)
[9] 李炜. 机器学习概述[J]. 科技视界, 2017(12): 149-149.
Li Wei. Overview of machine learning[J]. Science & Technology Vision, 2017(12): 149-149.(in Chinese)
[10] 薛丽霞, 孙伟, 汪荣贵, 等. 基于密度峰值优化的谱聚类算法[J]. 计算机应用研究, 2019(7).
Xue Lixia, Sun Wei, Wang Ronggui, et al. Spectral clustering algorithm based on density peak optimization[J]. Application Research of Computers, 2019(7).(in Chinese)
[11] 于文倩. 聚类相关知识简介[J]. 电子世界, 2014(11): 190-190.
Yu Wenqian. Introduction to clustering related knowledge[J]. Electronic World, 2014(11): 190-190.(in Chinese)
[12] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48- 61.
Sun Jigui, Liu Jie, Zhao Lianyu. Study on clustering algorithm[J]. Journal of Software, 2008, 19(1): 48- 61.(in Chinese)
[13] Shi J, Malik J. Normalized Cuts and Image Segmentation[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2000, 22(8): 888-905.
[14] 丁世飞, 贾洪杰, 史忠植. 基于自适应Nyström 采样的大数据谱聚类算法[J]. 软件学报, 2014, 25(9): 2037-2049.
Ding Shifei, Jia Hongjie, Shi Zhongzhi. Big data spectral clustering algorithm based on adaptive Nystrom sampling[J]. Journal of Software, 2014, 25(9): 2037-2049.(in Chinese)
[15] 王英博, 马菁, 宋晓倩. 基于最优投影的半监督谱聚类算法[J]. 计算机应用研究, 2018, 35(1): 97-100.
Wang Yingbo, Ma Jing, Song Xiaoqian. Semi-supervised spectral clustering algorithm based on optimal projection[J]. Application Research of Computers, 2018, 35(1): 97-100.(in Chinese)
[16] 刘颖莹, 刘培玉, 王智昊, 等. 一种基于密度峰值发现的文本聚类算法[J]. 山东大学学报: 理学版, 2016(1): 65-70.
Liu Yingying, Liu Peiyu, Wang Zhihao, et al. A text clustering algorithm based on density peak discovery[J]. Journal of Shandong University: Science Edition, 2016(1): 65-70.(in Chinese)
[17] 蔡忠伟, 李建东. 基于双谱的通信辐射源个体识别[J]. 通信学报, 2007, 28(2): 75-79.
Cai Zhongwei, Li Jiandong. Identification of communication radiation source based on bispectral[J]. Journal of Communications, 2007, 28(2): 75-79.(in Chinese)
[18] Chandran V, Elgar S L. Pattern Recognition using Invariants Defined from Higher Order Spectra to One-dimensional Inputs[J]. IEEE Trans. on Signal Processing, 1993, 41(1): 205-212.
[19] Tugnait J K. Detection of non-Gaussian Signals using Integrated Polyspectrum[J]. IEEE Trans. on Signal Processing, 1994, 42(12): 3137-3149.
[20] Liao X J, Bao Z. Circularly Integrated Bispectra: Novel Shift Invariant Features for High Resolution Radar Target Recognition[J]. Elecronics Letters, 1998, 34(19): 1879-1880.
[21] 尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015(1): 48-59.
Yi Baocai, Wang Wentong, Wang Lichun. Overview of deep learning research[J]. Journal of Beijing University of Technology, 2015(1): 48-59.(in Chinese)
[22] 沈先耿. 深度学习综述[J]. 数字化用户, 2017(11).
Shen Xiangeng. An overview of deep learning[J]. Digitized User, 2017(11).(in Chinese)

