1 引言
物联网于二十年前提出,在过去五年中得到了飞速发展[1-2],物联网可使大量物理对象接入整个网络[3],如移动终端、电脑、传感器以及车辆等,已成为第五代移动通信的重要组成部分。由于物联网中的物理对象大多是电池供电且无法充电其局限性是功率受限,而目前移动网络消耗了相当大的能量,例如全球约600万个蜂窝网消耗了120亿瓦的功率[4]。而物联网的快速增长显著增加了能源消耗,另外由于功率有限,物体对象的覆盖范围很小。因此,本文针对无线物联通信系统中的双跳中继协同传输[5-9]模型,利用源节点的信号能量进行功率分流设计,提出能量收集和信息传输的高能效传输算法。
中继协作网络因其可扩展网络覆盖,增加信道容量并提升系统的分集增益等优势而受到广泛研究[10-11]。目前已有部分文献对中继能效优化算法进行研究,文献[12]提出了单用户中继协作MIMO系统中节能资源分配方案,基于系统可实现的速率与总功率之间的比率,针对QoS(QoS,Quality of Service)和功率约束,对源和中继预编码矩阵进行优化。而文献[13]考虑了绿色通信,中继通过能量收集,基站通过电网供电的中继协作网络,以最大化基站能效为目的,满足特定的平均吞吐量。进一步的Li Fang等人提出了基于物理层网络编码的无线双向中继信道的能效优化问题,其通过将优化问题从无约束解决方案扩展到有约束的情况,以得到该优化问题的最优解[14]。以上文献并未充分考虑系统存在多类型节点的情况,尽管也有对中继网络的系统能效进行优化,但诸多研究在系统模型、目标函数和约束条件等方面均与本文存在较大差异。
中继的发送功率源于源节点的信号能量,为了满足目的端对能量收集的要求,需要对源端节点的发送功率进行优化。由于物联网通信系统中的物理对象能量受限,因此需提出更为高效的能量收集和信息传输算法。现有的国内外研究中已有一些功率分配算法,例如Angelakis提出了一种异构物联网系统的资源分配算法[15]。Zhang等提出了物联网睡眠协议的选择和休眠机制[16],Kotagi等设计了功率和资源块协同分配的LTE系统物联网[17]。Semasinghe等对物联网的资源分配、博弈论进行了总结回顾[18]。而诸多研究都未充分考虑物联网物理对象能量受限的特点,因此能量收集对于中继节点和目的节点都起着至关重要的作用。此外,在欧洲EARTH项目计划中,通过考虑发射功率、功率转换效率和硬件电路功耗以得到更高效的频谱效率[19]。
本文的中继节点和终端节点均进行无线能量收集,而中继节点则利用收集的能量进行终端节点的能量发送和信息传输设计,本文的创新贡献主要包括:
(1)中继节点利用源节点信号收集能量,进行终端节点能量收集和信息传输算法设计;
(2)获得了基于能效最大化准则的最优功率分配的渐近最优解;
(3)对所提算法进行了仿真和分析,验证了所提算法的有效性和正确性。
本文的结构安排如下:第1节对本文的研究背景进行介绍并进行了国内外研究分析;第2节描述本文的系统模型;第3节设计所提的能量收集和信息传输算法并推导功率分配的最优解;第4节对本文所提算法进行仿真和分析;第5节对本文进行总结。
2 系统模型
如图1所示,描述了双跳物联网无线网络的能量和信息传输的系统模型,由于物联网大规模覆盖等特点使得中继节点无电源充电,因此,在第一跳传输阶段,中继节点从源节点经由无线信道获取能量,同时利用该源节点接收所需信息。从中继节点到目的节点的第二跳传输阶段,中继节点利用从源节点收集到的能量进行信息发送,通过信息和能量传输的预编码算法设计将信号发送到目的节点1,同时目的节点2进行能量收集。
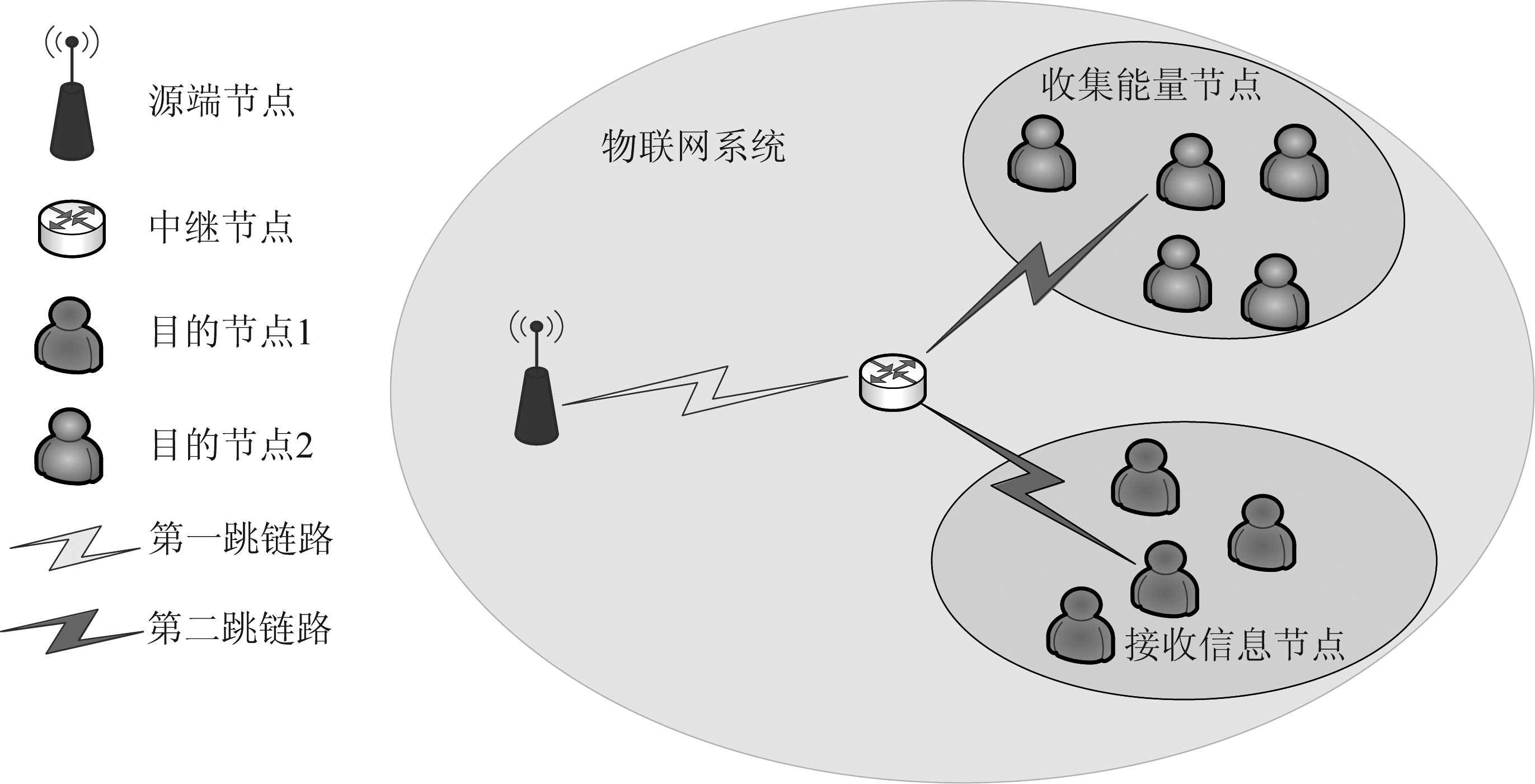
图1 中继协同的能量和信息传输系统模型
Fig.1 System model of energy and information transmission with relay cooperation
在第一跳物联传输阶段,中继节点接收到的信号由下式给出:
(1)
其中PS是物联网网络中源节点的发射功率,需进行信息传输和能量收集的优化,h～CN(0,1)是从源端到中继节点的无线信道,服从均值为零方差为1的循环对称复高斯分布,x是单位功率的发射信号,
是中继节点处的加性高斯白噪声(AWGN,additive white Gaussian noise),服从均值为零方差为
的循环对称复高斯分布。
中继节点接收到源节点的信号后,采用功率分流法收集能量(分流因子ρ):
(2)
其中0<ρ<1是功率分流因子,因此,中继节点处从所有接收到的信号中分离出信号之后的能量是
功率分流后的
则是中继节点接收的无线信号:
(3)
其中
是服从均值为零方差为的噪声,因此中继收集到的能量为:
(4)
中继节点的发送信号可表示如下:
(5)
其中yR,I是中继节点经过功率分流后接收到的无线信号,则:
(6)
在第二跳的传输中,目的节点1接收到的无线信号表示如下:
(7)
其中g～CN(0,1)是从中继节点到第一个接收信号的目的节点的无线信道,nI是第一个目的节点处的高斯白噪声,其中
同时,第二个目的节点收集能量可表示为:
(8)
其中f～CN(0,1)是从中继节点到收集能量目的节点的无线信道,服从均值为零方差为1的循环对称复高斯分布,
是第二个目的节点处的高斯白噪声。
3 能量收集和信息传输的预编码算法设计
本节将对源端进行预编码算法设计以实现绿色传输,在满足目的节点2所需的最小收集能量的前提下,对源节点的发送功率进行优化,最大限度地提高整个物联网通信系统能效的同时,满足第二个目的节点所需的最小能量。能效函数定义为瞬时吞吐量与硬件电路损耗的总功耗的比值。
通过合并等式(5)和(7),可得到从源端通过中继到达第一个目的节点的无线信号传输的表达式为:
(9)
其中
是通过中继到第一个目的节点的加性高斯白噪声。
基于等式(9),可得到第一个目的节点接收信号的SNR表达式:
(10)
对于收集能量的第二个目的节点,经过中继节点使用功率分流法从源端接收到的功率‖yE‖2为:
(11)
基于等式(10)和(11),在满足最小收集能量的前提下,最大化IoT系统的能效优化问题可表示为:
(12)
其中γ0>0是预设门限值,定义了在IoT网络的第二个目的节点处收集的最小能量。a>0和b>0是考虑了功率转换效率和硬件电路功耗成本的功耗模型中的参数,该模型在EARTH项目中得到了广泛应用[19]。本节目的是推导出其最优解析表达式,然而等式(12)中的目标函数与约束的联合优化中,ps是一个二次项,该优化问题是非凸优化。
为了解决这个难题,本文使用高信噪比近似法逼近等式(10)中的信噪比,在高信噪比情况下,可忽略噪声方差
(通常为1),因此等式(10)可以表示为:
(13)
把等式(13)代入等式(12),可获得:
(14)
等式(14)可以表示为(15),以便于使用拉格朗日乘子法求解:
(15)
由于约束
因此:
(16)
把等式(16)代入等式(15),得:
(17)
把等式(17)用拉格朗日函数表示:
(18)
其中λ是拉格朗日乘子。
通过对ps求一阶导数,并令其为0,可表示为:
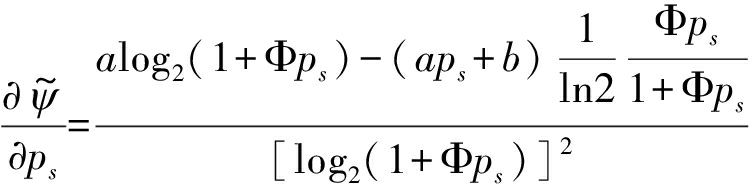
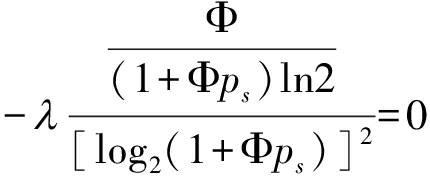
(19)
将式(19)整理如下:
(20)
因此,得到等式(20)的最优解为
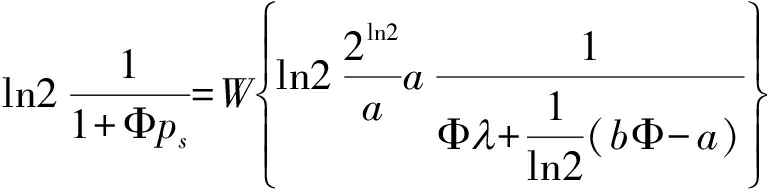
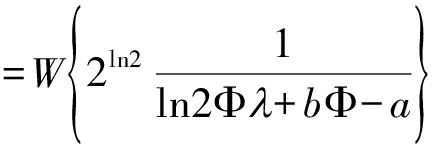
(21)
其中W{·}是朗伯函数[20],从而获得源节点的渐近最优发送功率为:
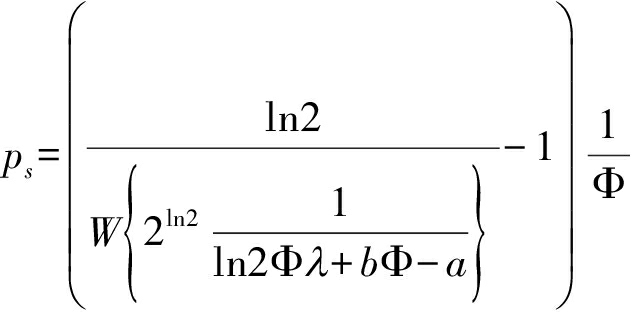
(22)
因此,通过上述推导和分析可根据双跳IoT系统中目的节点2收集的最小能量的任意值来计算源端最佳发送功率,而中继节点的发送功率全部来自源端。
4 仿真和分析
本节对本文所提方案实现的物联网系统能效进行了仿真和分析,其中蒙特卡罗循环次数为10000。第二目的节点通过无线传输收集能量,功耗(ptotal=apt+b)中的参数a的范围从5到10,b的范围从10到300。所有的噪声方差置为
信道服从瑞利衰落分布。
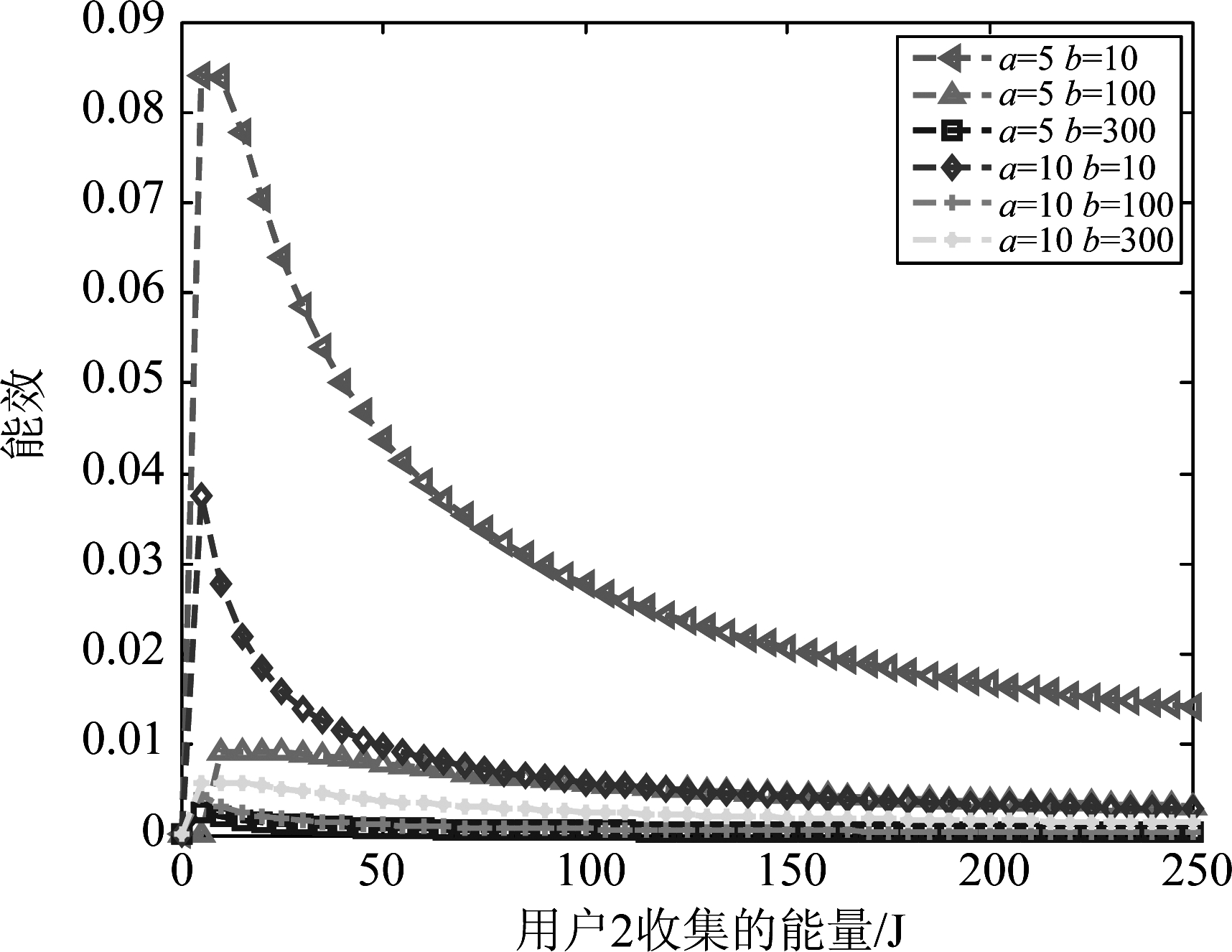
图2 功率分流因子ρ=0.5时,所提方案实现的IoT能效
Fig.2 Achieved energy efficiency of the whole IoT systems by the proposed scheme with ρ=0.5
图2描述功率分流因子ρ=0.5时,整个IoT系统的能效关于第二目的节点处所需的最小能量γ0的函数。由图可知,对于功耗模型的任意参数值,能效随着γ0的增加先上升后下降,这是由于吞吐量的增益远远大于低γ0时的功耗,表明了整个物联网系统的能效提高了。然而,与必须满足高γ0所增加的功率成本相比,吞吐量的增益是有限的,由图2可知,对于给定的b值,随着参数a的增加,最优点向左移动,也就是说随着参数a的增加最优点对应的γ0的值会减小。
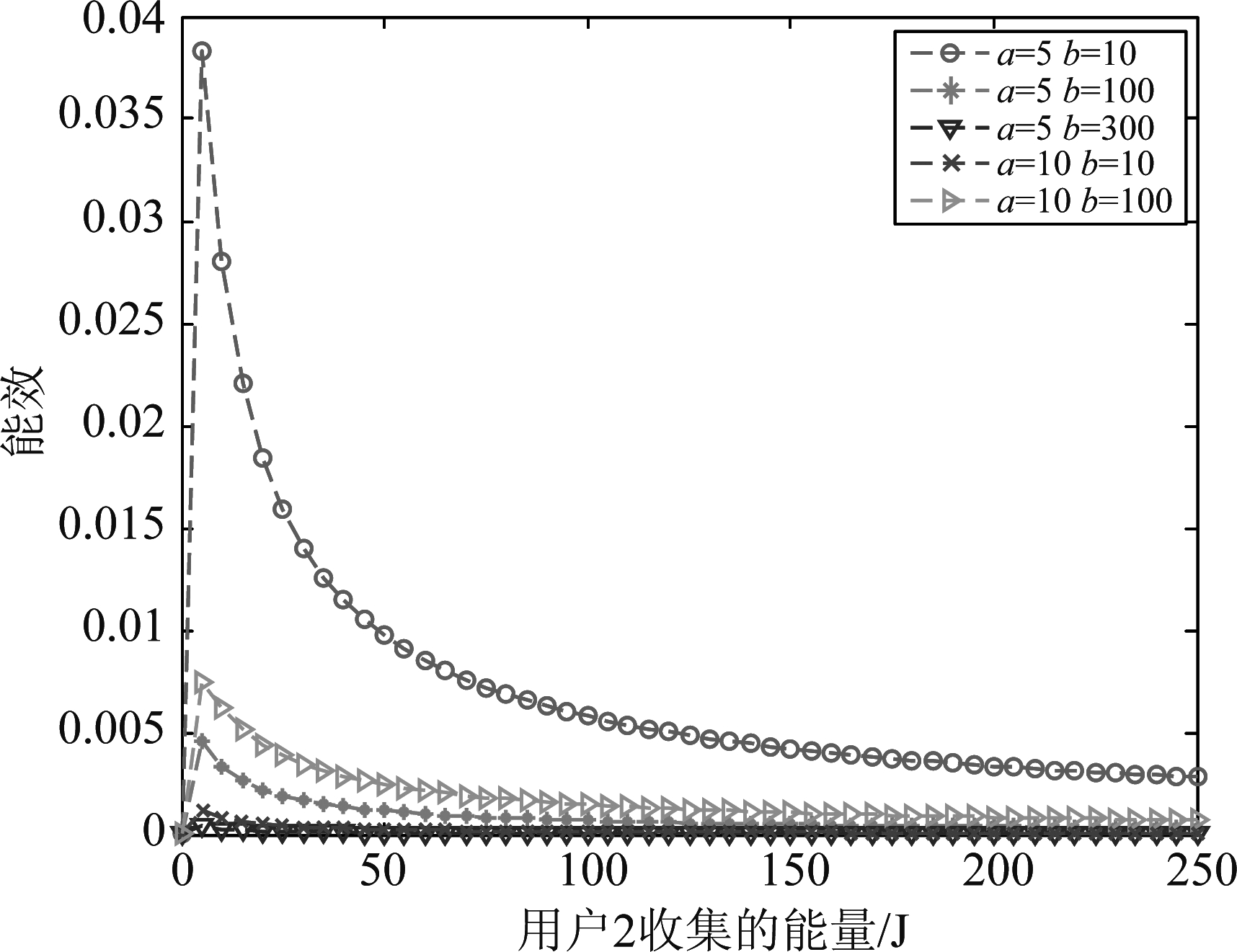
图3 功率分流因子ρ=0.9时,所提方案实现的IoT能效
Fig.3 Achieved energy efficiency of the whole IoT systems by the proposed scheme with ρ=0.9
图3与图2有相似趋势,不同的是图3对ρ=0.9时的极限情况进行了仿真和分析,由图可知当ρ很大时,尽管信息传输能力很强,但是能量收集能力降低,系统能效下降。
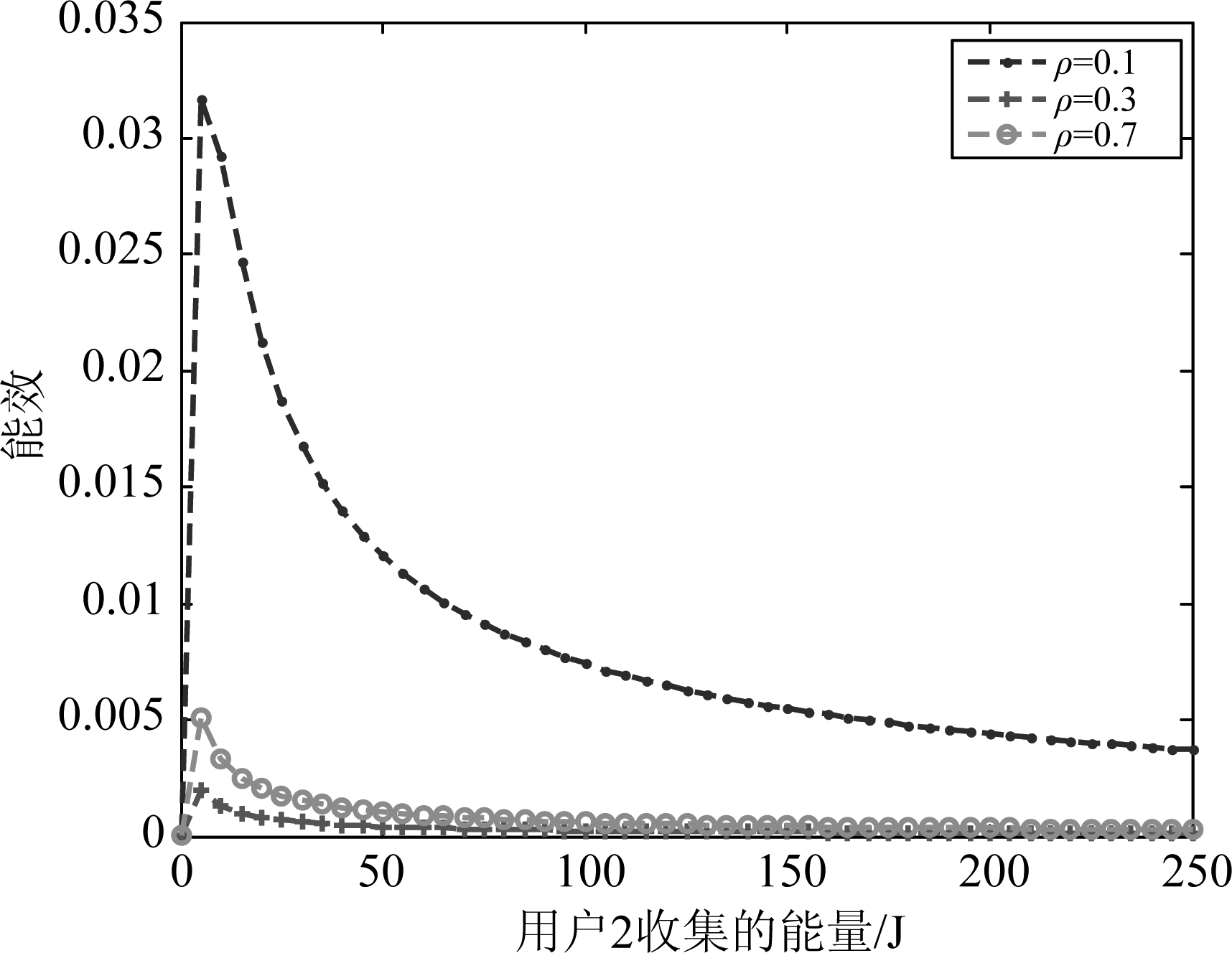
图4 a=5,b=10时,不同ρ值下,所提方案实现的IoT能效
Fig.4 Achieved energy efficiency of the whole IoT systems by the proposed scheme with different ρ and a=5,b=10
图4描述了在功耗参数a=5,b=10时,ρ分别为0.1、0.3、0.7时,目的节点2收集的能量和系统能耗的函数。由图可知,能效函数会随着ρ值的变化呈现出不同的趋势,这是因为ρ值同时决定着系统可以收集的能量和发送的信号,因此对源端的发送功率和功率分流因子ρ的联合优化将是本文的下一步研究重点。
图5描述了本文利用高信噪比近似法求解的能量收集和信息传输算法的渐近最优解与原始优化问题全局最优解的对比,由图可知,本文基于能效最大化优化准则所设计的中继协同无线物联系统能量收集和信息传输的渐近最优功率分配方案,与原始优化问题的全局最优解有着很小差距,可以作为一种求解该优化问题的简便方法。
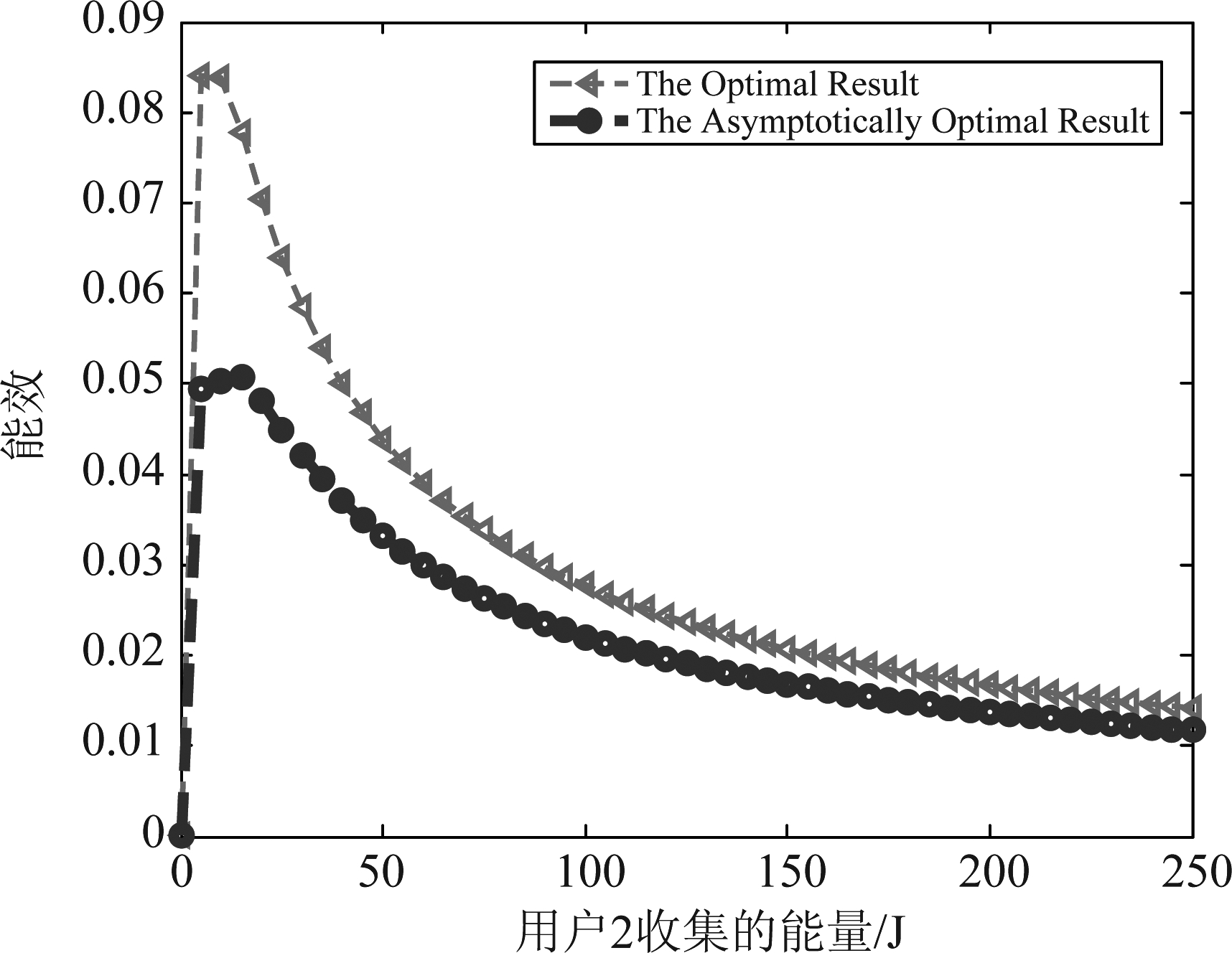
图5 渐近最优解和原始优化问题全局最优解的对比
Fig.5 The comparison between the asymptotically optimal result and the globally optimal result
5 结论
本文针对两跳无线物联通信系统,设计了中继节点利用收集的能量采用功率分流法进行能量收集和信息传输算法,其中算法是基于能效最大化优化准则,能效函数定义为瞬时吞吐量与硬件电路总功耗的比值,中继节点利用源节点发送的信号进行能量收集,考虑EARTH计划中实际的功率转换效率和硬件电路损耗的功耗因子,推导了中继协同的无线物联系统能量收集和信息传输的最优功率分配方案的解析解,由于优化问题是非凸问题,为了解决该问题,本文利用高信噪比近似法并通过拉格朗日算法和Lambert W函数获得了优化问题的渐近最优解,数值仿真验证了所提方案的正确性和有效性,当功率分流因子很小时,可实现的信息传输能力降低,而当很大时,尽管信息传输能力很强,但是能量收集能力降低,系统能效下降,因此对源端的发送功率、功率分流因子以及中继节点选择等参数的联合优化将是本文的下一步研究重点。
[1] Palattella M, Dohler M, Grieco A, et al. Internet of Things in the 5G Era: Enablers, Architecture, and Business Models[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(3): 510-527.
[2] Li Shancang, Xu Lida, Zhao Shanshan. 5G Internet of Things: A Survey[J]. Journal of Industrial Information Integration, 2018, 10: 1-9.
[3] Atzori L, Iera A, Morabito G. The Internet of Things: A survey[J]. Computer Networks, 2010, 54(15): 2787-2805.
[4] Ejaz W, Anpalagan A, Imran M A, et al. Internet of Things (IoT) in 5G Wireless Communications[J]. IEEE Access, 2016, 4: 10310-10314.
[5] Kramer G, Gastpar M, Gupta P. Cooperative Strategies and Capacity Theorems for Relay Networks[J]. IEEE Transactions on Information Theory, 2005, 51(9): 3037-3063.
[6] Adinoyi A, Yanikomeroglu H. Cooperative Relaying in Multi-antenna Fixed Relay Networks[J]. IEEE Transactions on Wireless Communications, 2007, 6(2): 533-544.
[7] 
, Yates R D. Bandwidth and Power Allocation for Cooperative Strategies in Gaussian Relay Networks[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1880-1889.
[8] Suraweera H A S H A, Smith P J S P J, Armstrong J A J. Outage Probability of Cooperative Relay Networks in Nakagami-m Fading Channels[J]. Communications Letters IEEE, 2006, 10(12): 834- 836.
[9] 韩玉洁, 杨绿溪. MIMO多中继辅助通信中基于最优功率分配的路由选择算法[J]. 信号处理, 2010, 26(1): 80- 85.
Han Yujie, Yang Lvxi. Routing Algorithm Based on Optimal Power Allocation in MIMO Multi-relay Assisted Communication[J]. Signal Processing, 2010, 26(1): 80- 85.(in Chinese)
[10] 冀保峰, 宋康, 李春国, 等. 聚合干扰下小小区网络的协作传输方案及性能分析[J]. 信号处理, 2015, 31(10): 1342-1353.
Ji Baofeng, Song Kang, Li Chunguo, et al. Cooperative Transmission Scheme and Performance Analysis of Small Cell Networks under Aggregation Interference[J]. Journal of Signal Processing, 2015, 31(10): 1342-1353.(in Chinese)
[11] Ji Baofeng, Li Yuqi, Meng Yinghui, et al. Performance analysis of two-way full-duplex relay with antenna selection under Nakagami channels[J]. EURASIP J. Wireless Commun. Netw., (2018) 2018: 265.
[12] Zappone A, Cao P, Jorswieck E A. Energy Efficiency Optimization in Relay-Assisted MIMO Systems With Perfect and Statistical CSI[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 443- 457.
[13] Zhao Ming, Zhao Jing, Zhou Wuyang, et al. Energy Efficiency Optimization in Relay-assisted Networks with Energy Harvesting Relay Constraints[J]. China Communications, 2015, 12(2): 84-94.
[14] Li Fang, Jie Xu, Ling Qiu. Energy Efficiency optimization for two-way relay channels[C]∥IEEE International Conference on Communications Workshops. IEEE, 2013.
[15] Angelakis V, Avgouleas I, Pappas N, et al. Allocation of Hegenerogenous Resources of an IoT Device to Flexible Services[J]. IEEE Internet of Things, 2016, 3(5): 691-700.
[16] Zhang Di, Zhou Zhenyu, Mumtaz S, et al. One Integrated Energy Efficiency Proposal for 5G IoT Communications[J]. IEEE Internet of Things Journal, 2016, 3(6): 1346-1354.
[17] Kotagi V J, Thakur R, Mishra S, et al. Breathe to Save Energy: assigning Downlink Transit Power and Resource Blocks to LTE Enabled IoT Networks[J]. IEEE Communications Letters, 2016, 20(8): 1607-1610.
[18] Semasinghe P, Maghsudi S, Hossain E. Game Theoretic Mechanisums for Resource Management in Massive Wireless IoT Systems[J]. IEEE Comm. Magazine, 2017, 55(2): 121-127.
[19] Auer G, et al. D2.3: Energy Efficiency Analysis of the Reference Systems, Areas of Improvements and Target Breakdown, Technical Report, INFSO-ICT-247733 EARTH (Energy Aware Radio and NeTwork TecHnologies), 2010.
[20] Valluri S R, Jeffrey D J, Corless R M. Some Applications of the Lambert W Function to Physics[J]. Canadian Journal of Physics, 2000, 78(9): 823- 831.
