1 引言
扩频通信因为其隐蔽性强,保密性高,抗干扰能力强等优点,在军事和商业通信中被广泛应用。软扩频技术,也称多序列扩频技术,它将直接序列扩频技术和编码技术相结合,克服了传统的直接序列扩频技术存在的带宽较宽,信息传输效率低等问题,并且具有一定的编码增益。现今,walsh码软扩频技术的应用越来越广泛,比如外军MarkⅦ Mode 5采用(16,4)的walsh软扩频编码技术,欧洲国家战地网使用的战术数字通信也提出使用(256,8)和(32,7)的正交矩阵编码扩频系统。另外,WCDMA应用(64,6)walsh码软扩频编码技术等[1]。 由于walsh码软扩频信号应用比较广泛,因此,论文主要研究walsh码软扩频信号。
针对扩频信号的盲解扩问题,当前已经有了一定的研究成果。文献[2]提出利用特征值分解法对直接序列扩频信号盲解扩。文献[3]采用奇异值分解法实现直接序列扩频信号盲解扩。文献[4]采用神经网络法实现直接序列扩频信号盲解扩。文献[5]利用压缩投影近似子空间跟踪法对直扩信号盲解扩。但上述算法多是针对传统直接序列扩频信号的,对于软扩频信号效果并不好。目前,软扩频信号盲解扩的方法不多,文献[6]首次应用聚类算法实现软扩频信号盲解扩,该算法可以估计延时时间和伪码序列规模数,但是对信噪比要求较高,计算量较大。文献[8]采用k-means聚类算法实现软扩频盲解扩,时间复杂度较低。但该算法的初始中心随机选择,聚类结果容易受到异常点和噪声影响。文献[9]采用改进k-means聚类算法实现软扩频盲解扩。该算法能克服随机选取初始聚类中心的缺陷,但随着搜索次数的增加,计算量有所增加。
针对现有walsh码软扩频信号盲解扩算法存在的不足,本文提出一种改进的密度峰聚类算法。该算法在已知伪码周期和码片速率的前提下,首先根据已知的伪码周期和码片速率对接收数据分段处理,得到数据矩阵,然后采用改进的密度峰聚类算法估计walsh软扩频信号的伪码序列规模数和伪码序列。该算法具有在较低信噪比情况下,实现walsh码软扩频信号盲解扩的特点。仿真结果表明,在信噪比较低时,本文算法能够准确估计接收的walsh码软扩频信号的伪码序列规模数和伪码序列,且时间复杂度相较于文献[9]所用算法有所降低。
2 软扩频模型及盲解扩问题的描述
软扩频信号发射端模型如图1所示。由于本文主要针对walsh码软扩频盲解扩,因此图1中扩频码序列选择器为walsh码产生器。
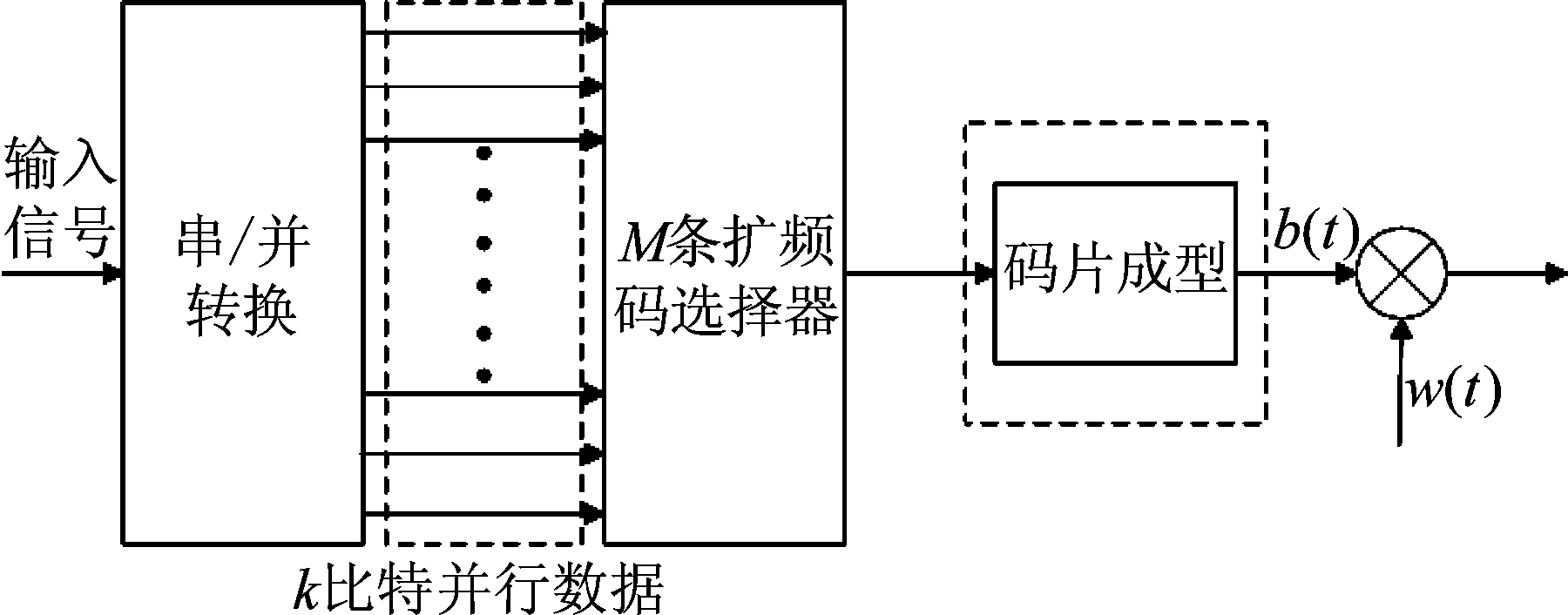
图1 软扩频信号发射端模型
Fig.1 Model of soft spread spectrum signal transmitter
将传输信息记为d(t),信息码d(t)经过串并转换后得到k比特的并行数据。并行数据共有M=2k个状态,依据每组信息码的状态选择M条伪码序列与其对应。
设传输的信息数据为:
(1)
其中an=±1,Tb为信息码元宽度,gb(t)是幅度为1且长度为1的矩形波。
将信息码元按k比特分组,则分组信息码可以表示为:
(2)
其中,![]() 是伪码周期。
是伪码周期。
k比特信息码权值为:
(3)
k比特信息码元根据计算的权值j从n条walsh码序列中选取M条伪码序列传输信息。尽管通过先验信息已知walsh码伪码序列长度n,但是伪码序列规模数M与伪码序列长度n不一定相等,即M≤n。因此,研究对软扩频信号伪码序列规模数的估计是很有必要的。
软扩频接收系统可以表示为:
(4)
其中Cj是由信息码的权值j确定。信息数据通过高斯白噪声信道后,接收到的软扩频信号可以表达为:
(5)
其中w(t)是均值为0,方差为1的高斯白噪声,并且与b(t)相互统计独立。
假设伪码速率Tc和伪码周期T=NTc已经估计出来[6],以Tc为采样速率对接收到的信号进行采样,得到离散的信号:
p(n)=b(t-τ)+w(t)|t=nTc=b(nTc-τ)+w(nTc)
(6)
其中τ为接收信号的延迟时间,τ∈[0,N-1]。
将采样后的离散序列分成若干段不重叠的序列,每个序列含有N个采样值。分段序列记为:
xm={x(mN-N),x(mN-N+1),
x(mN-N+2),…,x(mN-1)}
(7)
其中,m=1,2,…,SN,即X={x1,x2,…,xSN}。
在非合作通信过程,若想知道截获信号中的有用信息,需要知道M条伪码序列集合C={c1(t),c2(t),c3(t),…,cM(t)},从而进一步实现软扩频信号的盲解扩。
传统直接序列扩频信号是软扩频信号的一种特殊形式,直扩信号相当于k=1,伪码集合为:c1(t)=c2(t)=…=cM(t)时的软扩频信号。因此对软扩频信号盲解扩的研究有重要意义。
walsh码软扩频信号盲解扩问题就是对接收的软扩频信号,在少量先验信息甚至没有先验信息的情况下,采用盲解扩算法,估计伪码序列规模数和伪码序列。本文解决该问题主要分为两步:第一步,利用已知的伪码周期和码片速率,对接收的软扩频信号进行分段处理,得到数据矩阵。第二步,利用自动确定聚类中心的密度峰聚类算法估计软扩频信号的伪码序列规模数和伪码序列。
3 基于改进的密度峰聚类walsh码软扩频信号盲解扩算法
3.1 算法理论阐述
软扩频技术是将信息从信息空间映射到伪随机码空间,walsh码软扩频技术将walsh码作为伪随机码,实现对信息序列的扩频。文献[7]-[9]采用k-means算法实现软扩频信号盲解扩,但是算法需要提前预估最大伪码序列规模数,计算量较大,不适用于较大规模数据。Alex Rodriguez等人提出一种基于密度峰的聚类算法(clustering by fast search and find of density peaks 简称DPC)[11],其特点是不需预先指定聚类中心个数,但其密度峰聚类算法需要人工选择密度峰,容易出现少选或者错选聚类中心的问题。因此本文建立适用walsh码软扩频信号的盲解扩模型,将密度峰聚类算法应用于软扩频信号盲解扩,提出采用自动确定聚类中心的密度峰聚类算法实现walsh码软扩频信号盲解扩,有效降低算法复杂度,使之适合处理大规模数据。
密度峰聚类算法[10]主要计算局部密度ρi,数据点与具有较高局部密度数据点之间最短距离δi。
数据的局部密度有两种计算方式,分别是“截断核”和“高斯核”。
“截断核”:
(8)
其中,![]()
“高斯核”:
(9)
相较于“截断核”,使用“高斯核”计算的局部密度是连续的,不会出现不同数据具有相同局部密度的情况,因此,本文算法使用“高斯核”计算数据的局部密度。
数据点与具有较高局部密度数据点间最短距离δi,可通过计算数据点间欧氏距离得出。欧氏距离计算公式如式(10)所示:
i=1,2,…,SN j=1,2,…,SN
(10)
聚类中心局部密度较高,并且与局部密度较高的数据点间距离较大。因此,聚类中心点的ρi和δi数值较大。引入参数γi,γi计算公式如下所示:
γi=δiρi
(11)
当数据点为聚类中心时,γi数值较其他数据点的γi大,由此可以自动确定聚类中心,避免出现错误选择聚类中心的问题。
将γi从大至小排序。根据式(12)确定拐点位置。
ap=max{s|‖γs-1-γs|-|γs-γs+1‖>θ}
s=2,3,…,SN-1
(12)
其中,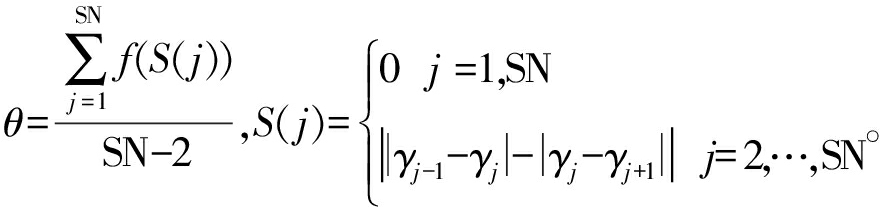
将n个数据间的距离按照从小到大排序,设为d1≤d2≤…≤dSN,利用数据点的邻居点占数据集样本点数的比例值P,按照式(13)计算dc。
dc=df(P/100)
(13)
其中f(P/100)表示P/100进行四舍五入取值,dc是判断数据点是否为聚类中心的阈值。若局部密度较高的数据点与已知聚类中心的最短距离大于dc,则两点都为聚类中心。否则,数据点为某聚类中心簇成员。
拐点之前数据点的γi值较大且相差较大,拐点之后数据点的γi值较小,且相差较小。将拐点之前的数据点称为潜在聚类中心。默认具有最大γi值的数据点为聚类中心,其他潜在聚类中心与实际聚类中心的最短距离小于dc时,将该数据组确定为聚类中心,否则将该数据组记为某聚类中心簇成员。
相较于文献[9]中利用k-means聚类算法解决软扩频信号盲解扩问题,改进的密度峰聚类算法减少了搜索次数,可以快速的估计出伪码序列规模数和伪码序列。
3.2 walsh码软扩频盲解扩步骤
根据文中对盲解扩算法的阐述,本文算法的具体步骤如下所示:
输入:数据矩阵X={x1,x2,…,xSN},数据点的邻居点总数占数据集样本点数的比例值P。
输出:伪码序列规模数,伪码序列。
Step 1 根据式(10)计算SN个样本组之间欧氏距离,得到距离矩阵dist(i, j)。
Step 2 根据P计算dc:将SN个样本组之间m=SN(SN-1)/2个欧氏距离从小到大进行排列。设有d1≤d2≤…≤dSN,那么dc=df(P/100),其中f(P/100)表示对P/100进行四舍五入取值。
Step 3 根据公式(9)和(10),计算每个数据点i的局部密度ρi和该点到具有更高局部密度数据点的最短距离δi。
Step 4 根据公式(11),计算数据点的γ值。然后,将γ从大至小排序,绘制γ排序图。根据γ排序图和公式(12)自动查找拐点ap,在排序图中,位于拐点之前的数据点为潜在聚类中心。
Step 5 默认具有最大γ值的数据点为一个实际聚类中心。根据式(10)计算点i与所有实际聚类中心的距离d(i, j),如果min(d(i, j))>dc,则点i被确定为一个新的实际聚类中心,否则点i被视为点j所属簇的成员。
Step 6 重复步骤5,直到i=ap,所得的聚类中心数目为伪码序列规模数,聚类中心即为伪码序列。
算法流程图如图2所示。
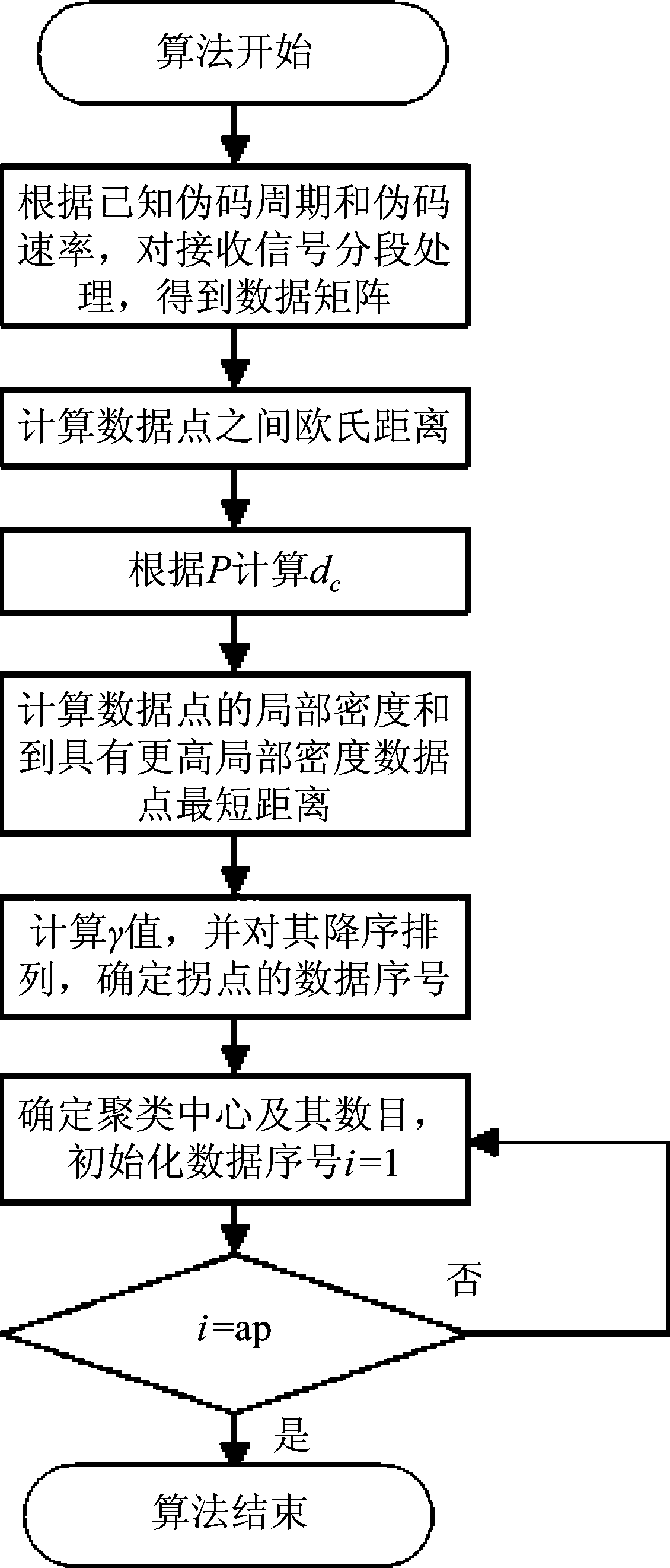
图2 改进密度峰聚类盲解扩算法流程图
Fig.2 The flow chart of blind estimation by improved density peak clustering
3.3 算法复杂度分析
实验采用SN个数据,算法第(1)步计算SN个数据之间的距离,时间复杂度是Ο(SN2),第(2)步中,将m个距离值排序的时间复杂度是Ο(m log m),第(3)步中计算每个数据的局部密度和到具有更高局部密度数据点的最短距离的时间复杂度是Ο(SN2),第(4)步中计算γ和对γ排序的时间复杂度是Ο(m log m),第(5)步和第(6)步中确定聚类中心和分配簇成员的时间复杂度是Ο(SN2)。由上述分析可得,本文算法的时间复杂度是Ο(m log m)。
传统k-means算法复杂度是Ο(m log m×α1×k),其中m是SN个数据之间的距离个数,k是聚类中心数目,α1是算法迭代次数。文献[9]所提改进的k-means算法由于选取初始聚类中心,与传统算法相比,其所用迭代次数α2相较于传统k-means算法的迭代次数α1减少,算法复杂度降低。由分析可知,本文所提改进的密度峰聚类算法复杂度相较于传统k-means算法和改进的k-means算法而言,时间复杂度有所降低。walsh码软扩频盲解扩算法的复杂度如表1所示。
表1 walsh码软扩频盲解扩算法复杂度比较
Tab.1 Comparison of walsh code blind spread spectrum expansion algorithm complexity

walsh码软扩频盲解扩算法算法复杂度k-means算法Ο(mlogm×α1×k)文献[9]所用改进k-means算法Ο(mlogm×α2×k)改进密度峰聚类算法Ο(mlogm)
4 仿真分析
本文使用改进的密度峰聚类算法实现walsh码软扩频盲解扩,在较低信噪比的情况下,准确估计伪码序列规模数和伪码序列是本文实验重点。实验采用的walsh码软扩频信号相关参数如下:
仿真信号为(8,3)时,伪码序列长度为N=8 chip,接收信号长度为1200 chip,信噪比SNR=0 dB,数据点的邻居点总数占数据集样本点数的比例值P=2。
仿真信号为(32,5)时,伪码序列长度为N=32 chip,接收信号长度为2000 chip,信噪比SNR=0 dB,数据点的邻居点总数占数据集样本点数的比例值P=3。
实验1 SNR=0 dB下验证改进密度峰聚类算法估计软扩频信号伪码序列规模数。
实验1结果见图3、图4。从图3和图4可以看出,信噪比SNR=0 dB时,每个数据点的gamma值γ(其计算公式见式(11))从大至小排序,构成γ决策图。决策图中,星型点为确定的聚类中心,圆心点为每个聚类中心的簇成员。拐点发生在数据序号30附近,gamma值8附近。拐点之前的数据点的γ值较大,且两两间隔较大。拐点之后的数据点,其γ值较小,前后间隔较小,重叠为一线。由图3可以看出,本文算法对接收的软扩频信号进行盲解扩,星型点数为8,即估计的伪码序列规模数为8,与(8,3)软扩频信号的伪码序列规模数相同。由图4可以看出,本文算法对接收的软扩频信号进行盲解扩,星型点数为32,即估计的伪码序列规模数为32,与(32,5)软扩频信号的伪码序列规模数相同。因此,改进的密度峰聚类算法在SNR=0 dB时,可以准确估计(8,3)和(32,5)软扩频信号的伪码序列规模数。
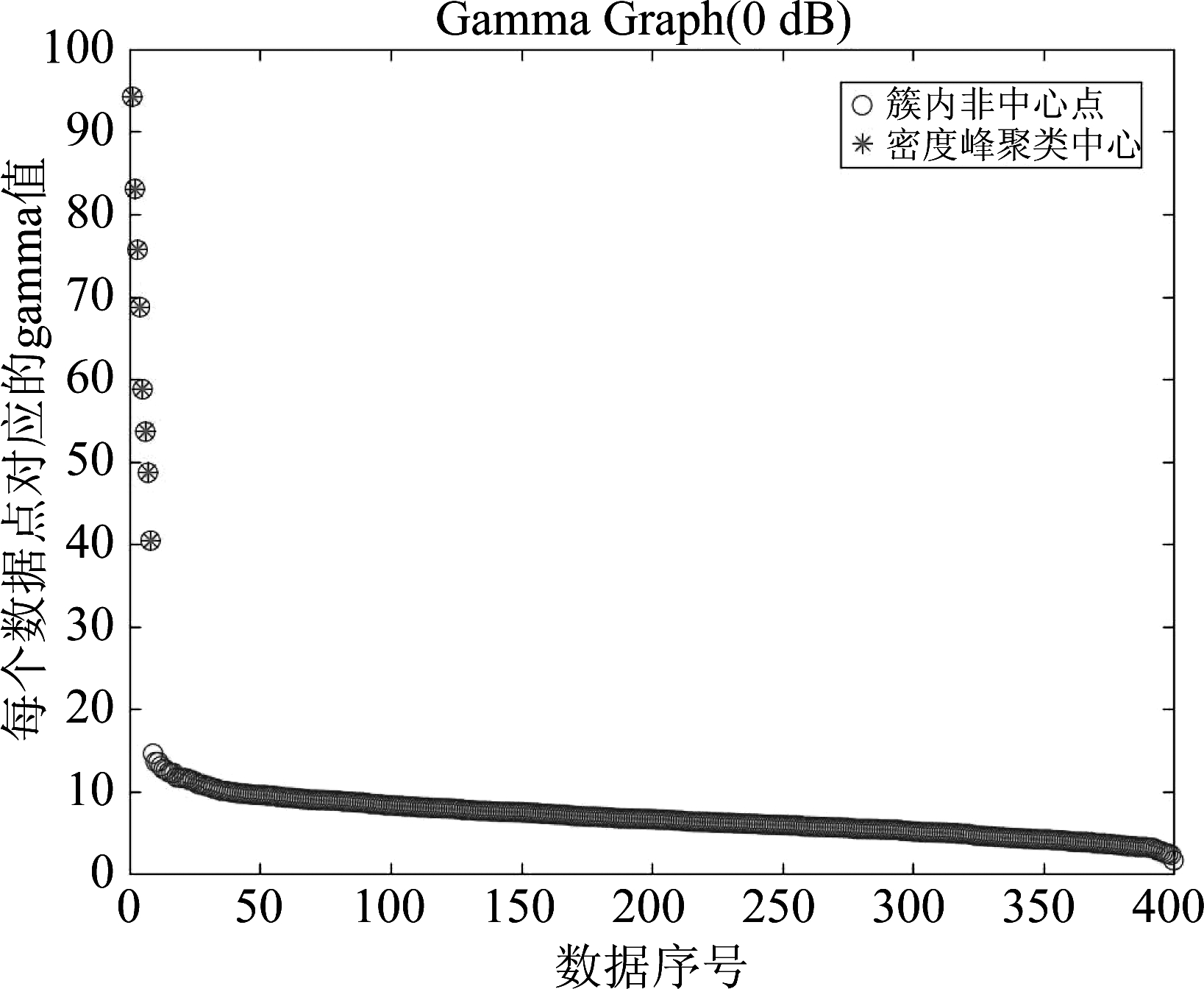
图3 SNR=0 dB时,(8,3)软扩频信号的gamma值γ的决策图
Fig.3 SNR=0 dB, decision graph of (8,3) soft spread spectrum signal

图4 SNR=0 dB时,(32,5)软扩频信号的gamma值γ的决策图
Fig.4 SNR=0 dB, decision graph of (32,5) soft spread spectrum signal
实验2 检验改进密度峰聚类算法估计软扩频信号伪码序列有效性。
图5为SNR=0 dB时利用本文提出的改进密度峰聚类算法对(8,3)软扩频信号伪码序列的估计值,图6为SNR=0 dB时(8,3)软扩频信号伪码序列的真实值。从图5可以看出,SNR=0 dB时,以0为阈值,幅度大于0的记为1,小于0的记为-1,估计结果与图6中(8,3)软扩频信号伪码序列的真实值一一对应。因此,改进的密度峰聚类算法能够准确估计(8,3)软扩频信号伪码序列。

图5 SNR=0 dB时(8,3)伪码序列估计值
Fig.5 SNR=0 dB, the estimated value of (8,3) soft spread spectrum

图6 SNR=0 dB时(8,3)伪码序列真实值
Fig.6 SNR=0 dB,the true value of (8,3) soft spread spectrum
实验3 检验信噪比大小对多种walsh码软扩频盲解扩算法性能的影响。
实验在不同信噪比取值下进行1000次蒙特卡洛仿真实验,算法错误估计伪码规模数概率随信噪比变化如图7所示。
由图7可以看出,传统k-means算法,改进k-means算法和改进密度峰聚类算法对接收软扩频信号盲解扩的错误概率随着信噪比提高而降低。传统k-means算法的性能较差,信噪比为0 dB时,错误估计概率达到10%以上,且因其随机选取初始聚类中心,错误估计概率变化较大,不能准确估计伪码序列规模数,仿真结果不稳定。改进的k-means算法性能最好,在接收信号信噪比大于-8 dB时,能准确估计出伪码序列规模数。本文所提算法当信噪比大于-4 dB时,对软扩频信号盲解扩错误概率为零,性能较好且仿真结果较稳定。另外,在相同信噪比条件下,聚类中心规模数为32时的伪码序列估计错误概率略大于聚类中心规模数为8的伪码估计错误概率。说明软扩频信号伪码长度越长,错误估计概率越大。有实验结果分析可知,本文所提盲解扩算法性能虽略低于改进k-means算法,但其运算复杂度大大低于改进k-means算法,更适合对数据规模较大的软扩频信号进行快速盲解扩。
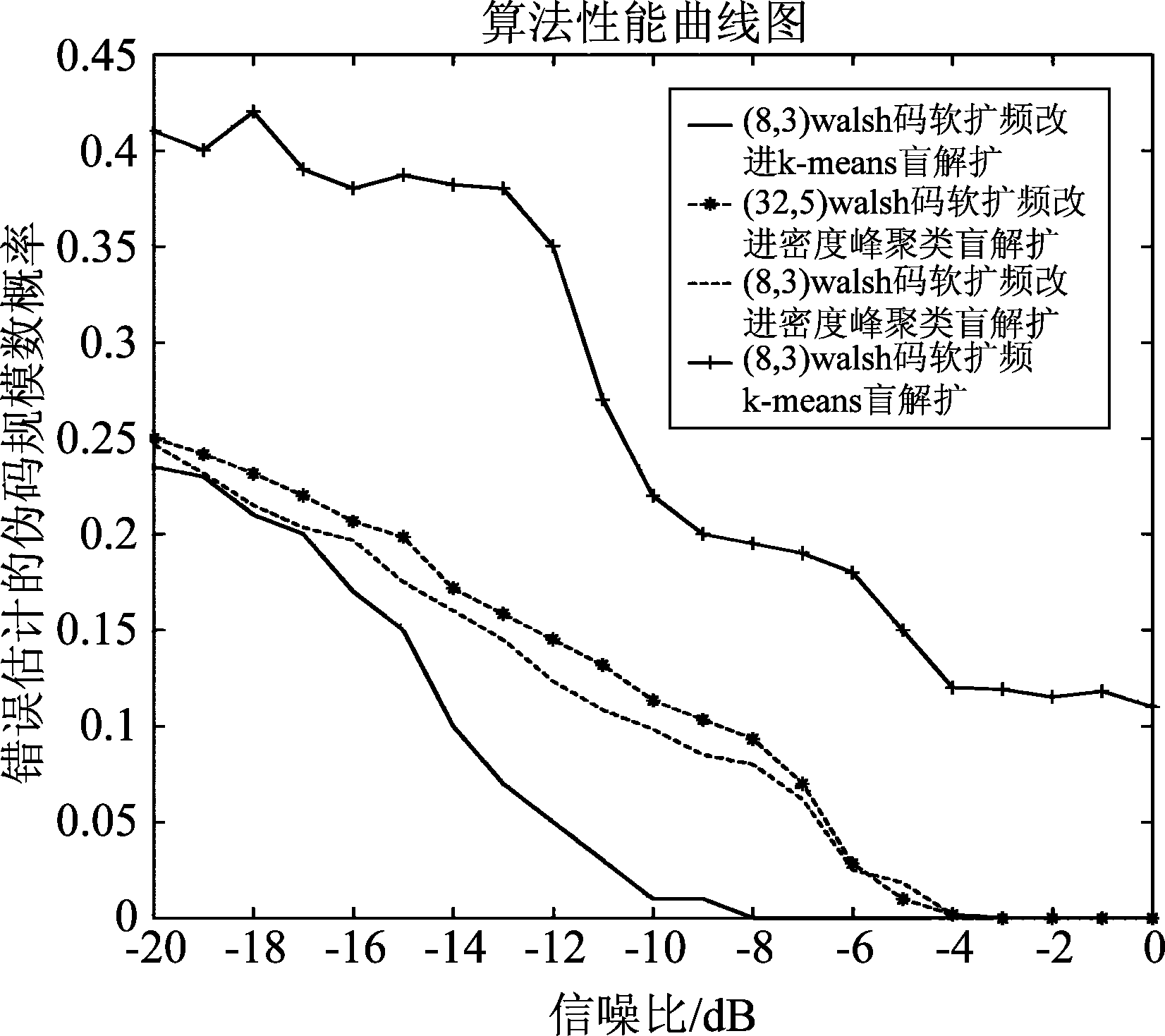
图7 多种软扩频信号盲解扩算法性能图
Fig.7 The performance curve of blind estimation of soft spread spectrum by multiple algorithm
5 结论
本文提出一种基于改进的密度峰聚类的walsh码软扩频信号盲解扩算法。该算法利用已知伪码周期和码片速率对接收软扩频信号进行分段处理,得到数据矩阵,然后利用改进的密度峰聚类算法估计软扩频信号的伪码序列规模数和伪码序列。分析及仿真实验表明,本文算法能够在较低信噪比条件下,实现对(8,3)和(32,5)walsh码软扩频信号盲解扩,并且算法复杂度较低。
[1] 周家晶, 唐友喜. JTIDS扩频序列的估计[J]. 电子科技大学学报, 2007, 36(5): 1054-1056.
Zhou J J, Tang Y X. Spread spectrum sequence estimation for JTIDS[J]. Journal of University of Electronic Science c and Technology of China, 2007, 36(5): 1054-1056.(in Chinese)
[2] Qui P Y, Huang Z T, Jiang W L, et al. Improved blind-spreading sequence estimation algorithm for direct sequence spread spectrum signal[J]. IET Signal Processing, 2008, 2(2): 139-146.
[3] 任啸天, 徐晖, 黄知涛, 等. 断码DS-SS信号扩频序列即信息序列联合估计方法[J]. 通信学报, 2012, 22(4): 169-175.
Ren X T, Xu H, Huang Z T, et al. Joint blinding estimation of the spread-spectrum sequence and information sequence for shot-code DS-SS signal[J]. Journal on Communications, 2012, 22(4): 169-175.(in Chinese)
[4] 张天骐, 周正中, 郭宗翔. 一种DS\SS信号PN码序列估计神经网络方法[J]. 信号处理, 2001, 17(6): 533-537.
Zhang T Q, Zhou Z Z, Guo Z X. A neural network approach to estimation of PN spreading sequence in DS/SS signal[J]. Signal Processing, 2001, 17(6): 533-537.(in Chinese)
[5] 吕明, 张洪波, 唐斌. 基于E-PASTd的盲扩频码序列估计算法[J]. 电子科技大学学报, 2007, 36(5): 886- 888.
Lv M, Zhang H B, Tang B. Blind estimation of PN spreading sequence based on E-PASTd[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(5): 886- 888.(in Chinese)
[6] Zhang T Q, Qian W R, Zhang G, et al. Parameter estimation of MC-CDMA signals based on modified cyclic autocorrelation[J]. Digital Signal Processing, 2016, 54: 46-53.
[7] 王航, 郭晓静, 王赞基. 基于聚类的软扩频信号盲解扩方法[J]. 电子与信息学报, 2009, 31(2): 422- 425.
Wang H, Guo X J, Wang Z J. Clustering based blind despread method of tamed direct sequence spread spectrum signals[J]. Journal of Electronic & Information Technology, 2009, 31(2): 422- 425.(in Chinese)
[8] 李军伟, 张天骐, 朱洪波, 等. 基于聚类的多进制扩频伪码序列盲估计方法[J]. 科学技术与工程, 2014, 14(2): 32-36.
Li J W, Zhang T Q, Zhu H B, et al. Clustering based blind estimation of PN sequences of mary spread spectrum system[J]. Science Technology and Engineering, 2014, 14(2): 32-36.(in Chinese)
[9] 张天骐, 杨强, 宋玉龙, 等. 一种k-means改进算法的软扩频信号伪码序列盲估计[J]. 电子与信息学报, 2017, 40(1): 226-234.
Zhang T Q, Yang Q, Song Y L, et al. Blind estimation PN sequence in soft spread spectrum signal of improved k-means algorithm[J]. Journal of Electronic & Information Technology, 2017, 40(1): 226-234.(in Chinese)
[10] 李涛, 葛洪伟, 苏树智. 自动确定聚类中心的密度峰聚类[J]. 计算机科学与探索, 2016, 10(11): 1614-1622.
Li T, Ge H W, Su S Z. Density peaks clustering by automatic Determination of cluster centers[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(11): 1614-1622.(in Chinese)
[11] Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[12] Wang S, Wang D, Li C, et al. Cluatering by fast search and find of density peaks with data field[J]. Chinese Journal of Electronics, 2016, 25(3): 397- 402.
[13] 赵知劲, 顾骁炜, 沈雷, 等. 非周期长码直扩信号的盲解扩[J]. 信号处理, 2014, 30(5): 511-516.
Zhao Z J, Gu X W, Shen L, et al. Blind despreading of non-periodic long code direct-sequence spread-spectrum signals[J]. Journal of Signal Processing, 2014, 30(5): 511-516.(in Chinese)
[14] 张天骐, 周正中, 林孝康, 等. 低信噪比长伪码直扩信号的盲估计方法[J]. 信号处理, 2008, 24(3): 370-376.
Zhang T Q, Zhou Z Z, Lin X K, et al. Approach to blind estimation of lower SNR long code DS signal[J]. Signal Processing, 2008, 24(3): 370-376.(in Chinese)
[15] Gu X L, Zhao Z J, Shen L. Blind estimation of pseudo-random codes in periodic long code direct sequence spread spectrum signal[J]. IET Communications, 2016, 10(11): 1273-1281.

