1 引言
随着能量采集技术的快速发展[1],文献[2]研究了基于时间切换和功率分配的放大转发中继协议,分别针对延迟受限和延迟容忍两种传输模式导出了中断概率和遍历容量的解析表达式。得到了在相对低的信噪比和高传输速率下,时间切换中继协议在吞吐量方面优于功率分配中继协议的结论。文献[3]研究了解码转发中继网络,推导了系统的可实现吞吐量和遍历容量的精确解析表达式。得到了以下结论:在各种信噪比条件下,功率分配中继方案的吞吐量性能都要优于时间切换中继方案的吞吐量性能。文献[4]研究了一个功率分配能量采集网络,获得了放大转发和解码转发协议下的最佳功率分配比的闭合形式。得到了在良好的协作链路中,放大转发协议比解码转发协议获益更多的结论。在源和目的地之间不存在直达链路时,文献[5]通过平衡能量采集阶段和信息传输阶段的持续时间来最大化系统吞吐量,推导出了最佳的时间分配。在多中继协助的双跳中继系统中,文献[6]研究了基于功率分配能量采集的同步无线信息和功率传输。每个中继节点使用分布式空时编码协助信息传输。针对解码转发和放大转发的中继协议提出了有效的算法，并求得了功率分配比的最优解。文献[7]给出了一种双跳全双工中继系统,基于时间切换中继协议分析了瞬时传输,延迟容忍传输和延迟受限传输,三种不同通信模式的可实现吞吐量。就系统吞吐量而言,瞬时传输最高,延迟容忍传输次之,延迟受限传输最小,因为延迟受限传输受到了传输速率的限制。文献[8]研究了基于功率分配能量采集协议的全双工中继传输方案。考虑功率分配在整个传输时间块内完成以及中继配置大规模天线的情况下,为了减弱中继自干扰对系统性能的影响, 提出了三种天线选择方案,并求出了系统遍历容量的近似闭合表达式。并基于发射功率和信道增益分析了三种方案的优缺点。考虑源和目的地之间存在直达链路时,文献[9]研究了基于时间切换能量采集协议的半双工放大转发协作中继方案,分析了同步无线信息和功率传输网络的吞吐量性能,并且基于时间切换和功率分配中继协议提出了自适应最大比合并协议,仿真验证了该协议可以选择更好的模式来实现通信。文献[10]研究了基于功率分配能量采集协议的半双工放大转发协作中继方案。采用高信噪比近似的方法得到了系统中断概率的闭合表达式,同时获得了最佳功率分配因子和分集阶数。
结合以上文献,还没有同时研究过源和目的地之间存在直达链路,中继工作在全双工模式下的吞吐量性能,然而这正是本文研究的重点,本文的结构如下。第2节介绍了系统整体传输架构。第3节研究了信息传输和系统吞吐量。第4节分析了最佳时间切换比。第5节介绍了自适应中继选择。第6节研究了最佳目的地选择。第7节参数仿真。第8节分析并总结全文。
2 系统模型
如图1是一个基于时间切换能量采集协议的全双工放大转发协作中继传输模型。由一个源(S)、一个全双工中继(R)和一个目的地(D)构成,源和目的地是单根天线,中继节点配备NR根天线。
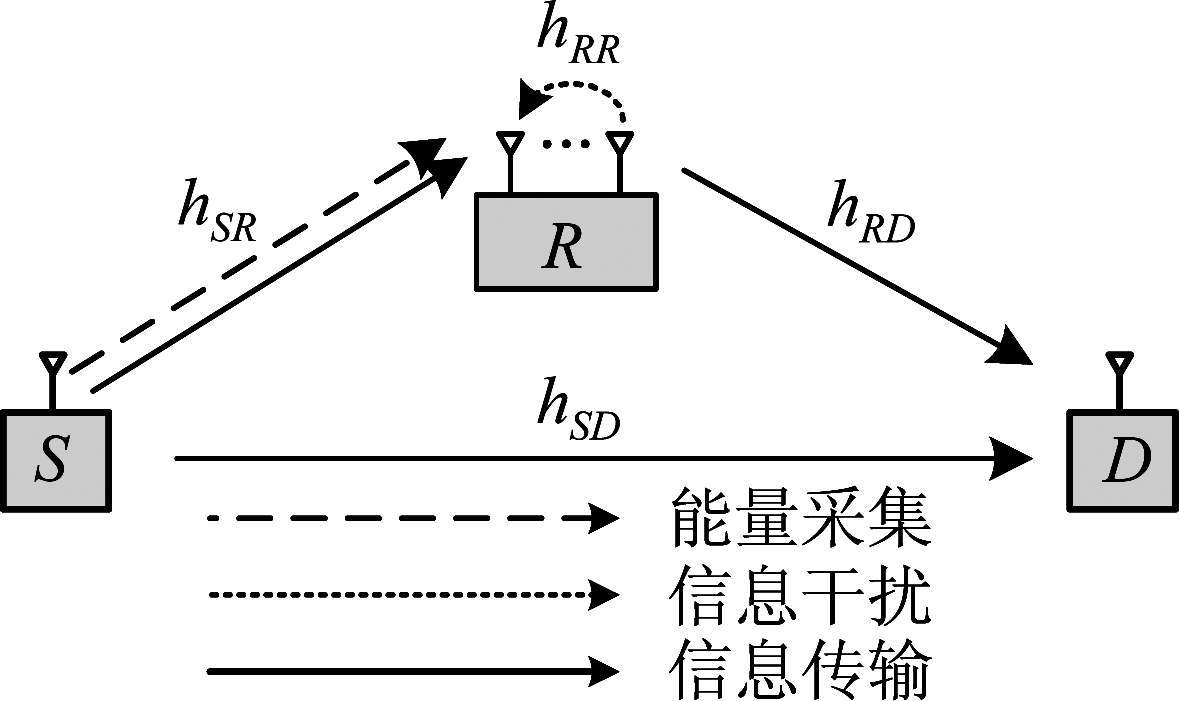
图1 协作通信网络中无线信息和功率传输的系统模型
Fig.1 The system model for wireless information and power transfer in a cooperative communication network
如图2是本文的传输时间块结构示意图。由图可知,整个时间块T内,源都可以通过直达链路传输信息到目的地。与此同时,T根据时间切换比α被分成两个不同的时隙,第一时隙αT内,中继节点进行能量采集。第二时隙(1-α)T内,全双工中继接收源信息的同时,放大转发源信息到目的地。
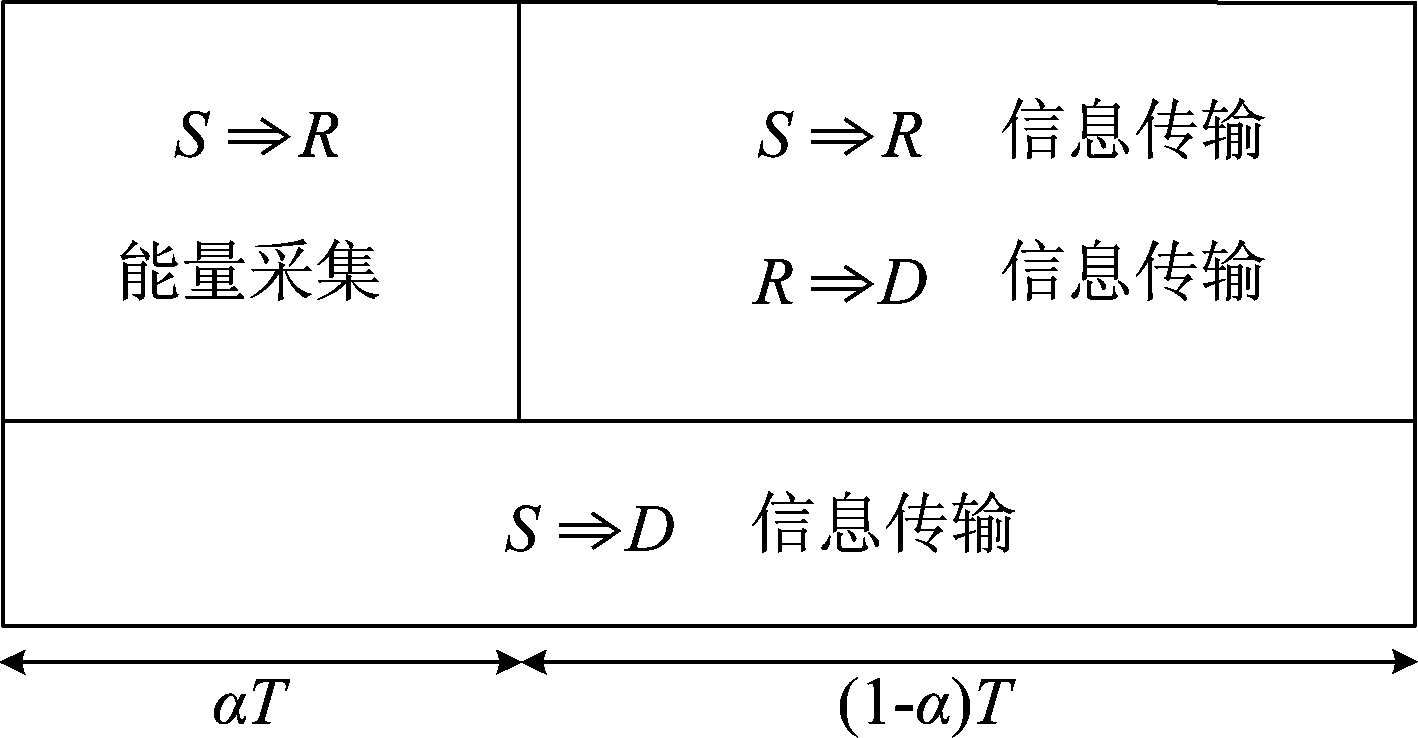
图2 传输时间块结构示意图
Fig.2 An illustration of transmission time-block structure
本文我们假设如下:
(1)所有信道从一个时间块到另一个时间块之间是遵循独立同分布准静止瑞利块衰落的,在每一个传输时间块T内,信道增益是一个常数。
(2)hij和
分别表示节点i和节点j之间的信道参数和距离(m代表路径损耗指数),λij表示节点i和节点j之间信道的平均信道增益,ni表示节点i接收到的均值为0方差为N0的加性高斯白噪声(i, j={S,R,D})。
3 吞吐量分析
本小节研究在延迟受限传输模式下,假定源节点发送速率是RS,由于无线信道是随机衰落的,中继传输可能会中断,系统平均吞吐量可表示为:
(1)
其中,t是信息传输持续时间,对于S⟹D信息传输t=T,对于S⟹R⟹D信息传输t=(1-α)T。
3.1 直达链路传输
由图1和图2可知,在整个时间块T内,源都可以通过直达链路直接传输信息到目的地。所以,此时目的地接收的信息和对应的信噪比分别为:
(2)
(3)
所以,在直达链路传输协议下,由式(3)可知,系统的中断概率和吞吐量分别是:
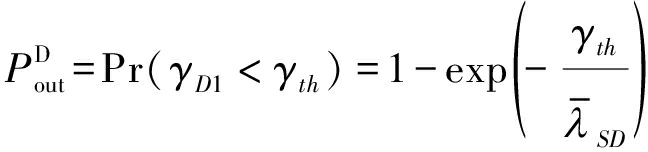
(4)
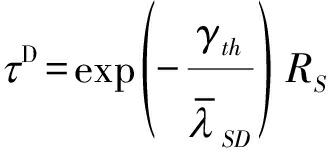
(5)
其中,
3.2 最大比合并传输
考虑到全双工系统中继自干扰的存在以及自干扰抑制技术的发展,可知自干扰是可以被抑制到噪声水平的[11]。并且,本小节考虑中继节点配备大规模天线,为了尽量减少中继的环路自干扰,中继同时选择收发天线。即:
(6)
其中,i表示中继用于接收信息的第i根天线, j表示中继用于发送信息的第j根天线。当中继配置的天线数NR趋于无穷大时,自干扰信道的信道增益可以等价于一个常数[8,12],即:
(7)
如图1和图2所示,第一时隙αT内,中继收到的信号是:
(8)
其中,xS表示节点S发送的信号,
[|xS|2]=1,[X]是对X求均值,|·|是绝对值运算符,PS表示源传输功率。考虑到中继接收到的噪声功率强度远远小于接收的信息功率强度以及后续闭合表达式的求解,在计算中继采集的能量时,忽略噪声功率。那么,在第一时隙αT内中继采集的能量为:
(9)
其中,η表示能量采集效率(0<η<1),所以,在第二时隙内中继的发送功率为:
(10)
其中,b=ηα/(1-α)。
由图1和图2可知,在第二时隙(1-α)T内,当源与目的地之间不存在直达链路时,中继收到的信号是:
(11)
其中,xR是中继转发的信息,[|xR|2]=1,有:
xR=GySR2
(12)
由于中继采用放大转发协议,所以中继放大转发因子可表示为:
(13)
由式(13)可知,中继节点是能量约束的,定义分母
为能量约束因子,可以保证中继用于信息传输的能量消耗低于中继采集的能量,从而确保中继能够正常传输信息而不至于中断。此时,目的节点接收的信息是:
(14)
考虑到本文中继采用的是放大转发协议,以及为进一步得到更加精准的吞吐量闭合表达式,在求解目的地信噪比时,考虑中继处的噪声。那么,此时目的端的信噪比和累积分布函数分别为:
(15)
其中,
(16)
其中,
表示第二类修正的n阶贝塞尔函数,详见文献[12]式(8.432.1)。
当源和目的地之间存在直达链路时,一方面源可以通过中继放大转发信息到目的地,另一方面源还可以通过直达链路直接传输信息到目的地,目的节点采用最大比合并技术,合并两路信息,此时,目的节点的信噪比和中断概率可以分别表示为:
γD=γD1+γD2
(17)
Pout=Pr(γD<γth)=Pr(γD1+γD2<γth)
=Pr(γD1<γth,γD2<γth-γD1)
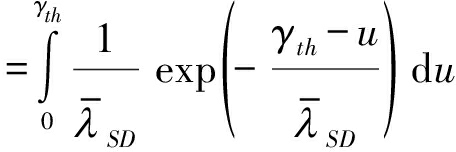
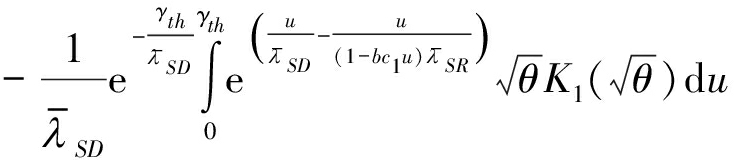
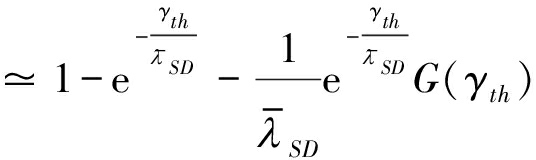
(18)
其中,N是一个控制近似复杂度准确度的参数，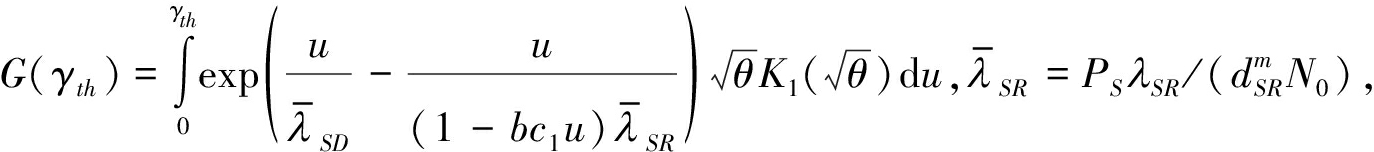
等式(a)用到了变量替换:令u=γth-q, fγD1(q)表示直达链路协议下目的端的概率密度。由G(γth)在数学上难以处理,我们利用高斯-切比雪夫正交[13]来获得G(γth)的近似值,即:
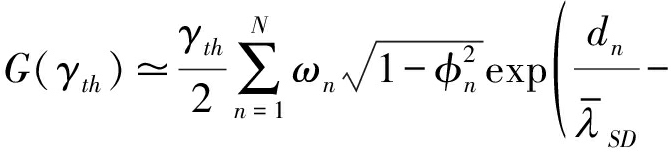
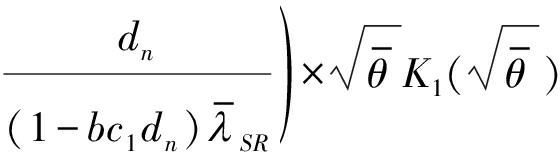
(19)
其中,
为求中断概率近似闭合表达式,假设中继配备大规模天线和采用自干扰抑制技术[11,14-15],中继自干扰可以忽略不计,并且考虑高信噪比条件下,PS/N0→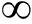
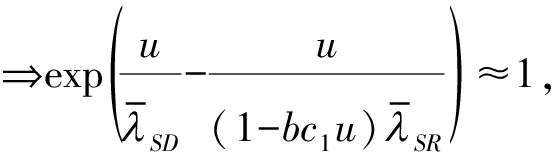有:
(20)
其中,
参考文献[16]中式(11.3.27),G(γth)可以表示为:
(21)
此时的中断概率为:
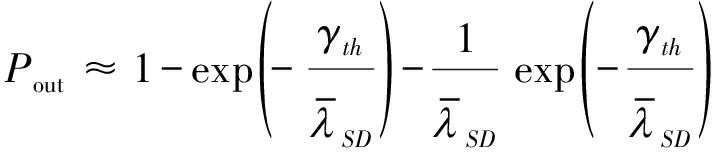
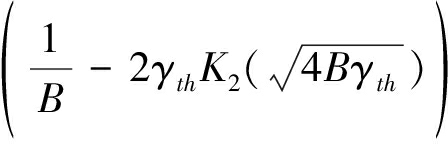
(22)
所以,在最大比合并传输协议下,系统吞吐量可以由中断概率表示为:
τ=(1-Pout)RS(1-α)
(23)
4 最佳时间切换比存在性分析
由图3可知,随着时间切换比α的增加,系统吞吐量先增大后减小,在0<α<1时,系统吞吐量最大值可表示为:
(24)
虽然以封闭形式求出最优解α*并不容易,但是可以借助于Mathematica来确定,通过求解可知,当0<α<1时,τ对于α的二阶导数都小于零的,即:τ是时间切换比α的凹函数,最佳时间切换比α*可以通过dτ/dα=0来获得。由于得到的闭合表达式比较复杂且冗长,在此不再写出,同时还可以通过一维搜索方法获得最优解α*。
5 自适应中继选择策略
本小节将图1扩展到有K个中继的协作网络,考虑中继采用自适应放大转发协议。该协议下中继会因为设置的速率阈值而中断,中继处设置一个能够正确放大转发的阈值Rt,由式(11)可得节点S到中继Rk链路互信息为
如果满足CSRk>Rt,认定中继能够正确放大转发源信息,设能够正确放大转发的中继集合记为D。同时设总的能够准确传输信息的中继个数是|D|。选择能使目的地瞬时接收信噪比(γD)最大的中继,即选择使Pout,k最小的中继k。
(25)
那么,系统中断概率为:
(26)
其中,Pr(|D|=L)表示存在L个中继可以准确放大转发源信息的概率,
表示能够正确放大转发的中继个数是L时目的节点的中断概率,分别有:
Pr(CSRk≤Rt)=Pr(γSRk≤γ)
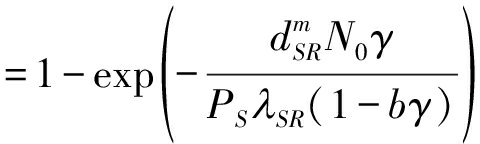
(27)
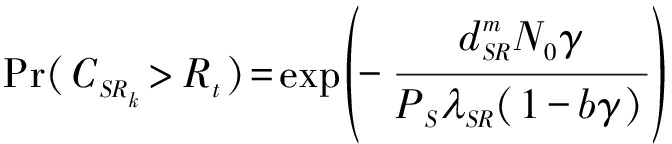
(28)
Pr(|D|=L)
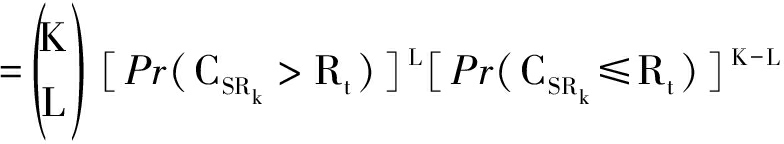
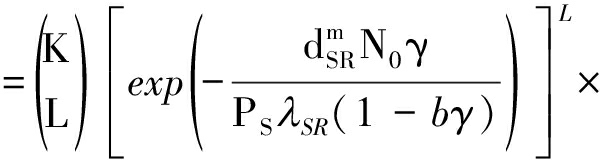
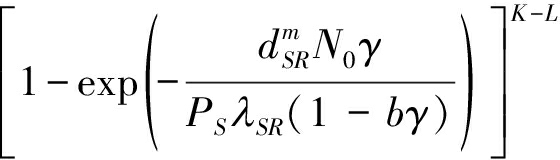
(29)
(30)
其中,γ=22Rt-1。
所以,采用自适应放大转发中继选择策略[17]时,系统的中断概率和吞吐量分别是:
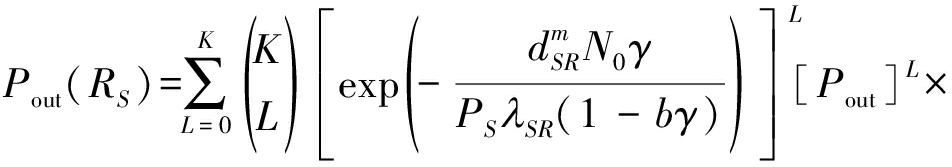
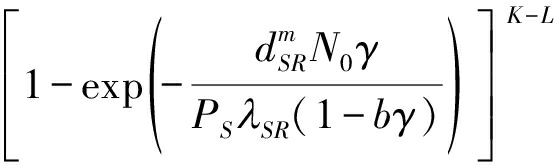
(31)
对于公式(31),由二项式定理可以化简为:
Pout(RS)=[Pout]L
(32)
τL=(1-[Pout]L)RS(1-α)
(33)
6 最佳目的地选择策略
基于图1的系统模型,考虑一个具有M个目的地的放大转发协作传输网络,中继节点是能量约束的,定义
为能量约束因子,可以保证中继用于信息传输的能量消耗低于中继采集的能量,从而确保中继能够正常传输信息而不至于中断。选择能使瞬时接收信噪比(γD)最大的目的地,即选择使Pout,m最小的目的地m。所以,最佳目的地可以由下式算出:
(34)
最佳目的地选择策略下系统存在M个目的地时,目的端累积分布函数可以由次序量统计原理[18]得:
FγD,M(y)=[FγD(y)]M
(35)
其中,FγD(y)是只有1个目的地时目的端的累积分布函数。
所以,存在M个目的地时系统的中断概率和吞吐量分别为:
Pout,M=[Pout]M
(36)
τM=(1-[Pout]M)RS(1-α)
(37)
7 数值结果与讨论
本小节,我们将对上述数值结果进行吞吐量分析,并用Monte-Carlo仿真加以验证。除另有阐述,系统参数默认设置为:源传输速率RS=2 bit/s,源发送功率PS=20 dB,能量采集效率η=0.8,路径损耗指数m=2.7,位置设置:源节点(0,0),中继节点(0.25,0.25),目的节点(3,0),这样设置的原因是由于能量采集在短距离是实用并且有效的,中继自干扰信道平均信道增益是0.01,其他信道的平均信道增益均设置是1,各节点接收到的噪声方差N0=1 W,中继配备天线数NR=10,近似准确度的参数N=20，中继个数是1，时间切换比α=0.31。为确保数据准确性与仿真便利性，蒙特卡洛仿真均执行105次循环。
图3绘制了时间切换比α对系统吞吐量的影响。由图可知,当0<α<0.7时,就系统吞吐量而言,本文算法比文献[7]中的算法大得多。例如,当时间切换比α=0.31时,相较于文献[7]中的算法,本文算法的吞吐量提高了0.16 bits/s/Hz,说明直达链路在提升系统吞吐量性能方面起到了至关重要的作用。并且随着α的增加,吞吐量曲线都是先上升到最大值(本文算法默认参数下的最佳时间切换比α=0.31)后减小,所不同的是,当α=0或者α=1时,文献[7]中的吞吐量会降为0。直达链路的系统吞吐量则不受α的影响,一直保持为一个常数,并且当α较大或较小时,都比文献[7]中算法的吞吐量要大,表明了直达链路存在的必要性。
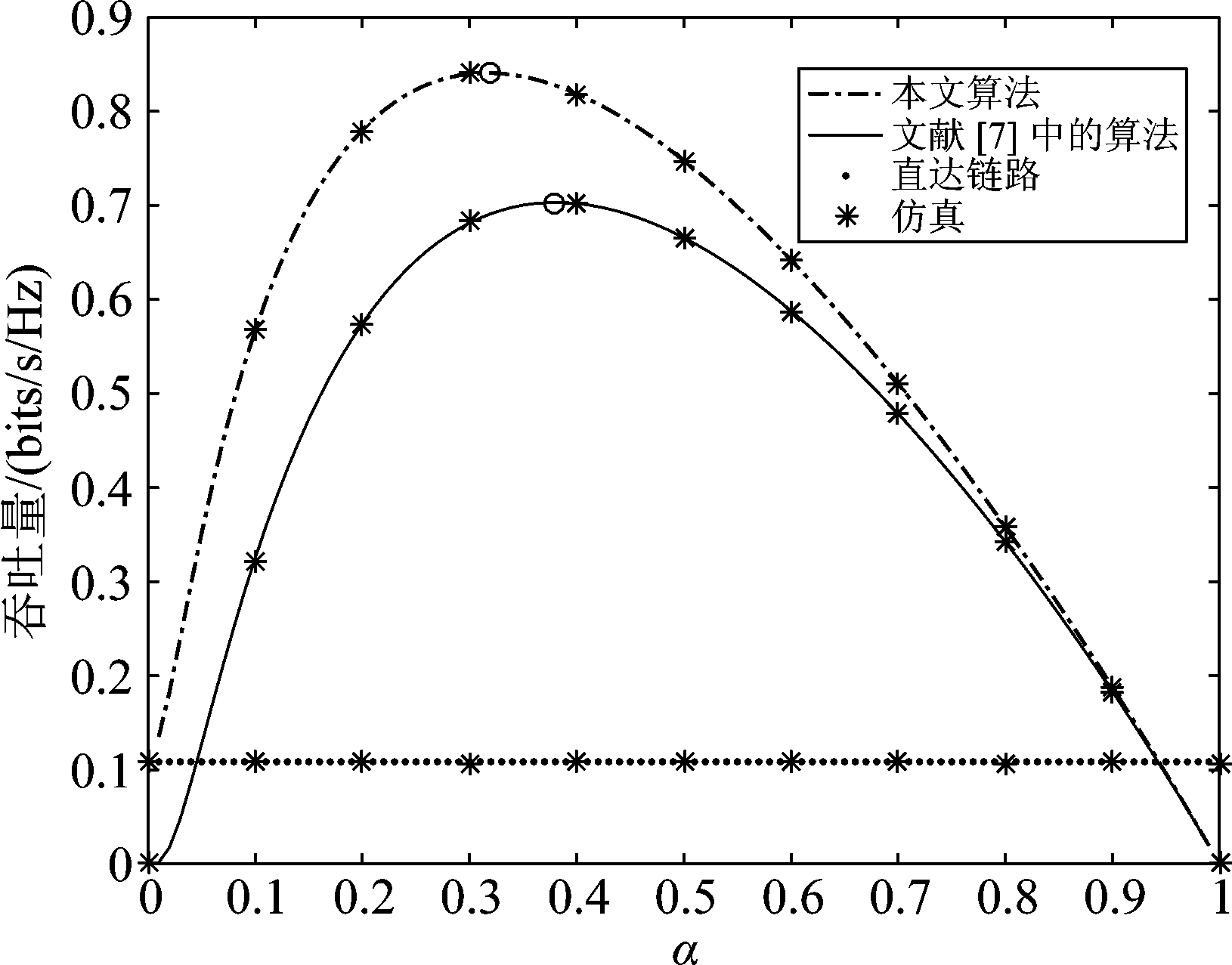
图3 吞吐量随时间切换比α的变化情况
Fig.3 Throughput with respect to the time switching ratio,α
图4描绘了三种算法的吞吐量随PS的变化趋势。由图可知,随着PS的增加,三种算法的吞吐量曲线都是上升的。在相同的源发送功率下(例如PS=30 dB),相较于文献[7]中的算法而言,本文算法的吞吐量提高了0.22 bits/s/Hz,体现了直达路径对于提升吞吐量性能具有显著的作用。本文算法的吞吐量大约是文献[9]中算法的两倍,体现了全双工技术和最小化中继自干扰的天线选择技术的优越性。
图5表示了三种算法的吞吐量随RS的变化趋势。由图可知,对于直达链路而言,吞吐量随着RS的增加是一直减小的,直到减小到0为止。然而,对于本文算法和文献[7]中的算法而言,吞吐量曲线都是随着RS的增加先上升到最大值再下降到0,并且在0～5 bit/s的源传输速率范围内,本文算法都表现出了较好的安全吞吐量性能,例如,当源传输速率RS=2.3 bits/s时,相较于文献[7]中的算法,本文算法的吞吐量提高了0.18 bits/s/Hz。
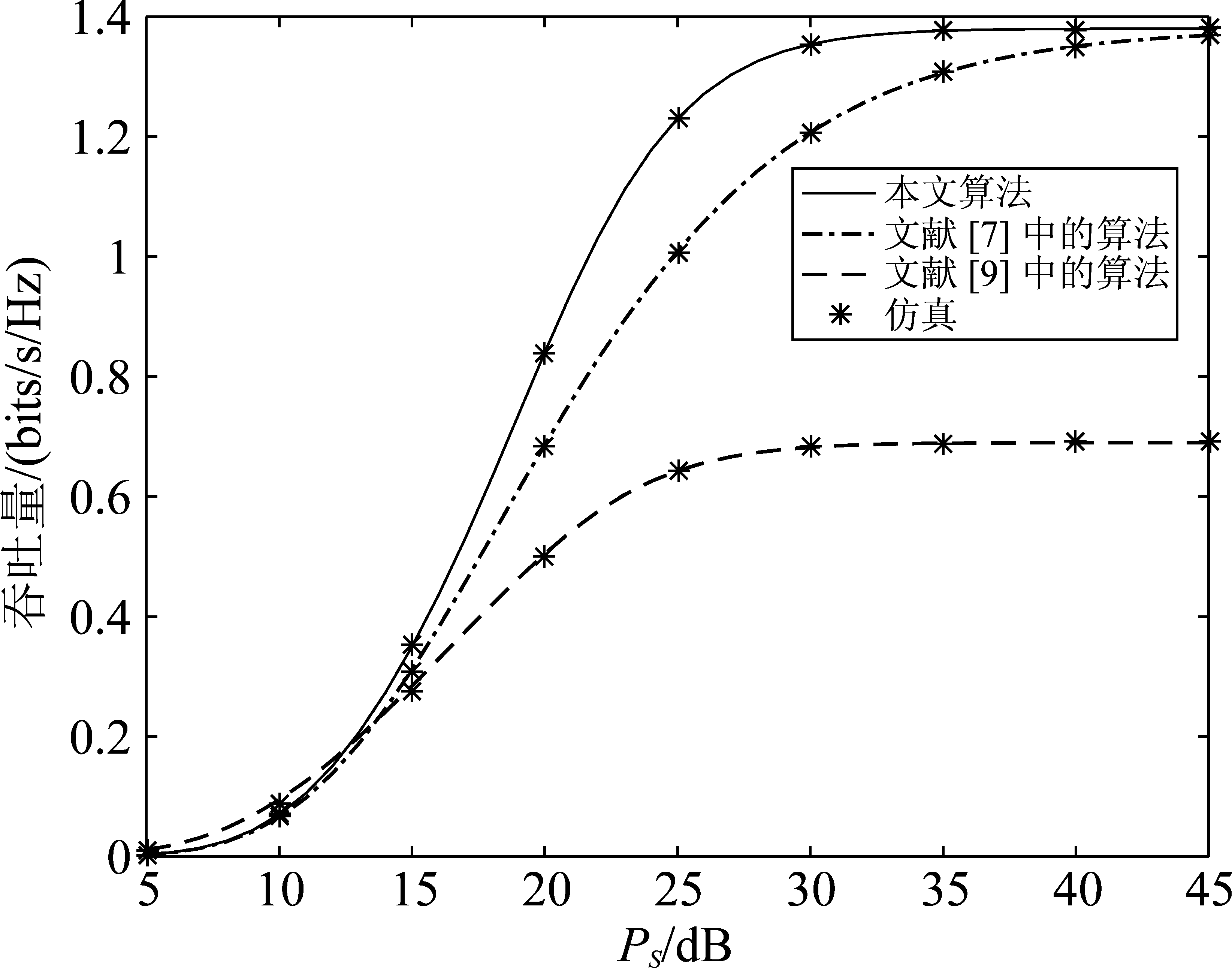
图4 吞吐量随发送功率PS的变化趋势
Fig.4 Throughput with respect to the transmit power, PS
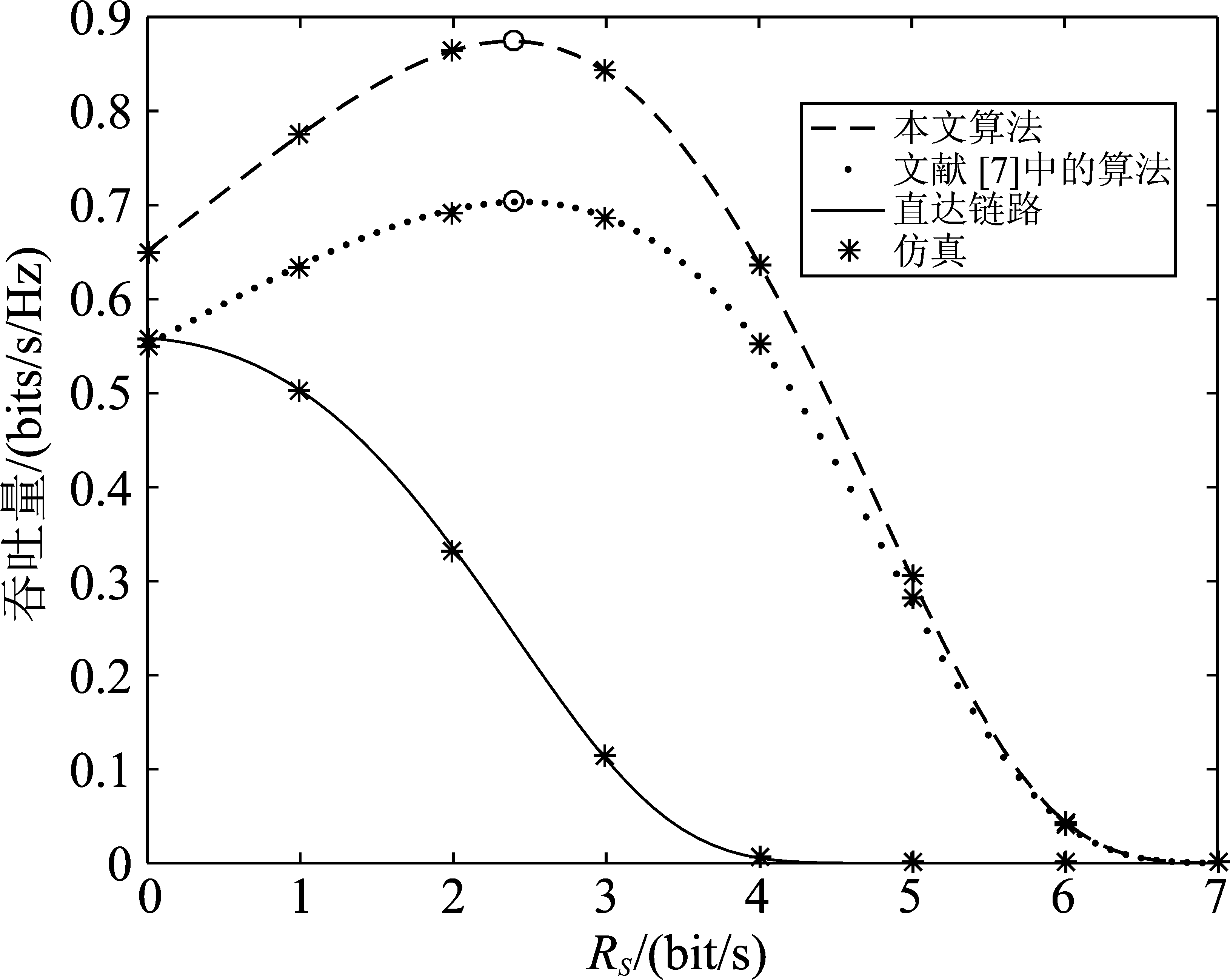
图5 吞吐量随传输速率RS的变化情况
Fig.5 Throughput with respect to the transmission rate, RS
图6表示了对于不同的能量采集效率η,源发送功率PS对本文系统吞吐量的影响。由图可知,在相同的源发送功率下(例如PS=25 dB)系统吞吐量性能会随着能量采集效率η的增加而显著提升。
图7表示了三种算法中能量采集效率η对吞吐量的影响,由图可知,本文算法和文献[7]中算法的吞吐量都随着能量采集效率η的增加而增加。当0<η<1时,就系统吞吐量而言,本文算法比文献[7]中的算法大得多。体现了直达链路对于提升吞吐量性能的突出作用。还可以看出,直达链路的吞吐量与能量采集效率η无关,因为,在直达链路中,源和目的节点都没有进行能量采集。
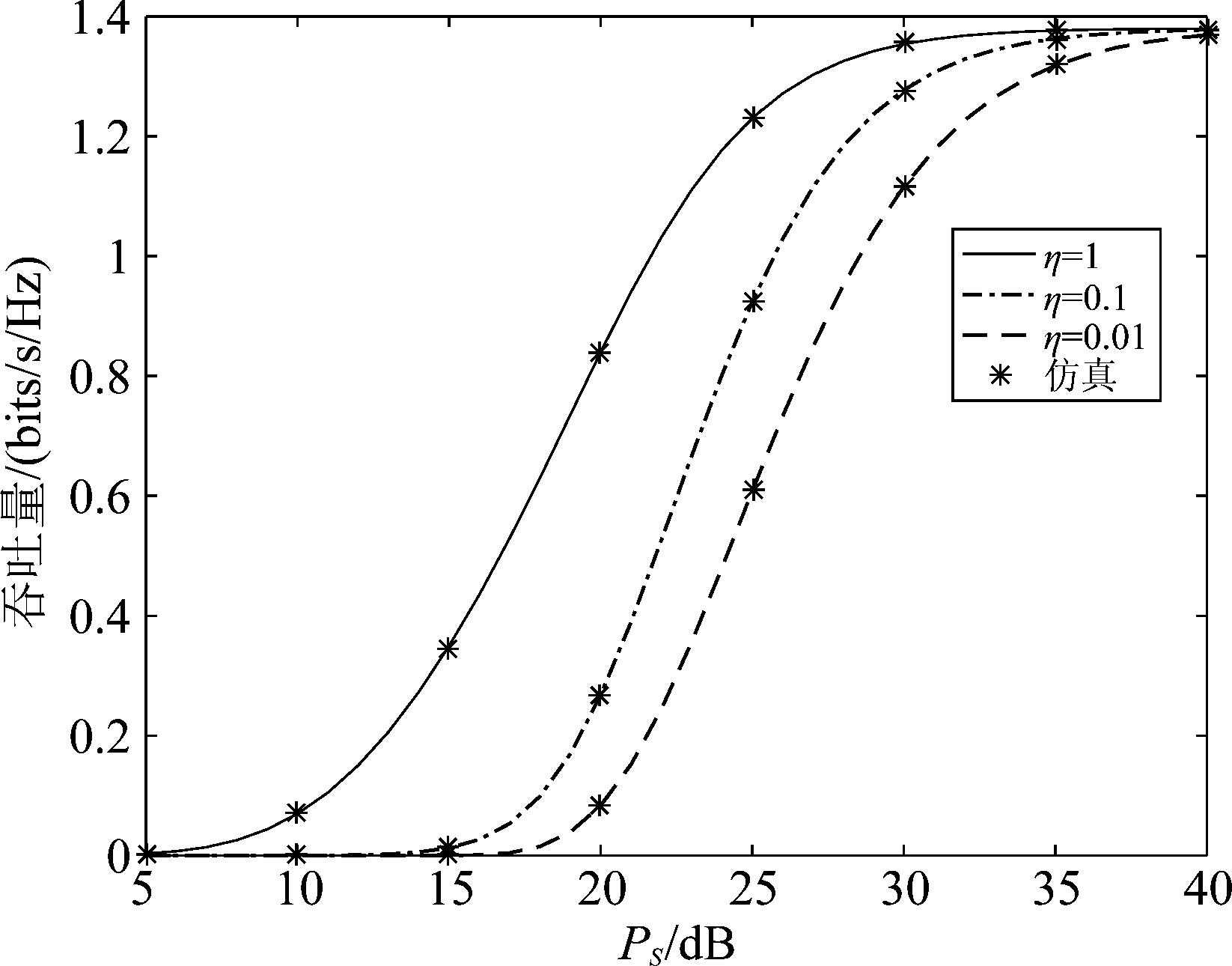
图6 对于不同的η值, 吞吐量随发送功率PS的变化趋势
Fig.6 Throughput with respect to the transmit power PS for different values of η
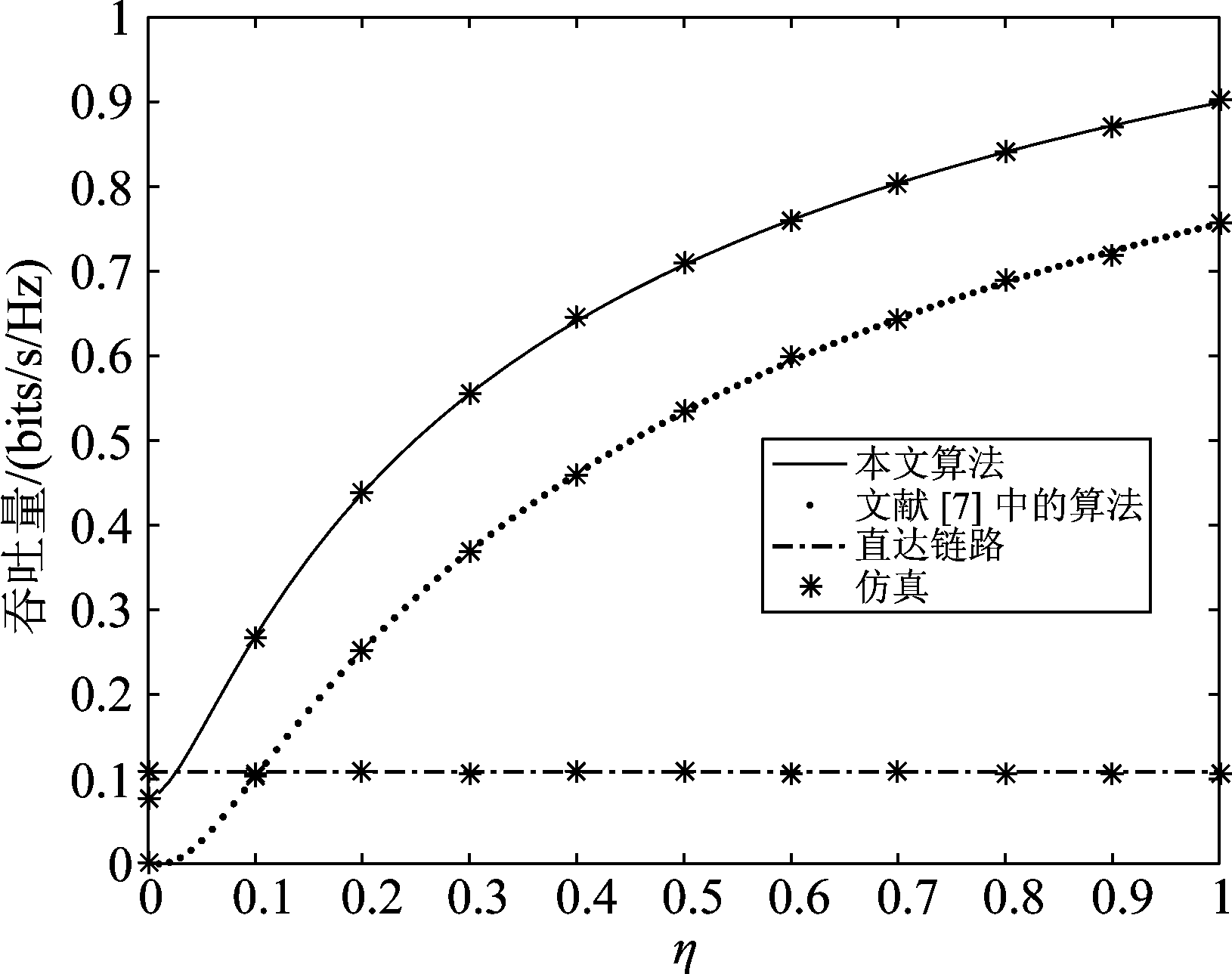
图7 吞吐量随能量采集效率η的变化情况
Fig.7 Throughput with respect to the energy harvesting efficiency,η
图8表示了对于不同的阈值Rt,源发送功率PS对系统吞吐量的影响。本图设置中继个数K=20,由图可知,当阈值Rt固定时,吞吐量曲线随着PS的增加而上升。同时,在同等发送功率条件下(例如PS=10 dB),当速率域值Rt越小时,系统吞吐量就越大。由公式CSRk>Rt可知,当速率域值Rt越小时,满足条件的中继个数|D|就会越大,即L越大,再由公式(33)可知,系统吞吐量就会越大,数值分析与仿真结果均表明,合理设置速率阈值可以有效改善系统吞吐量性能。
图9描述了对于不同的中继个数K,系统吞吐量随阈值Rt的变化趋势,由图可见,当中继个数K固定(例如K=4)时,随着阈值Rt的增大,系统吞吐量是逐渐减少的,直到减小到0为止。当阈值Rt固定(例如Rt=5.5 bit/s)时,即对于每一个中继而言,满足CSRk>Rt的概率将固定,当中继个数K越多,满足条件的中继个数|D|就越大,即L越大,同理由公式(33)可知,系统吞吐量就会越大,侧面也反应了中继个数对于提高吞吐量有着突出贡献。
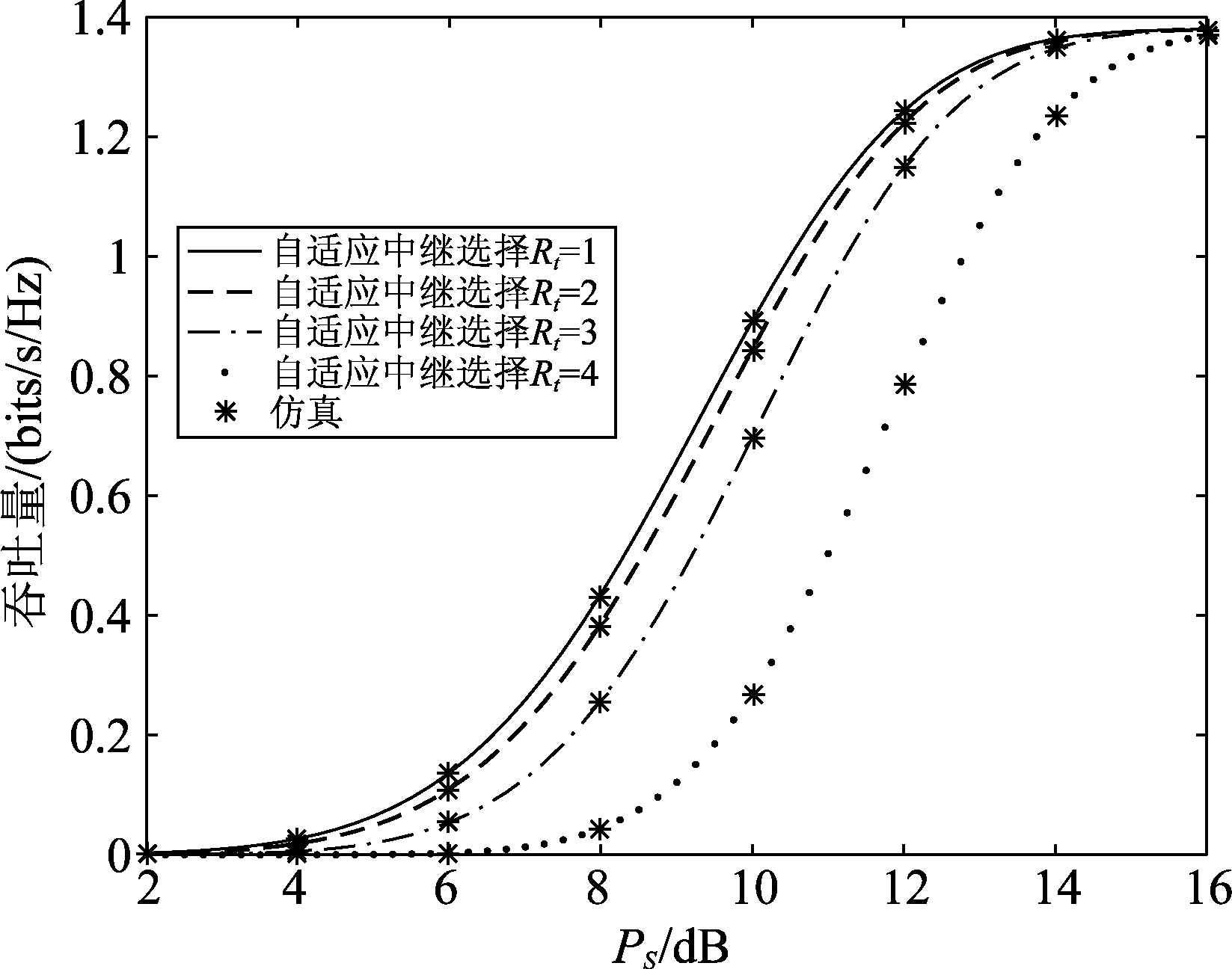
图8 对于不同的Rt值, 吞吐量随发送功率PS的变化情况
Fig.8 Throughput with respect to the transmit power PS for different values of Rt
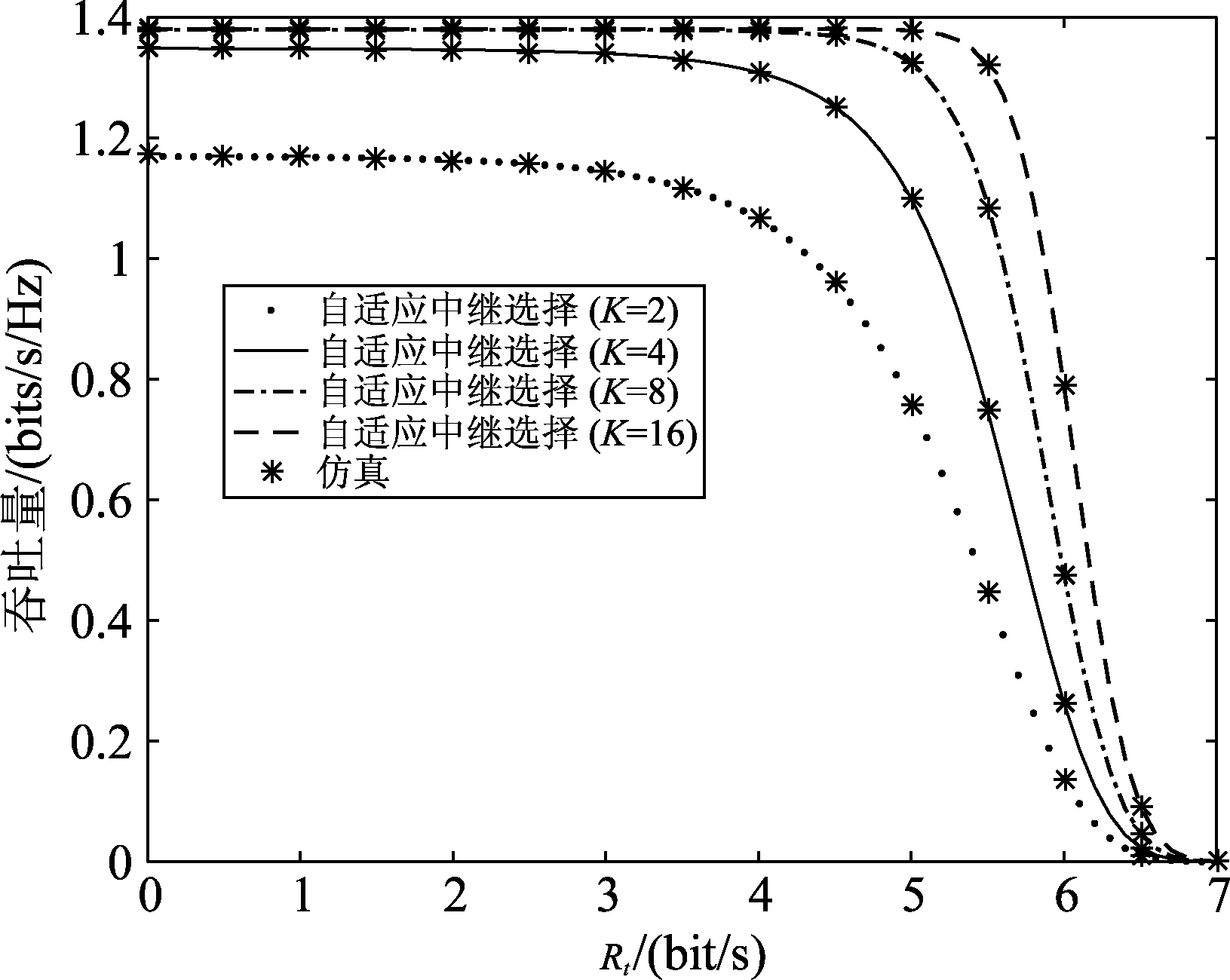
图9 对于不同的K值, 吞吐量随阈值Rt的变化趋势
Fig.9 Throughput with respect to the threshold Rt for different values of K
图10展示了对于不同的目的地个数M,系统吞吐量随源发送功率PS的变化情况。由图可知,当M固定时,吞吐量随PS的增加而增大。另外,在相同发送功率下(例如PS=15 dB),系统吞吐量会随着M的增加而显著上升。同样由公式(37)可知,当其他参数固定时,随着M的增加,系统吞吐量随之增加。
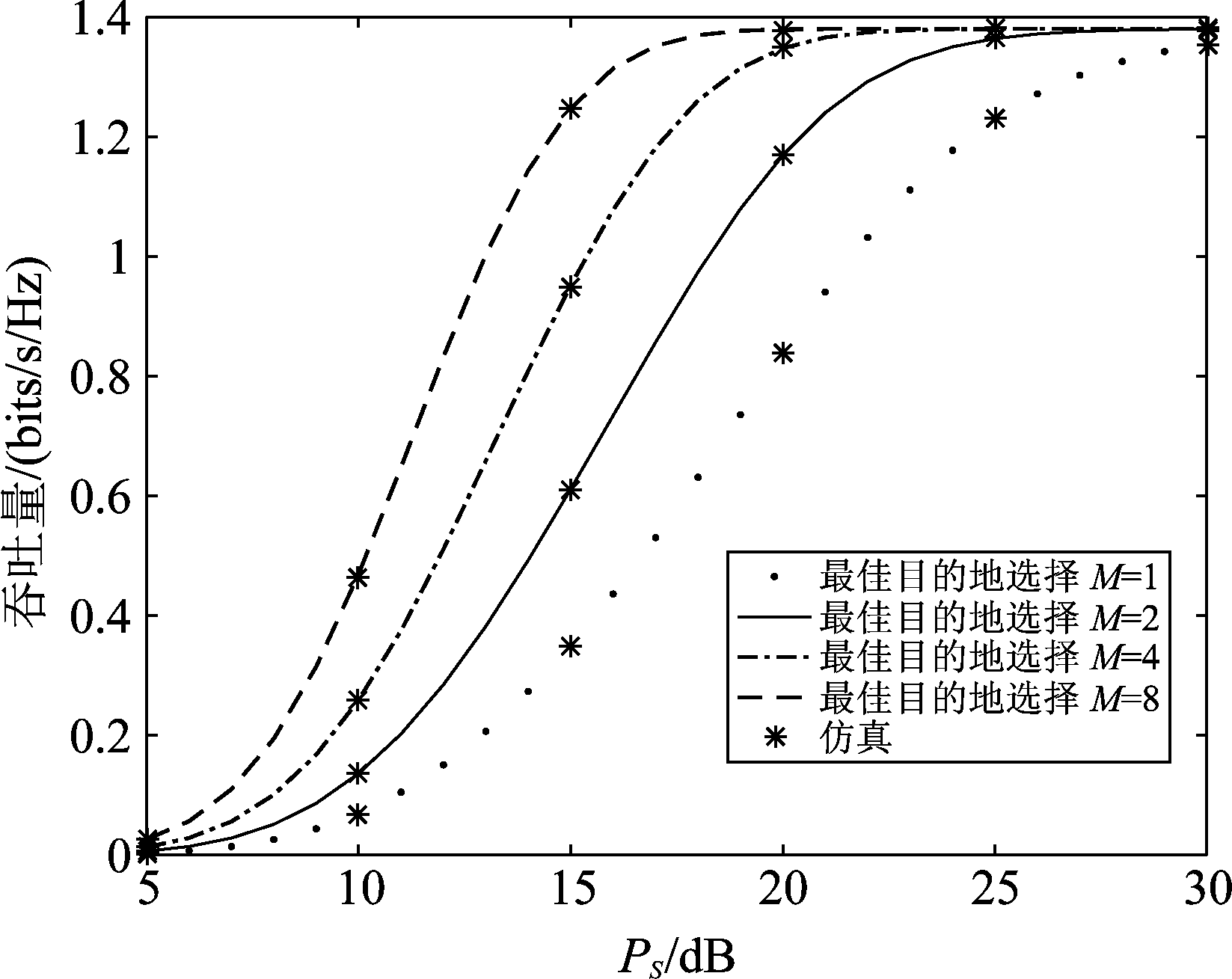
图10 对于不同的M值, 吞吐量随发送功率PS的变化趋势
Fig.10 Throughput with respect to the transmit power PS for different values of M
图11表示了对于不同时间切换比α,系统吞吐量随目的地个数M的变化曲线,设置了时间切换比α=0.31、α=0.36和α=0.41。由图可知,与α=0.36和α=0.41相比,最佳时间切换比α=0.31获得了更好的吞吐量性能。并且还可以看出,当时间切换比α固定时,增加目的地个数可以显著改善系统吞吐量性能,对于本文默认设置的系统参数而言,当目的地个数大概等于8时,系统吞吐量将达到最大值,之后保持不变。
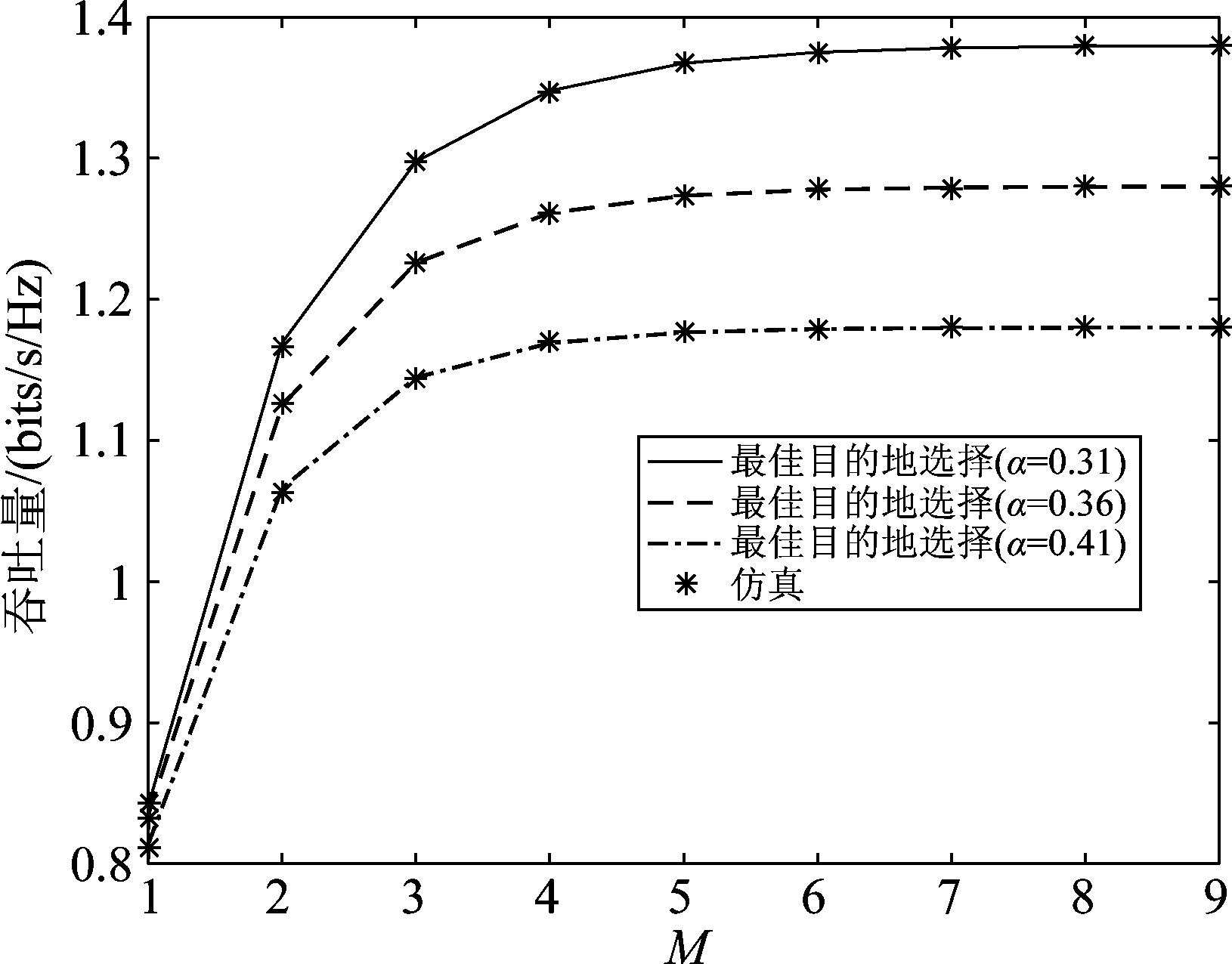
图11 对于不同的α值, 吞吐量随目的地个数M的变化情况
Fig.11 Throughput with respect to the number of destinations M for different values of α
8 结论
本文研究了基于时间切换能量采集的全双工放大转发协作中继网络。在延迟受限传输模式下推导出了中继自干扰增益为常数时系统吞吐量近似闭合表达式。对于不同的系统参数,理论分析和蒙特卡洛仿真均表明,相较于文献[7]中的算法和直达链路算法,本文算法表现出了更加优越的吞吐量性能。集中表现了源和目的地之间存在直达链路的有效性和必要性以及全双工和天线选择技术的优越性。考虑一个具有K个中继的自适应中继选择网络,得到了以下结论:中继个数K和阈值Rt都能显著提高系统吞吐量性能。在最佳目的地选择策略下,目的地个数M和源发送功率PS对提升系统吞吐量有重大作用。
[1] Zhou X, Zhang R, Ho C K. Wireless information and power transfer: Architecture design and rate-energy tradeoff[J]. IEEE Transactions on Communications, 2013, 61(11): 4754- 4767.
[2] Nasir A A, Zhou X, Durrani S, et al. Relaying protocols for wireless energy harvesting and information processing[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3622-3636.
[3] Nasir A A, Zhou X, Durrani S, et al. Throughput and ergodic capacity of wireless energy harvesting based DF relaying network[C]∥ICC 2014-2014 IEEE International Conference on Communications. IEEE, 2014: 4066- 4071.
[4] Yin S, Qu Z, Zhang L. Wireless information and power transfer in cooperative communications with power splitting[C]∥GLOBECOM 2015-2015 IEEE Global Communications Conference. IEEE, 2015: 1- 6.
[5] Zhao F, Wei L, Chen H. Optimal time allocation for wireless information and power transfer in wireless powered communication systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1830-1835.
[6] Liu Yuan. Wireless Information and Power Transfer for Multirelay-Assisted Cooperative Communication[J]. IEEE Communications Letters, 2016, 20(4): 784-787.
[7] Zhong C, Suraweera H A, Zheng G, et al. Wireless Information and Power Transfer With Full Duplex Relaying[J]. IEEE Transactions on Communications, 2014, 62(10): 3447-3461.
[8] 聂志巧, 赵睿, 方嘉佳, 等. 基于功率分配能量采集的全双工放大转发中继系统[J]. 信号处理, 2017, 33(4): 641- 648.
Nie Zhiqiao, Zhao Rui, Fang Jiajia, et al. Amplify and Forward Full Duplex Relaying Systems with Power Spitting Based Energy Harvesting[J]. Journal of Signal Processing, 2017, 33(4): 641- 648.(in Chinese)
[9] Zhao N, Hu F, Li Z. Simultaneous Wireless Information and Power Transfer Strategies in Relaying Network With Direct Link to Maximize Throughput[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8514- 8524.
[10] Lee H, Song C, Choi S H, et al. Outage probability analysis and power splitter designs for SWIPT relaying systems with direct link[J]. IEEE Communications Letters, 2017, 21(3): 648- 651.
[11] Riihonen T, Werner S, Wichman R. Mitigation of loopback self-interference in full-duplex MIMO relays[J]. IEEE Transactions on Signal Processing, 2011, 59(12): 5983-5993.
[12] Gradshteyn I S, Ryzhik I M. Table of integrals, series, and products[M]. Academic Press, 2007.
[13] Neumaier A. Introduction to numerical analysis[M]. Texts in Applied Mathematics, 1974: 719-720.
[14] 谭星, 赵睿, 王聪, 等. 协作干扰下的非可信中继与全双工目的节点系统的遍历安全容量分析[J]. 信号处理, 2017, 33(5): 734-740.
Tan Xing, Zhao Rui, Wang Cong, et al. Ergodic Secrecy Capacity of Untrusted Relay and Full Duplex Destination Systems with Cooperative Jamming[J]. Journal of Signal Processing, 2017, 33(5): 734-740.(in Chinese)
[15] Chen G, Gong Y, Xiao P, et al. Dual Antenna Selection in Secure Cognitive Radio Networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(20): 7993- 8002.
[16] Abramowitz M, Stegun I A. Handbook of mathematical functions with formulas, graphs, and mathematical tables[M]. New York, Dover, 1972.
[17] 林鸿鑫, 赵睿, 贺玉成, 等. 过时信道状态信息下的机会式中继选择系统的安全性能分析[J]. 信号处理, 2016, 32(7): 810- 818.
Lin Hongxin, Zhao Rui, He Yucheng, et al. Secrecy Performance Analysis of Opportunistic Relay Selection Systems with Outdated CSI[J]. Journal of Signal Processing, 2016, 32(7): 810- 818.(in Chinese)
[18] Shrestha A P, Kwak K S. Secure opportunistic scheduling with transmit antenna selection[C]∥PIMRC 2013-2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. IEEE, 2013: 461- 465.
