1 引言
利用相干检测器对海杂波中有用信号进行检测时需要借助于参考样本来估计海杂波的协方差矩阵。常用的估计算法包括样本协方差矩阵(sample covariance matrix, SCM)、归一化样本协方差矩阵(normalized sample covariance matrix, NSCM)[1]和最大似然(maximum likelihood, ML)估计算法[2]等。当均匀的参考样本足够多时,上述估计算法在无干扰的杂波背景下获得了较好的检测性能[3- 4]。但是当均匀的参考样本数量有限时,会导致估计的协方差矩阵奇异。为此,学者们提出了各种解决办法,丁昊等人挖掘了协方差矩阵关于次对角线的斜对称结构[5];于涵等人提出了用于检验散斑协方差矩阵估计性能的白化度评价方法[6];文献[7]在距离多普勒域考虑到在相邻样本之间具有相同的杂波特性,借助杂波在角度-多普勒域的内在稀疏性提出了基于稀疏贝叶斯学习的协方差矩阵估计算法。文献[8-9]借助于色加载算法有效提高了非均匀场景下协方差矩阵的估计精度。上述的估计算法主要是为了解决有限的均匀参考样本导致估计的协方差矩阵奇异这一问题。在不需要参考样本的前提下,简涛等人提出了修正最大似然(modified maximum likelihood,MML)估计协方差矩阵[10]。
随着雷达距离分辨率的提高,高距离分辨率海杂波具有空间部分均匀性,其表现为在空间上邻近的参考样本具有相同的功率,而较远距离的参考样本具有不同的功率。如果能采用对参考样本进行分组,将相同功率的参考样本分成一组,使得空间部分均匀的参考样本演变成组内均匀、组间不均匀的样本,则有可能减小由样本的空间部分均匀性对协方差矩阵估计的影响。文献[11-14]已表明采用分组策略确实可以减小协方差矩阵的估计误差,进而提高检测器的检测性能。另外,在实际的海洋环境下,假目标干扰也是不可避免的,干扰的存在必然会增加协方差矩阵估计的误差[15-16]。考虑到海杂波的空间部分均匀性和假目标干扰的不可避免性,本文采用分组机制,对海杂波的参考样本进行分组处理,并利用纹理的最大后验估计值作为每组的加权系数,将空间部分均匀的样本演变成组内均匀的样本,提出了分组加权样本协方差矩阵估计算法(grouped weighted sample covariance matrix, GW-SCM)。考虑到假目标干扰的存在,进一步利用协方差矩阵之间的差异提出了一致性因子,以确定干扰所在的分组,并剔除干扰。最后通过实测数据验证了本文所提分组加权算法的可行性。
本文安排如下,第2节对问题进行建模,介绍了二元假设检验,球不变随机向量模型和检测算法;第3节详细介绍了本文提出的GW-SCM和相应的干扰剔除算法,并给出了算法流程图;在第4节中,结合实测数据验证了本文所提算法的有效性;最后,在第5节总结全文。
2 问题描述
海杂波背景下多脉冲(或多阵元)相干雷达目标检测问题可以采用二元假设检验来表达:
H0∶zr=cr r=0,…,R
(1)
式中,向量zr∈CN×1和cr∈CN×1分别表示距离单元r的观测值和杂波回波。N表示积累脉冲数,r为距离单元编号,r=0表示被检测单元,r=1,…,R表示参考单元。α是与目标和信道影响有关的未知确定性参数,p∈CN×1为已知的多普勒导向矢量,p=[1,exp(j 2πfdTc),…,exp(j 2πnfdTc),…,exp(j 2π(N-1)fdTc)]T/N(其中fd表示目标的多普勒频率,Tc表示脉冲重复周期,上标T表示转置),且满足pΗp=1(上标H表示共轭转置)。假设cr,r=1,…,R与c0是独立同分布(independent and identically distributed, IID)的球不变随机向量(spherically invariant random vector, SIRV)杂波[14],其表达形式为:
(2)
式中,散斑gr是IID均值为0的复圆高斯随机向量,gr~CN(0,M),散斑的协方差矩阵M表示杂波在时间上的相关特性。纹理τr是一个非负的随机变量,其概率密度函数(probability density function,PDF)为f(τr),反映了杂波功率在不同距离单元之间的起伏变化。τr与gr是相互独立的。
考虑到海杂波的空间部分均匀性和存在的假目标干扰,本文提出了一个分组机制,其主要有两个目的,其一,不分组的情况下海杂波的参考样本是空间部分均匀的,分组后参考样本演变为组内均匀,即实现了部分均匀的参考样本在组内的空间均匀化;其二,由于存在的假目标会增加协方差矩阵估计误差,我们需要定位干扰在空间上的位置,并将其剔除,利用分组策略后,可以实现干扰的准确定位与剔除。
分组的具体实现过程为:将R个参考单元分为G组,每组包含hg(g=1,2,…,G)个单元,则![]() 令
令
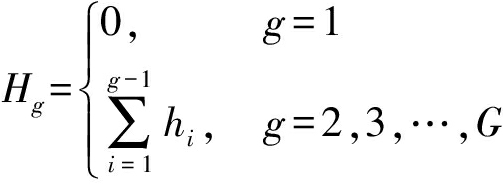
(3)
其中,Hg表示前g-1个分组内所有距离单元数之和。定义h=[h1,…,hg,…,hG]。
由于假设相邻距离单元的纹理τr具有相同功率水平,即同一组内具有相同的纹理值,则分组后的纹理τr可表示为:
τr=Sg,Hg+1≤r≤Hg+hg,g=1,2,…,G
(4)
借助于文献[17],在杂波协方差矩阵M已知的情况下提出的归一化匹配滤波器(normalized matched filter, NMF),
(5)
在实际的雷达环境下,协方差矩阵M需由参考样本估计获得。接下来,本文将估计海杂波的协方差矩阵![]()
3 协方差矩阵估计算法
3.1 GW-SCM估计算法
利用参考样本来估计海杂波的协方差矩阵,典型的算法之一就是SCM估计,这意味着参考样本具有相同的统计特性[1]。这个假设成立与否取决于海杂波是否具有空间均匀性。SCM估计算法为:
(6)
SCM估计协方差矩阵时设计简单、计算量小,它是高斯白噪声中的最大似然协方差矩阵估计算法。在低分辨雷达中,SCM估计算法能够较好的工作。随着雷达分辨率的提高,邻近分辨单元的杂波样本逐渐趋于空间部分均匀甚至非均匀,杂波不再具有相同的统计特性,SCM必然导致较大的估计误差。
考虑到海杂波的空间部分均匀性,为了将相同功率的海杂波分成一组,以实现将部分均匀的海杂波转换成组内均匀的海杂波,本节提出了GW-SCM估计算法,其具体过程如下:
第1步:计算纹理的相关系数,确定分组依据。
高分辨雷达下,海杂波表现为显著的“三非”特性,即非高斯特性、时间上的非平稳特性和空间上的非均匀性[18]。海杂波由纹理调制散斑构成,考虑到纹理在空间上具有相关性,首先,提取纹理,然后计算纹理在空间上的相关特性。利用接收回波zr估计海杂波的纹理为:
(7)
纹理在空间距离上的相关系数ρ(k)为[19]:
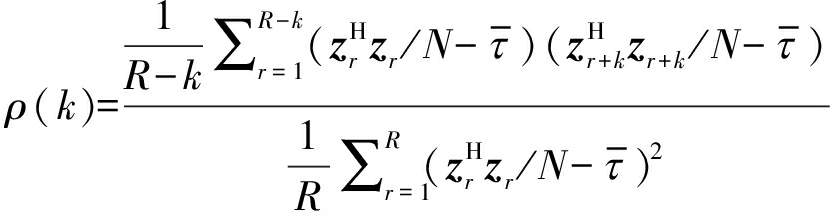
(8)
其中,k为距离单元间隔数,1≤k≤R-1。ρ(k)反映了纹理在距离上的相关特性,如果纹理在距离上是高度相关的,则ρ(k)≈1;否则,如果纹理在距离上是高度不相关的,则ρ(k)≈0。
利用纹理的相关系数ρ(k)可以确定海杂波空间分组的依据。文献[19]给出距离相关长度定义为ρ(k)从1衰减为1/e时所对应的距离间隔。当ρ(k)小于1/e=0.3679时,近似认为纹理在空间距离上是不相关的,则无法通过相干累积来获得能量上的增益,通过式(8)计算出ρ(k)从1衰减为1/e时对应的距离间隔即可作为每组的长度hg。需注意,应保证N≤hg/2以确保由每组参考样本估计得到的协方差矩阵是非奇异的。
第2步:计算每组的协方差矩阵。
由SCM算法估计出每组的协方差矩阵,表达式为:
(9)
第3步:计算每组的加权系数。
考虑到每组的协方差矩阵具有相同的功率,而组间的协方差矩阵具有不同的功率,且每组的协方差矩阵对估计海杂波总的协方差矩阵贡献不一致,引入一个加权系数来衡量每组所占权重。为此,基于逆伽马分布的纹理,本文引入了纹理的最大后验估计值作为加权系数,其表达形式为[14,20]:
(10)
其中,βg和ηg分别为第g组纹理分布的尺度参数和形状参数,βg和ηg可以通过矩估计算法得到。公式(10)的证明详见附录A。
第4步:利用加权系数计算GW-SCM为
(11)
3.2 存在干扰时的GW-SCM估计算法
由于在实际的海洋环境下,假目标干扰是不可避免的[21]。本节主要研究存在假目标干扰的情况下,协方差矩阵的分组加权估计算法。通过对海杂波的空间样本进行分组,可以更好地定位假目标所在的分组,并将其剔除,以确保协方差矩阵的准确估计。
本节中前3步的算法与第3.1节前3步的算法相同,不再赘述。
第4步:确定干扰所在的分组。
如果某组样本中含有假目标,则该组的协方差矩阵估计值必与其他组的协方差矩阵估计值存在较大的差异,为了衡量协方差矩阵之间的差异,参考一致性因子[19]的定义形式,本文引入参数θ,
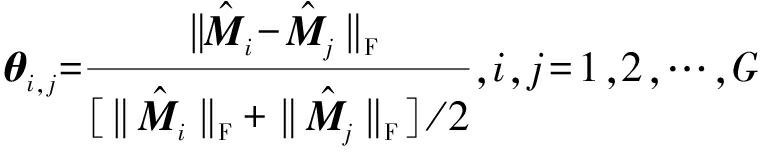
(12)
其中,‖·‖F表示矩阵的F范数。θ为G×G阶的实对称方阵,其对角线元素为零。θ反映了不同距离上协方差矩阵的一致性,θ的值越小,空间区间上的协方差矩阵越一致,则认为该距离区间的海杂波是均匀的。θ的值越大,空间区间上的协方差矩阵相差较大,则认为该距离区间的海杂波是部分均匀或非均匀的。假设第g组的某距离单元含有假目标,该假目标导致海杂波在空间上偏离均匀性,则反映在该方阵的第g行或者第g列上的元素明显大于非本行或非本列的元素,依据该矩阵的均值作为阈值来判断某行或者某列的元素是否明显偏大,由此可以确定假目标所在的分组,并将其剔除。
第5步:计算干扰剔除后的GW-SCM为
(13)
式中,Q为剔除假目标干扰所在的分组后剩余的分组。
将公式(13)代入公式(5),即为干扰剔除的GW-SCM ANMF检测器。
图1显示了本文提出的GW-SCM算法的具体流程图。在计算复杂度方面,SCM需要O(RN2)次的浮点乘法运算,GW-SCM需要O(RN3)次的浮点乘法运算。

图1 GW-SCM算法流程图
Fig.1 Flow chart of GW-SCM
4 实验结果与性能分析
本节将利用实测数据来分析本文所提算法的性能,并与对比算法进行比较。实测数据名为TFA10_007[22],该数据为Fynmeet雷达在2006年采集的,雷达载频为9 GHz,距离分辨率为15 m,脉冲重复频率为2.5 kHz,VV极化模式。该数据含有99973个时间脉冲,64个距离单元,删去3个含有目标的单元,剩下61个为纯海杂波单元。由于该数据的测试目标为一艘小船,在整个观测时间内,雷达采用跟踪模式对小船进行监测,由于我们无法知道小船的运动参数(径向速度、加速度、转动速度等),我们无法利用小船的相位信息对小船进行能量上的相干累积,所以我们在实验中采用仿真的目标和实测的海杂波数据来验证我们算法的有效性。
仿真目标回波A0(n)为
A0(n)=α0exp(j(2πnfdTc+φ))
(14)
式中, fd为目标的多普勒频率,在实验中设fd=-100 Hz;φ为均匀分布在[-π,π]上的随机初始相位;幅度α0用来调节信杂比(signal-to-clutter ratio, SCR),定义为
(15)
式中,Pc是待检测单元杂波的平均功率。设定虚警概率为Pf=10-3。
4.1 GW-SCM 恒虚警分析
我们利用仿真的海杂波数据验证了GW-SCM的恒虚警特性。将纹理建模为逆伽马分布,散斑建模为高斯向量,其均值为0,协方差矩阵为Mi, j=ρ|i-j|,0< ρ<1,虚警概率为Pf=10-3。利用公式(13),我们分析了ANMF检测器的门限随协方差矩阵参数ρ的变化情况,如图2所示,可以看出,随着参数ρ从0.1变化到0.9,检测器的门限在0.9附近,波动很小,可以得出结论:ANMF检测器对公式(13)估计的GW-SCM有恒虚警特性。
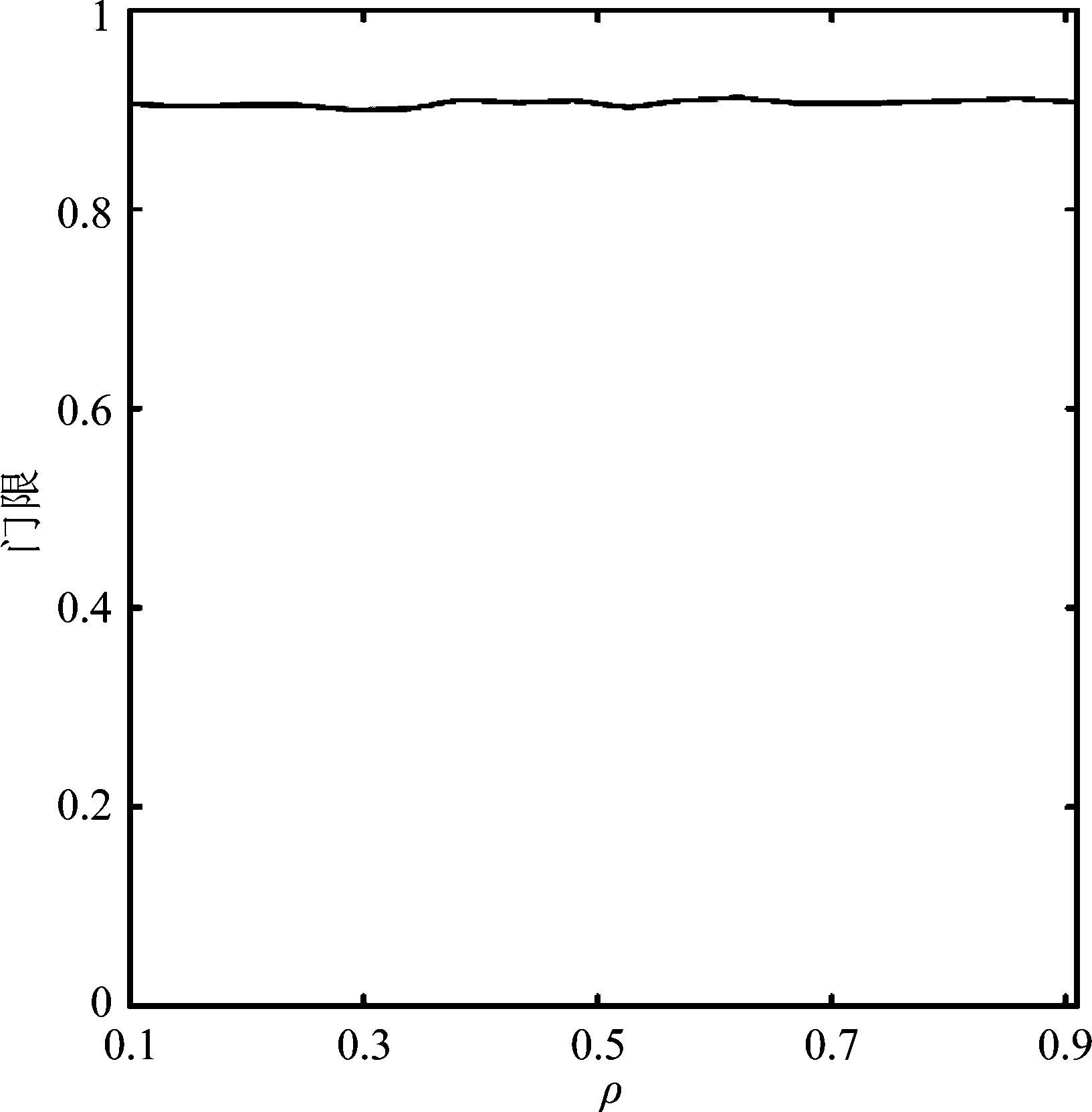
图2 ANMF检测器的门限协方差矩阵参数ρ的变化曲线
Fig.2 Curves of the threshold of ANMF with the parameter ρ of covariance matrix
4.2 纹理拟合情况分析
在现有文献中,已有学者对纹理采用逆伽马分布[23]、广义伽马分布、伽马分布和逆高斯分布建模[24],这里本文将对这四种分布的纹理进行对比分析。广义伽马分布的PDF为:
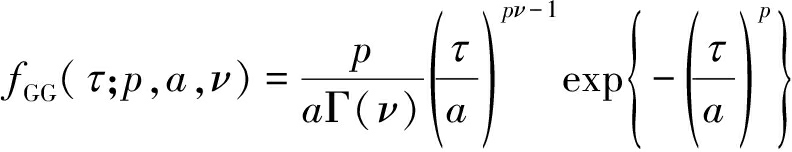
(16)
式中,Γ(·)是伽马函数;p>0为功率参数;a>0为尺度参数;ν>0为形状参数。
逆伽马分布的PDF为:
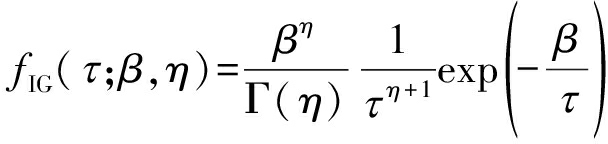
(17)
式中,β>0为尺度参数;η>0为形状参数。
伽马分布的PDF为:
(18)
式中, β>0为尺度参数;α>0为形状参数。
逆高斯分布的PDF为:
(19)
式中, μ>0为尺度参数;λ>0为形状参数。
为了分析纹理的分布情况,我们采用了以下的拟合方式:首先,根据接收的杂波数据zr通过公式(7)计算出纹理![]() 然后求得纹理的直方图,最后,用相应分布的PDF并调整分布的参数来拟合实际的纹理的直方图图像,以达到最佳的拟合效果。图3显示了原始杂波的纹理分布拟合情况与逆伽马分布、广义伽马分布、逆高斯分布和伽马分布的对比。从图3中可以看出,逆伽马分布能较好的拟合原始杂波的纹理,逆高斯分布在曲线的上升段拟合较好,在尖峰位置出现偏离,而广义伽马分布与伽马分布拟合时存在较大的偏差,尤其在纹理的概率密度函数的尖峰位置,这说明假定纹理为逆伽马分布是成立的。
然后求得纹理的直方图,最后,用相应分布的PDF并调整分布的参数来拟合实际的纹理的直方图图像,以达到最佳的拟合效果。图3显示了原始杂波的纹理分布拟合情况与逆伽马分布、广义伽马分布、逆高斯分布和伽马分布的对比。从图3中可以看出,逆伽马分布能较好的拟合原始杂波的纹理,逆高斯分布在曲线的上升段拟合较好,在尖峰位置出现偏离,而广义伽马分布与伽马分布拟合时存在较大的偏差,尤其在纹理的概率密度函数的尖峰位置,这说明假定纹理为逆伽马分布是成立的。
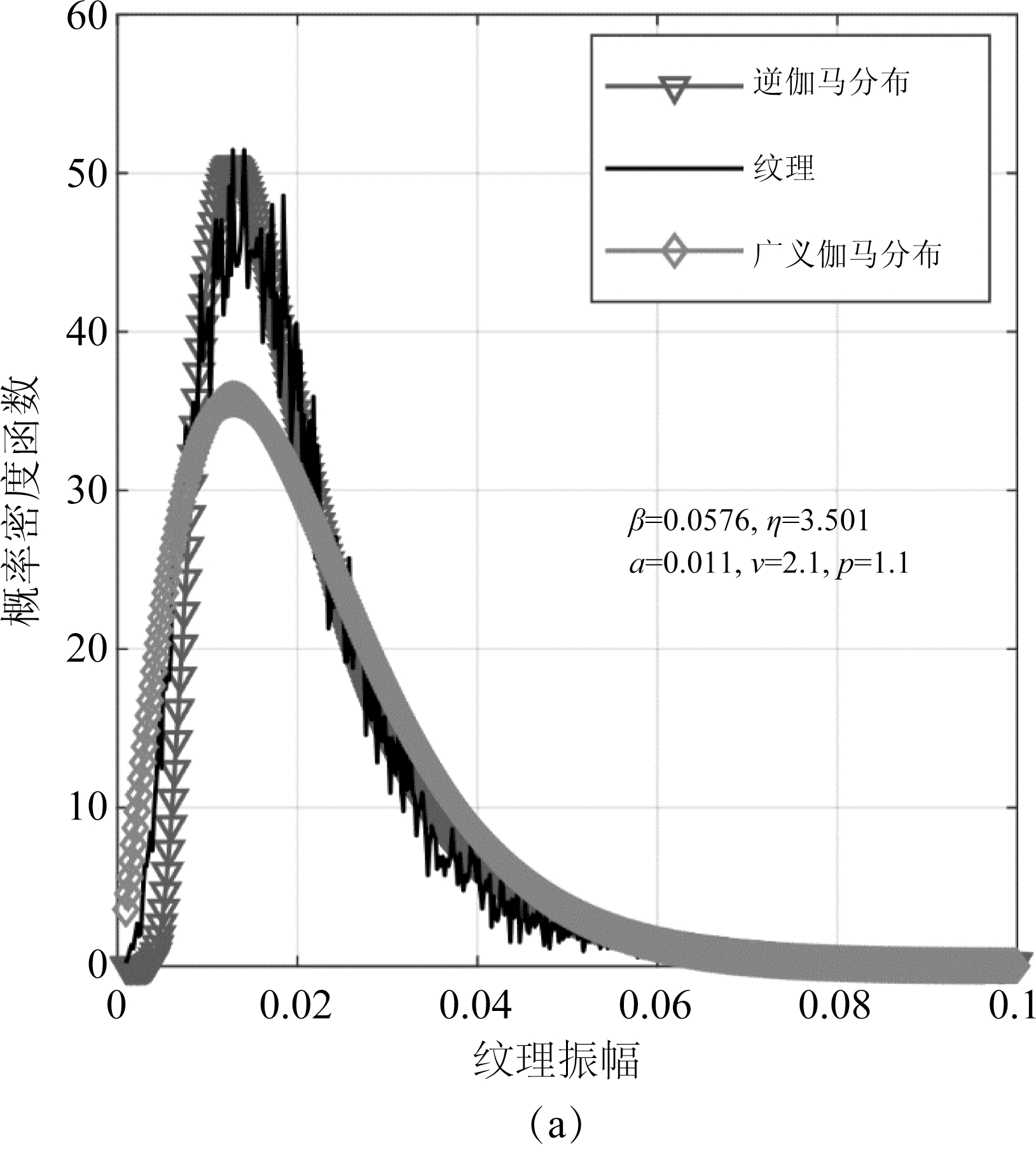
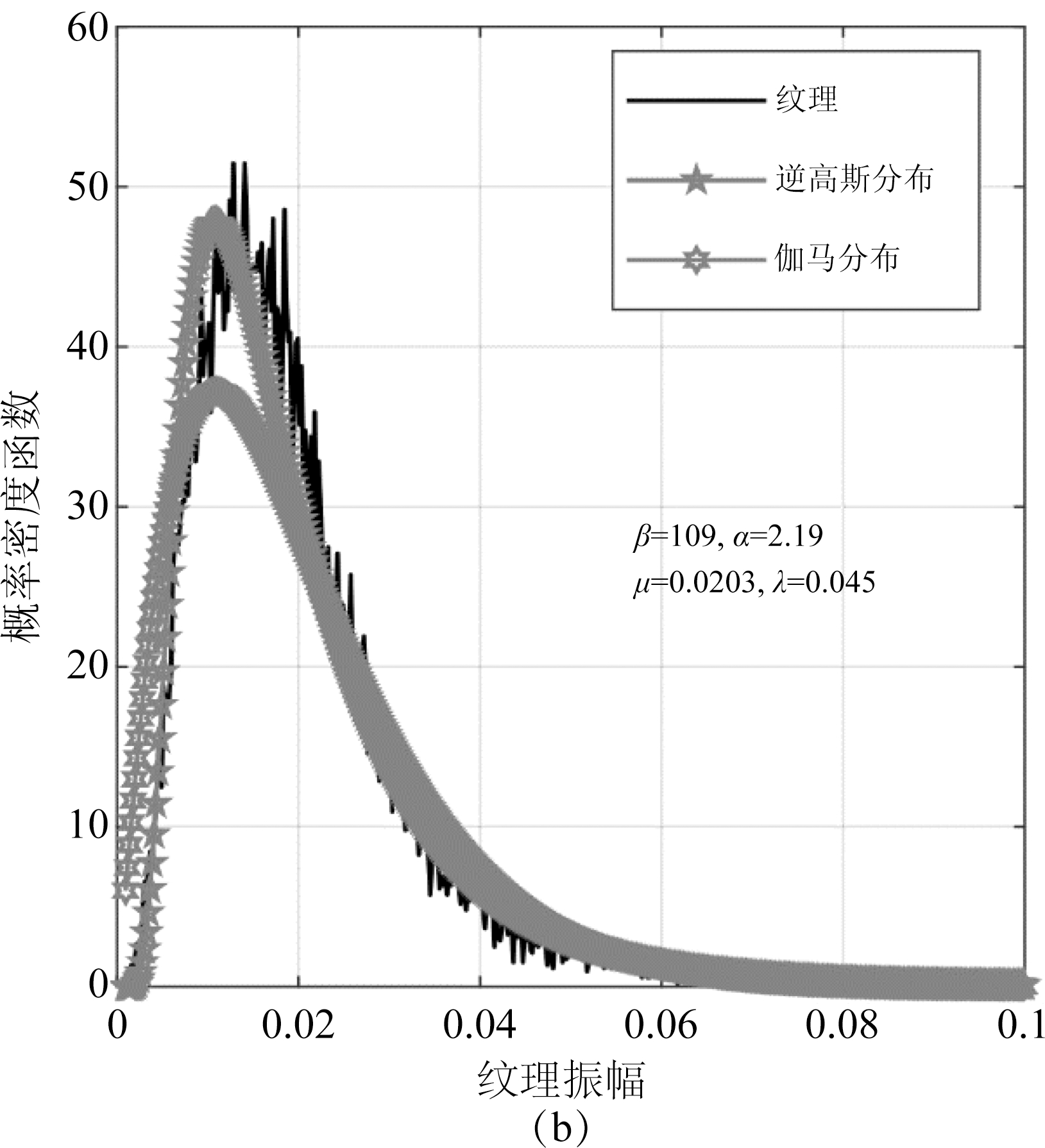
图3 原始杂波纹理采用逆伽马分布、广义伽马分布、逆高斯分布和伽马分布拟合的曲线
Fig.3 Fitting curves of texture in real sea clutter by inverse Gamma distribution, generalized Gamma distribution, inverse Gaussian distribution and Gamma distribution
4.3 不同分组情况下的实验性能比较
实验参数设置为:情况1,N=4,G=6,h=[10,10,10,10,10,10];情况2,N=4,G=4,h=[15,15,15,15]。图4显示了不同分组情况下,3.1节所介绍的GW-SCM算法的检测性能。G=6时的检测性能略微优于G=4时的检测性能。为了解释在均匀分组情况下不同分组大小所导致性能差异的原因,我们接下来分析了纹理在距离上的相关系数ρ(k),如图5所示。实验参数为N=4,曲线为300次实验结果的平均值。
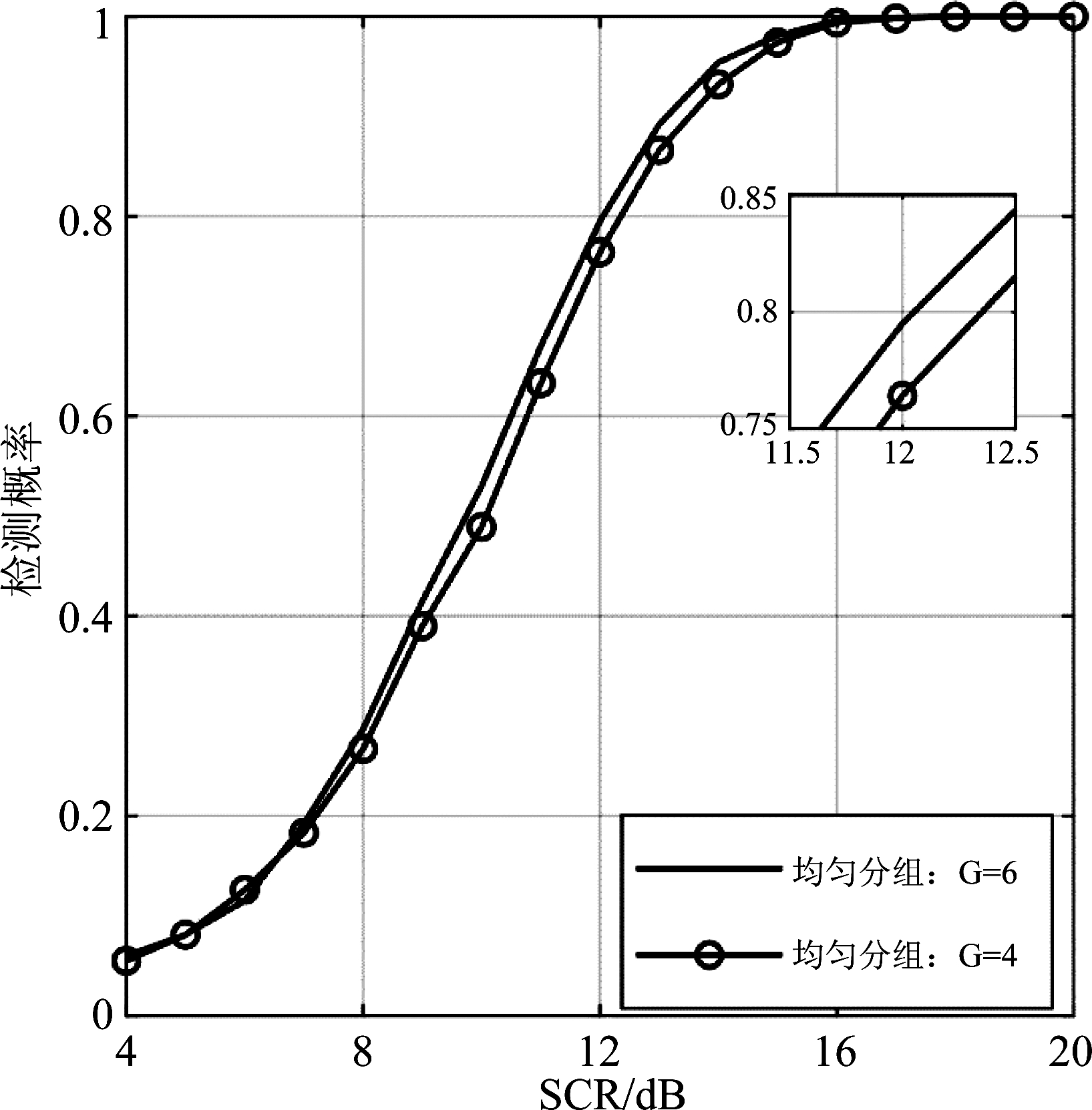
图4 不同分组情况下ANMF的检测概率随SCR变化曲线
Fig.4 Detection probability of ANMF versus SCR in different group cases
从图5可以看出,纹理的相关系数随着距离单元间隔的增加呈现出递减的趋势,这说明距离单元越远,纹理彼此之间的相关性越小。距离单元间隔为10的情况下(对应G=6)纹理的相关系数约为0.35,距离单元间隔为15的情况下(对应G=4)纹理的相关系数约为0.25,小于1/e(图5中横线所示),故将15个距离单元分为一组时,组内纹理已具备去相关特性,参考样本的相关特性已发生了改变,势必给协方差矩阵估计带来误差,因此对于均匀分组情况,G=6时的检测性能略微优于G=4时的检测性能。
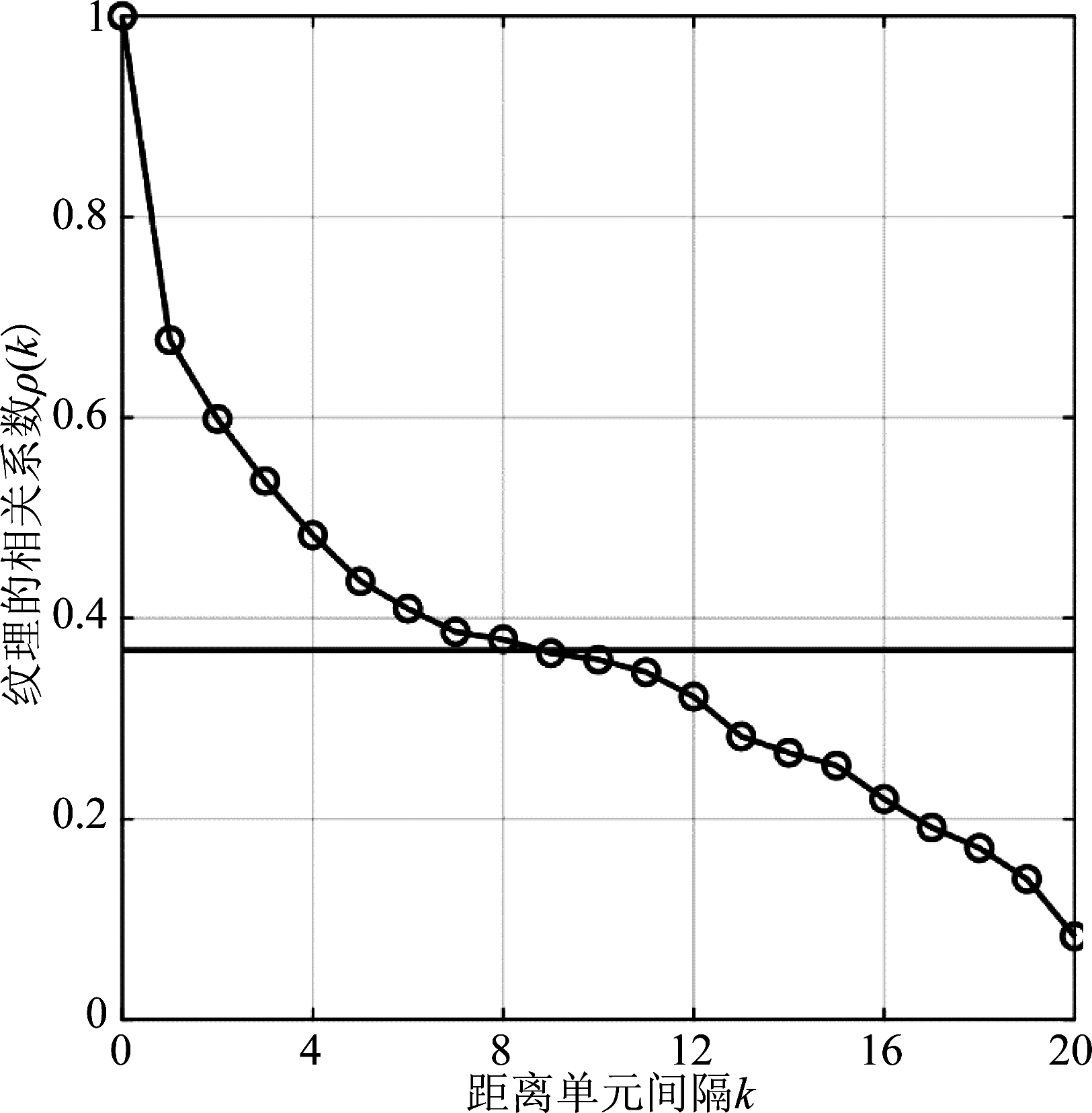
图5 纹理在不同距离单元间隔的相关系数
Fig.5 Correlation coefficient of texture in different range cell interval
根据图4和图5的实验结果可以得出结论:均匀分组的情况下,合理的分组能提高检测器的检测性能。
4.4 分组和不分组情况下的实验性能比较
图6为不分组与均匀分组情况下,ANMF的检测概率随SCR的变化情况,其实验参数为:不分组时N=4,G=1,R=60;均匀分组时N=4,G=6,h=[10,10,10,10,10,10]。从图6中可以看出,均匀分组的检测性能优于不分组的检测性能,受限于实测数据的距离单元数,分组后每组的参考样本数为hg=10,hg/N=2.5,每组用来估计协方差矩阵的参考样本数明显变少,当组内样本在空间上是完全均匀的,会带来约3 dB的性能损失[25]。即使分组情况下有3 dB的性能损失,依然优于不分组情况下的检测性能约0.1 dB,如果我们有足够多的参考样本,则分组后的性能增益至少为3.1 dB。这说明不分组时各距离单元的样本并不是完全均匀的,进一步验证了本文提出的分组策略的必要性。
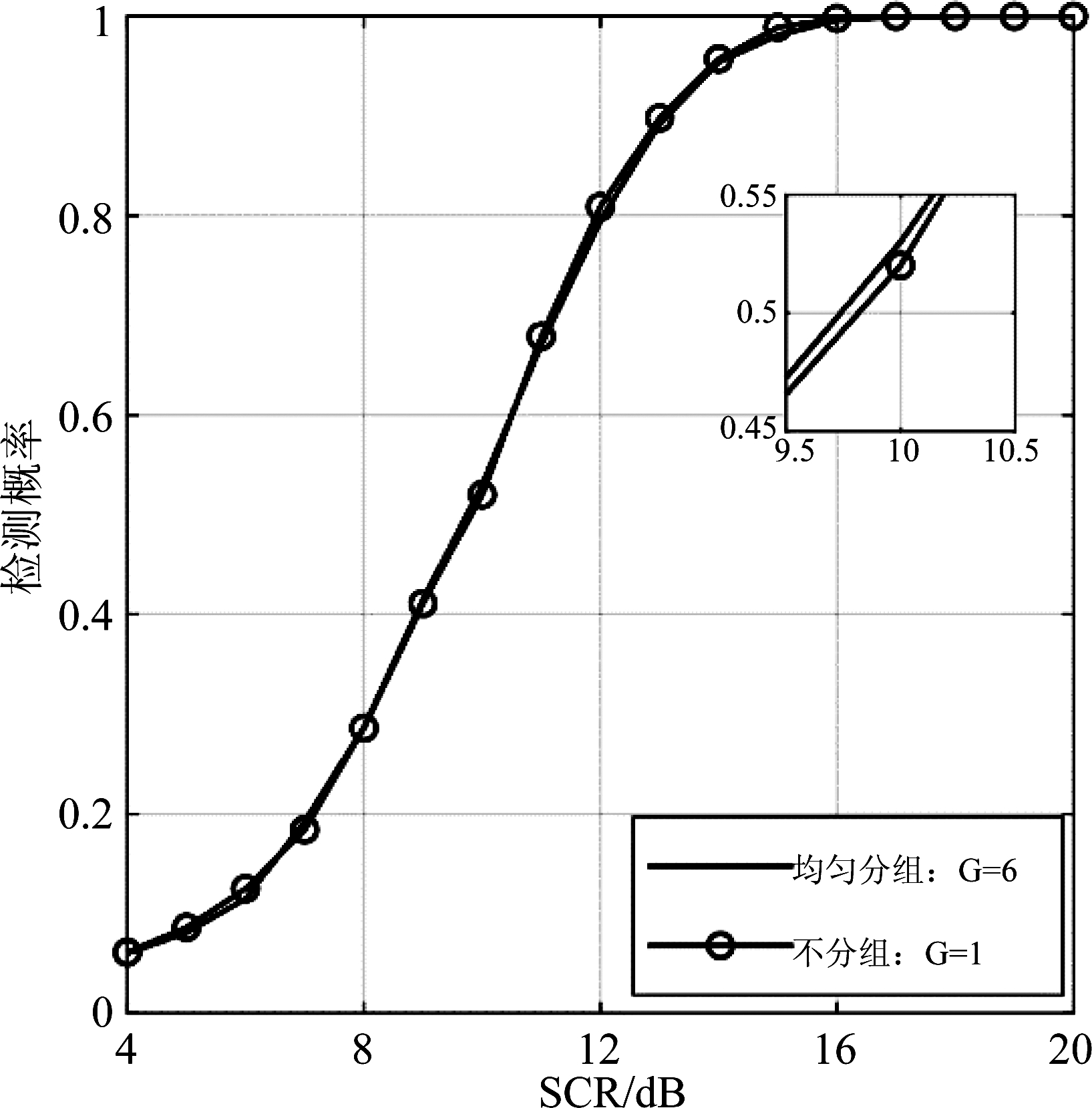
图6 不分组和均匀分组情况下ANMF的检测概率随SCR变化曲线
Fig.6 Detection probability of ANMF versus SCR in the without group case and in the average group case
4.5 不剔除干扰和剔除干扰情况下的实验性能比较
为了比较存在干扰时检测器的检测性能,本文将在某个距离单元上加上假目标干扰,假目标定义为
I(n)=Bexp(j(2πnfiTc+ϑ))
(20)
式中, fi为干扰的频率,在实验中设fi=-800 Hz;ϑ为均匀分布在[-π,π]上的随机初始相位;幅度B用来调节干杂比(interference-to-clutter ratio, ICR),定义为
ICR=10log10(B2/Pc)
(21)
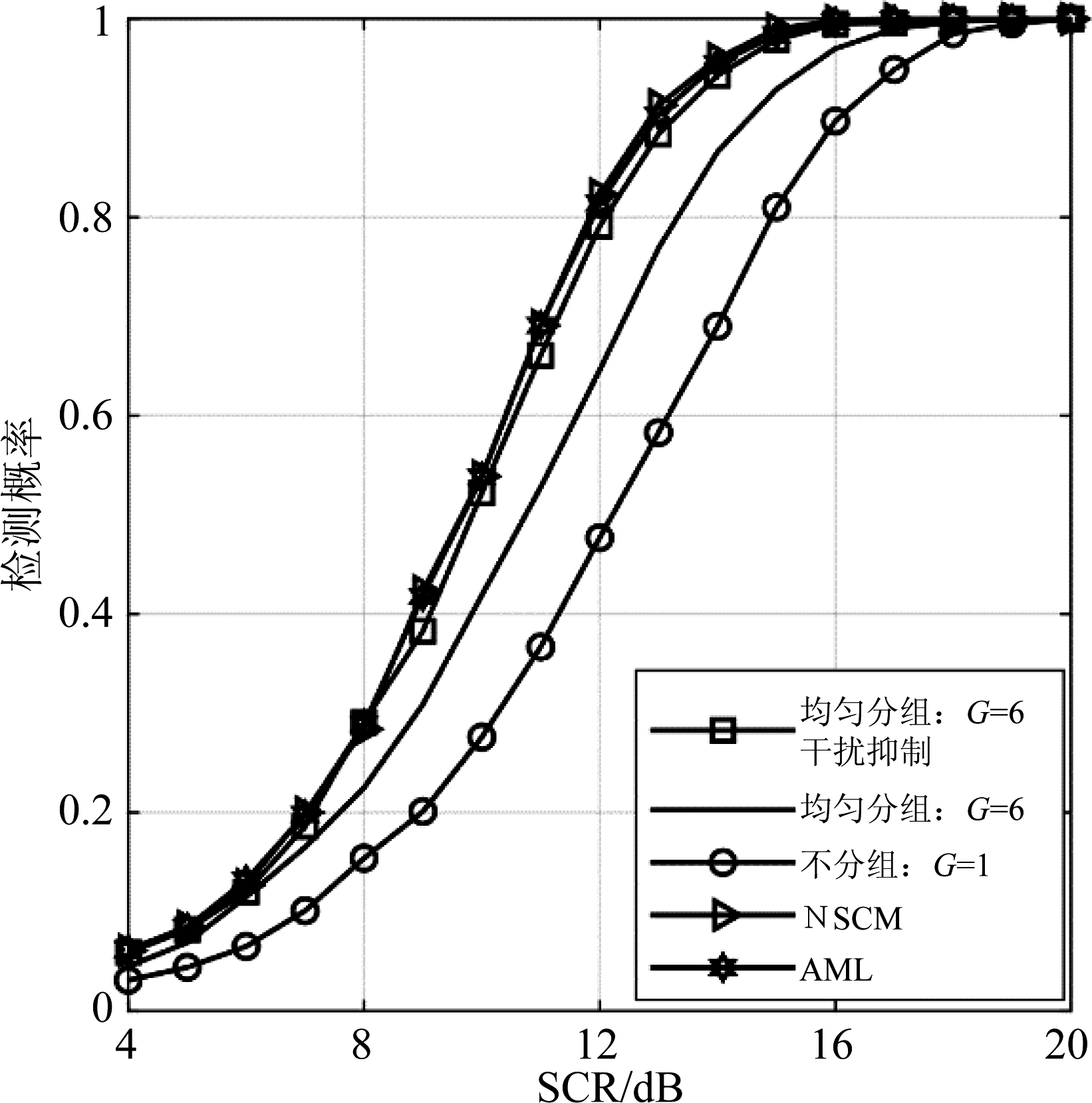
图7 ICR=30 dB下五种算法的检测概率随SCR变化曲线
Fig.7 Detection probability of five detectors versus SCR with ICR=30 dB
图7为存在干扰且ICR=30 dB时,不分组、均匀分组不去干扰和均匀分组去干扰情况下ANMF检测器的检测性能,同时对比了NSCM和AML估计算法的检测性能,其实验参数为:不分组时N=4,G=1,R=60;均匀分组时N=4,G=6,h=[10,10,10,10,10,10]。从图7中可以看出,当ICR=30 dB,采用传统的SCM算法,在不分组情况下(如图7圆圈标记线所示),检测器的性能最差;采用G=6的分组而不剔除干扰时(如图7黑色实线所示),检测器的性能优于不分组情况约2 dB,其原因是本文在分组算法中引入的加权系数对各组的协方差矩阵进行了不同比例的加权,该加权系数对于真实的杂波环境具有自适应性,干扰所在组的权重是最小的,起到了初步抑制干扰的作用;采用G=6的分组剔除干扰时(如图7方形标记线所示),检测器的性能优于不剔除干扰情况约1 dB,优于不分组情况约3 dB,其原因是本文采用θ来衡量各组协方差矩阵差异时,找到了干扰所在的分组,并将其进一步剔除,使得在协方差矩阵估计时只有纯杂波,实现了干扰的两步剔除,故而其检测性能最佳。同时,我们也发现,本文提出的均匀分组去干扰情况下ANMF检测器的检测性能与NSCM和AML估计的ANMF检测器的检测性能相当,其主要原因有两方面,一方面,NSCM和AML估计算法对纹理能量进行了归一化处理,实现了初步剔除干扰的目的;另一方面,如果我们不受限于实测数据的距离单元数,即分组后每组的参考样本数若满足hg/N≫2.5,则不会带来由于RMB准则导致的3 dB的性能损失[25],若我们可以获得足够多的参考样本数据,则我们的算法可以优于NSCM和AML算法至少3 dB。
5 结论
针对海杂波的协方差矩阵估计问题,考虑到海杂波的空间部分均匀性和假目标干扰的不可避免性会给协方差矩阵估计带来误差,本文提出分组加权协方差矩阵估计算法,并利用纹理的最大后验估计值作为每组的加权系数,实现了部分均匀的参考样本在组内的空间均匀化。进一步提出了衡量协方差矩阵之间差异的一致性因子,以确定假目标所在的分组,并最终剔除假目标。利用实测数据验证了算法的可行性。实验结果表明,首先,均匀分组的情况下,合理的分组能提高ANMF检测器的检测性能;其次,由于加权系数对于真实的杂波环境具有自适应性,干扰所在组的权重是最小的,起到了初步抑制干扰的作用;最后,采用干扰剔除算法,使得在估计协方差矩阵时只有纯杂波,其检测性能得到进一步的提升。
附录A
假设每组的参考样本具有相同的纹理值,海杂波的纹理服从逆伽玛分布[16],其PDF为:
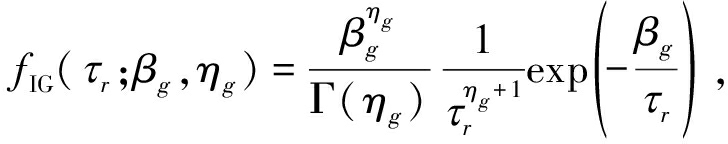
g=1,2,…,G,Hg+1≤r≤Hg+hg, τr>0
(A1)
根据式(4)有:
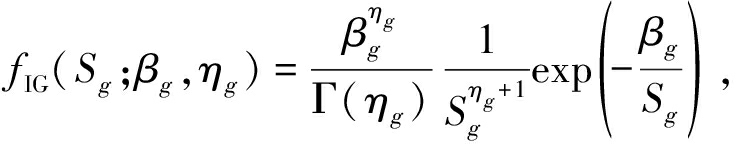
g=1,2,…,G
(A2)
其中,Γ(·)表示伽玛函数,βg为尺度参数,ηg为形状参数。
在Sg条件下,参考样本zr,r=1,2,…,R的PDF为:
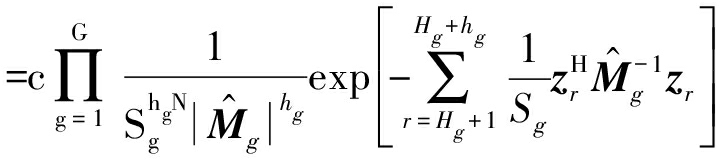
(A3)
结合式(A2)和(A3),在Sg确知的情况下,其PDF为:
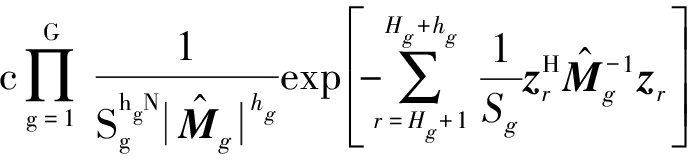
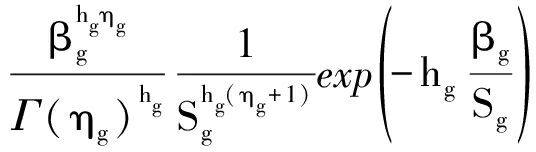
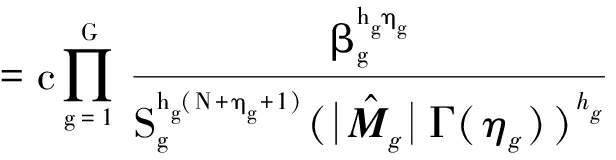
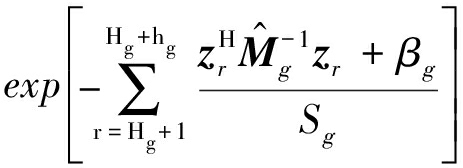
(A4)
为了获得Sg的最大后验估计,需要最大化后验函数f(Sg|z1,z2,…,zR),
f(Sg|z1,z2,…,zR)
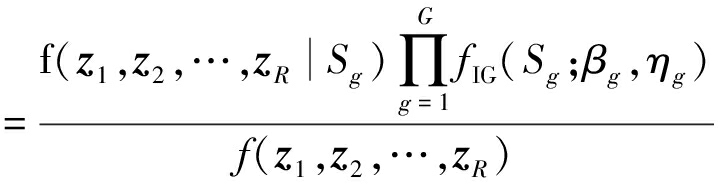
(A5)
则Sg的最大后验估计的数学表达形式为:
(A6)
因此,![]() 可以通过
可以通过![]() 对Sg求导的算法得到,令
对Sg求导的算法得到,令
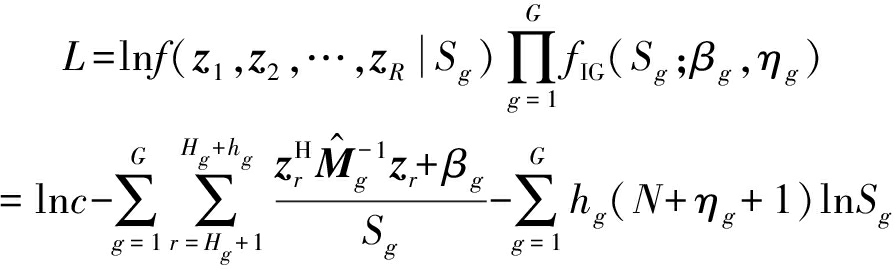
(A7)
由![]() 可得,Sg的最大后验估计为:
可得,Sg的最大后验估计为:
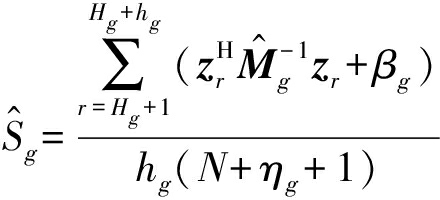
(A8)
为了简化运算,本文将zr固定在每组内的某个距离单元,则公式(A8)近似为公式(10)。
[1] Gini F, Greco M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter[J]. Signal Processing, 2002, 82(12): 1847-1859.
[2] Pulsone N B, Raghavan R S. Analysis of an adaptive CFAR detector in non-Gaussian interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 903-916.
[3] 何友, 简涛, 苏峰, 等. 非高斯杂波协方差矩阵估计算法及CFAR特性分析[J]. 中国科学: 信息科学, 2011, 41(1): 90-99.
He Y, Jian T, Su F, et al. CFAR assessment of covariance matrix estimators for non-Gaussian clutter[J]. Scientia Sinica Informationis, 2011, 41(1): 90-99.(in Chinese)
[4] 谢洪森, 邹鲲, 杨春英, 等. 海杂波协方差矩阵估计及其对目标检测性能的影响[J]. 系统工程与电子技术, 2011, 33(10): 2174-2178.
Xie H S, Zou K, Yang C Y, et al. Sea clutter covariance matrix estimation and its impact on signal detecton performance[J]. Systems Engineering and Electronics, 2011, 33(10): 2174-2178.(in Chinese)
[5] 丁昊, 薛永华, 黄勇, 等. 均匀和部分均匀杂波中子空间目标的斜对称自适应检测算法[J]. 雷达学报, 2015, 4(4): 418- 429.
Ding H, Xue Y H, Huang Y, et al. Persymmetric adaptive deterctors of subspace signals in homogeneous and partially homogeneous clutter[J]. Journal of Radars, 2015, 4(4): 418- 429.(in Chinese)
[6] 于涵, 水鹏朗, 杨春娇, 等. 用于检验散斑协方差矩阵估计性能的白化度评价方法[J]. 雷达学报, 2017, 6(3): 285-291.
Yu H, Shui P L, Yang C J, et al. Whitening degree evaluation method to test estimate accuracy of speckle covariance matrix[J]. Journal of Radars, 2017, 6(3): 285-291.(in Chinese)
[7] Wu Q, Zhang Y D, Amin M G, et al. Space-time adaptive processing and motion parameter estimation in multistatic passive radar using sparse Bayesian learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 944-957.
[8] 时艳玲. 空间非均匀海杂波的协方差矩阵估计新算法[J]. 系统工程与电子技术, 2013, 35(11): 2239-2243.
Shi Y L. New covariance matrix estimation algorithm for spatial non-homogeneous sea clutter[J]. Systems Engineering and Electronics, 2013, 35(11): 2239-2243.(in Chinese)
[9] 张圣鹋, 何子述, 李军, 等. 一种稳健的知识辅助STAP色加载系数优化算法[J]. 电子与信息学报, 2016, 38(8): 1942-1949.
Zhang S M, He Z S, Li J, et al. A robust colored-loading factor optimization aproach for KA-STAP[J]. Journal of Electronics & Information Technology, 2016, 38(8): 1942-1949.(in Chinese)
[10] 简涛, 黄晓冬, 王捷, 等. 基于修正最大似然估计的距离扩展目标检测器[J]. 武汉大学学报: 信息科学版, 2016, 41(6): 791-796.
Jian T, Huang X D, Wang J, et al. Range-spread target detector based on modified maximum likelihood estimation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 791-796.(in Chinese)
[11] Conte E, Maio A De, Ricci G. Covariance matrix estimation for adaptive CFAR detection in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 415- 426.
[12] 顾新锋, 简涛, 何友, 等. 协方差矩阵结构的广义杂波分组估计算法[J]. 宇航学报, 2012, 33(12): 1794-1800.
Gu X F, Jian T, He Y, et al. Generalized clutter-clustered estimation of covariance matrix structure[J]. Journal of Astronautics, 2012, 33(12): 1794-1800.(in Chinese)
[13] 顾新锋, 简涛, 何友, 等. 局部均匀背景中距离扩展目标的GLRT检测器及性能分析[J]. 电子学报, 2013, 41(12): 2367-2373.
Gu X F, Jian T, He Y, et al. GLRT detector of range spread target in local homogeneous background and its performance analysis[J]. Acta Electronica Sinica, 2013, 41(12): 2367-2373.(in Chinese)
[14] Shi Y L. Three GLRT detectors for range distributed target in grouped partially homogeneous radar environment[J]. Signal Processing, 2017, 135(6): 121-131.
[15] 刘维建, 谢文冲, 王永良. 部分均匀环境中存在干扰时机载雷达广义似然比检测[J]. 电子与信息学报, 2013, 35(8): 1820-1826.
Liu W J, Xie W C, Wang Y L. Generalized likelihood ratio test for airborne radar with jamming in partially homogeneous environments[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1820-1826.(in Chinese)
[16] Rabideau D J. Clutter and jammer multipath cancellation in airborne adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 565-583.
[17] Conte E, Lops M, Ricci G. Adaptive detection schemes in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1058-1069.
[18] 丁昊, 董云龙, 刘宁波, 等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5): 499-516.
Ding H, Dong Y L, Liu N B, et al. Overview and prospects of research on sea clutter property cognition[J]. Journal of Radars, 2016, 5(5): 499-516.(in Chinese)
[19] 施赛楠, 水鹏朗, 杨春娇, 等. 基于逆高斯纹理空间相关性的雷达目标检测[J]. 系统工程与电子技术, 2017, 39(10): 2215-2220.
Shi S N, Shui P L, Yang C J, et al. Radar target detection based on spatial correlation of inverse-Gaussian texture[J]. Systems Engineering and Electronics, 2017, 39(10): 2215-2220.(in Chinese)
[20] Bandiera F, Besson O, RicciI G. Knowledge-aided covariance matrix estimation and adaptive detection in compound-Gaussian noise[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5391-5396.
[21] Shi Y L, Xie X Y. Adaptive diagonal loading covariance matrix estimator in spatially heterogeneous sea clutter[C]∥2nd International Workshop on Materials Engineering and Computer Sciences(IWMECS 2015), 2015: 470- 475.
[22] Herselman P L, Baker C J, Wind H J De. An analysis of X-band calibrated sea clutter and small boat reflectivity at medium-to-low grazing angles[J]. Int. J. Navig. Obs. 2008, 14: 347518.
[23] 丁昊, 王国庆, 刘宁波, 等. 逆Gamma纹理背景下两类子空间目标的自适应检测方法[J]. 雷达学报, 2017, 6(3): 275-284.
Ding H, Wang G Q, Liu N B, et al. Adaptive detectors for two types of subspace targets in an inverse Gamma textured background[J]. Journal of Radars, 2017, 6(3): 275-284.(in Chinese)
[24] 任双桥, 刘永祥, 黎湘, 等. 广义K分布杂波模型参数估计[J]. 电子学报, 2006, 34(12): 2278-2281.
Ren S Q, Liu Y X, Li X, et al. Parameters estimation for generalized K-distributed clutter model[J]. Acta Electronica Sinica, 2006, 34(12): 2278-2281.(in Chinese)
[25] Reed I S, Mallett J D, Brennan L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 853- 863.



