1 引言
随着国民经济和航空运输业的迅速发展,机场运输流量日益增加。据统计,2017年全国运输机场的旅客吞吐量为11.48亿人次、邮货吞吐量为1617.73万吨,同往年相比均有大幅度增长。然而由于机场建设缺少科学性指导,使得机场容量无法满足日益增长的流量需求,机场延误问题依旧突出。据民航局相关部门统计,2017全年民航平均航班延误率高达29%,甚至在7月份达到了49.24%[1]。机场延误会对乘客、航空公司、机场运行人员等造成严重影响,给民航的正常运转带来挑战。而机场延误预测算法的研究,不仅可以提前预知机场拥堵时间点,为民航相关部门的运行决策提供理论指导[2-3],还可以间接反映未来机场航班需求量和容量的关系[4-5],为机场建设提供参考,具有非常重要的研究价值。
针对机场延误预测问题,国内外学者已经展开了一些研究,所采用的方法大多是线性回归、支持向量机、决策树等传统算法[6-12]。文献[6]基于非线性回归模型,对五个大型枢纽机场的航班延误情况进行了预测,通过增加航空信息网特征,其预测准确率最高为85%;文献[9]首先利用模糊线性回归模型来拟合机场延误与天气和交通流量之间的关系,利用该回归模型可得到估计延误,然后通过比较实际延误和估计延误,进一步得到评估延误的连续性能基准。但是该方法仅仅考虑了天气和交通流量这两个特征与机场延误的线性关系,并没有分析其他影响因素。文献[10]利用逻辑回归和决策树这两个机器学习模型,来预测机场地面延迟的发生。通过实验对比,逻辑回归可比决策树取得更好的预测结果,但其准确率也只有84%。由于这些机场延误预测方法均是针对小数据样本进行训练,处理能力有限,导致预测准确率难以提高,如若增大训练样本,这些传统数据处理方式和预测算法又将面临着计算瓶颈。
近年来,一些学者开始尝试利用神经网络对机场延误情况进行预测[13-17]。文献[13]利用浅层的ANN对机场空域进行延误预测,但是在面对严重且持续性延误状况时,该模型的预测结果并不理想;文献[16]提出一种多输入层ANN对肯尼迪机场航班进行延误预测,该方法可对原始数据中的离散特征进行处理,其预测准确率可达86%;文献[17]融合了气象因素和航班因素,并利用双通道卷积神经网络对融合后的数据进行特征提取,融合气象信息后其预测结果正确率为92.1%。但是以上方法较少考虑机场状态信息的时间相关性,事实上前一时刻机场的延误对后续机场是否延误的影响很大。并且这些方法没有充分考虑机场延误原始数据的特征属性。对于不同的数据特征,应该利用不同的编码方式分别对其进行处理,可以充分发挥模型算法的性能。因此,针对这些问题,需要对机场延误预测方法做进一步的探索和研究。
LSTM[18]网络目前在计算机视觉、语音识别、自然语言处理等方面得到了广泛应用,不仅具备神经网络自动提取数据特征的优点,并且相比于同为深度学习模型中表现出色的其他神经网络,LSTM模型具有记忆性,对于时序数据有较好的拟合效果,可以更好的利用机场延误数据的时间相关性。为此,本文提出一种基于混合编码和LSTM网络的机场延误预测模型,该模型包括数据预处理、特征提取和分类预测三部分。在数据预处理部分考虑到机场延误数据的特征取值多样性,提出了一种混合编码方法。在特征提取部分为更加充分利用海量机场延误数据信息,以及机场延误问题本身的时间传递性,设计了基于LSTM的神经网络结构,该网络结构可充分挖掘海量机场延误信息的特征,从而进一步提高模型的预测能力。
2 基于混合编码和LSTM网络的机场延误预测模型
图1为本文提出的机场延误预测模型,主要包括3个部分:(1)数据预处理:对机场数据、航班数据和气象数据实施数据预处理,得到按照时间排序的数据串作为后续LSTM网络的输入。(2)特征提取:将数据输入到LSTM网络中,利用网络的结构特点,对数据进行空间特征提取和时间特征提取。(3)分类预测:在LSTM网络的后面连接一个Softmax分类器,将机场延误预测问题转为分类问题,预测出机场是否发生延误。
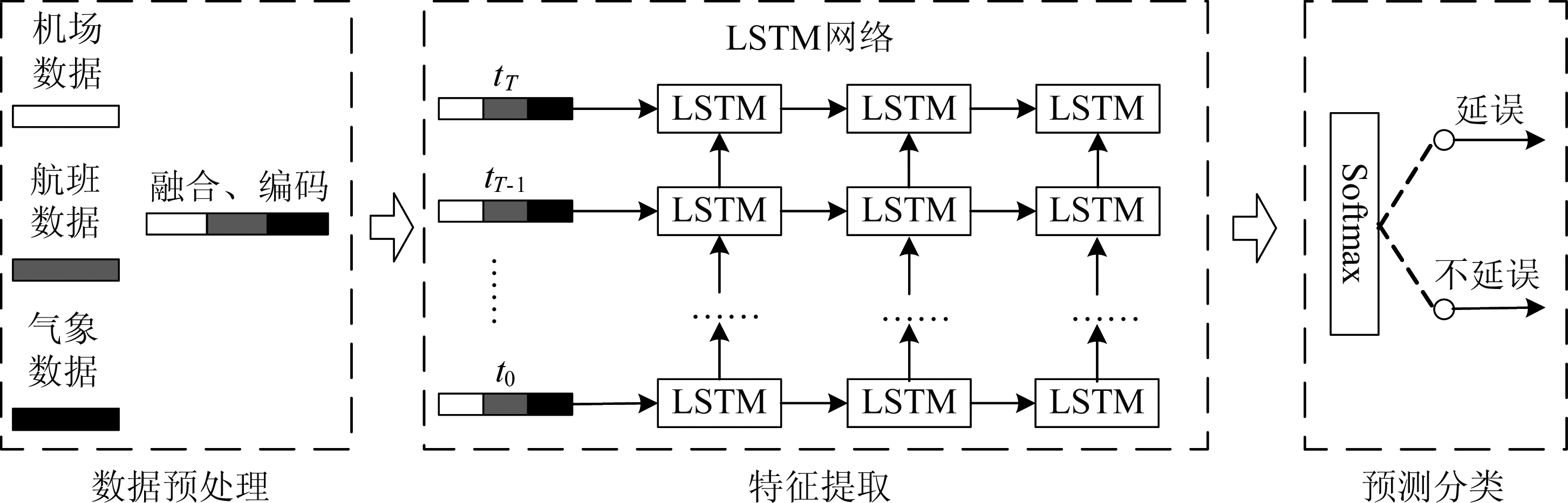
图1 机场延误预测模型
Fig.1 Airport delay prediction model
2.1 数据预处理
本文模型实验数据为2016-2017年美国亚特兰大机场的航班运行数据和气象数据,其中航班数据来自于交通运输统计局(Bureau of Transportation Statistics,BTS)的航班准时性数据(Airline On-Time Performance Data, AOTP),气象数据来自于国家海洋和气候管理局(National Oceanic and Atmospheric Administration, NOAA)提供的本地气候质量监控数据(Quality Controlled Local Climatological Data,QCLCD)。
根据航班数据和气象数据原始特征的属性,对其重新划分和定义,得到以下三种数据:
机场属性数据定义为A,包括日期(Date)、时间(Time)、机场ID(AirportID)、机场所在城市ID(CityMarketID)、机场所在州代码(StateFips),共5个特征属性。
航班数据定义为F,包括年(Year)、季度(Quarter)、月(Month)、日(DayofMonth)、星期几(DayOfWeek)、尾翼号(TailNum)、航班号(FlightNum)、航线号(AirlineID)、承运人(Carrier)、起飞/降落机场ID(OriginAirportID/DestAirportID)、起飞/降落城市ID(OriginCityMarketID/DestCityMarketID)、起飞/降落所在州代码(OriginStateFips/DestStateFips)、计划起飞/降落时间(CRSDepTime/CRSArrTime)、起轮/放轮时间(WheelsOff/WheelsOn)、航程(Distance),共15个特征属性。
气象数据定义为W,包括日期(Date)、时间(Time)、观测站类型(StationType)、机场天气状态(SkyCondition)、干球华氏温度(DryBulbFarenheit)、干球摄氏温度(DryBulbCelsius)、湿球华氏温度(WetBulbFarenheit)、湿球摄氏温度(WetBulbCelsius)、露点华氏温度(DewPointFarenheit)、露点摄氏温度(DewPointCelsius)、相对湿度(RelativeHumidity)、风向(WindDirection)、风速(WindSpeed)、能见度(Visibility)、观测站气压(StationPressure)、海平面气压(SeaLevelPressure)、记录类型(RecordType)、高度(Altimeter),共18个特征属性。
数据预处理过程包括了数据融合、混合编码和时间序列的构造。下面给出数据预处理的步骤:
(1)数据融合:以日期、航班起飞/降落时间以及天气观测时间这3个特征作为键值,对机场数据A、航班数据F和气象数据W融合后得到数据集R。
(2)混合编码:数据的混合编码过程如图2所示,首先将数据R的特征属性分为离散性和连续性两种,对连续性特征进行Min-Max[17]归一化编码,然后将离散性特征分为低维特征和高维特征,低维特征的编码方式为One-Hot[17]编码;高维特征的编码方式为Mean-Encoder[19]编码,最后得到编码后的数据集E。
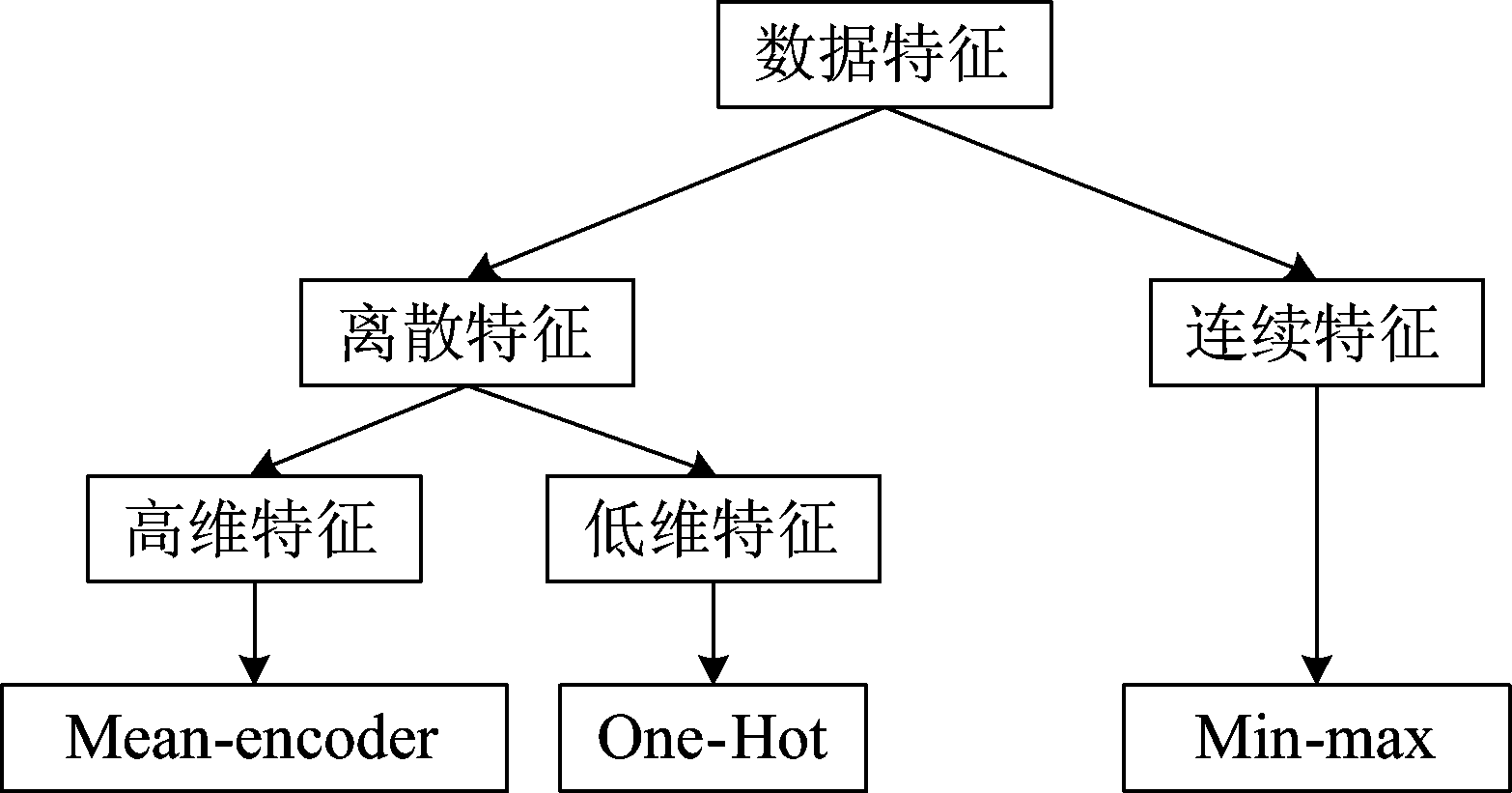
图2 数据混合编码过程
Fig.2 Data hybrid coding process
对于离散性数据,比较常用的方法是采用One-Hot编码,使数据特征的欧式距离都为![]() 从而使重要性保持一致。但是,对于取值结果穷举数高达几百甚至几千的高基数离散性特征来说,One-Hot编码方法在实际运用中并不能得到令人满意的结果,为此根据文献[19]提出的Mean-Encoder编码方法理论知识,以及数据R中离散特征基数分布的统计结果,提出了以100为阈值,将R的离散特征分为高基数离散特征和低基数离散特征两类,分别对其进行Mean-Encoder和One-Hot编码的混合编码方法。
从而使重要性保持一致。但是,对于取值结果穷举数高达几百甚至几千的高基数离散性特征来说,One-Hot编码方法在实际运用中并不能得到令人满意的结果,为此根据文献[19]提出的Mean-Encoder编码方法理论知识,以及数据R中离散特征基数分布的统计结果,提出了以100为阈值,将R的离散特征分为高基数离散特征和低基数离散特征两类,分别对其进行Mean-Encoder和One-Hot编码的混合编码方法。
下面对Mean-Encoder的算法进行说明,为方便后续算法的描述,首先给出如下定义:本文为一个二分类问题,分类对象y共有两个不同的取值,分别是延误和不延误,具体取值表示为yi,i∈(0,1);该分类对象某一个离散性特征ν共有k个不同种类,使用νj来表示其中的一个种类,0≤j≤k。则离散特征νj的编码可由表1给出的算法步骤求得。
表1 Mean_Encoder算法步骤
Tab.1 Algorithm steps of Mean_Encoder

根据表1给出的算法步骤,Mean-Encoder算法的思想是将离散特征ν的k个不同类别,均表示为ν为该类别时y等于不同值时的概率。该概率估算为先验概率和后验概率的一个凸组合,λ为先验概率的权重,本文在经过大量实验后,该权重函数的可调参数m和f的值设为了40和3。
(3)时间序列的构造:为适应LSTM网络结构特点,需要对编码后的数据E在时间维度上进行分割,得到最终网络输入的时间序列串Et。图3(a)为基于时间段的序列构造方法,预测结果为时间段T内机场的平均延误状态。该方法首先将编码后的数据按照时间顺序排列,然后以时间T为间隔,依次对数据进行分割,但是由于每个时间段内机场的运行航班数量相差较大,使每个序列串包含的数据个数不一样,即图中l1,l2,l3……的值不相等,造成LSTM网络循环迭代的时间长度不一致。为解决该问题,本文采用了基于时刻的序列构造方法(如图3(b)所示)。根据统计分析结果,大型枢纽机场内航班的起飞和降落时间基本可以覆盖全天24小时,为此将预测结果设为机场内每一个运行航班起飞或降落时刻的机场延误状态,输入为该时刻以及前l-1时刻的数据, 来保证每个序列包含的数据个数统一。具体实现方法是以宽度为l,步长为1的分割窗口在时间维度上进行滑动分割,得到n-l个输入序列(l≪n),每个序列的长度均为l。每条序列对应的预测结果为第l时刻的机场延误状态。
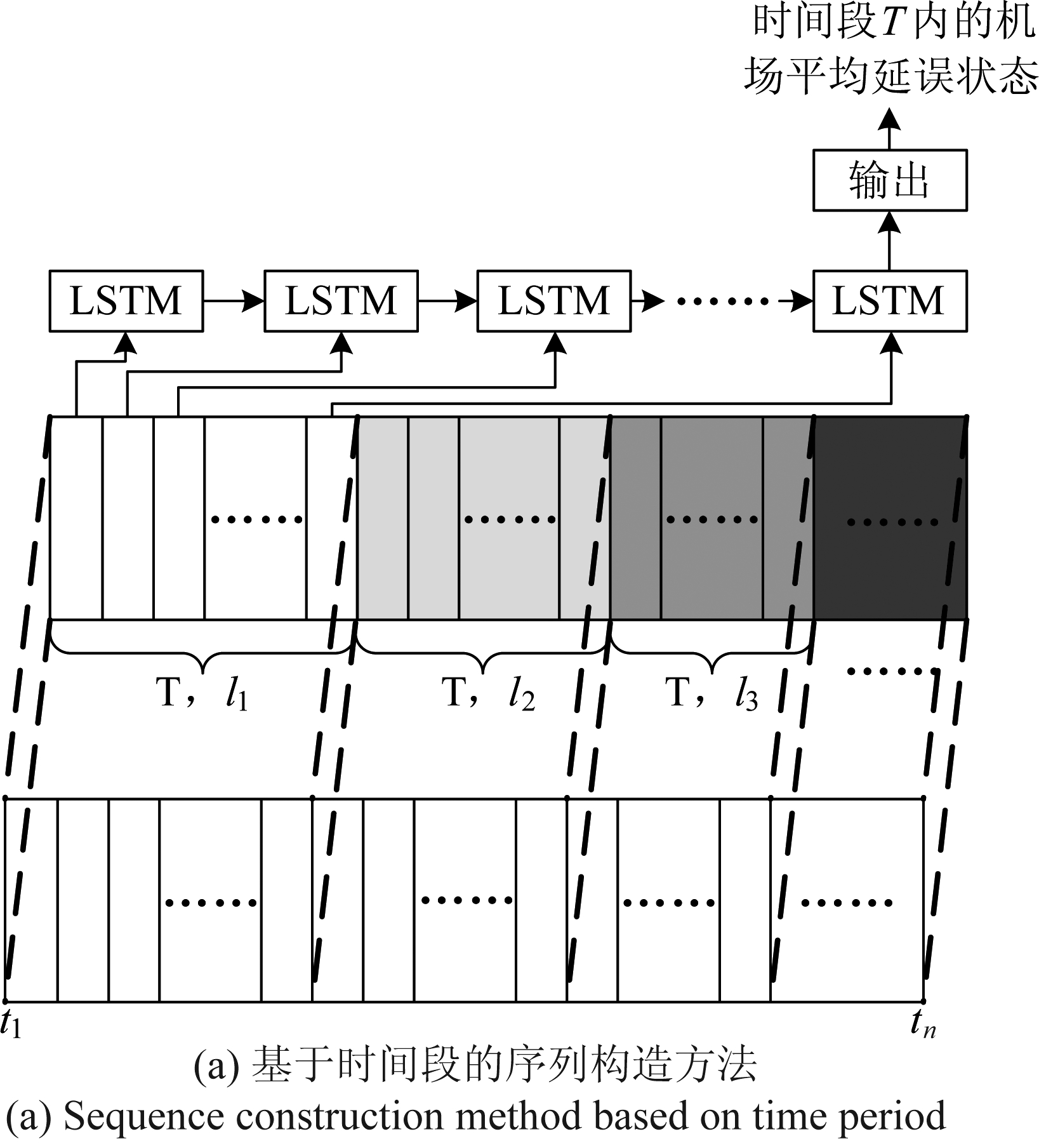
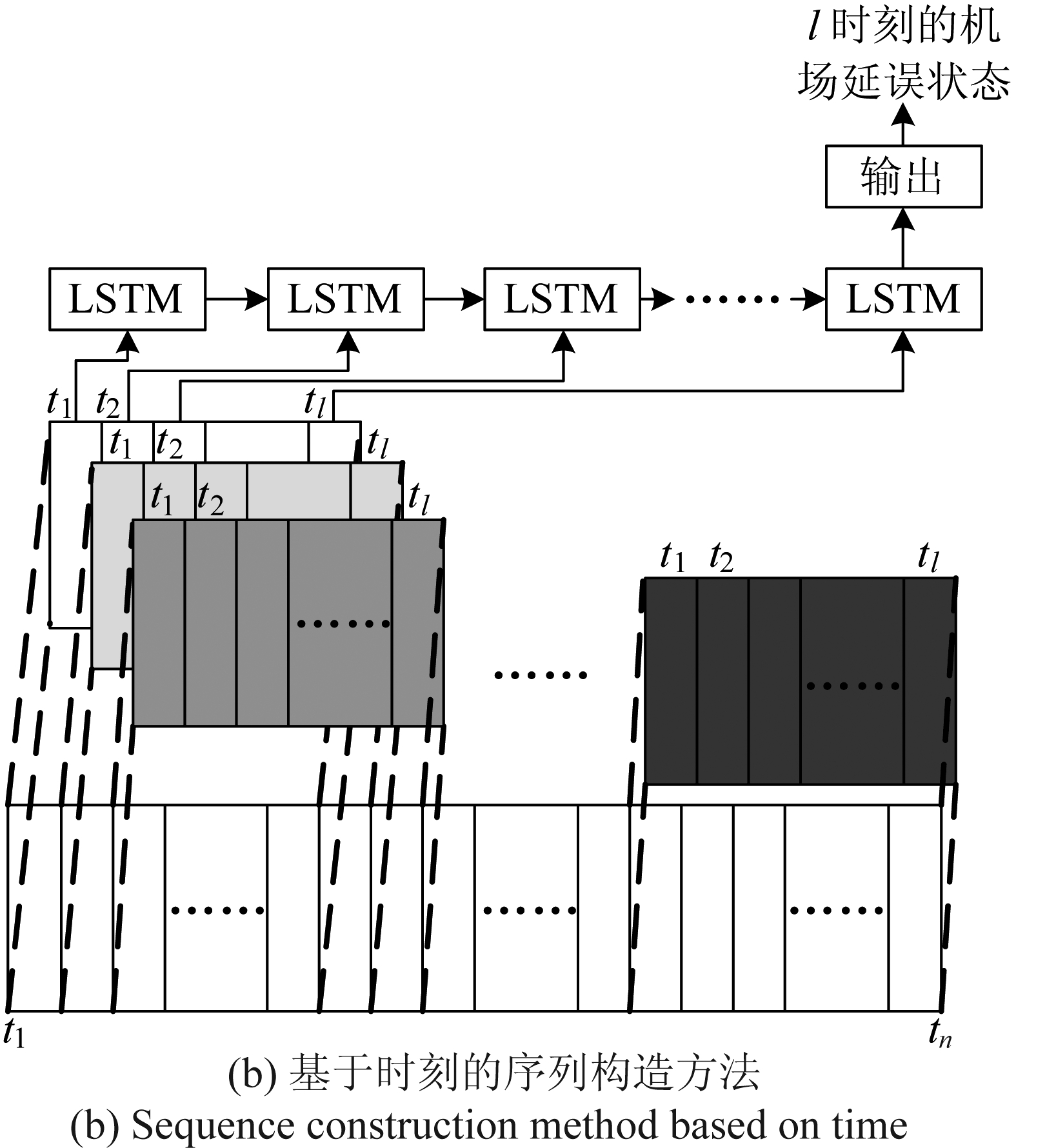
图3 时间序列构造方法
Fig.3 Construction method of time series
2.2 特征提取
机场延误数据具有很强的时间相关性,利用LSTM网络来完成机场延误数据的特征提取,可以有效利用过去时刻机场延误状态对当前时刻的影响,同时LSTM网络可以弥补简单循环神经网络[20](Recurrent Neural Network, RNN)无法记忆长时间信息的问题。
图4(b)为LSTM的单元结构示意图,为了方便对比,图4(a)给出了的RNN单元结构示意图。从图中可以看出LSTM网络单元相比RNN增加了多个门单元和记忆单元,用于保持和传递长时间信息,提高网络的有效性。
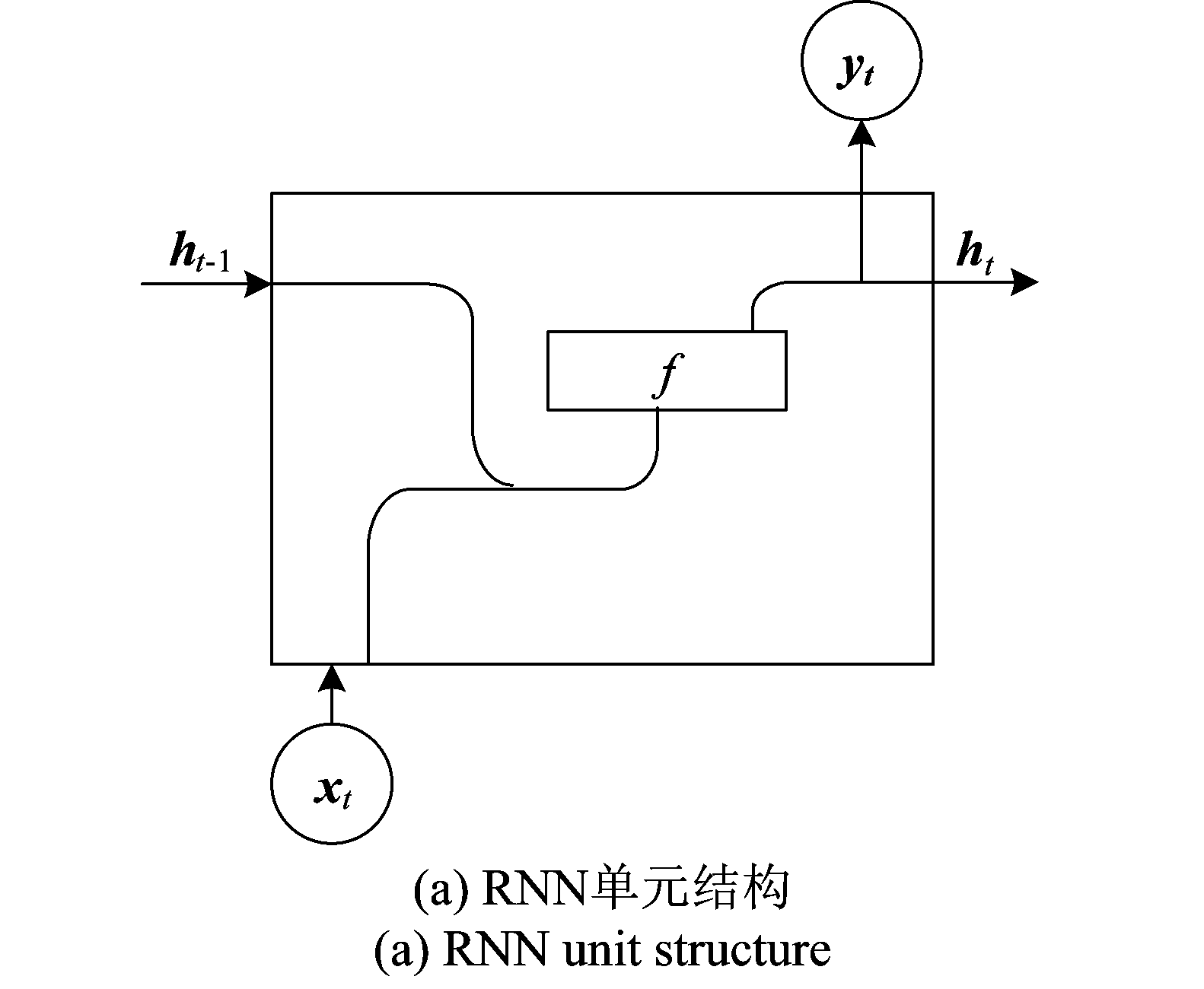
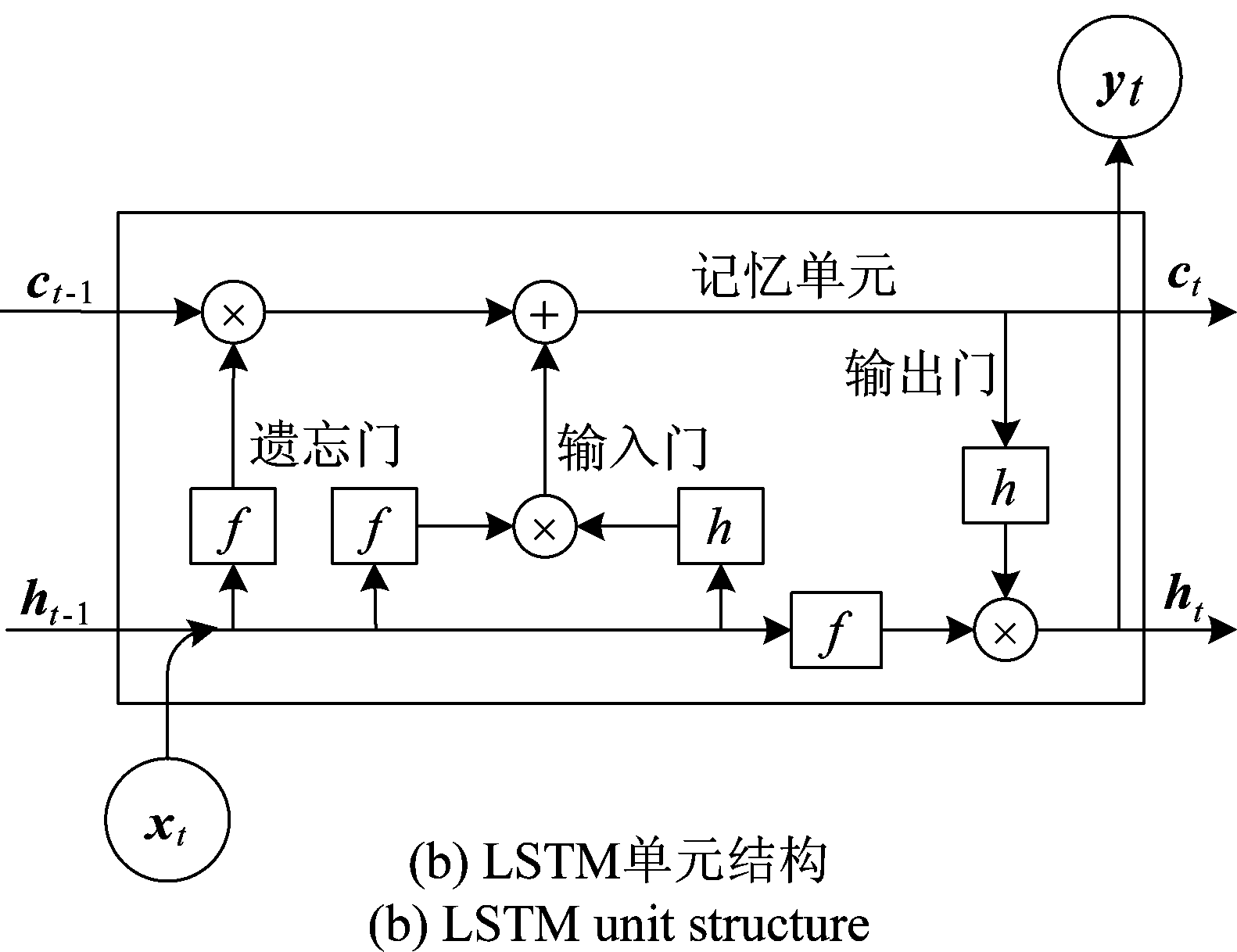
图4 RNN和LSTM单元结构对比
Fig.4 Comparison of RNN and LSTM unit structure
图4(b)中的f(·)和h(·)分别代表不同的激活函数。定义xt为t时刻的输入,ht为t时刻的隐藏层状态,it为t时刻的输入门输出,ft为t时刻的遗忘门输出,ot为t时刻的输出门输出,那么上述定义可分别表示为公式(1)~(3):
it=f(ωxixt+ωhiht-1+bi)
(1)
ft=f(ωxfxt+ωhfht-1+bf)
(2)
ot=f(ωxoxt+ωhoht-1+bo)
(3)
公式(3)中ωxi、ωxf、ωxo为输入门、遗忘门和输出门的输入权重矩阵,ωhi、ωhf、ωho为对应每个门的反馈权重矩阵,bi、bf和bo则为每个门对应的偏置向量。LSTM的记忆功能主要依靠单元的中间状态,![]() 和ht为LSTM输入函数、输出函数和隐藏层对应的中间状态。
和ht为LSTM输入函数、输出函数和隐藏层对应的中间状态。![]() 可以表示为公式(4):
可以表示为公式(4):
(4)
其中ωxc、ωhc和bc为对应的权重矩阵和偏置向量。ct则可以表示为公式(5),LSTM单元的状态更新过程包含两部分,分别为状态ct和状态ht的更新,如公式(5)、(6)所示:
(5)
ht=oth(ct)
(6)
表2为本文使用的LSTM网络结构配置图。将原始数据进行数据预处理后,可得到维度为(b,l,f)的网络输入数据,其中b为网络的批处理数量,l为每条数据的时间序列长度,f为编码后数据的特征维度。本文共设计实现了LSTM1、LSTM3、LSTM5三个网络结构,分别代表隐藏层为1、3、5的LSTM网络。网络第1层均包括了维度转换1、神经单元数量为128的全连接和维度转换2,维度转换1的目的是将三维输入数据转换压缩为二维矩阵,维度转换2的目的则是将二维矩阵中的时间维度单独提出来,形成一个三维数据。在LSTM隐藏层的配置上,每一层神经单元个数均为128,时间步长为l。
2.3 预测分类
根据中国民航航空局发布的《航班正常管理规定》[21],“航班延误”是指航班实际到港挡轮时间晚于计划到港时间超过15分钟的情况。近来一些参考文献在此基础上把延误情况进行细分,得到多个不同的延误等级,但是为了实验设置更加有依据,本文按照航班延误的定义,将延误时间在15分钟以内的情况划分为不延误状态,反之划分为延误状态,即将机场延误预测问题转化为一个二分类问题。同时,在后续实验中对比了不同分类精度下LSTM网络的预测准确率。
特征分类部分共有两层:全连接和Softmax[22]分类器。其中,全连接层的输出特征图维度为(1×1)×m,m为分类类别数,本文所涉及的是二分类问题,所以这里的m为2。网络训练使用交叉熵作为代价函数来计算损失值,其表达式为式(7)
表2 LSTM网络结构配置
Tab.2 LSTM network structure configuration
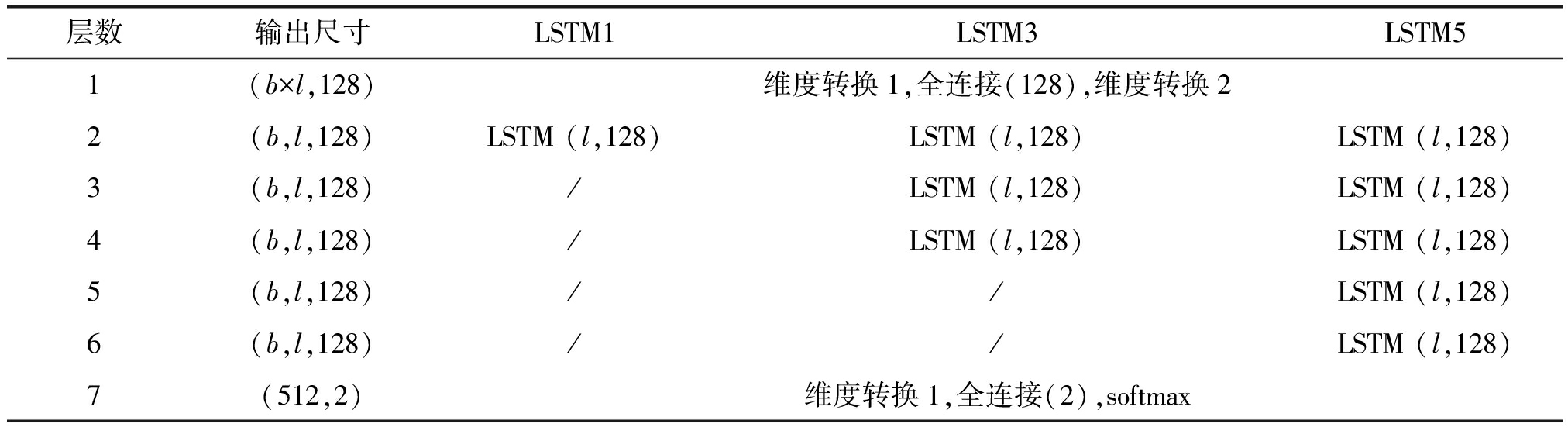
层数输出尺寸LSTM1LSTM3LSTM51(b×l,128)维度转换1,全连接(128),维度转换22(b,l,128)LSTM (l,128)LSTM (l,128)LSTM (l,128)3(b,l,128)/LSTM (l,128)LSTM (l,128)4(b,l,128)/LSTM (l,128)LSTM (l,128)5(b,l,128)//LSTM (l,128)6(b,l,128)//LSTM (l,128)7(512,2)维度转换1,全连接(2),softmax
(7)
式中,p(x)为期望输出,q(x)为实际输出,H(p,q)为交叉熵,该式子刻画的实际输出与期望输出的距离,也就是说交叉熵越小,两个概率分布越接近,则训练的拟合函数越接近真实情况,预测准确率越高。
为了更好的评估LSTM网络在机场延误预测问题上的有效性,本文采用的评价准则:
(8)
其中,N为测试集中总的数据量,C表示模型预测的延误状态与实际延误状态相同的记录数。
3 实验
本节先介绍了实验所使用的平台、参数配置和数据集。然后,基于LSTM模型讨论了隐藏层层数、时间步长数和编码方式对预测精度的影响,确定了面向机场延误预测的LSTM网络结构。最后,基于机场延误数据对比了ANN[13]、VGG[23]和LSTM模型的预测结果和训练时间。
3.1 实验环境与参数配置
实验所使用计算机的配置如下:处理器为英特尔至强Xeon E5-1620,CPU频率为3.60 GHz;内存为16.00 GB;操作系统为Ubuntu14.04 (64位);图形加速卡为GeForce GTX TITAN Xp;深度学习开发平台为Tensorflow 1.3.0。
表3给出了机场延误预测模型中涉及的参数名称与对应的参数值,学习率的变化策略为分别在迭代6万次和8万次的时候进行衰减,每次衰减10倍。
表3 机场延误预测神经网络参数表
Tab.3 Airport delay prediction neural network parameters
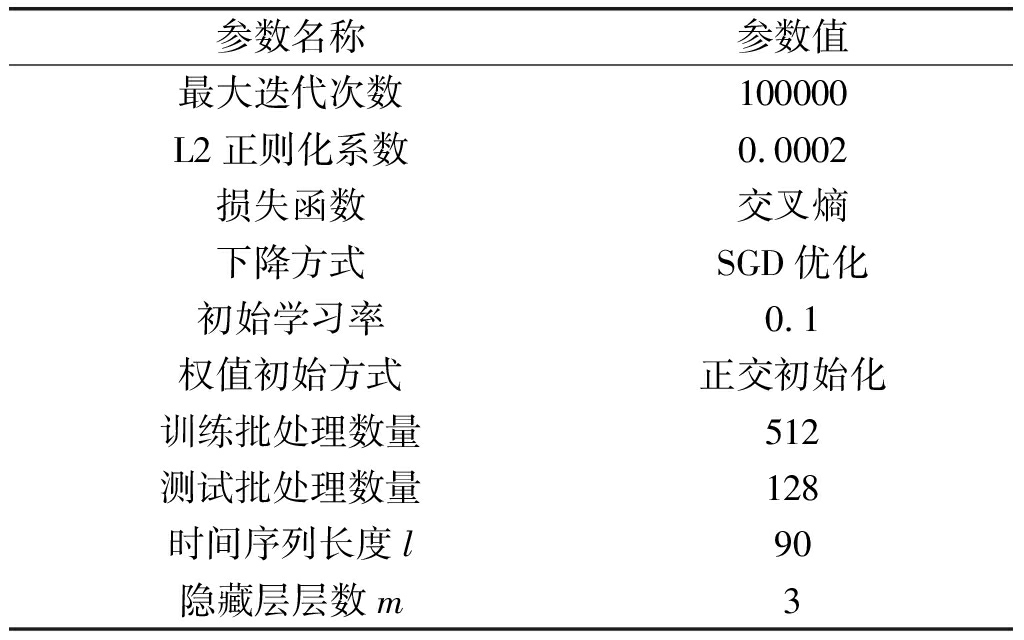
参数名称参数值最大迭代次数100000L2正则化系数0.0002损失函数交叉熵下降方式SGD优化初始学习率0.1权值初始方式正交初始化训练批处理数量512测试批处理数量128时间序列长度l90隐藏层层数m3
3.2 时间步长数对预测结果的影响分析
由于LSTM网络每层只有最后一个时刻的输出,使得网络对输入序列的长度比较敏感。如果网络的时间步长过大,会导致训练时间过长,甚至会产生梯度消失和梯度爆炸的现象;如果网络的时间步长过小,则输入数据的时间相关性不能被充分学习。但是由于计算能力不足,本文只对l取值为30、60、90的时间步长进行为了分析。表4给出了时间步长取不同值时,对应的预测准确率。
表4 不同时间步长的预测准确率对比
Tab.4 Comparison of prediction accuracy for different time steps

网络名称测试准确率/%LSTM3-3093.19LSTM3-6093.34LSTM3-9094.01
从表4中可以看出,增加时间步长数,测试准确率会得到逐步提高,说明通过时间相关特性考虑范围越广,对预测结果的影响越大。
图5为LSTM3-30、LSTM3- 60、LSTM3-90三个网络结构对应的损失值,从图中可以看出,LSTM3-90对应的损失值最小,且没有出现不稳定的情况,说明当LSTM网络的时间步长数l增加至90时,网络仍然能够被很好的训练。为此,下面实验中涉及到的时间步长数均为90。
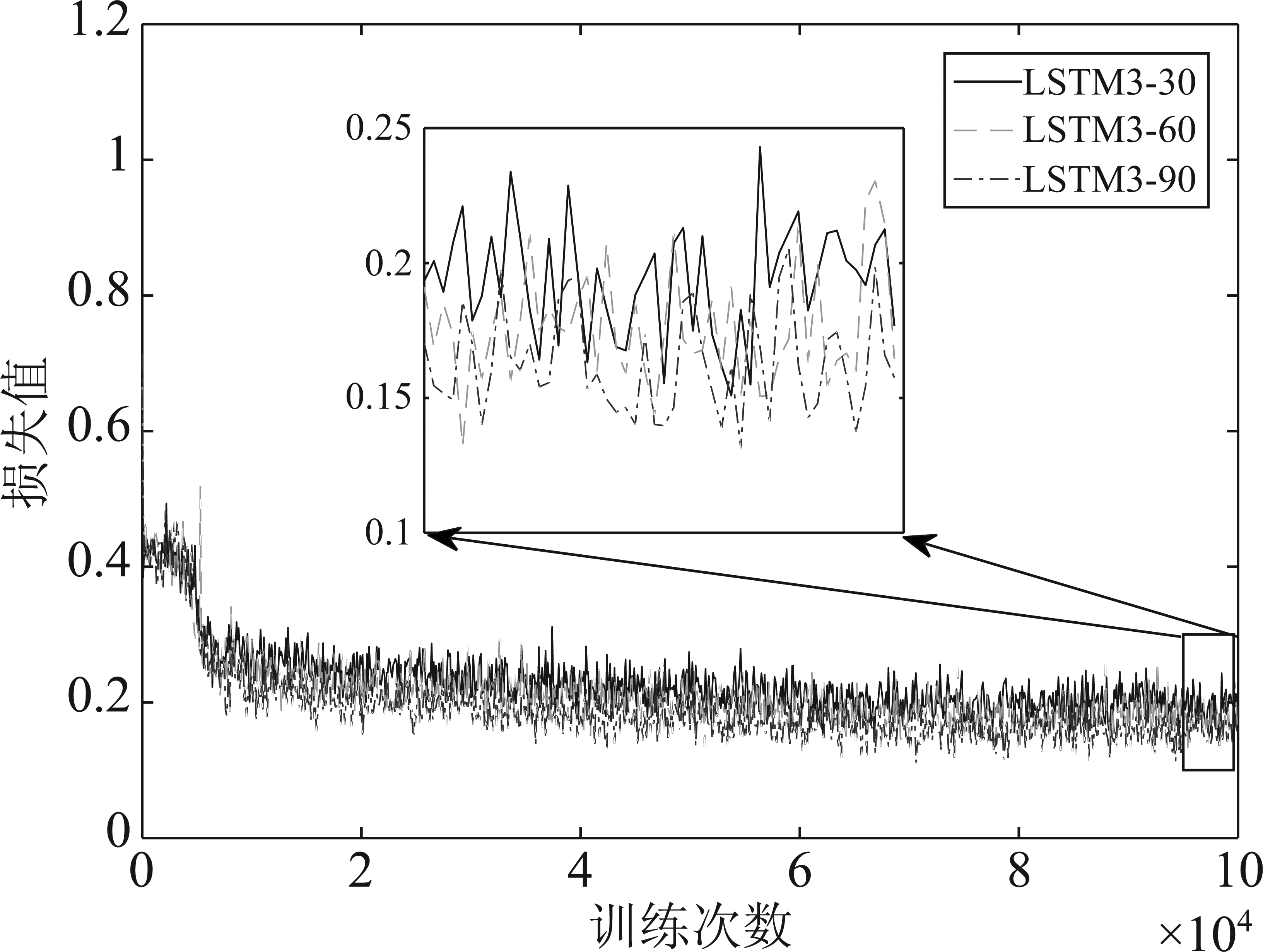
图5 不同时间步长的损失值对比
Fig.5 Comparison of loss values at different time steps
3.3 隐藏层层数对预测结果的影响分析
为确定面向机场延误预测问题的LSTM网络可训练深度,本文对LSTM1、LSTM3和LSTM5网络进行了训练测试,预测结果如表5所示,当LSTM网络的隐藏层层数等于3时,其预测结果的准确率最高为94.01%。但是当隐藏层增加至5层时,预测准确率开始下降。
由表5可知,LSTM5出现了随着网络层数增加预测准确率不升反降的现象,为进一步探索该现象原因,图6给出了LSTM1、LSTM3和LSTM5第一层对应的梯度值。这是因为神经网络模型在反向传导过程中进行隐藏层权重以及误差项的更新,如果网络第一个隐藏层的梯度值随迭代次数变化能一直保持稳定,则表征该网络其他隐藏层均能保证信息的有效传递。从图6可以明显看出,LSTM5网络梯度值锐减,基本分布在10-5量级,相比其他两种网络结构大概减少了10-2。这说明LSTM网络在权值更新过程中存在梯度消失问题,难以充分地进行特征提取,进而导致预测准确率降低。所以本文LSTM网络的隐藏层层数设计为3层。
表5 不同隐藏层层数的测试准确率对比
Tab.5 Comparison of test accuracy of different hidden layers

网络名称测试准确率/%LSTM193.15LSTM394.01LSTM588.86
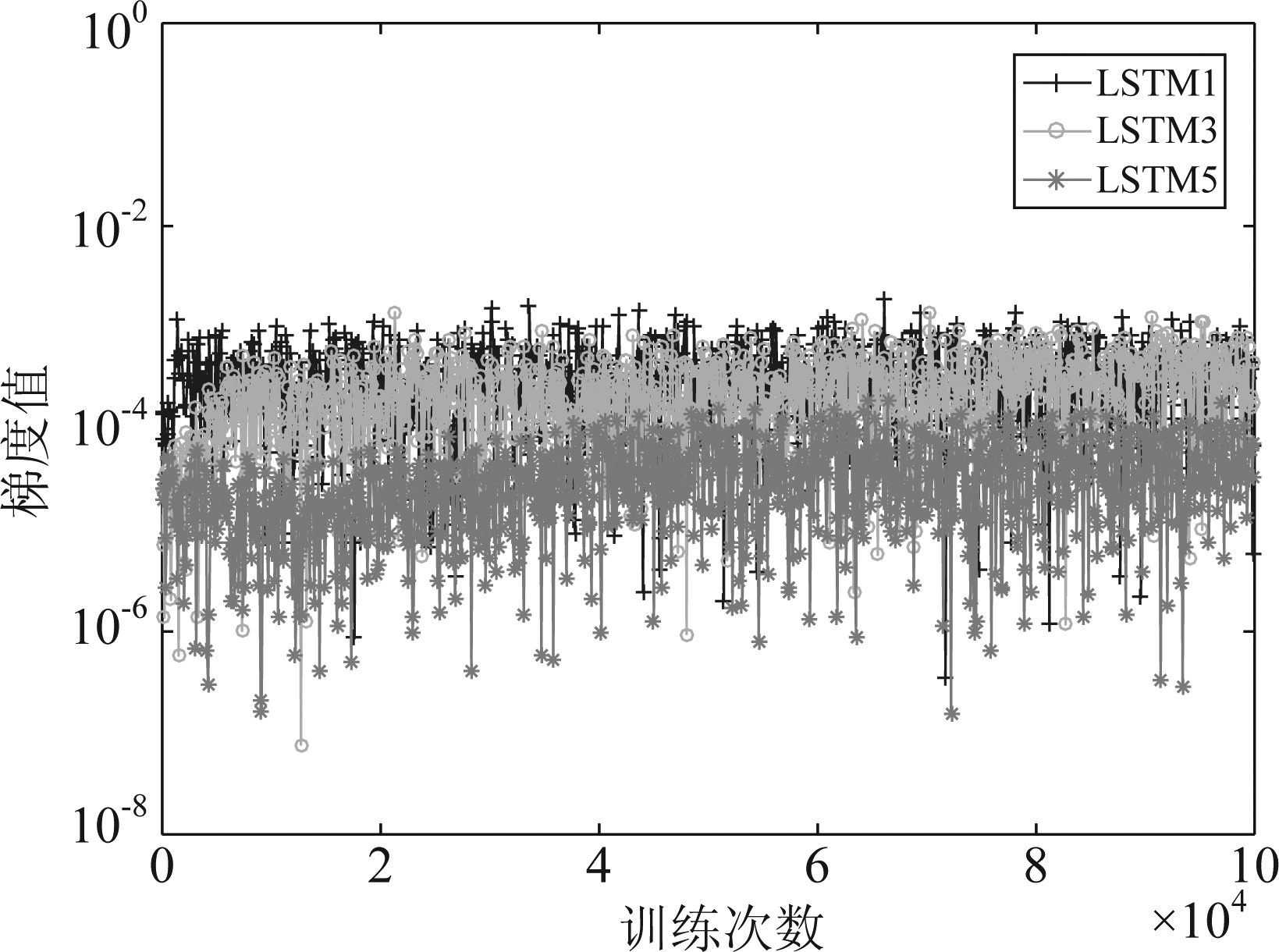
图6 不同隐藏层层数的梯度值对比
Fig.6 Gradient value comparison of different hidden layer levels
3.4 编码方式对预测结果的影响分析
为研究混合编码方法的有效性,下面基于机场延误数据和LSTM3网络对OneHot编码、频次编码、混合编码进行了对比,三种编码方法所对应的预测结果如表6所示。前面章节已经对OneHot编码和本文所提的混合编码进行了介绍,这里不再赘述。频次编码是处理离散性特征的一种常用编码方式,其思想是利用对特征取值的频次统计结果,将频次最高的取值值编码为0,其次为1,依此类推[17]。由表6中的预测准确率可知,使用OneHot编码时预测准确率最低,频次编码的预测结果提高为93.27%,混合编码方法的预测准确率最高为94.01%。这是因为虽然频次编码加入了概率统计信息,但是相比Mean-encoder方法来说,这些统计信息都比较宏观粗糙,并且混合编码是针对离散性特征的不同特点,进行了细化,使得网络可以更加容易充分的进行特征提取。
表6 编码方式对预测结果的影响分析
Tab.6 Analysis of the influence of coding methods on prediction results

编码方法预测准确率/%OneHot89.41频次编码93.27混合编码94.01
3.5 分类精度对预测结果的影响
为探索机场延误预测模型对分类精度的敏感性,分别设计了类别为二和五的网络模型,其中五分类的划分标准可参考文献[17]。实验结果如表7所示,可以看出网络LSTM1、LSTM3和LSTM5在不同分类精度下的测试准确率相差0.73%~1.37%。通常情况下,模型的分类越精细,对类别的分辨率越低,本文所使用的LSTM3网络在进行五分类预测时,准确率降低为93.29%,但是由于网络中时序信息的增加和混合编码的优势,相比文献[16]所提模型,LSTM3网络具有更高的预测准确率。
表7 不同分类类别的测试准确率对比
Tab.7 Comparison of test accuracy of different classification category
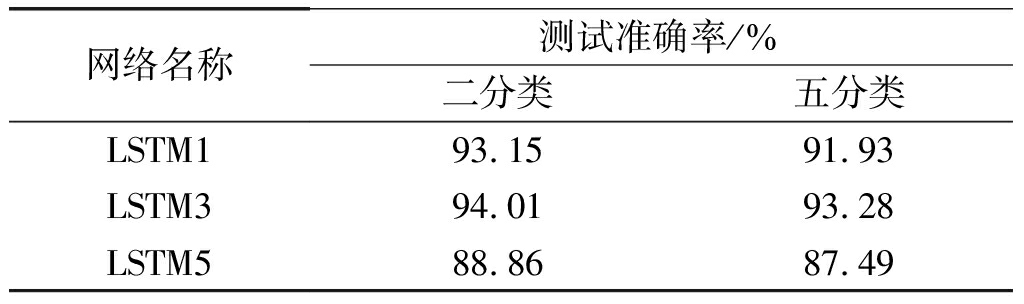
网络名称测试准确率/%二分类五分类LSTM193.1591.93LSTM394.0193.28LSTM588.8687.49
3.6 不同神经网络模型对比
为了验证LSTM网络在处理机场延误预测问题的优势,本文使用了ANN和VGG两种网络结构作为对照组。ANN不同隐藏层之间采取的是全连接方法,这里设计了层数为1、3、5的网络结构,对应网络名称为ANN1、ANN3、ANN5。当神经网络深度增加时,模型对计算机性能的要求越来越高,模型的收敛也越来越困难。VGG是基于文献[23]提出的经典卷积神经网络,包括了若干个重复出现的3×3卷积核和2×2最大池化。这里基于机场延误数据实现了VGG16和VGG19,对于时序性数据集,由于卷积神经网络没有考虑时间维度上数据的关联性,所以在具体实现策略上,需要将其映射到空间维度上进行卷积,这样的操作必定会丢失一部分数据信息,特别是长时间距离的信息。
表8为ANN、VGG和LSTM网络的测试准确率对比。由表中数据可以看出,ANN网络在隐藏层层数为3层时,预测准确率最高,可达到90.34%,但是随着层数的继续增加,出现了梯度消失的现象,ANN5的测试准确率随着网络层数的增减不升反降。VGG网络作为一种卷积神经网络,通过局部感知参数共享的方式能大幅度降低网络训练参数,其训练时间最短,但是因为其思想是将时域数据转换至空域进行卷积,预测效果并不能达到要求,而且随着网络层数的加深,也出现了预测精度下降的情况。而本文采用的LSTM3网络结构,虽然其训练时间较长,但是测试准确率比ANN和VGG网络高3.67%~11.65%,证明了利用LSTM网络来解决机场延误预测问题更加有效。
表8 不同网络结构的测试准确率对比
Tab.8 Comparison of test accuracy of different network structures
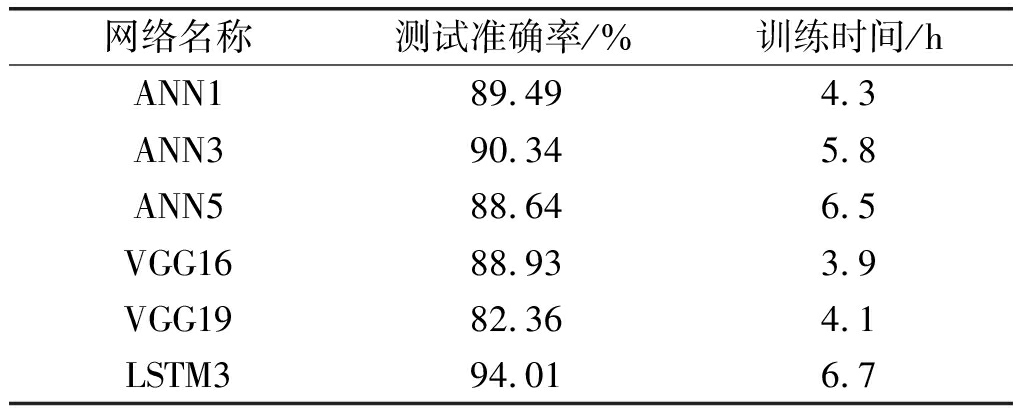
网络名称测试准确率/%训练时间/hANN189.494.3ANN390.345.8ANN588.646.5VGG1688.933.9VGG1982.364.1LSTM394.016.7
图7表示各个网络结构随迭代次数变化的损失值大小,损失值越小,说明模型预测值与真实值大小越接近。图7的实验结果表明,随着训练迭代次数的增大,模型逐渐趋于收敛,训练集损失值最终减少到一个固定的范围。其中,ANN5和VGG19的损失值最大,大约分布在0.4左右,与测试准确率的结果相对应,而LSTM5的损失值最低,大约为0.2,证明了LSTM网络的预测结果更加接近于真实值。
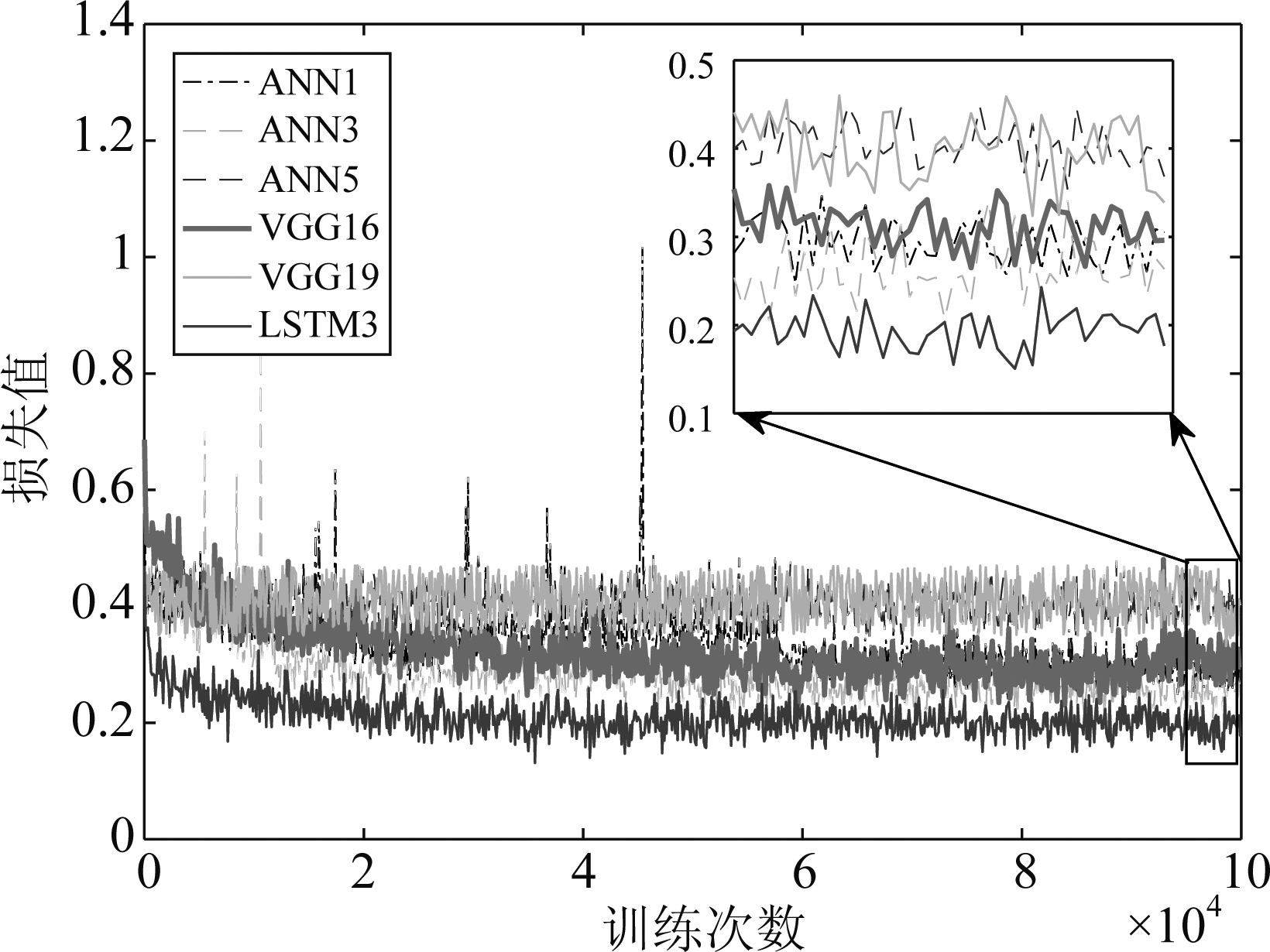
图7 不同网络结构的损失值对比
Fig.7 Comparison of loss values of different network structures
图8为不同各个网络结构第一层梯度值随迭代次数的变化曲线。由图8中可以明显看出ANN5和VGG19的梯度值出现了锐减,进一步说明了这两个网络梯度消失的问题,LSTM3和ANN1、VGG16的梯度值比较接近且值最大,大约在10-3左右,说明这三个网络可以更加完备的表达数据信息。
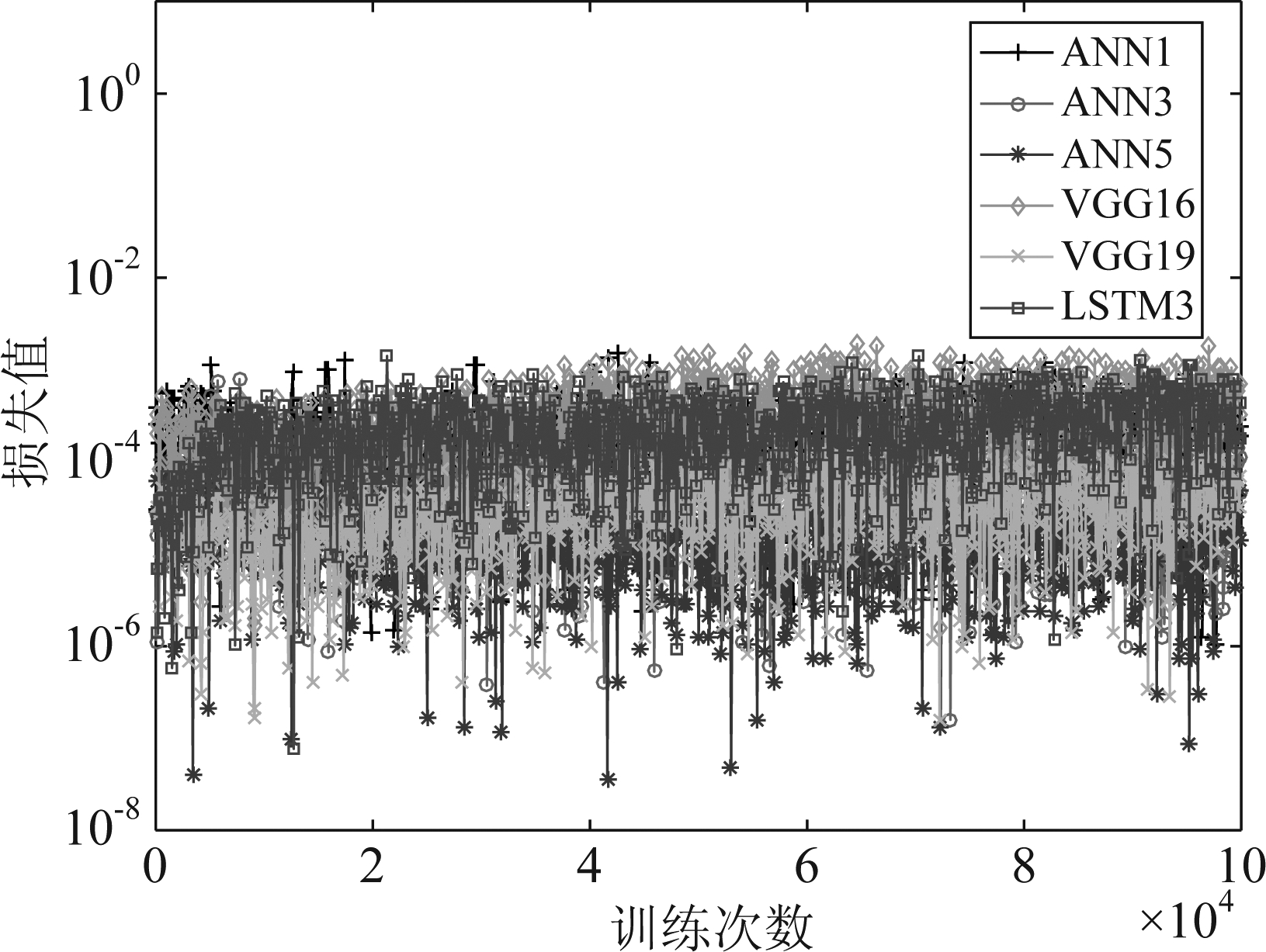
图8 不同网络结构的梯度值对比
Fig.8 Gradient value comparison of different network structures
3.7 LSTM网络在不同机场应用的对比
前面小节利用亚特兰大机场的实际运行数据对机场延误预测模型进行了讨论,并确定了模型最佳的超参数设置,下面将对LSTM网络在不同机场应用的普适性进行验证。表9给出了4个代表性机场的延误预测准确率,分别是亚特兰大机场(ATL)、洛杉矶机场(LAX)、肯尼迪机场(JFK)和拉瓜迪亚机场(LGA)。根据美国机场的吞吐量统计,亚特兰大机场位居第一,洛杉矶机场紧随其后,肯尼迪机场处于平均水平,而拉瓜迪亚机场则比较靠后。由表9给出的结果可以看出,对于中大型国际机场,本文所提方法均可以达到比较好的预测准确率,其中洛杉矶机场的预测准确率甚至大于亚特兰大机场的结果,但是对于小型机场,由于其原始数据量比较小,网络不能得到训练,拉瓜迪亚机场预测准确率只有89.52%。
表9 LSTM网络应用于不同机场的测试准确率
Tab.9 The test accuracy of LSTM network at different airports

机场名称机场代码测试准确率/%亚特兰大机场ATL94.01洛杉矶机场LAX94.21肯尼迪机场JFK93.89拉瓜迪亚机场LGA89.52
4 结论
本文创新性提出一种基于混合编码和长短时记忆网络的机场延误预测方法,通过实验结果分析,根据数据特征取值的不同特点针对性编码,同时利用LSTM网络来学习机场延误数据的时间依赖关系,可使模型的物理含义更加符合机场延误事件特点,提高预测准确率,可进一步优化空管、航空公司等部门的决策。下一步将针对深层LSTM网络的梯度消失问题,继续探索LSTM网络在航班延误预测问题中的应用,同时争取与国内空管部门达成合作,对我国民航具体情况进行分析研究。
[1] 中国民用航空局. 2017年全国民航航班运行效率报告[OL]. http:∥www.caac.gov.cn/XWZX/MHYW/201803/P020180329429997641224.pdf.2018.3.
CACC. 2017 National civil aviation flight operation efficieucy report[OL]. http:∥www.caac.gov.cn/XWZX/MHYW/201803/P020180329429997641224.pdf.2018.3.(in Chinese)
[2] 吴薇薇, 孟亭婷, 张皓瑜. 基于机场延误预测的航班计划优化研究[J]. 交通运输系统工程与信息, 2016, 16(6): 189-195.
Wu Weiwei, Meng Tingting, Zhang Haoyu. Flight plan optimization based on airport delay prediction[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(6): 189-195.(in Chinese)
[3] Nayak N, Zhang Y. Estimation and comparison of impact of single airport delay on national airspace system with multivariate simultaneous models[J]. Transportation Research Record, 2011, 2011(2206): 52- 60.
[4] Eads G, Kiefer M, Mehndiratta S. Short-term delay mitigation strategies for san francisco international airport[J]. Transportation Research Record Journal of the Transportation Research Board, 2001, 1744(1): 44-51.
[5] 韩淑敏. 机场运行可预测性分析与优化[D]. 天津:中国民航大学, 2016.
Han Shumin. Analysis and optimization of the airport operational predictability[D]. Tianjing: Civil Aviation University of China, 2016.(in Chinese)
[6] 罗谦, 张永辉, 程华, 等. 基于航空信息网络的枢纽机场航班延误预测模型[J]. 系统工程理论与实践, 2014, 34(S1): 143-150.
Luo Qian, Zhang Yonghui, Cheng Hua, et al. Study on flight delay prediction model based on flight networks[J]. Systems Engineering-Theory & Practice, 2014, 34(S1): 143-150.(in Chinese)
[7] Deutschmann A. Prediction of airport delays based on non-linear considerations of airport systems[C]∥The 28th International Congress of the Aeronautical Sciences. Brisbane: ICAS, 2012: 1-5.
[8] 徐涛, 丁建立, 顾彬, 等. 基于增量式排列支持向量机的机场航班延误预警[J]. 航空学报, 2009, 30(7): 1256-1263.
Xu Tao, Ding Jianli, Gu Bin, et al. Forecast warning level of flight delays based on incremental ranking support vector machine[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1256-1263.(in Chinese)
[9] 张静, 徐肖豪, 王飞, 等. 基于模糊线性回归模型的机场延误性能评估[J]. 交通运输工程学报, 2010, 10(4): 109-114.
Zhang Jing, Xu Xiaohao, Wang Fei, et al. Airport delay performance evaluation based on fuzzy linear regression model[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 109-114.(in Chinese)
[10] Mukherjee A, Grabbe S, Sridhar B. Predicting ground delay program at an airport based on meteorological conditions[C]∥The 14th AIAA Aviation Technology, Integration, and Operations Conference. Texas: AIAA, 2014: 2014-2713.
[11] 郭野晨风, 李杰, 胡明华, 等. 基于简化WITI指标的机场延误预测方法[J]. 交通运输系统工程与信息, 2017, 17(5): 207-213.
Guo Yechenfeng, Li Jie, Hu Minghua, et al. Airport delay prediction method based on simplified WITI index[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(5): 207-213.(in Chinese)
[12] 吴仁彪, 李佳怡, 屈景怡. 融合气象数据的并行化航班延误预测模型[J]. 信号处理, 2018, 34(5): 505-512.
Wu Renbiao, Li Jiayi, Qu Jingyi. Parallel flight delay prediction model based on fusion of meteorological data[J]. Journal of Signal Processing, 2018, 34(5): 505-512.(in Chinese)
[13] Noboru T, Ryosuke K, Akihide S, et al. Prediction of delay due to air traffic control by machine learning[C]∥AIAA Modeling and Simulation Technologies Conference, 2017: 191-199.
[14] Baspinar B, Ure N K, Koyuncu E, et al. Analysis of delay characteristics of european air traffic through a data-driven airport-centric queuing network model[J]. IFAC-PapersOnLine, 2016, 49(3): 359-364.
[15] Kim Y J, Choi S, Briceno S, et al. A deep learning approach to flight delay prediction[C]∥IEEE. 2016 IEEE /AIAA 35th Digital Avionics Systems Conference. New York: IEEE, 2016: 67-72.
[16] Khanmohammadi S, Tutun S, Kucuk Y. A new multilevel input layer artificial neural network for predicting flight delays at JFK airport[J]. Procedia Computer Science, 2016, 95: 237-244.
[17] 吴仁彪, 李佳怡, 屈景怡. 基于双通道卷积神经网络的航班延误预测模型[J]. 计算机应用, 2018, 38(7): 2100-2112.
Wu Renbiao, Li Jiayi, Qu Jingyi. Flight delay prediction based on dual-channel convolutional neyral networks[J]. Journal of Computer Applications, 2018, 38(7): 2100-2112.(in Chinese)
[18] Hochreiter S, Schmmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[19] Micci-barreca D. A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems[J]. ACM SIGKDD Explorations Newsletter, 2001, 3(1): 27-32.
[20] Tsoi C A, Shaohua T. Recurrent neural networks: a constructive algorithm and its properties[J]. Neuro Computing, 1997, 15(3- 4): 309-326.
[21] 中华人民共和国交通运输部. CCAR300—2016, 航班正常管理规定[S]. 北京: 中华人民共和国交通运输部, 2016.
Ministry of Transport of the People’s Republic. CCAR300—2016, Normal flight regulations[S]. Beijing: Ministry of Transport of the People’s Republic, 2016.(in Chinese)
[22] Duan K, Keerthi S S, Chu W, et al. Multi-category classification by soft-max combination of binary classifiers[C]∥Proceedings of the International Workshop on Multiple Classifier Systems. Berlin: Springer-verlag, 2003: 125-134.
[23] Simonyan K, Zisserman A. Vary deep convolutional networks for large-scale image recognition[EB/OL].[2015- 4-10]. https:∥arxiv.org/abs/1409.1556.pdf.


