1 引言
晴空湍流(clear air turbulence,CAT)是威胁航空安全的一种极端危险性气象目标,因其不伴有明显的天气现象且尺度较小,雷达回波较弱,常规机载气象雷达难以探测,对飞行安全威胁极大[1]。当飞机误入晴空湍流时,会引起飞机颠簸,严重影响旅客的乘机舒适度,剧烈颠簸甚至造成人员受伤和巨大经济损失[2]。据报道,2017年5月1日俄罗斯航空从莫斯科飞往曼谷航班途中发生剧烈晴空颠簸,导致27人受伤[3]。最新研究表明,随着全球气候变化引起的二氧化碳浓度增加,到2050年跨大西洋冬季中高强度的晴空湍流发生频率将提高40%～170%[4-5]。
对于民航飞机,根据国际民航界统一标准,速度谱宽大于5 m/s的气象目标为湍流[6]。根据这一标准,机载气象雷达可依据气象目标回波的谱宽来检测湍流,通过估计的目标回波谱宽与这一门限相比即可实现。本质上说,机载气象雷达通过对回波进行多普勒处理来探测湍流,即估计回波的一阶和二阶谱矩(平均多普勒频率和谱宽)。常规的多普勒处理方法为脉冲对处理(Pulse Pair Processing,PPP)[7-8],PPP复杂度低,能够满足机载气象雷达检测目标的实时性,但是它仅适用于高信噪比的情况[9]。对于含水量很小的CAT,由于回波信噪比低,利用PPP法估计谱宽时误差较大,因而不再适用。
目前,有些地基多普勒雷达已经具备CAT探测能力。WSR 88D雷达是美国建设的新一代地基天气雷达网的重要组成部分,其采用的VCP31/VCP32两种晴空观测模式主要通过发射宽脉冲和降低雷达采样时的天线转速,增加样本积累数来提高雷达对弱回波或晴空回波的探测能力[10-11]。由于载机平台的高速运动,该方法不适用于机载气象雷达。为有效检测CAT,机载气象雷达可通过采用相控阵体制增加积累脉冲数来有效提升回波信噪比[12]。相控阵雷达采用多个天线接收回波信号,相对于传统的单天线雷达,其接收的回波信号中包含目标空域信息,可通过空时积累改善回波信噪比[13]。文献[14]提出一种基于最优空时自适应处理方法的低空风切变风速估计方法,在信噪比低时可有效估计风场速度。但由于增加空间维采样,最优空时自适应处理方法中协方差矩阵维数较大,导致算法运算量较大,实际应用中受限。
在低信噪比条件下,本文引入空时体制,提出了一种基于降秩多级维纳滤波器(Reduced-Rank Multistage Wiener Filter, RR-MWF)[15]的回波谱矩估计方法。RR-MWF是一种有效的降维空时自适应处理方法,能降低计算复杂度。传统多级维纳滤波算法只适用于常规点目标,针对分布式湍流目标,首先将算法推广,即构建适用于分布式目标的空时导向矢量,然后在此基础上构造降秩变换矩阵和标量维纳滤波器。最后,利用最小均方误差准则求解适用于分布式气象目标的自适应RR-MWF权矢量来处理回波信号,从而进行噪声抑制和信号匹配,估计谱矩。另外,还给出了快速算法,进一步降低运算量。仿真实验分析证明,所提方法能有效估计低信噪比的晴空湍流回波谱宽,实现CAT检测。
2 信号模型
图1给出了机载相控阵气象雷达探测CAT的示意图,天线阵列等效为均匀线阵。当检测湍流时,首先通过天线阵列接收气象目标的回波,继而对接收的空时二维信号进行多普勒处理,获取气象目标的谱宽信息。首先,给出机载相控阵雷达的接收信号模型。
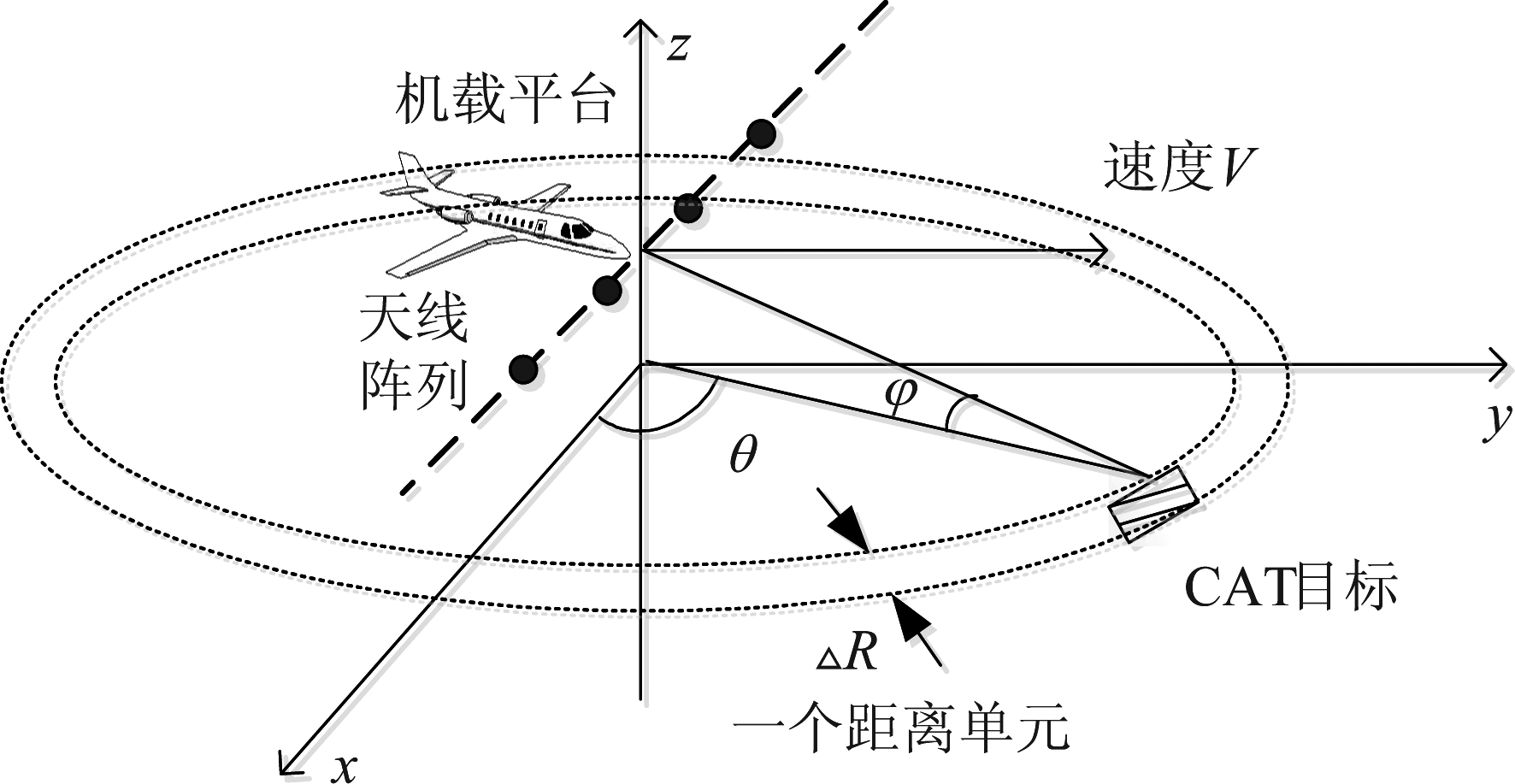
图1 机载相控阵气象雷达探测CAT
Fig.1 Schematic of CAT detection by airborne phased array weather radar
假设飞机以水平匀速V直线飞行,N元均匀线阵沿航向垂直方向放置,阵元间隔为d,雷达发射信号波长为λ,脉冲重复频率为fr,一个相干处理时间内脉冲数为K,θ和φ分别是天线波束指向的方位角和俯仰角。
晴空湍流属于分布式目标,由大量的气象粒子组成。当被电磁波照射时,在一个距离单元内分布着的大量散射点都会反射电磁波,各散射点的回波信号叠加在一起形成了该距离单元的雷达回波。用s(n,k)表示第n个阵元第k个脉冲对一个距离单元内气象目标的空时二维采样数据[16],即
(1)
其中
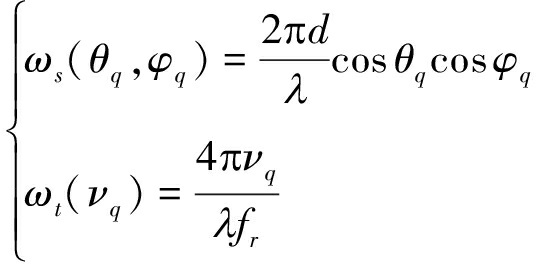
(2)
式(1)中Q表示波束范围内的气象目标散射点个数,Aq表示第q个散射粒子回波信号的幅度,Rq表示第q个散射粒子与雷达之间的斜距,θq,φq,νq分别表示第q个散射点的方位角、俯仰角和其相对飞机的径向速度,ωs(θq,φq)、ωt(νq)分别表示第q个散射粒子的空间角频率和时间角频率。文献[17]表明气象回波信号的功率谱近似服从高斯分布,根据多普勒频率与速度的关系可得散射点的速度分布亦为高斯分布。在后续的仿真实验中,假设某距离单元的气象粒子平均径向速度为ν0,多普勒速度谱宽为σν0时,可通过高斯随机信号的生成方法仿真得到一个距离单元内Q个散射点的速度νq。则一个距离单元中晴空湍流回波的阵列形式可写为[16]
(3)
由于检测CAT时机载气象雷达处于高空平视状态,可不考虑地杂波的影响[18],则雷达回波信号包括湍流回波信号和噪声。用X表示一个距离单元内雷达回波信号,用n表示加性高斯白噪声,则
X=S+n
(4)
某距离单元的雷达回波信号X可表示为[16]
(5)
3 利用降秩多级维纳滤波器的回波谱矩估计方法
最优空时处理器直接处理接收的空时二维数据时计算量大[16],为了降低计算量,采用降秩多级维纳滤波器估计谱矩。
3.1 分布式气象目标的空时导向矢量
在雷达信号处理中,一般需要构建目标的参数化模型以实现后续的匹配滤波。传统多级维纳滤波算法只适用于常规点目标,由于气象目标属于分布式目标,所以需要将算法推广。这里构建适用于分布式目标的空时导向矢量,准确描述其空域和时域分布特性。某距离单元适用于分布式目标的空时导向矢量可表示为[16]
U=Us(θ,φ)N×1⊗Ut(fd,σf)K×1
(6)
其中, fd为归一化平均多普勒频率,σf表示回波的归一化多普勒谱宽,⊗表示Kronecker积。Us(θ,φ)N×1为空间导向矢量,Ut(fd,σf)K×1为时间导向矢量,并且可以分别表示为[19]
Us(θ,φ)N×1=us(θ,φ)⊙gs(θ,φ)
(7)
Ut(fd,σf)K×1=ut(fd)⊙gt(σf)
(8)
其中,⊙为Hadamard积,
(9)
表示该距离单元中,天线波束指向上点目标的空间导向矢量,
(10)
为信号的角度扩展函数[20],其中,
表示θ方向上的角度扩展,σφ表示φ方向上的角度扩展,
(11)
表示多普勒频率为fd的点目标的时间导向矢量,
(12)
表示多普勒频率扩展函数。
3.2 基本原理
多级维纳滤波器(Multistage Wiener Filter, MWF)是维纳滤波器的一种多级等效实现形式,其基本原理是将输入信号进行多级分解,再进行多级标量维纳滤波,最后输出误差信号[15]。将MWF在r级分解处截断,得到秩r的RR-MWF,其原理如图2[13]。
当用RR-MWF估计目标回波的谱矩时,图2中X为机载相控阵雷达接收的空时二维回波,U是根据3.1节构造的适用于分布式目标的空时导向矢量,B是阻塞矩阵(即BU=0),d0是初始期望信号,hi是Xi-1和di-1之间的归一化互相关函数,Bi是hi的零空间,Xi-1、di和wi分别是第i级的输入信号、参考信号和维纳权矢量[15]。则可根据降秩维纳滤波器原理[15,21]得出此时自适应输出权矢量为
WRR-MWF=U-BHTrWd=
(13)
其中,Tr是等效降秩变换矩阵,Wd后向维纳滤波器,RX=E[XXH]为雷达回波信号的协方差矩阵。
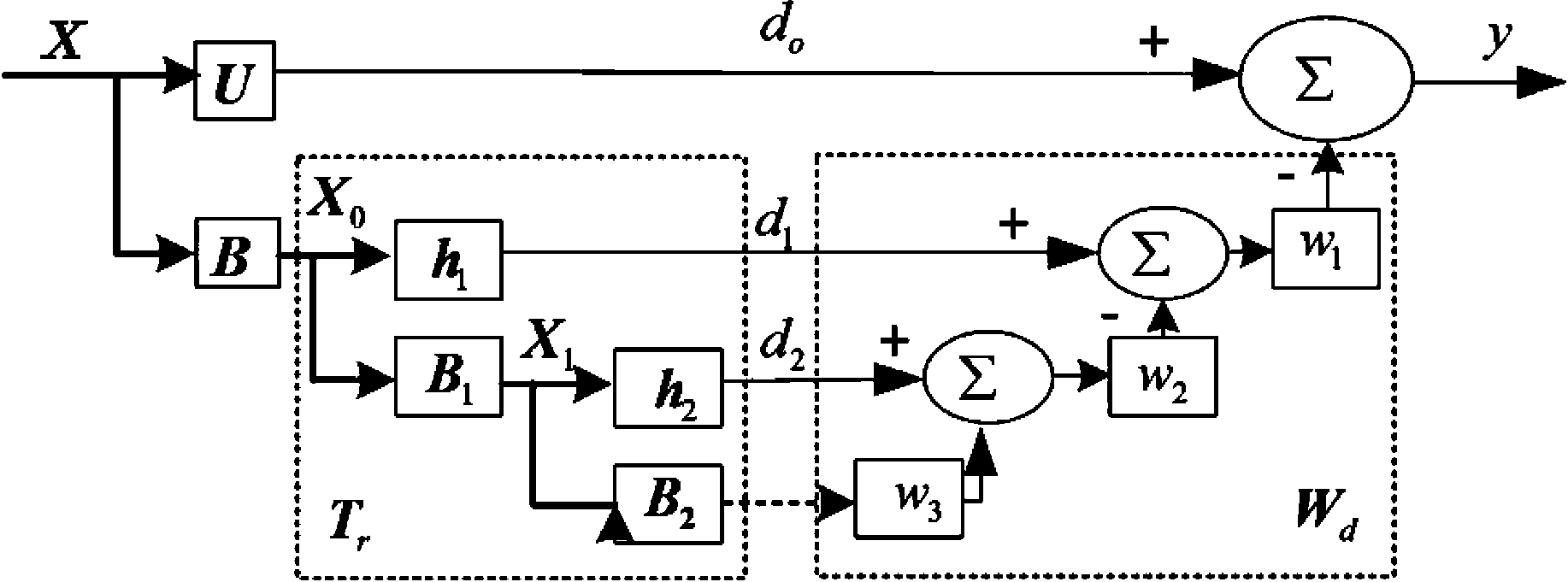
图2 降秩多级维纳滤波器
Fig.2 Reduced-Rank Multistage Wiener Filter model
根据式(13)可以将降秩多级维纳滤波器简化为降秩多级维纳滤波器等效形式,如图3。
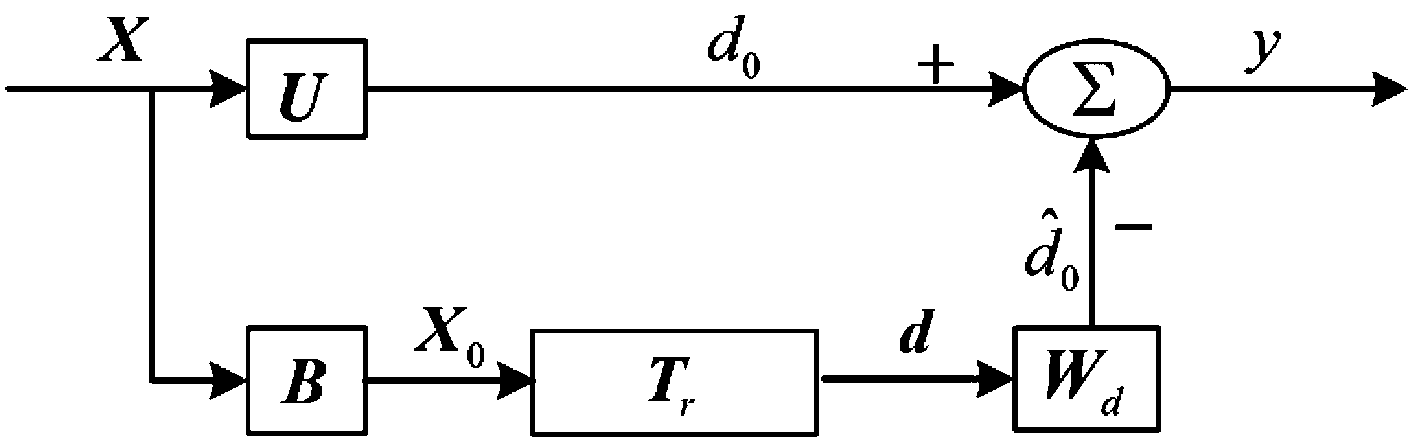
图3 RR-MWF等效形式
Fig.3 The equivalent RR-MWF model
首先对接收的空时数据X进行预处理。上支路中,当重构的空时导向矢量U所用平均多普勒频率、多普勒谱宽与气象目标的平均多普勒频率、多普勒谱宽相匹配时,上支路中得到的初始期望信号含有噪声和气象目标回波。而下支路中,空时二维数据经过阻塞矩阵B阻塞了气象目标回波,X0中只含有噪声[15],将d0和X0送入降秩多级维纳滤波器进行自适应滤波。
降秩多级维纳滤波器中,首先,用前向分解滤波器构成的降秩变换矩阵Tr对X0进行降秩处理,然后用后向维纳滤波器Wd进行标量维纳滤波。根据多级维纳滤波器的原理,Wd使得
逼近d0中与X0相关的信号分量,因此实现自适应干扰对消,可以得到噪声抑制后的输出信号y,即气象目标回波。可将y称为估计的代价函数,并表示为
(14)
若选择能准确描述气象目标的空时导向矢量U,上下两支路的噪声互相抵消,气象目标信号有效输出,则使得y取最大值。此时,用于重构气象目标的空时导向矢量U所假设的平均多普勒频率和谱宽即为该距离单元回波的平均多普勒频率和谱宽估计值,即
(15)
如图4,给出了代价函数在不同(fd,σf)处的取值,可以看出在假设的归一化平均多普勒频率和归一化多普勒谱宽处(fd 0=0,σf 0=0.0286),代价函数达到最大值。由此可见,对回波信号所有可能的平均多普勒频率和多普勒谱宽区间进行二维搜索,根据式(15)即可估计出待检测距离单元回波的多普勒谱宽。
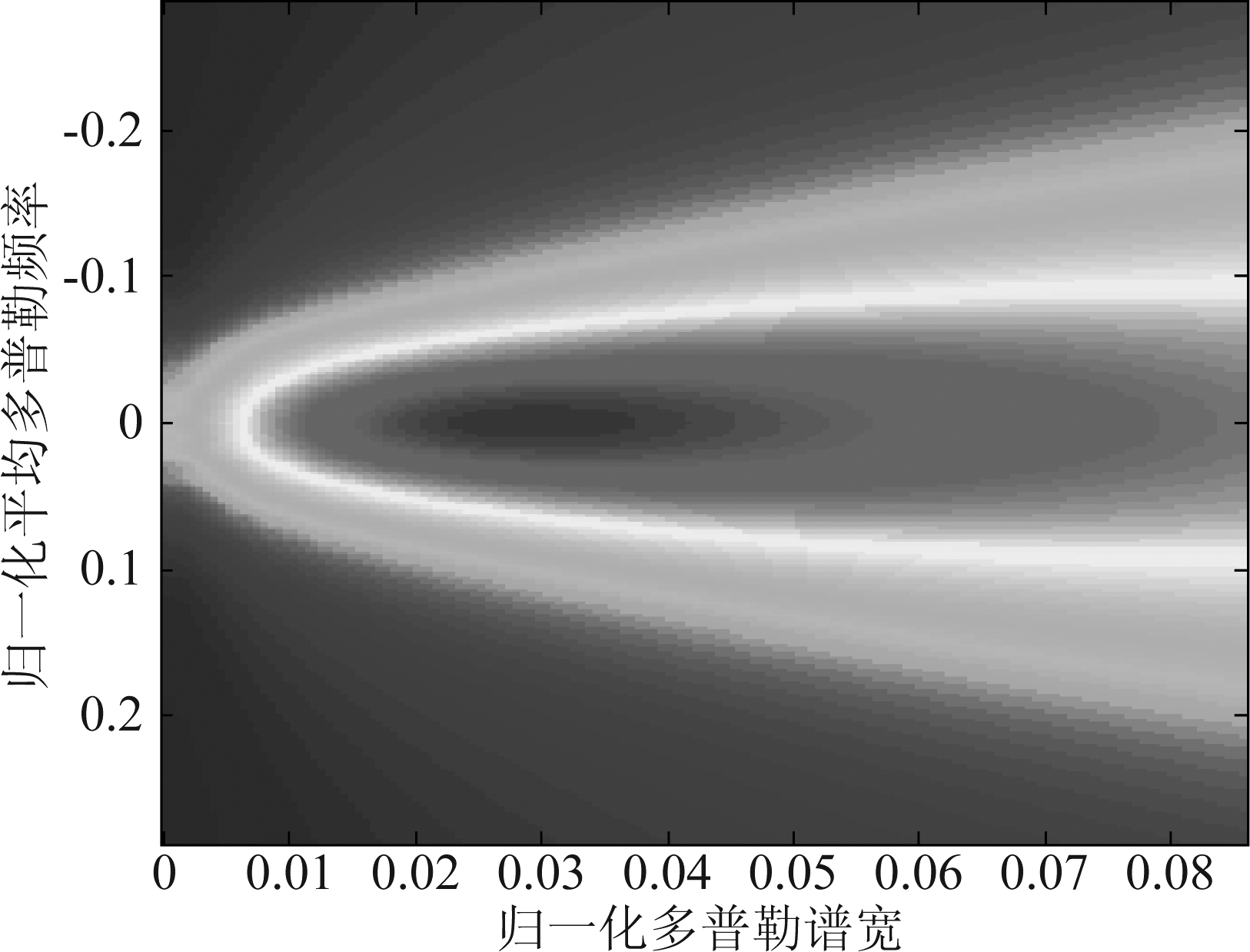
图4 基于RR-MWF谱矩估计的代价函数(fd 0=0,σf 0=0.0286)
Fig.4 The cost function of RR-MWF estimator (fd 0=0,σf 0=0.0286)
3.3 估计步骤
综上所述可得到算法的实现步骤:
步骤1 设定气象目标可能的平均多普勒频率和谱宽,由式(6)构造气象目标对应的空时导向矢量;
步骤2 由式(13)计算秩r降秩多级维纳滤波器权矢量;
步骤3 根据式(14)利用自适应输出权矢量处理空时二维回波数据得出代价函数y;
步骤4 改变空时导向矢量U中的平均多普勒频率和谱宽,重复步骤1～3,二维搜索y的峰值,此时空时导向矢量中设置的平均多普勒频率和谱宽即为所求。
3.4 算法复杂度分析
设降秩多级维纳维纳滤波器的秩为r,接收的空时数据来自某一距离单元。则RR-MWF前向递推中,Xi+1=Bi+1Xi的总计算量为
的总计算量为r(NK-(r-1)/2),后向递推中都是标量运算。由此可得,RR-MWF的计算复杂度为O((NK)2)。而对于基于最优空时自适应处理的谱宽估计方法,计算最优权矢量需要对NK×NK的协方差矩阵求逆,计算复杂度为O((NK)3),当数据维数大时计算量非常大不适用于工程应用。可见,基于RR-MWF的谱宽估计方法运算量明显降低。
4 实验结果与分析
4.1 快速算法
为了进一步简化算法的复杂度,首先仿真分析了代价函数的收敛情况。验证发现平均多普勒频率和谱宽是不耦合的,因此可将二维搜索简化为两个一维搜索实现,进一步降低运算量。
图5是在设定不同谱宽条件时,代价函数随平均多普勒频率的变化曲线,其中的每条曲线都在fd=0处达到峰值,表明任意设定多普勒谱宽都不会影响准确估计回波的平均多普勒频率。图6是在设定平均多普勒频率时,代价函数随谱宽的变化曲线,其中只有当设定fd=0时,代价函数在真实值σf=0.0286处达到峰值。以上实验表明,平均多普勒频率与多普勒谱宽是不耦合的,可以先估计平均多普勒频率,再估计谱宽。
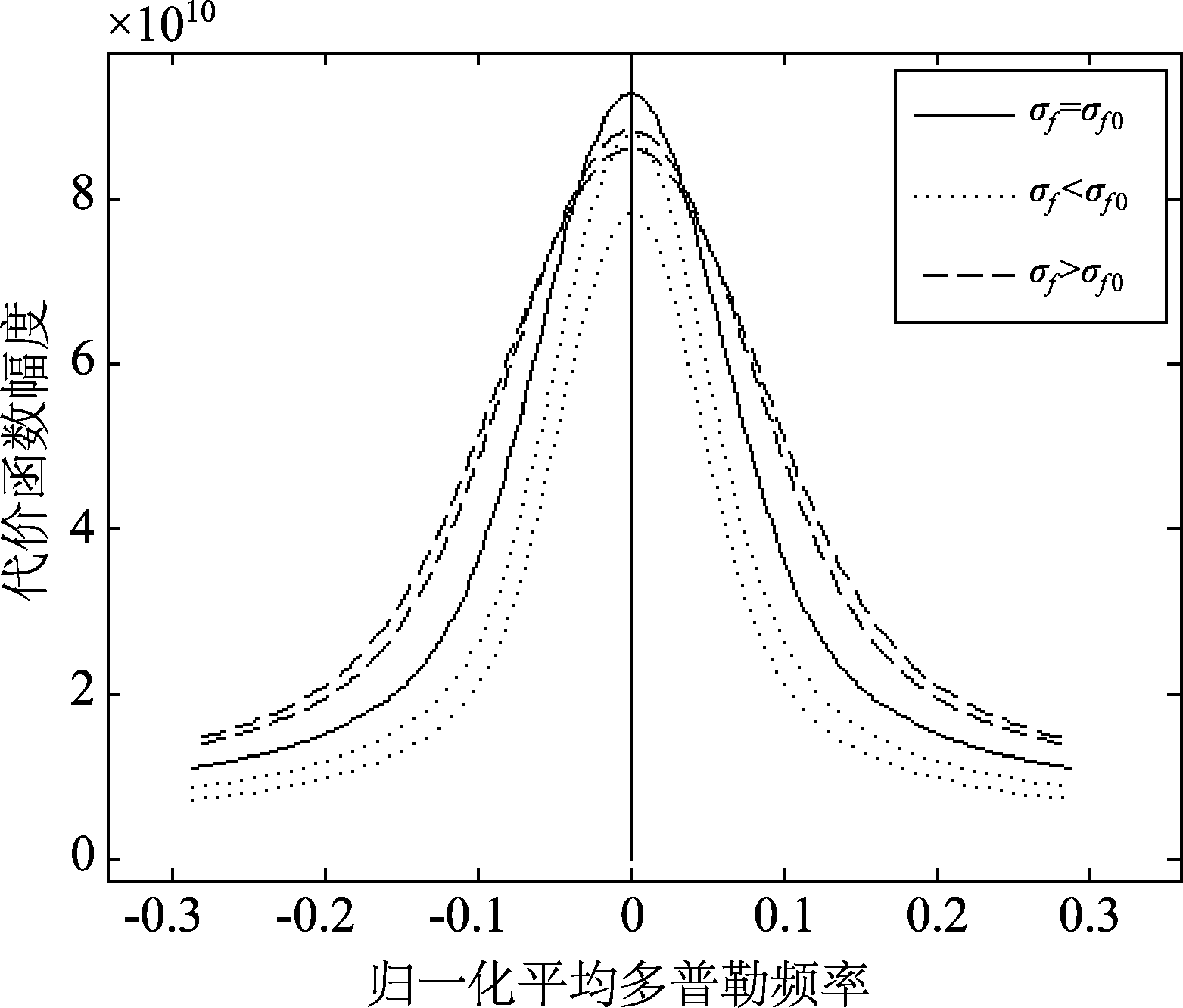
图5 不同平均多普勒频率的代价函数值(σf 0=0.0286)
Fig.5 The values of the cost function at different mean Doppler frequencies (σf 0=0.0286)
利用这一特点,即可以先假设谱宽为某个任意合理常数,对平均多普勒频率进行一维搜索,得出平均多普勒频率估计值
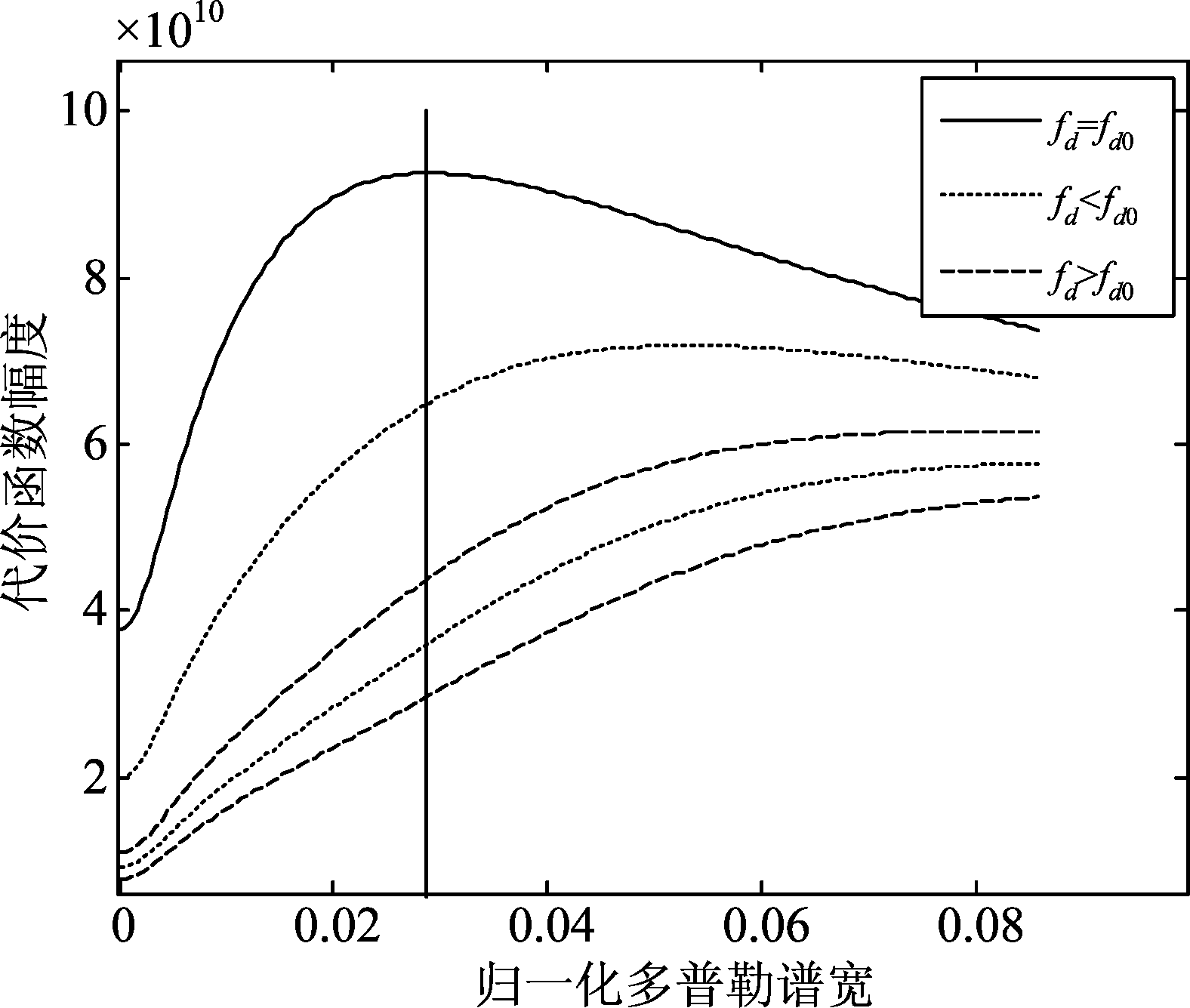
图6 不同谱宽的代价函数值(fd 0=0)
Fig.6 The values of the cost function at different Doppler spectrum widths (fd 0=0)
(16)
得出
后,再对多普勒谱宽进行一维搜索
(17)
即可估计出回波谱宽,从而将式(16)和式(17)替换式(15)搜索代价函数峰值来估计回波谱矩,进一步降低算法的运算量。
4.2 仿真结果分析
假设湍流分布于飞机前方7500～16500 m范围内,其他仿真参数设定情况见表1。
表1 仿真参数
Tab.1 Simulation parameters
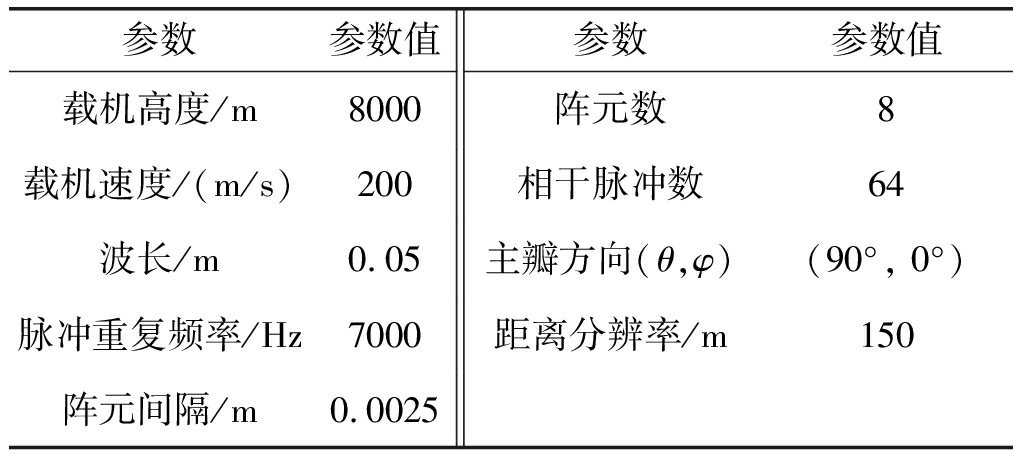
参数参数值参数参数值载机高度/m8000阵元数8载机速度/(m/s)200相干脉冲数64波长/m0.05主瓣方向(θ,φ)(90°, 0°)脉冲重复频率/Hz7000距离分辨率/m150阵元间隔/m0.0025
为分析基于降秩多级维纳滤波器谱宽估计算法的性能,不失一般性,设置湍流的平均多普勒频率fd 0=0,多级维纳滤波的分解级数为8,按照上述的快速算法对雷达回波进行谱宽估计。
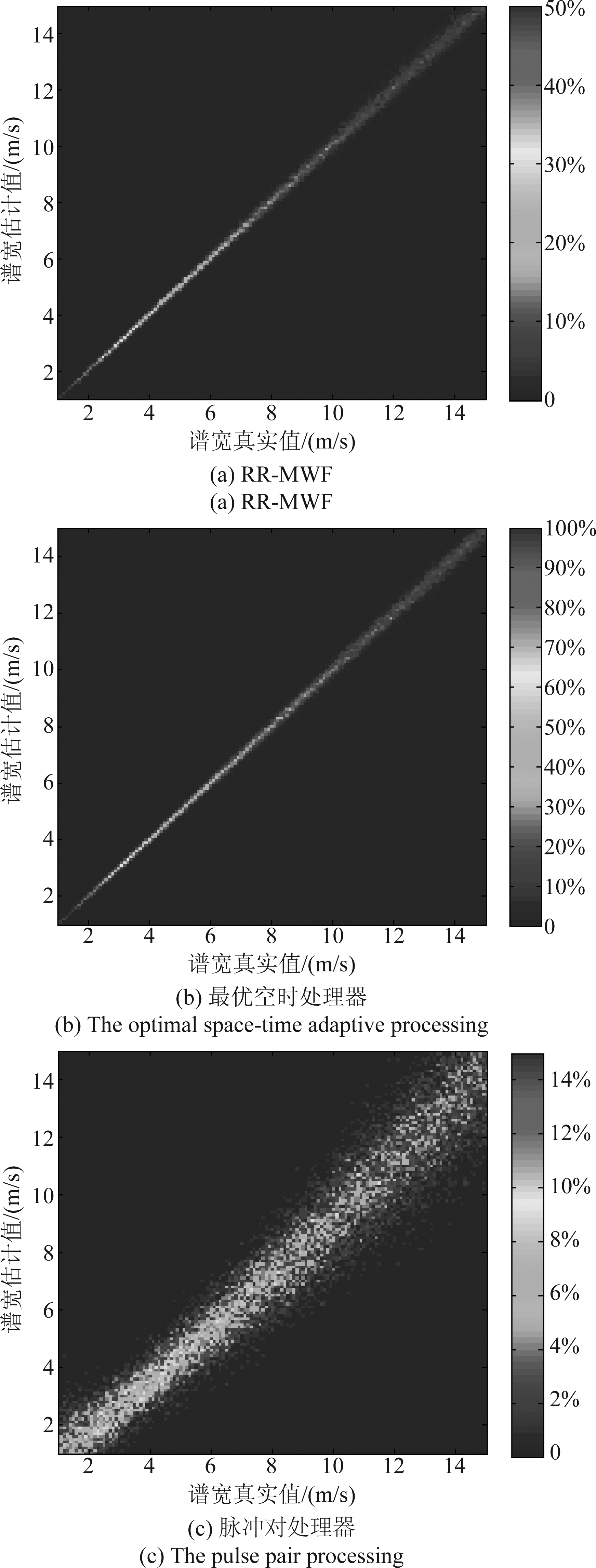
图7 三种算法的谱宽估计结果(SNR=20 dB)
Fig.7 The results of spectral width estimation for the three methods (SNR=20 dB)
首先,通过估计值的分布直观对比分析本文方法和PPP法。假设信噪比为20 dB,设置不同的多普勒谱宽值,每种情况都进行100次Monte Carlo实验,统计每种情况下估计值的分布情况,如图7所示,(a)、(b)、(c)分别为利用本文方法、最优空时处理器和PPP法估计的结果。图7中,横坐标是假设的谱宽值,纵坐标是谱宽估计值,用0%到100%表示估计值在各个取值范围内所占百分比。根据图示结果可知,利用PPP法估计谱宽的估计值分布分散,即估计偏差较大;而基于RR-MWF和最优空时处理器的谱矩估计结果相近且估计值分布集中在真实值附近,即估计偏差小,准确度高。可见,基于空时自适应处理的方法性能优于PPP法。
为进一步进行性能对比,下面通过统计不同信噪比时的估计误差进行分析。设湍流目标归一化多普勒谱宽σf 0=0.0286,比较了在不同信噪比情况下,三种算法谱宽估计的均方误差,如图8所示,图中均方误差转化为分贝值表示。由图可见,当信噪比低时RR-MWF估计器和PPP法估计谱宽得出的均方误差相差很大,在信噪比低于10 dB时,RR-MWF估计器性能明显优于PPP,表明了其在低信噪比时的有效性。
随着信噪比增加,RR-MWF估计器和最优空时处理器算法的谱宽估计均方误差下降快,在信噪比低(SNR=5 dB)时,均方误差已经接近平稳值。信噪比较高时,PPP法谱宽估计的均方误差比利用其余两种方法估计的均方误差小,这是由于搜索步长引起的,而PPP法无需搜索。
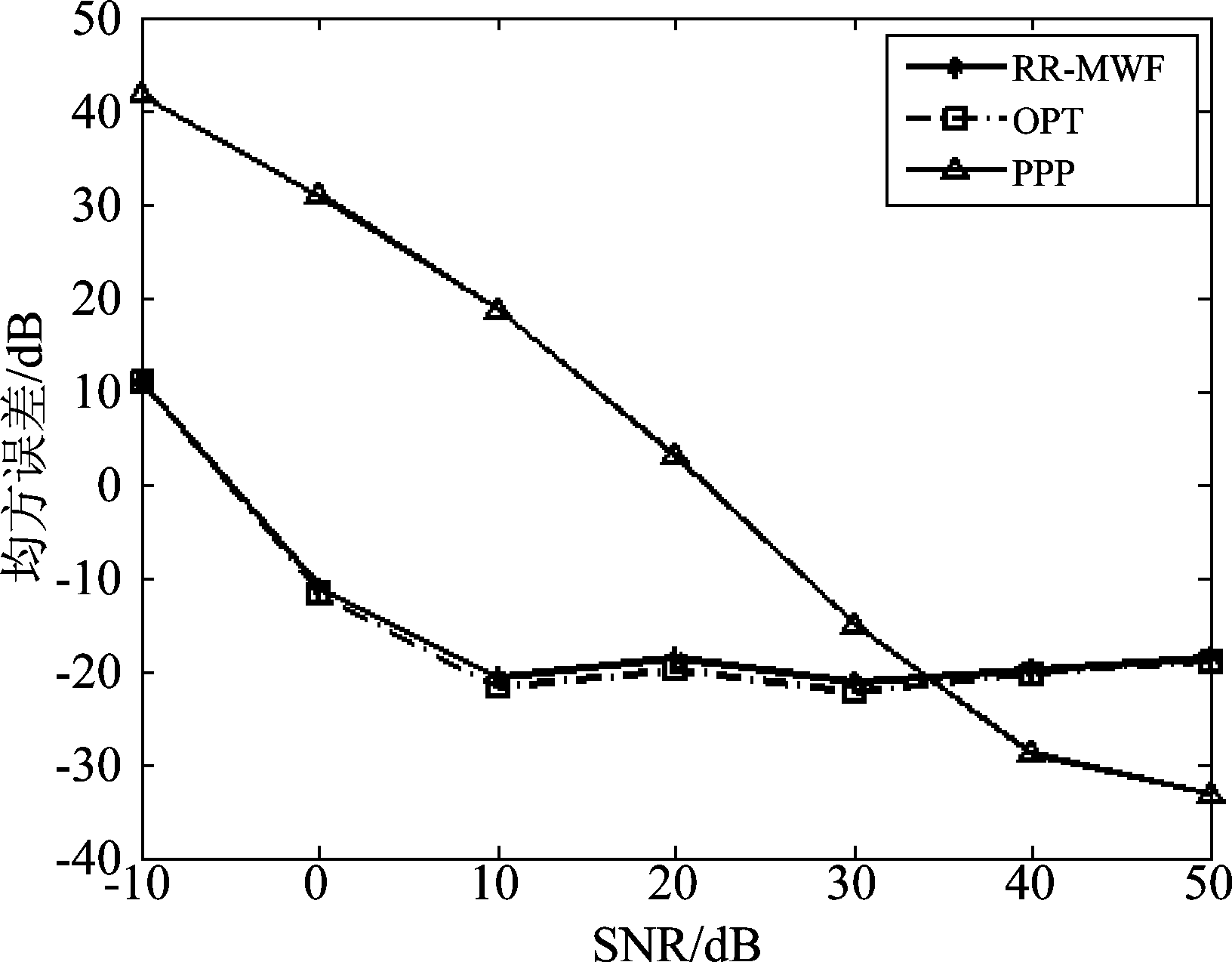
图8 三种算法的多普勒谱宽估计均方误差
Fig.8 The MSEs of spectrum width estimation for the three methods
如图9所示,RR-MWF算法估计的均方误差仅仅比最优处理器算法的低2 dB左右,可见两种算法之间的性能相近,说明RR-MWF算法在运算量降低的同时,可获得准最优的性能。以上仿真实验和运算量分析表明,本文方法能有效估计低信噪比下的气象目标的雷达回波谱宽,且运算量相对最优空时处理大大下降。
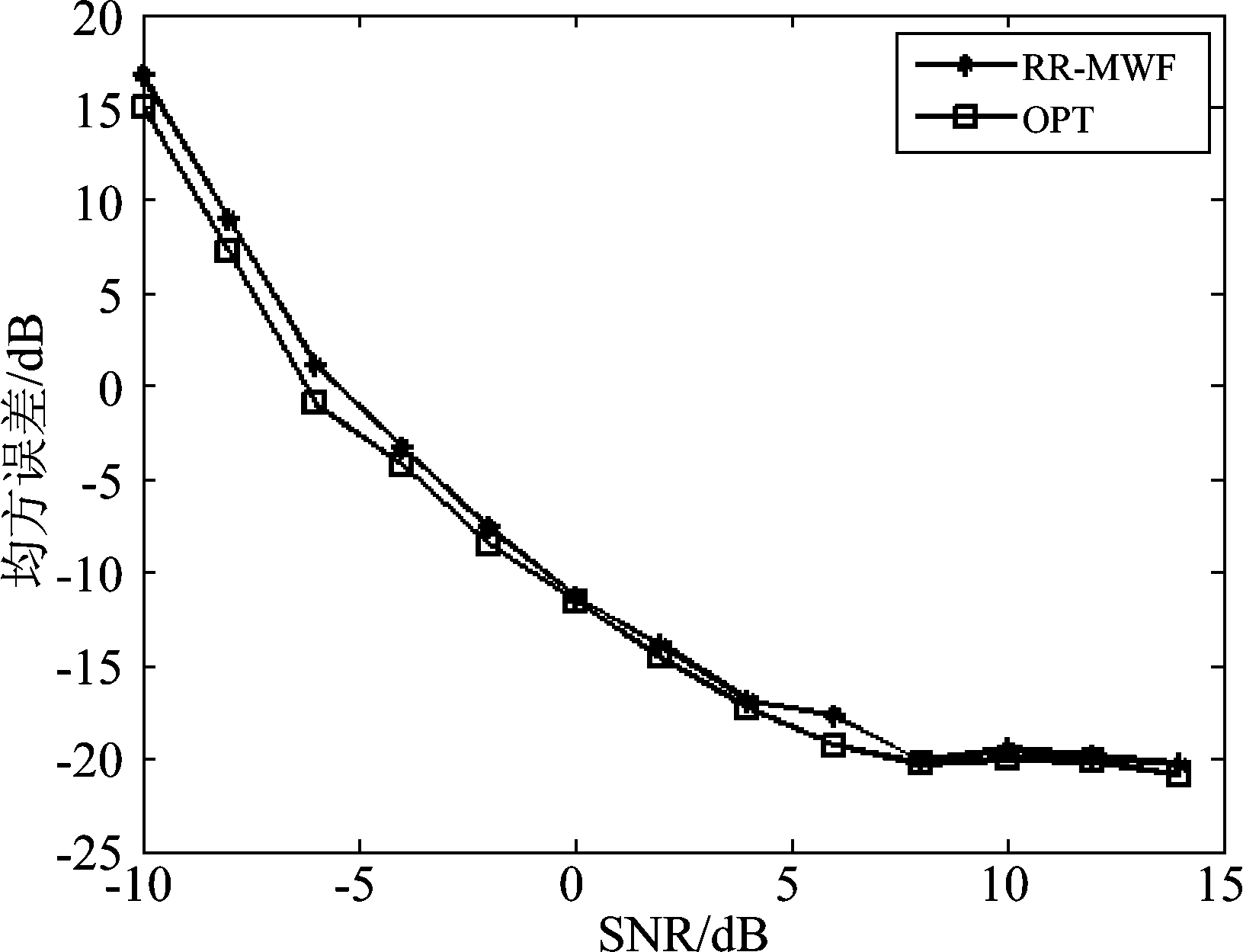
图9 RR-MWF和最优空时处理器的多普勒谱宽估计均方误差
Fig.9 The MSEs of spectrum width estimation for RR-MWF and optimal estimator
5 结论
针对常规机载气象雷达检测晴空湍流时回波信噪比低,在雷达引入空时体制的基础上提出了一种基于RR-MWF的回波谱矩估计方法。所提方法利用空时联合处理提高信噪比,并构造了适用于分布式气象目标的自适应RR-MWF权矢量来处理雷达回波,从而进行噪声抑制和信号匹配,估计谱矩。经过谱矩估计仿真实验得出,可利用平均多普勒频率与多普勒谱宽是不耦合的特点,进一步将二维搜索简化为一维搜索,从而能进一步降低算法的运算量。最后,仿真结果表明降秩多级维纳滤波器与最优空时处理器相比运算量降低,并且可实现准最优性能。在信噪比低于10 dB时,提出的RR-MWF估计器明显优于常规的脉冲对法,体现了低信噪比时的有效性。因此,本文提出的方法可用于机载气象雷达CAT检测。
[1] Storer L N, Williams P D, Joshi M M. Global Response of Clear-Air Turbulence to Climate Change[J]. Geophysical Research Letters, 2017, 44(19): 9976-9984.
[2] 周林, 黄超凡. 近10年晴空湍流的研究进展[J]. 气象科技, 2015, 43(1): 91-96.
Zhou Lin, Huang Chaofan. Advances in Clear Air Turbulence Researches in Last Ten Years[J]. Meteorological Science and Technology, 2015, 43(1): 91-96.(in Chinese)
[3] AeroInside.[Online]. Available: https:∥www.aeroinside.com/item/9477/aeroflot-b773-near-bangkok-on-may-1st-2017-turbulence-injures-36.
[4] Williams P D. Increased Light, Moderate, and Severe Clear-Air Turbulence in Response to Climate Change[J]. Advances in Atmospheric Sciences, 2017, 34(5): 576-586.
[5] Williams D, Joshi M. Intensification of Winter Transatlantic Aviation Turbulence in Response to Climate Change[J]. Nature Climate Change, 2013, 3(7): 644- 648.
[6] Collins R. Collins WXR-2100 MultiScanTM Radar Fully Automatic Weather Radar[J]. Internet Citation, Jan, 2003, 1: 1OPP.
[7] 卢晓光, 吴仁彪. 基于RELAX的气象雷达回波参数化谱矩估计方法[J]. 信号处理, 2011, 27(8): 1250-1253.
Lu Xiaoguang, Wu Renbiao. A Parametric Spectral Moments Estimation Algorithm for Weather Radar Echoes Employing RELAX[J]. Signal Processing, 2011, 27(8): 1250-1253.(in Chinese)
[8] Warde D A, Torres S M. Improved spectrum width estimators for Doppler weather radars[C]∥Proc. 8th Eur. Conf. Radar Meteorol. Hydrol.(ERAD). 2014: 8.
[9] 吴仁彪, 卢晓光, 李海, 等. 机载前视风切变检测气象雷达的研究进展[J]. 数据采集与处理, 2014, 29(4): 496-507.
Wu Renbiao, Lu Xiaoguang, Li Hai, et al. Overview on airborne forward-looking weather radar with windshear detection capability[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 496-507.(in Chinese)
[10] Melnikov V M, Zrni
D S, Doviak R J, et al. Prospects of the WSR- 88D Radar for Cloud Studies[J]. Journal of Applied Meteorology and Climatology, 2011, 50(4): 859- 872.
[11] Miller M A, Johannes V, et al. Detection of Nonprecipitating Clouds with the WSR- 88D: A Theoretical and Experimental Survey of Capabilities and Limitations[J]. Weather and Forecasting, 1998, 13(4): 1046-1062.
[12] Lipor J. MIMO Radar Transceiver Design for High Signal-to-Interference-Plus-Noise Ratio[D]. Doctoral Dissertation, 2013.
[13] 洪玺, 王文杰, 殷勤业. 基于多级维纳滤波器的空时自适应信号处理及其在无线通信系统中的应用[J]. 信号处理, 2017, 33(3): 430- 436.
Hong Xi, Wang Wenjie, Yin Qinye. Multistage Wiener Filter Based Space and Time Adaptive Signal Processing and Its Application in Wireless Communication Systems[J]. Journal of Signal Processing, 2017, 33(3): 430- 436.(in Chinese)
[14] 吴仁彪, 张彪, 李海, 等. 基于空时自适应处理的低空风切变风速估计方法[J]. 电子与信息学报, 2015, 37(3): 631- 636.
Wu Renbiao, Zhang Biao, Li Hai, et al. Speed estimation for low-attitude windshear based on space-time adaptive processing[J]. Journal of Electronics and Information Technology, 2015, 37(3): 631- 636.(in Chinese)
[15] 王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009.
Wang Yongliang, Ding Qianjun, Li Rongfeng. Adaptive Array Processing[M]. Bejing: Tsinghua University Press, 2009.(in Chinese)
[16] 王永良, 彭应宁. 空时自适应信号处理[M]. 北京: 清华大学出版社, 2000.
Wang Yongliang, Peng Yingning. Space-Time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2000.(in Chinese)
[17] 卢晓光. 机载气象雷达信号处理若干关键技术研究[D]. 天津: 天津大学, 2014.
Lu Xiaoguang. Research on Key Techniques of Signal Processing for Airborne Weather Radar[D]. Tianjin: Tianjin University, 2014.
[18] Alitz O J, Moos D P. Vector phase angle change distribution processor[P]. U.S. Patent: 4, 600, 925, 1986-7-15.
[19] Doviak R J, Zrinc D S. Doppler Radar and Weather Observations[M]. 2nd ed. USA: Dover Publications, 2006: 1-100.
[20] Boyer E, Larzabal P, Adnet C. Parametric Spectral Moments Estimation for Wind Profiling Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(8): 1859-1868.
[21] Zhang Ming, Lu Rui, Zhu Shitao, et al. DOA Estimation Based on Reduced-rank Multistage Wiener Filter[J]. Procedia Computer Science, 2017, 107(C): 652- 656.
