1 引言
近年来,无人机、无人艇等新型无人装备取得长足发展,美国海军当前已经可以同时利用多艘高速快艇协同,实施海上“蜂群”攻击,完成作战任务。可以说无人装备的问世在一定程度上创新了海军的作战方式,同时也对现有的预警和防御系统提出了挑战。因此,无人装备的发展对我国专属经济区、沿海边境线、重要港口、重要海面平台(如南海钻井平台)等的安全防御与保护造成了重大威胁,对以无人艇为代表的海上无人装备的监控、预警和防御迫在眉睫。
传统地基平台的雷达受视距限制难以进行大范围的海面区域保护;机载或舰载平台可以实现大范围的海面区域保护,但杂波干扰强、依赖天气并且成本高;星载平台的雷达功能强大但重访时间长、造价昂贵、系统复杂,因此现有的系统难以对专属经济区、沿海边境线、重要港口、重要海面平台进行有效的防护。前向散射雷达(FSR)系统具有结构简单、功耗低等优点,非常利于对海面运动目标进行检测,能够在各种环境中较好地工作(如近海、岛礁、深海钻井平台等),具有较强生存能力。
对FSR空中地面目标的相关研究已经比较成熟,Glaser在1985年通过黑体近似与巴比涅原理对当前前向散射的基本原理进行了论述,为现在的FSR信号建模分析打下了基础[1]。Chapurskiy提出SISAR成像技术,指出了SISAR用于目标成像的可行性以及用于目标识别的潜力[2]。西安电子科技大学对空中目标的信号建模、回波分析及SISAR成像进行了研究并完成了实验验证[3-4]。北京理工大学对基于导航星无源的前向散射雷达目标探测与识别进行了研究[5-6]。此外,北京理工大学还与英国Birmingham大学展开合作,给出了地面运动目标的精确信号模型,并提出了针对地面运动目标的速度及穿越点的位置估计方法[7-8]。
在海面目标FSR研究方面,英国伯明翰大学研究了基于目标的能量谱和多普勒频率以及改进的匹配滤波检测海面运动目标的方法,并对运动接收机下的回波进行了采集分析[9-11]。英国的Daniel采用C波段雷达采集了不同海面目标的回波,证明了对回波进行处理实现目标分类的可行性[12]。总体来说当前对海面FSR的研究较少,没有一个系统的考虑海浪起伏的模型来描述前向散射雷达海面回波信号,没有对FSR海面目标的多径效应进行分析。
本文对海浪起伏及多径干扰的影响进行建模分析,将不同风速下的海浪起伏与海面运动目标前向散射的回波信号模型相结合;同时,根据海面实际情况,给出了多径干扰下的回波信号模型,比较分析了海浪起伏和多径干扰对目标回波信号的影响,给出了仿真结果及分析。
2 FSR海面目标探测信号建模
2.1 考虑海浪影响的信号建模
海浪的起伏主要受风速变化影响,而海面目标的相关参数也会受到这种运动起伏的影响[13]。因此,设计前向散射雷达海面目标运动模型时,需要考虑海浪起伏对回波信号造成的影响[14]。为方便研究,将海浪作为一个平稳随机过程处理,可建模为多个周期与初相不同的余弦波的叠加[15]
(1)
根据线性波动理论,当我们不考虑海面表面的张力影响时,在数值上,波数和角频率的关系应满足如下公式:
代表重力加速度,D代表水深,当波长小于两倍水深的时候,我们可以简化得到
代表第n个余弦波的η(t)为海面有风浪时相对于静止海面的瞬时高度,an代表第n个余弦波的振幅,服从瑞利分布,ωn代表第n个余弦波的角频率,kn代表第n个余弦波的波数,在数值上kn=2π/λn,我们认为φn是在(0,2π)范围内服从均匀分布,x为波点位子,通常取一个固定位置,为了研究方便,可取x=0,t为时间[16]。
下面对低风速时域海面进行模拟,我们选择风速度为7 m/s,也就是轻浪情况下的最大风速,这样有利于后续结论的引出,仿真频段为0.4～3.4 rad/s,频率增量为0.1 rad/s,得到7 m/s风速下海面相对于静止海面的瞬时高度随时间的变化,如下图1所示。
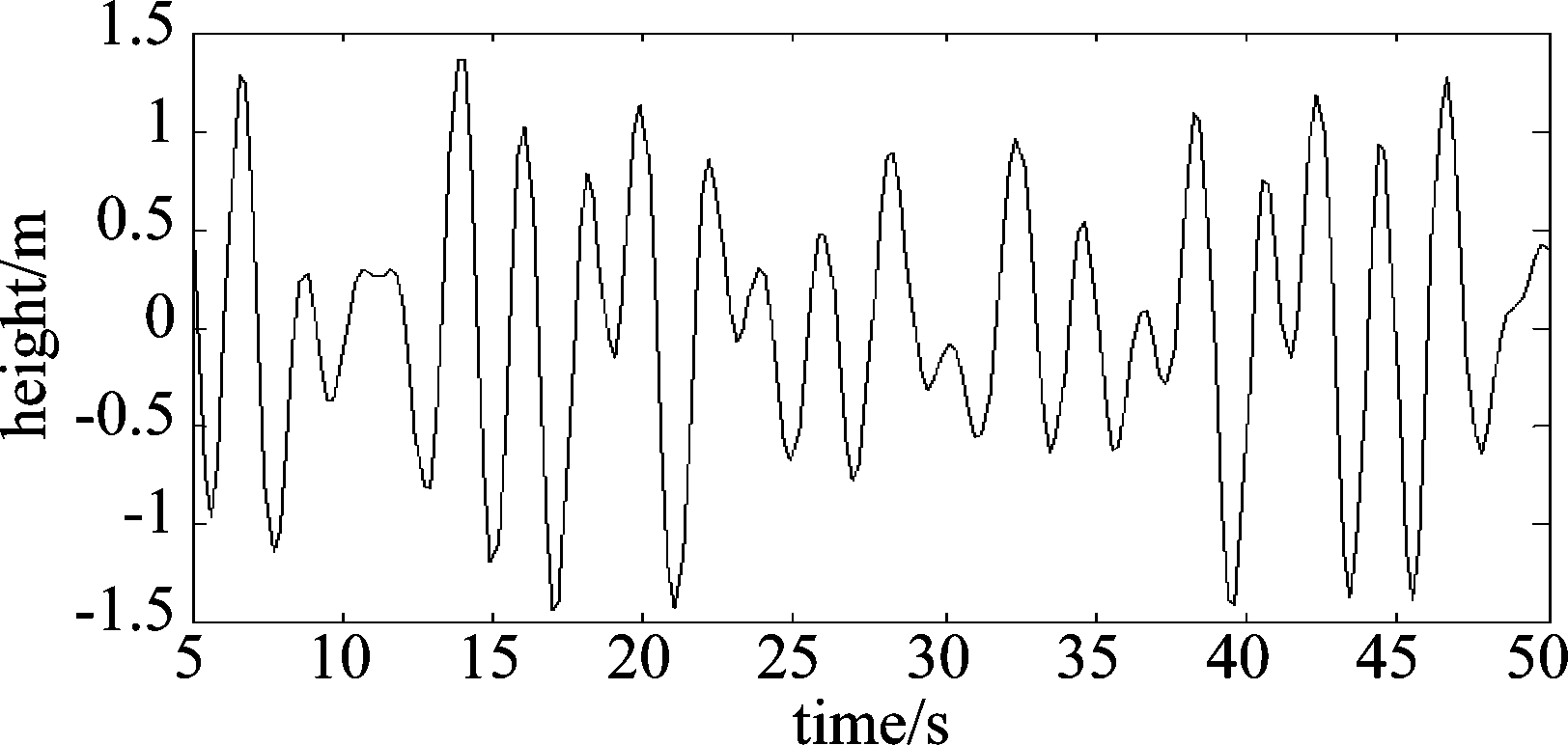
图1 轻浪下海浪高度模拟结果
Fig.1 Simulation results of sea wave height in light waves
图2 海浪模型下FSR系统结构
Fig.2 FSR system structure under sea wave model
得到风速与海浪高度的对应结果,我们就可以将海浪起伏的数学模型代入到传统前向散射信号模型中。如图2所示为前向散射雷达的系统结构,发射机位置T为中心,沿着x、y、z方向延伸建立空间直角坐标系。
R所示为接收机位置,Q为目标穿越基线的位置,φ为目标穿越基线的夹角,dT为发射机到Q点的距离,dR为接收机到Q点的距离,设置P点为运动目标,坐标为(xp,yp,zp),以P点为中心设立局部坐标系,x′,y′,z′轴分别与x,y,z轴平行,rc1,rc2分别为目标到发射机和接收机的距离,αν为目标在发射机方向上的俯仰角,βν为目标在接收机方向上的俯仰角, α和β 为目标在发射机和接收机方向的衍射角。
根据巴比涅原理以及场强分布公式,我们可以将目标的前向散射信号表示为:
(2)
A为发射信号的幅值,k为发射波的个数,设目标上任意一点在以p点为中心的坐标系中坐标为(x′,y′,z′), r1为发射机到目标上任意一点的距离,r2为接收机到目标上任意一点的距离,则r1,r2可以表示为:
(3)
其中rc1,rc2是目标中心点到发射机和接收机之间的距离
xp=ν·t·sin φ,yp=dT+ν·cos φ·t,zp=zp
(4)
目标的衍射角α1,α2被近似表示为目标的方位向观测角αh,βh,近似表示为:
cos α+cos β=cos ανcos αh+cos βνcos βh
≈cos αh+cos βh
(5)
而目标阴影轮廓像的指示函数用εT(x′,z′)来表示:
(6)
代入可得:
(7)
令
在目标航迹固定的情况下,海浪对信号模型的影响主要表现在侧影指示函数εT(x′,z′)的变化,我们可以将海浪的起伏变化代入对
的计算中,那么有
(8)
其中,hmin和hmax分别为目标侧影轮廓的最低点和最高点,于是我们可以得到海浪影响下海面目标前向散射的信号模型:
(9)
2.2 多径干扰下FSR信号建模
首先,照射到海面目标的雷达波由两部分组成,即由远端雷达直接照射到目标上的直接照射波和首先照射到海面然后经海面反射到目标上的雷达波。于是有如图所示下r1+r2,r3+r2,r1+r4,r3+r4四条路径组成的雷达波:雷达-目标-雷达,雷达-海面-目标-雷达,雷达-目标-海面-雷达,雷达-海面-目标-海面-雷达。
图3 多径干扰模型下FSR系统结构
Fig.3 FSR system structure under multipath interference model
事实上,除以上四种主要途径外还有更多的高次反射路径,但是根据理论研究和长期观测到的结果均表明,在海面与目标的相互作用下,高次的海面路径对雷达接收机回波的贡献通常非常小,因此我们为了简化问题,忽略三次及更高次的海面反射对回波的影响[17]。
假设在发射机和接收机之间海面具有相同的反射特性,反射系数用Γ表示。那么,四条路径上传播的信号可以分别表示为:
接收信号为
回波信号可以表示为:
Γejk(r3+r2)+Γejk(r1+r4)+Γ2ejk(r3+r4)]dx′dz′
(10)
对r1,r2,r3,r4作二阶泰勒近似可得:
(11)
其中,a为发射机高度,a′为接收机高度,
分别表示每条传播路径上目标的复轮廓函数。
(12)
(13)
(14)
(15)
用
(x′)表示多径干涉下目标复轮廓函数:
(16)
海面反射系数垂直极化和水平极化条件的值可以由下式计算得到:
(17)
在发射机接收机高度远小于基线距离的情况下,擦掠角极小,不管垂直极化还是水平极化,Γ都可近似为-1[15],那么复轮廓函数可简化为:
(18)
海面运动目标信号模型在时域的回波信号模型可表示为:
(19)
3 仿真与讨论
本部分对前向散射雷达海浪下与多径干扰下的回波信号进行仿真,以考察海浪起伏与多径干扰对回波幅度和相位的影响。仿真参数如表1。
表 1 FSR仿真参数
Tab.1 Simulation parameters for FSR
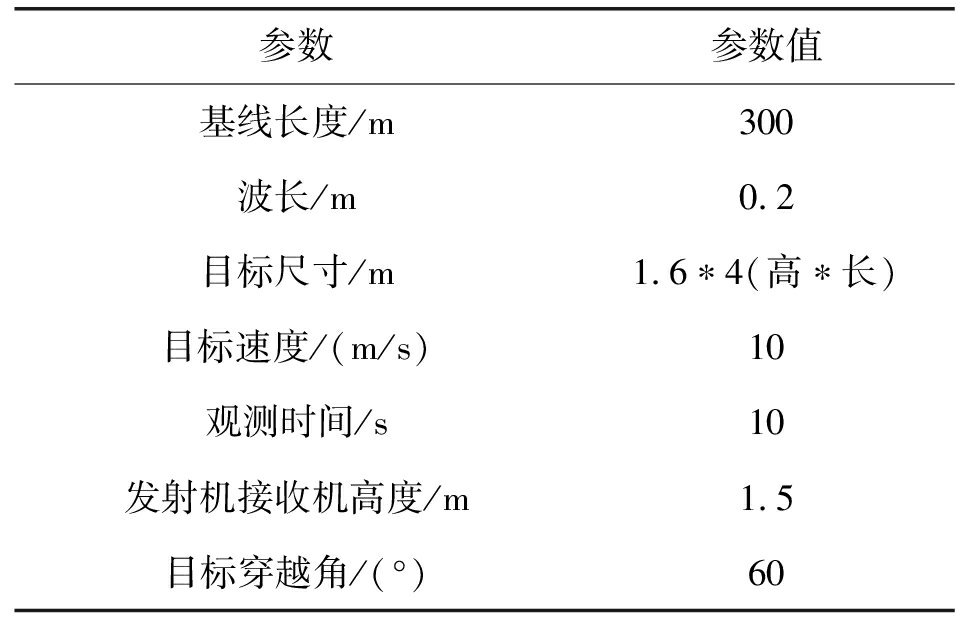
参数参数值基线长度/m300波长/m0.2目标尺寸/m1.6∗4(高∗长)目标速度/(m/s)10观测时间/s10发射机接收机高度/m1.5目标穿越角/(°)60
不同风速海浪下目标幅度的仿真结果如图4。
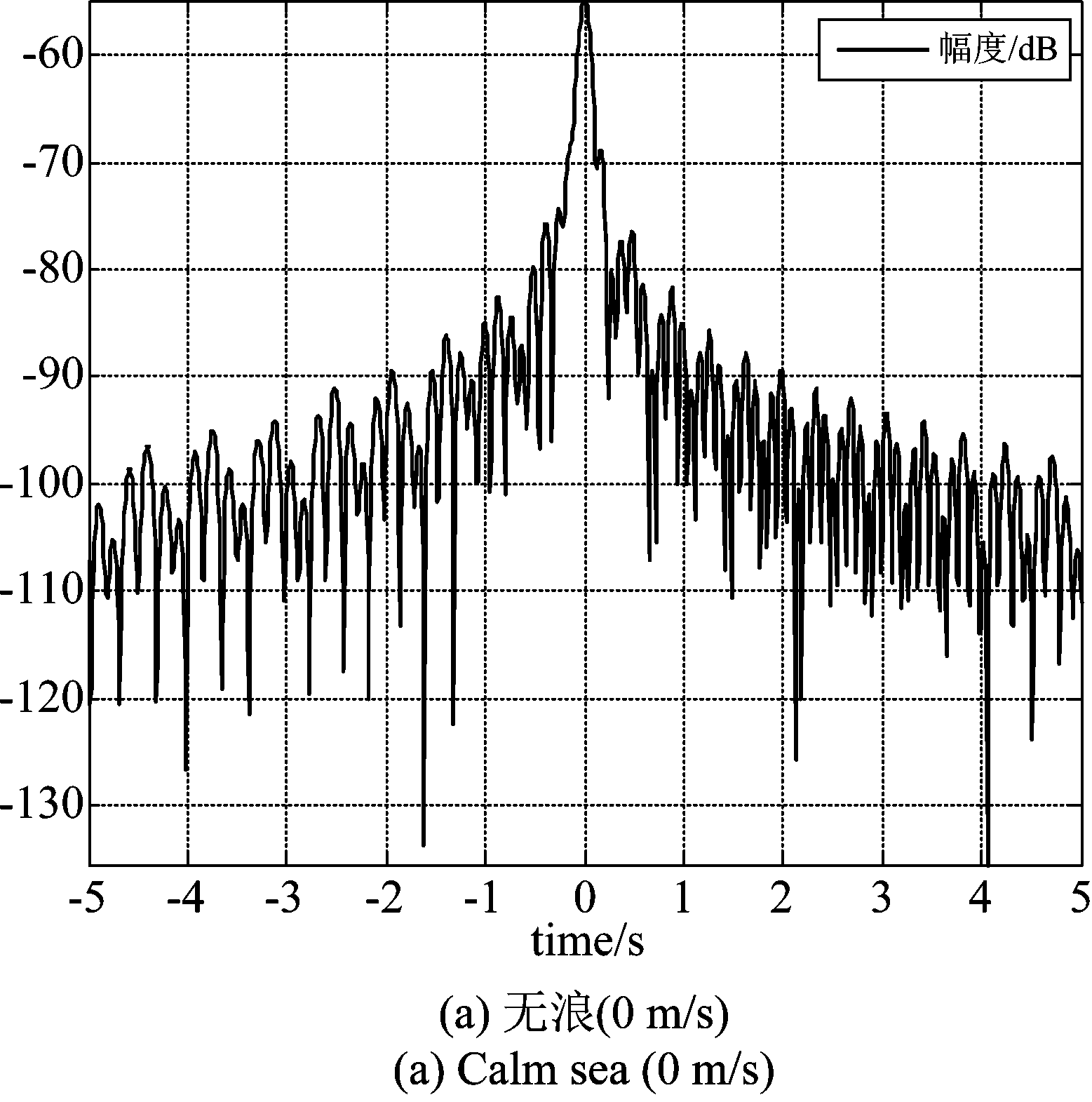
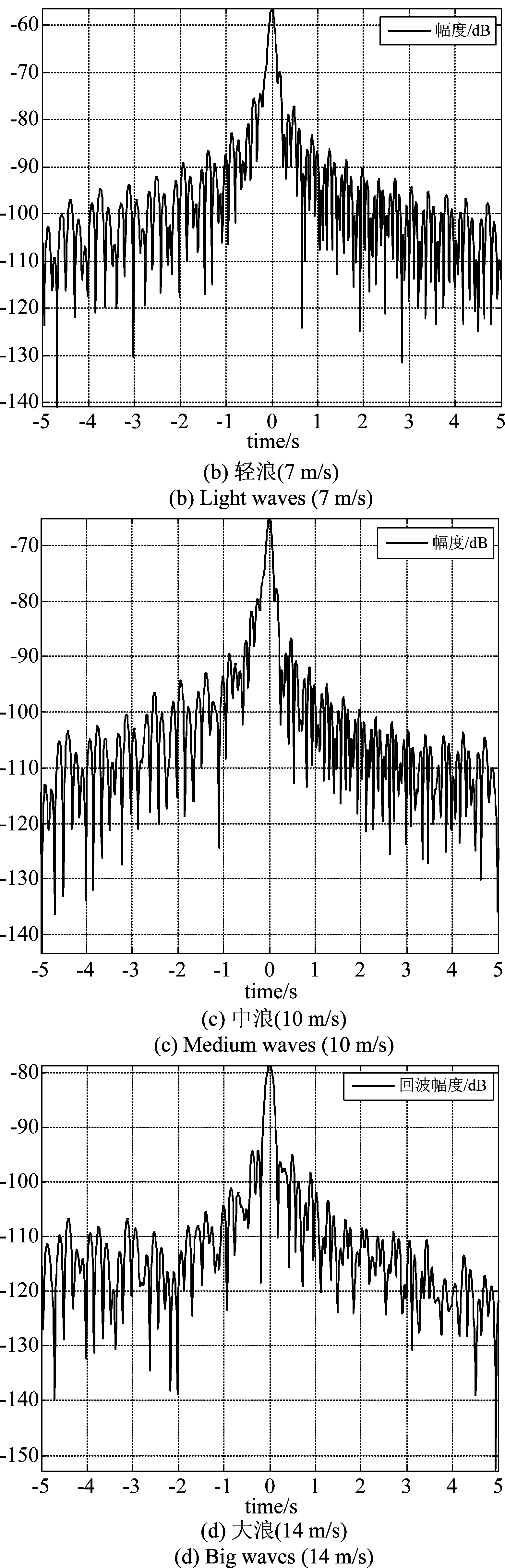
图4 不同海浪下回波幅度
Fig.4 Echo amplitude in different wave
接着,对不同风速下的回波相位进行仿真,得到无浪、中浪、大浪与无风状态下的比较如图5。
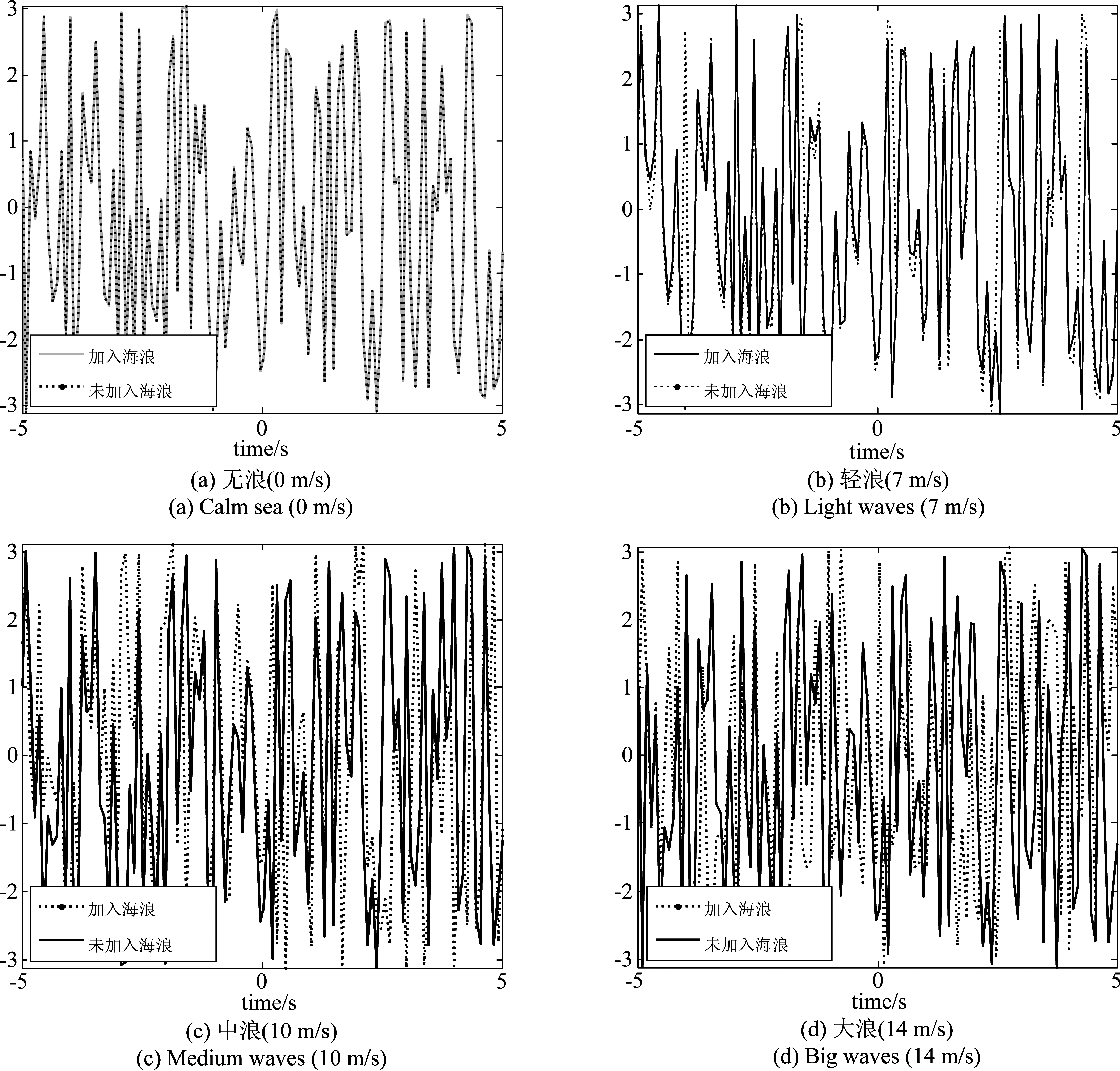
图5 不同海浪下回波相位
Fig.5 Echo phase in different wave
通过对不同风速下海浪的目标回波幅度和相位分析,我们可以看到,当风速很小一直到7 m/s的量级,回波的幅度和相位都没有发生明显的变化,通过观察信号幅度的仿真结果,可以看出目标回波信号幅度呈现出sinc函数的特性,这是由前向散射雷达的原始模型决定的,目标回波信号的模型可以表示为无数个幅度、相位不同但调频斜率相同的Chirp信号的叠加形式,而每一个子Chirp信号可以侧影轮廓上一个纵向切段的前向散射信号,由于我们采用的是1.6 m*4 m矩形目标进行仿真,由于侧影轮廓像和目标回波信号的傅里叶变换关系,目标的回波信号在时域呈现出Sinc特性,这也从侧面证明了仿真结果的正确性。随着风速的增大,到了中浪的量级,回波幅度已经产生了明显的减小,而相位的影响更为明显,这种状况一直延续到大浪,说明风速到达中浪之后相位已经完全混乱,不利于后续的信号处理过程。
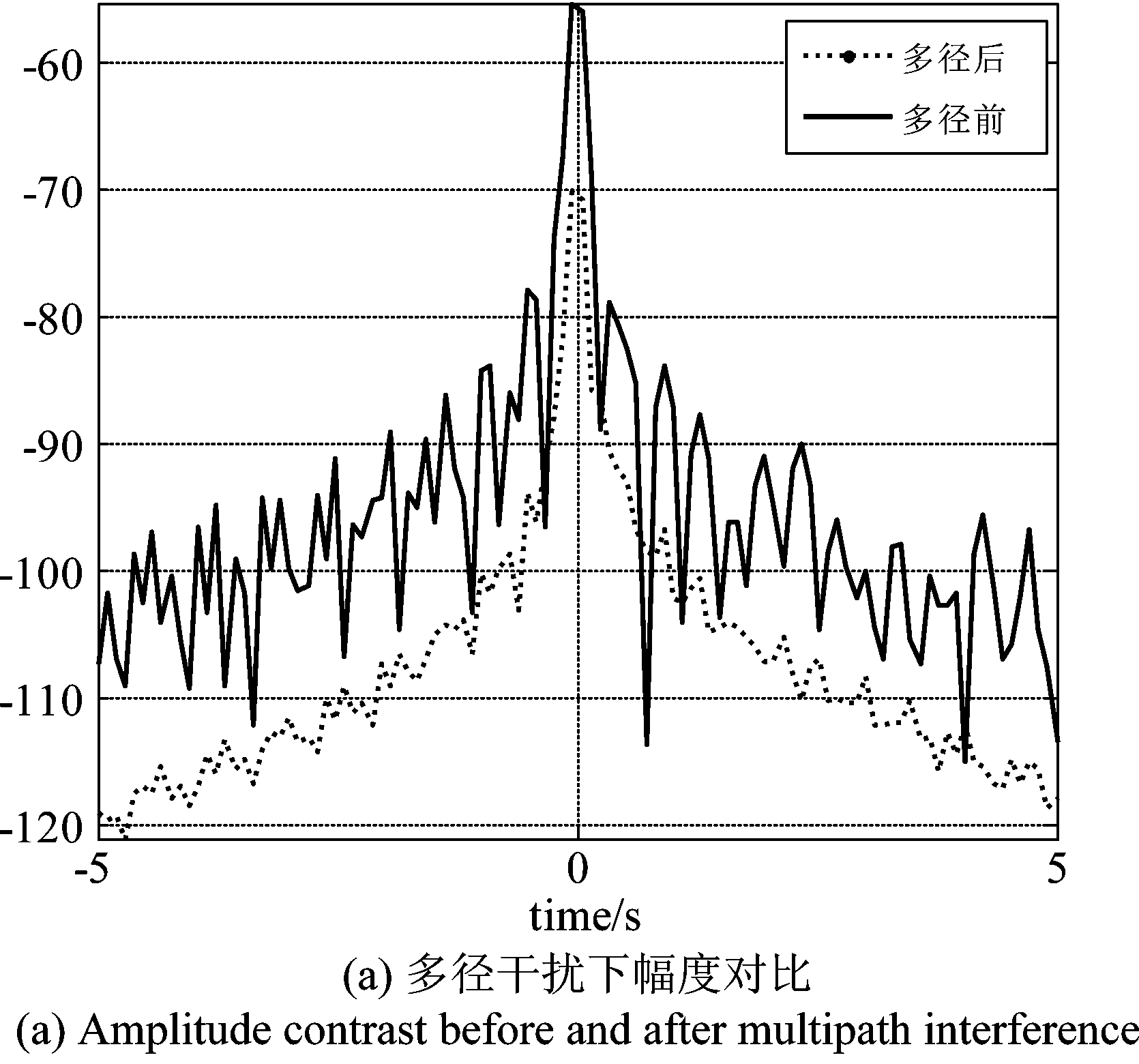
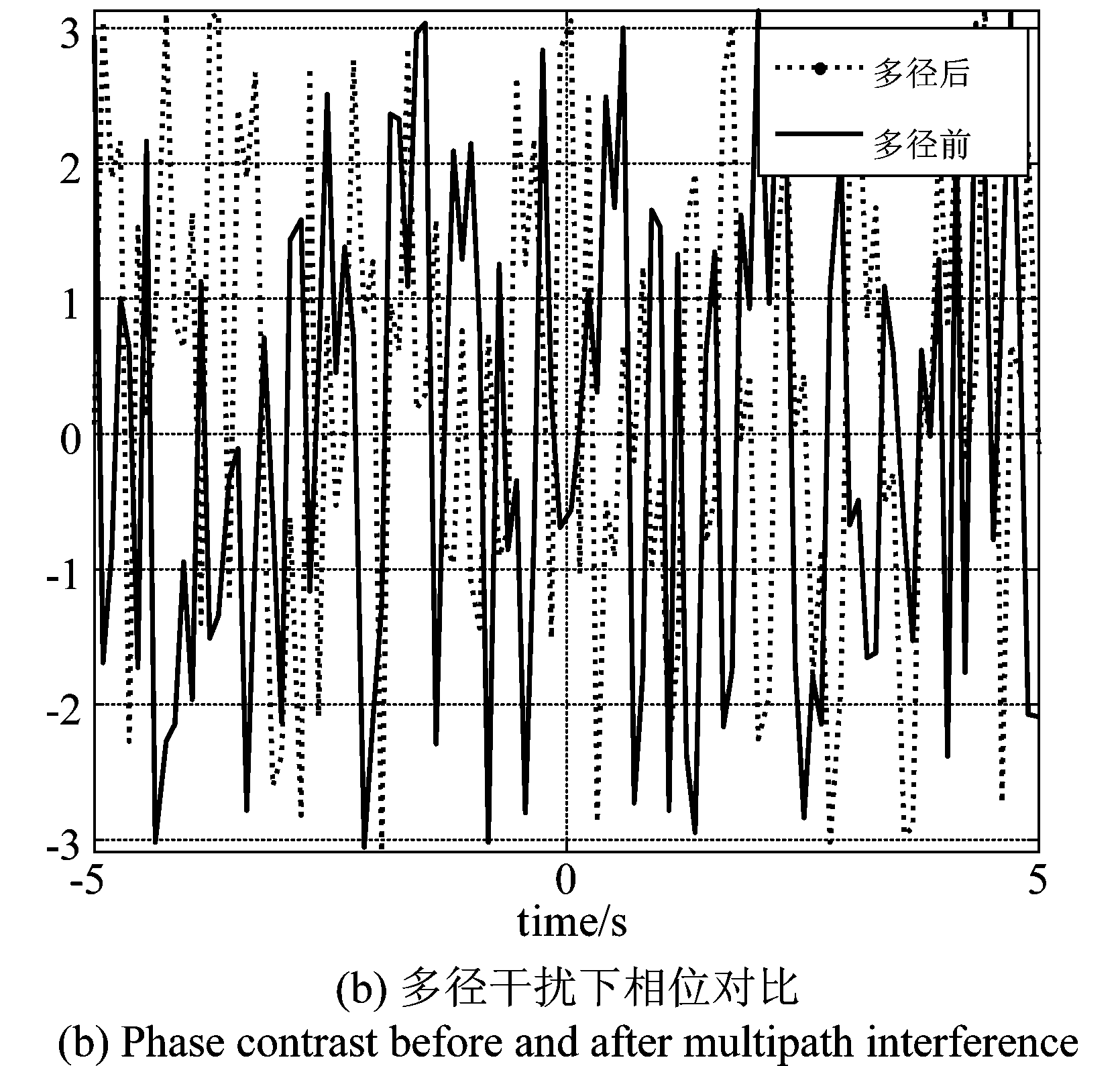
图6 多径干扰下回波幅度相位仿真结果
Fig.6 Simulation results of amplitude and phase under multipath interference
可以看到,多径干扰对回波信号的幅值和相位均产生了重大影响:回波幅度产生较大幅度衰减,结合多径干扰会引起信号衰落的特性,证明了仿真的正确性;目标的回波相位产生了大幅度的紊乱,这对以后的信号处理将带来十分不利的影响。
4 结论
本文首先给出了海浪起伏下和多径干扰下的前向散射海面目标回波信号模型。然后基于回波信号模型,对比分析了不同风速下海浪与多径干扰对海面目标回波特性的影响,并通过仿真结果侧面印证了建模的正确性。结果表明:
在轻浪及更低的海情下,FSR海面目标的回波幅度和相位没有产生明显的改变。随着风速的增大,回波幅度逐渐减小,回波相位在中浪情况下与未加入海浪相比已经呈现出明显的杂乱状态。多径干扰会对信号的回波幅度和相位产生重大影响,这种影响体现在回波幅度的大幅度衰减,信号相位呈现出与中浪及大浪海情下类似的明显杂乱状态。
由于海浪起伏的随机性,当风速过高的时候,海浪的影响难以通过现实的数学模型进行补偿,而且之前的仿真对象都是基于目标本身,真实情况下随着海浪的增强,海尖峰的出现会大大提高检测的难度[15]。通过对FSR海面目标回波信号的幅度和相位在不同风速海浪下的仿真结果,结合7 m/s已是轻浪中的最高量级,可以得出当前对海面前向散射雷达的研究应主要在轻浪及以下范围内讨论。
由于多径干扰的客观存在性,结合多径干扰下的仿真情况,我们认为在低风速海浪下对海面目标进行前向散射回波特性分析时应主要考虑多径干扰的影响,通过对多径干扰造成的信号幅度和相位的变化进行补偿,将对海面目标的后续信号处理乃至SISAR成像产生积极影响。
[1] Glaser J I. Some results in the bistatic radar cross section (RCS) of complex objects[J]. Proceedings of the IEEE, 1989, 77(5): 639- 648.
[2] Chapurskii V V. Reconstruction of the images of objects on the basis of one-dimensional radio holograms synthesized for small diffraction angles[J]. Radiotekhnika I Elektronika, 1988, 33: 1747-1756.
[3] 张涛, 张群, 罗斌凤, 等. 基于时频分析的双基地前向散射雷达侧影成像[J]. 电子学报, 2001, 29(6): 726-729.
Zhang Tao, Zhang Qun, Luo Binfeng, et al. Bistatic forward scattering radar profile imaging based on time-frequency analysis[J]. Acta Electronica Sinica, 2001, 29(6): 726-729.(in Chinese)
[4] 张涛, 罗永健, 张群, 等. SISAR侧影像的校正及特征提取[J]. 电子与信息学报, 2002, 24(11): 1634-1640.
Zhang Tao, Luo Yongjian, Zhang Qun, et al. Profile correction and feature extraction for SISAR[J]. Journal of Electronics and Information Technology, 2002, 24(11): 1634-1640.(in Chinese)
[5] Hu C, Liu C, Wang R, et al. Detection and SISAR Imaging of Aircrafts Using GNSS Forward Scatter Radar: Signal Modeling and Experimental Validation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017: 1-1.
[6] Liu C, Hu C, Wang R, et al. GNSS forward scatter radar detection: Signal processing and experiment[C]∥International Radar Symposium. IEEE, 2017.
[7] Long T, Hu C, Mikhail C. Ground moving target signal model and power calculation in forward scattering micro radar[J]. Science in China Series F (Information Science), 2009, 52(9): 1704-1714.
[8] Cheng H, Antoniou M, Cherniakov M, et al. Quasi-optimal signal processing in ground Forward Scattering Radar[C]∥IEEE Radar Conference, 2008.
[9] Ritchie M, Fioranelli F, Woodbridge K, et al. Simultaneous data collection of small maritime targets using multistatic radar and forward scatter radar[J]. IET Radar Sonar Navigation, 2017, 11(6): 937-945.
[10] Behar V, Kabakchiev C, Garvanov I. Marine target classification and parameter estimation using Forward Scattering Radar[C]∥International Radar Symposium, 2012.
[11] Abdullah N F, Rashid N E A, Ibrahim I P, et al. FSR vehicles classification system based on hybrid neural network with different data extraction methods[C]∥International Conference on Radar. IEEE, 2018.
[12] Kabakchiev C, Garvanov I, Cherniakov M, et al. Bistatic UWB FSR CFAR for maritime target detection and estimation in the frequency domain[C]∥International Radar Symposium, 2011.
[13] 黄勇, 陈小龙, 关键. 实测海尖峰特性分析及抑制方法[J]. 雷达学报, 2015, 4(3): 334-342.
Huang Yong, Chen Xiaolong, Guan Jian. Characteristics analysis and suppression method of measured sea spike[J]. Journal of Radar, 2015, 4(3): 334-342.(in Chinese)
[14] Chen Xiaolong, Guan Jian, Bao Zhonghua, et al. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002-1018.
[15] 许小剑. 时变海面雷达目标散射现象学模型[M]. 北京: 国防工业出版社, 2013, 2): 28-29.
Xu Xiaojian. Phenomenological model of radar target scattering from time-varying sea surface[M]. Beijing: National Defense Industry Press, 2013, 2): 28-29.(in Chinese)
[16] 朱洪华, 蔡建立. 不规则海浪的仿真[J]. 电脑知识与技术(学术交流), 2007, 3(13): 202-203.
Zhu Honghua, Cai Jianli. Simulation of irregular waves[J]. Computer Knowledge and Technology (Academic Communication), 2007, 3(13): 202-203.(in Chinese)
[17] 焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007, 1): 11-15.
Jiao Peinan, Zhang Zhongzhi. Radar environment and radio wave propagation characteristics[M]. Beijing: Electronic Industry Press, 2007, 1): 11-15.(in Chinese)
