1 引言
分布式雷达是一种新体制雷达,由多部小口径雷达联网组成雷达阵列进行协同工作,在很长的基线上分布,通过相参处理,可以等效合成大孔径天线,具有很高的角度分辨率和测角精度。此外,相对于传统的大孔径雷达,分布式雷达还具有机动性强、生存能力强、成本低、可靠性强等优点。因此,分布式雷达得到了各国的重视和大力发展,并被认为是下一代雷达的重点发展方向。法国航天研究所、美国的林肯实验室、国内的北京理工大学、西安电子科技大学、电子科技大学等单位均已开展分布式雷达的相关研究[1- 4]。但是由于分布式雷达阵的稀疏布置,在雷达节点均匀布置时,将会产生明显栅瓣,严重影响阵列的方向图性能。此外,在实际应用场景中,由于地形、雷达单元的口径、雷达间的互耦效应等多方面因素,会对阵列节点的位置有多种约束。通过对分布式雷达节点位置进行优化设计,可以在保证阵列其他性能不变和满足多约束的基础上抑制栅瓣,降低峰值旁瓣电平,提高雷达系统性能。
阵列节点位置设计可看作一个数学优化问题,因此许多数学优化方法被应用于阵列节点设计中。1997年H. Lebret和S. Boyd将凸优化算法应用到阵列方向图综合中[5];2008年,Keizer提出了迭代傅里叶变换算法(Iterative Fourier Transform, IFT)[6],大大降低了计算复杂度,但是只适用于源于均匀阵列的稀疏阵列设计;2008年美国杜克大学Q. H. Liu课题组为减少阵元数量首次应用Matrix Pencil Method(MPM)综合具有笔形波束方向图的稀布直线阵列[7],但是不能实现对阵元数量的精确控制;2018年,D. Pinchera提出了Inflating-Deflating Exploration Algorithm(IDEA)[8],通过对阵元模拟位置的放缩迭代的寻找最优阵元位置。这些方法虽然在一定条件下可以快速找到阵元最优位置及其激励,但是受限条件较多,可添加的约束有限,只适用于特定场景,不适用于分布式雷达节点位置的优化设计。此外,许多全局优化算法及其改进方法也被提出并被应用于阵列优化设计,如遗传算法[9](Genetic Algorithm, GA)、粒子群算法[10](Particle Swarm Optimization, PSO)等,这些方法灵活、简便,得到了广泛的研究与应用。
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的一种寻优算法,因其对最优化问题的求解具有普适性和灵活性,广泛的应用于各种领域的优化问题中。1994年,R. L. Haupt首次将遗传算法应用于阵列稀疏设计中[9],在均匀的阵列栅格上选择若干节点位置作为有效阵元的放置位置。2006年,陈客松提出了实值编码的改进遗传算法(Modified Genetic Algorithm,MGA),并应用于稀布线阵的设计中[11],但是由于编码方法的原因,使得算法受初始化影响较大,导致寻优结果易陷入局部最优。文献[12]和文献[13]分别将遗传算法与迭代傅里叶算法和凸优化算法结合,提高了算法的收敛速度和全局搜索能力,得到了更低峰值旁瓣的阵列,但是只适用于稀疏阵列的设计。
针对以上问题,本文提出了一种基于遗传算法的分布式雷达的节点位置优化设计方法。该方法首先采用了一种基于最小间距的实值映射编码方法,将节点位置的映射值作为染色体编码,并初始化种群;然后采用一种对种群进行先增广后收缩的选择算子,同时剔除未满足其他约束的解;再采用一种自适应广义交叉算子和广义变异算子,根据种群的聚集程度自适应的调整交叉概率和变异概率;最后经过反复迭代得到最优解,实现分布式雷达节点位置的优化。
2 分布式雷达模型
如图1所示,M个雷达单元非均匀的排布在长度为L的基线上,由于分布式雷达的孔径较大,目标回波无法被视为平面波,因此采用菲涅尔模型构建导向矢量:
a=[a1,a2,…,aM]
(1)
(2)
(3)
其中k=2π/λ,λ为雷达信号波长,xi为第i个雷达单元节点位置的坐标,u=sin θ,R0为目标到阵列中第一个雷达单元的距离。
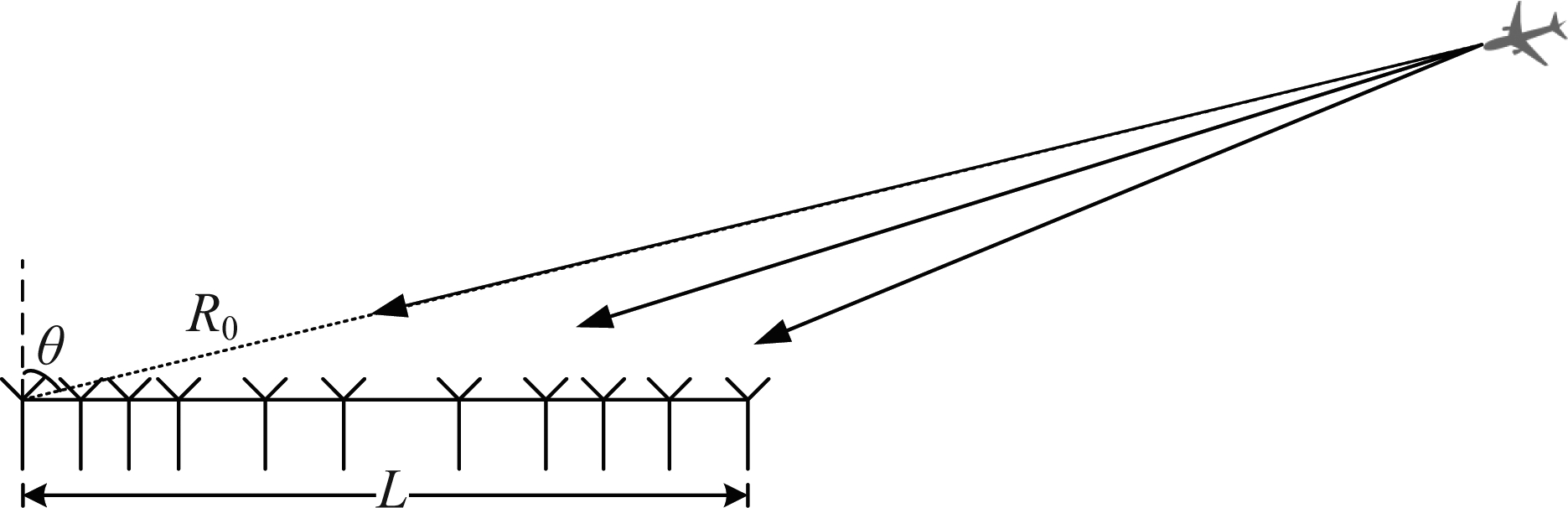
图1 分布式雷达线阵几何模型
Fig.1 Geometry model of distributed radar line array
由于在实际应用场景中有时需对不同型号的雷达进行组网,因此每个节点上的雷达的方向图可能不完全相同,则阵列方向图FF表示为:
FF(u)=EF(u)AF(u)
(4)
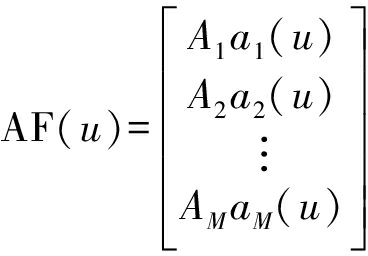
(5)
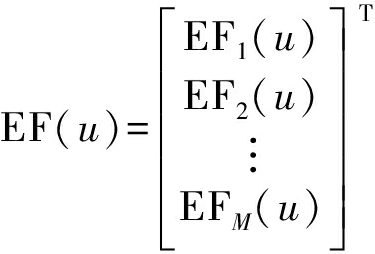
(6)
其中θ为方位角;Am为第m个阵元的激励,在优化对象为节点位置时,可令Am=1,m=1,2,…,M;EF(u)为单元因子,即阵元的方向图;AF(u)为阵因子,决定于天线阵列的阵元的数量、激励分布、位置分布以及阵列的结构,与阵元的辐射特性无关。
在实际场景中,由于分布式雷达口径很大,地形对雷达单元的放置位置有诸多限制:如在基线上的某一段不能放置阵元;为保证阵列有确定的主瓣宽度,需要约束阵列孔径,即约束阵列两端阵元位置不变;由于每个阵元都是一部雷达,在阵元间距较小时,强互耦效应严重影响阵列的性能,因此要对阵元间距进行最小距离约束。以峰值旁瓣电平(PSLL)最低作为优化目标来抑制栅瓣的电平,以阵元位置x=[x1,x2,…,xM]T为优化对象,则优化问题的数学模型可以写为:
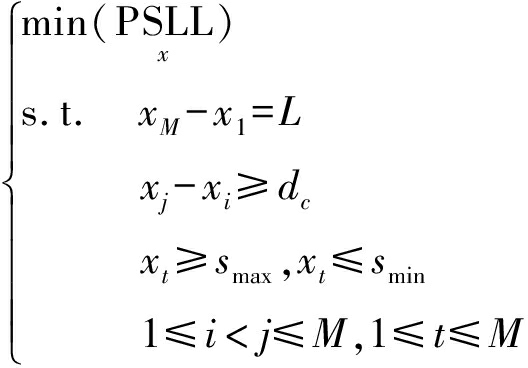
(7)
PSLL=max![]()
(8)
其中,dc为约束的最小阵元间距,smin和smax分别为基线上不可放置阵元约束的最小值和最大值,u0=sin(θ0),θ0的取值区间为排除主瓣之外的区域。
3 基于遗传算法的分布式雷达节点位置优化设计方法
遗传算法步骤简单,方法灵活,非常适用于解决分布式雷达阵列节点设计这一多约束优化问题。文献[11]中提出的改进的遗传算法通过提出一种新的实值编码方法,有效避免在交叉和变异过程中出现不可行解,减小了搜索空间,提高了算法的效率;但是由于分布式雷达阵列单元的超稀疏分布,阵元数量过少,该方法会导致搜索空间的离散化和实际搜索空间减小,最终寻优结果陷入早熟。针对以上问题,本文提出一种多约束遗传算法。首先,在实值编码方法的启发下提出一种实值映射编码方法,简化了预处理和后处理的步骤;然后提出一种对种群先增广后收缩的选择算子,减小初始化种群对优化结果的影响;最后通过自适应的交叉和变异处理保证种群后期的多样性,防止结果早熟。下面对本文提出方法的步骤进行详细阐述。
3.1 实值映射编码及初始种群的创建
为保证阵列的孔径为L,令阵元的位置为:
x=[x1,x2,…,xM]T=[0,d1+dc,…,di+idc,…,L]T,1≤i≤M-2
(9)
d=[d1,d2,…,dM-2]T
(10)
0≤di<dj≤SP=L-(N-1)dc,1≤i<j≤M-2
(11)
其中d为包含阵元位置信息的一条染色体,是阵元位置的实值映射。该编码方法可以在可行解空间不变的同时,将搜索空间从大小为L的空间映射到大小为SP的空间,在满足了约束的同时减小了搜索空间。
在初始种群的创建中,在[0,SP]上取M-2个随机数,并从小到大排序,则可以得到一个个体,其染色体为d=[d1,d2,…,dM-2]T,个体数为N的种群的染色体可以被记为矩阵形式:
D=[d1,d2,…,dN]
(12)
3.2 适应度函数的构造及适应度计算预处理
为解决分布式雷达容易出现的栅瓣和高旁瓣问题,将优化目标设置为降低分布式雷达阵列方向图的峰值旁瓣电平,则阵元位置为x的个体适应度函数可以写为:
(13)
其中b为适应度函数调整参数。由于在算法迭代一定次数后,种群中各个体的PSLL数值差距较小,需要对其进行修正以提高选择算子的效率和性能。可以将b设置为与种群中最高峰值旁瓣值相关:
(14)
式中α∈[0,1],为调整参数。
由于迭代中的个体染色体d为阵元位置实值x的映射,因此在计算种群适应度时,需要对种群染色体进行预处理:
X′=D+C=
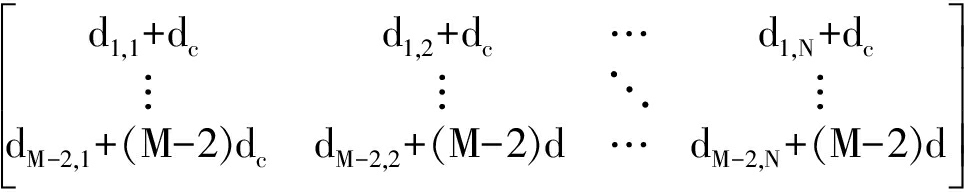
(15)
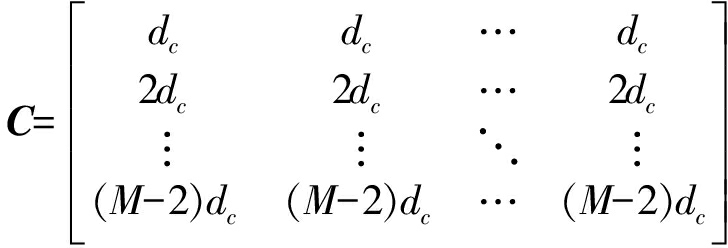
(16)
(17)
式中,0和L分别是值为0和L、长度为N的行向量。
3.3 对种群先增广后收缩的选择算子
按照3.1中离散的实值编码方法构建种群,虽然理论上的搜索空间是[0,SP],但在算法的一次运行中,由于交叉算子仅对不同染色体上的基因值进行互换操作而不会改变基因值,变异算子虽然能够产生新的基因值,但是较小的变异概率导致其产生的新基因值十分有限且随机性很强,因此实际的搜索空间基本是由初始化种群中染色体上各个基因值组成的离散空间,最终寻优的结果即为初始种群中所有基因值通过组合寻优得到的最优值,而非整个理论搜索空间中的最优值,当种群容量较小时,优化结果极容易陷入局部最优。针对这一问题,本文提出了一种对种群先增广后收缩的选择算子,用于在种群中增大扰动,提高算法的全局搜索能力。
将种群进行复制,然后将复制的种群中的个体进行两两融合:

(18)
(19)
式中,1为元素全部为1的(M-2)×N的矩阵,r为元素为(0,1)内随机数的(M-2)×N的矩阵,m∘n=[m1n1,m2n2,…,mNnN]表示m,n两个矩阵的Hadamard积。
将D′与D合并为个体数为2N的增广新种群Dtemp并对其进行选择操作,由式(18)、(19),D′是原种群D在扰动机制下保存了一定原种群信息得到的衍生种群。通过在选择前对种群的增广,增强了对种群的随机扰动,增大了实际搜索空间。再采用轮盘赌方法和精英策略结合的选择策略,在保留种群精英的基础上,在Dtemp中采用轮盘赌的方法选择N个满足约束条件的个体作为下一代的父代,对不满足约束的个体进行剔除。
3.4 自适应的广义交叉算子和广义变异算子
在本文中的实值映射编码方式下,个体染色体向量上的每一个值都直接包含个体对应阵元的位置信息。广义交叉算子首先根据交叉概率判定是否对种群中的两个基因进行交叉操作,若是,则再随机选择两个染色体上的位置并进行交换。类似的,广义变异算子首先根据变异概率判定是否对种群中的某个基因进行变异操作,若是,则再随机选择染色体上的位置用新的随机数代替。需要注意的是,在完成广义交叉和广义变异操作后,由于染色体上数据的改变,需要重新对染色体进行排序,以保证染色体上的数据升序排列。
阵列结构设计无实时性的要求,对时间复杂度需求较低,对优化结果要求较高,因此本文参考文献[14]提出一种自适应交叉概率pc和变异概率pm:
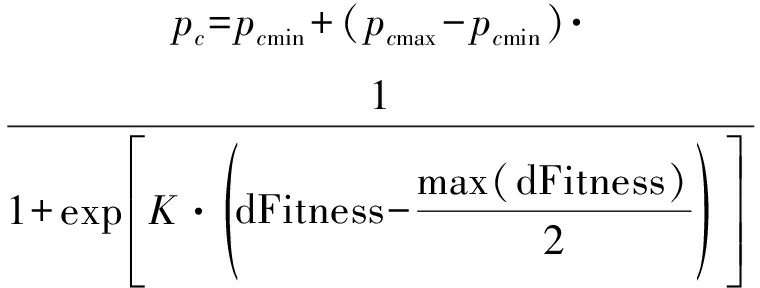
(20)
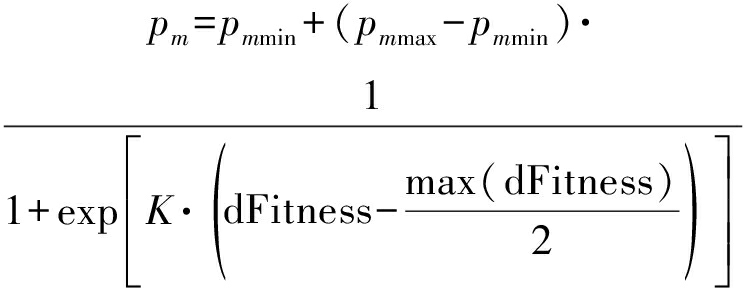
(21)
dFitness(i)=Fitnessmax(i)-Fitnessavg(i)
(22)
其中,pcmax,pcmin和pmmax,pmmin分别为交叉概率和变异概率的上限和下限,Fitnessmax(i)和Fitnessavg(i)分别表示第i代种群中的个体适应度函数的最大值和均值,dFitness(i)反映了该代中个体聚集程度,K为调节参数。根据种群中个体的聚集程度调整变异概率和交叉概率,在种群中个体聚集程度高的时候提高交叉概率和变异概率,防止结果早熟。
3.5 算法流程
本文提出的方法与遗传算法的流程基本一致。首先对种群进行初始化,得到初代种群;然后进行种群的繁衍迭代:进行种群的适应度计算,并根据种群的适应度更新交叉和变异概率,接着对种群进行先增广后收缩的选择处理,然后依次进行广义交叉和变异处理;重复迭代过程直至满足了终止条件。相比文献[11]中的方法,本方法移除了对种群的后处理,改进了对种群适应度计算的预处理,步骤更为精简;采用先增广后收缩的选择处理,降低了初始化种群对算法结果的影响。本文提出的基于多约束遗传算法的流程图如图2所示。
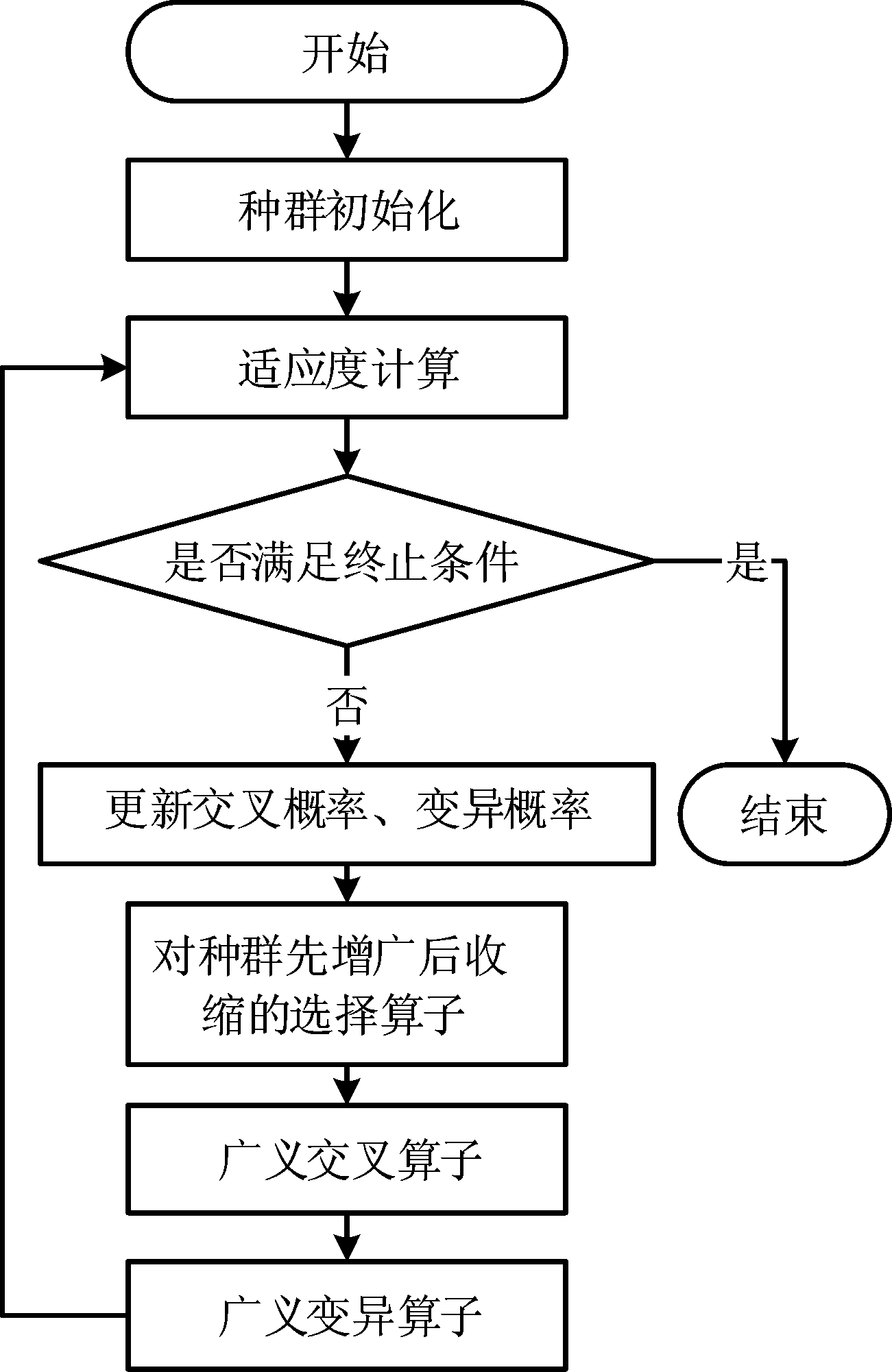
图2 算法流程图
Fig.2 Flowchart of the proposed algorithm
4 仿真实例
仿真条件:在300 m的基线上布置12部雷达,其中第一台为主雷达,其他为相同的辅助雷达,载频为3 GHz,约束雷达间最小间距为2 m,模拟实际场景约束在100~110 m的位置上禁止放置雷达单元。采用本文提出的方法和文献[11]中的方法分别进行独立的200次仿真,由于文献[11]中的方法受初始化种群和种群规模影响较大,而本文所提方法中进行了一次种群的增广并对增广后的种群进行适应度计算,为使得两种方法的总计算量相近,故令本文方法种群规模为500;文献[11]方法的种群规模为1000。为模拟实际情景,设主雷达和辅助雷达的有效口径分别为:7 m2,1 m2,其方向图如图3所示,分别为:
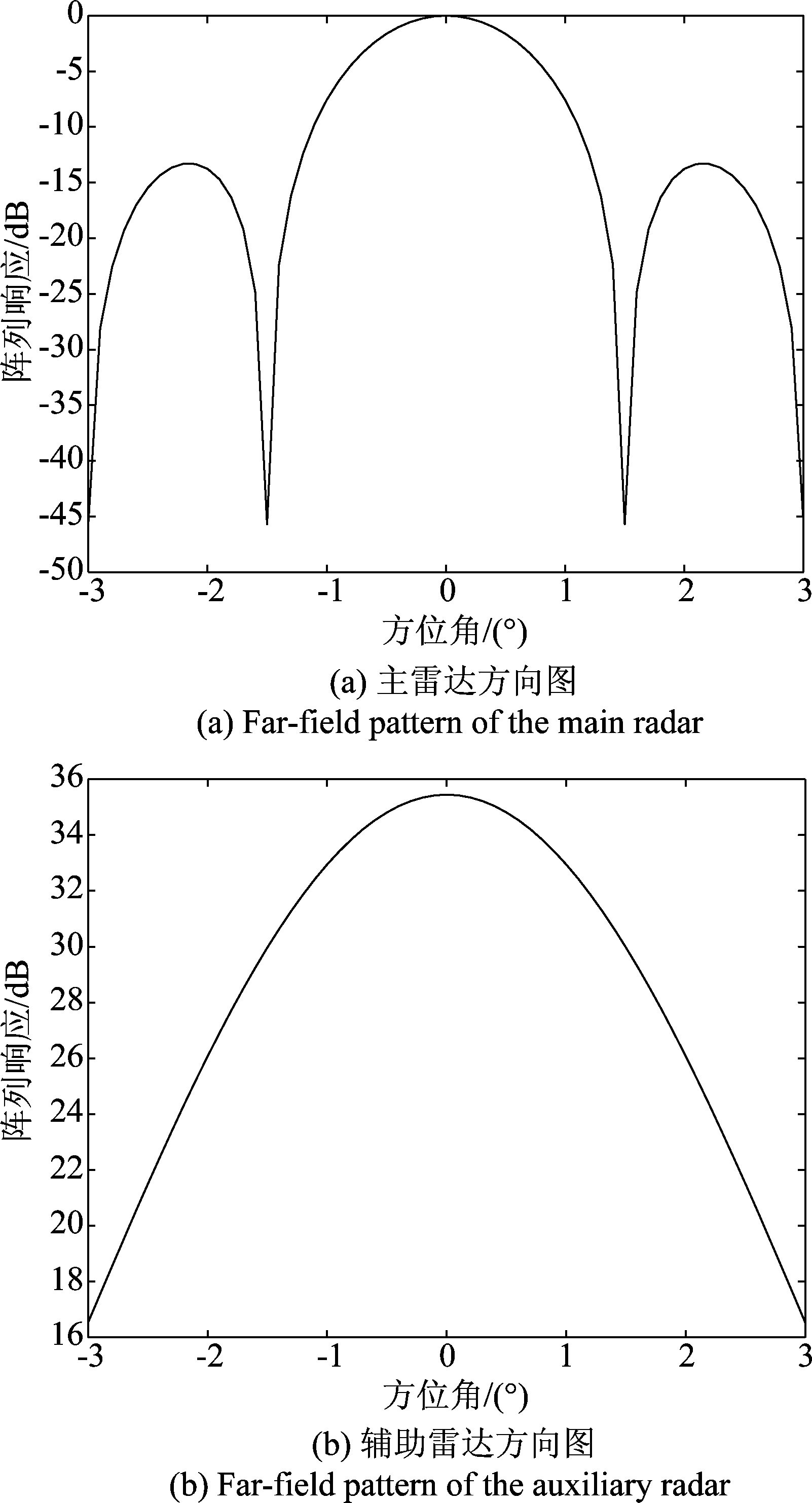
图3 主雷达和辅助雷达方向图
Fig.3 Far-field pattern of the main radar and auxiliary radar
(23)
(24)
(25)
(26)
其中,Gm,Ga分别为主雷达和辅助雷达单元的增益,Sm,Sa分别为其有效面积。
仿真结果:采用本文提出的方法和MGA得到的最优阵列节点位置如表1所示,雷达单元非均匀地布置在0~300 m的基线上,在100~110 m的区域内没有布置雷达,且相邻的雷达单元间距均大于2 m。其方向图如图4所示,均匀排布阵列的方向图中,在±0.31°、±0.63°等附近均有明显栅瓣,而经过优化设计的阵列方向图中,栅瓣均被明显抑制,本文方法得到的最优阵列可以将峰值旁瓣降低至-5.368 dB,比文献[11]中方法得到的最优阵列低0.862 dB,但是主瓣宽度略有展宽,约为0.015°。在算法寻优性能方面,本文方法得到的最优阵列、最差阵列以及200次平均和文献[11]的收敛曲线如图5所示,本文所提方法寻优速度在迭代早期与文献[11]中方法基本相同,随着迭代代数增加,文献[11]的方法在150代左右基本收敛,而本文的方法则由于在选择步骤中对种群进行了先增广后收缩的扰动以及自适应的变异率,使得种群中保持有高的种群多样性,因此在300~600代依然保持有较好的搜索能力。在仿真耗时方面,在配置cpu型号为i5 3230M的个人PC上,采用本文方法耗时平均为37.68 min,采用文献[11]中方法耗时平均为30.14 min。综上,本文的方法可以有效实现栅瓣、旁瓣抑制的效果,并以降低收敛速度和增加优化时长为代价,提高了算法的全局寻优能力,能够得到旁瓣更低的阵列。
表1 优化分布式雷达阵列节点位置
Tab.1 Elements location of the optimal distributed radar
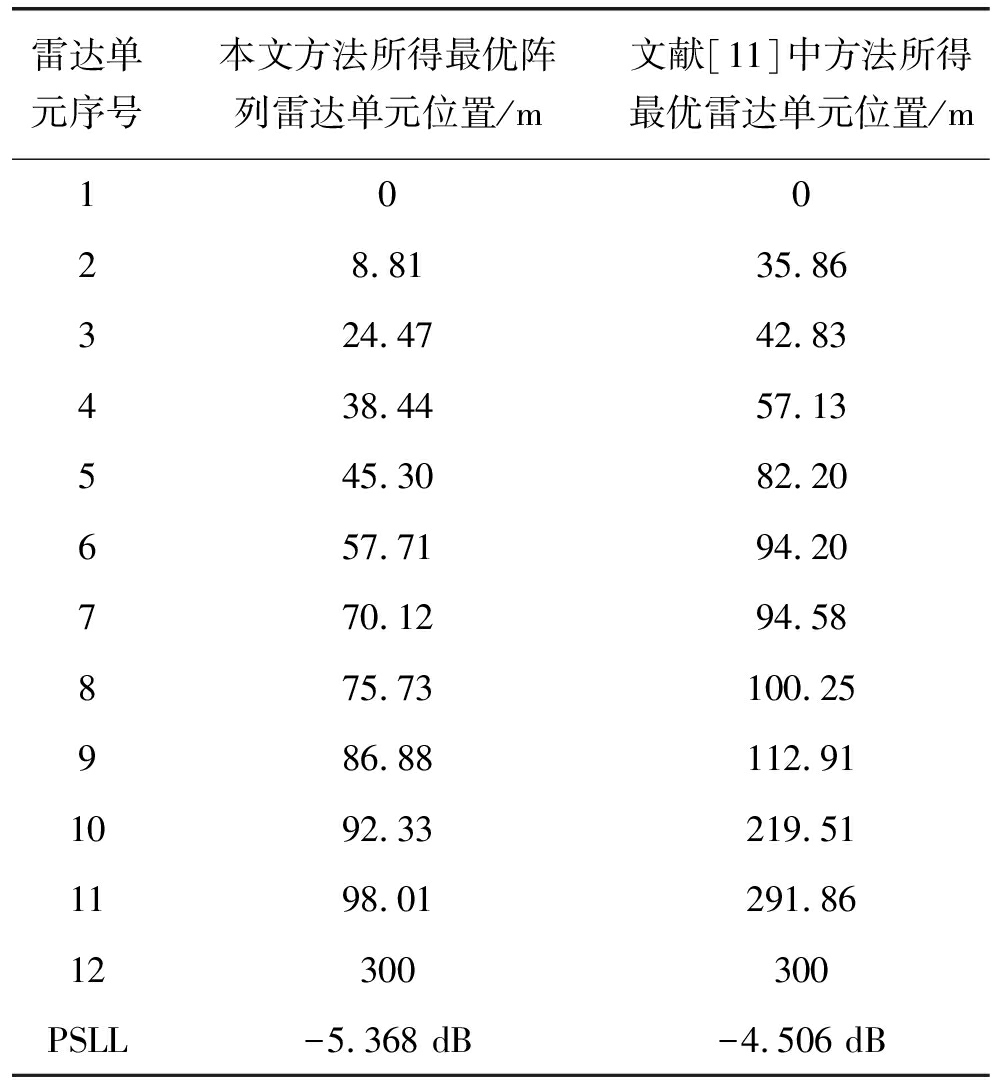
雷达单元序号本文方法所得最优阵列雷达单元位置/m文献[11]中方法所得最优雷达单元位置/m10028.8135.86324.4742.83438.4457.13545.3082.20657.7194.20770.1294.58875.73100.25986.88112.911092.33219.511198.01291.8612300300PSLL-5.368dB-4.506dB

图4 阵列方向图
Fig.4 Far-field pattern of the optimal solution
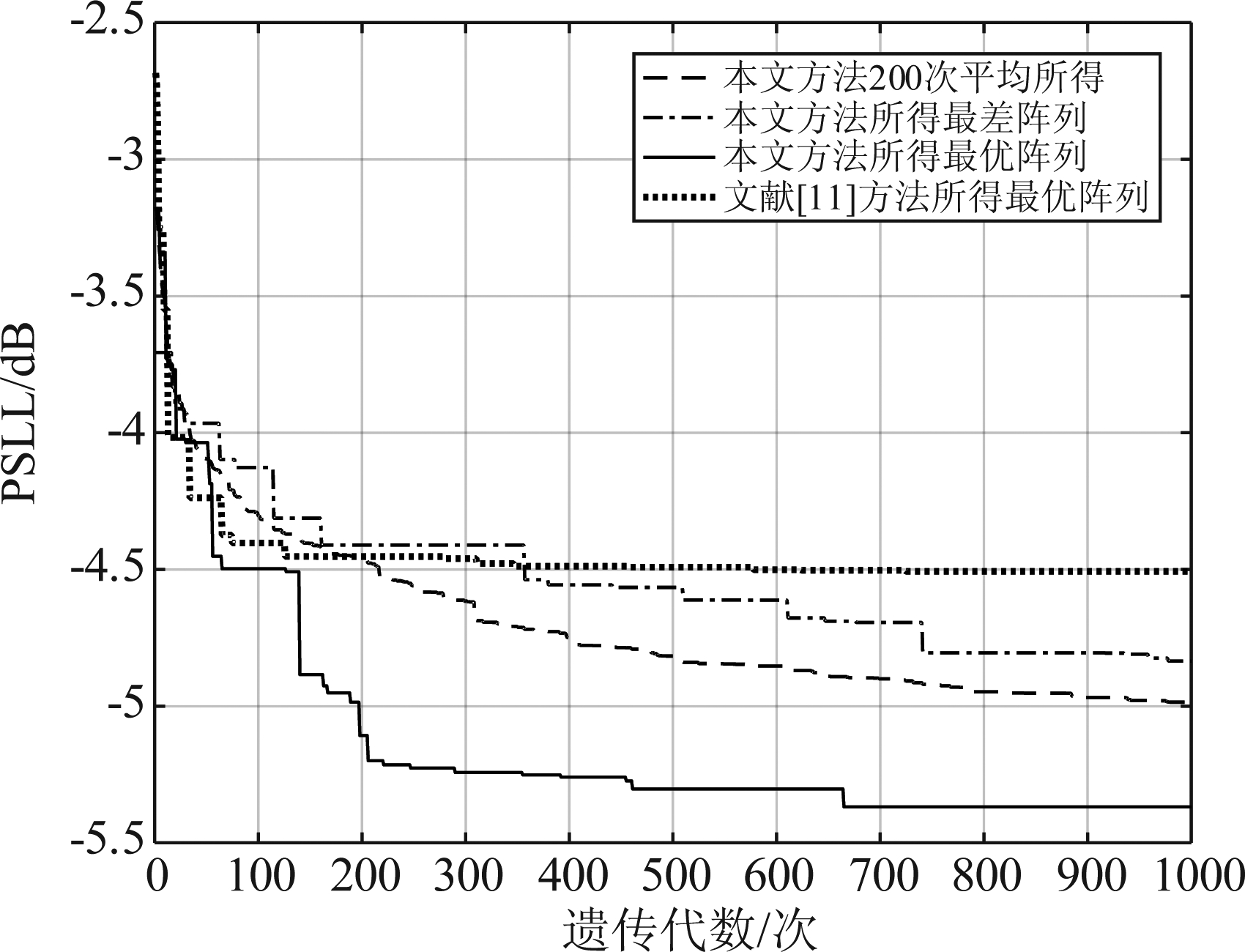
图5 算法收敛曲线
Fig.5 Convergence of the methods
5 结论
分布式雷达具有阵元数量少、分布口径大、实际应用场景约束多等特点,针对以上特点,本文基于多约束遗传算法提出了一种优化分布式雷达节点位置的方法。该方法基于阵元最小间距对节点位置进行实值映射编码,提高了优化效率;并通过对种群先增广后收缩的选择算子,降低初始化种群对算法结果的影响;同时采用了一种自适应的广义交叉和变异处理,根据种群的适应度调整交叉率和变异率,以提高算法后期的种群多样性,提高算法的优化性能。仿真实例表明,采用该方法进行分布式雷达的节点位置优化,可以稳健、有效的得到无明显栅瓣、低旁瓣电平且满足多约束的阵列,并且相较于已有方法,该方法简单易行,全局搜索能力强。
[1] 殷丕磊. 地基宽带分布式全相参雷达技术研究[D]. 北京: 北京理工大学, 2016.
Yin Pilei. Research on Ground-Based Wideband Distributed Coherent Aperture Radar[D]. Beijing: Beijing Institute of Technology, 2016.(in Chinese)
[2] Yang Xiaopeng, Yin Pilei, Zeng Tao, et al. Applying Auxiliary Array to Suppress Mainlobe Interference for Ground-Based Radar[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 433- 436.
[3] Feng Han Zhe, Liu Hong Wei, Yan Jun Kun, et al. A fast efficient power allocation algorithm for target localization in cognitive distributed multiple radar systems☆[J]. Signal Processing, 2016, 127: 100-116.
[4] 张帅. 分布式雷达抗干扰与目标检测方法研究[D]. 成都: 电子科技大学, 2017.
Zhang Shuai. Research of Distributed Radar Technology Against Jamming And Target Detection[D]. Chengdu: University of Electronic Science and Technology of China, 2017.(in Chinese)
[5] Yan Chuang, Yang Peng, Xing Zhiyu, et al. Synthesis of Planar Sparse Arrays With Minimum Spacing Constraint[J]. IEEE Antennas & Wireless Propagation Letters, 2018, PP(99): 1-1.
[6] Keizer, Will P M N. Linear Array Thinning Using Iterative FFT Techniques[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(8): 2757-2760.
[7] Liu Yanhui, Nie Zaiping, Liu Qinghuo. Reducing the Number of Elements in a Linear Antenna Array by the Matrix Pencil Method[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(9): 2955-2962.
[8] Pinchera D, Migliore M D, Panariello G. Synthesis of Large Sparse Arrays Using IDEA (Inflating-Deflating Exploration Algorithm)[J]. IEEE Transactions on Antennas and Propagation, 2018: 1-1.
[9] Haupt, R. L. Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(7): 993-999.
[10] Jin N, Rahmat-Samii Y. Advances in Particle Swarm Optimization for Antenna Designs: Real-Number, Binary, Single-Objective and Multiobjective Implementations[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3): 556-567.
[11] Chen Kesong, He Zihui, Han C. A Modified Real GA for the Sparse Linear Array Synthesis With Multiple Constraints[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(7): 2169-2173.
[12] Cui Can, Li Wentao, Ye Xiutiao, et al. Hybrid Genetic Algorithm and Modified Iterative Fourier Transform Algorithm for Large Thinned Array Synthesis[J]. IEEE Antennas & Wireless Propagation Letters, 2017, PP(99): 1-1.
[13] Fu Yu, Guo Zhigui, Wang Haowen, et al. Optimization of planar thinned antenna array based on genetic and convex hybrid algorithm[C]∥Progress in Electromagnetic Research Symposium. IEEE, 2016.
[14] Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1994, 24(4): 656- 667.



