1 引言
近年来,城区环境中的低小慢目标如小型无人机越来越多,对空中监管和空中安全带来了巨大的安全隐患。对城市地区低小慢目标的探测是当前雷达技术领域所面临的紧迫任务。由于低小慢目标的背景复杂,且考虑电磁辐射的影响,所以对雷达探测提出了很高的要求。基于民用4G通信信号的外辐射源雷达其通信基站基本实现全面覆盖,无电磁污染且可形成多基地组网探测系统已成为人们的研究热点。4G通信技术采用的是LTE(Long Term Evolution,长期演进)标准,文献[1]对LTE信号能否用作外辐射源雷达照射源进行了可行性分析,得出LTE信号是可行的。对微弱目标的探测,一种有效的方法是增加积累时间。但长时间相参积累会引起走动问题。由于通信基站的双(多)基地构型,目标的径向速度引起跨距离单元走动,当目标有切向速度或本身有加速度时会产生跨多普勒单元走动,且目标运动速度越快,发生走动的现象越明显,严重影响积累增益。为解决距离走动问题,keystone变换是用于校正目标在相参积累时间内发生距离走动的一种常用方法。keystone变换是最早应用于动目标SAR成像领域的一种常见的距离走动校正技术,其主要优势是不需要目标的具体运动信息就能实现多个目标的距离走动补偿[2]。文献[3]提出了基于keystone变换的微弱目标检测方法,在无目标运动速度信息条件下实现了距离走动补偿。文献[4]提出了基于keystone变换的米波双基地雷达长时间相参积累算法,通过在距离频域-方位时域利用keystone变换实现距离走动校正,利用FFT实现长时间相参积累,有效提高了回波信噪比。文献[5]研究了基于keystone变换的OFDM雷达信号距离走动校正方法,实现了高速运动目标和长时间积累的脉间距离走动补偿,提高了雷达输出信噪比。为补偿多普勒走动,文献[6]提出基于包络插值和分数阶傅里叶变换的数字电视辐射源雷达走动补偿算法,使长时间相参积累不受限与距离走动和多普勒走动。文献[7]提出STFT-Hough的变换方法,通过无交叉数据滑动窗截取信号和多普勒频率取峰值补偿了多普勒走动展宽,且大大降低了算法的计算复杂度。文献[8]公开了一种基于天基双基地雷达的动目标长时间相参积累方法,能够实现相位补偿,改善多普勒相位的影响。文献[9]提出了一种基于keystone变换和FRFT的机动弱目标检测算法。文献[10]针对高速高机动目标,提出了两种长时间相参积累检测方法,即Radon-分数阶傅里叶变换和Radon-分数阶模糊函数,能够同时补偿长时间积累过程中的距离和多普勒走动,提高积累增益。
上述研究成果大都针对单基地雷达进行讨论,而对基于LTE信号的双多基地雷达系统进行慢速微弱目标回波的长时间相参积累技术未有研究。由于手机基站的密集部署使得目标到基站的距离一般较短,长时间积累时相对转角较大,会引起目标散射特性的空变,影响目标回波相参积累效果。本文即针对上述问题开展研究,结构如下:第2节对目标的散射特性建模,给出目标的回波信号模型;第3节对回波信号的距离走动和多普勒走动特性进行理论分析,提出了基于keystone变换和FRFT的走动校正方法,同时分析了目标的散射特性对回波能量和参数估计的影响;第4节用所提方法对理想点目标回波进行计算机仿真处理,对比分析校正前后的仿真结果,并仿真分析了目标散射特性对回波能量和参数估计的影响。
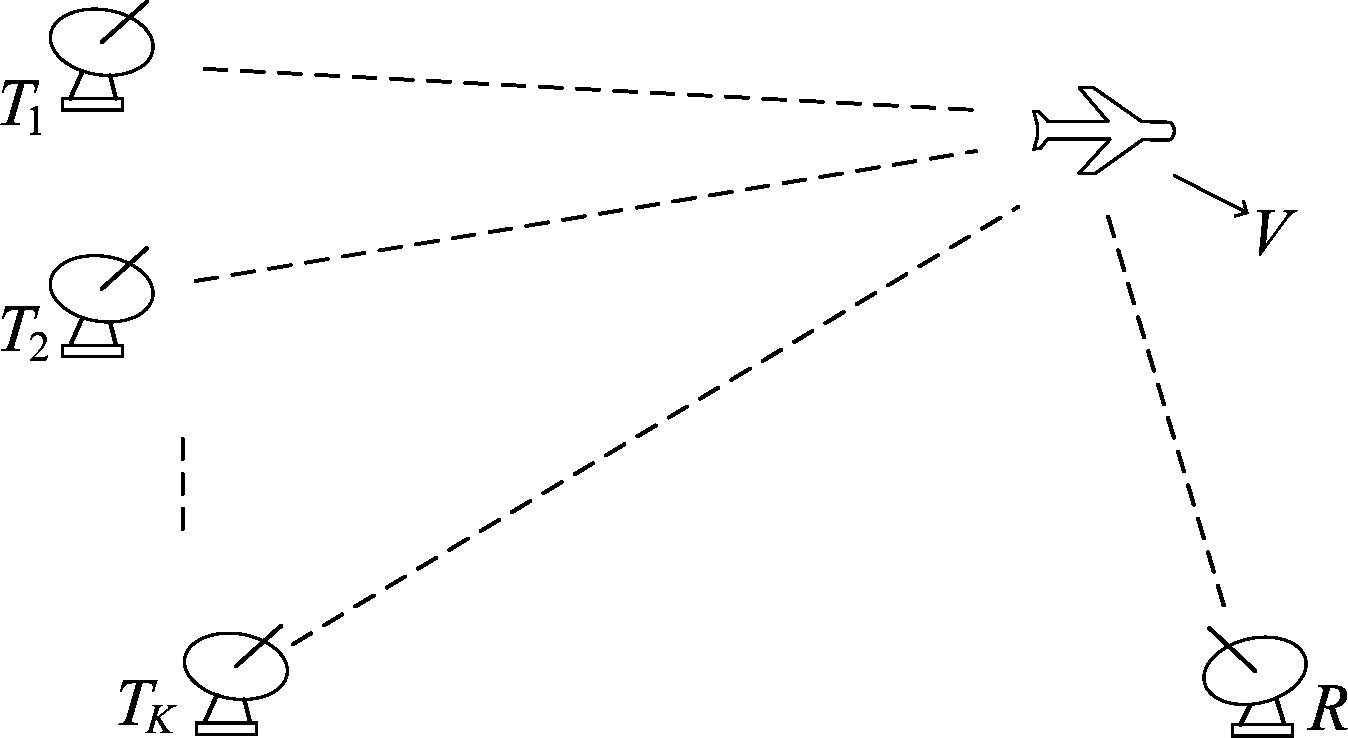
图1 外辐射源雷达系统示意图
Fig.1 The schematic diagram of the passive bistatic radar
2 信号模型
假定外辐射源雷达系统由K个手机基站(辐射源)和1个接收节点构成,其中各手机基站分别位于Tk,k=1,…,K,接收节点位于R,且假设目标以速度V匀速运动,则该雷达系统示意图如图1所示。雷达接收节点通过接收目标反射的由手机基站辐射的LTE通信体制下的OFDM信号[11]进行低小慢目标探测。假设K个手机基站发射的信号相互正交,即
其中sti(t)和stj(t)分别表示第i个手机基站和第j个手机基站的发射信号,且手机基站Tk与T1的时间同步误差为Δτk,频率同步误差为Δfk,相位同步误差为Δθk,k=1,…,K,其中Δτ1=Δf1=Δθ1=0。
2.1 接收信号模型
假设手机基站以Tr为间隔重复发射脉冲信号,N表示手机基站在相参积累时间内发射的脉冲总数,n=0,…,N-1。用RTk,RRe和RTa,n分别表示第k个手机基站、接收节点的位置矢量和发射第n个脉冲时目标的位置矢量。那么第k个手机基站、目标和接收节点之间的传播延时τkn的表达式为:
(1)
其中RTa,n=RTa,0+nTrV。
假设目标散射的空变特性用Θ(k,n)表示,则雷达接收节点接收到的回波信号为:
(2)
其中stk(t)表示第k个手机基站的发射信号,αk为回波衰减系数。式(2)经下变频后表示为:
exp[-j 2π(fc-Δfk)(t-Δτk)]
(3)
其中fc为载频。
这里对目标散射的空变特性进行二阶建模,即
Θ(k,n)=ak·(nTr)+bk·(nTr)2
(4)
其中ak,bk为任意参数。
3 信号处理方法
当目标与雷达之间发生相对运动时,通常进行多普勒处理时不考虑距离走动带来的影响。但长时间相参积累使得对微弱小目标探测时就会发生跨距离单元走动。由于目标的距离走动在积累时间内不能超过半个距离单元,所以在相参积累之前利用keystone变换对距离走动进行校正。由于外辐射源雷达其固有的双(多)基地构型及目标运动速度等因素,使得长时间相参积累期间跨越多个距离单元的同时也跨越多个多普勒单元,所以在距离走动补偿的基础上通过FRFT补偿多普勒走动。
3.1 回波信号走动分析
下面公式推导回波信号在积累时间内距离走动和多普勒走动的产生。
构建第p个手机基站的发射信号stp(t),经过匹配滤波处理得到:
Sr1(f,n)=|αp|2|Xp( f )|2exp[jΘ(p,n)]
exp[-j 2π(f+fc-Δfp)τpn]
(5)
其中Xp( f )是发射信号复包络的傅里叶变换。
令ΔR=τpnc,由式(1)得:
ΔR=|RTp-RTa,n|+|RRe-RTa,n|
(6)
由于目标与雷达站的相对距离短,积累时间长,需对式(6)采用Taylor二阶展开以提升近似精度;可得:
(7)
其中ΔRp=|RTp-RTa,0|+|RRe-RTa,0|,ΔVp=VT(eTp-Ta+eRe-Ta),
这里
式(7)代入式(5)得:
Sr1(f,n)≈|αp|2|Xp( f )|2exp[jΘ(p,n)]
(8)
3.2 回波信号走动校正
令Θ(p,n)=a(nTr)+b(nTr)2,对式(8)引入keystone变换:(f+fc-Δfp)n=fcm,由于keystone补偿后, f的一阶、二阶项很小可忽略,于是有:
(9)
其中λ=c/fc,相应的距离时域信号为:
(10)
从式(10)可看出,信号的峰值位置始终位于ΔRp/c处,即keystone变换将原本位于不同距离单元的回波信号校正到同一距离单元内,补偿了距离走动,回波能量在距离向聚焦。
3.3 相位FRFT处理
从式(10)看出,信号的多普勒频率在慢时间域近似为LFM信号,传统的傅里叶变换不能使慢时域目标回波的能量得到有效集聚。信号的FRFT可解释为信号的时间轴在时频平面的旋转,定义式为[12-13]:
Fα[s](u)=
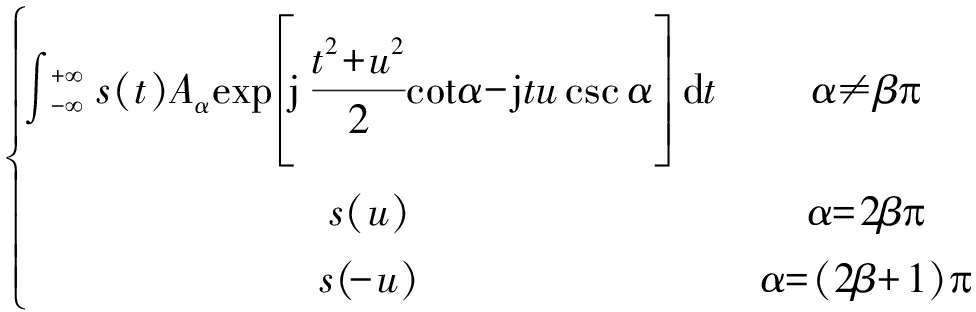
(11)
式中,
取整数,α为旋转角度,与变换阶数p的关系为α=pπ/2,p∈(-2,2],u为分数阶傅里叶变换域。
记
把式(10)代入式(11)得:
(12)
当旋转角度与慢时域目标回波信号的调频率相匹配时,即μ=-cotα0/(2π),则
|Fα0[sr2(τ,m)](u)|=|AAαδ(2πfdc-ucscα0)|
(13)
可见,经过FRFT处理后,慢时域信号在FRFT域呈现冲激函数,信号能量得到最大程度的积累,有利于后续检测处理。此时,最佳FRFT域u0满足u0cscα0=2πfdc。
3.4 目标散射特性的影响分析
对慢时域信号进行FRFT,信号能量在参数平面 (α, u) 上形成二维分布,通过阈值搜索此二维平面的峰值点,可确定信号的最佳旋转角度,即
(14)
根据FRFT域峰值点坐标(α0,u0),目标散射空变特性模型参数可表示为:
(15)
由式(13)和(15)可看出,目标散射的空变特性对目标回波能量无影响,对速度估计有影响。
4 计算机仿真与分析
在仿真中,考虑由一个手机基站T和一个接收机R构成的探测系统,假设T、R及目标分布在同一个双基地平面,且目标在1/2积累时间的位置与T、R构成正三角形,T与R相距1000 m,目标沿60°方向远离手机基站和接收节点飞行。假设噪声为复高斯白噪声。仿真参数设置为:
表1 仿真参数
Tab.1 Simulation parameters
参数参数值载频/GHz1.8信号带宽/MHz20脉冲重复时间/ms5采样率/MHz40脉宽/ms0.5积累时间/s5运动速度/(m/s)20SNR/dB-50,-56,-60
4.1 点散射目标仿真
图2给出了不同SNR条件下应用本文算法得到的回波距离多普勒图,作为对比同时给出了补偿前的FFT相参处理结果(如图3所示),可看出,补偿前目标表现很明显的距离走动和多普勒走动,补偿后(如图2(a),图2(b)和图2(c)所示)走动现象消失,目标回波能量聚焦,出现了回波峰值,这说明所提算法能够有效地进行走动校正,提高积累增益。当SNR较低时,如图2(c)所示,由于噪声能量较高,相对于图2(a)和图2(b)来说,目标峰值不易得到,若SNR更低时,经FRFT处理后,目标完全淹没在噪声中,检测困难。在各个SNR条件下分别进行8次Monte Carlo仿真,如图4所示,从图中可知,在各SNR下得到的仿真结果与理论结果之差都在1 dB以内,定量说明了所提算法可以有效提高回波SNR,为城区环境中小目标检测提供了一种新的技术途径。
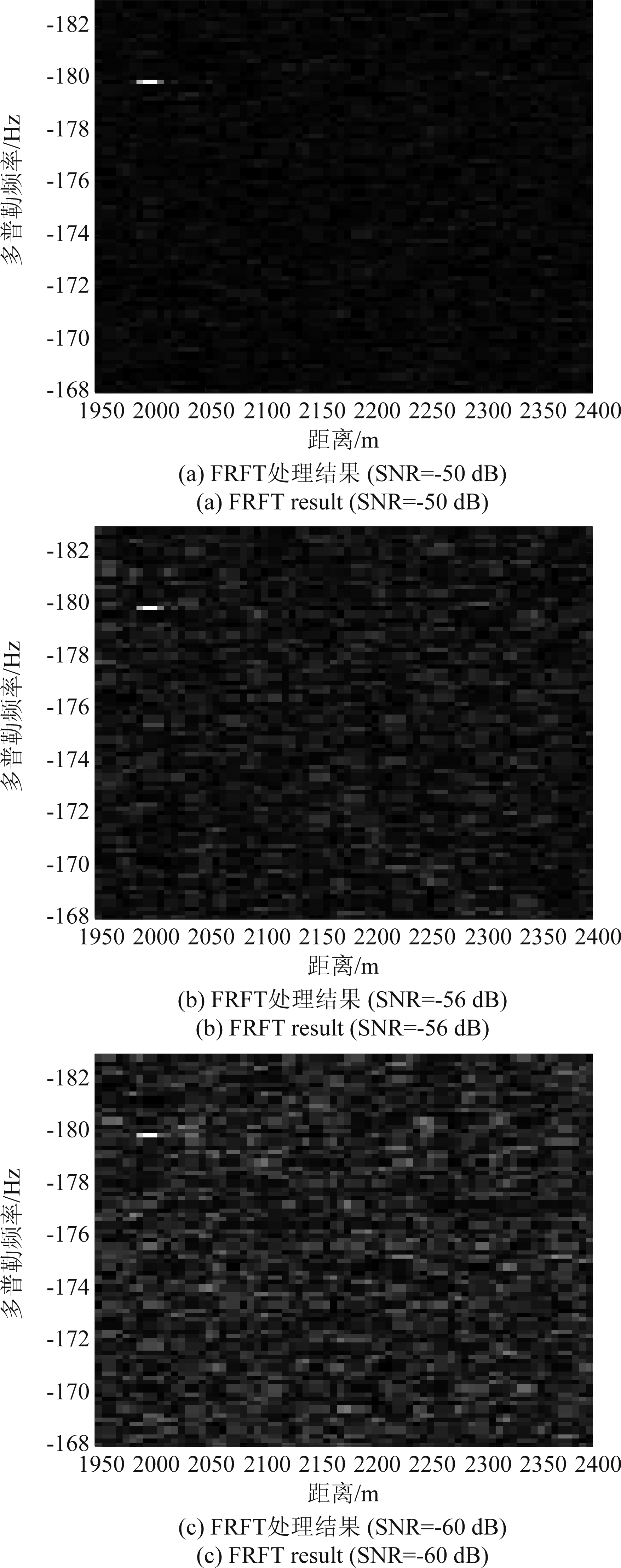
图2 不同SNR条件下的回波距离多普勒图
Fig.2 Range-Doppler plot of echo with different SNR
图3 FFT处理结果(SNR=-50 dB)
Fig.3 FFT result (SNR=-50 dB)
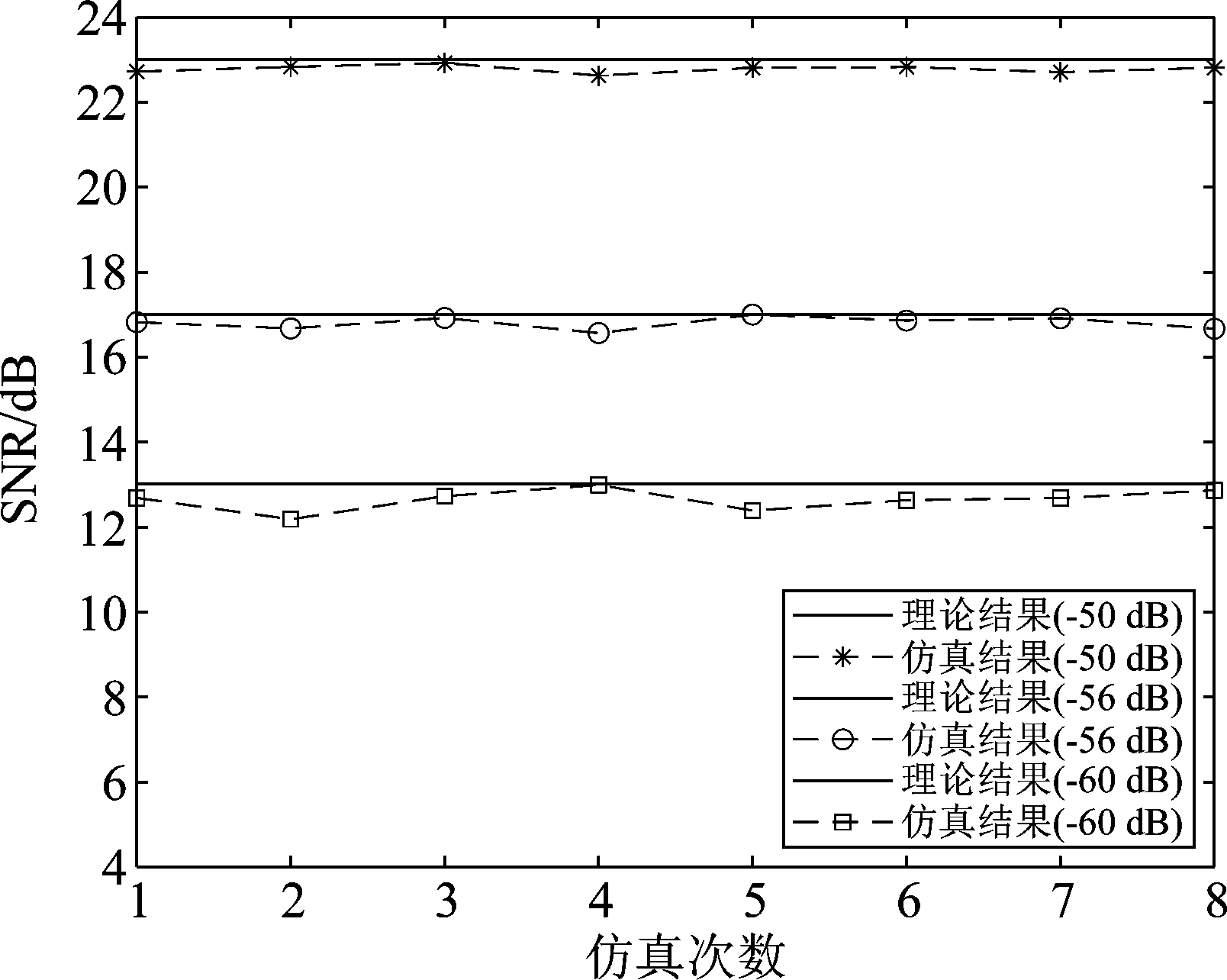
图4 8次 Monte Carlo仿真
Fig.4 8 Monte Carlo simulations
4.2 目标散射空变仿真
在给出的典型目标散射空变特性模型下,设置参数a和b,如表2所示。对引入散射特性的目标回波进行长时间相参积累,得到目标散射空变对回波能量和参数估计的影响,如图5所示。从图5(a)可看出,引入目标散射空变特性与不引入比较,目标的回波能量差别稳定在3 dB以内,这说明目标散射空变特性对回波能量无影响;图5(b)和(c)的纵轴分别表示理论推导和仿真两种情况下,ΔVp和
的真值与估计值的偏差随参数a和b的变化情况,其中仿真结果与理论计算结果的偏差在5%范围内,且都关于参数a和b呈线性变化,这说明目标散射空变特性对速度估计具有一定的影响。
表2 参数a和b
Tab.2 Parameters of a and b
参数参数值a/rad-16葩/3-8葩/3028葩/540葩/3b/rad-葩/5-葩/80葩/45葩/12
图5 目标散射特性对回波能量和参数估计的影响
Fig.5 Influence of target scattering characteristics on echo energy and parameter estimation
5 结论
针对城区环境中微弱慢速小目标的检测问题,本文提出了一种基于LTE信号的长时间相参积累算法。首先,在回波模型中引入了满足多项式的目标散射模型;其次,理论分析了目标距离走动和多普勒走动特性,提出了用keystone变换校正距离走动,用FRFT补偿多普勒走动的长时间相参积累算法,并分析了目标散射空变性对回波能量和速度参数估计的影响;最后,仿真结果验证了所提方法的有效性,且表明对于多项式散射模型的目标,其散射空变性对回波能量无影响,对速度参数估计具有一定的影响。由于keystone变换和FRFT都是线性的,因此所提算法也能够推广到多个目标环境。
此外,5G技术已受到广泛关注,研究基于5G信号的长时间相参积累算法具有重要的意义,未来我们将致力于研究基于5G信号的外辐射源雷达系统对微弱慢速小目标的检测问题。
[1] 黄硕. LTE信号的被动雷达波形分析[D]. 天津: 天津大学, 2012.
Huang Shuo. Wave analysis of LTE signals for passive radars[D]. Tian Jin: University of Tian Jin, 2012.(in Chinese)
[2] Perry R P, Dipietro R C, Fante R L. SAR imaging of moving target[J]. IEEE Trans on AES, 1999, 35(1): 188-200.
[3] 张顺生, 曾涛. 基于keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 1675-1678.
Zhang Shunsheng, Zeng Tao. Weak target detection based on keystone transform[J]. Acta Electronic Sinica, 2005, 33(9): 1675-1678.(in Chinese)
[4] 战立晓, 汤子跃, 朱振波. 米波双基地雷达长时间相参积累算法[J]. 信号处理, 2013, 29(3): 351-359.
Zhan Lixiao, Tang Ziyue, Zhu Zhenbo. Long term coherent integration algorithm for metric-band bistatic radar[J]. Journal of Signal Processing, 2013, 29(3): 351-359.(in Chinese)
[5] 张卫, 顾红, 苏卫民. 基于keystone变换的OFDM信号距离走动校正方法[J]. 数据采集与处理, 2013, 28(4): 421- 424.
Zhang Wei, Gu Hong, Su Weimin. Range walk correction of OFDM signal radar with keystone transform[J]. Journal of Data Acquisition and Processing, 2013, 28(4): 421- 424.(in Chinese)
[6] 杨金禄, 单涛, 陶然. 数字电视辐射雷达的相参积累徙动补偿方法[J]. 电子与信息学报, 2011, 33(2): 407- 411.
Yang Jinlu, Shan Tao, Tao Ran. Method of migration compensation in coherent integration for digital TV based passive radar[J]. Journal of Electronics and Information Technology, 2011, 33(2): 407- 411.(in Chinese)
[7] 张丹, 吕晓德, 杨鹏程, 等. 外辐射源雷达多普勒徙动补偿新方法[J]. 雷达科学与技术, 2017, 15(4): 375-380.
Zhang Dan, Lv Xiaode, Yang Pengcheng, et al. A new doppler migration compensation method for passive radar[J]. Radar Science and Technology, 2017, 15(4): 375-380.(in Chinese)
[8] 曾涛, 刘飞峰, 冯文玲, 等. 一种天基双基地雷达的动目标长时间相参积累方法[P]. 中国: 201510382112.2, 2015.12.02.
Zeng Tao, Liu Feifeng, Feng Wenling, et al. A long term coherent accumulation method for moving target of space-based Bistatic radar[P]. China: 201510382112.2, 2015.12.02.(in Chinese)
[9] 郭云飞, 周森山, 赵尚宇. 基于Keystone-FRFT的机动弱目标检测算法[J]. 杭州电子科技大学学报: 自然科学版, 2015, 35(1): 97-100.
Guo Yunfei, Zhou Senshan, Zhao Shangyu. A maneuvering weak target detection algorithm based on keystone-FRFT[J]. Journal of Hangzhou Dianzi University: Natural Science Edition, 2015, 35(1): 97-100.(in Chinese)
[10] 关键, 陈小龙, 于晓涵. 雷达高速高机动目标长时间相参积累检测方法[J]. 信号处理, 2017, 33(3A): 1- 8.
Guan Jian, Chen Xiaolong, Yu Xiaohan. Long-time coherent integration-based detection method for high-speed and highly maneuvering radar target[J]. Journal of Signal Processing, 2017, 33(3A): 1- 8.(in Chinese)
[11] 施祥同. OFDM雷达信号波形设计方法与仿真实现[D]. 长沙: 国防科学技术大学, 2010.
Shi Xiangtong. OFDM Radar Waveform Design Methods and Simulation[D]. Chang Sha: National University of Defense Technology, 2010.(in Chinese)
[12] Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Trans. Signal Processing, 1996, 44(9): 2141-2150.
[13] 陶然, 邓兵, 王越. 分数阶Fourier变换在信号处理领域的研究进展[J]. 中国科学 E辑 信息科学, 2006, 36(2): 113-136.
Tao Ran, Deng Bing, Wang Yue. Research progress of fractional Fourier transform in signal processing[J]. Science In China Ser. E Information Science, 2006, 36(2): 113-136.(in Chinese)
