1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)作为重要的一种成像雷达,具备全天时、全天候的优势,自发明之初便被广泛应用于军用、民用领域,是有源遥感探测的重要手段之一。合成孔径雷达通过发射线性调频信号与平台与目标间的相对运动,对距离向和方位向进行脉冲压缩处理,从而获得高分辨率图像[1]。而定标技术是获取高精度SAR图像的重要环节之一。未经定标的系统不仅系统稳定性差,测量重复率差,且其图像无法精确地反映出来实际地物的散射特性[2-3]。
传统定标技术分为内定标与外定标。斜距定标作为外定标技术的重要组成部分,是获取高精度SAR图像的重要环节。传统的斜距定标方法通过定位定向系统(Position and Orientation System,POS)辅助数据和地面控制点的坐标对斜距进行测量,其测量精度受到 POS 系统测量精度的限制[4-7]。但对POS系统精度的强依赖性,将导致系统成本过高,系统复杂性增加等问题。而SAR方位向提供的信息除进行方位向压缩外,还可通过处理子孔径的相位进行距离测量。利用合成孔径雷达中基本的“走-停”模型,引入子孔径相位精确处理的概念,将传统雷达的测角原理与合成孔径雷达算法处理相结合。在提供一种新的测角模型的同时,利用Cramer-Rao界对其测角性能进行评价,并根据测角与测距定位的关系,将其应用于斜距定标中。经分析该方法在保证一定定标精度的情况下,减少了对地面控制点的精确位置测量与系统POS长时稳定精度的依赖,是由数据域提供的一种新的定标方式。
本文主要讨论合成孔径雷达方位向信息新的处理应用方法,结合雷达测角,实现合成孔径雷达子孔径相位测角、定标。内容安排如下:第2节介绍了合成孔径雷达子孔径相位测角模型及测角误差的Cramer-Rao界分析,第3节推导了合成孔径雷达子孔径相位法测角精度与测距定位精度的关系,针对测距定位精度与传统斜距定标方法进行了对比。
2 SAR子孔径相位测角精度分析
2.1 SAR子孔径相位测角模型
根据合成孔径雷达(SAR)成像原理,结合其成像所使用的“走-停”模型,可以利用相邻PRT之间雷达信号的收发模拟测角雷达实现测角,其重要的一个保证条件为SAR发射信号间具有相参性。
首先构造SAR子孔径相位测角模型,验证其满足测角的基本假设:各阵元接收电磁波为平行关系。SAR子孔径测角模型如图1所示。其中V为平台运动速度,h为飞机飞行高度,θd为下视角,Rc为中心距,R为目标-波束斜边距,θa为方位向波束宽度,PRT为脉冲重复时间。
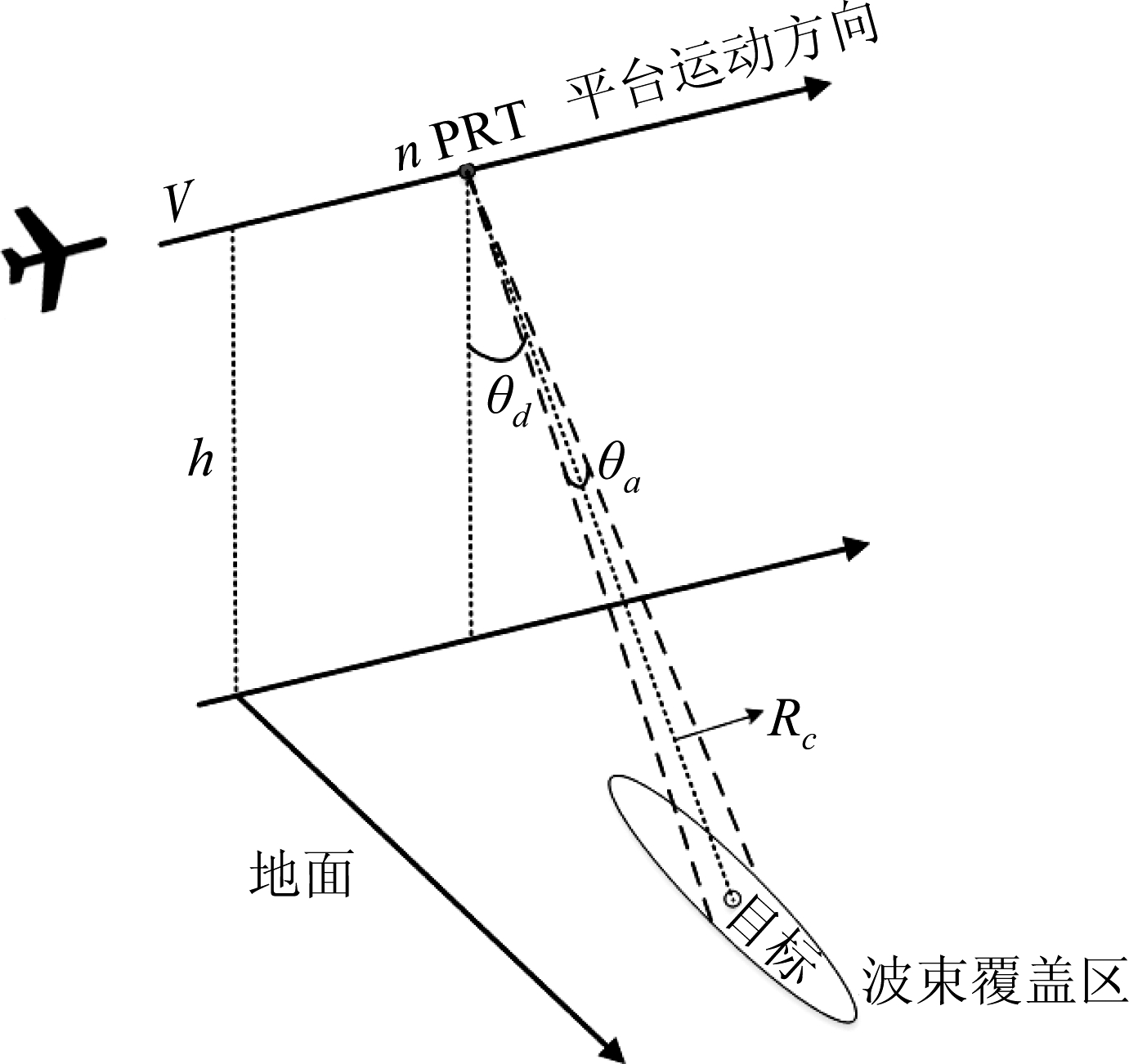
图1 SAR子孔径相位测角模型
Fig.1 SAR angle measurement model based on subaperture phase
当雷达波束第一次照射到目标(1 PRT)时,其与目标的距离为
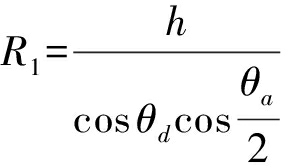
(1)
当平台运动到下一个PRT时,其与目标的距离为
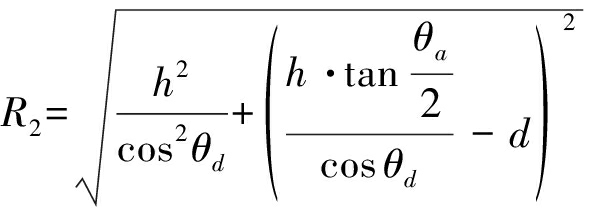
(2)
其中,对于合成孔径雷达,d=PRT·V。
此时,飞行方向与平台-目标连线的夹角为
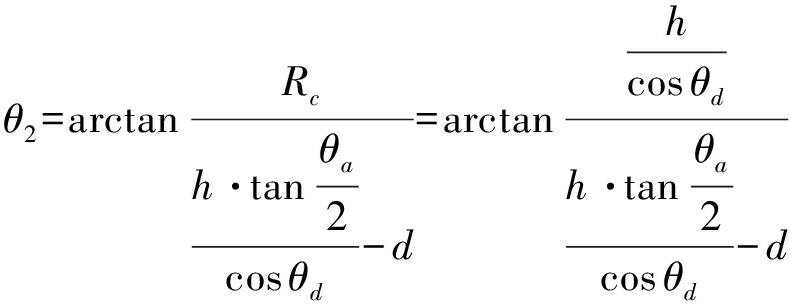
(3)
对比前一个PRT,其夹角变化为
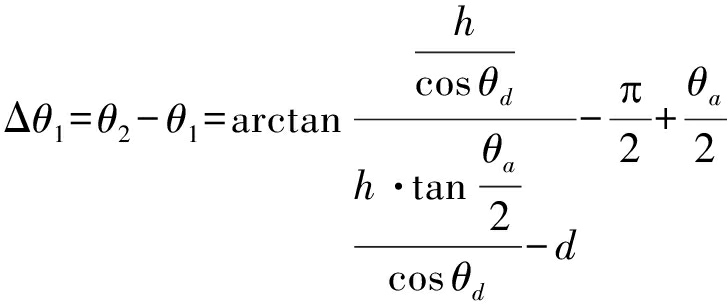
(4)
当
时
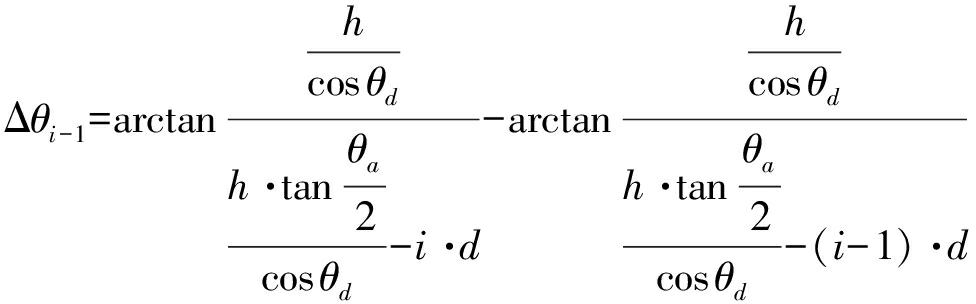
(5)
以Ka波段SAR系统为例,结合实际情况代入具体数据进行分析。雷达载频设置为35 GHz,PRF为3.125 kHz,下视角为70°,平台飞行高度为914 m,飞行速度为70 m/s,方位向波束角近似为10°,则
(6)
考虑极限情况时,当θi=90° 时,i≈10437,此时Δθi-1=8.382*10-6 rad,其角度变化曲线如图2所示。
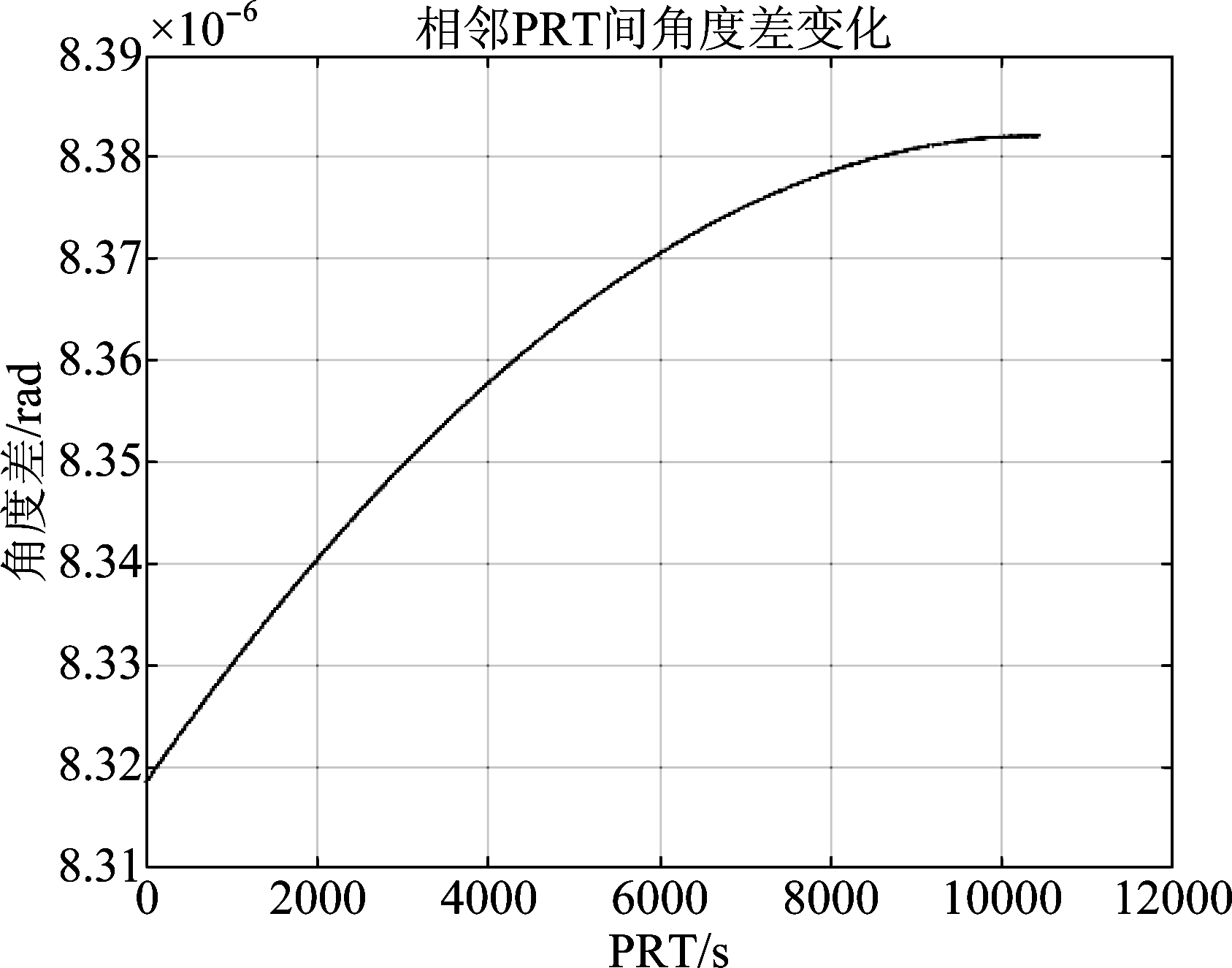
图2 不同相邻PRT间角度差变化
Fig.2 Angle difference change with different PRT
由图2可以看出,当
时,相邻PRT间子孔径接收回波与平台运动方向的夹角相对较小,因此在使用子孔径相位模型时,可以近似认为目标回波来波角度相同,满足角度估计的基本假设。
2.2 SAR子孔径相位测角精度Cramer-Rao界推导
Cramer-Rao界是衡量参数无偏估计方法的标准,是参数估计方差的下限,本节将利用这一数学工具进行方法精度分析。下面针对简单情况下的双PRT子孔径相位测角的Cramer-Rao界进行数学推导与仿真。
结合SAR成像原理,在利用两个相邻PRT进行角度估计时,电磁波与子孔径基线夹角θ可通过两相邻PRT接收信号的相位差得到。因此实际上有两个待估参量:一个是参考PRT的相位α,另一个是θ。一般情况下,我们只关心θ的估计精度。
α和θ已知情况下,对于相同时刻的多次采样,若PRT 0服从均值为ejα的复高斯分布,信号形式可表示为s0[n]=ejα+w0[n],则PRT 1服从均值为
的复高斯分布,信号形式可表示为
其中,w0[n],w1[n]均为均值为0的复高斯分布。这里需要注意的是,雷达接收信号并不服从复高斯分布,这里所指其分布是针对于同一时刻下不同随机噪声下的采样。
PRT 0和PRT 1的联合概率密度为:
(7)
式(7)中,
上标T为普通转置,H为Hermit转置。分别对s0[n]与s1[n]求取相位,并作差反解出
构成θ的无偏估计[8]。根据式(7)中的概率密度函数与Fisher信息阵的定义,可计算2阵元联合估计的Fisher信息阵为:
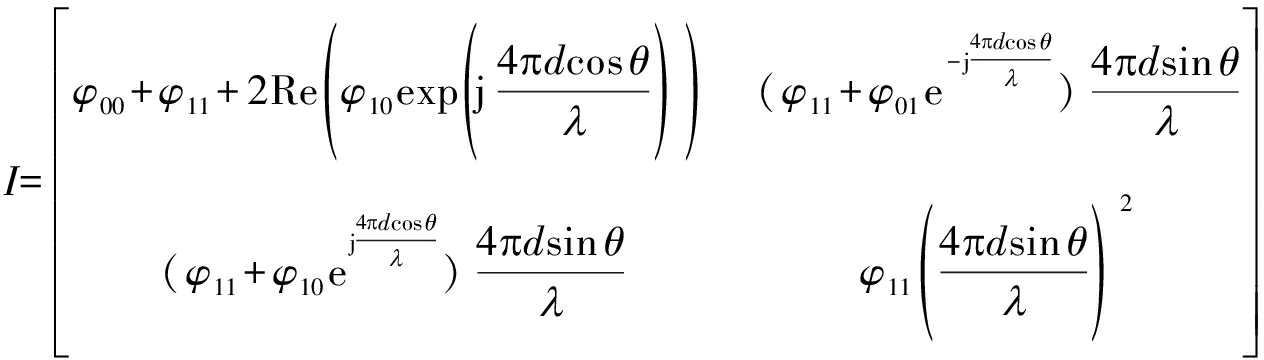
(8)
根据Cramer-Rao界推导可得θ的无偏估计量方差下限为
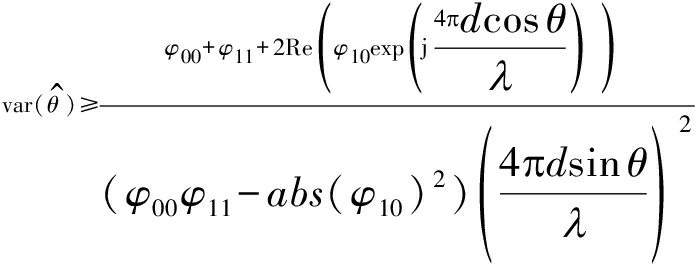
(9)
由于PRT 0与PRT 1相互独立,因此φ01=φ10=0。则上式可化简为
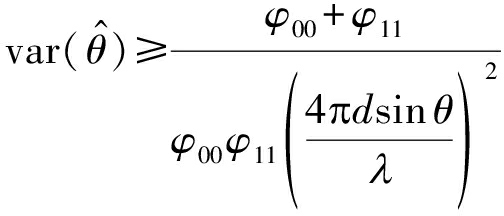
(10)
上式中,φ00,φ11由协方差矩阵∑求得,∑与各PRT采样方差有关。
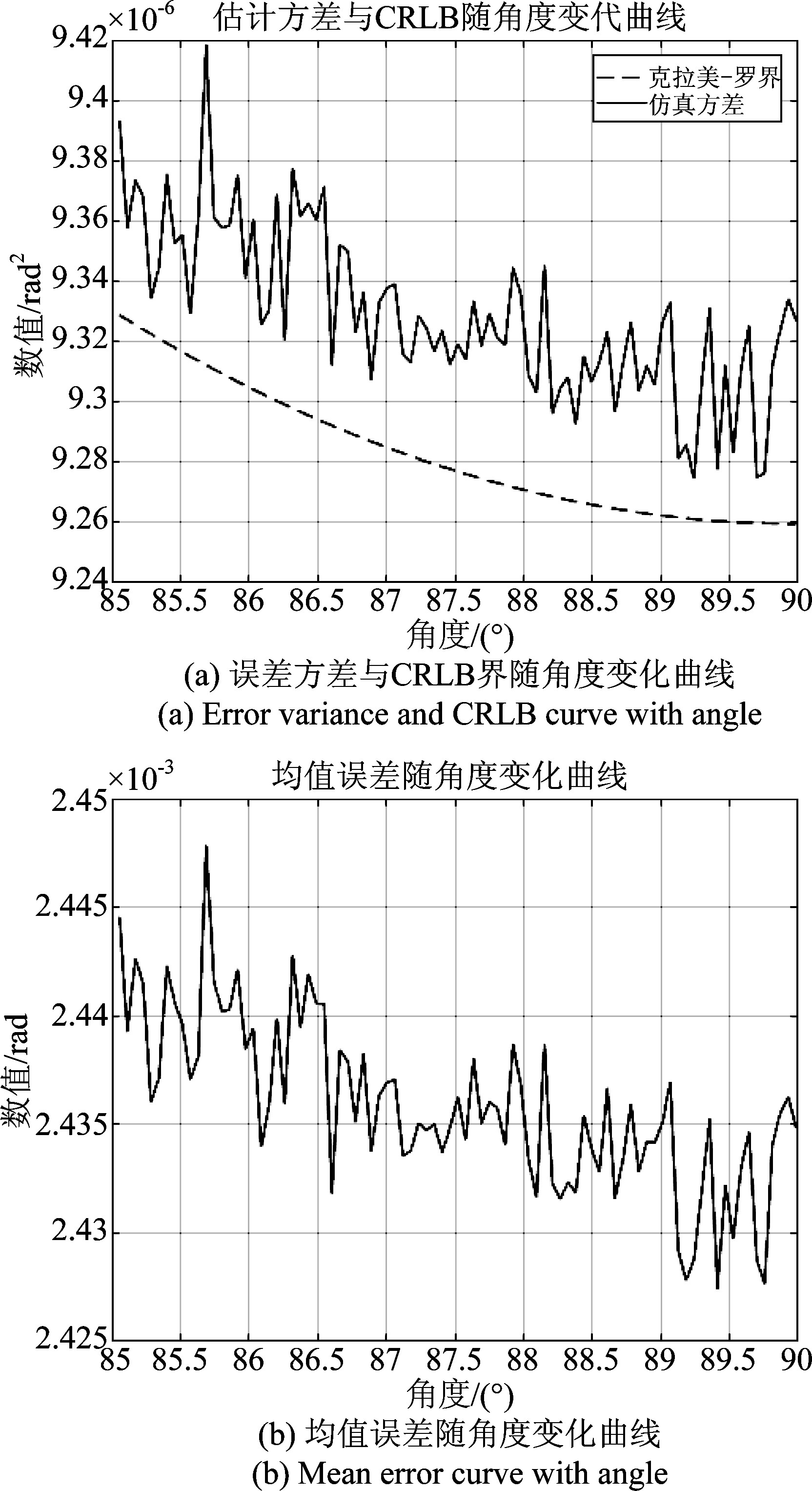
图3 测角性能分析
Fig.3 Angle measurement performance analysis
图3(a)为采用500000次蒙特卡洛实验,使用Ka波段SAR系统参数,信噪比仍选取20 dB时,仿真的估计方差与Cramer-Rao界随角度变化曲线,图3(b)为均值误差曲线。在角度变化范围选取上,根据其方位向波束宽度,结合具体SAR参数,选择角度范围为85°～90°。
由图3可知,在使用Ka波段SAR系统参数下,当选取子孔径PRT数目为2时,其Cramer-Rao界与方差在10-6数量级,均值误差为10-3数量级。
为进一步分析构成子孔径的PRT个数与Cramer-Rao界的关系,下面推导n个PRT的Cramer-Rao界表达通式。n个PRT的Fisher信息阵表达式为
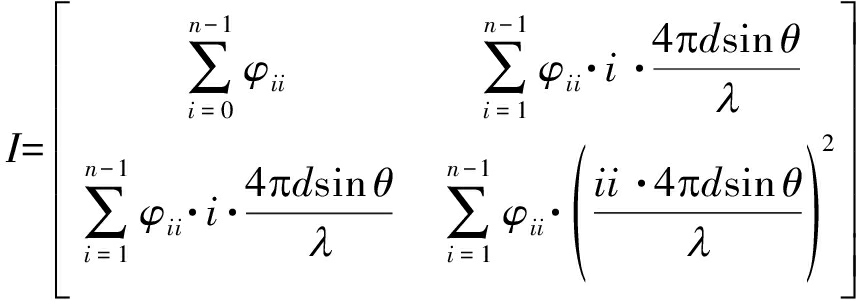
(11)
可得n个PRT时θ无偏估计量的方差下限为:
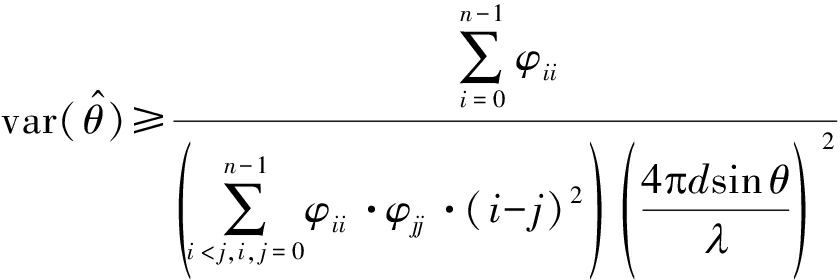
(12)
通过选取不同子孔径对其Cramer-Rao界、误差方差及均值误差进行仿真计算可知,选取的子孔径数目越多,其Cramer-Rao界、误差方差及测角均值误差越小。图4根据式(12)仿真了当角度为86.0886° 时,不同子孔径阵元个数下Cramer-Rao界的变化。从中看出,随着子孔径个数的增加,其Cramer-Rao界不断减小。当阵元个数增加到80时,其Cramer-Rao界为10-10数量级,其均值误差为10-5数量级。
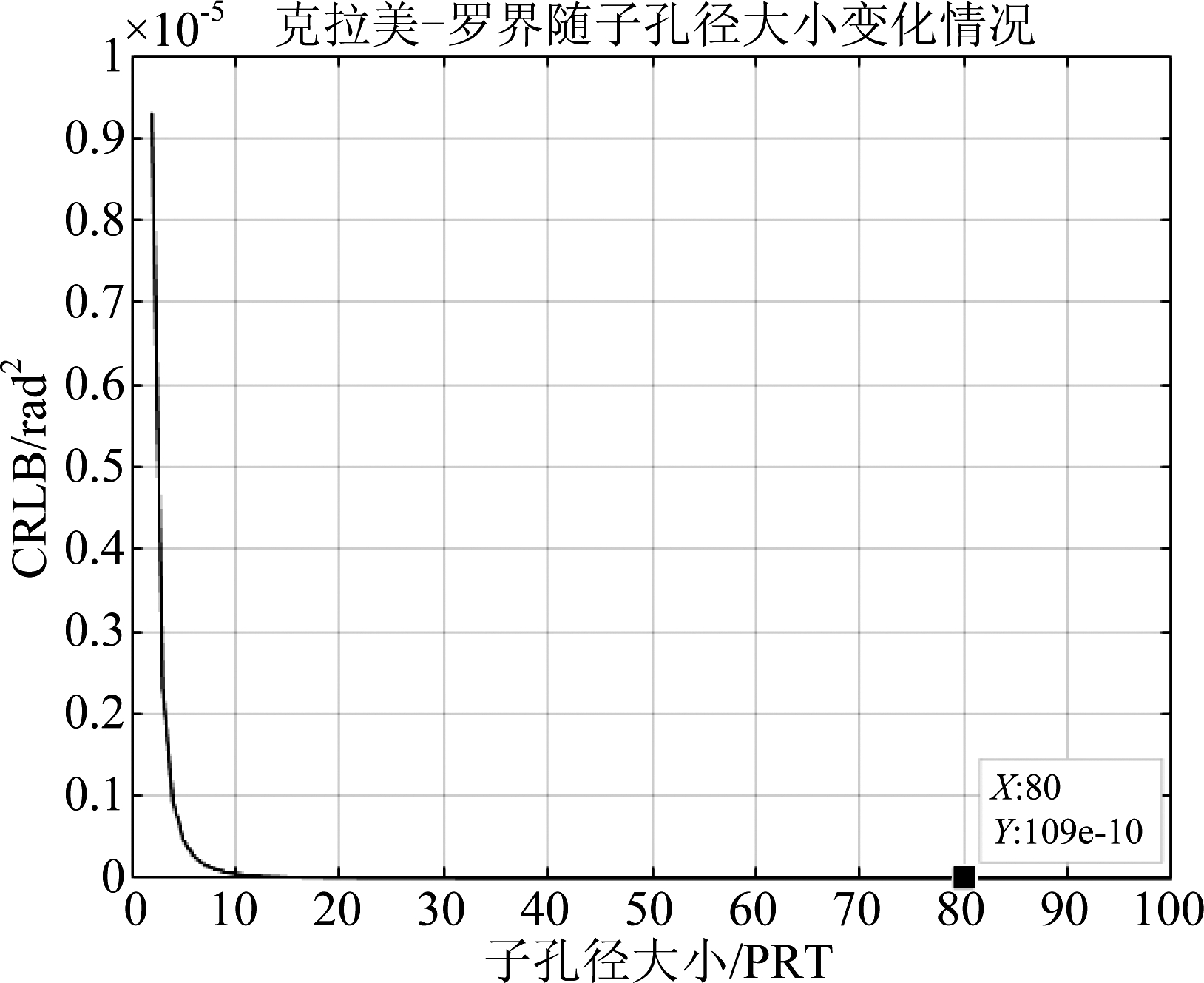
图4 不同子孔径长度下CRLB曲线
Fig.4 CRLB curve with subaperture length
3 SAR子孔径相位法定位测距应用
3.1 SAR子孔径相位测距定位原理
根据SAR成像原理,选取m个PRT作为一段子孔径,选取每段的第一个PRT作为参考测角阵元,当测角精度为θerror时,第i个子孔径所在阵列测得的角度为:
(13)
其中,θi为第i个子孔径所在阵列的真实角度。利用不同子孔径获得的角度估计值,计算可得目标与雷达的斜距估计值为:
(14)
通过以上推导,构建出了测角精度与测距精度之间的关系,为其进一步仿真可行性验证打下了基础。
3.2 仿真定位可行性分析
根据上一小节推导的测角精度与测距精度的关系,以及之前对于不同阵元个数下Cramer-Rao界的变化,仍使用Ka波段SAR系统参数,仿真了子孔径长度为80个PRT时不同测角精度对雷达定位目标距离精度的影响。其测角精度范围由其Cramer-Rao界推演得到,当m=80时,在2.2节所用雷达系统参数下,测角误差均值为10-5rad,测角精度仿真范围设置在10-5rad附近。
图5显示了不同控制条件对斜距定标精度的影响,计算结果不仅可以为该方法参数的选择提供参考,还可为下节中与传统斜距定标方法的对比提供数据支撑。图5中主要结论总结如表1所示。这里对图5(c)进行特别说明。通过图5(c)中曲线的变化可以看出本方法对于飞行速度误差不敏感,相较于一般的惯导系统,并没有对测速精度有很大的依赖性。
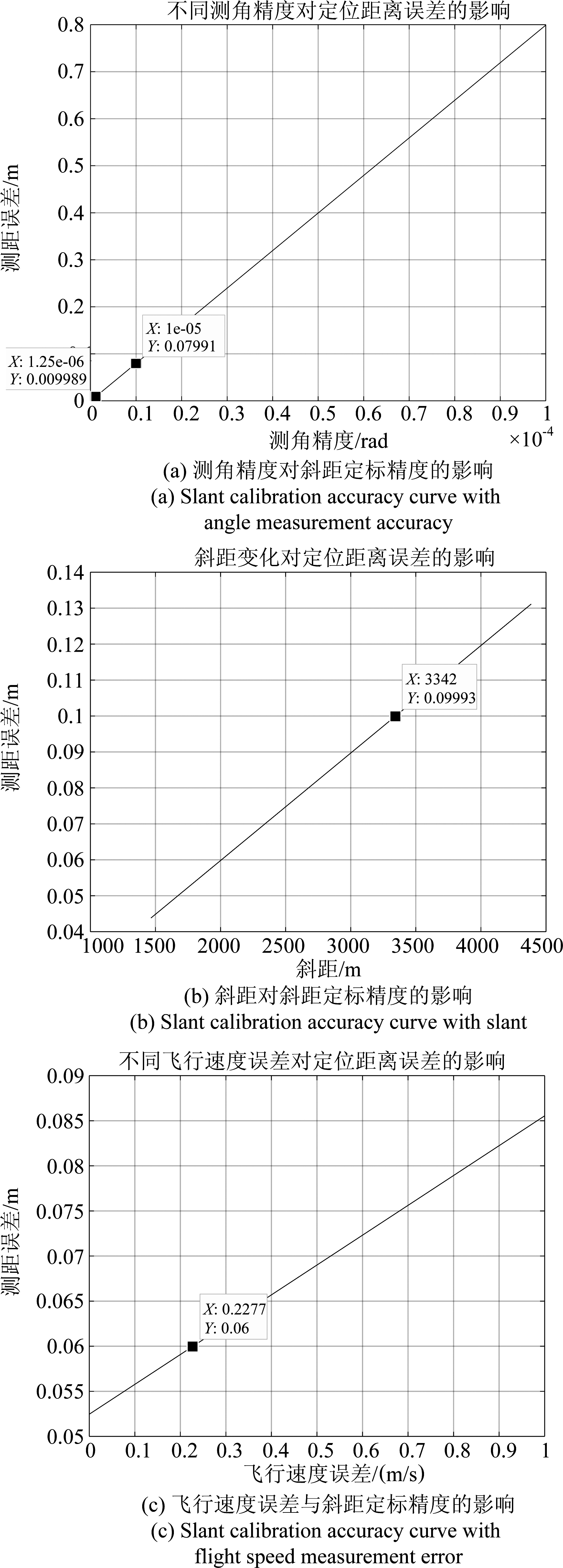
图5 不同因素对斜距定标精度的影响
Fig.5 Slant calibration accuracy curves with different factors
通过上述分析可以看出,传统斜距定标方法由于利用平台与控制点的精确几何关系从而受到POS系统精度制约。而本文提出的方法完全利用雷达数据进行角度估计并获取精确斜距值,进而实现斜距定标,减少了对地面控制点位置的精确定位及系统POS系统的长时高精度要求。即使使用80个PRT,在仿真系统参数下,仅需保证POS在0.0256 s内的测速精度。在具体精度对比上,以POS 510系统为例,当定位精度均为0.06 m时,其对速度估计精度的要求如表2所示。通过表2可以看出,本文方法在速度估计精度较低的情况下提供了与POS 510相同斜距定标精度。下面将把本文斜距定标方法应用到实际数据处理中进行检验。
表1 不同因素对斜距定标的影响
Tab.1 Influence of different factors on the calibration of slant range
影响变量影响趋势测角精度测角精度越高,斜距定标精度越高斜距斜距越近,斜距定标精度越高速度测量误差速度测量误差越小,斜距定标精度越高
表2 定位精度0.06 m时两种方法速度估计精度要求
Tab.2 Speed estimation accuracy requirements of two methods when positioning accuracy is 0.06 m
定位方法子孔径相位法POS510速度估计精度要求≤0.2277m/s≤0.02m/s
3.3 SAR子孔径相位测距定位法应用
斜距误差对SAR成像的精确利用有着重要意义,斜距误差一方面会引起方位调频率误差和残余运动误差[7],进而影响图像的方位向聚焦;另一方面还会引起高程反演误差。目前,斜距误差通常通过测量地面控制点和载机轨迹信息利用空间几何关系进行标定[9-10]。
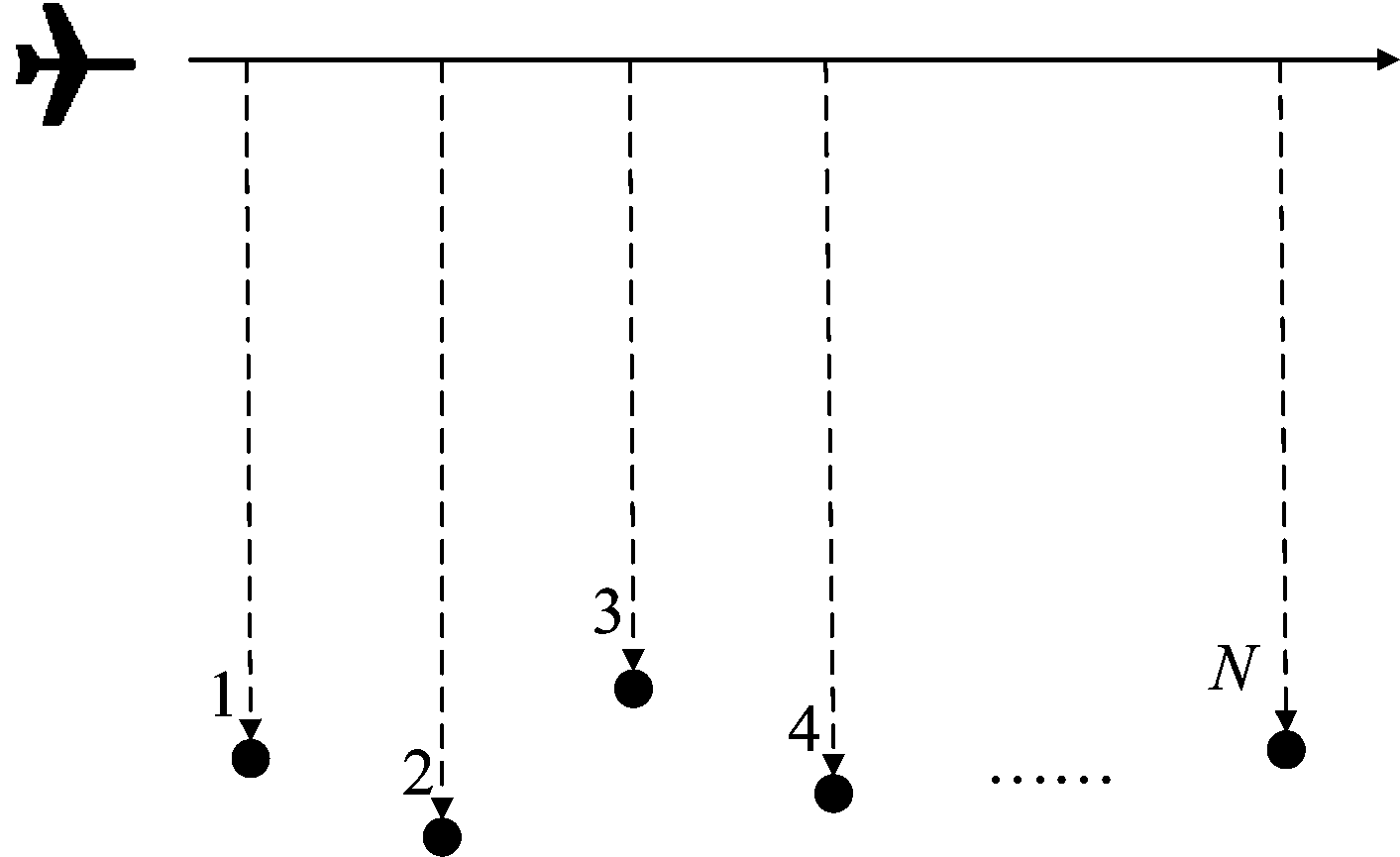
图6 斜距定标控制点示意图
Fig.6 Slant calibration control point diagram
斜距定标需预先选取N个地面控制点,如图6所示,利用已知控制点坐标可得:
(15)
其中,(xiGCP,yiGCP,ziGCP)表示第i个控制点的三维几何位置,(xi,yi,zi)表示雷达波束中心照射在第i个控制点时主天线的三维位置,Δr为所需标定的斜距误差,ri表示第i个控制点在SAR图像上的斜距,其计算公式如式(16)所示:
(16)
上式中,c表示光速,τ0表示定标前的系统采样时延, ji表示第i个控制点在SAR图像中的列号,δr 为斜距采样间隔。通过以上两式便可求出斜距误差Δr。
由于载机的轨迹信息受到POS精度的限制,因此利用系统与目标空间几何关系进行斜距定标受POS精度制约,与此同时,精度高的POS价格较为昂贵,在一些对成本要求较高的SAR系统中难以保证斜距定标的精度。从原理上可以看出,子孔径相位定标法完全利用雷达数据,减少了对地面控制点位置的精确定位及系统POS系统的长时高精度要求,即使使用80个PRT,在仿真系统参数下,仅需保证POS在0.0256 s内的精度。
此外,通过仿真分析可知,在一定的雷达参数设置、子孔径PRT数目以及飞行高度下,利用SAR子孔径而非POS与雷达系统信息得到的距离向定位精度可以达到cm级,在某些较优条件下,甚至可以达到0.01 m附近。通过对目前斜距定标方法的调研可知,传统斜距定标方法由于受到POS精度的限制,定标精度较为粗糙。以POS 510系统为例,其后处理速度误差为0.02 m/s时,可提供 0.05 m 的后处理定位精度,此时综合考虑定标点位置测量误差、图像处理误差、大气误差等因素的影响,由传统斜距定标方法可获得的最高斜距定标精度大约为 0.06 m[11]。而结合上一小节仿真结果可以看出,当速度误差为0.1 m/s时,SAR子孔径相位梯度定标方法的距离定位精度为0.05577 m,在速度误差更大的情况下提供了更高的定标精度。因此,其可以作为一种新的斜距定标方法,并取得更好的斜距定标精度。
4 结论
本文利用合成孔径雷达子孔径相位,提出了一种新的斜距定标方法。该方法将传统阵列测角原理与合成孔径雷达子孔径相结合,在运动误差较大的情况下可获得较高的斜距定标精度。通过计算推导与仿真结果可以看出,与传统斜距定标方法对比,该方法在速度误差较大时,其斜距定标精度不逊于传统方法,而且不需要地面控制点的精确坐标,是一种基于数据处理的斜距定标新方法。
[1] Curlander J C, Mcdonough R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. Wiley, 1991: 1-22.
[2] Freeman A. SAR calibration: an overview[J]. IEEE Trans. Geosci. Remote Sensing, 1992, 30(6): 1107-1121.
[3] Zyl J J V, Chapman B D, Dubois P, et al. The effect of topography on SAR calibration[J]. IEEE Transactions on Geoscience & Remote Sensing, 1993, 31(5): 1036-1043.
[4] Mallorqui J J, Bara M, Broquetas A. Sensitivity equations and calibration requirements on airborne interferometry[C]∥IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120). IEEE, 2000, 6: 2739-2741.
[5] Huang J, Zeng Q, Jiao J, et al. High precision airborne SAR geometric calibration and geolocation based on an improved near range model[C]∥Geoscience & Remote Sensing Symposium. IEEE, 2015.
[6] Montazeri S, Gisinger C, Eineder M, et al. Automatic Detection and Positioning of Ground Control Points Using TerraSAR-X Multiaspect Acquisitions[J]. IEEE Transactions on Geoscience & Remote Sensing, 2018, PP(99): 1-20.
[7] 毛永飞. 机载双天线干涉SAR误差补偿与定标技术研究[D]. 北京: 中国科学院研究生院, 2012.
Mao Yongfei. Research on compensation and calibration for airborne dual-Antenna interferometric SAR[D]. Beijing: Institute Of Electronics Chinese Academy Of Scences, 2012.(in Chinese)
[8] Steven M. Kay. 统计信号处理基础: 估计与检测理论[M]. 罗鹏飞, 张文明, 刘忠，等,译. 北京: 电子工业出版社, 2014: 20-32.
Steven M. Kay. Fundamentals of Statistical Signal Processing[M]. Luo Pengfei, Zhang Wenming, Liu Zhong, et al. translate. Beijing: Publishing House of Electronics Industry, 2014: 20-32.(in Chinese)
[9] 张薇. 机载双天线干涉SAR定标方法研究[D]. 北京: 中国科学院电子学研究所, 2009.
Zhang Wei. Research on calibration method of airborne dual-antenna interferometric SAR[D]. Beijing: Institute of Electronics, Chinese Academy of Sciences,2009.(in Chinese)
[10] 邬俊, 徐刚. ISAR机动目标联合高分辨成像和参数估计[J]. 信号处理, 2018,34(11): 1355-1361.
Wu Jun, Xu Gang. High-resolution Inverse Synthetic Aperture Radar Imaging of Maneuvering Targets Joint with Parameter Estimation[J]. Journal of Signal Processing, 2018,34(11): 1355-1361.(in Chinese)
[11] 曾友兵. 高精度机载InSAR外定标方法研究[D]. 北京: 中国科学院电子学研究所, 2016.
Zeng Youbing. Research on Interferometric Calibration Method for High Precision Airborne InSAR System[D]. Beijing: Institute of Electronics, Chinese Academy of Sciences, 2016.(in Chinese)
