1 引言
迁飞是昆虫躲避不良生境/开拓时空新资源的特殊行为对策,也是导致虫害异地暴发和病害大流行的重要原因。重大农林害虫(如粘虫、褐飞虱、小地老虎等)和草原害虫(如草地螟、牧草盲蝽、东亚飞蝗等)均具有较强的迁飞能力。迁飞性虫害在我国常年发生面积约70亿亩次,造成近400亿斤粮棉重大损失[1],严重威胁我国的粮食生产安全,已成为制约农业持续稳定发展的重大瓶颈问题。若能实现迁飞昆虫的有效监测,不仅可以对我国迁飞性昆虫的群落结构、种群波动、物种关系以及害虫暴发致灾的生物学和生态学机理进行深入分析,促进迁飞昆虫学的理论发展;还可以建立虫害早期精准预警新体系,为实现“源头”治理提供必要的决策信息和情报支持,从根本上保障我国的粮食生产安全。
雷达(Radar)是无线电检测和测距(Radio detection and ranging)的缩写。昆虫雷达通过发射一束电磁波射向空中迁飞的昆虫,虫体(具有与雨滴相似的性质)引起电磁信号向四周反射,部分反射信号被雷达接收,利用雷达的定向和测距功能,可以计算出昆虫迁飞的方位、高度、位移和种群密度等参数,可为获取昆虫高空飞行的行为学参数提供新的研究手段。
从1968年英国昆虫学家Rainey在尼日尔首次用雷达对夜间迁飞的沙漠蝗成功观测至今[2],昆虫雷达已经历了半个世纪的发展,极大地促进了迁飞昆虫学的研究。最开始出现的昆虫雷达为扫描雷达体制。1971年,英国建成一部波长3.2 cm的X频带扫描昆虫雷达,于1972年在沙特阿拉伯对沙漠蝗的迁飞进行了野外观测[3]。此后,澳大利亚、美国和中国相继建成X频段扫描昆虫雷达,通过对迁飞昆虫的观测,取得重要研究成果[4]。基于扫描昆虫雷达,可测量迁飞昆虫群体的共同定向、密度、数量等参数,但是无法实现个体昆虫参数的测量,并且数据处理费时费力。
70年代中期,英国首先研制出垂直波束雷达(Vertical Looking Radar,VLR)[5]。该雷达为线性极化体制,波束垂直向上观测,并以波束中心为轴快速旋转。线极化方向随着波束旋转,因而将雷达极化方式称为旋转极化。1975年和1978年,该雷达在马里进行了2次观测,成功的检测到了个体昆虫的朝向和振翅频率[6]。80 年代中期,在VLR的基础上,英国将章动原理移植到VLR的设计中,研制成功ZLC(Zenith-pointing Linear-polarized Conical-scan, 垂直波束线极化圆锥扫描)制式的第二代VLR[7]。第二代VLR用于观测中、大型昆虫,可测量昆虫个体的飞行速度、方向和朝向,还可测量与昆虫的大小、形状有关的3个RCS(Radar-Cross Section,雷达散射面积)参数,用于昆虫质量估计[8]。计算机控制该雷达的整机运行,观测数据的计算分析也由计算机自动完成,极大的降低了昆虫观测的费用,而且实时性得到很大的提高,可以全季节或者全年的不间断观测,实现了长期的自动监视。第二代VLR出现至今已超过三十年,目前仍是应用最广泛的昆虫雷达。
昆虫雷达的创制和应用,尤其是第二代VLR的应用,促使迁飞昆虫学由定性研究发展到定量分析,拓展了迁飞昆虫学研究领域的广度和深度,使人们对昆虫的高空飞行行为有了新的认识[9]。然而,当前昆虫雷达仍有以下不足:(1)非相参雷达体制,仅能测量目标回波幅度信息,而无法获得相位信息;(2)距离分辨率低(45 m@英国VLR,50 m@澳大利亚VLR),且距离采样不连续,当同一距离单元存在多个目标时,无法有效测量目标参数;(3)极化方式单一,测量效率低,数据处理复杂且参数反演成功率低。
为了解决传统昆虫雷达的不足,本团队开发了一种基于全极化的相参雷达,该雷达工作在Ku频段,采用同时全极化体制,可同时测量目标HH、HV、VH和VV(H,Horizontal,水平;V,Vertical,垂直;HV表示垂直极化发射、水平极化接收的目标回波,其第一个字母表示雷达接收的极化方式,第二个字母表示雷达发射的极化方式,其他缩写同上)极化回波[10];发射波形采用调频步进频体制,距离分辨率高达0.2 m。该雷达采用金属球和倾斜的金属丝进行极化定标,可测量目标朝向和振翅频率,并已通过外场实验成功验证。
2 基于全极化的相参雷达
2.1 系统
该雷达系统参数如表1所示,雷达如图1所示。雷达为相参体制,中心频率16.2 GHz,采用调频步进频波形,共40个子脉冲,每个子脉冲采用chirp信号,子带宽20 MHz,步进频高分辨合成后,总带宽800 MHz,可实现0.2 m的距离分辨率。雷达采用同时全极化体制[11],发射链路和接收链路均包括H极化和V极化两个通道,天线为双极化抛物面天线。在发射信号时,H极化和V极化信号分别通过双极化天线的H端口和V端口同时发射出去,两种极化信号采用正交的相位编码隔离。在接收信号时,H极化和V极化同时接收,对H极化接收的信号进行相位解码,得到HH和HV信号;对V极化接收的信号进行相位解码,得到VH和VV信号,由此实现同时目标散射矩阵(SM,Scattering Matrix)测量。雷达配备伺服,可工作在扫描模式,也可以工作在垂直对天静止波束模式。
表1 全极化相参雷达系统参数
Tab.1 The fully polarimetric coherent radar system parameters
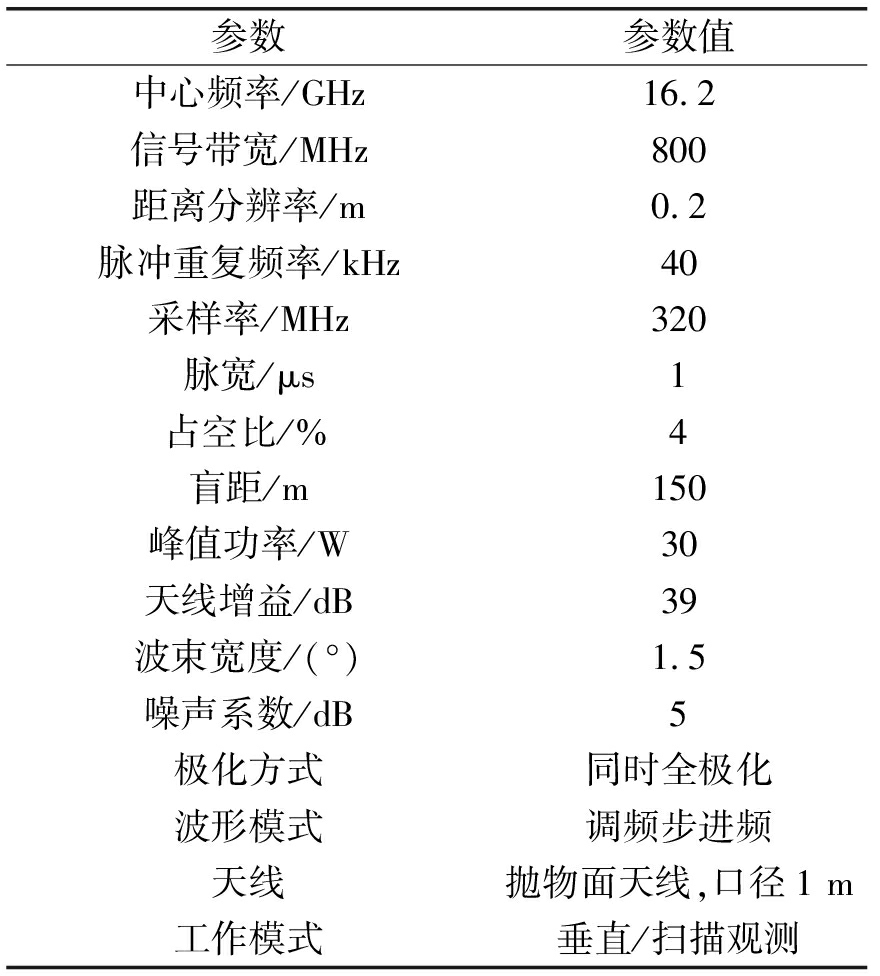
参数参数值中心频率/GHz16.2信号带宽/MHz800距离分辨率/m0.2脉冲重复频率/kHz40采样率/MHz320脉宽/μs1占空比/%4盲距/m150峰值功率/W30天线增益/dB39波束宽度/(°)1.5噪声系数/dB5极化方式同时全极化波形模式调频步进频天线抛物面天线,口径1m工作模式垂直/扫描观测
图1 全极化相参雷达
Fig.1 The fully polarimetric coherent radar
2.2 极化定标
SM包含了目标全部极化信息,在目标识别方面有很大的应用潜力[12-14]。该雷达可测量目标SM,然而雷达收、发链路均有H和V两个极化通道,通道之间会存在增益和相位不一致,双极化天线会存在两种极化信号的相互泄露串扰,因此,雷达直接测量的SM存在极化误差,需要进行极化定标。极化定标是指用雷达测量散射矩阵已知的标准定标体,解算极化误差,并在实际测量时补偿极化误差,还原目标真实SM的过程。
全极化相参雷达采用单目标校准技术[15],该技术仅测量一个金属球即可实现极化定标。考虑收、发链路极化误差,雷达测量的SM可建模为:
M=RCSCT=
(1)
其中,
和
分别表示接收和发射通道间幅、相误差矩阵,Rh和Th分别为发射和接收时水平极化通道幅、相特性,Rν和Tν分别为发射和接收时垂直极化通道幅、相特性;
为发射和接收时,天线的交叉串扰误差矩阵,c为极化串扰因子,式(1)中第一个C为接收天线的交叉极化串扰矩阵,第二个C为发射天线的交叉极化串扰矩阵,由于该雷达是单基地雷达,收、发共用同一天线,因此这里假设发射和接收时,天线的交叉极化串扰相同,C为对称矩阵是假设H和V极化之间的串扰互易,由于天线是无源器件,该假设是合理的;
为目标真实SM。
金属球的真实散射矩阵为:
(2)
其中,so为金属球的共极化RCS。将式(2)带入式(1)中,可得到金属球SM测量值表达式:
(3)
由式(3)可以解得参数c的值:
(4)
其中
(5)
由式(1)可得未知目标的SM测量值为
(6)
联合式(3)、式(4)和式(6),可以解得目标的SM的4个元素:
(7)
(8)
(9)
(10)
如果金属导体球到雷达的距离r0和未知目标到雷达的距离ru不相同,则需要在校准后的PSM乘上距离补偿因子(ru/r0)2e-2ik0(r0-ru)。
需要注意的是,由于式(4)中c的符号无法确定,该方法校准后的SM的交叉极化项(shν和sνh)存在180°相位模糊。这里采用测量N°金属丝朝向的方法判断c的符号,判断方法如下:
(1)测量N°金属丝的散射矩阵,N°∈(10°,80°);
(2)假定c的符号为“+”(或“-”),对金属丝进行极化校准;
(3)利用2.3节介绍的朝向提取方法计算金属丝朝向,若计算的朝向为N°,则c的符号为“+”(或“-”),若计算的朝向为-N°,则c的符号为“-”(或“+”)。
需要注意的是,N的最优值为45,此时散射矩阵的交叉极化项最强,测量误差最小;N越接近0或90,散射矩阵的交叉极化项越小,测量误差越大。
2.3 昆虫朝向估计
传统昆虫雷达为旋转极化体制,测量目标的极化方向图(不同极化方向的目标回波功率[16]),利用估计方法(如最小二乘法)估计昆虫朝向。全极化相参雷达可直接测量目标SM,因此采用基于目标SM的朝向提取方法[16]。
该方法是基于“当极化方向平行于昆虫体轴时,回波功率最大”的假设,利用最优极化理论,从SM中直接提取使回波功率最大时的极化方向,该方向即为昆虫朝向。最优极化理论揭示,当雷达极化方式为目标散射矩阵的主特征向量时,目标回波功率达到最大值,因此,可以从目标主特征值向量中提取昆虫朝向。
假设极化定标后,目标散射矩阵为
(11)
其中,shh、shν、sνh和sνν均为复数,对于本雷达(单基地)shν=sνh。目标的大特征值和对应的主特征向量可表示为
(12)
(13)
其中
κ=shνejβ/(λ-shh)
(14)
为提取昆虫朝向,将主特征向量写成椭圆极化的形式
(15)
其中,φ为极化方向,τm为椭圆角。
令式(13)与式(15)相等,即可得到昆虫朝向:
(16)
需要注意的是,式(16)仅在λ≠shh时成立,当λ=shh昆虫朝向为0°,因此可将式(16)改写为
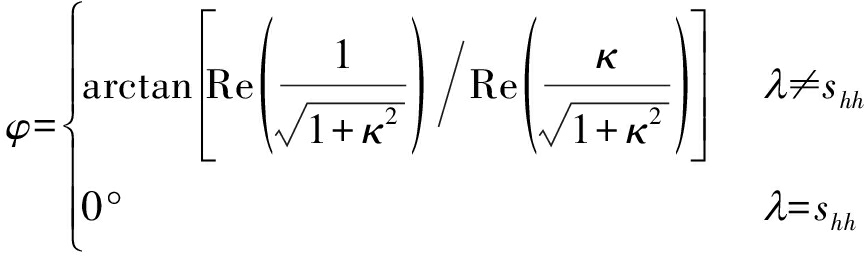
(17)
2.4 振翅频率提取
相比于传统VLR旋转波束,全极化相参雷达工作时波束垂直对天静止观测,更易于测量昆虫振翅频率。研究表明,昆虫振翅会调制回波幅度,同时也会调制回波相位,且利用相位调制可提取精度更高的振翅频率[17]。传统VLR为非相参雷达,仅能测量目标回波强度,只能使用幅度调制提取振翅频率;全极化相参雷达为相参雷达体制,可测量目标回波相位,因此,将采用文献[17]中基于相位调制的振翅频率提取方法。
全极化相参雷达可测量目标4路(HH、HV、VH、VV)极化回波,提取振翅频率时,选择其中回波最强(信噪比最高)的一路信号。振翅频率处理方法如下:
(1)提取目标回波相位;
(2)对相位做差分处理,去除低频成分;
(3)对差分相位做傅里叶分析;
(4)振翅调制会在频域数据中振翅频率处形成以零频为中心对称的小尖峰,找到小尖峰的位置即可提取振翅频率。
3 实验验证
2018年9～10月,课题组在云南省澜沧拉祜族自治县开展了极化定标实验和夜间垂直对空观测实验,下面将基于外场实测数据验证极化校准、朝向和振翅频率测量的有效性。
3.1 极化定标
极化定标实验场景如图2所示。金属球直径15 cm,由无人机悬吊在60 m高度,距雷达的地面距离300 m。雷达通过调整方位角和俯仰角对准金属球。金属丝测量场景类似图2,所用金属丝直径1.5 mm,长40 cm,其一端通过尼龙线系在无人机上(同金属球),另一端通过尼龙线连到地面,由实验人员手持尼龙线控制金属丝朝向,使其在垂直于雷达视线的平面内的朝向尽量接近45°(实际操作存在±10°误差)。实验假设c的符号为“+”,极化定标后提取朝向为38°(主要由实验角度误差导致),与实验设定朝向基本一致,所以c的符号确定为“+”。
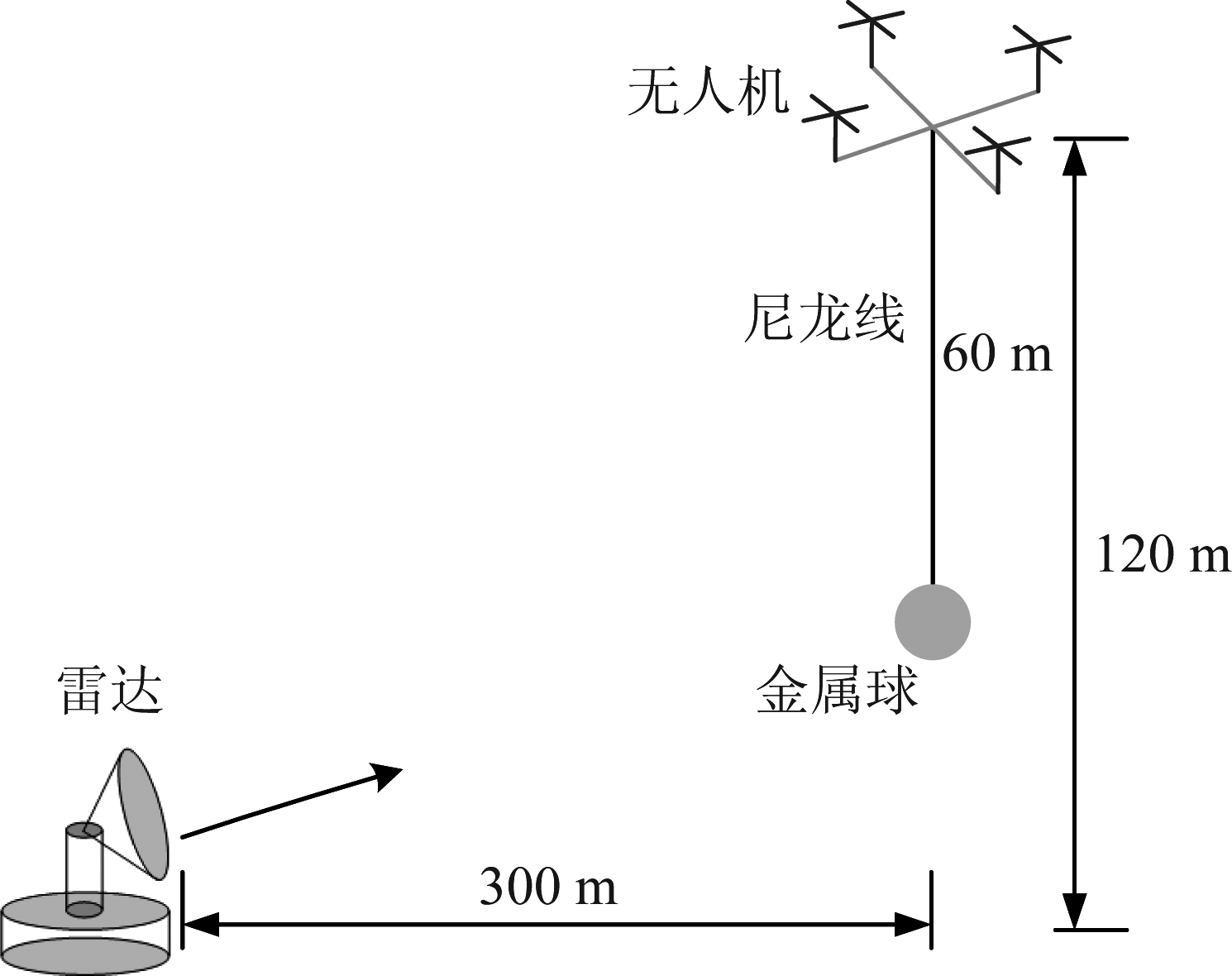
图2 极化校准实验场景
Fig.2 Polarization calibration experiment scene
将同一金属球测量2次(相隔2天),其中一次作为定标体,另一次作为目标,进行极化定标。极化定标前后极化方向图(理论上,金属球的极化方向图为标准圆形)如图3所示,极化方向图P的计算公式为:
(18)
其中,α为极化方向,S为目标散射矩阵。从图3可看到,定标前极化方向图误差较大;定标后极化方向图为较标准的圆形。定标后,系统极化隔离度为41 dB、通道间幅度不一致为0.1 dB、通道间相位不一致为5.5°。因此,该极化定标算法可较好的定标全极化相参雷达。
图3 校准前后金属球极化方向图
Fig.3 The metal ball polarization pattern before and after polarization calibration
3.2 昆虫朝向估计
基于2018年9月20日夜间雷达垂直对空观测采集的自由飞行昆虫数据,我们分析了雷达朝向测量昆虫朝向方法的有效性。首先,利用2.2节给出的极化定标方法,对目标SM进行极化定标,然后用朝向估计方法从定标后的SM中估计昆虫朝向。图4是3只昆虫的朝向提取结果,其中蓝色曲线是基于昆虫SM反演的极化方向图,红色直线是提取的朝向,可看到,所提取的朝向均为回波功率最大的方向。因此,雷达可成功提取昆虫朝向。
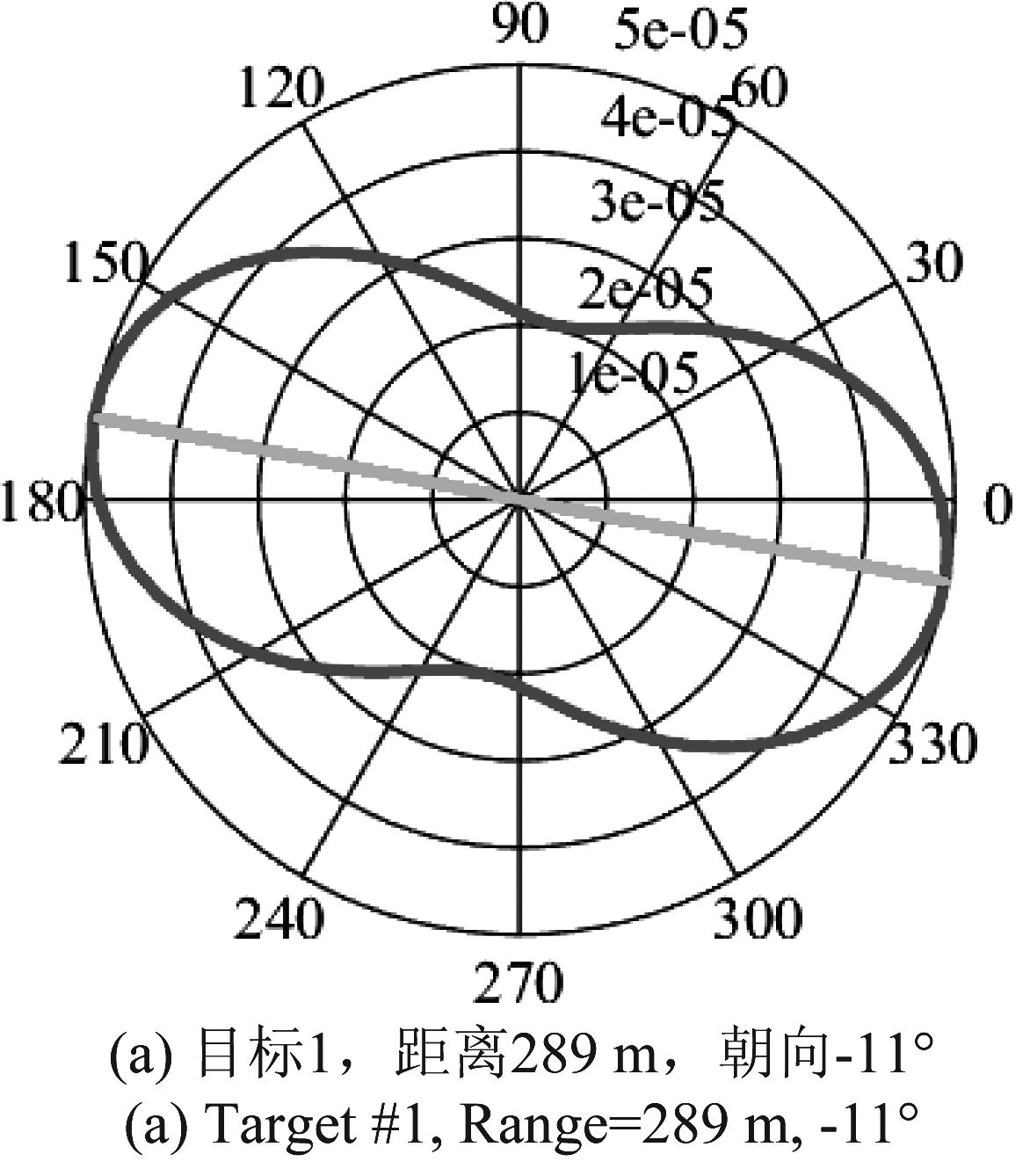
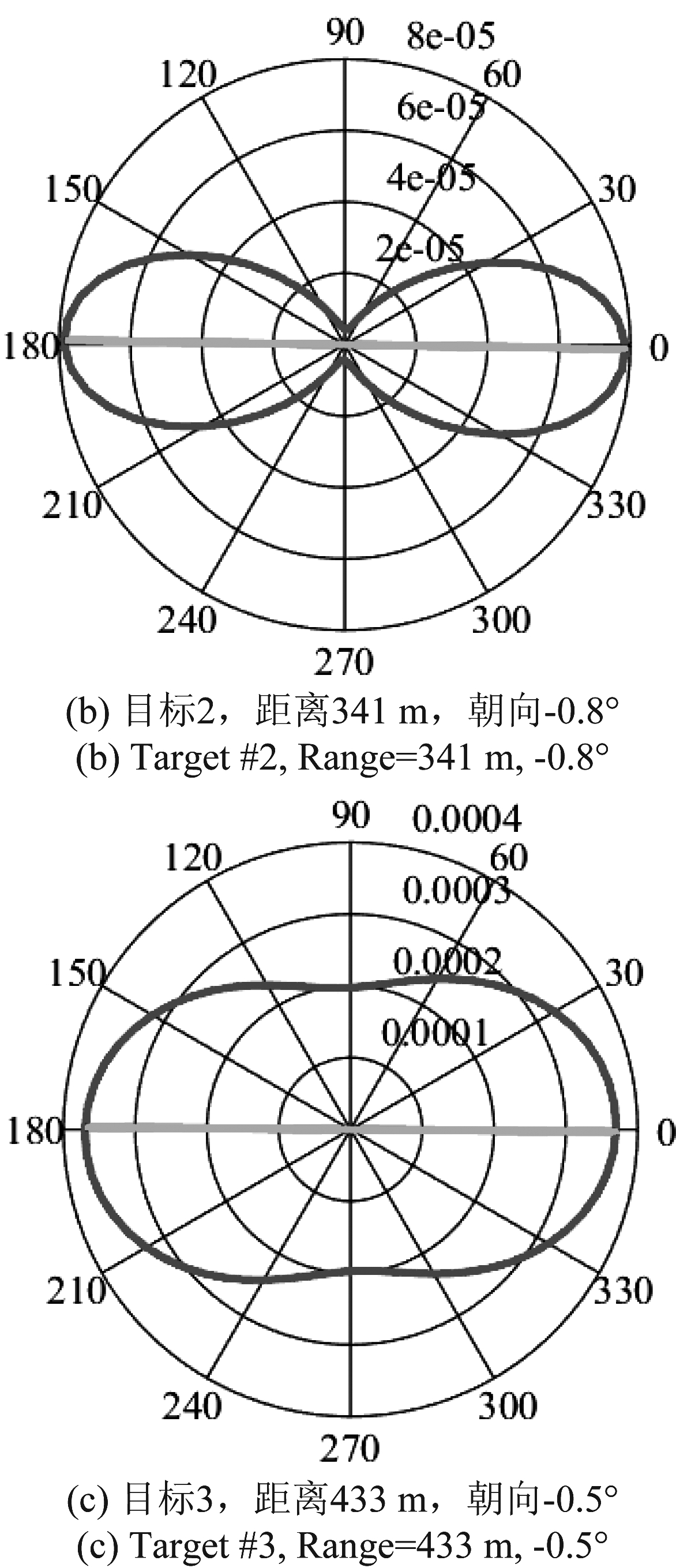
图4 昆虫朝向测量结果
Fig.4 The insect orientation measurement results
3.3 昆虫振翅频率提取
基于振翅频率提取方法,我们分析了图4中3只昆虫对应的振翅频率,图5所示的是对差分相位做傅里叶分析后的频域结果,可明显看到关于零频对称的尖峰,其对应的频率即为振翅频率,三只昆虫的振翅频率分别为36 Hz、53 Hz和28 Hz。因此,全极化相参雷达可成功提取昆虫振翅频率。
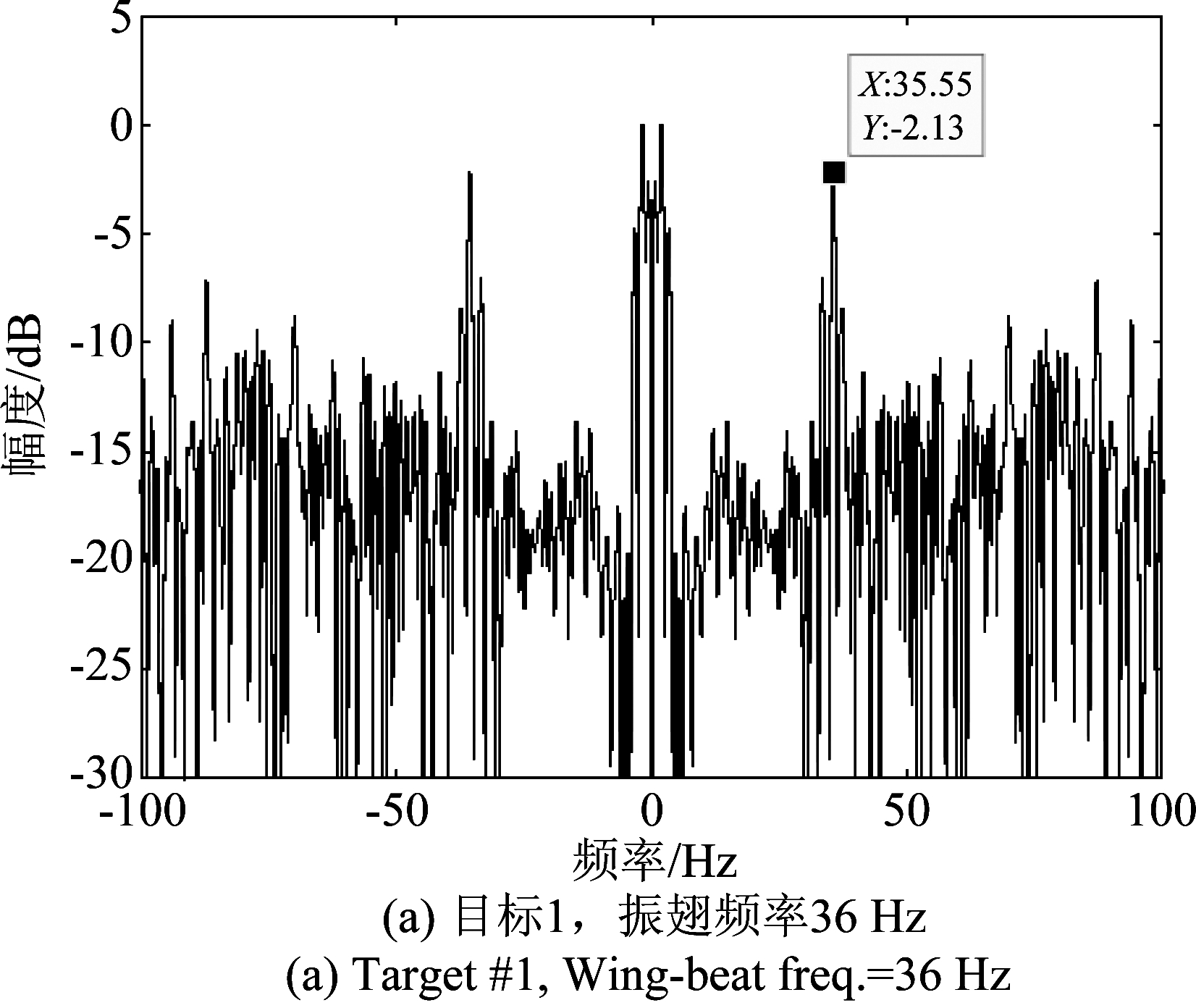
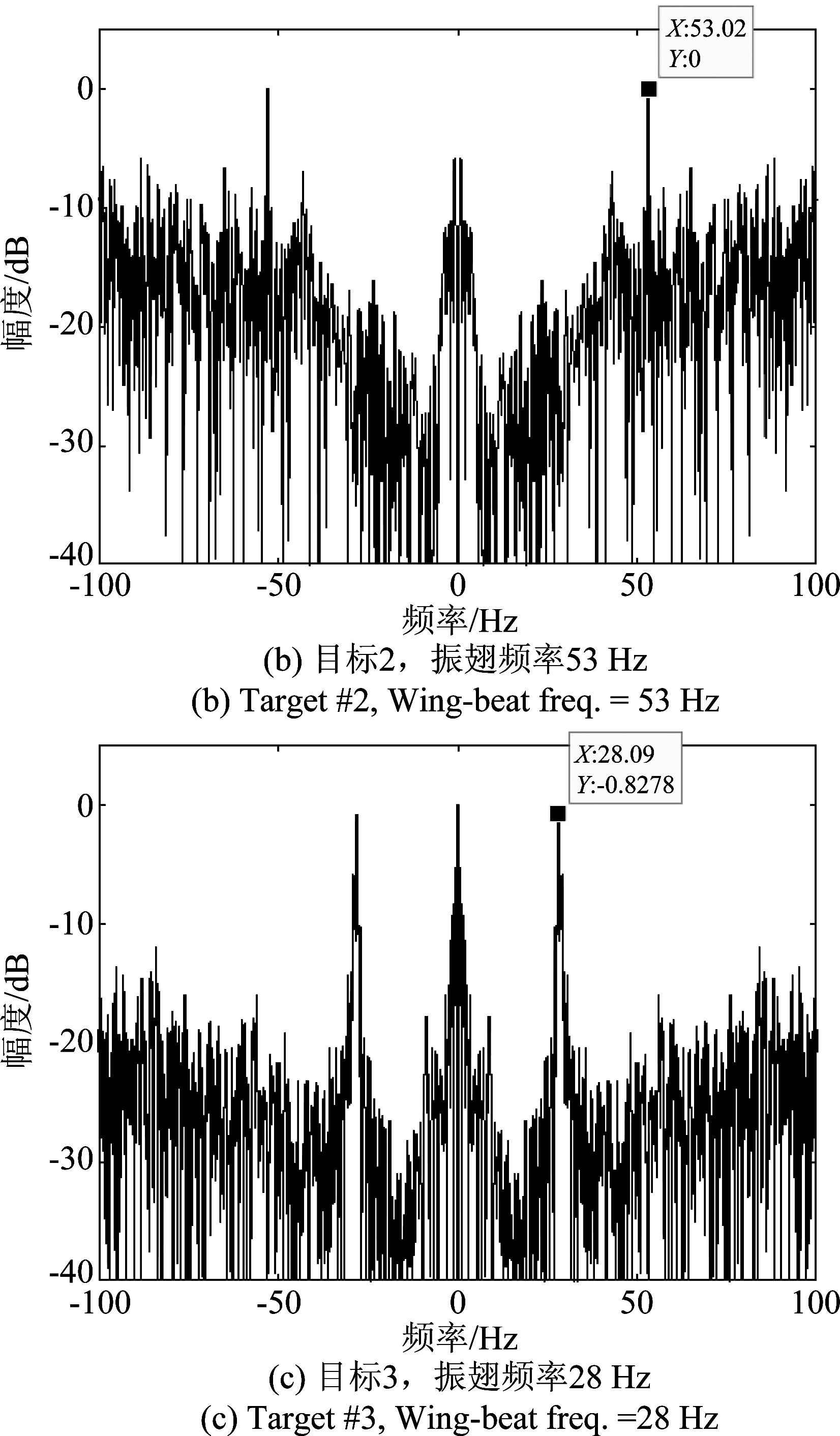
图5 昆虫振翅频率测量结果
Fig.5 The insect wing-beat frequency measurement results
4 结论
本文介绍了一种基于全极化的相参雷达,该雷达工作在Ku频段,采用同时全极化体制,调频步进频波形,距离分辨率高达0.2 m,可扫描观测也可以垂直对天静止波束观测,可测量昆虫朝向和振翅频率。雷达采用单目标校准技术进行极化定标,定标体为一个金属球和一段金属丝,实验时不需要精确控制金属丝的朝向,实际实施难度小,实验证明,采用该校准技术,雷达可实现较高精度的极化校准。雷达可直接测量目标SM,采用基于SM的昆虫朝向估计方法测量昆虫朝向,采用基于相位调制的昆虫振翅频率提取方法测量昆虫振翅频率,基于外场自由飞行昆虫观测实验,成功验证了雷达测量昆虫朝向和振翅频率的能力。
[1] 中华人民共和国农业部. 中国农业统计资料2013[M]. 北京: 中国农业出版社, 2014.
The Ministry of Agriculture of the People’s Republic of China. Statistics on Chinese agriculture 2013[M]. Beijing: China Agriculture Press, 2014.(in Chinese)
[2] Schaefer G W. Radar studies of locust, moth and butterfly migration in the Sahara[J]. Proceedings of the Royal Society of London, 1969, C34: 39- 40.
[3] Riley J R. Radar observations of individual desert locusts (Schistocerca gregaria (Forsk.)(Orthoptera: Locustidae))[J]. Bulletin of Entomological Research, 1974, 64: 19-32.
[4] Drake V A, Farrow R A. The influence of atmospheric structure and motions on insect migration[J]. Annual Review of Entomology, 1988, 33: 183-210.
[5] Reynolds D R, Riley J R. Radar observations of concentrations of insects above a river in Mali, West Africa[J]. Ecological Entomology, 1979, 4(2): 161-174.
[6] Riley J R, Reynolds D R. Radar-based studies of the migratory flight of grasshoppers in the middle Niger area of Mali[J]. Proc R Soc Lond B Biol Sci, 1979, 204(1154): 67- 82.
[7] Bent G A. Developments in detection of airborne aphids with radar[C]∥1984 British Crop Protection Conference-Pests and Diseases, 1984: 665- 674.
[8] Riley J, Reynolds D. Radar monitoring of locusts and other migratory insects[J]. Tropical Agriculture, 1993.
[9] Hu Gao, Lim K S, Horvitz N, et al. Mass seasonal bioflows of high-flying insect migrants[J]. Science, 2016, 354(6319): 1584-1587.
[10] Hu Cheng, Li Wenqing, Wang Rui, et al. Insect flight speed estimation analysis based on a full-polarization radar[J]. Science China Information Sciences, 2018, 61(10): 109306.
[11] 刘勇, 李永祯, 王雪松, 等. 基于正交互补序列的瞬时极化测量编码波形设计[J]. 信号处理, 2009, 25(9): 1353-1359.
Liu Yong, Li Yongzhen, Wang Xuesong, et al. The coding Waveform design for instantaneous polarization measurement based on orthogonal complementary sequences[J]. Signal Processing, 2009, 25(9): 1353-1359.(in Chinese)
[12] Hu Cheng, Li Weidong, Wang Rui, et al. Accurate Insect Body Length Extraction Based on the Invariant Target Parameters[C]∥2018 IEEE International Conference on Computational Electromagnetics (ICCEM). IEEE, 2018: 1-3.
[13] 韩萍, 陈丽丽. 基于极化交叉熵和 Yamaguchi 分解的飞机目标检测方法[J]. 信号处理, 2017, 33(3): 389-396.
Han Ping, Chen Lili. Airplane Detection Algorithm of Polarimetric SAR Image Based on Polarimetric Cross Entropy and Yamaguchi Decomposition[J]. Journal of Signal Processing, 2017, 33(3): 389-396.(in Chinese)
[14] 刘勇, 梁伟, 周宏潮, 等. 雷达目标一维全极化特征提取方法[J]. 信号处理, 2014, 30(5): 544-552.
Liu Yong, Liang Wei, Zhou Hongchao, et al. One-dimensional Fully Polarimetric Characteristic Extraction Method of Radar[J]. Journal of Signal Processing, 2014, 30(5): 544-552.(in Chinese)
[15] Sarabandi K, Ulaby F T. A convenient technique for polarimetric calibration of single-antenna radar systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(6): 1022-1033.
[16] Hu Cheng, Li Weidong, Wang Rui, et al. Accurate insect orientation extraction based on polarization scattering matrix estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1755-1759.
[17] Wang Rui, Hu Cheng, Fu Xiaowei, et al. Micro-Doppler measurement of insect wing-beat frequencies with W-band coherent radar[J]. Scientific Reports, 2017, 7(1): 1396.
