1 引言
随着雷达对抗的日趋激烈,吊舱、有源诱饵技术日趋成熟,雷达系统面临欺骗式干扰的巨大挑战,主瓣干扰对抗也是当前世界雷达界难题和热点。随着数字射频存储器技术的发展[1],通过对信号进行截获、采样、存储、转发,与目标回波精准相似的假目标能够被复制出来,增强了欺骗性。而来源于主瓣方向的欺骗式干扰更是对雷达系统的威力和生存能力带来了严峻的考验。目前针对有源欺骗式干扰的主要对抗措施是利用干扰信号和有用信号在时域[2]、频域[3]、空域和极化域[4-5]等方面的差异进行区分,采取信号处理达到从干扰背景中提取有用信息的目的。然而基于波形捷变的方法可会导致高的距离旁瓣,限制了雷达输出信干比的提高和对干扰的抑制性能。基于目标极化特征的方法在干扰机采用极化调制时难以奏效。此外,可在分布式多基地雷达系统[6]中同时利用目标的空间去相关特性和干扰信号同源的特点实现干扰抑制,但并不适用于单基地雷达系统。实际上,传统雷达对抗主瓣欺骗式干扰有一定难度,因此,在新体制雷达下挖掘目标和干扰的多参数信息成为抗主瓣欺骗式干扰的一种重要途径。
近年来提出的频率分集阵列(frequency diverse array, FDA)雷达受到学者的广泛关注[7-9]。然而FDA的发射方向图的距离角度依赖性体现在发射端,必须要结合多输入多输出(multiple-input multiple-output, MIMO)技术来分离发射端信号来获取发射自由度。FDA-MIMO近几年在军用民用等领域得到了广泛应用,如机载FDA空时二维处理(space-time adaptive processing, STAP)雷达距离模糊杂波抑制[10-11],合成孔径雷达高分辨率无模糊成像[12-13],距离角度估计[14-15]等。鉴于FDA-MIMO雷达发射维包含距离维信息,因此可以具有更高信号处理灵活度。因此可以利用真实目标与主瓣欺骗式干扰的距离信息差异来进行辨别。文献[16]研究了FDA-MIMO雷达自适应距离角度二维波束形成方法,并提出了一种基于直接数据域的稳健距离-角度二维波束形成方法,可用来抑制欺骗式干扰。然而该方法假定由同一假目标产生器(false target generation, FTG)产生的假目标在发射-接收维具有相同的导向矢量,而这一假设条件仅是众多实际情况中的特例。此外,采用自适应波束形成的方法需要解决非均匀样本挑选的问题。
通常假目标由FTG将截获的雷达波形延迟若干个脉冲之后再转发出去。基于对真实目标先验信息的粗估计,在逐个距离门补偿后[16],通过真、假目标在发射空间频率上的差异,在联合发射-接收二维频率域来对其进行区分。本文考虑一种非自适应波束形成的方法,即固定权向量为指向目标的导向矢量,而非利用样本数据计算协方差来获取自适应权。通过选择合适的频率步进量,可以使得假目标位于波束形成方向图的零点,从而有效地对抗主瓣欺骗式干扰。
2 FDA-MIMO雷达主瓣欺骗式干扰模型
不失一般性,考虑由M个发射阵元,N个接收阵元组成的等距线阵,其发射频率以Δf线性递增。在FDA MIMO系统中,第m个阵元发射频率为:
fm=f0+(m-1)Δf,m=1,2,…,M
(1)
其中f0为参考阵元(第一个阵元)频率。在窄带条件下,假设远场某位置(R0,θ0)处存在单点目标源,则第n个阵元接收的来自该目标的反射信号可表示为:
(2)
其中假设不同阵元发射的信号φm(t)彼此正交,且满足
其中τ为任意时延,( )*表示共轭运算。其中β为点目标复散射系数;双程时延
d为阵元间距,
为公共延迟时间。则第n个阵元接收第m个阵元发射的信号在经匹配滤波φm(t-τ0)exp{j2πfmt}后的输出为
(3)
其中
波长
则雷达接收到的目标信号矢量可表示为
xS=[y11,y12,…,y1N,y21,…,yMN]T
=ξSb(θ0)⊗a(R0,θ0)
(4)
其中⊗表示Kronecker积;a(R0,θ0)∈CM×1和b(θ0)∈CN×1分别为发射和接收导向矢量,其表达形式分别如下:
a(R0,θ0)
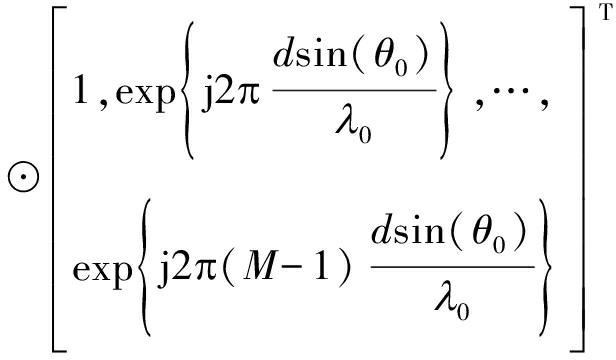
(5)
(6)
其中⊙表示Hadamard积。可见目标距离维信息包含在发射导向矢量里。对接收信号的处理过程如图1所示。
假设FTG位于(Rj,θj)处。且存在L个假目标,第n个阵元接收到的第l个假目标信号经匹配滤波后,得到
(7)
其中,
为第n个接收阵元与FTG的双程时延;τl为对于第l个假目标的调制时间。对于主瓣欺骗式干扰有
相当于假目标实际所在的位置对应的时延,可以将其可等效为
其中Rl为假目标等效位置。进一步,第l个假目标的接收信号快拍矢量形式为
xl=[Jl,11,Jl,12,…,Jl,1N,Jl,21,…,Jl,MN]T
=ξlb(θj)⊗a(Rl,θj)
(8)
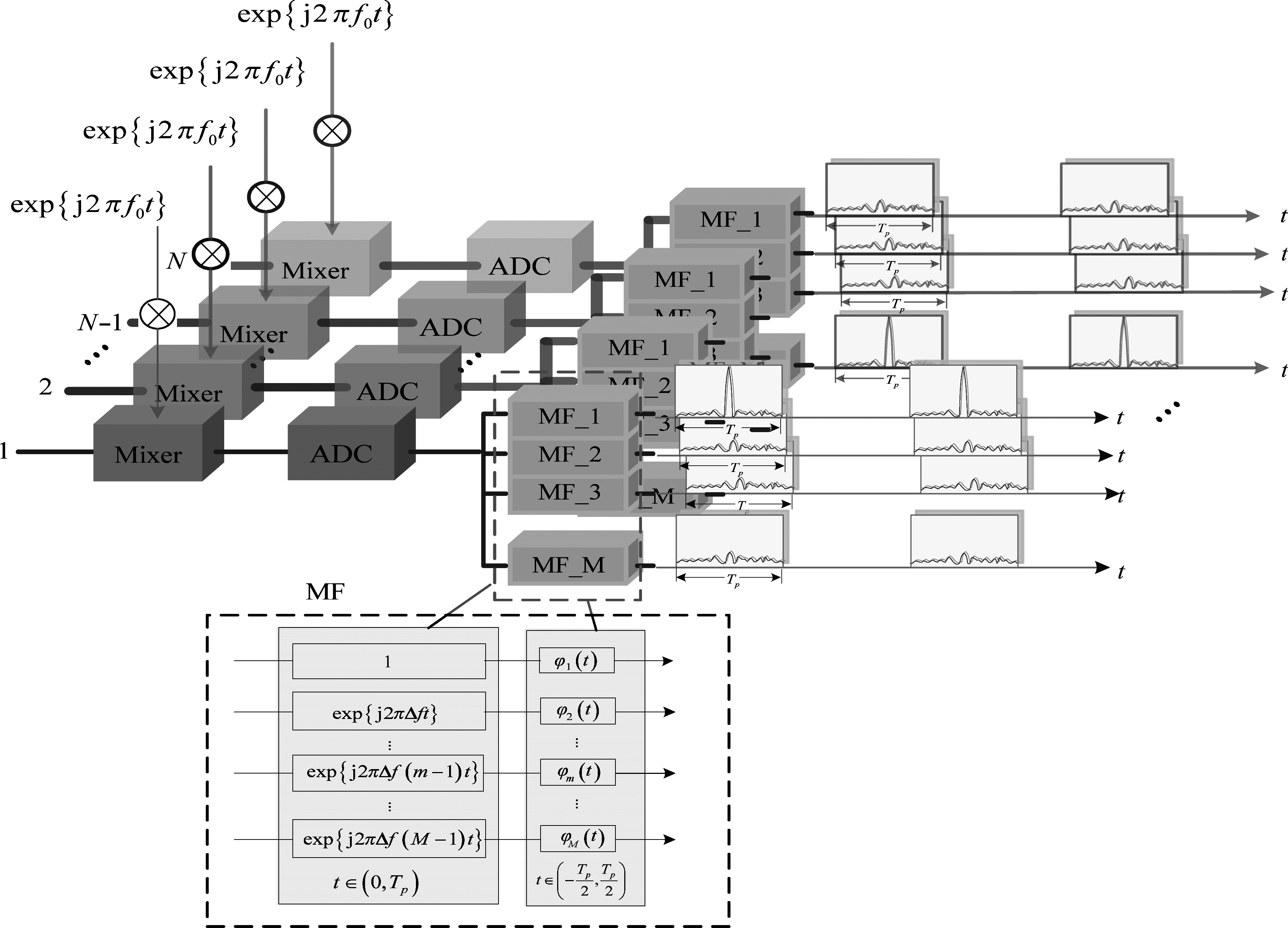
图1 FDA-MIMO接收信号处理图
Fig.1 Received signal processing of FDA-MIMO system
由此可得,FDA MIMO雷达的接收信号可表示为
(9)
其中,xS为真实目标信号分量;xl为第l个假目标信号分量;n表示噪声分量。
3 非自适应波束形成抗主瓣欺骗式干扰原理
本文假设真实目标的距离和角度信息已知(例如,在搜索阶段完成目标信息的粗估计),这是鉴别真、假目标的重要前提。根据发射导向矢量,则对于真实目标和假目标的发射空间频率可以表示为
(10a)
(10b)
由同一个干扰机转发出来的假目标信号,其接收空间频率相同,均为
本质上,区分干扰机的后向散射信号与转发假目标信号是利用了存储延迟时间的信息。因此,可以考虑对回波信号按距离门进行发射角频率补偿[16],补偿之后的目标信号与第l个假目标信号对应的发射空间频率可以分别表示为
(11a)
(11b)
其中,
表示最大无模糊距离,且fr为脉冲重复频率,p为假目标延迟脉冲数。
如图2所示,经过补偿后,干扰机产生的假目标信号在发射-接收二维空间频率域是离散分布的,等效距离模糊重数一致的假目标具有相同的空间谱分布。而对于真实目标,由于其发射、接收空间频率相同,即
因此真实目标在发射-接收二维空间频率域是沿对角线分布的。对于阵元数为M的阵列,其最多可形成M-1个零点,可以抑制M-1个假目标。FDA-MIMO雷达非自适应波束形成抗干扰的原理在于让假目标位于天线方向图的零点位置。补偿后真、假目标发射空间频率差值可以表示为
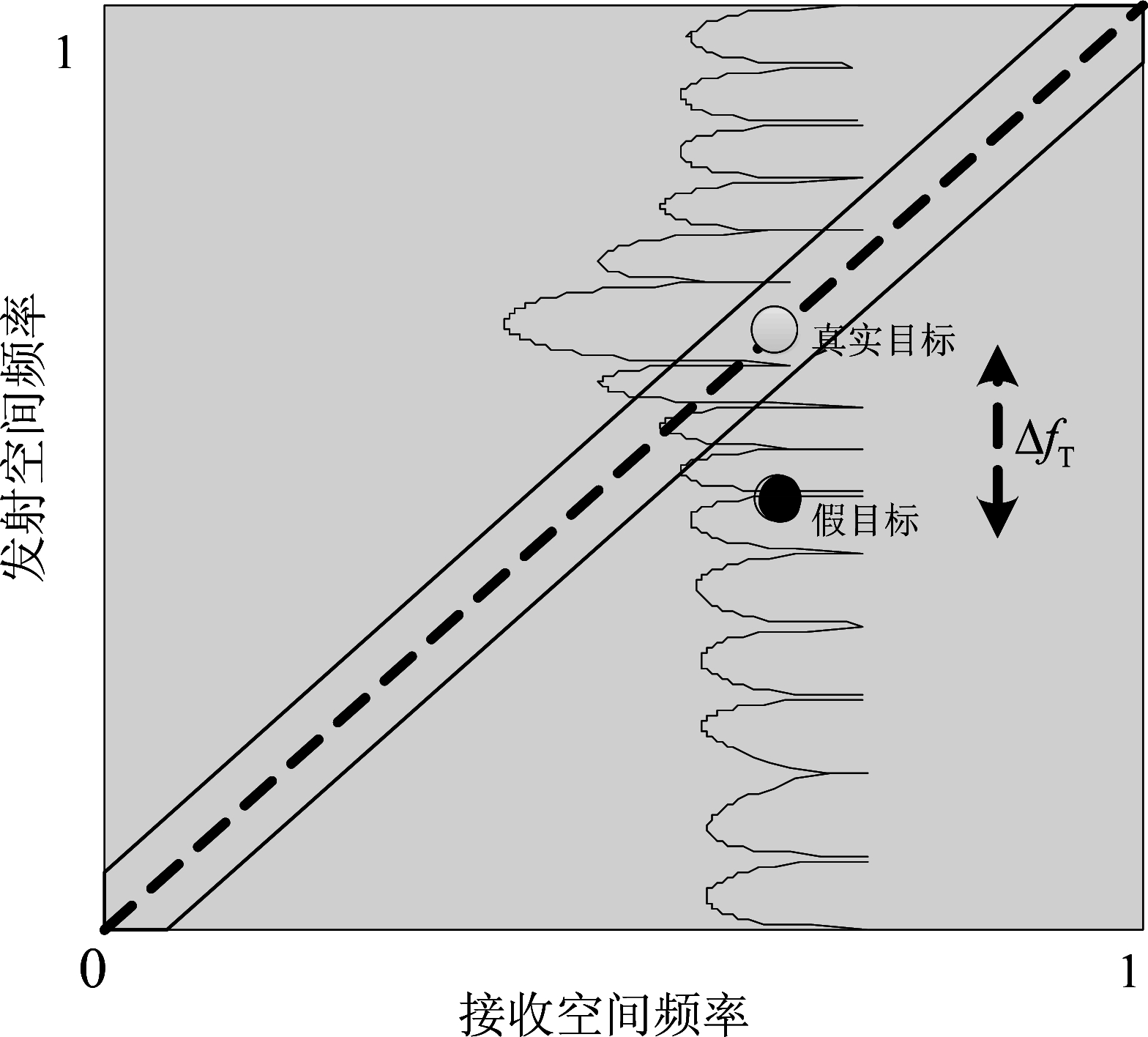
图2 真、假目标频谱分布
Fig.2 Frequency spectra locations of real and deceptive targets
(12)
其中,z为
的整数部分,q为小数部分,且q∈[0,1)。在空间频率轴[-0.5,0.5]范围上,不同距离模糊区域的信号以ν为间距排列。由于相位差具有2π周期性,可忽略整数部分u的影响。为了能分辨出不同模糊区域的真、假目标,需要保证真假目标的发射空间相位差不为2π的整数周期倍,否则真、假目标发射空间频率一样。由于pz为整数,因此可以忽略,则要求
ΔfT=pν≠z,z∈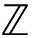
+
(13)
通常,雷达系统中通常设计满足
即载频和PRF是倍数的关系,因此每个天线初相是相同的,且主瓣都指向同一个方向,因此传统雷达无法对欺骗式干扰进行抑制。在FDA-MIMO雷达中,脉冲间真、假目标等效的发射波束主瓣指向有一定的偏移量,即不同阵元发射初相是变化的。因此,可以推算出了频率步进量的计算公式
Δf=(z+q)fr
(14)
当目标的角度为0°时,即固定权向量为全1的列矢量,补偿后的FDA-MIMO的发射方向图可以表示为:
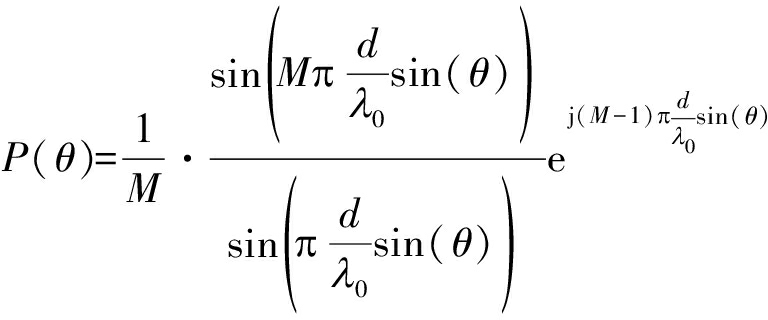
(15)
由式(15)可以计算得当
且
时,方向图值为0,进一步可以计算得第一个零点所对应的发射空间频率
即当真、假目标延迟脉冲数相差为1时,选择
假目标位于第一个零点,相应的频率步进量
此时,转发延迟为1～M-1个PRT的欺骗式假目标均位于波束形成的零点,可以被有效抑制。当延迟脉冲数为M个,则普通波束形成抗干扰失效,此时假目标的发射频率与真实目标相同。类似地,当真、假目标延迟脉冲数相差为p时,则频率步进量有效取值为:
(16)
接收数据通过发射-接收二维波束形成器,权矢量可以表示为:
(17)
其中,
4 仿真实验
本节通过仿真数据来验证所提非自适应波束形成方法对主瓣距离欺骗式干扰抑制的有效性。由于FDA-MIMO有效抗主瓣干扰的前提是假目标相比于真实目标至少延迟一个脉冲。本节假设一共有500个距离门,每个距离门大小为30 m。假设预设的真实目标不存在距离模糊,且位于第300个距离门。FTG产生3个假目标,均存在距离模糊。假目标1,假目标2和假目标3分别延迟了2、5、6个脉冲,且分别位于第100个、第400个和第350个距离门。表1给出了具体的仿真参数。
图3给出了FDA-MIMO雷达基于非自适应波束形成抗主瓣欺骗式干扰结果。图3(a) 给出了Capon谱分布,可见真实目标由于收发频率相同,因此沿主对角线分布,而对于假目标,与真实目标存在
的发射频率偏差。图3(b) 给出了发射-接收二维非自适应波束形成器响应,即二维方向图。图3(c) 对比了MIMO与FDA-MIMO雷达的匹配滤波0°剖面,可见,对于MIMO雷达,由于没有距离维自由度,仅靠角度维自由度无法抑制距离欺骗式干扰信号。而FDA-MIMO雷达,由于同时具有角度和距离维的自由度,采用非自适应波束形成抑制假目标后,预设的真实目标处会形成峰值。
表1 FDA-MIMO雷达系统仿真参数
Tab.1 Parameters of the FDA-MIMO system
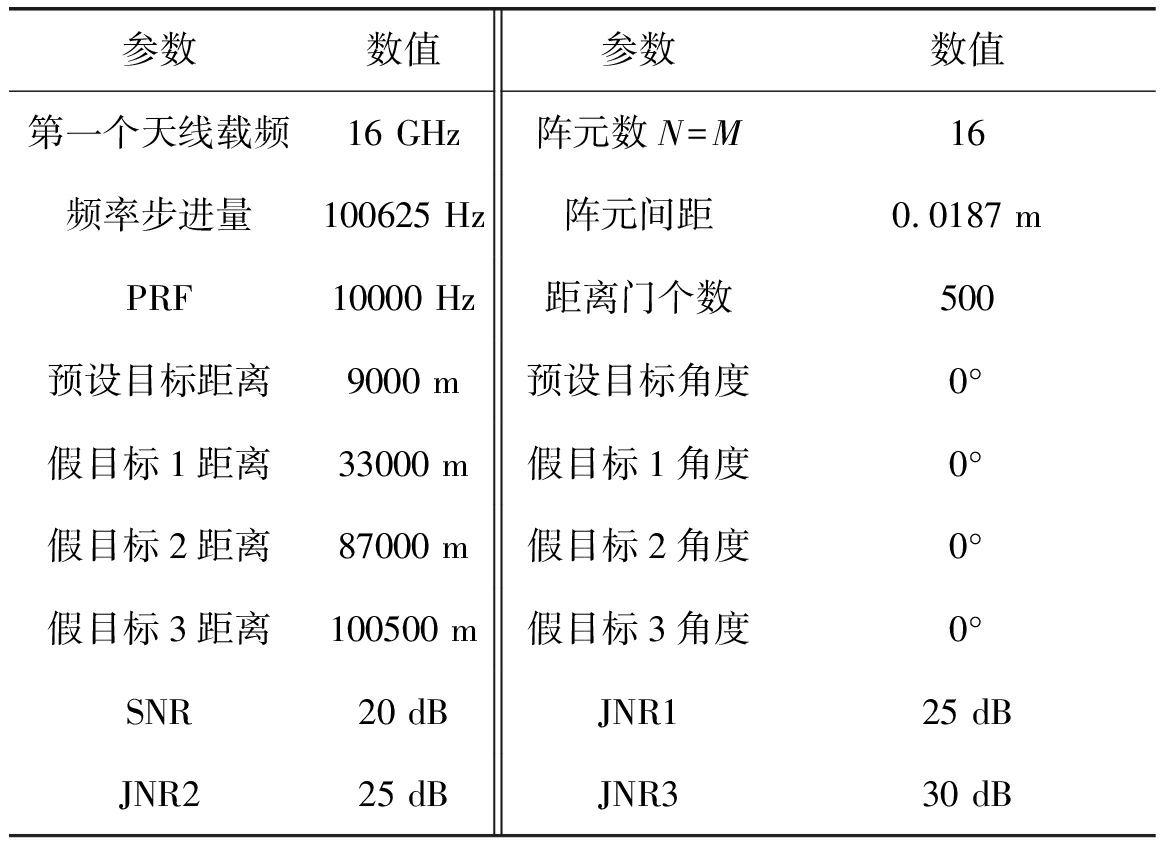
参数数值参数数值第一个天线载频16GHz阵元数N=M16频率步进量100625Hz阵元间距0.0187mPRF10000Hz距离门个数500预设目标距离9000m预设目标角度0°假目标1距离33000m假目标1角度0°假目标2距离87000m假目标2角度0°假目标3距离100500m假目标3角度0°SNR20dBJNR125dBJNR225dBJNR330dB
图3 FDA-MIMO雷达非自适应波束形成主瓣距离欺骗式干扰抑制
Fig.3 Main-beam deceptive jamming suppression with non-adaptive beam-forming in FDA-MIMO radar
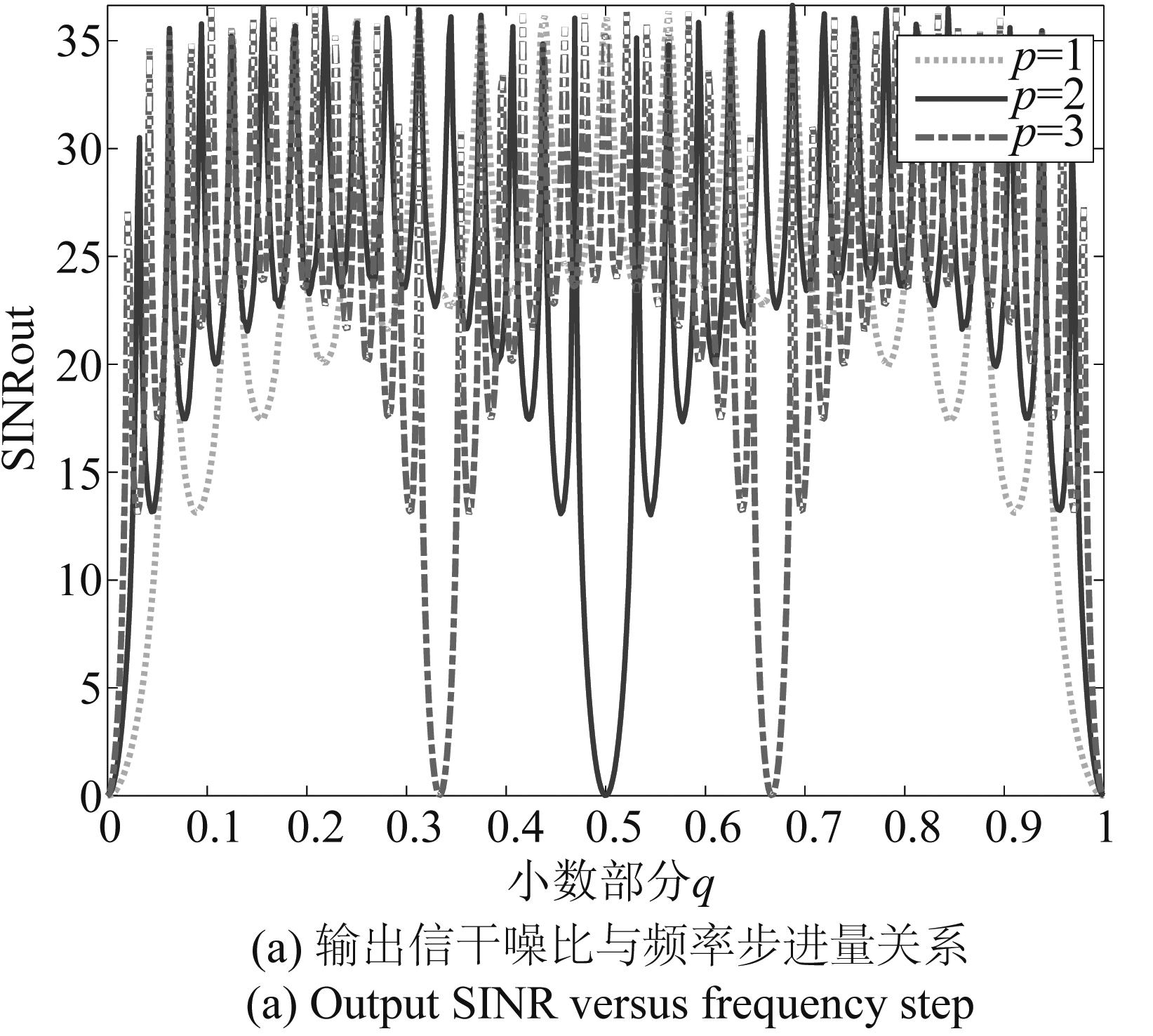
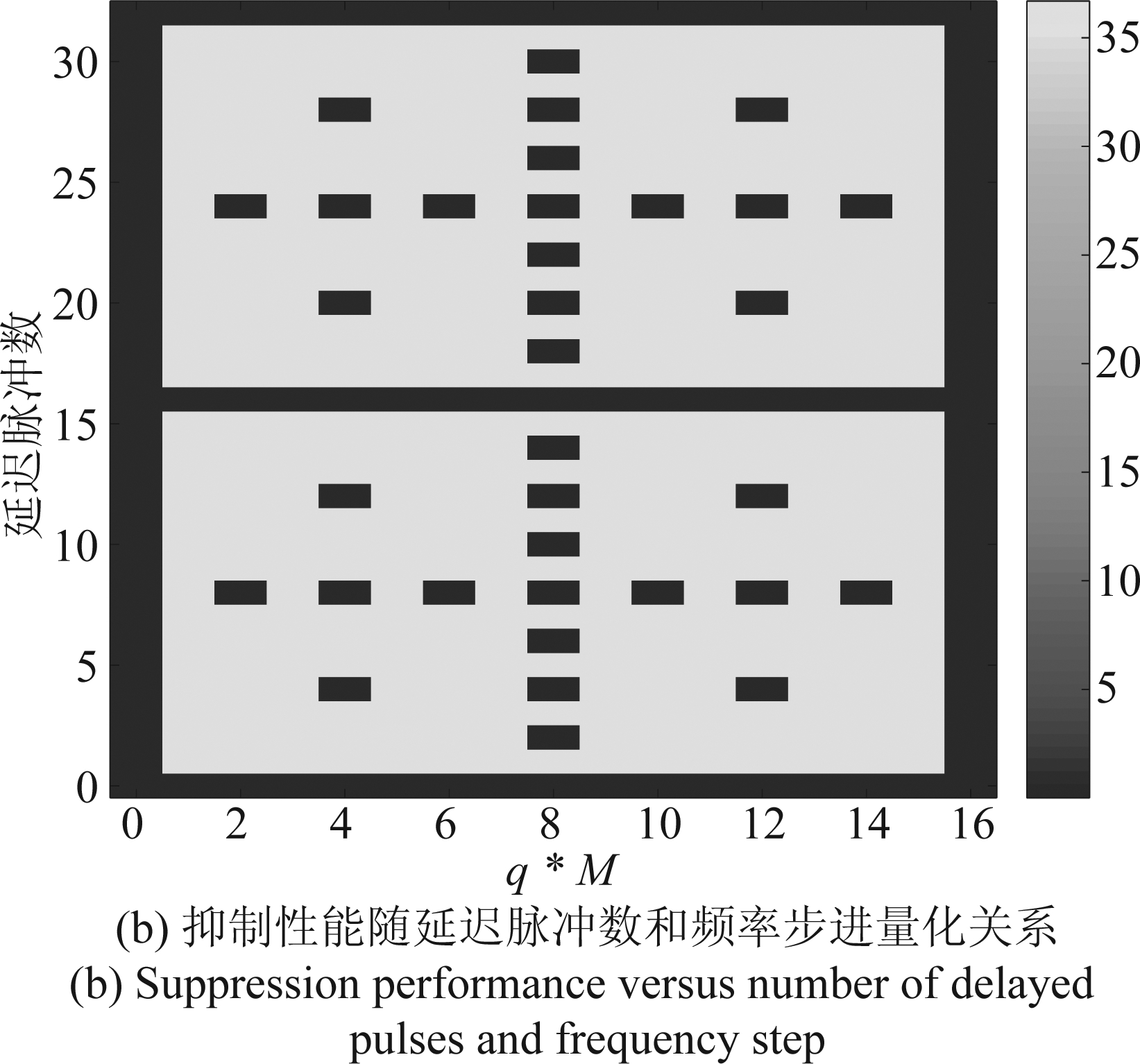
图4 频率步进量的选择
Fig.4 Selection of frequency step
图4(a) 给出了普通非自适应波束形成随频率步进量的变化,仿真实验中对比了延迟脉冲数分别为p=1,2,3时的输出信干噪比。仿真结论与公式(16)一致。图4(b) 给出了非自适应波束形成性能随延迟脉冲数和频率步进量的关系,其中黄色部分表示干扰能被有效地抑制。这里频率步进量取离散值,如前文所述,在给定频率步进量
时,当延迟脉冲数为M个,则普通波束形成抗干扰失效(蓝色部分),此时假目标的发射频率与真实目标相同。同样的,给定频率步进量为其他离散值时,当延迟脉冲数导致假目标的发射频率与真实目标相同(发生模糊),则抗干扰失效。
5 结论
本文针对FDA-MIMO雷达体制,提出一种基于非自适应波束形成的主瓣欺骗式干扰抑制方法。FTG通过将截获的雷达信号延迟一个或多个脉冲周期转发形成具有不同距离频率的假目标,经过距离补偿,在联合发射-接收频域上,真实目标和假目标的发射频率不同,因此可以利用这一差异实现真假目标的识别与欺骗式干扰的抑制。通过选择合适的频率步进量,利用非自适应波束形成,可以成功抑制位于方向图零点位置的假目标。
[1] 周超, 刘泉华, 曾涛. DRFM间歇采样转发干扰辨识算法研究[J]. 信号处理, 2017, 33(7): 911-917.
Zhou Chao, Liu Quanhua, Zeng Tao. Research on DRFM repeater jamming recognition[J]. Journal of Signal Processing, 2017, 33(7): 911-917.(in Chinese)
[2] Feng Qingqing, Xu Huaping, Wu Zhefeng, et al. Deceptive jamming suppression for SAR based on time-varying initial phase[C]∥in Proc. of the IEEE International Geoscience and Remote Sensing Symposium, 2016: 4996- 4999.
[3] Li Yuntao, Jia Xin, Chen Yongguang, et al. Frequency agility MIMO-SAR imaging and anti-deception jamming performance[C]∥in Proc. of the XXXIth URSI General Assembly and Scientific Symposium, 2014: 1- 4.
[4] Xiang Zhe, Chen Boxiao, Yang Minglei. Transmitter/receiver polarisation optimization based on oblique projection filtering for mainlobe interference suppression in polarimetric multiple-input-multiple-output radar[J]. IET Radar Sonar Navigation, 2018, 12(1): 137-144.
[5] 罗双才, 唐斌. 一种空域-极化域联合的雷达欺骗干扰抑制算法[J]. 信号处理, 2012, 28(3): 443- 448.
Luo Shuangcai, Tang Bin. An algorithm of radar deception jamming suppression based on the joint processing in spatial and polarizational domains[J]. Signal Processing, 2012, 28(3): 443- 448.(in Chinese)
[6] Yang Chaoqun, Feng Li, Zhang Heng, et al. A novel data fusion algorithm to combat false data injection attacks in networked radar systems, IEEE Trans. Signal Inform. Process. over Networks, 2018, 4(1): 125-136.
[7] Wang Wenqin, Dai Miaomiao, Zheng Zhi. FDA Radar Ambiguity Function Characteristics Analysis and Optimization[J].IEEE Transactions on Aerospace & Electronic Systems, 2018, 54(3): 1368-1380.
[8] Antonik P, Wicks M C, Griffiths H D, et al. Frequency diverse array radars[C]∥in Proc. of the IEEE Radar Conference, 2006: 215-217.
[9] 李星星, 向龙, 熊智敏, 等. 频分MIMO雷达分解迭代稳健自适应波束形成算法[J]. 信号处理, 2018, 34(6): 631- 640.
Li Xingxing, Xiang Long, Xiong Zhimin, et al. Decomposition and iteration robust adaptive beamforming algorithm for frequency diverse MIMO radar[J]. Journal of Signal Processing, 2018, 34(6): 631- 640.(in Chinese)
[10] Xu Jingwei, Zhu Shengqi, Liao Guisheng. An Adaptive Range-Angle-Doppler Processing Approach for FDA-MIMO Radar Using Three-Dimensional Localization[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 309-320.
[11] Xu Jingwei, Zhu Shengqi, Liao Guisheng. Range Ambiguous Clutter Suppression for Airborne FDA-STAP Radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1620-1631.
[12] Farooq J, Temple M A, Saville M, et al. Exploiting frequency diverse array processing to improve SAR image resolution[C]∥in Proc. of the IEEE Radar Conference, 2008: 1-5.
[13] Wang Chenghao, Xu Jingwei, Liao Guisheng, et al. A Range Ambiguity Resolution Approach for High-Resolution and Wide-Swath SAR Imaging Using Frequency Diverse Array[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 336-346.
[14] Xu Jingwei, Zhu Shengqi, Liao Guisheng. Range ambiguous clutter suppression for airborne FDA-STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1620-1631.
[15] Xiong Jie, Wang Wenqin, Gao Kuandong. FDA-MIMO Radar Range-Angle Estimation: CRLB, MSE, and Resolution Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 284-294.
[16] Xu Jingwei, Liao Guisheng, Zhu Shengqi, et al. Deception jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 115: 9-17.
[17] Xu Jingwei, Liao Guisheng, Zhu Shengqi, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Transactions on Signal Processing, 2015, 63(13): 3396-3410.
