1 引言
微振动是指目标或目标组成部分发生的微小往复运动[1]。微振动现象在自然界和工程界普遍存在,例如昆虫、飞鸟的振翅运动,人体的呼吸、心跳引起的胸腔运动,说话声引起的声带振动,强风吹过或重型车辆经过引起的建筑物、桥梁颤动,车辆发动机工作导致的车身振动等等。获取这些微振动信息,对辨识目标类别、分析目标健康状态等有重要作用。目前常用的微振动测量方法可分为接触式和非接触式两类。接触式测量主要依靠机械测量、电测量及光纤测量等技术手段,需要传感器紧贴被测目标。其中,机械测量主要利用惯性原理进行动测量,测量精度低,动态范围小;电测量主要采用电阻式、电感式、电容式、压电式等传感器将动转换成电信号测量,测量灵敏度高,但难于绝缘处理,易受外界电磁场干扰,且容易损坏;光纤测量通过动改变光信号传输状态实现动测量,测量灵敏度极高,但需要在目标内部预埋置光纤,使用局限性大。非接触测量主要依靠激光、红外、声波测量[2-3],以及雷达测量等技术手段,不需要接触目标即可获得目标微振动信号,具备极高的使用灵活性。其中,激光测量动灵敏度高,但在有遮挡及烟、雨、雾等条件下无法正常工作,红外测量受外界热源干扰严重,声波测量在噪声较大的环境下无法工作,而雷达测量可穿透一定障碍物,且不容易受天气及环境因素影响,是一种可靠的非接触微振动测量技术手段,广泛应用于目标识别、生命体征监测、建筑物/桥梁安全监测等领域。
本文重点关注特定目标上由声压变化激励的微弱机械振动高精度雷达测量应用。在该应用中,目标的微振动主要对雷达回波相位进行调制,形成多普勒调制边带[1]。当目标场景中有强杂波存在时,即使杂波背景完全静止,雷达系统工作频率不稳定仍然导致杂波随时间变化,一部分杂波能量以系统相位噪声的形式逸散到振动调制边带上,对振动调制信号形成压制,这是导致强杂波环境下微振动信号提取精度差的主要因素[5- 6]。
基于杂波图对消、脉冲对消、横向滤波等传统雷达杂波抑制算法只能抑制静止杂波,对变化杂波无改善。时间自适应滤波[7- 8]方法对抑制杂波背景本身随时间的缓慢变化有一定效果,但仍无法抑制由系统工作频率不稳定导致的杂波捷变。因此,传统雷达杂波抑制方法对上述问题改善效果不大。
在雷达测振特定领域,针对强杂波抑制的主流技术是载波自适应对消技术[6]。该技术需要在雷达射频接收机前端构造射频自适应对消电路,通过该电路实时生成与杂波幅度相等、相位相反的对消信号并从雷达回波信号中减去,从而达到杂波抑制目的。由于射频对消电路响应时间极短,能动态跟踪因系统工作频率不稳定而导致的杂波捷变,因此载波对消技术能有效提升强杂波环境下的微振动信号解调精度。但是,针对宽带信号的载波对消电路复杂度极高,远超过雷达系统本身,硬件上难以实现对复杂场景的自适应对消。
本文主要针对由系统工作频率不稳定导致强杂波环境下微振动信号提取精度恶化问题,提出一种基于差分共轭相乘的微振动信号提取方法。该方法可以不增加系统复杂度,利用纯信号处理手段实现相位噪声对消和微振动信号的高精度提取。
本文后续章节安排如下,第2小节首先构建了强杂波环境下的目标场景回波模型,分析杂波微振动信号解调信噪比的影响,其次基于该模型提出一种适用于微振动高精度信号提取的共轭差分相乘方法,能有效改善输出信噪比,最后通过仿真和实测数据验证该方法的有效性;第3节对全文进行归纳总结。
2 强杂波环境下的目标微振动信号提取方法
2.1 强杂波环境下的微振动目标回波建模与杂波影响分析
如图1所示,设观测场景中包含单一微振动目标和杂波背景,目标与雷达的初始距离为R0,由目标振动导致的径向距离变化为M(t),满足|M(t)|≪λ,λ为系统工作波长,并假设杂波背景随时间变化可忽略。
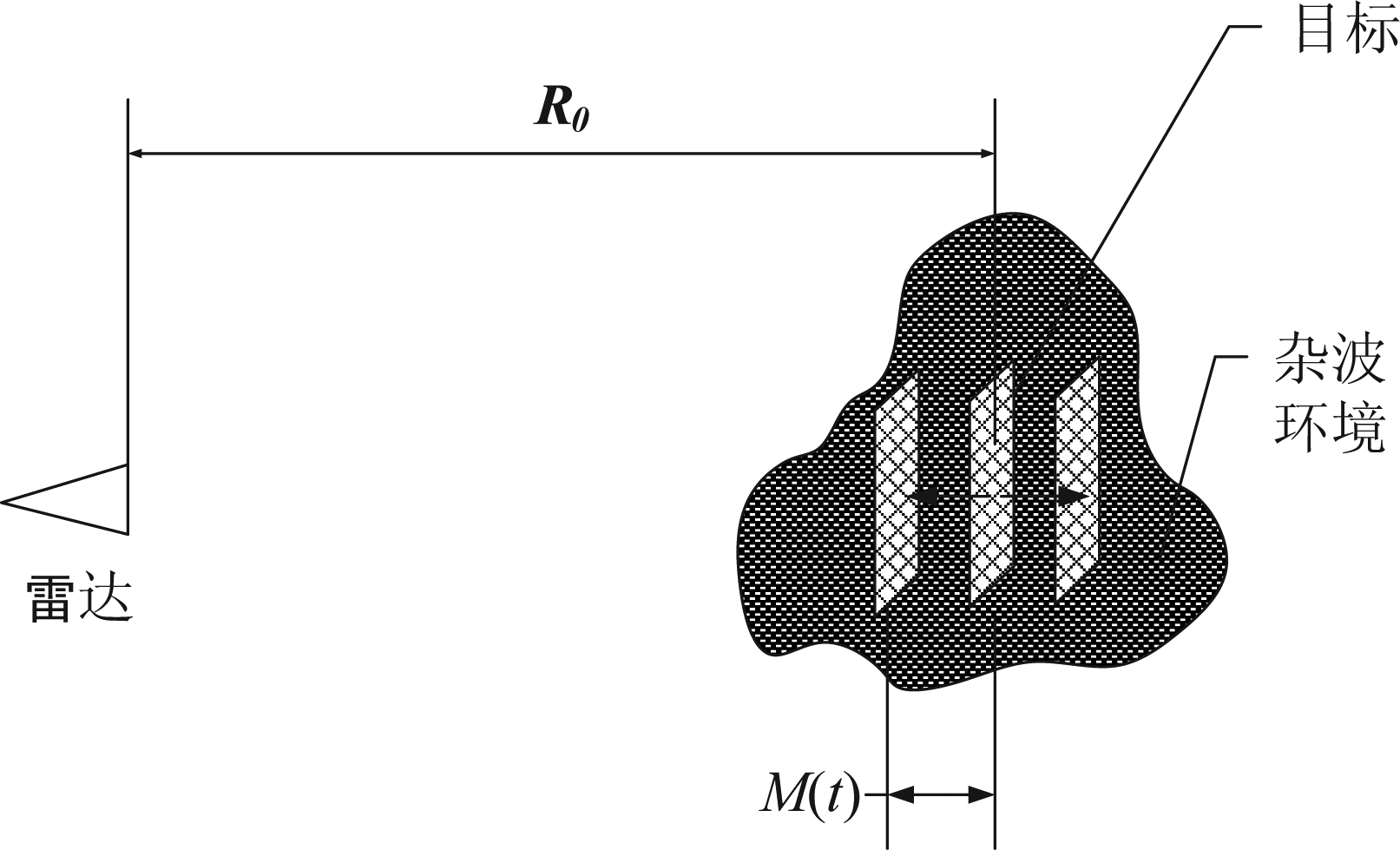
图1 微振动目标测量场景示意图
Fig.1 Scene of radar measurement for micro-vibration target
对宽带雷达回波做一维高分辨处理,得到观测场景的高分辨距离像。提取距离像中包含微振动目标的距离分辨单元,当忽略系统热噪声时,该单元复信号可以表征为[9]:
sr(t)=Kr·exp{jφr}
=Kd·exp{jφd(t)}+Kc·exp{jφc(t)}
(1)
其中,Kr和φr为目标单元一维像的幅度和相位,Kd和φd为振动目标的幅度和相位,Kc和φc为同距离分辨单元内杂波的幅度和相位,φd和φc可表示为:
(2)
φc(t)=φc0+φcn(t)
(3)
其中, φd0是目标回波初始相位,φc0是目标所在距离分辨单元内所有杂波相参合成后的杂波等效初始相位,φdn(t),φcn(t)分别是系统工作频率不稳定导致的目标回波及杂波所携带的噪声相位。如果距离分辨单元在1 m以下,可以近似认为φdn(t)=φcn(t)=φn(t)。
将(2)～(3)代入到式(1)得到一般情况下回波相位与目标振动间的函数关系如下:
(4)
为了分析方便考虑以下两种极端情况:
1)无杂波情况
该情况下信杂比
根据公式(4)有
(5)
此时,回波相位中包含静止相位、振动调制相位、噪声相位。其中,静止相位项可以通过高通滤波滤除;振动调制相位与目标振动成线性比例关系,调制倍数为
噪声相位是一种宽带有色噪声,其功率谱密度分布在全多普勒带宽范围内,必定覆盖目标振动所在的频率范围,形成与振动信号的竞争关系,是影响振动信号提取的主要因素之一。
2)杂波远强于目标情况
该情况下信杂比
根据公式(4)有
(6)
此时,回波相位中仍然包含静止相位、振动调制相位与噪声相位三项。其中,振动调制相位仍与目标振动成线性比例关系,调制系数是无杂波情况下的
倍。由于
且|cos(φd0-φc0)|≤1,该调制系数远小于无杂波情况。
比较式(5)、(6)结果可见,有强杂波存在时的与无杂波存在时恶化了
(7)
其中,AF为信噪比恶化因子,SΦNR|SCR→∞ ,SΦNR|SCR→0 分别是SCR→∞及SCR→0情况下,振动调制相位功率与噪声相位功率之比。如该式所示,强杂波导致振动调制信噪比下降,下降幅度不小于SCR恶化程度。
2.2 基于差分共轭相乘法的高精度目标微振动信号提取方法及信噪比改善性能分析
令I(t)=ReSr(t),Q(t)=ImSr(t),φm(t)=4πM(t)/λ,当|M(t)|≪λ时,公式(1)可以用1阶泰勒展开近似,即有
I(t)=Kdcos(φd0)+Kccos(φc0)-Kdsin(φd0)φm(t)-
(Kdsin(φd0)+Kcsin(φc0))φn(t)
Q(t)=Kdsin(φd0)+Kcsin(φc0)+Kdcos(φd0)φm(t)+
(Kdcos(φd0)+Kccos(φc0))φn(t)
(8)
对上式求时间导数,去掉其中直流分量有
(9)
其中,
是两个均值为零、相互独立的非高斯随机过程。因此,式(9)构成典型的两路盲信号混叠形式,M为系数未知的2×2混叠矩阵。
对式(9)解混叠的过程相当于求M逆矩阵M-1的过程,可以通过各种经典盲信号分离方法求解,但此处对M矩阵形式有一定模型认知,可以直接对该矩阵求逆,得到
W=
(10)
其中,W为M的伴随矩阵,与M-1只差一个常数因子。
因此,对
可做如下估计,即
=(Kdcos(φd0)+Kccos(φc0))I′(t)+
(11)
其中,Sr0=Kdexp(jφd0)+Kcexp(jφc0)可以视为Sr(t)的时间平均值,()*求复共轭运算。对式(11)的结果进行积分得到动信号输出
(12)
在实际信号处理过程中,式(8)与式(12)的微分和积分运算用脉冲间的慢时间差分和序列求和运算替代。并且为了提升信号处理实时性,式(11)中的
用其瞬时值
替代,即有
(13)
其中,Δt是1个相参积累周期(CPI),对应第n个脉冲重复周期。将上列公式描述的振动信号提取方法称作差分共轭相乘法。
对该方法,存在det{M}=KdKcsin(φc0-φd0)=0的情况,即式(9)不构成两组独立观测,具体分解为如下两种情况:
情况1 |φc0-φd0|=4π|Rc-R0|/λ→0,即杂波的等效散射中心位置与动目标位置近似重合,由于雷达距离分辨率通常远大于工作波长,而杂波等效散射中心体现的是距离单元内所有散射中心相参叠加的综合效果,因此该情况在实际工作环境中很难发生;
情况
即杂波的等效散射中心与动目标间距恰好为在工作波长的半整数倍,该情况在实际工作环境中有一定几率发生,需要雷达具有一定的载波频率调整能力,当判断发生上述问题时(例如可计算输出信号短时功率谱的峰值信噪比,当小于某特定门限时),可通过变换工作波长,回避|Rc-R0|趋近工作波长半整数倍的情况。在具体实施时,可以将雷达设计成双载波交替发射的工作体制,或者在步进频体制下选同不同步进频范围进行高分辨合成。
综上,基于差分共轭相乘法的目标微振动信号提取方法的处理流程如图2所示。
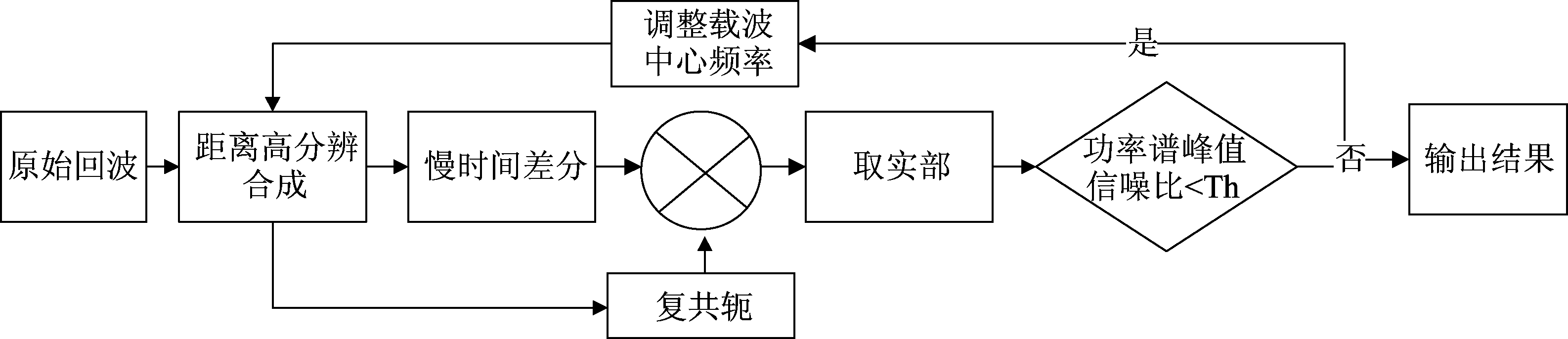
图2 差分共轭相乘法处理流程图
Fig.2 Diagram of conjugate cross multiplication method
2.3 仿真与实测数据验证
2.3.1 仿真结果
设置雷达系统工作参数与目标场景参数如表1所示。为了模拟系统相位噪声对振动信号提取的影响,代入设定工作频段的雷达系统相位噪声典型值进行仿真,如表2所示,利用分段线性插值拟合成连续相位噪声曲线。仿真场景主要模拟室内环境,场景回波中主要来自若干个孤立目标回波。本仿真中,场景回波只包含1个振动目标的回波以及1个与目标在同一距离分辨单元内强散射点回波(杂波)。
表1 雷达参数与仿真场景参数列表
Tab.1 the parameter of the radar and the scene
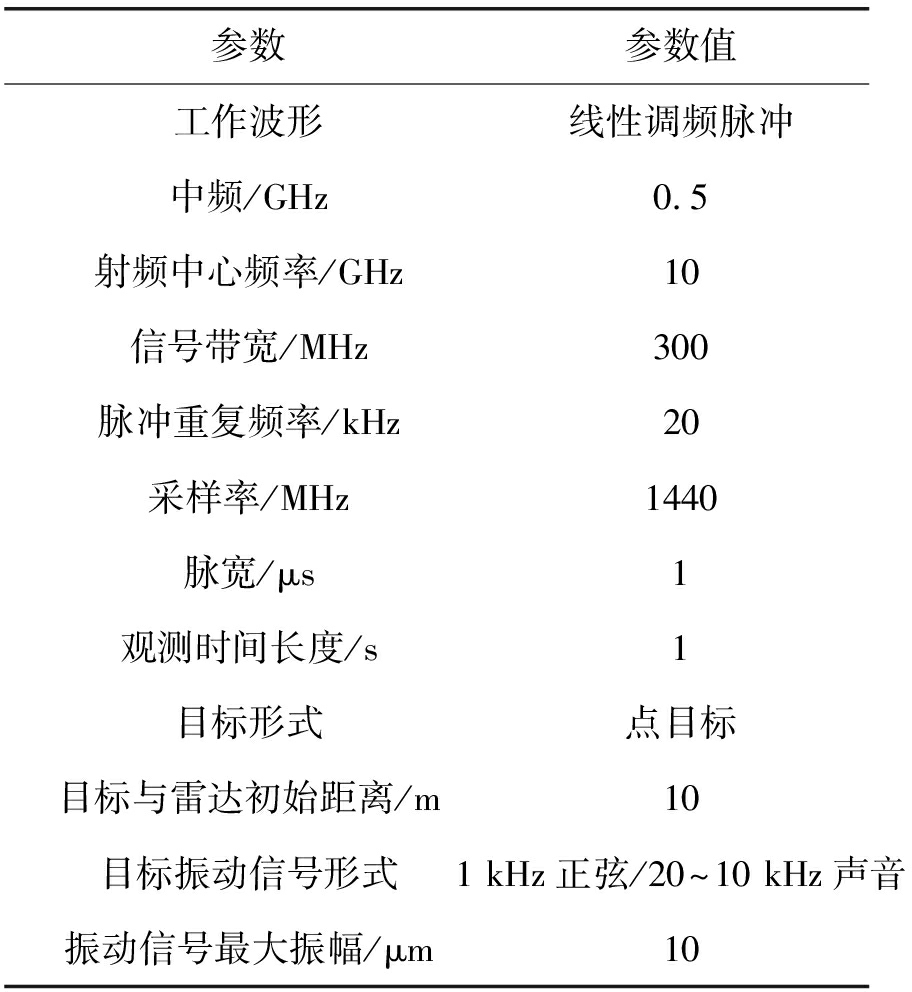
参数参数值工作波形线性调频脉冲中频/GHz0.5射频中心频率/GHz10信号带宽/MHz300脉冲重复频率/kHz20采样率/MHz1440脉宽/μs1观测时间长度/s1目标形式点目标目标与雷达初始距离/m10目标振动信号形式1kHz正弦/20～10kHz声音振动信号最大振幅/μm10
根据上述参数设置进行目标场景回波仿真,采用基于回波相位直接解调和共轭交叉相乘法从回波中提取微振动信号并归一化到单位振动幅度,记输出结果分别为MPE(t)与MCM(t),比较这两种方法的精度。记归一化的原始振动信号为MAC(t),用相对均方根误差(RMSE)表征不同算法的信号提取精度,即
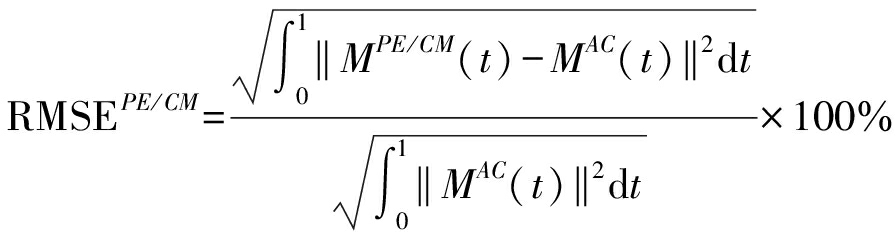
(14)
表2 X波段雷达典型相位噪声水平
Tab.2 The typical phase noise level for the X-band radar
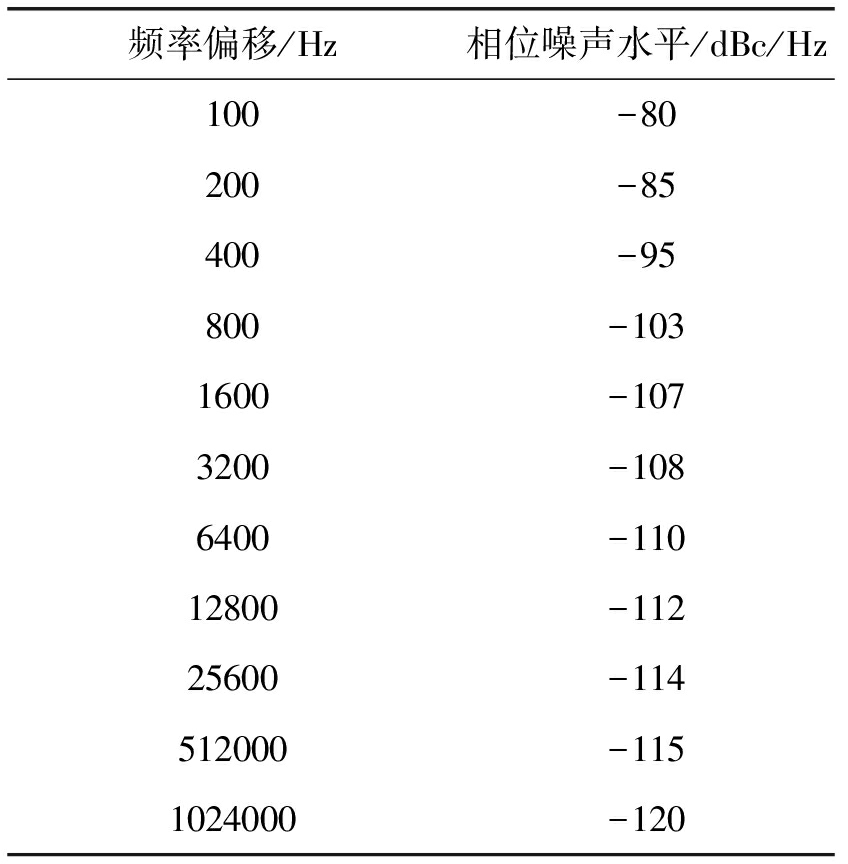
频率偏移/Hz相位噪声水平/dBc/Hz100-80200-85400-95800-1031600-1073200-1086400-11012800-11225600-114512000-1151024000-120
同时,定义后一种方法相对前一种方法的精度改善因子定义为:
(15)
仿真结果如图3所示。图3(a)显示了有杂波(SCR=-20 dB)和无杂波两种情况下观测场景的高分辨一维像(HRRP),其中有杂波情况下场景回波主要由杂波贡献,比无杂波情况回波强度高约20 dB,图3(b)～(g)和(h)～(m)分别是模拟目标以1 kHz正旋振动及受外界音频声压驱动、振动幅度最大不超过10 μm情况下回波处理结果。表3罗列了不同SCR条件下,回波相位直接提取与共轭交叉相乘法提取振动信号的精度及改善因子。结果表明,在强杂波条件下,共轭交叉相乘法提取振动信号精度显著优于回波相位直接提取振动信号,但改善程度随SCR下降而有一定程度降低,到SCR≤-50 dB情况下误差显著。
2.3.2 实测数据结果
实测数据采集雷达设备工作参数如表1所示。实测数据采集试验场景为如图4所示,其中目标为定制装饰画,该装饰画背后有高灵敏度金属膜片,可响应周边环境声压变化并形成机械振动。试验过程中,在装饰画附近通过电脑播放一段声音,引起膜片振动,关闭木门后通过雷达对装饰画进行照射并录取回波,通过信号处理提取回波中调制的微振动信号,与原始播放信标进行对比并分析振动提取精度。
如图5(a)所示,试验场景中的主要存在两个强反射点,分别来自于房门及会议室后墙壁。后一个强散射点回波主要包括后墙壁散射回波成分(强杂波),及装饰画散射回波成分(目标回波),墙壁回波构成对装饰画回波上微弱振动信号提取的主要干扰。对该场景下采集到的回波进行处理,得到如图5(c)～(d)、(f)～(g)结果,分别对应从回波相位中直接取振动信号及通过共轭交叉相乘法取振动信号所得结果及其对应的短时傅里叶变换谱。对比由图5(b)、(e)给出的真实播放信号进行对比,后者精度显著高于前者。根据公式(11)、(12)具体计算得到,回波相位直接提取的相对均方根误差为100%,基于共轭交叉相乘法提取的相对均方根误差为40.48%,后者相对于前者改善7.78 dB。
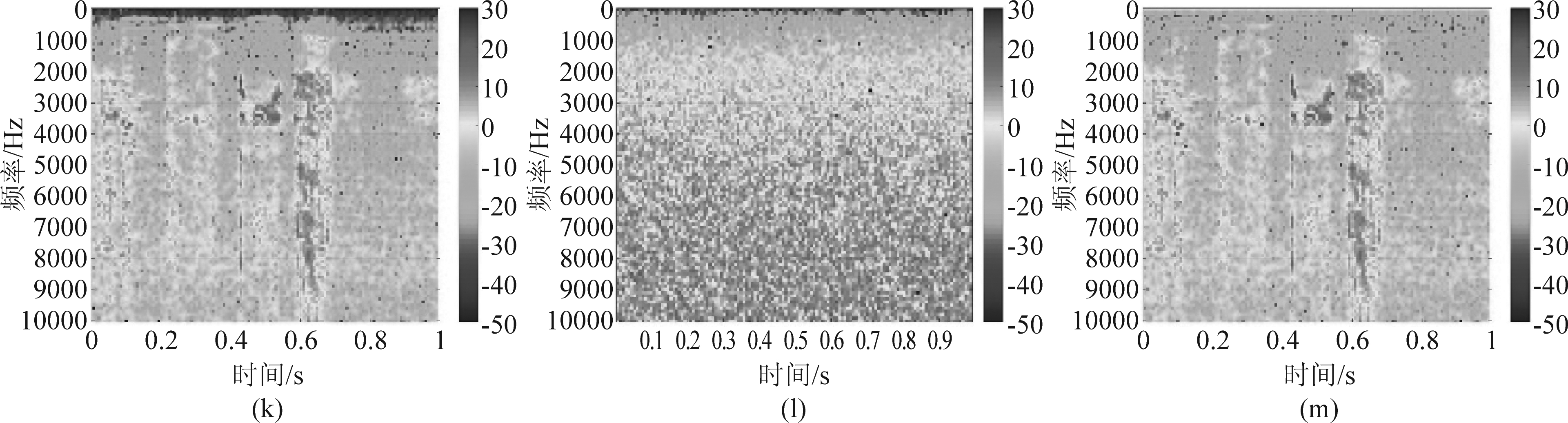
图3 SCR=-20 dB条件下仿真数据信号处理结果:(a)有无杂波情况下的场景HRRP;(b) 1 kHz正弦信号;(c) 1 kHz回波相位直接提取振动信号;(d) 1 kHz差分共轭相乘法提取振动信号;(e) 1 kHz信号频谱;(f) 1 kHz回波相位直接提取振动信号短时傅里叶变换谱;(g) 1 kHz差分共轭相乘法提取振动信号短时傅里叶变换谱;(h) 播放声音信号;(i) 声音回波相位直接提取振动信号;(j) 声音差分共轭相乘法提取振动信号;(k) 声音信号频谱;(l) 声音回波相位直接提取振动信号短时傅里叶变换谱;(m) 声音差分共轭相乘法提取振动信号短时傅里叶变换谱
Fig.3 Simulation data signal processing results under SCR=-20 dB condition: (a) scene HRRP with or without clutter; (b) 1 kHz sinusoidal signal; (c) 1 kHz echo phase directly extracts the vibration signal; (d) 1 kHz differential conjugate multiplication method to extract the vibration signal; (e) 1 kHz signal spectrum; (f) 1 kHz echo phase directly extracts the short-time Fourier transform spectrum of the vibration signal; (g) 1 kHz differential conjugate multiplication method to extract the short-time Fourier transform spectrum of the vibration signal; (h) play sound signal; (i) sound echo phase directly extracts vibration signal; (j) sound differential conjugate multiplication method extracts vibration signal; (k) sound signal spectrum; (l) sound echo phase directly extracts vibration signal for short time Fourier transform spectrum; (m) sound differential conjugate multiplication method to extract short-time Fourier transform spectrum of vibration signal
表3 仿真精度分析
Tab.3 Analysis of the micro-oscillation extraction accuracy
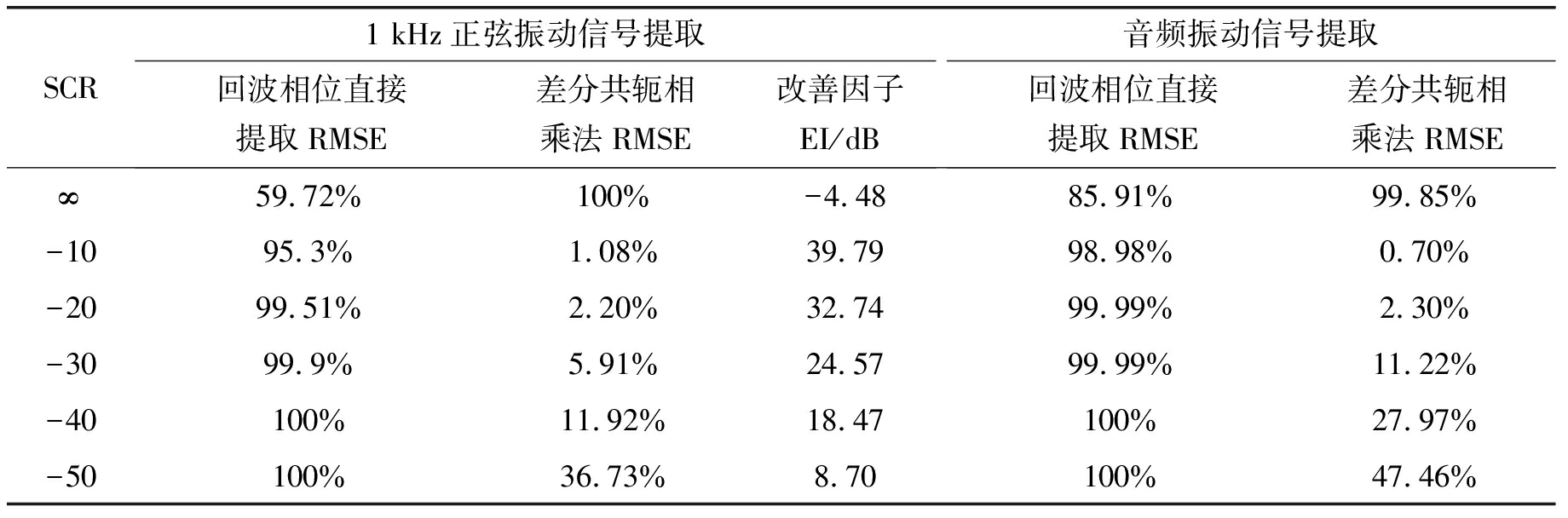
SCR1kHz正弦振动信号提取回波相位直接提取RMSE差分共轭相乘法RMSE改善因子EI/dB音频振动信号提取回波相位直接提取RMSE差分共轭相乘法RMSE改善因子EI/dB∞59.72%100%-4.4885.91%99.85%-1.31-1095.3%1.08%39.7998.98%0.70%43.02-2099.51%2.20%32.7499.99%2.30%32.76-3099.9%5.91%24.5799.99%11.22%19-40100%11.92%18.47100%27.97%11.07-50100%36.73%8.70100%47.46%6.48
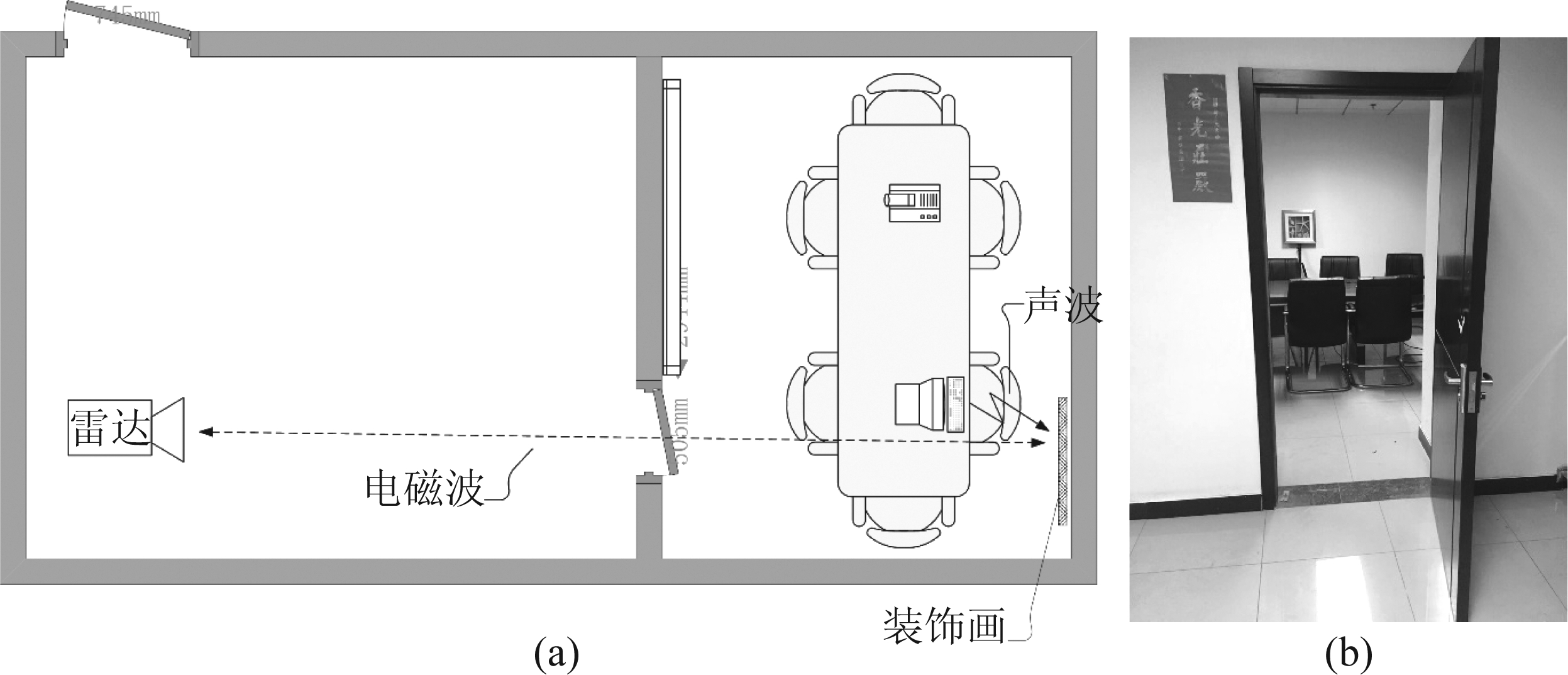
图4 试验场景描述:(a) 试验场景示意图; (b) 试验场景实景照片
Fig.4 Description of the experimental scene: (a) schematic diagram of the experimental scene; (b) experimental scene photo
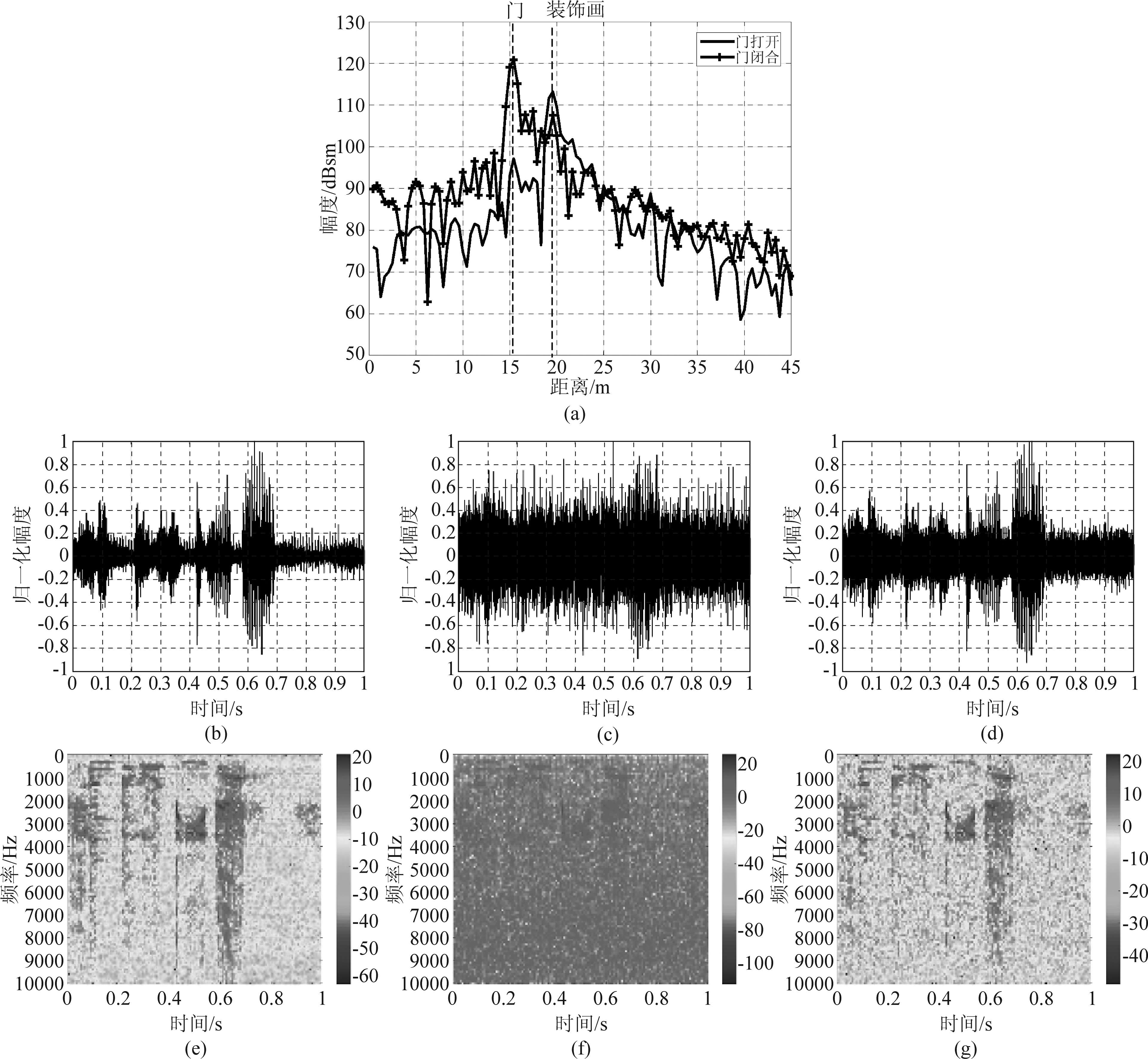
图5 实测数据信号处理结果:(a) 门打开与闭合情况下的场景HRRP;(b) 原始播放信号;(c) 回波相位直接提取振动信号;(d) 差分共轭相乘法提取振动信号;(e) 原始信号频谱;(f) 回波相位直接提取振动信号短时傅里叶变换谱;(g) 差分共轭相乘法提取振动信号短时傅里叶变换谱
Fig.5 The measured data signal processing results: (a) the scene HRRP when the door is open and closed; (b) the original playback signal; (c) the echo phase directly extracts the vibration signal; (d) the differential conjugate multiplication method extracts the vibration signal; (e) original signal spectrum; (f) echo phase direct extraction of short-time Fourier transform spectrum of vibration signal; (g) differential conjugate multiplication method for extracting short-time Fourier transform spectrum of vibration signal
3 结论
在利用雷达对强杂波环境中目标微振动信号进行提取时,低信杂比导致雷达回波相位中的目标振动调制成分被雷达系统内部相位噪声压制,难以有效提取到目标上的微动信号。本文提出适用于强杂波环境目标微动提取的差分共轭相乘法,实现了动提取信号输出信噪比增强。通过仿真和试验验证了该方法的有效性。理论和仿真分析忽略了系统热噪声和调幅噪声对结果的影响,需要在进一步工作中细致分析。
[1] Chen V C. Analysis of radar micro-Doppler with time-frequency transform[C]∥Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing, 2000: 463- 466.
[2] 陈维锋, 彭晋川, 顾建华, 等. 地震救助生命搜索与定位技术研究进展[J]. 地震地磁观测与研究, 2003, 24(6): 89-94.
Chen W F, Peng J C, Gu J H. Recent development of victim location technologies and devices for post-earthquake search and rescue[J]. Seismic Geomagnetic Observation and Research, 2003, 24(6): 89-94.(in Chinese)
[3] 王书伟, 张晗, 张鸣. 人体生命信息探测系统中的传感器技术[J]. 红外, 2008, 29(12): 24-26.
Wang S W, Zhang H, Zhang M. Sensor techniques in human life information detection systems[J]. Infrared, 2008, 29(12): 24-26.(in Chinese)
[4] 杨琪, 邓彬, 王宏强, 等. 太赫兹雷达目标微动特征提取研究进展[J]. 雷达学报, 2018(1): 22- 45.
Yang Q, Deng B, Wang H Q, et al. Advancements in research on micro-motion feature extraction in the terahertz region[J]. Journal of Radar, 2018(1): 22- 45.(in Chinese)
[5] 胡程,廖鑫,向寅,等.一种生命探测雷达微多普勒测量灵敏度分析新方法[J].雷达学报,2016,5(5):455- 461.
Hu C, Liao X, Xiang Y, et al. Novel Analytic Method for Determining Micro-Doppler Measurement Sensitivity in Life-detection Radar[J]. Journal of Radar, 2016,5(5):455- 461.(in Chinese)
[6] 钱鉴, 季晓勇. 载波对消与微弱动的微波遥测[C]∥第三届全国物理及其应用学术研讨会, 2006.
Qian J, Ji X Y. Microwave telemetry with carrier cancellation and weak motion[C]∥The 3rd National Symposium on Physics and Its Applications, 2006.(in Chinese)
[7] 贺峰. 宽带/超宽带雷达运动人体目标检测与特征提取关键技术研究[D]. 长沙：国防科学技术大学, 2011.
He F. Researches on key techniques of wide band/ultra-wide band radar detection and signature extraction of locomotor human targets[D]. Changsha:National University of Defense Science and Technology, 2011.(in Chinese)
[8] Melvin W L. A STAP overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19-35.
[9] 李奥林. 基于高分辨雷达测量的目标微弱振动高精度提取方法研究[D]. 北京: 北京理工大学, 2018.
Li A L. Research on high precision extraction method of weak vibration of target based on high resolution radar measurement[D]. Beijing: Beijing Institute of Technology, 2018.(in Chinese)
