1 引言
GEO SAR是运行在约36500 km高度上的合成孔径雷达,可以实现约1/3的全球覆盖[1]。GEO SAR可对灾害区域实现每天1.5-2.5 h的监测,因此在灾害预防、灾害急救、形变检测等方面具有广大的前景[2- 4]。然而在单星GEO SAR中,中高倾角(15°以上)的方案要求系统具有大面积的天线和高功率,而近零倾角的方案则具有超长合成孔径时间的缺陷。为了降低近零倾角GEO SAR方案的合成孔径时间,2015年意大利米兰理工大学提出分布式GEO SAR概念——Advanced Radar Geosynchronous Observation System (ARGOS)[5]。系统使用N=6颗GEO SAR形成NTOT=N(N+1)/2个等效相位中心。通过优化卫星的位置使得相位中心尽可能均匀,从而理论上可以将合成孔径时间下降为单星SAR的1/NTOT。原来在近零倾角GEO SAR中8 h的脉冲积累时间可以下降到35 min左右,因此可以用于大气相位屏检测等应用。同时系统还具有提高信噪比的优势,在不改变天线尺寸的基础上可以进一步降低卫星的发射功率。
合成孔径雷达的模糊度是SAR系统设计的重要问题,已经成为衡量雷达性能的重要指标[6]。严重的模糊噪声将导致雷达最终图像分辨率的恶化以及强目标图像的重复出现,即“鬼影”。对于低轨SAR而言,模糊度的研究已经较为成熟,通常在距离时域、方位频域求得模糊区位置。由于低轨SAR中卫星的运动通常可视为直线运动,因此慢时间与多普勒频率的关系可根据几何关系求解得到[7]。对于低轨斜视模式SAR,由于地面为平面模型,因此也可通过几何关系获得模糊区位置。
分布式GEO SAR可分解为双基地GEO SAR的叠加。对于GEO SAR而言,全孔径时间成像将获得很高的方位向分辨率,甚至优于2 m[8]。对于当前5~20 m分辨率的观测需求而言,部分孔径时间即可满足要求。然而目前已有SAR模糊度的计算大多基于频域方法,这等效于积累时间为全孔径时间[9]。在部分孔径时间模式下,目标的多普勒带宽将低于场景的瞬时多普勒带宽,因而传统基于方位频域的模糊度计算方法将不再适用。此外,双基地GEO SAR中,地球球形表面不可忽略,且收发卫星速度可能不一致,使得单基地SAR模糊区的计算方法失效。
文献[10]就滑动聚束SAR给出了时域计算方法。针对每个慢时间点,先获得目标的多普勒频率,然后根据模糊数与几何关系获得多普勒模糊区的位置,最后通过天线增益计算方位模糊度。但该文献研究的是单基地SAR以及场景为平面的情况,未讨论双基地和地球球形表面时模糊区的计算问题。目前GEO SAR模糊度的研究主要以单基地SAR[9, 11]为主。文献[9]针对地球球形表面给出星载单基地SAR的模糊位置计算方法,但其模糊度计算方法仍为频域方法,且未讨论双基地情况下模糊区的计算。文献[12]针对单基地GEO SAR的模糊度进行了系统参数设计,文献[13]考虑了提出考虑距离徙动影响的时序设计方法,并仿真了设计结果下的模糊度,这些文献均未讨论双基地情形和时域方法。
本文给出了考虑地球球形表面的双基地GEO SAR模糊区位置的近似计算方法,然后给出分布式GEO SAR模糊度的时域计算方法。针对单基地GEO SAR、双基地GEO SAR、多基地GEO SAR等多种模式,给出了模糊度的仿真和分析。
2 分布式GEO SAR模糊度计算方法
分布式GEO SAR的示意图如图1所示。共有N个GEO SAR卫星线性排列并且同时收发信号,共可形成NTOT=N(N+1)/2个等效相位中心(PC)。所有卫星的运动速度相同,并且与运动方向一致。容易知道PC随着卫星的运动而运动,并且与卫星的速度方向一致。通过设计卫星的位置使得PC间的基线尽可能均匀,理想情况下PC在全孔径完全均匀排列。这时整个孔径被分成NTOT段同时采集信号,从而可以将合成孔径时间降低为单星SAR的1/NTOT[5]。对于分布式GEO SAR,如果是一发多收并且发射机也同时接收的情况,那么脉冲重复频率(PRF)需要满足发射时刻与回波到达时刻不互相重叠的条件,如果发射机不接收,则PRF仅需满足多普勒带宽和场景宽度要求。如果是多发多收的情况,考虑到波形的正交性问题,可以采用时分正交波形。
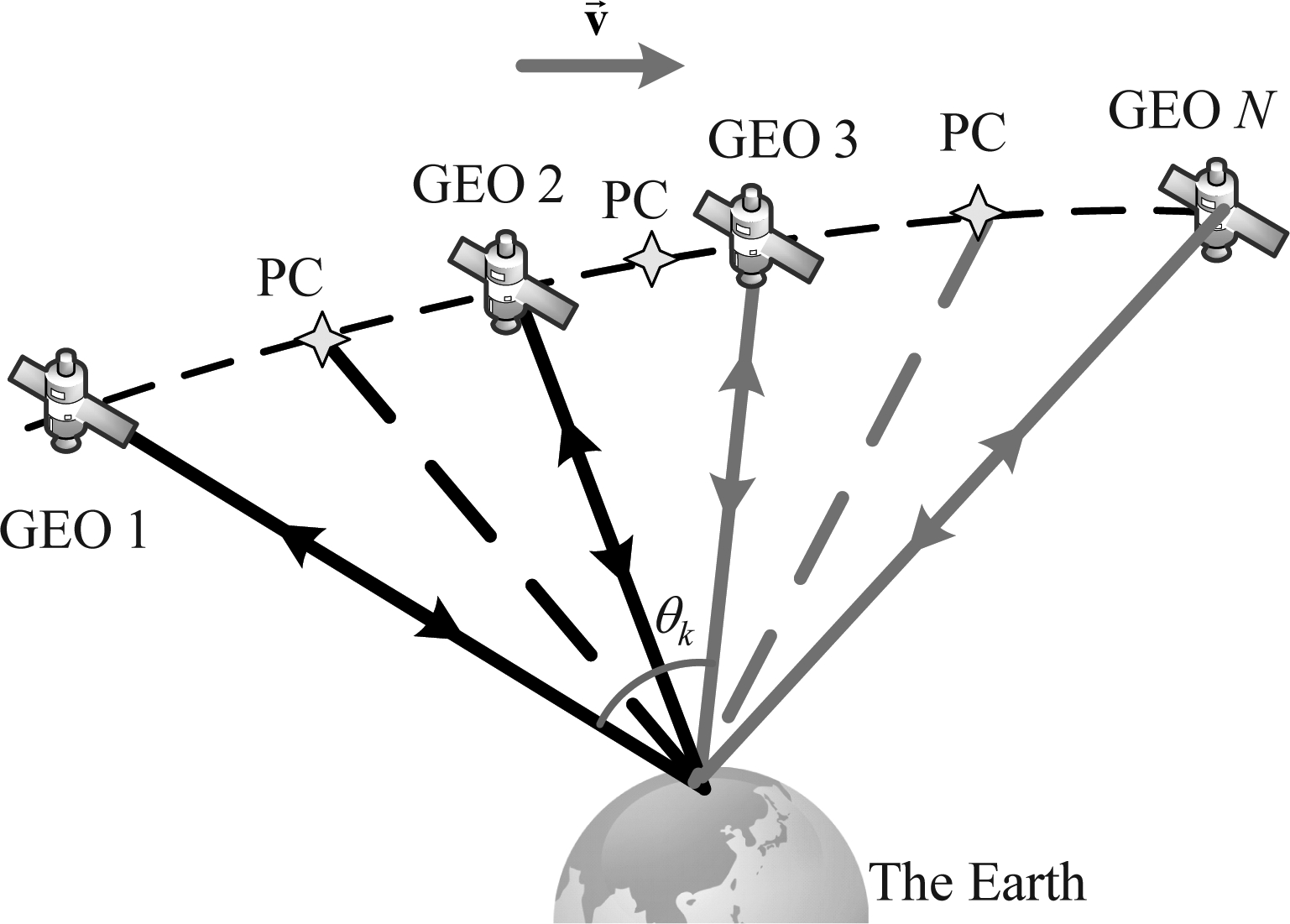
图1 分布式GEO SAR构型示意
Fig.1 Geometric structure of distributed GEO SAR swarm
在传统SAR(包括低轨星载SAR和机载SAR)的条带模式中,模糊度的计算通常在距离时域、方位频域中进行的,这是因为天线沿着方位向扫描,沿方位向的点具有相同的多普勒历史,因而可以使用频域方法进行统一计算[6]。在聚束模式与滑动聚束模式中,对于方位向任意一个点目标,由于在合成孔径时间内几何关系明确、几何参数易于表示,因而也可获得多普勒频率与目标偏离波足中心角度的关系,因此也可用方位频域方式计算系统模糊度[14]。在假设场景具有一致的散射率下,常规模糊度的计算公式为
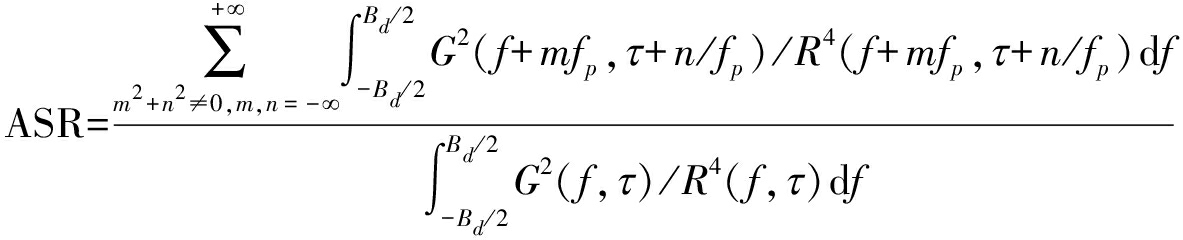
(1)
其中Bd表示信号方位向带宽, fp=PRF,G(f,τ)表示天线方向图,R(f,τ)表示斜距, f为多普勒频率。当m=0,n≠0时,上述公式表示距离模糊的计算方法,当m≠0,n=0时,上述公式表示方位模糊的计算方法。模糊区的位置如图2所示,距离模糊区沿着等多普勒线,且是目标所在的等多普勒线与各个同心圆的交点;多普勒模糊区沿着等距离线,是目标所在的等距离线与各个等多普勒线的交点;而耦合模糊区是其余交点。
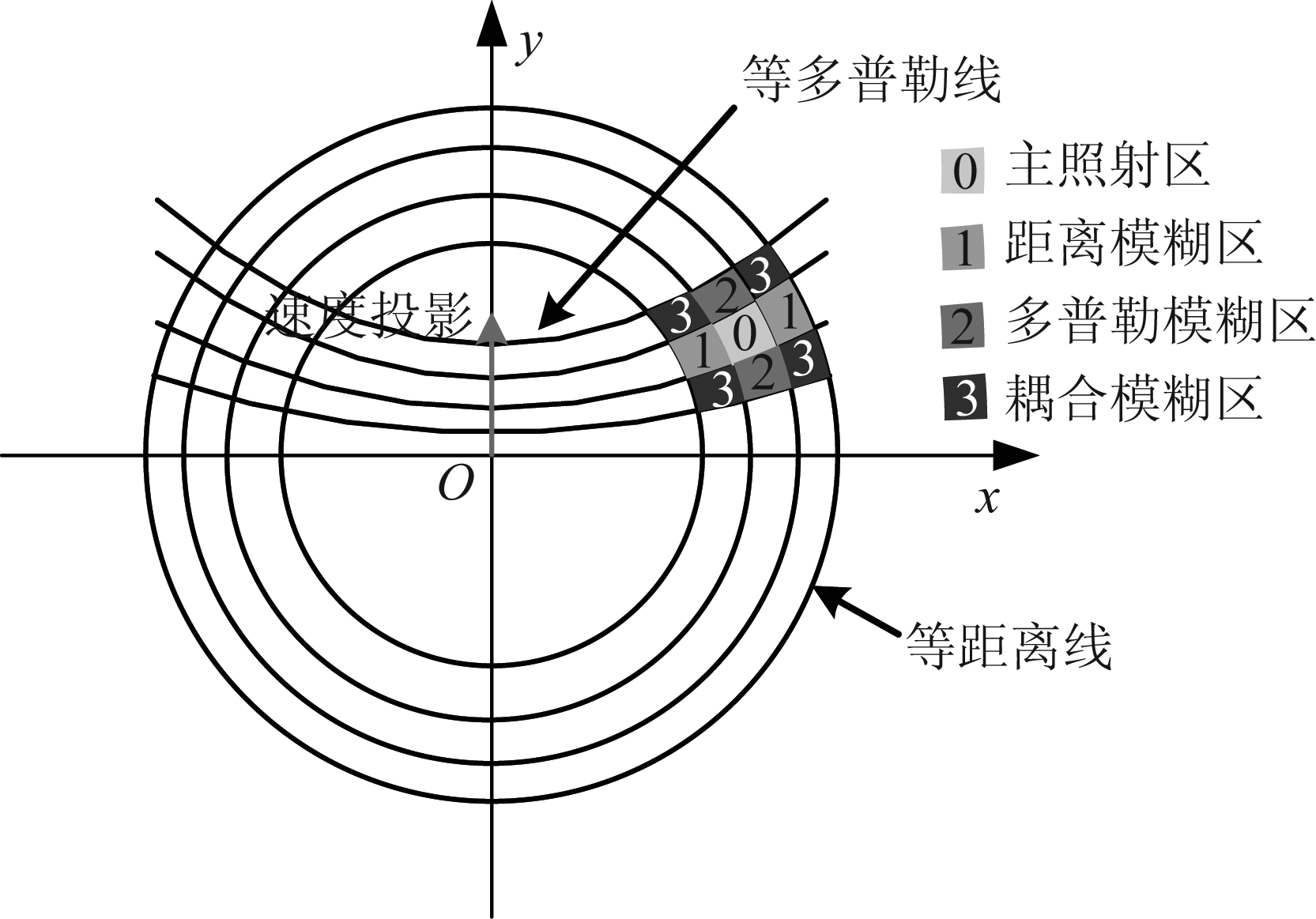
图2 传统SAR模糊区示意
Fig.2 Ambiguity positions for traditional SAR
但对于L波段GEO SAR而言,不施加波束控制情况下的全孔径成像分辨率非常高,甚至优于2 m[8],远远高于通常L波段的分辨率设计值。因此,为了达到10 m甚至5 m分辨率的成像结果,仅需部分合成孔径时间即可。对于不同方位位置的目标,回波信号多普勒范围有所不同。此外,由于地球自转的影响,使得GEO SAR在诸多轨道位置呈现出显著的不规则曲线轨迹,给目标多普勒计算带来困难。因此,使用方位频域的模糊度计算方法将带来一定的误差。
在传统SAR当中,由于无需考虑地球球形表面,因而模糊区的计算方法简单易行。而在GEO SAR中,地球的球形需加以考虑,此时可以使用联立求解方程的方法获得模糊区位置[9]。对于分布式GEO SAR,考虑到收发分置的双基地GEO SAR相位中心,模糊区的求解方法需加以修正。当收发卫星距离远小于斜距时,距离模糊区准确位置与使用相位中心的计算结果非常接近。经过评估,即使在模糊距离达5000 km的情况下,地面距离模糊区的精确位置与近似位置仅相差15 m以内,这个误差对于天线增益计算而言可以忽略不计。假设要求解的模糊区位置为(x,y,z),相位中心位置为(xPC,yPC,zPC),收发卫星的速度分别为![]() 模糊区距离和多普勒频率分别为R、fd,则模糊区的位置可通过求解以下公式获得
模糊区距离和多普勒频率分别为R、fd,则模糊区的位置可通过求解以下公式获得
x2+y2+z2=r2
(2)
(x-xPC)2+(y-yPC)2+(z-zPC)2=R2
(3)
νx(xT-x)+νy(yT-y)+νz(zT-z)+ux(xR-x)+
uy(yR-y)+uz(zR-z)=-fd·λR
(4)
其中r为地球半径,λ为信号波长。公式(4)和(3)相减,并令
C2=-(νxxT+νyyT+νzzT+uxxR+uyyR+uzzR+fd·λR)
a=(νx+ux)
b=(νy+uy)
c=(νz+uz)
(5)
则方程变为xPC·x+yPC·y+zPC·z+C1=0且a·x+b·y+c·z+C2=0。令
(6)
则可将x、y用z表示为
y=Az+A0
x=Bz+B0
(7)
结合公式(2)可以得到![]() 令
令
α=(A2+B2+1)
β=(B0B+A0A)
(8)
则得到
(9)
当Δ=β2-αγ<0时,表示指定距离模糊值与多普勒模糊值的模糊区不存在。根据公式(9)可以得到z的值,结合公式(7)可以得到相应的x、y的值。上述计算方法可用于计算任意双基地GEO SAR模糊区的位置。多基地GEO SAR可以分解为多个双基地组合。
我们考虑圆形天线,假设各个天线有效直径为D,对于特定收发卫星,天线方向图(幅度)可表示为
(10)
其中ΔφT(m,n,ta)为发射卫星到模糊区(m,n)目标的斜距与发射卫星天线法线夹角,ΔφR(m,n,ta)为接收卫星到模糊区(m,n)目标的斜距与接收卫星天线法线夹角。
这里我们给出分布式GEO SAR模糊度的时域计算方法。首先对地面进行网格划分,然后对慢时间进行划分。对于任意一个地面网格、任意一个慢时间点、任意一个收发组合,首先计算该慢时间时刻此收发组合对当前地面网格的斜距R0和多普勒频率fd0,进而选定距离模糊值m·c·PRT/2和多普勒模糊值n·PRF(对应模糊区斜距R=R0+m·c·PRT/2,多普勒频率fd=fd0+n·PRF)。使用公式(2)到(9)可以获得地面模糊区的位置,进而可计算模糊区对当前收发组合的增益。对所有收发组合增益求和,得到当前模糊区的有效增益。当m=n=0时,就可以得到主区的有效增益。对所有时间点求积分,得到主区和模糊区的能量。选定多个模糊值,并计算场景点的模糊比,计算公式为
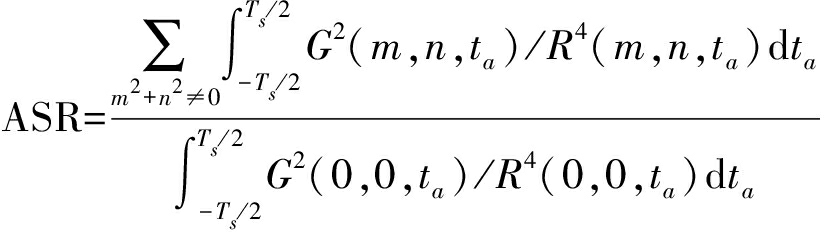
(11)
3 仿真与讨论
我们选取文献[9]中的传统频域计算方法作为参考,仿真本文所提出的模糊度时域计算方法。仿真采用的GEO SAR参数如表 1所示。一共4个卫星,卫星的星下点轨迹重合,都是“小8”形状,如图3(左)所示。卫星1和4的初始位置重合,但速度方向不一致。卫星1~3的速度方向基本一致。单基地模式下仅卫星1工作,双基地模式下卫星1、4工作,多基地模式下卫星1~3工作。由于文献[9]中的方法是针对单基地SAR,未涉及双基地GEO SAR模糊区计算,因此设计双、多基地GEO SAR时,使用本文提出的模糊区近似计算方法。考虑到GEO SAR地球自转不可忽略,我们仿真偏航和不偏航两种情况,分别对应正侧视模式和斜视模式。
卫星1全轨多普勒带宽如图3(右)所示,我们选取赤道处进行仿真。取PRF=80 Hz,单基地成像时间取1000 s(全孔径时间约为5400 s),对应5 m方位分辨率。双基地GEO SAR成像时间与单基地一致。多基地GEO SAR包含卫星1~3,均匀分布形成5个相位中心。由于卫星间距按照分辨率设计,因此多基地GEO SAR的合成孔径时间为1000/5=200 s。
表1 GEO SAR仿真参数
Tab.1 Simulation parameters for GEO SAR
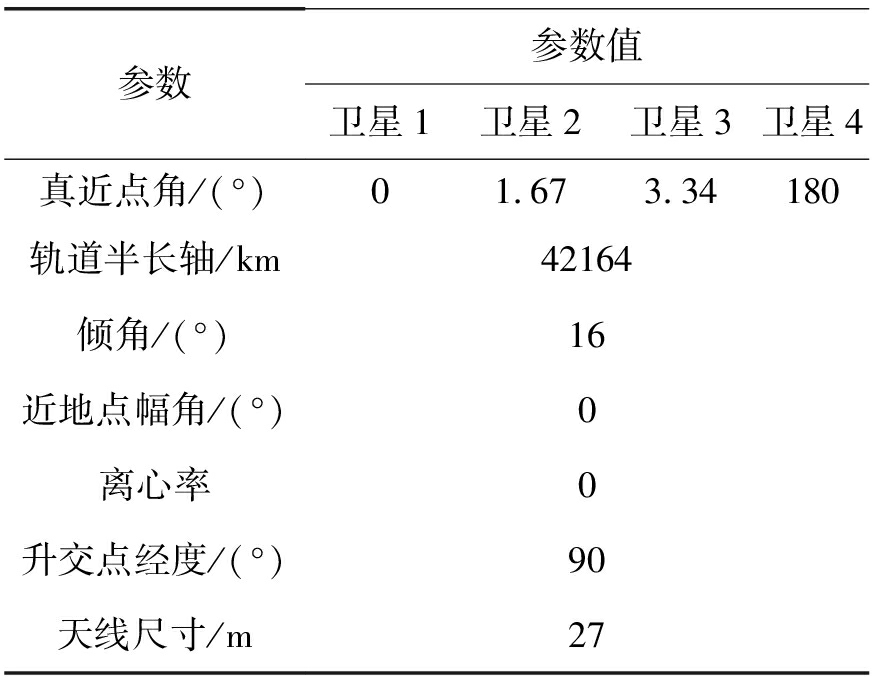
参数参数值卫星1卫星2卫星3卫星4真近点角/(°)01.673.34180轨道半长轴/km42164倾角/(°)16近地点幅角/(°)0离心率0升交点经度/(°)90天线尺寸/m27
本文提出的模糊度时域计算方法和参考频域计算方法得到的模糊度如图4所示。从仿真结果,我们有以下结论:
•使用传统频域方法和时域方法得到的模糊度结果有所差异。对于不同的构型,时域方法得到的模糊度趋势总是接近抛物线,而传统频域方法得到的模糊度的趋势随着构型而变化。
•传统方法与本文时域方法的差异程度与系统构型息息相关。在正侧视模式下,本文方法与传统方法得到的结果差异较小,而斜视情况下,这个差异将扩大。这是因为传统频域方法等效于全孔径时域方法,而斜视情况下波足的运动方向与地距向耦合严重,因此沿着地距向场景的点的天线增益在长孔径照射时间内会发生变化,使得最终模糊度变得较为平滑。
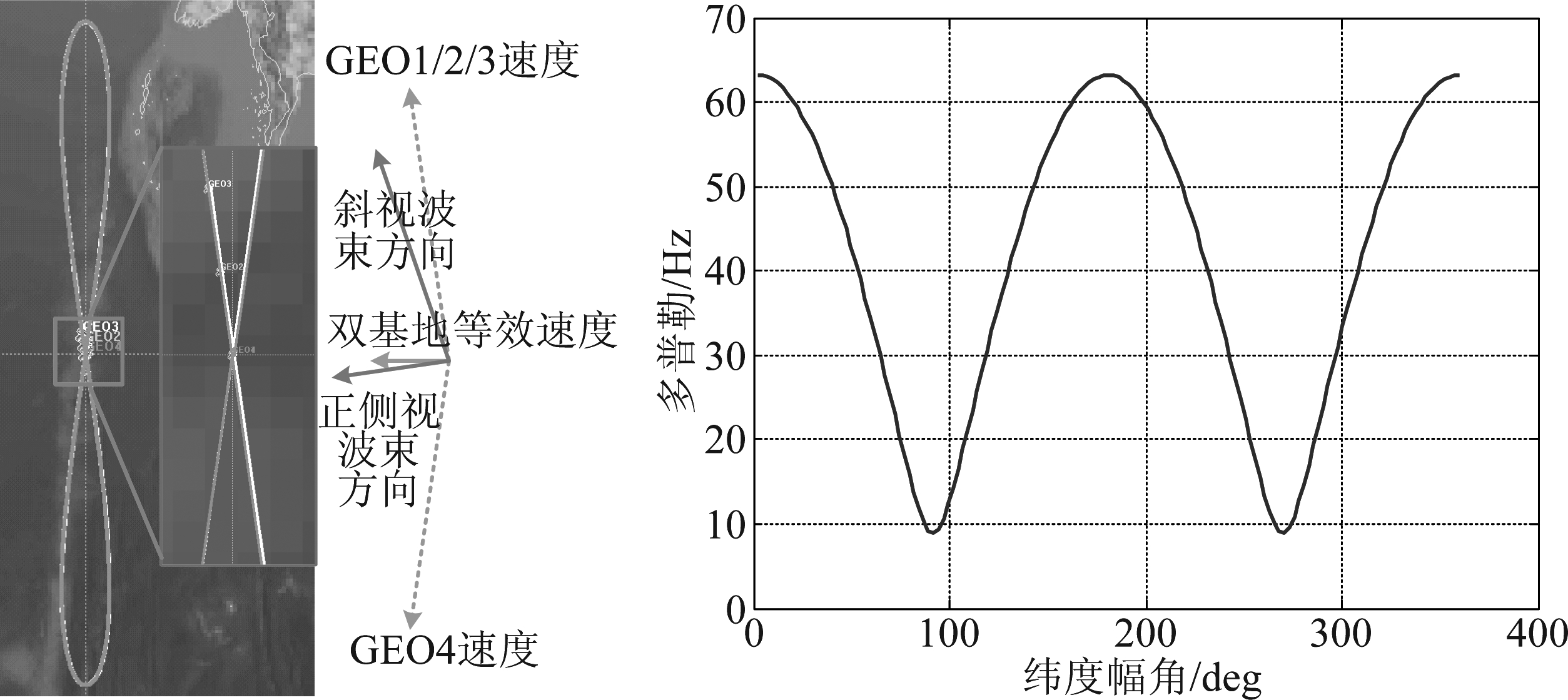
图3 GEO SAR星下点示意图(左)及全轨多普勒带宽(右)
Fig.3 Nadir track (Left) and full orbit Doppler bandwidth (Right) of GEO SAR
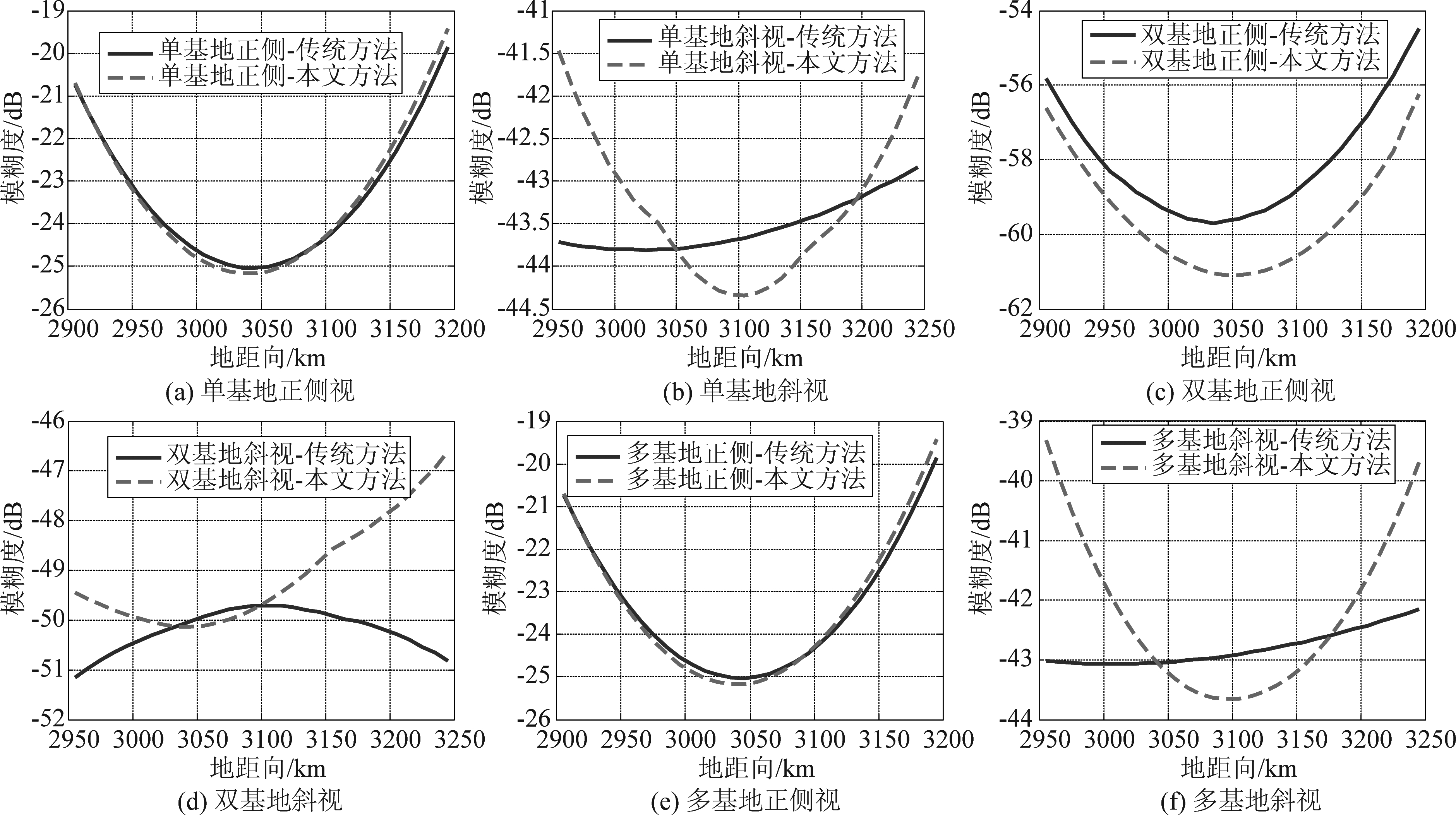
图4 本文方法和参考方法的模糊度仿真结果
Fig.4 GEO SAR ambiguity calculated by the proposed method and reference method
•对于单基地和多基地情况,斜视将引起模糊度性能得到提升。这是因为斜视情况下等距离线和等多普勒线不再正交,在GEO SAR中这种非正交特性更加明显,如图5所示。这将导致距离模糊区与多普勒模糊区之间的间隔与最小间距相比大大增加,使模糊区与天线主瓣方向的夹角更大,因此模糊区具有更低的天线增益。
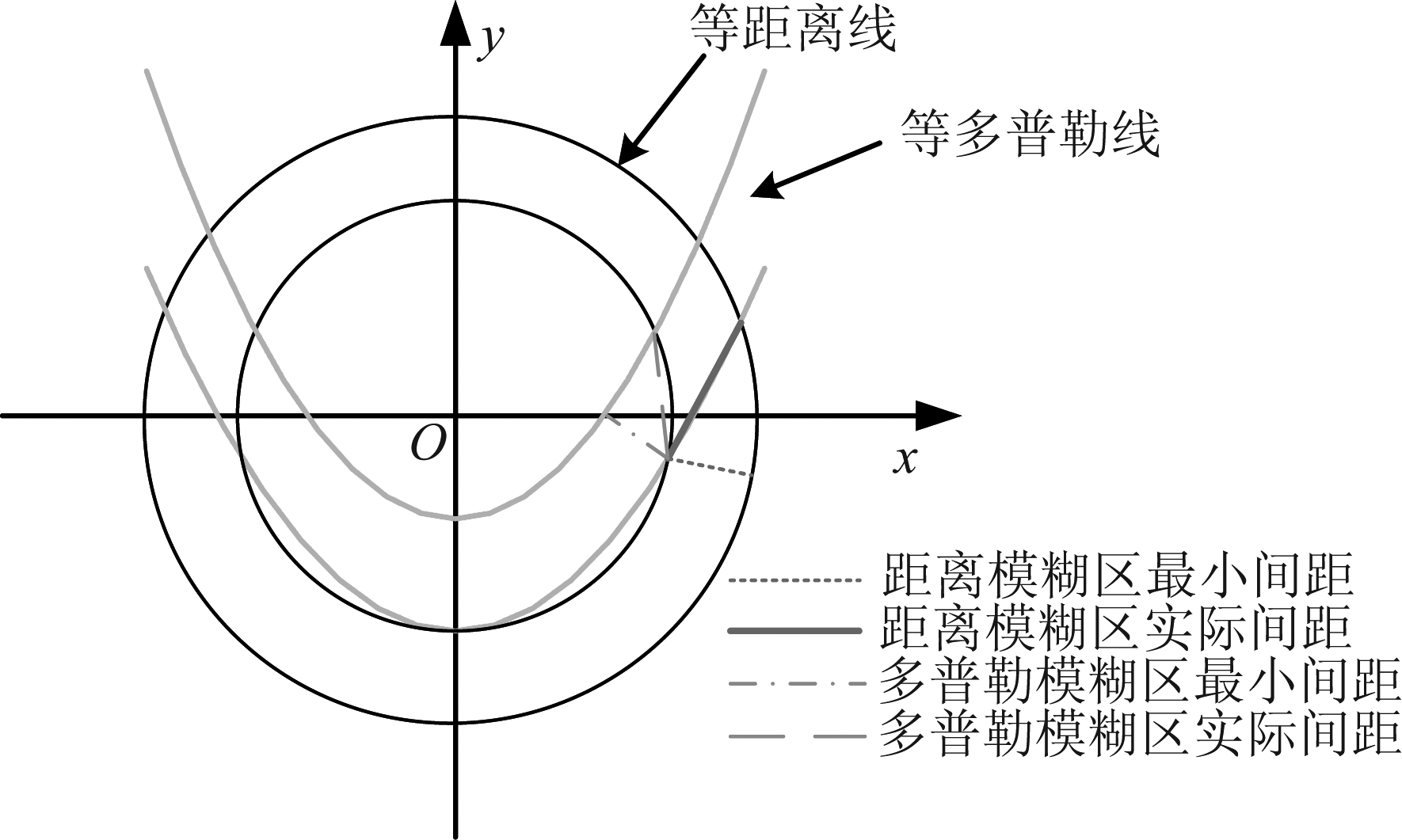
图5 等距离线与等多普勒线非正交示意
Fig.5 Non-linearity of iso-range and iso-Doppler lines
•双基地GEO SAR的模糊度与等效速度的大小和方向密切相关。如图3(左)所示,双基地等效速度相比于单基地速度,在大小和方向上都发生了明显的变化。等效速度大小下降使得场景多普勒带宽下降,域单基地的PRF(80 Hz)相比小得多,因此模糊度性能相比单基地大大提升。此外,斜视模式的波束方向与等效速度之间的正交性更好,因此斜视模式的模糊度反而要大于正侧视模式。事实上,双基地模式下的斜视角应当使用等效速度进行计算。在本例中,波束虽然相对于发射卫星速度而言是斜视的,但是对于等效速度而言斜视角反而更小。
4 结论
本文首先给出双基地GEO SAR模糊区的近似计算方法,然后给出分布式GEO SAR模糊度的时域计算步骤。基于此,对比分析了单基地GEO SAR、双基地GEO SAR和多基地GEO SAR的模糊度。结果表明,斜视情况下时域计算方法与传统的频域计算方法差异较大,并且差异性与卫星构型与斜视角有关,斜视情况将提高模糊度性能。在非全孔径时间成像下,宜采用模糊度时域计算方法。此外,双基地GEO SAR的模糊度具有一定特殊性,其模糊性能与等效速度的大小和方向相关。波束方向与等效速度的方向影响了双基地GEO SAR的模糊度,二者夹角正交性越高,则模糊度越大。对于GEO SAR而言,采用扫描模式既可以满足分辨率要求,还可以大大增加成像覆盖区域。扫描模式下的模糊度分析是下一步的研究工作。
[1] Long T, Hu C, Ding Z, et al. Geosynchronous SAR: System and Signal Processing[M]. Springer, 2018.
[2] Mao E-K, Long T, Zeng T, et al. State-of-art of Geosynchronous SAR[J]. Signal Processing (Xinhao Chuli), 2012, 28(4): 451- 462.
[3] 毛二可, 曾涛, 胡程, 等. 基于地球同步轨道合成孔径雷达的双基地探测系统: 概念及潜力[J]. 信号处理, 2013, 29(3): 285-292.
Mao Erke, Zeng Tao, Hu Cheng, et al. Bistatic detection based on Geosynchronous SAR: Concept and Potentiality[J]. Journal of Signal Processing, 2013, 29(3): 285-292.(in Chinese)
[4] 张欣, 黄普明, 王伟伟, 等. 二维stolt插值解耦合的GEO SAR成像算法[J]. 信号处理, 2016, 32(12): 1418-1424.
Zhang Xin, Huang Puming, Wang Weiwei, et al. 2-D Stolt Interpolation to Correct Coupling Algorithm for GEO SAR Imaging[J]. Journal of Signal Processing, 2016, 32(12): 1418-1424.(in Chinese)
[5] Guarnieri A M, Broquetas A, Recchia A, et al. Advanced Radar Geosynchronous Observation System: ARGOS[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(7): 1406-1410.
[6] Li F K, Johnson W T K. Ambiguities in Spacebornene Synthetic Aperture Radar Systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(3): 389-397.
[7] Curlander J C, Mcdonough R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. New York: Wiley, 1991.
[8] Chen J, Sun G C, Wang Y, et al. An Analytical Resolution Evaluation Approach for Bistatic GEOSAR Based on Local Feature of Ambiguity Function[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 2159-2169.
[9] Dong X, Ding Z, Wang J. Ambiguities in high squint mode SAR[C]∥Proceedings of the EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, F 23-26 April 2012, 2012.
[10] 王万林, 谭小敏, 田栋轩. 星载滑动聚束SAR的成像性能[J]. 空间电子技术, 2017, 14(3): 20-26.
Wang Wanlin, Tan Xiaomin, Tian Dongxuan. Imaging Performance of Spaceborne Slip SAR[J]. Space Electronic Technology, 2017, 14(3): 20-26.(in Chinese)
[11] 李财品, 何明一. 地球同步轨道 SAR 方位模糊度研究[J]. 信号处理, 2015, 31(6): 694-701.
Li Caipin, He Mingyi. Study on Azimuth Ambiguity for Geosynchronous Earth Orbit SAR[J]. Journal of Signal Processing, 2015, 31(6): 694-701.(in Chinese)
[12] Rodon J R, Broquetas A, Guarnieri A M, et al. A Ku-band geosynchronous Synthetic Aperture Radar mission analysis with medium transmitted power and medium-sized antenna[C]∥Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, F 24-29 July 2011, 2011.
[13] Li C, He M. Timing design for geosynchronous SAR[J]. Electronics Letters, 2016, 52(10): 868- 870.
[14] 唐禹, 王岩飞, 张冰尘. 滑动聚束SAR成像模式研究[J]. 电子与信息学报, 2007, 29(1): 26-29.
Tang Yu, Wang Yanfei, Zhang Bingchen. A Study of Sliding Spotlight SAR Imaging Mode[J]. Journal of Electronics and Information Technology, 2007, 29(1): 26-29.(in Chinese)



