1 引言
MIMO雷达是本世纪初被引入到雷达领域的一种新型雷达体制,随着近几年电路集成、信号处理和天线设计等技术的发展进步变得更具吸引力。MIMO雷达系统基于“多输入多输出”的思想,在发射端设置多个天线阵元,发射信号相互正交,接收端使用多个天线阵元同时接收目标的散射回波,从而形成多对收发组合通道,形成远大于实际阵列长度的等效孔径。这种阵列结构的优点在于几乎无需时间积累便可以获得目标区域的一次“快拍”数据,且系统通过空间卷积的方法使用较少的收发天线阵元便获得足够的空间谱采样,保证系统分辨率的同时避免了庞大的天线系统带来的成本问题。
现阶段MIMO雷达的主要的研究方向有MIMO雷达阵列设计和波形优化、目标监测与识别和成像技术研究等。在成像技术研究领域,Daniel等提出了一种适用于频率分集MIMO雷达成像的快速重构算法,主要基于加速傅里叶技术实现多站成像[1]。Zhuge X等将合成孔径雷达中的距离徙动算法(Range Migration Algorithm, RMA)应用到三维近场MIMO阵列成像,获得了高质量的成像结果[2],设计了一种用于隐匿武器监测的超宽带成像系统[3]。Bleh等设计了一种用于远场三维成像的W波段的FMCW MIMO雷达系统[4]。Jeon等设计了一种用于高分辨成像的W波段MIMO雷达[5]。此外,MIMO雷达成像技术在穿墙雷达、癌症监测等领域也得到了发展应用[6-7]。聂臻霖等设计了耐高温高压、高粉尘的MIMO雷达,应用于工业高炉冶炼中的粉料成像识别[8]。韩兴斌等从空间谱采样的角度分析了基于MIMO体制的分布式多通道雷达成像问题[9]。国防科技大学的王怀军比较全面地研究了MIMO雷达的成像算法,对经典的反向投影成像算法,距离偏移算法等加以改进后应用于MIMO雷达成像,并进行了原理性实验验证,也提出了融合成像处理算法,克服MIMO成像雷达频谱缺失的问题[10]。经典的标准BP成像算法由于不受天线阵列拓扑的限制和不存在平面波近似而得到了最为广泛的应用,且成像精度最高,但缺陷在于对大景深宽视角场景成像时运算量巨大,限制了成像系统的实时性。对应用于边坡场景的MIMO雷达系统,天线波束宽度可达120°,成像距离可达几千米,较大的场景范围带来了巨大的运算量。
总的来讲,近年来MIMO雷达成像算法理论已基本成熟,但成像处理算法的计算量仍然是制约MIMO雷达工程应用中快速成像的瓶颈。本文从MIMO雷达成像原理出发,提出了一种适用于大景深、宽视角场景的快速成像算法,该算法通过相位中心近似补偿解决了近场成像散焦问题,通过方位向分块Dechirp实现方位向的快速聚焦,通过仿真和实验数据验证了算法的有效性。
2 MIMO雷达阵列构型及回波建模
2.1 MIMO雷达阵列几何构型
MIMO成像雷达工作原理如图1所示,MIMO雷达收发阵列拓扑为一维线阵,有M个发射阵元和N个接收阵元,那么根据多输入多输出的原理,收发阵元组合得到的数据观测通道为MN个,相当于存在MN个虚拟阵元,大大扩展了原有物理接收阵元孔径,得到大孔径的等效阵列。以线阵所在位置为x轴,设发射天线阵元坐标为xT,m(m=1,2,...,M),接收天线阵元坐标为xR,n(n=1,2,...,N),则极坐标格式下雷达信号从第m个发射阵元发出,经散射点P(ρ0,θ0)被第n个接收阵元接收的距离分别是
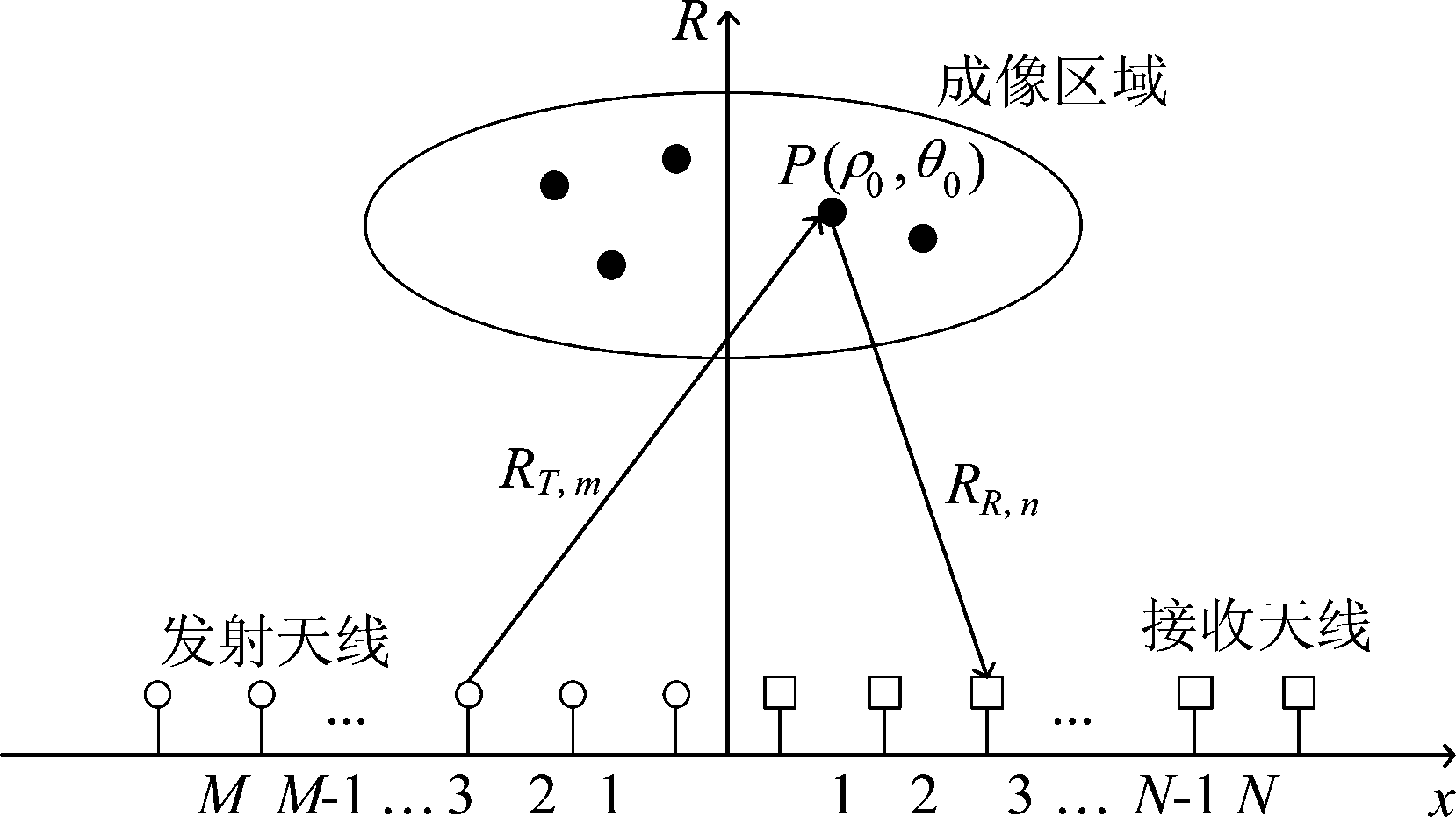
图1 MIMO雷达数据采集几何示意图
Fig.1 Data acquisition geometry of MIMO radar
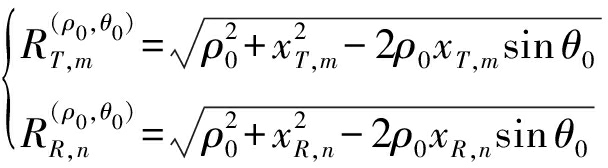
(1)
其中T表示发射阵元, m表示发射阵元的编号, R表示接收阵元, n表示接收阵元的编号。
设光速为c,则相应的双程时延为
(2)
2.2 系统参数与回波建模
MIMO雷达系统发射调频连续波(Frequency Modulated Continuous Wave, FMCW),该信号相当于一个占空比1的脉冲信号,所以不需要很高的峰值功率,用较低功率的固态放大器便可以满足要求。接收端采用Dechirp接收体制,使回波信号和本振信号进行混频得到较小的差频带宽,从而降低了对回波数据接收通道、后端A/D采集设备的要求,在民用市场极具竞争力。
由于MIMO雷达回波特性和阵列拓扑有很大关系,本文不涉及MIMO雷达阵列设计,表1给出一组MIMO雷达系统主要参数,图2给出该参数下MIMO雷达天线的几何构型。如图2,雷达系统有16个发射天线,32个接收天线,发射天线间距为d,接收阵元间距为8d。
表1 MIMO雷达系统主要参数
Tab.1 Parameters of MIMO radar
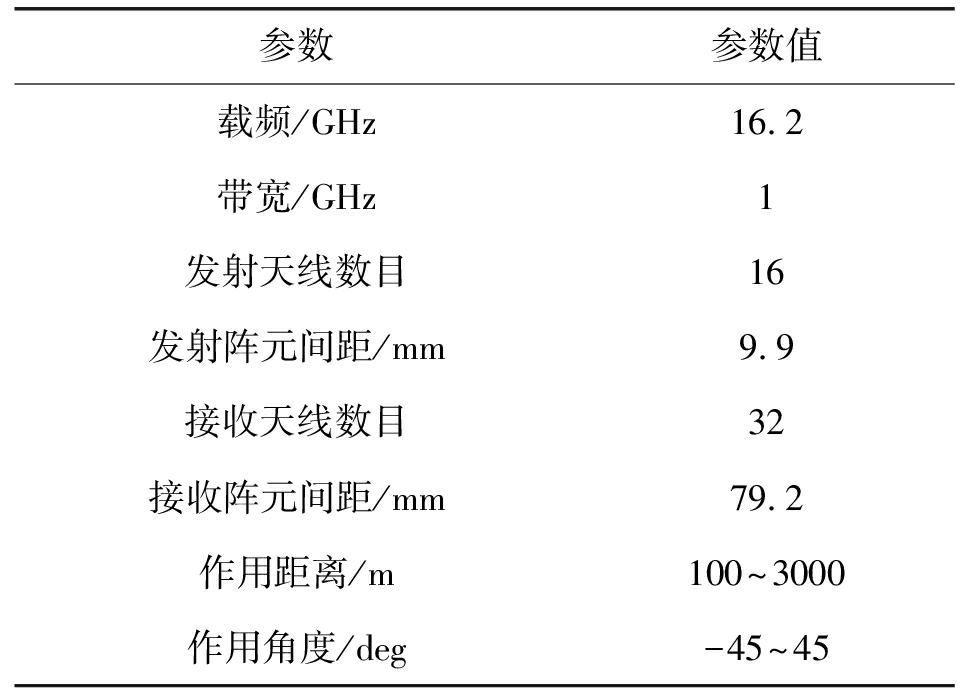
参数参数值载频/GHz16.2带宽/GHz1发射天线数目16发射阵元间距/mm9.9接收天线数目32接收阵元间距/mm79.2作用距离/m100~3000作用角度/deg-45~45
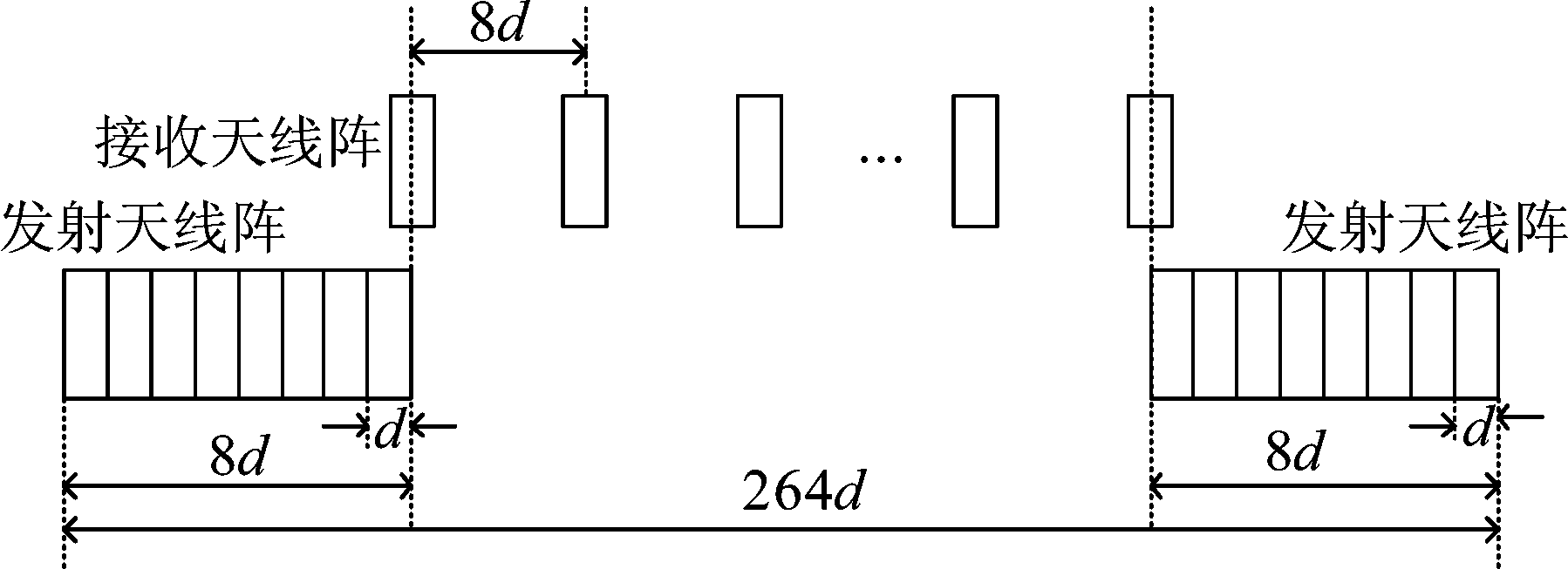
图2 MIMO雷达天线拓扑结构
Fig.2 Antenna topology of MIMO radar
一个脉冲周期内的接收到的回波信号为:
(3)
其中Tp为脉冲宽度, fc为载频,γ为调频斜率。为便于分析,这里假设回波信号的幅度包络为1。进行解线频调处理并去残余视频相位后得到的距离压缩信号如(4)式。
(4)
其中rect(xn/L)是方位向采样包络,代表方位向收发阵元组合的通道采样,从而限定雷达方位采样范围为-L/2到L/2。为表述方便,认为L是MIMO成像雷达的等效阵元形成的孔径。pr(·)为距离压缩后的信号包络函数。c为光速, fc为载频。实际上,由于近场情况下各目标的等效虚拟孔径不重合,若进行虚拟阵元等效,还需补偿等效的阵元近似误差,这个在后续步骤中讨论。
3 MIMO雷达快速成像算法原理
3.1 算法概述
基于信号模型(4)给出图3所示的MIMO雷达快速成像算法整体流程,进行PCA误差补偿后,按虚拟阵元的顺序进行数据重排,然后利用Keystone变换实现距离徙动校正,通过方位分块Dechirp原理实现方位向聚焦。下面给出该算法的详细说明和推导过程。
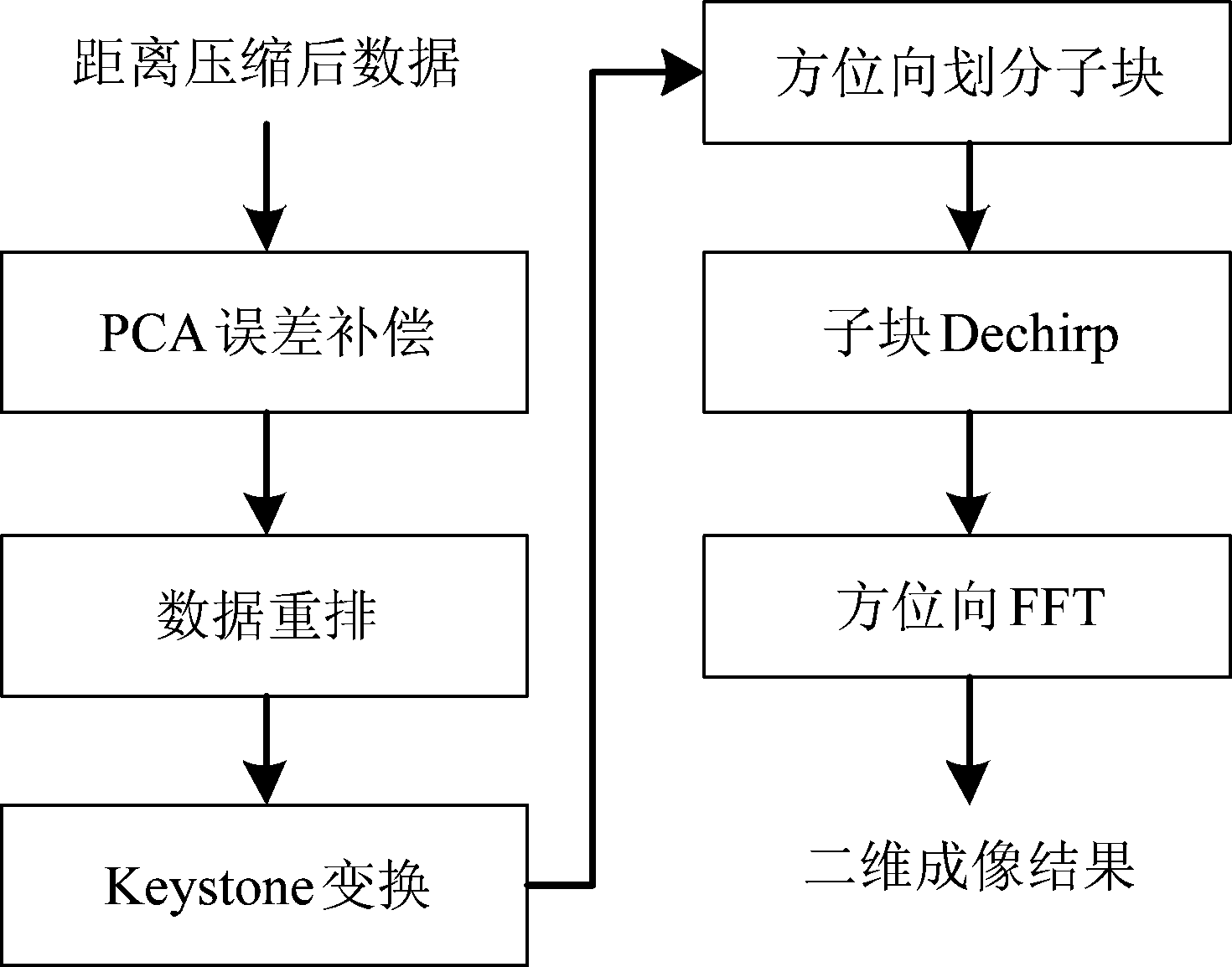
图3 算法流程图
Fig.3 Algorithm processing flow
3.2 相位中心近似误差分析
对于收发分置的雷达系统,发射天线和接收天线独立地发射和接收信号,那么可以近似认为在发射和接收天线的相位中心的连线的中点发射和接收信号,此点称为“等效相位中心”。如图4所示,假设雷达在Tm处发射信号,Rn处接收信号,那么C点为等效相位中心,可认为在C点放置一个收发同置的天线阵元。那么等效天线阵元C点的坐标为
(5)
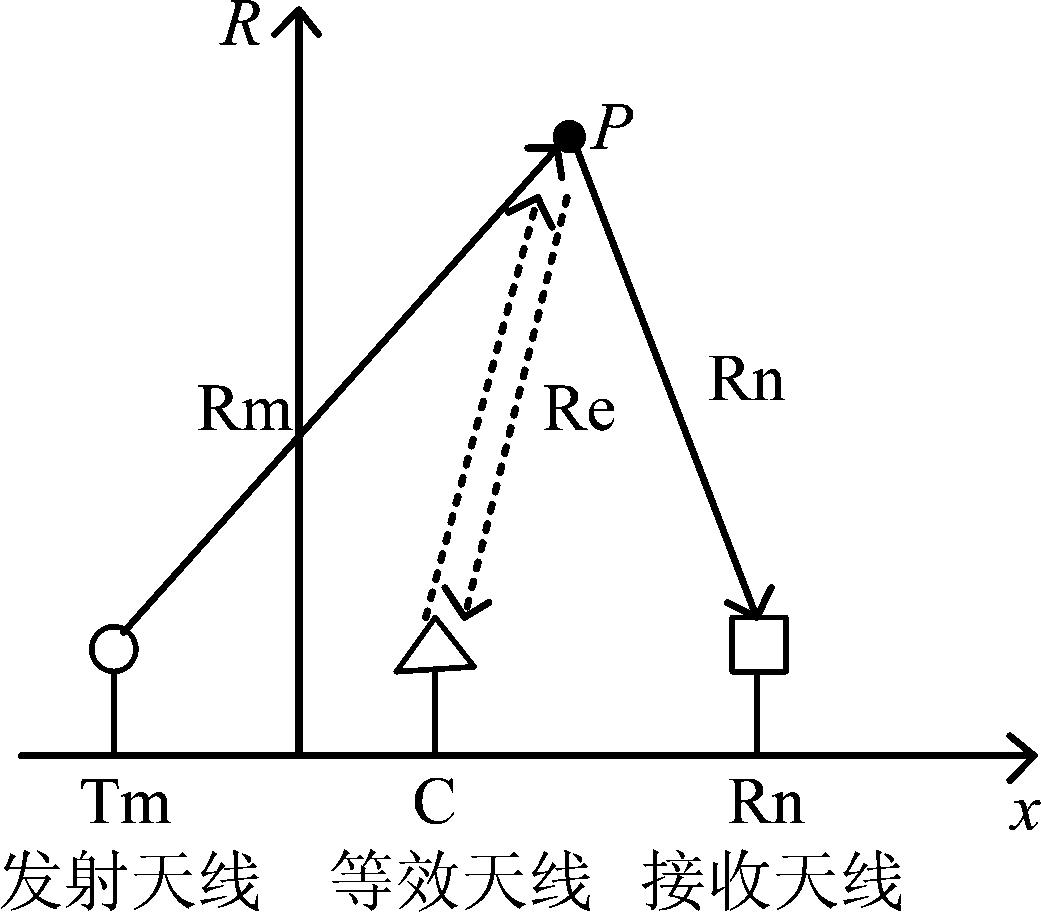
图4 一对收发阵元组合的等效相位中心
Fig.4 Equivalent phase center of transceiver array elements
在满足远场平面波近似的条件下,相位中心等效带来的近似误差可以忽略,但是在近场条件下,近似误差会导致图像质量下降,主瓣分裂,旁瓣抬高。一般来讲,合成阵列雷达的近远场的临界条件为目标到阵列中心和阵列两端的双程波程差小于λ/4,对于上述参数的MIMO雷达系统,近远场临界距离约347 m[11]。结合式(5),相位中心等效带来的距离误差为
(6)
忽略泰勒展开后的三阶及以上项,得到需要补偿的等效相位中心近似误差为如式(7)所示,从中可以看出,该误差随着目标的距离和方位角变化,即具有空变性。为保证误差补偿的准确性采用分块误差补偿的方式:在每一个距离线按一定原则划分子块,然后将每一子块的方位角正弦的中心作为参考点,补偿该误差。
(7)
误差补偿后,每一对收发组合的方位采样可变为其等效相位中心的方位采样,相应的阵列采样也可等效为虚拟阵元采样,然后将MIMO的回波数据按照虚拟阵元的顺序进行重新排列。补偿后的回波信号模型为
(8)
由于MIMO雷达虚拟等效孔径相对于雷达作用距离很小,通过对(8)进行泰勒展开,可以发现回波信号中距离徙动的二阶及以上项通常小于距离分辨率的1/4,可以忽略;方位相位历程的三阶及以上项小于π/8,可以忽略。所以式(8)可以合理简化为
(9)
3.3 距离向处理
仍以点目标P为研究对象,由于MIMO信号的距离徙动简化为距离线性走动,可以利用Keystone变换实现距离徙动校正[12]。Keystone变换是在距离频域实现,所以首先对(9)进行距离向FFT得到:
(10)
其中f表示基带频率,pr(·)代表距离频域的包络。从相位第二项可以看出距离徙动量随着目标方位角变化而具有空变性。无法通过频域线性相位的相乘来直接校正。
对方位变量进行Keystone变换,即引入虚拟方位采样变量xm,k,令xe,k=xm,kfc/(f+fc),将变量替换后的距离频域信号进行IFFT,得到距离徙动校正后的时域回波信号如式(11)所示。
(11)
3.4 方位向处理
方位向处理中的子块Dechirp是在伪极坐标系(ρ-sin θ)域进行的,等价于距离多普勒域,通过对二维时域的信号进行方位FFT得到。为了更直观地实现ρ-sin θ域的变换,先对(11)进行方位变量等价替换,令![]() 得到:
得到:
(12)
其中Ka(ρ0,θ0)可以看作方位向的调频率,依赖于目标的位置坐标(ρ0,θ0),
(13)
子块划分前,需要进行方位向FFT变到ρ-sin θ域,得到的变换结果为:
(14)
其中,Bsin θ(ρ0,sin θ0)为方位向支撑域宽度:
(15)
式(14)表示信号在伪极坐标域分布在其真实位置(ρ0,θ0)附近,距离宽度由距离压缩结果pr(·)决定,方位向宽度由Bsin θ(ρ0,sin θ0)决定。那么整个场景的回波信号占据了ρmin~ρmax、方位向sin θmin~sin θmax范围内,由于Ka(ρ0,θ0)随目标位置变化,不能使用统一的参考函数去斜。所以采用将各距离门的数据在sin θ域划分为Δsin θ(ρ)的Nsin θ(ρ)个子块的方法,其中划分宽度Δsin θ(ρ)的依据是保证子块Dechirp后的残余相位误差小于π/8,即:
(16)
图5给出了子块划分宽度上限随距离的变化曲线,可以看出随着距离的增大,分段宽度增大,相应的划分的子段个数随之减小,在一定距离后无需划分子块,便可满足误差要求。
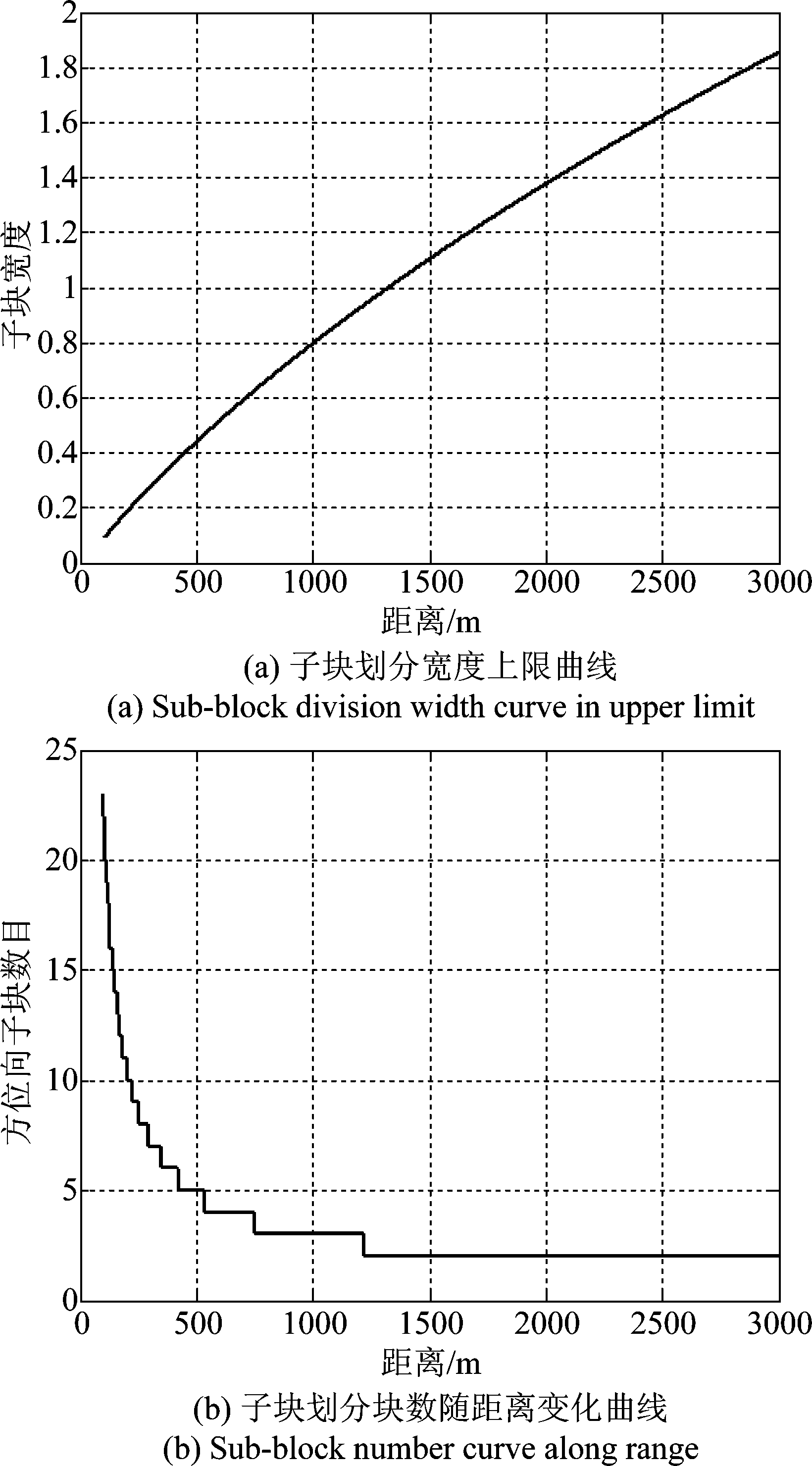
图5 方位向子块划分宽度和划分块数
Fig.5 Azimuth sub-block division width and number of sub-blocks
图6给出了在一个距离门内信号划分的示意图,浅灰部分代表不同方位角处的信号能量,1、2、3为三个子段的序号,子段方位角中心分别为sin θ1、sin θ2、sin θ3。然后对各子段信号做时域Dechirp处理,参考信号以子段中心点(ρi,sin θi)为参考,为
(17)
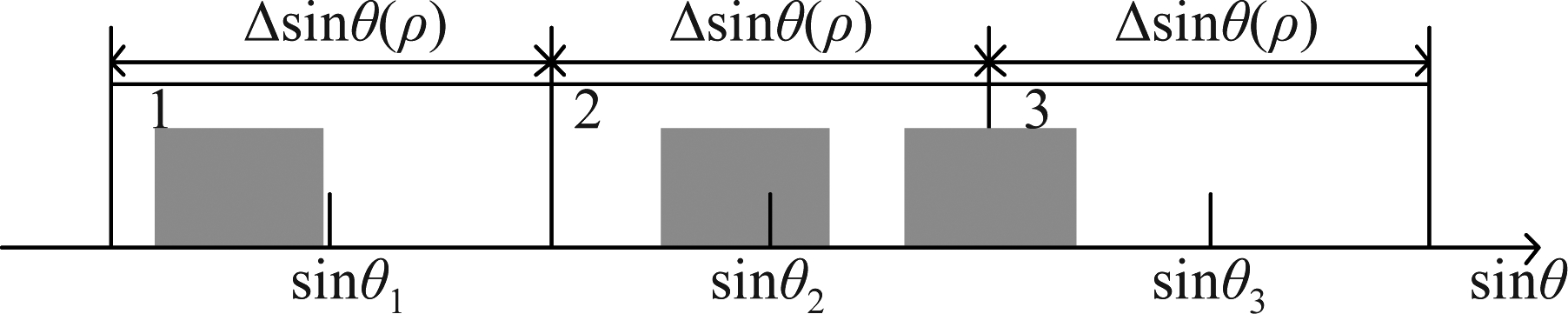
图6 方位向子段划分示意图
Fig.6 Schematic diagram of sub-blocks division along the azimuth
子区间Dechirp的结果为:
Sd(ρ,xλ;i)=S(ρ,xλ;i)·ref(ρ,xλ;sin θi)
(18)
将各区间子块在二维时域相加,得到整个方位范围的结果:
(19)
最后,进行方位向FFT变换回ρ-sin θ域,得到二维聚焦的MIMO图像。
3.5 算法运算量分析
这里根据算法的浮点运算量(FLOP)来分析处理开销。假设距离向采样点数为Nr,方位向采样点数为Na,压缩后的二维数据矩阵大小为Nr×Na。设Keystone变换插值核长度为M,方位划分距离门ρ的分段数目为m(ρ),则本算法的整体运算量为
距离向处理包括距离向FFT、Keystone变换和距离向IFFT:
5Nrlog2(Nr)Na+2(2M-1)NrNa+5Nrlog2(Nr)Na
(20)
方位向处理包括方位FFT、子块Dechirp处理和方位FFT聚焦:
5Nrlog2(Na)Na+[5Nalog2(Na)+8Na]·
(21)
假设Nr=Na=N,则本算法运算的时间复杂度为O(N2log2N),优于BP算法复杂度O(N3)。
4 算法验证
4.1 仿真实验验证
以2.2节中系统参数和极坐标(100 m,45°)处点目标进行仿真,对本文提出的算法的精度和性能加以验证。图7(a)为回波距离压缩且重排后的二维时域信号,可以看到明显的距离徙动;图7(b)为目标进行Keystone变换校正距离徙动后的结果;然后将信号变换到ρ-sin θ域,按式(16)进行方位向子块Dechirp处理,得到最终的成像结果图7(c)、(d),对成像结果的二维分辨率及峰值旁瓣比进行评估,如表2所示。从时间开销看,本文算法仅需7 s即可成像,相比于传统BP算法约需要30 s,大大提高了运算速度。图8给出了相位中心近似误差对近场目标成像的影响,未补偿前方位向主瓣分裂,旁瓣抬高,栅瓣较高,误差补偿后可以得到良好的方位聚焦效果。所以,本算法可以兼顾近远场大场景成像,在保证算法精度的前提下运算效率远优于BP算法。
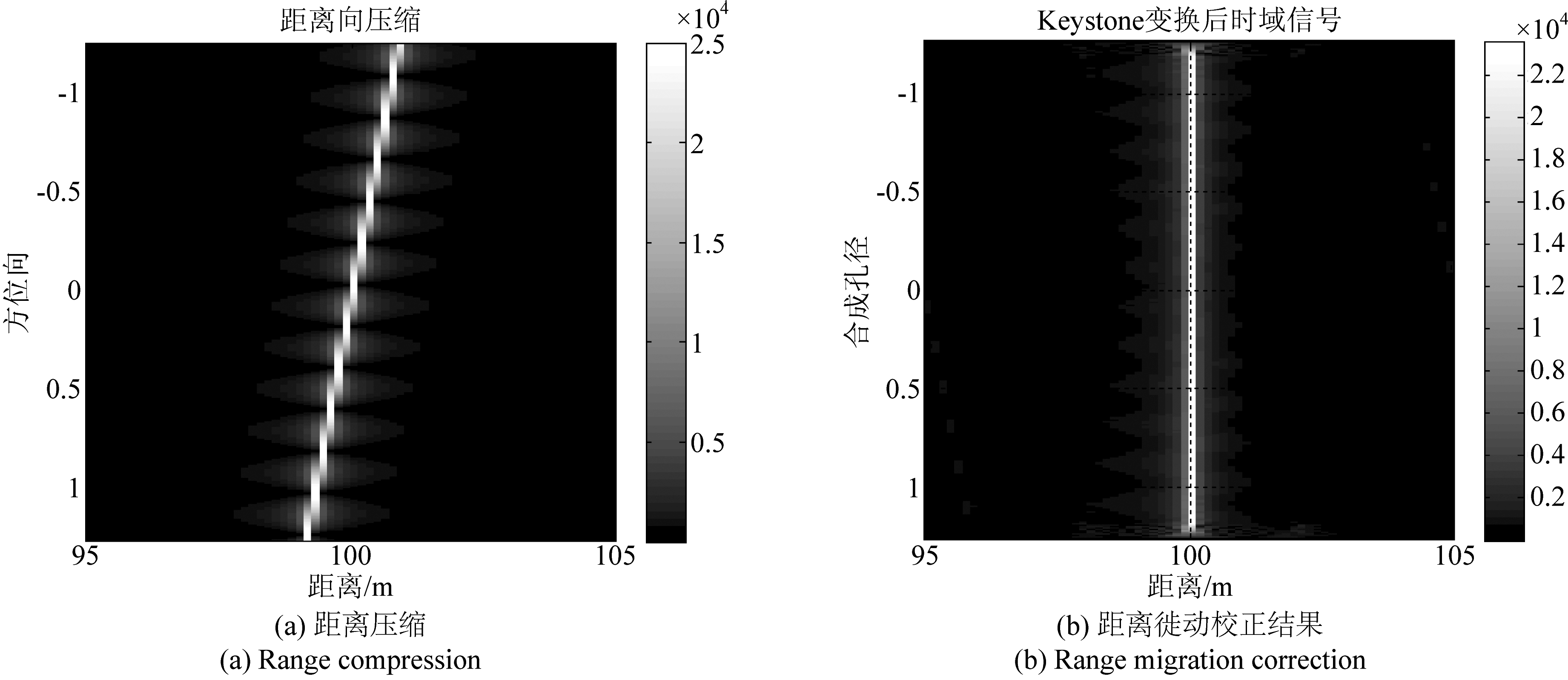
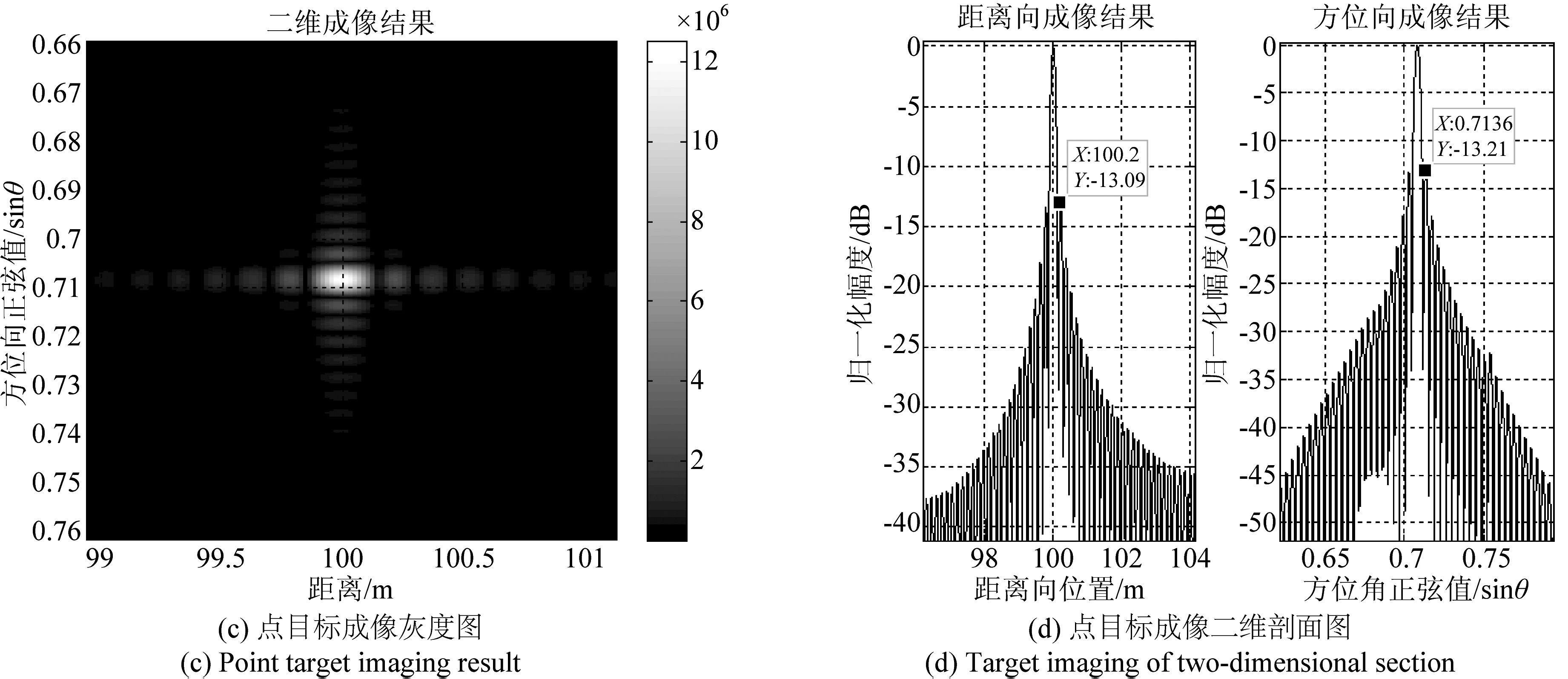
图7 成像处理过程
Fig.7 Imaging process
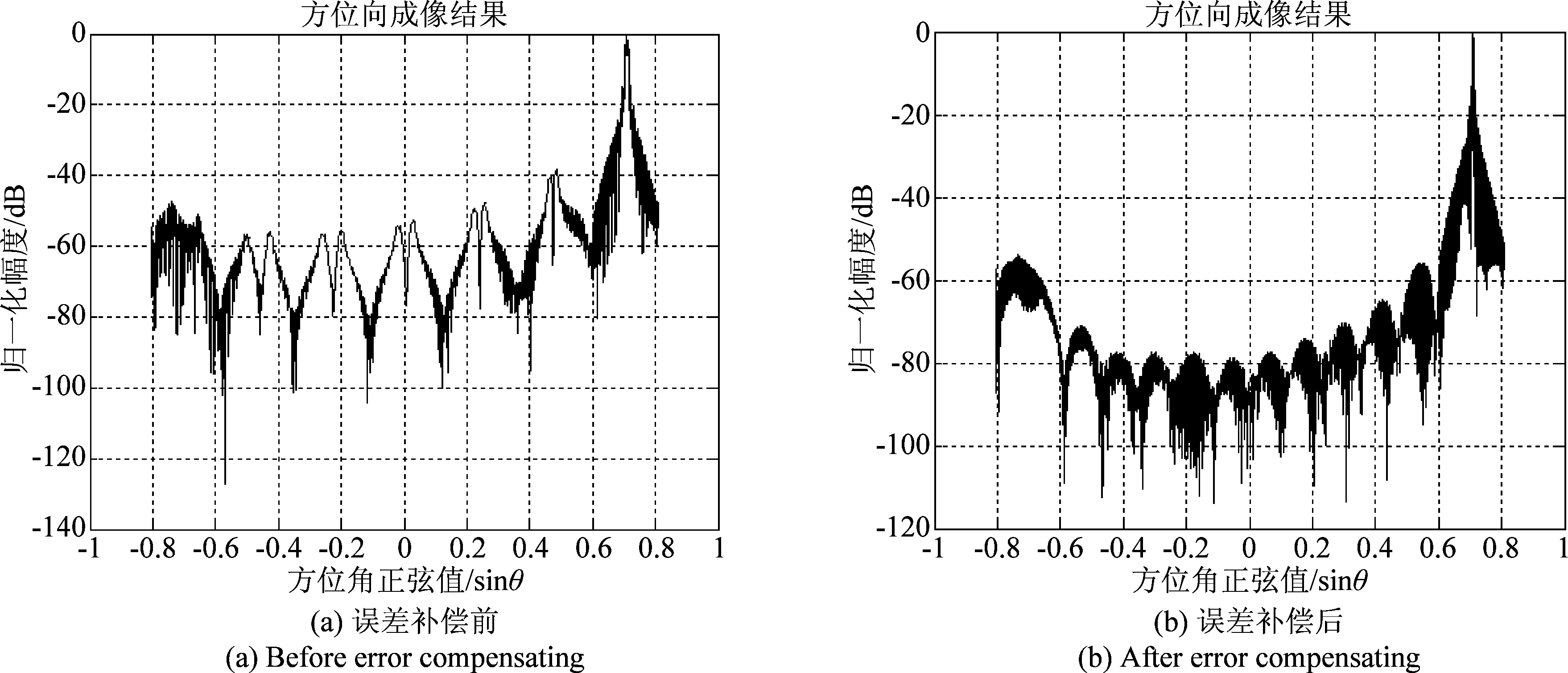
图8 PCA误差补偿前后方位向成像结果对比图
Fig.8 PCA error compensating comparison in azimuth
表2 成像结果性能分析
Tab.2 Performance analysis of imaging result

性能指标测量值(理论值)距离向分辨率/m0.14(0.15)方位向分辨率/mrad3.33(3.65)距离向峰值旁瓣比/dB-13.21(-13.26)方位向峰值旁瓣比/dB-13.09(-13.26)
4.2 外场实验验证

图9 成像场景光学图片
Fig.9 Optical picture of the imaging scene
使用本文提出的成像算法对地基MIMO雷达的外场实验得到的实测数据进行了处理。图9为利用实验室的MIMO雷达系统对河北某矿区进行探测的目标场景光学图,场景距离范围为200~850 m,方位视场为-45°~45°,场景中放置一角反射器作为定标器。MIMO雷达系统为Ku波段调频连续波体制,通过分时发射FMCW以区分回波信号,雷达参数同2.2节参数一致,带宽选用0.4 GHz,含有16个发射阵元和32个接收阵元,等效孔径长度约为2.53 m,实际采集到的原始回波数据经过了100次的快拍积累。图10(a)、(b)分别为利用本文的算法和BP成像算法得到的成像结果,对角反的性能分析如表3所示。可以看到二者成像结果基本一致,较强的散射区域如中央公路、角反射器等均清晰可见,标准BP算法成像约需要102 s,而利用本文成像算法用时仅26 s。因此,本算法在保证成像精度的要求下极大地节约了时间成本,满足了系统对于大景深宽视角场景快速成像的实时性要求。

图10 成像结果对比
Fig.10 Comparison of imaging results
表3 角反射器性能分析
Tab.3 Performance analysis of corner reflector
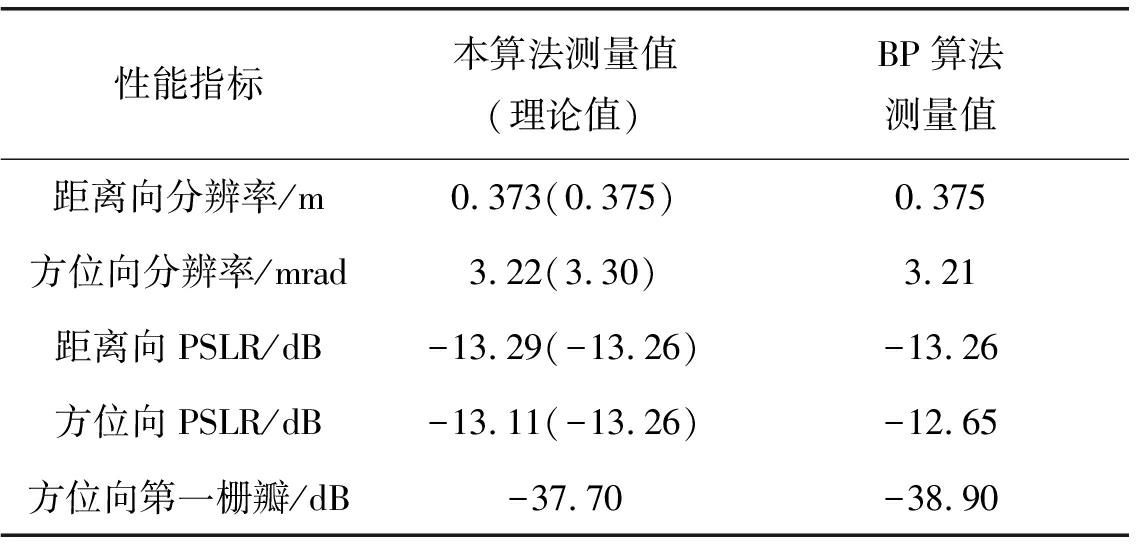
性能指标本算法测量值(理论值)BP算法测量值距离向分辨率/m0.373(0.375)0.375方位向分辨率/mrad3.22(3.30)3.21距离向PSLR/dB-13.29(-13.26)-13.26方位向PSLR/dB-13.11(-13.26)-12.65方位向第一栅瓣/dB-37.70-38.90
5 结论
本文提出了一种适用于地基MIMO雷达系统的大景深宽视角场景快速成像算法,适用距离范围可兼顾近远场且适用视角范围大。该方法基于实验室MIMO雷达系统建立信号模型,将MIMO收发阵列进行虚拟阵元等效,并补偿近场阵元等效带来的距离误差,距离向利用Keystone变换校正距离徙动,方位向利用分块Dechirp实现快速聚焦。最后,通过仿真实验和外场实验验证了算法的有效性:仿真数据证明了算法处理流程的正确性,图像分辨率、峰值旁瓣比等性能指标均达到了理论要求。外场实验选取大景深、宽视角场景,对算法的实际处理能力及时间花销进行评估,验证了该算法在保证成像精度的前提下运算效率优于BP算法,可以更好地满足系统实时性的要求。
[1] Daniel L Marks, Okan Yurduseven, David R. Smith. Fourier Accelerated Multistatic Imaging: A Fast Reconstruction Algorithm for Multi-Input-Multiple-Output Radar Imaging[J]. IEEE Access, 2017, 5: 1796-1809.
[2] Zhuge X, Yarovoy A G. Three-Dimensional Near-Field MIMO Array Imaging Using Range Migration Techniques[J]. IEEE Transactions on Image Processing, 2012, 21(6): 3026-3033.
[3] Zhuge X, Yarovoy A G. A sparse aperture MIMO-SAR-based UWB imaging system for concealed weapon detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 509-518.
[4] Daniela Bleh, Markus Rosch, Michael Kuri, et al. W-Band Time-Domain Multiplexing FMCW MIMO Radar for Far-Field 3-D Imaging[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(9): 3474-3484.
[5] Se-yeon Jeon, Min-Ho Ka, Seungha Shin, et al. W-Band MIMO FMCW Radar System With Simultaneous Transmission of Orthogonal Waveforms for High-Resolution Imaging[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(11): 5051-5064.
[6] Klemm M, Leendertz J, Gibbins D, et al. Microwave radar-based differential breast cancer imaging: imaging in homogeneous breast phantoms and low contrast scenarios[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(7): 2337-2344.
[7] Wang Wu, Lu Biying, Song Yongping, et al. Parallel Realization of Moving Target Imaging in 2D MIMO Through-Wall Radar Applications[A]. IEEE Beijing Section. Proceedings of 2015 IEEE International Conference on Communication Problem-Solving(ICCP)[C]. IEEE Beijing Section, 2015: 145-148.
[8] 聂臻霖, 陈先中, 侯庆文. 基于高炉料线的 MIMO 成像雷达设计[EB/OL]. 北京: 中国科技论文在线[2018- 09-14]. http:∥www.paper.edu.cn/releasepaper/content/201809-26.
Nie Zhenglin, Chen Xianzhong, Hou Qingwen. Design of MIMO Imaging Radar Based on Blast Furnace Feed Line[EB/OL]. Beijing: Chinese scientific papers online[2018- 09-14]. http:∥www.paper.edu.cn/releasepaper/content/201809-26.(in Chinese)
[9] 韩兴斌, 胡卫东, 郁文贤, 等. 分布式多通道雷达成像技术[J]. 电子与信息学报, 2007, 29(10): 2354-2358.
Han Xingbin, Hu Weidong, Yu Wenxian, et al. Distributed multi-channel radar imaging technology[J]. Journal of Electronics and Information, 2007, 29(10): 2354-2358.(in Chinese)
[10] 王怀军. MIMO雷达成像算法研究[D]. 长沙: 国防科学技术大学, 2010.
Wang Huaijun. Research on MIMO radar imaging algorithm[D]. Changsha: National University of Defense Technology, 2010.(in Chinese)
[11] Hu Cheng, Wang Jingyang, Tian Weiming, et al. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays[J]. Sensors, 2017, 17(3), 598- 602.
[12] 杨旭, 皮亦鸣, 李晋, 等. 采用二阶Keystone变换的机动目标ISAR成像算法[J]. 信号处理, 2018, 34(11): 1297-1306.
Yang Xu, Pi Yiming, Li Jin, et al. ISAR Imaging Algorithm of Maneuvering Targets Using the Second-Order Keystone Transform[J]. Journal of Signal Processing, 2018, 34(11): 1297-1306.(in Chinese)



