1 引言
随着电子技术的发展和传感器精度的提高,观测目标将会占据传感器的多个分辨单元且对目标的空间信息感兴趣,从而使得一个目标在一个采样周期内可能产生多个量测点,这种目标就被看作为扩展目标,该目标的跟踪问题也被称为扩展目标跟踪[1- 4](Extended target tracking/Extended object tracking, ETT/EOT)。扩展目标跟踪系统不仅能提供目标精确的运动信息,同时也包含着目标的形态信息,即它对目标[4]的动态和空间信息进行了同时估计。
Gilholm等人[5- 6]提出广泛使用的模型,观测数目服从泊松分布,其中泊松率γ是目标状态的函数,即采用PPP来模拟空间扩展和测量数量。大多数ETT算法都是将目标近似为刚性形状,如矩形、椭圆和星凸形状。随机矩阵模型假定目标的形状可以用一个椭圆近似,观测按照高斯分布围绕在目标几何中心的周围。文献[7]是最早使用随机矩阵方法(Random Matrix Method, RMM)对扩展目标的运动状态和物理扩展进行估计。与依赖于椭圆形状的随机矩阵模型相比,随机超平面模型(Random Hypersurface Model, RHM)[8-9]不再将扩展目标形状局限于椭圆,而是使用更一般的星凸(star convex)形状来近似目标轮廓。为了参数化形状,文献[10]和[11]实现了高斯过程(Gaussian Processes, GP),即通过一个高斯过程自动学习目标形状,从而能够对任意形状的目标给出其轮廓的解析表达式。在文献[12]中,扩展目标由一组反射点建模,期望最大化(Expectation Maximization, EM)算法用于处理未知关联。在文献[13]和[14]中,明确地参数化了具有方向和半轴长度的椭圆,并使用乘法噪声来形成非线性测量方程。
多目标跟踪的关键问题是测量与目标之间的关联是未知,如果假设给定测量值的原点独立于所有其他测量值,即多个度量可以被分配给一个目标,则该模型被称为“多对一”模型[15-16],聚类和划分就是传统数据关联方法使用的最直观的解决方案之一,如概率假设密度滤波器[17],概率多假设跟踪[18-19]或JPDA[20]滤波器。另一类扩展目标跟踪数据关联方法就是通过置换门控区域中所有测量的全部可能组合,直接解决多个测量到目标的关联。假设每种组合均匀分布,并且需要每种组合的增益[21-22],这种方法即使通过迭代的改进[23]也使计算候选测量组合的复杂性非常高。Streit基于[5]和[6]的模型提出了JPDA强度滤波器[24](JPDA intensity filter, JiFi),用来估计每个扩展目标的强度函数,避免了大量的关联概率计算。Granstrom等人提出了一种基于采样的随机优化方法[25]来获得最可能的关联。
由于扩展目标在每个时刻可产生多个量测,再满足点目标跟踪的假设条件,如果依然采用传统的量测关联算法,随着目标数和量测数的增多,运算量将呈指数增长,必然会导致组合爆炸问题,故需修改假设条件将点目标跟踪的联合概率数据关联算法推广到多扩展目标跟踪将成为本文的研究重点。本文针对该问题,提出了基于PPP模型的JPDA滤波器。假设杂波和来自目标的测量的数目都是泊松分布且相互独立的,则每个采样间隔产生的泊松分布的概率函数与传统目标跟踪方法中的检测概率[6]具有相似的作用,所以在本文中没有使用显式的检测概率。对于扩展目标的形状估计,采用的是通过递归结合各个测量值来明确估计椭圆形扩展目标的方向和半轴长度[13]。泊松模型能够确定计算出边缘关联概率(本文的重要公式)并使用其结果分别更新每个扩展目标状态向量的运动参数和形状参数。
本文的其余部分的结构如下。第2节简单介绍扩展目标的测量模型和运动模型,以及推导出测量的预测和更新的相关向量参数;第3节首先推导出对扩展目标进行测量的JPDA,然后描述JPDA滤波器的更新步骤;第4节详细描述本文提出的新算法步骤;第5节在两种不同的场景中测试该算法并分析算法的性能;第6节对本文进行总结。
2 建模及估计
对于扩展目标,除了用目标的运动模型描述目标状态如何随时间演化(如目标状态包括位置、速度、加速度和转弯率等),还需要用目标的形状模型来描述目标的空间几何形状。
假设时间步k时扩展目标的运动参数如下:
(1)
其中
表示目标的位置,
表示目标的速度,甚至还可以表示目标的加速度和转弯率等。
根据文献[13]扩展目标椭圆参数化描述,假设时间步k时扩展目标的形状参数如下:
pk=[ak,lk,1,lk,2]T∈R3
(2)
其中ak∈[-π,π)表示椭圆的方向,lk,1和lk,2∈R+表示椭圆的两个半轴长度。
扩展目标的状态向量xk由运动参数rk和形状参数pk组成。
xk=[rk,pk]T
(3)
2.1 测量模型
假设扩展目标在每个时间步k时产生不同数量的独立二维笛卡尔测量
其中Mk表示时间步k时测量的个数,每个独立的测量
是与扩展目标运动参数和形状参数相关的乘法噪声测量模型[13,26],它的基本构造是目标的运动质心与随机缩放的椭圆半轴以及测量噪声的和。
(4)
对上式(4)进行紧凑化简可写成:
(5)
其中H=[I20]和
表示方向的旋转矩阵,
表示乘法噪声。注意,在本文中,假设
是一个高斯噪声,用协方差为
的高斯分布来匹配椭圆的均匀分布[14]。
2.2 运动模型
根据扩展目标的运动参数和形状参数,可以假设其遵循线性马尔可夫模型:
(6)
(7)
其中
和
分别是运动参数和形状参数的转换矩阵,
和
分别是其协方差矩阵为
和
的零均值高斯过程噪声。注意:由于每个扩展目标的椭圆形状的大小可能不相同,故对其形状模型可以单独模拟。
2.3 测量预测
由于扩展目标的运动参数和形状参数的时间演化均遵循线性马尔可夫模型,因此,可以使用卡尔曼滤波器预测相关公式,即
(8)
(9)
(10)
(11)
2.4 测量更新相关参数
如果只对
进行线性测量更新,那么扩展目标的形状参数则无法观测[26],所以针对扩展目标的运动参数和形状参数提出了两步测量更新。首先,利用采集到的原始测量值对运动参数进行更新;然后,通过对的不相关转换[27]得到伪测量
对形状参数进行更新。注意,扩展目标的运动参数和形状参数是相互独立的,因此在使用的过程中并没有重复计算测量值。
2.4.1 运动参数
由上文式(5)易得到目标的运动状态是线性,形状参数是非线性的,并通过上一步估计的
来近似pk可把式(5)调整如下
(12)
根据卡尔曼滤波器[5,28],可得预测的观测向量、互协方差和新息协方差如下,
(13)
(14)
(15)
2.4.2 形状参数
为了能够利用线性估计器中测量中包含的信息,通过采用原始测量的2倍克罗内克积来构造伪测量。此外,将测量偏移其期望值,使得伪测量的期望和协方差是原始测量的第二和第四中心矩。总之,伪测量如下定义
(16)
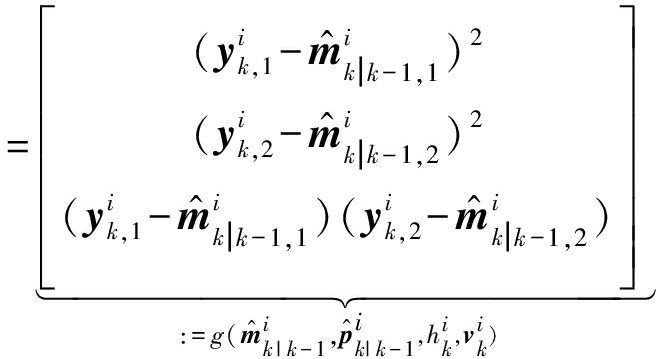
(17)
其中
(18)
根据式(15),设
(19)
(20)
(21)
假设式(15)可写为
(22)
然后,根据第二和第四中心矩的定义可得
(23)
(24)
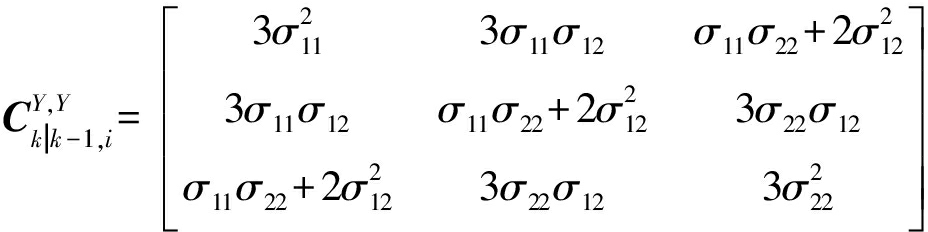
(25)
其中
为了计算扩展目标的形状参数的互协方差
根据泰勒级数展开,式(17)的伪测量方程围绕
和
进行线性化
(26)
其中
和
是式(17)的关于运动参数(x和y两列)和形态参数的雅可比行列式。注意,因为的期望值为零,并且它与形状参数不相关,因此,在计算互协方差时只有重要,故互协方差可写为
(27)
其中
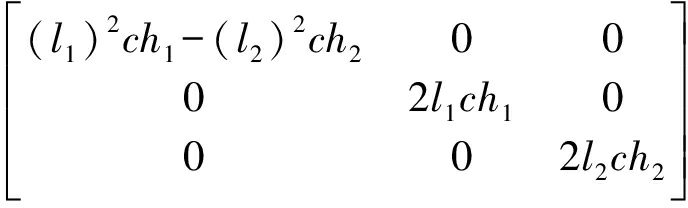
(28)
其中
由于下文要JPDA测量更新中在用到以上相关参数,故本节把文[13]滤波器中的相关知识进行了详细梳理。
3 数据关联
假设
表示k时刻的一组可用的测量,
表示一组未知的扩展目标,其中Nk表示时间步k时目标的个数。每次测量都来自扩展目标或者杂波,其中每个扩展目标产生测量的数量都服从泊松分布,杂波的数量是均值为λ0的泊松分布。假设杂波是在监视区域内密度为ρ的均匀分布。在本文中,扩展目标跟踪主要是从以下两个方面与传统的点目标跟踪进行区别的:(1)状态向量不仅包含目标的运动参数,还包含目标的形状(方向和大小)参数;(2)每个扩展目标至少产生一个测量。所以,测量到目标的分配及Xk的估计是解决本文多扩展目标跟踪的关键。
3.1 PPP
在本文中采用PPP对扩展目标进行测量建模[5,6]。每个扩展目标
产生
个测量,其中服从均值为λi的泊松分布,即
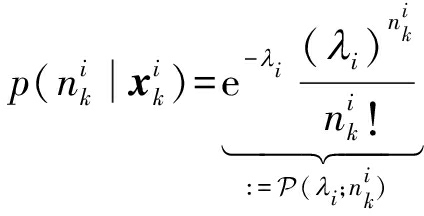
(29)
其中λi在监视区域内的泊松率与传统点目标跟踪中的检测概率充当相似的角色。当
表示目标漏检,由扩展目标产生的测量y是来自空间分布
的独立随机抽取,假设关联事件θ将测量集Zi分配给扩展目标xi,即
(30)
其中
是指定目标xi的测量yj的空间分布,具体详情将在3.3节中描述。对于多扩展目标Xk,有
(31)
3.2 空间分布
如2.1节所述,为了对空间分布进行建模,测量模型是将形状参数与测量相关联的显式测量函数构建而成的[14]。根据扩展目标由运动参数
和形状参数
组成的,且和是均值分别为
和以及相应的协方差为
和
的高斯分布,JPDA滤波器的数据关联可由以下公式定义:
(32)
其中
是在时间步k时扩展目标i的运动参数的量测的一步预测,
是其新息协方差。注,式(32)与文献[29]的公式(2)相同,其中非均匀泊松过程的空间依赖的速率函数是λiGij。
3.3 JPDA
在时间步k时,Mk个测量需要分配给Nk个目标或者背景杂波,其中测量值与扩展目标之间的映射是“多对一”且随时间的变化测量值是未知的,即可将多个测量值分配给一个扩展目标。故关联假设可以用一个1×Mk随机矩阵
表示,其中
(33)
以上关联隐式指定如下:
是所有分配给扩展目标i的测量集;
是杂波的测量集;
是的基数;
是杂波的数量,如
在本文中,给定一个关联事件θ和
时,可得到
p(θ|Xk)=p(θ,T|Xk)=p(θ|T,Xk)p(T|Xk)
(34)
结合公式(29),可得
(35)
假设T相等的不同关联事件是均匀分布的,即
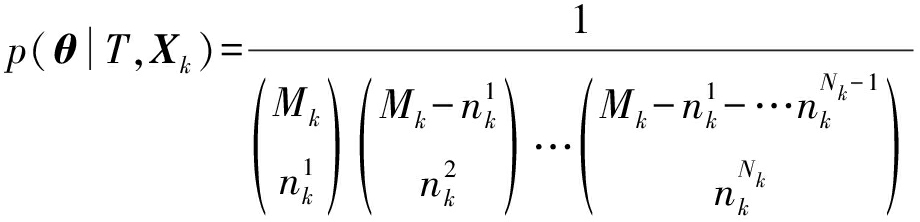
(36)
由式(34)、(35)和(36)可得,
(37)
根据式(31)和(37)以及贝叶斯规则,可得关联事件θ的后验概率为下式,
p(θ|Zk,Xk)∝p(Zk|θ,Xk)p(θ|Xk)
(38)
测量j与扩展目标i的边缘关联概率为
βij=p(θi=j|Zk,Xk)
(39)
(40)
式(39)是在杂波和目标都为泊松模型的情况下推导出来的:根据文献[5- 6],泊松模型的似然对应于PMHT[30]中使用的似然性,即多个测量被独立的分配给不同扩展目标,其中参数λi表示泊松均值。基于以上原因,本文中的边缘关联概率可用文献[29]中“多对一”的测量对目标的关联思想以及LMIPDA[15]等类似的方式进行简,则可得
(41)
(42)
其中
(43)
3.4 JPDA测量更新
在确定了边缘关联概率之后,通过结合边缘关联概率以JPDA方式分别更新每个扩展目标状态向量的运动参数和形状参数。如果已知测量的原点,则跟踪滤波器将独立且顺序地更新每个扩展目标状态向量的运动学参数和形状参数。给定以概率βij分配给第i个目标的测量值yj,依据传统的PDA方法[31]将扩展目标的运动参数和形状参数的状态与状态协方差分别进行更新,
(44)
(45)
(46)
(47)
其中
是测量
的期望值,
是伪测量
的期望值,
和分别是
和的互协方差以及与之间的协方差,
和
分别是和的互协方差以及与之间的协方差。
4 基于PPP模型的JPDA算法
根据上文的推导结果,对基于PPP模型的多扩展目标跟踪的JPDA算法进行了归纳。为了清晰,该算法具体步骤如下:
第1步,给定扩展目标的初始状态
(48)
第2步,扩展目标的运动参数和形状参数的状态的一步预测
(49)
(50)
第3步,运动参数的量测的一步预测
(51)
第4步,运动参数和形状参数的预测协方差
(52)
(53)
第5步,运动参数的新息
(54)
第6步,运动参数和形状参数的新息协方差
(55)
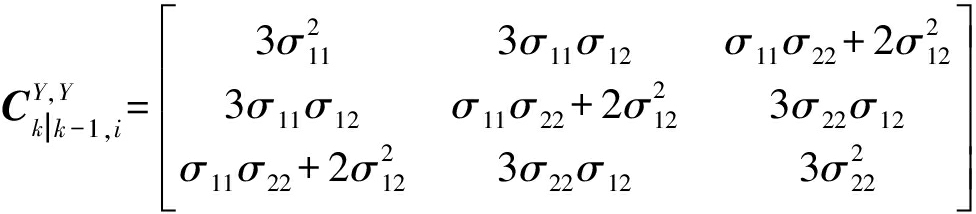
(56)
第7步,形状参数的量测的一步预测
(57)
第8步,形状参数的新息
(58)
第9步,计算每个联合事件概率
(59)
其中
第10步,根据联合事件概率计算边缘关联概率βij,k
(60)
其中
(61)
第11步,JPDA滤波器的运动参数和形状参数的状态更新
(62)
(63)
第12步,JPDA滤波器的运动参数和形状参数的状态协方差更新
(64)
(65)
第13步,循环第2步至第12步,直到完成对扩展目标的跟踪。
5 仿真实验
本节的主要目的在于通过仿真实验验证第4节中提出的算法在两种高杂波场景中应用的有效性,并将其与其他滤波器[32]进行了对比。
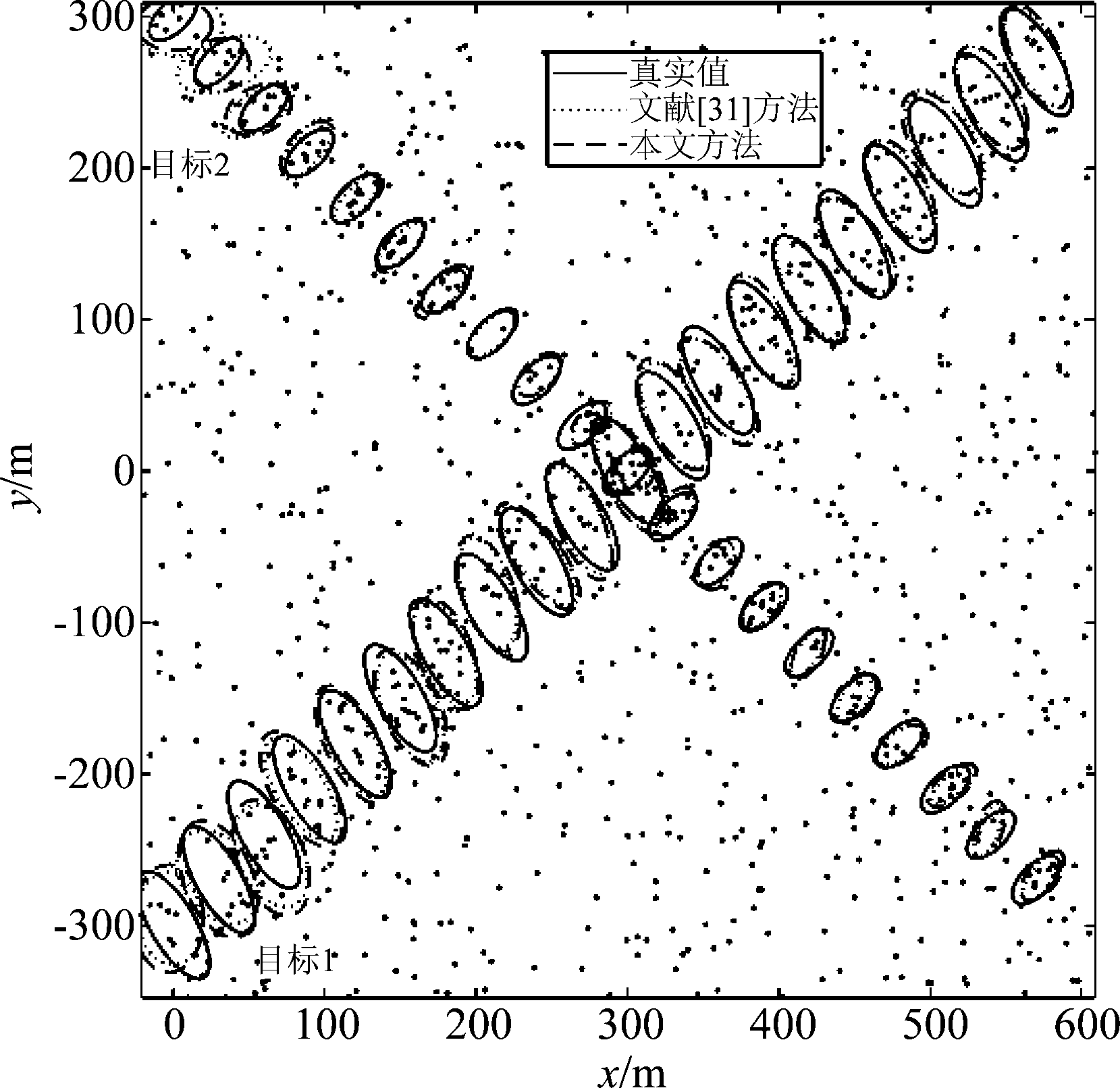
图1 模拟场景1
Fig.1 Simulation scenario 1
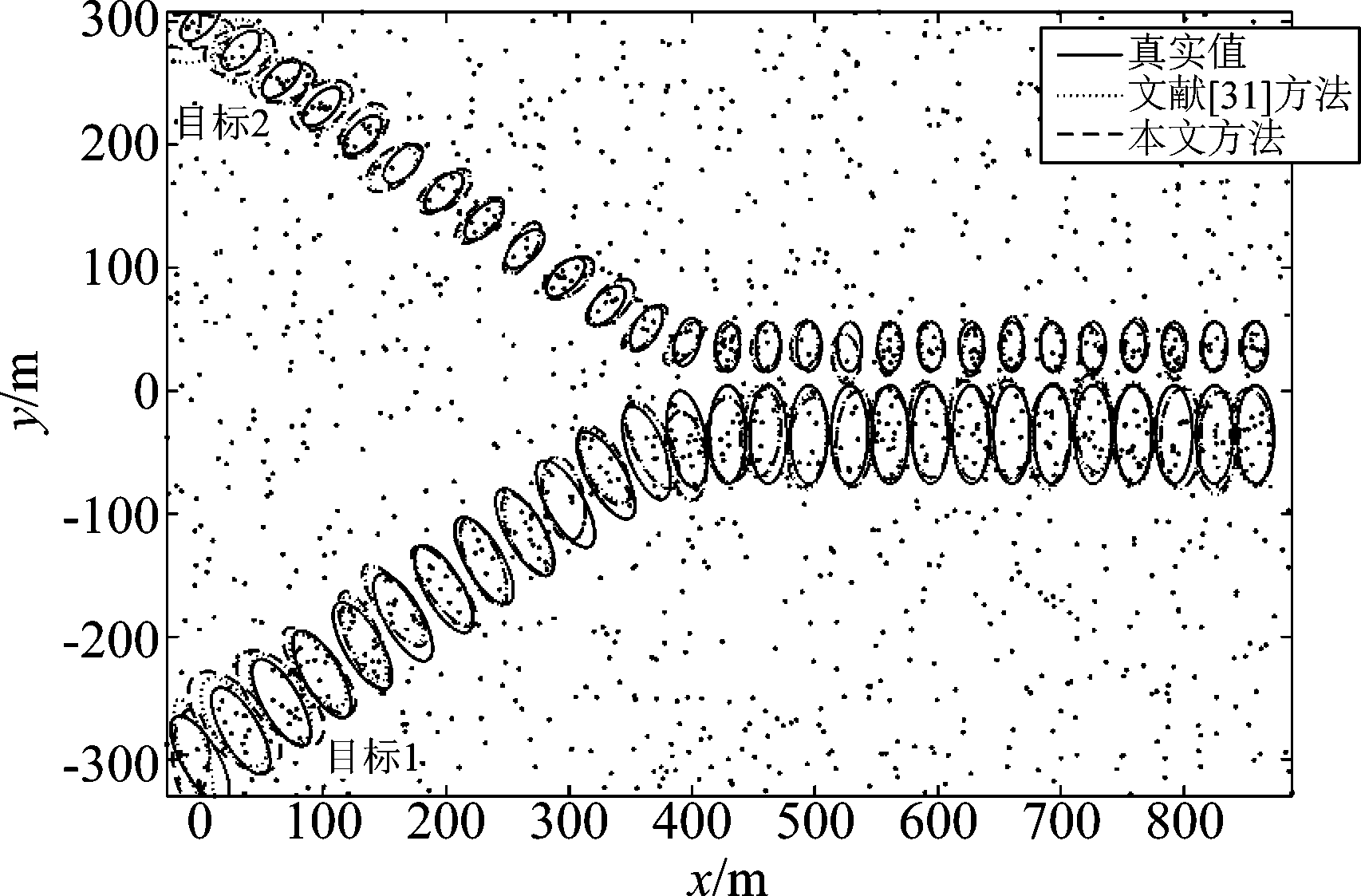
图2 模拟场景2
Fig.2 Simulation scenario 2
在第一个场景中,模拟两个目标交叉运动的轨迹,在第二场景中,模拟两个目标在空间上慢慢接近的运动轨迹。在这两种情况下,目标1的初始位置为(0 m,-300 m),地面实况椭圆的半轴长度为[40 m,15 m],生成的测量服从泊松分布,均值为9;目标2的初始位置为(0 m,300 m),地面实况椭圆的半轴长度为[20 m,10 m],生成的测量服从泊松分布,均值为7;杂波也为泊松分布,均值为40。两个目标在两种场景中均为恒速移动,其仿真结果如图1和图2,发现本文方法与文献[31]方法都能比较准确的跟踪目标运动。
在两种场景下,运行200次蒙特卡罗对两种方法每个时间帧的平均计算时间进行了比较如下图3和图4。由于本文算法中减少了计算测量更新中的运动参数和形状参数的互协方差和新息协方差的复杂度,所以本文提出的方法比文献[31]提出的方法时间复杂度低。
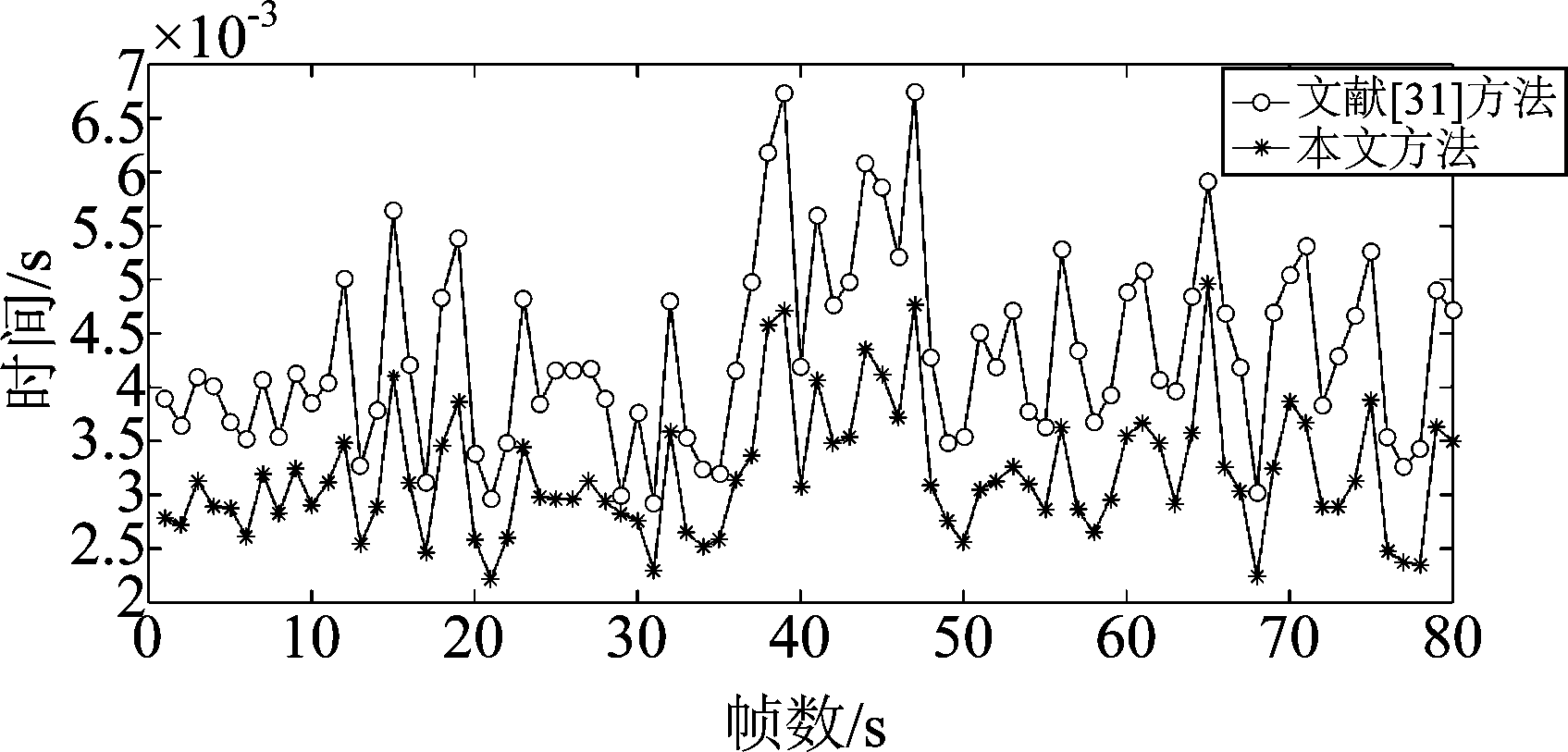
图3 场景1的平均计算时间
Fig.3 Mean computation time of the scenario
图4 场景2的平均计算时间
Fig.4 Mean computation time of the scenario 2
本文使用的算法性能评价指标为最优次模式分配(Optimal Sub-patten Assignment, OSPA)距离[33]:
(66)
其中,n是在两个椭圆x和
选取的等距样本点数,如
和
是集合{1,2,…,n}所有排列组合。由于OSPA距离的计算复杂度通常是样本数的立方,为了减少计算负担,在本实验模拟中样本点数取4。
通过图5和图6分析可看出,本文提出方法相较文献[31]提出方法性能较好。本文和文献[31]所使用方法中都是假设目标基数已知,且都能在两种具有挑战的场景下正确区分目标,但本文使用PPP模型下的当前有效测量的边缘关联概率和一种新的滤波器算法结合进行测量更新的算法对扩展目标进行跟踪时保持了更好的跟踪性能。
图5 场景1的平均OSPA距离
Fig.5 Mean OSPA distance of the scenario 1
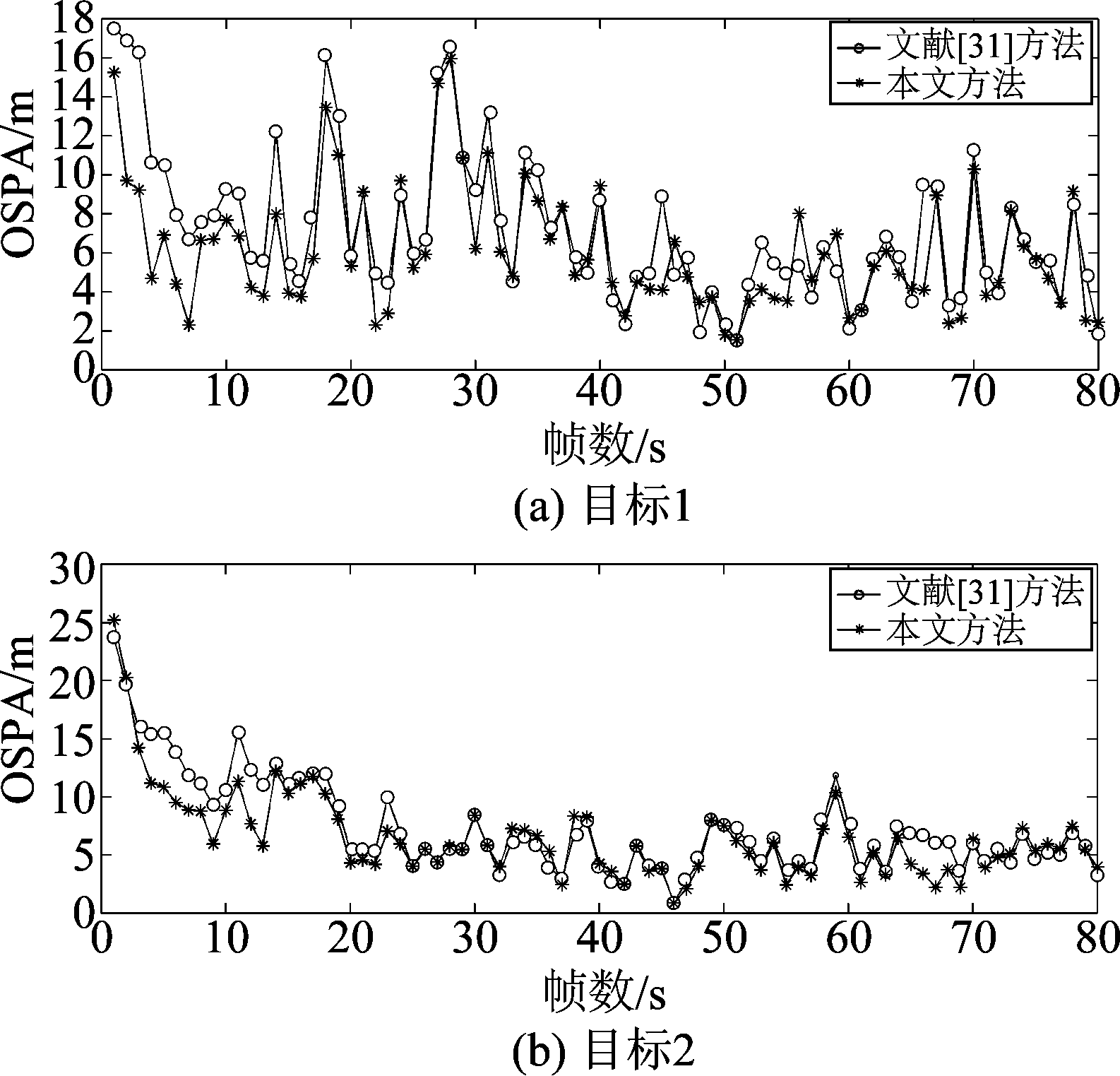
图6 场景2的平均OSPA距离
Fig.6 Mean OSPA distance of the scenario 2
6 结论
由于扩展目标会产生各自的空间分布,本文提出了一种基于PPP模型的多扩展目标的JPDA跟踪算法。它不需要对可能的测量集组合进行排列,且当扩展目标个数固定时,计算运动目标的边缘关联概率对目标进行测量更新,其跟踪性能较好且运算时间较快。在未来,我们将继续研究跟踪性能良好的扩展目标跟踪算法。
[1] Mihaylova L, Carmi A Y, Septier F, et al. Overview of Bayesian sequential Monte Carlo methods for group and extended object tracking[J]. Digital Signal Processing, 2014, 25(1): 1-16.
[2] Vermaak J, Ikoma N, Godsill S J. Sequential Monte Carlo framework for extended object tracking[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(5): 353-363.
[3] 赵维娓. 基于随机有限集多扩展目标跟踪方法的研究[D]. 兰州: 兰州理工大学, 2017.
Zhao Weiwei. Research on methods of multiple extended targets tracking based on random finite set[D]. Lanzhou: Lanzhou University of Technology, 2017.(in Chinese)
[4] Granström K, Baum M. Extended object tracking: introduction, overview and applications[J]. Journal of Advances in Information Fusion, 2017, 12(2): 139-174.
[5] Gilholm K, Godsill S, Maskell S, et al. Poisson models for extended target and group tracking[C]∥Signal and Data Processing of Small Targets, 2005.
[6] Granström K, Salmond D. Spatial distribution model for tracking extended objects[J]. IEE Proceedings on Radar, Sonar and Navigation, 2005, 152(5): 364-371.
[7] Koch J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.
[8] Baum M, Hanebeck U D. Random hypersurface models for extended object tracking[C]∥IEEE International Symposium on Signal Processing and Information Technology, 2010: 178-183.
[9] Baum M, Hanebeck U D. Extended object tracking with random hypersurface models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 50(1): 149-159.
[10] Wahlström N, Özkan E. Extended target tracking using Gaussian processes[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4165- 4178.
[11] Hirscher T, Scheel A, Reuter S, et al. Multiple extended object tracking using Gaussian processes[C]∥International Conference on Information Fusion, 2016.
[12] Bordonaro S Willett P, Shalom Y B, et al. Extended object tracking with exploitation of range rate measurements[J]. Journal of Advances in Information Fusion, 2017, 12(2): 228-242.
[13] Yang Shishan, Baum M. Extended Kalman filter for extended object tracking[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2017: 4386- 4390.
[14] Yang Shishan, Baum M. Tracking the orientation and axes lengths of an elliptical extended object[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2017: 1-15.
[15] Musicki D, La Scala B. Multi-target tracking in clutter without measurement assignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 877- 896.
[16] Hue C, Cadre J P L, Perez P. Tracking multiple objects with particle filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 791- 812.
[17] Granstrom K, Orguner U. A PHD filter for tracking multiple extended targets using random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671.
[18] Wieneke M, Koch W. A PMHT approach for extended objects and object groups[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2349-2370.
[19] 孙进平, 付福其, 付锦斌, 等. 应用超图匹配的多假设群目标跟踪方法[J]. 信号处理, 2017, 33(11): 1497-1504.
Sun Jinping, Fu fuqi, Fu Jinbin, et al. Multiple hypothesis group target tracking using hypergraph matching[J]. Journal of Signal Processing, 2017, 33(11): 1497-1504.(in Chinese)
[20] Vivone G, Braca P. Joint probabilistic data association tracker for extended target tracking applied to X-Band marine radar data[J]. IEEE Journal of Oceanic Engineering, 2016, 41(4): 1007-1019.
[21] Habtemariam B, Tharmarasa R, Thayaparan T, et al. A multiple-detection joint probabilistic data association Filter[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 461- 471.
[22] Schuster M, Reuter J, Wanielik G, et al. Probabilistic data association for tracking extended targets under clutter using random matrices[C]∥International Conference on Information Fusion, 2015: 961-968.
[23] Xie Yifan, Huang Yuan, Song Taek Lyul. Iterative joint integrated probabilistic data association filter for multiple-detection multiple-target tracking[J]. Digital Signal Processing, 2018, 72(1): 232-243.
[24] Streit R. JPDA intensity filter for tracking multiple extended objects in clutter[C]∥International Conference on Information Fusion, 2016.
[25] Granström K, Renter S, Fatemi M, et al. Pedestrian tracking using Velodyne data—Stochastic optimization for extended object tracking[C]∥IEEE Intelligent Vehicles Symposium (IV), 2017.
[26] Baum M, Faion F, Hanebeck U D. Modeling the target extent with multiplicative noise[C]∥Proceedings of the 15th International Conference on Information, 2012: 2406-2412.
[27] Jian Lan, Li X Rong. Nonlinear estimation by LMMSE-based estimation with optimized uncorrelated augmentation[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4270- 4283.
[28] Sarkka S. Bayesian Filtering and Smoothing[M]. Cambridge University Press, 2013: 51- 63.
[29] Baum M. Linear-time JPDAF based on many-2-many approximation of marginal association probabilities[J]. Electronics Letters, 2015, 51(19): 1526-1528.
[30] Willett P, Ruan Ya, Streit R. PMHT: problems and some solutions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 738-754.
[31] Blackman S, Robert Popoli R. Design and analysis of modern tracking systems[M]. Artech House Press, 1999: 325- 402.
[32] Yang Shishan, Thormann K, Baum M. Linear-time joint probabilistic data association for multiple extended object tracking[C]∥2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), 2018: 6-10.
[33] Yang Shishan, Baum M, Granström K. Metrics for performance evaluation of elliptic extended object tracking methods[C]∥2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), 2016: 523-528.
