1 引言
每年有数以亿计的昆虫为寻找适宜的生存环境进行大范围、远距离迁飞。昆虫,尤其是蝗虫、稻飞虱、草地螟等害虫的突然、大规模迁飞,往往给迁入地带来严重的经济损失,如何做好昆虫迁飞的预测预警成为当前社会领域亟待解决的难题之一。昆虫多在夜间高空飞行,此时传统光学设备的观测效果有限,雷达作为远距离探测的工具,可以实现对目标空域的全天时、全天候监测,为观测空中虫群提供了新手段,它的应用与发展推动迁飞昆虫学由定性研究发展到定量分析,在昆虫迁飞领域有着不可替代的作用[1-3]。
1950年,英国昆虫学家Rainey提出了用雷达观测沙漠蝗迁飞的设想[4],并于1968年首次在尼日尔利用改造的航海雷达对沙漠蝗的夜间迁飞现象进行了雷达观测,取得了空前成功[5],这标志着昆虫雷达学的诞生。此后的几十年来,昆虫雷达学取得了长足的进步,英国、美国、澳大利亚及中国等国的研究人员研制了包括机载昆虫雷达、扫描昆虫雷达、垂直昆虫雷达、跟踪昆虫雷达等多种体制的昆虫雷达[6-7]。其中,具备垂直上指、偏振旋动、波束章动、锥形扫描(Zenith-pointing Linearly-polarized Conical-scan, ZLC)制式的垂直观测雷达(Vertical Looking Radar, VLR)实现了昆虫个体速度、方向、头部朝向以及体型等多种参数测量,并且具有自动化与无人值守的特点,实现了迁飞性害虫的长期自动监测,成为现今使用最为广泛的昆虫雷达[8-11]。
1990年,澳大利亚的Drake博士建成了两部ZLC制式的VLR,命名为昆虫监测雷达(Inset Monitoring Radar, IMR),其数据采集模块上使用模拟门控峰值保持电路和低速模拟数字转换器(Analog to Digital Converter, ADC)来采集不同高度的目标回波。由于低速ADC需要足够的时间进行模拟回波的数字化,因此将雷达175~1300 m的探测范围分为15个宽度为25 m的距离门,相邻距离门之间的间隔为50 m,IMR在距离门上的不连续导致无法有效分析昆虫上升下降率。2018年,Drake对IMR进行了升级,将数据采集模块中的模拟门控峰值保持电路和低速ADC更换为120 MHz采样率的高速ADC,使雷达具备了连续采集完整回波的能力,使昆虫上升下降率测量成为可能。Drake基于升级后IMR,开发了相应的目标检测关联程序,根据得到目标高度随时间的变化关系,使用线性拟合的方法实现了昆虫的上升下降率提取[12]。但是由于IMR的距离分辨率仅为7.5 m,无法得到昆虫个体的精细轨迹;其使用的目标检测依旧为固定门限检测,航迹关联与线性拟合的上升下降率测量在实现上也较为复杂,不利于数据的进一步分析。与昆虫上升下降率研究类似,近期鸟类上升下降率研究也取得一定进展。2019年,康奈尔大学的Cecilia Nilsson利用X波段跟踪雷达观测了瑞典南部的雨燕繁殖区内雨燕个体与群体的飞行特性,实验结果验证了雨燕在黄昏时成群上升至高空、黎明时成群下降至低空,并在黄昏与黎明之间以个体在高空飞行的互作关系[13]。
为解决现有IMR在昆虫上升下降率提取中存在的上述问题,本文利用本团队开发的高分辨全相参昆虫雷达,提出了一种基于Radon变换的昆虫上升下降率提取算法。该算法采用脉冲多普勒(Pulse Doppler, PD)积累与单元平均恒虚警检测(Cell-averaging Constant False Alarm Rate, CA-CFAR)实现对昆虫目标的检测与快时间/慢时间一维距离像数据矩阵向二值化航迹矩阵的转换。在此基础上,基于线性Radon变换将目标关联与航迹的线性拟合问题转化为参数域上的峰值检测问题,从而实现目标上升下降率的快速测量。最后,通过实测数据处理,结果验证了算法的有效性。
2 基于Radon变换的昆虫上升下降率提取
2.1 系统与算法流程
本团队研制的高分辨全相参昆虫雷达如图1所示,其硬件上主要由双极化抛物面天线、射频分机、数字分机、二维伺服转台及其附属设备组成。雷达参数设计如表1所示,其采用调频步进频体制,理论距离分辨率为0.1875 m(实测距离分辨率为0.2 m),同时该雷达具有全极化和全相参测量能力,能够实现目标的精确测量。

图1 高分辨全相参昆虫雷达
Fig.1 High-resolution phase-coherent insect radar
表1 高分辨全相参昆虫雷达系统参数
Tab.1 The system parameters of high-resolution
phase-coherent insect radar
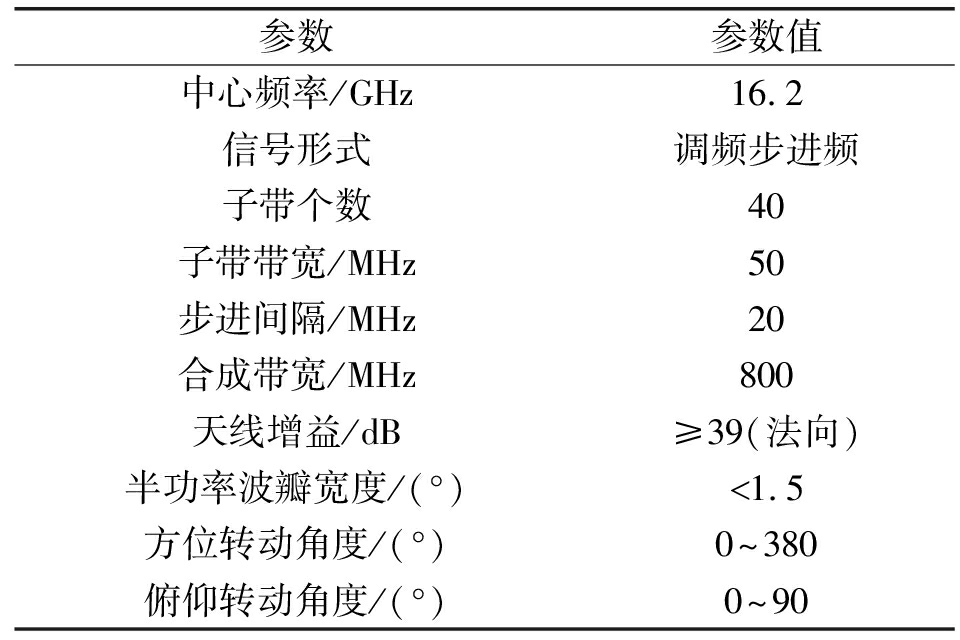
参数参数值中心频率/GHz16.2信号形式调频步进频子带个数40子带带宽/MHz50步进间隔/MHz20合成带宽/MHz800天线增益/dB≥39(法向)半功率波瓣宽度/(°)菝1.5方位转动角度/(°)0~380俯仰转动角度/(°)0~90
基于Radon变换昆虫上升下降率提取算法的实现流程如图2所示,主要利用高分辨全相参昆虫雷达系统得到高分辨一维距离像,将一定时间内的高分辨一维距离像按时间排列组成快时间/慢时间数据矩阵。首先对其经过PD积累与CA-CFAR处理转化为二值化航迹矩阵,即:将检测到目标位置置为1,未检测到目标位置置为0;再使用Radon变换将二值化航迹矩阵转化到参数域;最终通过检测参数域峰值提取昆虫上升下降率。接下来将分“PD积累与CA-CFAR”和“Radon变换”详细说明算法的实现流程。
2.2 PD积累与CA-CFAR
由于直接对快时间/慢时间数据矩阵进行Radon变换存在结果中出现复杂彩色条纹的问题,增加了峰值检测的难度,因此需要对其进行二值化处理。本算法中采用的是PD积累+CA-CFAR的方法,对目标矩阵进行检测,将快时间/慢时间数据矩阵中,过门限的位置置1,未过门限的位置置0,从而实现二值化。
PD积累是对每个距离单元所对应的慢时间数据都进行频谱分析,由此将快时间/慢时间数据矩阵转化为快时间/多普勒频率矩阵[14]。经过脉冲多普勒处理,回波信号的静止杂波将集中在零频附近,便于实现运动昆虫与静止杂波的分离;同时作为一种有效的相参积累方式,PD积累还可以有效提高目标信噪比,提高雷达检测性能。本算法采用依次对慢时间对应的每一列数据进行离散傅里叶变换的处理方式,具体实现形式如图3所示。
CA-CFAR是最常用的CFAR检测器之一,在给定参考单元数2M、保护单元数2N及虚警概率Pfa的情况下,利用该算法对被测单元两侧各M个参考单元进行平均杂波包络估计,得到杂波功率水平估计Z为
(1)
其中,xn和yn分别表示被测单元左侧和右侧的功率水平。自适应门限判决的标称化因子T为
(2)
由此,可以确定CA-CFAR的检测门限为
(3)
其中,H1表示有目标的假设,H0表示没有目标的假设。
图2 基于Radon变换的昆虫上升下降率测量算法实现流程
Fig.2 Schematic of the ascent and descent rate extraction algorithm based on Radon transformation
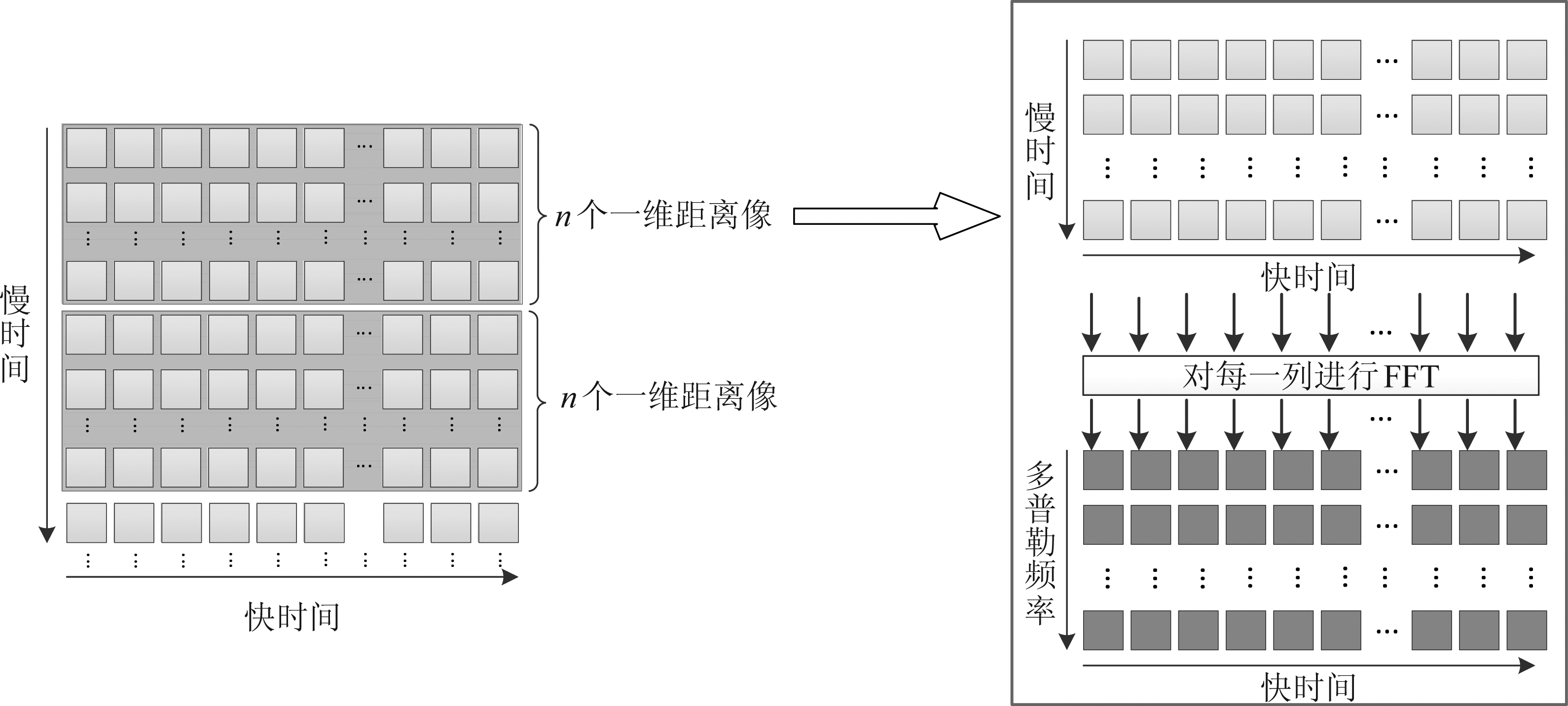
图3 脉冲多普勒处理
Fig.3 Pulse Doppler processing
2.3 Radon变换
Radon变换是由数学家Radon最早提出的一种沿路径进行积分投影的积分变换。对于一个定位在平面D上的二维图像F(x,y),其Radon变换为
(4)
其中,δ(·)为冲击函数,δ(p-xcos θ-ysin θ)表示当p=xcos θ+ysin θ时函数值为1,其余情况函数值为0,因此Radon变换为函数F(x,y)在沿着直线p=xcos θ+ysin θ下的积分[15]。Radon变换通过对二值图像F(x,y)中的直线或线段进行线性积分,将其从平面D中的一条直线转化为θ-p域的一个点,通过检测θ-p域中的峰值点从而提取平面D中的直线参数[16]。
针对一幅二值图像,如图4(a)和(b)所示,Radon变换以图像中心为坐标原点,对图像进行积分投影,即:沿垂直于投影方向开始,计算这一列上所有像素的灰度值之和作为在该角度的Radon变换值,如此计算到最后一列。图5(a)仿真了100×100的二值图像,其中左下角包含一条斜率为45°的线段。通过对二值图像进行Radon变换,得到结果如图5(b)所示,其中的极亮点(对应峰值点)位置横坐标为45°,即:原图像中存在有一条与图像坐标原点呈45°直线。
考虑垂直昆虫雷达在进行观测时,昆虫穿越雷达波束多为匀速直线运动,反映到雷达快时间/慢时间图像中呈直线(如图6所示),因此可以利用Radon变换对雷达快时间/慢时间图像进行处理,通过检测θ-p域中的峰值点,进而提取昆虫的上升下降率。
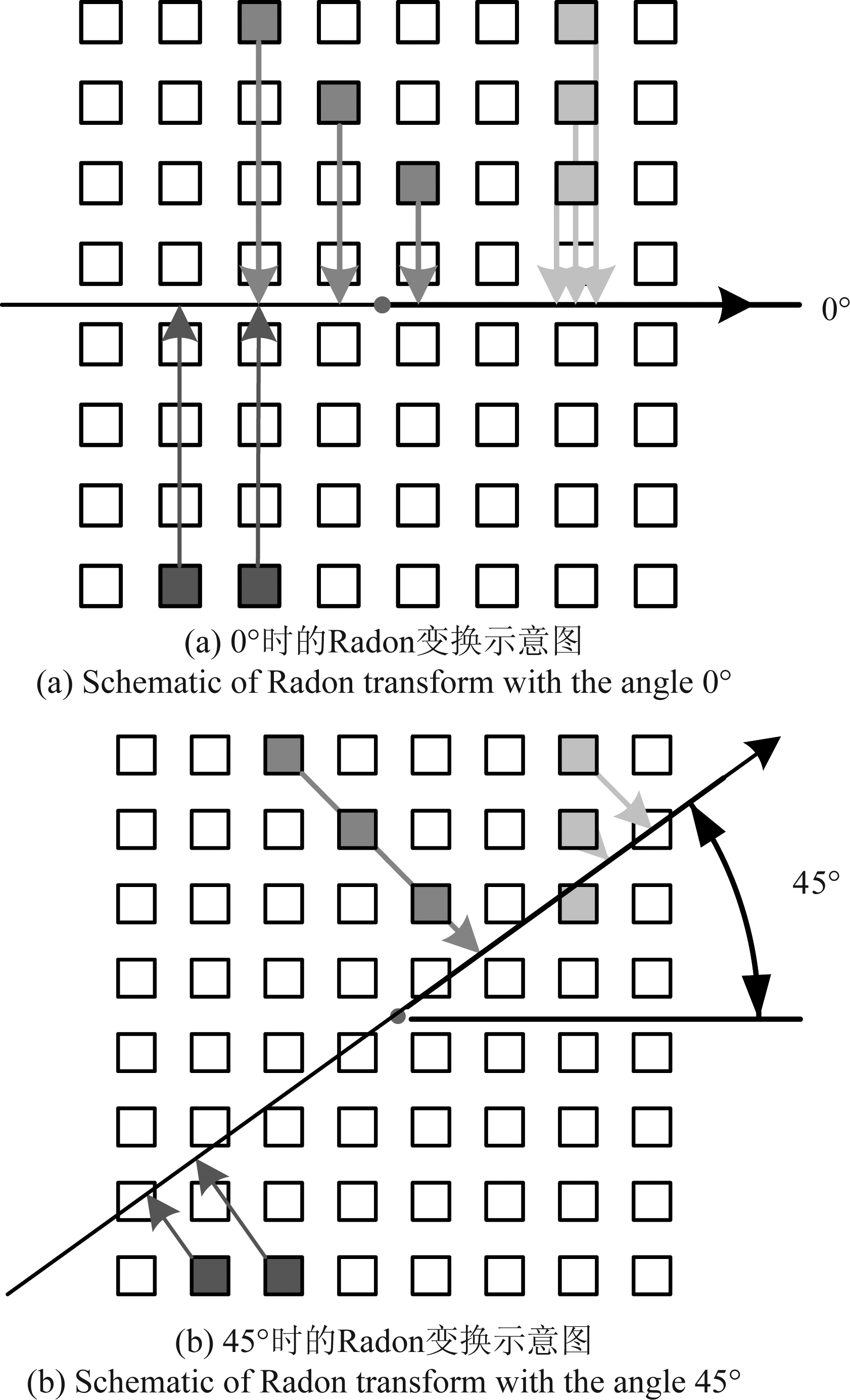
图4 Radon变换示意图
Fig.4 Schematic of Radon transform
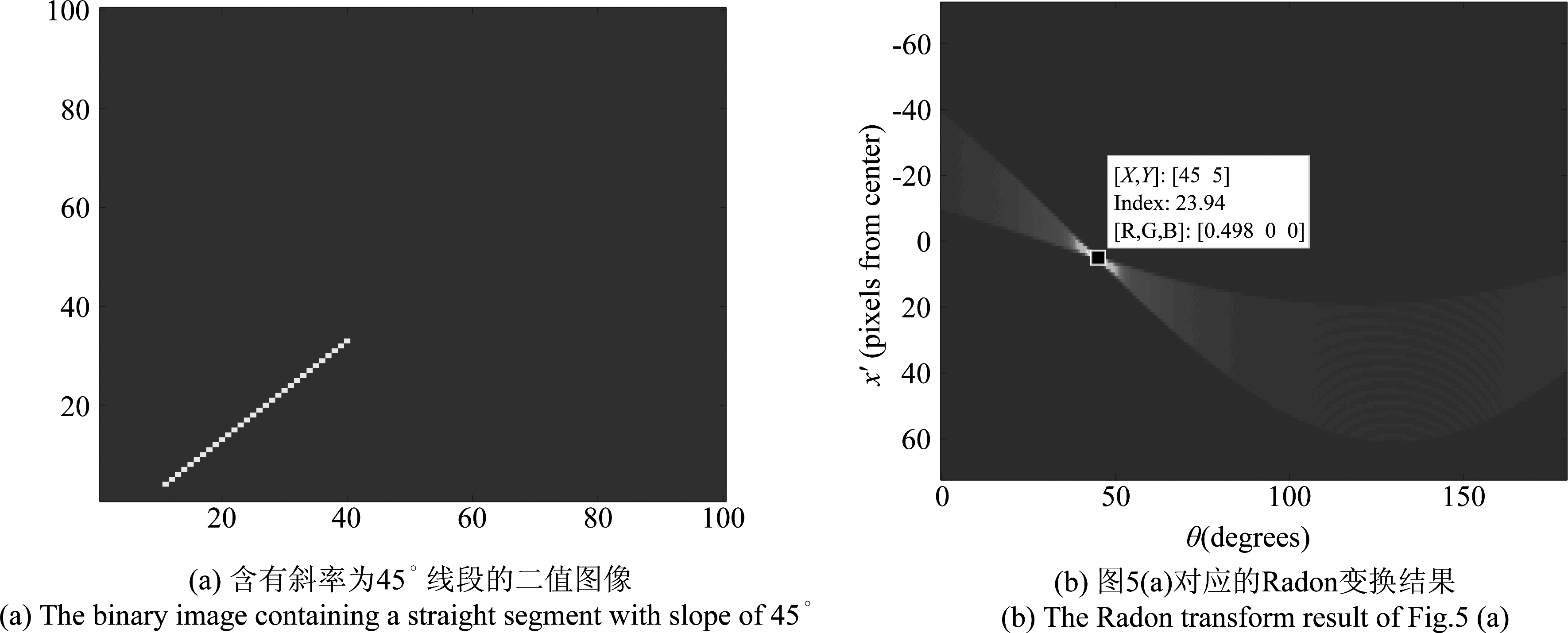
图5 仿真100×100含有45°斜率直线的二值图像及其Radon变换结果
Fig.5 Simulation of 100×100 binary image containing a straight segment with slope of 45° and the corresponding Radon transform result
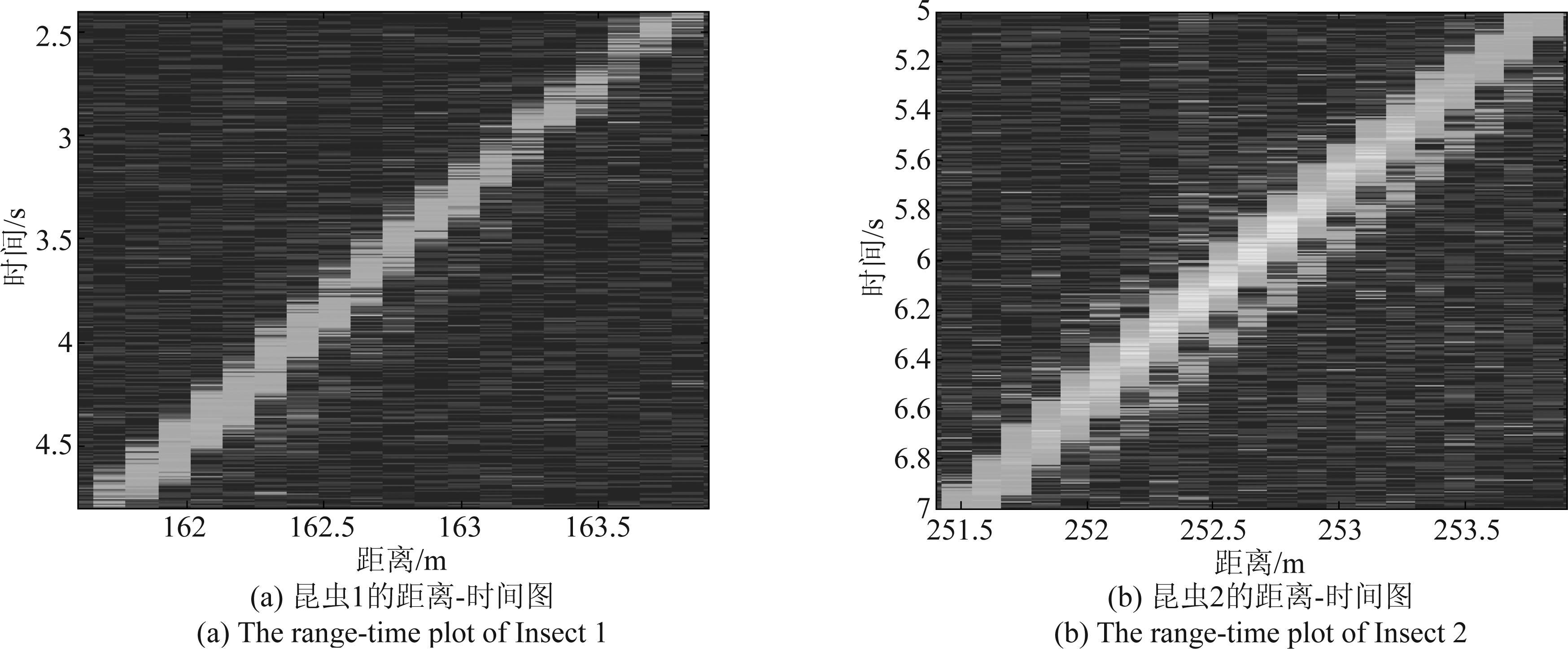
图6 2016年6月廊坊观测部分昆虫的距离-时间结果
Fig.6 The range-time plot of insects at Langfang in June, 2016
3 实验验证
本部分将以本团队于2018年7月16日晚在内蒙古锡林浩特采集的实验数据为例,详细解释基于Radon变换的昆虫上升下降率测量算法的实现过程及有效性。
3.1 PD积累与CA-CFAR
考虑到高分辨全相参昆虫雷达采集数据较多,这里选取时间长度为3 s的数据进行分析,数据采集时间为2018年7月16日晚22时39分42秒,雷达垂直对天照射,实验场景如图7所示。绘制3 s时间内的快时间/慢时间结果如图8所示,其中,横坐标为目标距离,纵坐标为数据采集时间,由上至下表示时间的推移,昆虫的航迹反映为图8中的亮色线。从图8中可以看出,雷达观测到大量目标,其高度大体呈下降趋势,且航迹多为直线。

图7 内蒙古锡林浩特实验中雷达垂直观测场景图
Fig.7 The experimental scene of radar vertical looking in XilinHot, Inner Mongolia

图8 2018年7月16日22时39分42秒内蒙古观测昆虫的距离-时间结果
Fig.8 The range-time plot in XilinHot, Inner Mongolia at 22:39:42 16th June 2016 with time duration of 3 seconds
由于昆虫一般飞行速度小于10 m/s且高分辨全极化雷达的距离分辨率为0.1875 m,考虑在积累时间内目标尽量不会产生跨距离单元徙动,因此在本研究中设定PD积累时间为20 ms,CA-CFAR虚警率为1×10-7。通过对图8中的数据进行PD积累与CA-CFAR处理,可以得到处理后的二值图像如图9所示。从结果可以看出,图9中的黄色线与图8中的亮色线一一对应,由此说明PD积累与CA-CFAR能够较为准确的实现快时间/慢时间数据矩阵到二值化航迹矩阵的转化。
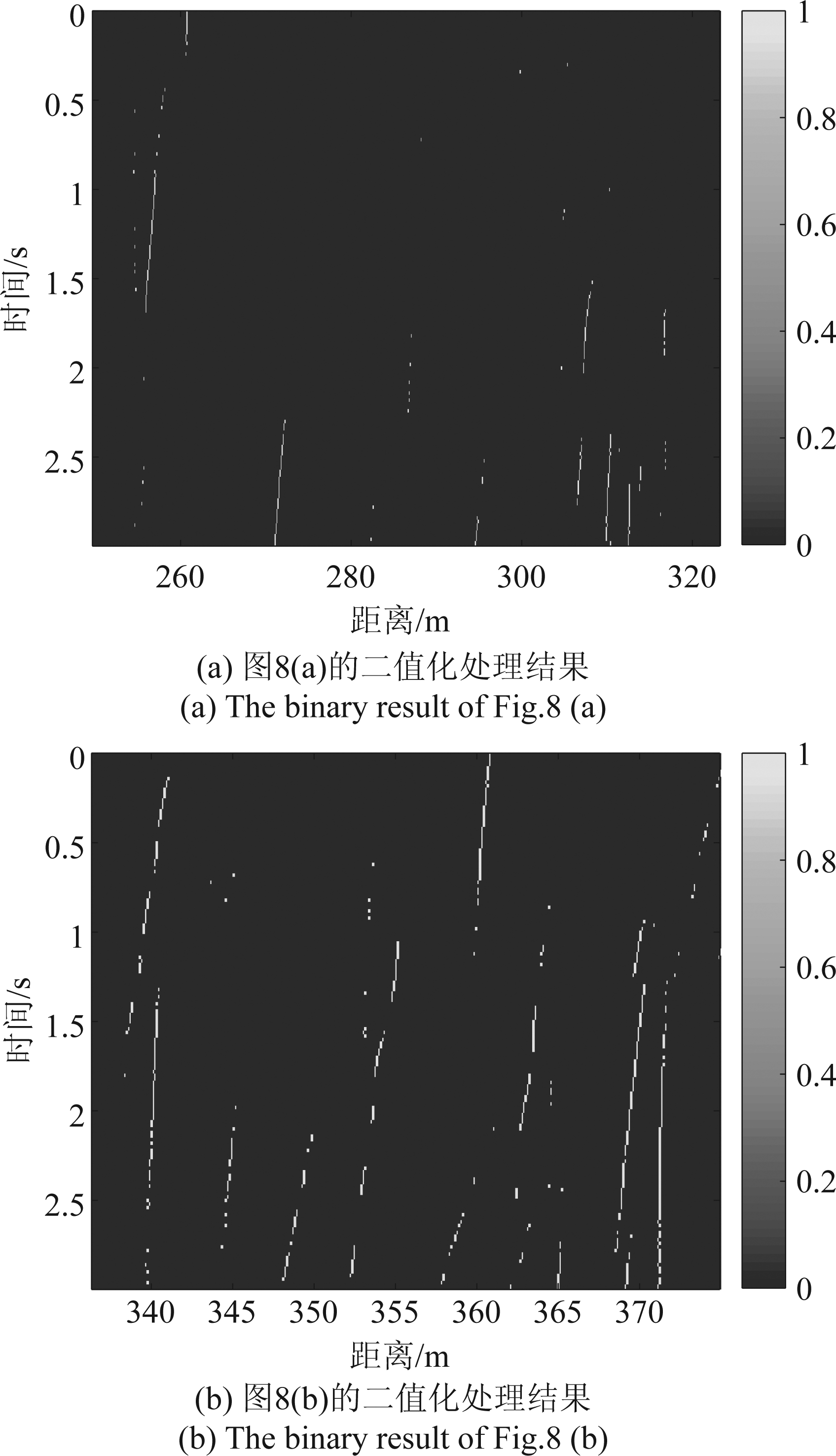
图9 对图8中距离-时间图的二值化处理结果
Fig.9 The binary result of the corresponding range-time plot in Fig.8
3.2 Radon变换与昆虫上升下降率提取
对3.1节处理得到的二值图像进行0°~180°的Radon变换,得到的θ-p域结果如图10所示,通过检测图10中的局部极大值,即:图10中红色椭圆位置,可以得到距离-时间坐标系下直线对应的斜率和截距。通过绘制其中2个局部极大值代表的直线,得到部分结果如图11所示,其中白色的位置波动的直线表示原始二值化航迹,深色直线为Radon变换局部极大值对应的斜率和截距所代表直线。从结果可以看出,即使一条航迹在检测过程中断为若干条,经过Radon变换后其斜率与截距也基本保持一致,因此Radon变换提取到的局部极大值依然可以实现对航迹的准确直线拟合,从而证明了基于Radon变换进行上升下降率提取算法的有效性。
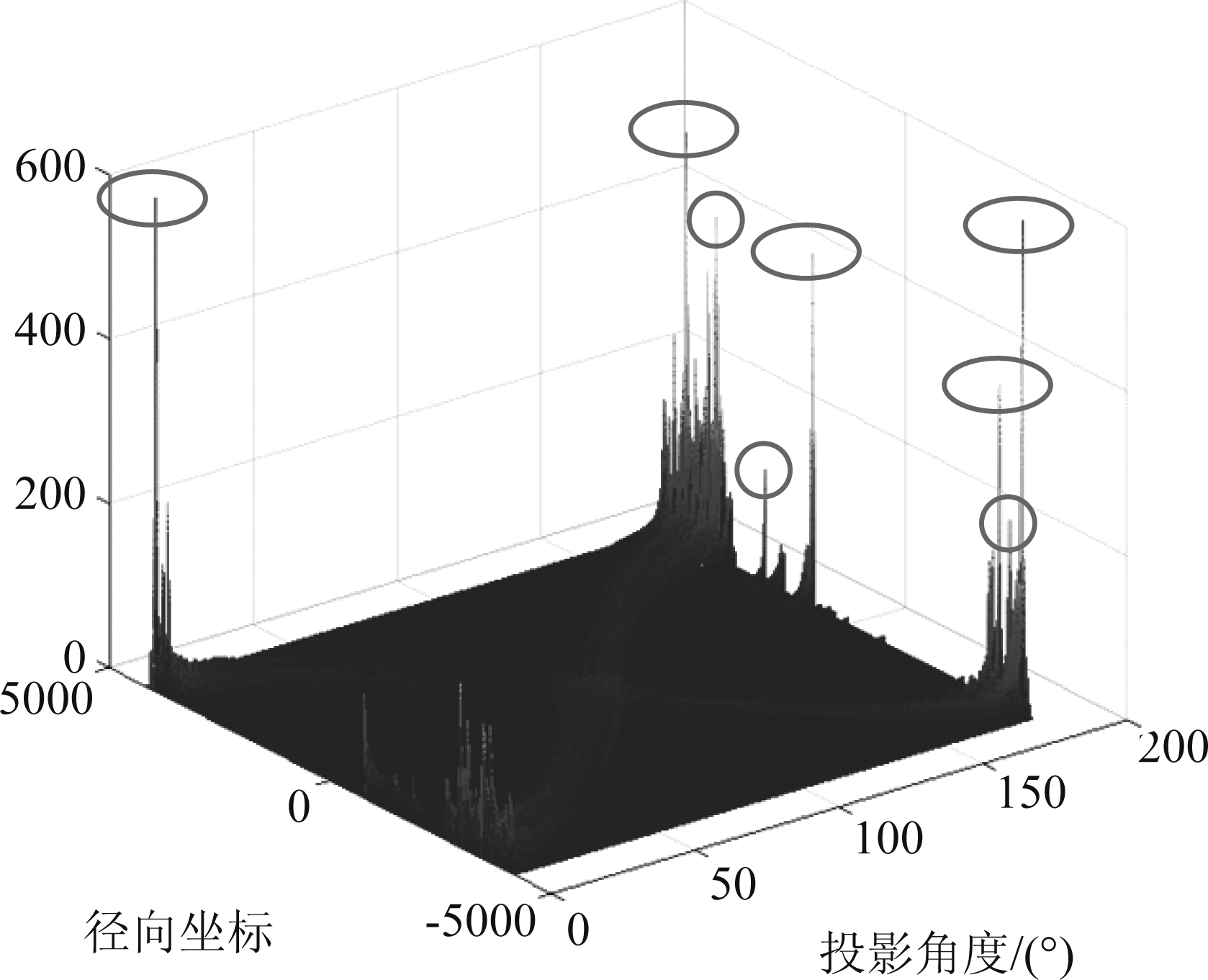
图10 对图9中二值图像的0°~180° Radon变换结果
Fig.10 The Radon transformation result of the binary result in Fig.9 with theta 0°~180°
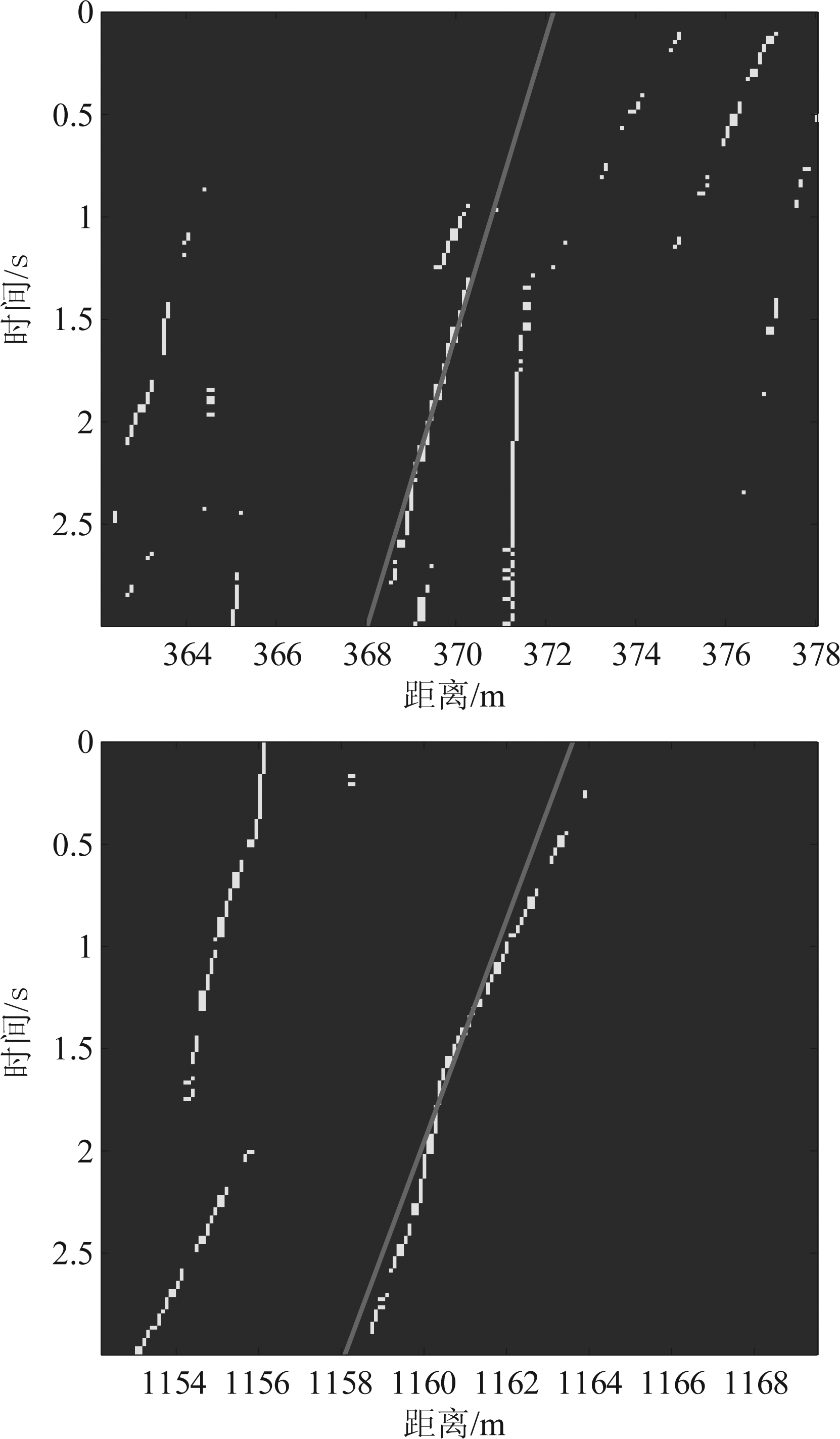
图11 Radon变换提取航迹结果
Fig.11 The result of the extracted trace based on the result of Radon transformation
4 结论
本文基于本团队开发的高分辨全相参昆虫雷达系统,提出了一种基于Radon变换的昆虫上升下降率提取算法。该算法以高分辨全相参昆虫雷达测得的快时间/慢时间数据矩阵为输入,首先通过PD积累与CA-CFAR检测将数据矩阵转化为Radon变换能够处理的二值图像,再通过Radon变换将包含多目标航迹信息的二值图像转化到参数域,通过查找参数域峰值得到昆虫航迹斜率,从而实现上升下降率的提取。基于外场实测数据,成功验证了该算法的有效性。相较于传统的多目标关联算法,本算法实现简单,可为昆虫上升下降率研究提供借鉴。
[1] Riley J R. Remote sensing in entomology[J]. Annual Review of Entomology, 1989, 34(1): 247-271.
[2] Chapman J W, Smith A D, Woiwod I P, et al. Development of vertical-looking radar technology for monitoring insect migration[J]. Computers and Electronics in Agriculture, 2002, 35(2-3): 95-110.
[3] 封洪强. 雷达昆虫学40年研究的回顾与展望[J]. 河南农业科学, 2009(9): 121-126.
Feng Hongqiang. Review and prospect of radar entomology for 40 years[J]. Journal of Henan Agricultural Sciences, 2009(9): 121-126.(in Chinese)
[4] Rainey R C. Observation of desert locust swarms by radar[J]. Nature, 1955, 175(4445): 77.
[5] Schaefer G W. Radar studies of locust, moth and butterfly migration in the Sahara[J]. Proceedings of the Royal Entomological Society of London, 1969, 34(33): 39- 40.
[6] Schaefer G W, Rainey R C. An airborne radar technique for the investigation and control of migrating pest insects[J]. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 1979, 287(1022): 459- 465.
[7] 翟保平. 追踪天使——雷达昆虫学30年[J]. 昆虫学报, 1999(3): 315-326.
Zhai Baoping. Tracking angels-radar entomology for 30 years[J]. Acta Entomologica Sinica, 1999(3): 315-326.(in Chinese)
[8] Smith A D, Riley J R, Gregory R D. A method for routine monitoring of the aerial migration of insects by using a vertical-looking radar[J]. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 1993, 340(1294): 393- 404.
[9] Harman I T, Drake V A. Insect monitoring radar: analytical time-domain algorithm for retrieving trajectory and target parameters[J]. Computers and Electronics in Agriculture, 2004, 43(1): 23- 41.
[10] 张智, 张云慧, 姜玉英, 等. 雷达昆虫学研究进展及应用前景[J]. 植物保护, 2017, 43(5): 18-26.
Zhang Zhi, Zhang Yunhui, Jiang Yuying, et al. Research progress and application prospect of radar entomology[J]. Plant Protection, 2017, 43(5): 18-26.(in Chinese)
[11] Hu Cheng, Li Weidong, Wang Rui, et al. Accurate insect orientation extraction based on polarization scattering matrix estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1755-1759.
[12] Drake V A, Wang H. Ascent and descent rates of high-flying insect migrants determined with a non-coherent vertical-beam entomological radar[J]. International Journal of Remote Sensing, 2018, 40(3): 1-22.
[13] Nilsson C, Bäckman J, Dokter A M. Flocking behaviour in the twilight ascents of common swifts apus[J]. Ibis, 2019.(Online)
[14] Richards M A. Fundamentals of radar signal processing[M]. Tata McGraw-Hill Education, 2005.
[15] Deans S R. Hough transform from the Radon transform[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1981(2): 185-188.
[16] Wang Liqiang, Ying Hao. Radon transform and forstner operator applying in buildings contour extraction[C]∥2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, 2009: 415- 419.


