1 引言
作为探测信息的工具,雷达在军事领域中得到了广泛的应用并发挥了重要作用。相对于传统的相控阵雷达, MIMO雷达的每个阵元都有独立的波形产生器,可以发射相互独立的波形,在接收端匹配滤波后形成等效发射波束,实现波形分集[1]。同时,MIMO雷达因此具备了波形捷变的能力,并在发射波形信号的设计方面具有很高的自由度。因而MIMO雷达发射波形的设计和优化成为了一个重要的研究方向。由于MIMO雷达将相互正交的长序列波形调制在多个天线上发射,并通过多个接收天线对回波信号进行处理,因此回波信号不可避免地会产生各信号分量之间的相互模糊。为了降低不同目标回波间的相互干扰,将各信号分量进行分离,需要各信号之间具有较小的互相关能量,因此有必要对长序列正交信号波形设计进行研究。
智能优化算法是MIMO雷达正交波形设计的有效方法。文献[2]采用改进的Fletcher-Reeves算法,并以自相关旁瓣和互相关的四次方和为代价函数进行了正交信号波形设计。文献[3]利用模拟退火算法和邻域搜索的方法对正交多项码和正交频率编码波形进行了优化设计,得到了比较低的自相关旁瓣。文献[4]使用了遗传算法和邻域搜索的方法,提升了波形的性能和优化速度。文献[5]在遗传算法得到初始解的基础上使用和声算法搜寻邻域最优解。文献[6]使用遗传算法产生了任意长度的正交四相码。
为了进一步提高波形的性能,需要使用更优的优化算法。量子遗传算法是遗传算法的改进算法,有着较强的全局搜索能力和较快的收敛速度,并已广泛应用于雷达领域之中,如文献[7-9]。文献[7]将量子遗传算法应用于激光成像图像雷达中,提高了搜索目标的速度与精度。文献[8]使用量子遗传算法解决了敏捷成像卫星调度问题。文献[9]将量子遗传算法应用在微信信号去噪处理中,有效提升了信号的信噪比。
本文使用量子遗传算法,在伪随机相位编码信号(PPC)的基础上,对正交信号波形进行了优化设计,旨在降低长序列的正交信号波形的互相关峰值。最终得到的正交信号波形与遗传算法得到的结果相比,收敛速度得到显著提高,且具有更低的互相关峰值。
2 信号模型和设计准则
MIMO雷达波形设计的问题需要从多个方面考虑,包括自相关特性、互相关特性、峰值因子、能量谱形状和多普勒特性等。自相关特性主要是自相关旁瓣峰值电平和主瓣宽度,在强回波中检测弱目标等情况下,对波形的自相关特性提出了很高的要求,需要足够窄的主瓣和足够低的旁瓣;互相关特性主要包括互相关峰值电平和互相关平均电平,更低的互相关值有利于降低信号之间的干扰;峰值因子即波形的最大幅度与均方根幅度之比,反映了雷达发射机功率的有效性;能量谱形状与频带利用和硬件实现有关,平坦、紧凑的能量谱形状可以更有效地利用频带,同时也更容易硬件实现;而多普勒特性主要与信号的时间长度有关,长度越长,多普勒特性越好。
多个信号之间的正交性能主要通过互相关特性体现。对于信号s1(t),s2(t),…,sN(t),其互相关函数为:
(1)
当两个波形完全正交时,有:
rij(τ)=0
(2)
但在工程实现上,理想的正交波形很难实现,大多数情况下使用的正交波形事实上都是准正交波形[6],即其互相关函数式(1)不为0。为了提高波形之间的正交特性,降低信号之间的干扰,需要波形的互相关值尽可能小。一般通过互相关的峰值电平和平均电平来衡量波形的互相关特性,因此,本文将正交波形的设计准则定为,在满足自相关旁瓣峰值电平小于一定值的约束条件下,使互相关峰值电平尽量小。
正交波形有多种实现方式,需从其中选择一种作为信号模型进行优化设计。传统的MIMO雷达使用的正交信号有正交点频脉冲信号(SFP)、伪随机相位编码信号(PPC)、正交离散频率编码信号(DFCW)、正交频分复用线性调频信号(OFDM-LFM)、伪随机相位-有符号线性调频信号(PSC)和伪随机相位-离散频率编码信号(PDF)等。其中,SFP和OFDM-LFM无法实现相参波束合成,而PSC在互相关和自相关旁瓣区中表现出的一系列“矮峰”是由子脉冲Chirp调制产生的,因此无法进行有效的优化。而DFCW可视为PDF的一种特例(无子脉冲随机相位调制)。综合考虑需要满足多个波形、互相关峰值可以优化和可以实现相参波束合成等条件,应从PPC和PDF中比较选择。其中,由于码长(子脉冲个数)为N的PDF波形不但和同码长的PPC波形一样有N个相位值,而且还有N个频率值,因此在使用同样的优化算法时,PPC波形的用时远远短于PDF波形,且在相同带宽的限制之下,PDF波形的自相关和互相关性能并不明显优于PPC波形,因此选择PPC波形作为优化设计的信号模型[10]。
假设MIMO雷达有M个发射阵元,其中第i个阵元发射的信号为si(t),i=1,2,…,M,每个信号包含N个子脉冲,对于PPC信号,信号集表示为[11,12]
{si(t)=a(t)ejφi(p),p=1,2,…,N}, i=1,2,…,M
(3)
其中
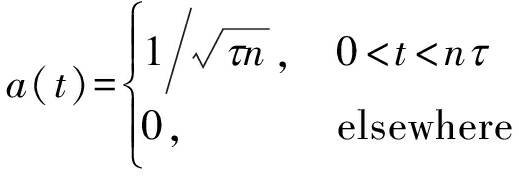
(4)
τ是子脉冲宽度,φi(p)是子脉冲的相位。如果采用K相编码,则子脉冲的相位φi(p)只能取2π/K的整数倍[13]。即
(5)
因此,PPC信号的互相关函数为:
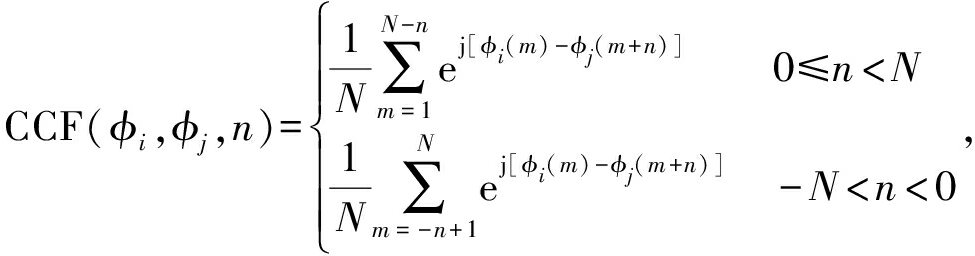
i≠j
(6)
因此,根据设计准则,对于一组阵元发射的信号x(包含M个信号x1,x2,…,xM),其优化函数设计为在满足自相关旁瓣峰值电平的约束条件下,求任意两个波形之间的互相关峰值电平,并取其中的最大值,如式(7)所示:
(7)
其中CCF(xi,xj,n)为两个波形之间互相关函数,如式(6)。而g(x)则是求每个波形的自相关旁瓣峰值电平,并取其中的最大值,如式(8)所示。L则是设定的自相关旁瓣峰值电平的约束值。式(7)中函数在g(x)>L时取1,大于归一化的互相关峰值电平,代表当一个信号的自相关旁瓣峰值不满足约束条件时,认为该信号的性能很差,而不需要讨论其互相关特性。
(8)
其中,ACF(xi,n)为每个波形的自相关函数:
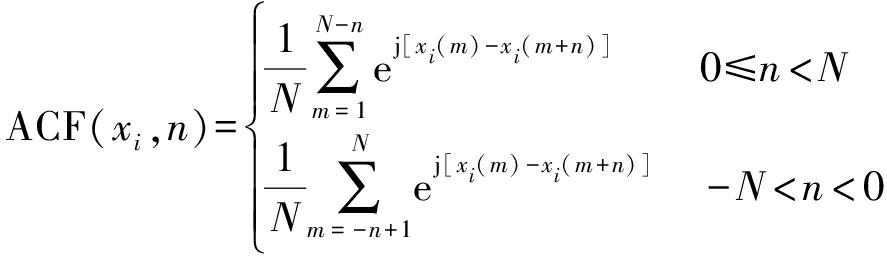
(9)
3 基于量子遗传算法的波形设计
这一节主要讨论如何利用量子遗传算法进行正交波形设计。首先对量子遗传算法进行介绍,然后对量子旋转门的旋转策略进行了调整,最后以信号的自相关旁瓣峰值电平和互相关峰值电平作为评价标准,建立了适应度函数,并给出了算法的步骤和流程图。
3.1 量子遗传算法
为了优化多相编码信号的互相关性能,需要用到人工智能类优化算法,遗传算法就是其中较为经典的一种智能优化算法。但是在面对复杂的大规模计算的问题时,遗传算法暴露出搜索速度较慢、容易“早熟”陷入局部极值等缺点。因此我们使用量子遗传算法进行波形设计。量子遗传算法[14]是在遗传算法的基础上引入了量子计算后形成的算法。与传统的遗传算法一样,量子遗传算法也包括构造种群、计算适应度、种群更新的方法。但与前者不同的是,量子遗传算法的比特位是量子比特位,而非确定的经典的比特位。量子比特位借鉴了量子理论,表示为|0〉和|1〉两个态的任意中间态,描述为
|φ〉=α|0〉+β|1〉
(10)
其中,复数α和β表示相对应的比特状态的概率幅,且其模满足归一化条件
|α|2+|β|2=1
(11)
|α|2表示测量值取|0〉的概率,|β|2表示测量值取|1〉的概率。
由于量子遗传算法的染色体处于叠加态或者纠缠态,因此传统遗传算法的选择、交叉、变异操作无法应用在量子遗传算法中,而是使用量子门代替,其中主要应用的是量子旋转门和量子非门。量子旋转门的作用是在最优个体信息的指导下,对量子比特的概率幅的角度进行旋转,以实现量子状态的改变。这样,子代种群将不会由父代群体杂交决定,而是由父代种群中的最优个体与当前染色体向该最优个体靠拢之后的概率幅决定。旋转后的概率幅[14]为:
(12)
其中Δθ为旋转角,旋转角的方向与大小取值如表1所示,其中xi代表当前染色体的第i个基因位,而bi代表父代的最优染色体的第i个基因位,δ为旋转角的步长,用于控制算法的收敛速度,而s(αi,βi)为旋转角的调整方向。而f(x)和f(b)分别代表当前染色体和最优染色体的适应度函数值。本文对旋转角的调整策略进行了优化,使用的调整策略是,当xi=bi时,代表当前染色体和最优染色体的第i位基因相同,因此不做调整,旋转角为0;当xi≠bi时,将当前染色体的适应度f(x)与父代的最优染色体的适应度进行比较,并给定旋转角的方向和大小,使得染色体的概率幅向适应度函数值更小的方向演化。旋转角的步长δ随着迭代次数进行调整,在迭代次数较小的时候选择更大的步长可以加快算法收敛,而在迭代次数较大的时候选择较小的步长可以防止早熟陷入局部极值。
表1 旋转角调整策略
Tab.1 Adjustment strategy of the rotation angle
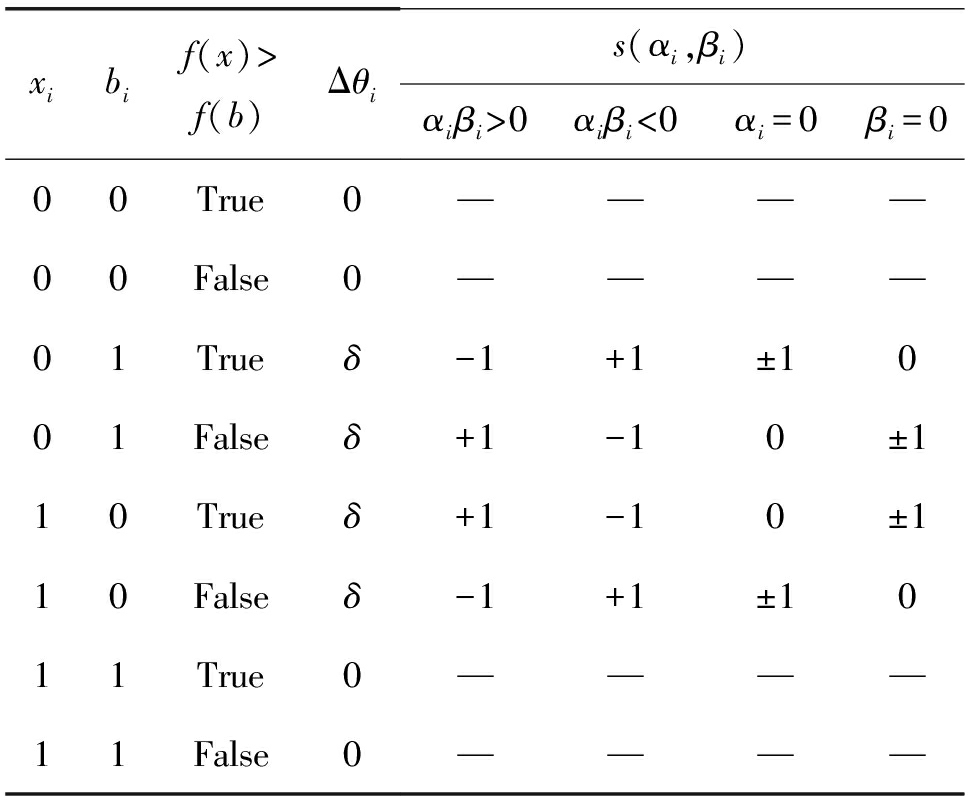
xibif(x)>f(b)Δθis(αi,βi)αiβi>0αiβi<0αi=0βi=000True0————00False0————01Trueδ-1+1±1001Falseδ+1-10±110Trueδ+1-10±110Falseδ-1+1±1011True0————11False0————
为了避免早熟,提高算法的局部搜索能力,在通过量子旋转门之后,使用量子非门模拟染色体的变异。变异的具体方法为,首先以事先给定的概率从种群中选择若干个体,并按确定的概率确定若干个基因位,对这些基因位执行量子非门操作,模拟染色体的变异。量子非门的操作实际上是改变原先坍缩到某一个状态的倾向,使其以该程度的倾向坍缩到另一个状态。变异后的概率幅为
(13)
量子遗传算法的流程图如图1所示。
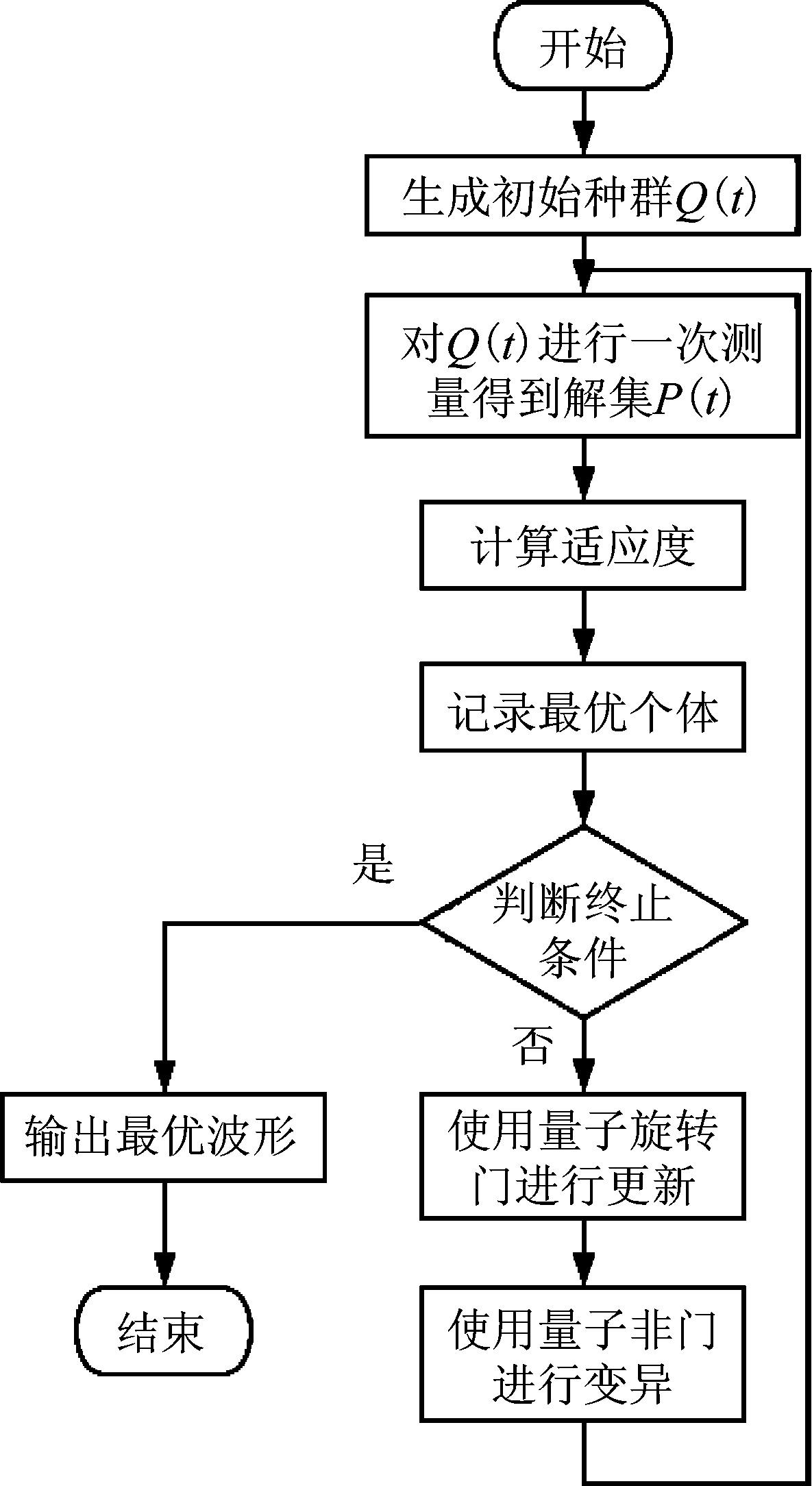
图1 量子遗传算法流程图
Fig.1 Flow chart of quantum genetic algorithm
与传统的遗传算法相比,量子遗传算法最大的不同之处在于使用了量子比特而不是经典的确定的比特。这样在搜索过程中,量子遗传算法可以用更少的个体表达更丰富的种群,提高种群的多样性,并提高了全局搜索能力,防止过早收敛到局部极值。同时,由于采用了旋转角的调整策略,量子遗传算法拥有较快的收敛速度[14]。
3.2 正交信号波形设计过程
这一节介绍基于量子遗传算法对正交信号波形优化设计的具体过程,具体步骤为:
步骤1 给定种群大小、最大迭代次数、旋转角步长、变异概率等算法参数。
步骤2 利用随机相位编码初始化种群并生成解集:
将种群定义为
Q(t)={qt,1,qt,2,qt,3,…, qt,n}
(14)
t是迭代次数,n是种群中的个体数目。对于种群中的每一个个体,都有
(15)
l为每个个体的量子比特数,满足
l=M·N·K
(16)
M为正交信号波形的数量即阵元数,N为波形的码长,K为每个相位角所占用的比特数。
然后将所有概率幅都进行随机初始化。与初始化为![]() 相比,随机初始化可以增大个体间的差异,增加种群多样性,防止过早收敛。根据种群的概率幅状态生成含n个个体的二进制解集P(t):
相比,随机初始化可以增大个体间的差异,增加种群多样性,防止过早收敛。根据种群的概率幅状态生成含n个个体的二进制解集P(t):
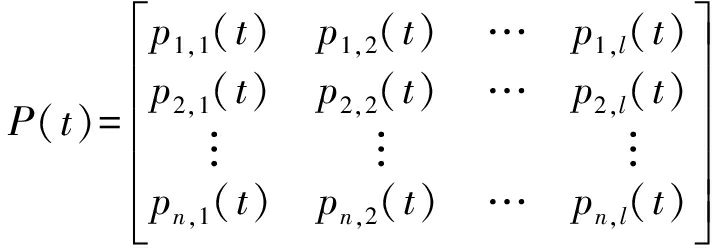
(17)
步骤3 计算种群中每个个体的适应度,并记录最优个体:
对于步骤2中生成的二进制解集P(t),首先将其转化为波形集。将每K比特的数据作为一组(例如pi,K(j-1)+1(t),pi,K(j-1)+2(t),…,pi,Kj(t)),并将其转化为一个相位:
(18)
这样将二进制解集转化为了由相位构成的波形集φ(t):
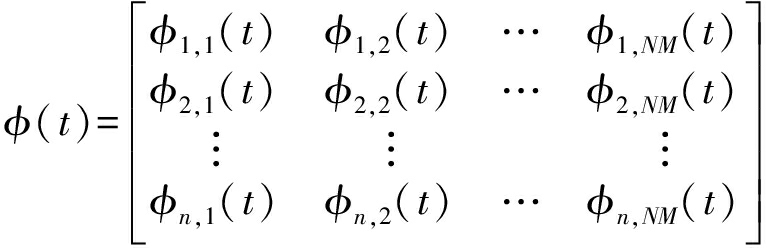
(19)
矩阵(19)的每一行都是一个个体。对于每个个体Θs(t),都包含长度为N的M个波形:
Θs(t)=[Θs,1(t),Θs,2(t),…,Θs,M(t)]
(20)
其中,
Θs,i(t)=[φs,N(i-1)+1(t),φs,N(i-1)+2(t),…,φs,Ni(t)]
(21)
然后将式(7)作为适应度函数,求Θs(t)的适应度值:
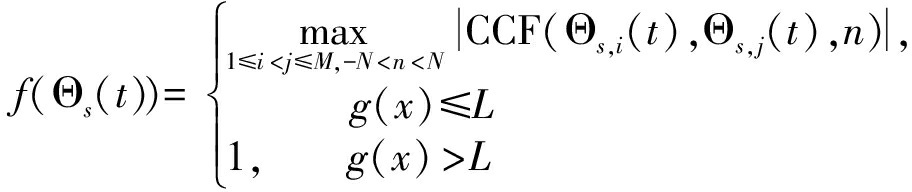
(22)
在对所有个体的适应度进行比较之后,选取适应度函数最小的个体为当前种群的最优个体。比较当前种群的最优个体与原先记录的最优个体,若当前种群的最优个体优于记录的最优个体,则更新记录,否则仍然使用原先的最优个体。
步骤4 在最优个体的信息的指导下,根据表1所述旋转角调整策略,通过量子旋转门对Q(t)进行种群进化。
步骤5 对使用量子非门模拟种群的基因突变:
以给定的概率选择Q(t)中的若干个体,并选择个体中的若干基因位,对这些基因位使用量子非门进行种群变异,变异之后的基因位将会将自身的两个概率幅互换。以此保持种群多样性,避免选择压力。
步骤6 利用进化与变异后的种群概率幅生成新的解集,并将其由二进制转换为相位集。
步骤7 计算新的种群的个体的适应度,并更新最优个体记录。
步骤8 判断是否达到最大迭代次数。若否,迭代次数加一并转到步骤4,继续进行循环;若是,则结束迭代计算,并输出最优个体信息。
4 仿真实验
为了验证使用量子遗传算法进行MIMO雷达正交信号波形优化设计的效果,这里使用MATLAB进行了实验验证。给定的参数如表2所示。为了加快算法收敛,在前500次迭代中使用3倍旋转角。利用量子遗传算法进行优化设计,迭代10000次后,得到的波形的自相关函数如图2(a)~(c)所示,其中横坐标为时延,纵坐标为对数形式的自相关函数。可以得到,自相关旁瓣的峰值为-23.8 dB,因此可以得出结论,所得波形具有良好的自相关特性。图2(d)~(f)是所得波形的互相关曲线,其中横坐标为时延,纵坐标为对数形式的互相关函数。可以得到,互相关的峰值为-27.0 dB,因此可以得出结论,所得波形具有良好的互相关特性。
表2 仿真参数
Tab.2 Simulation parameters
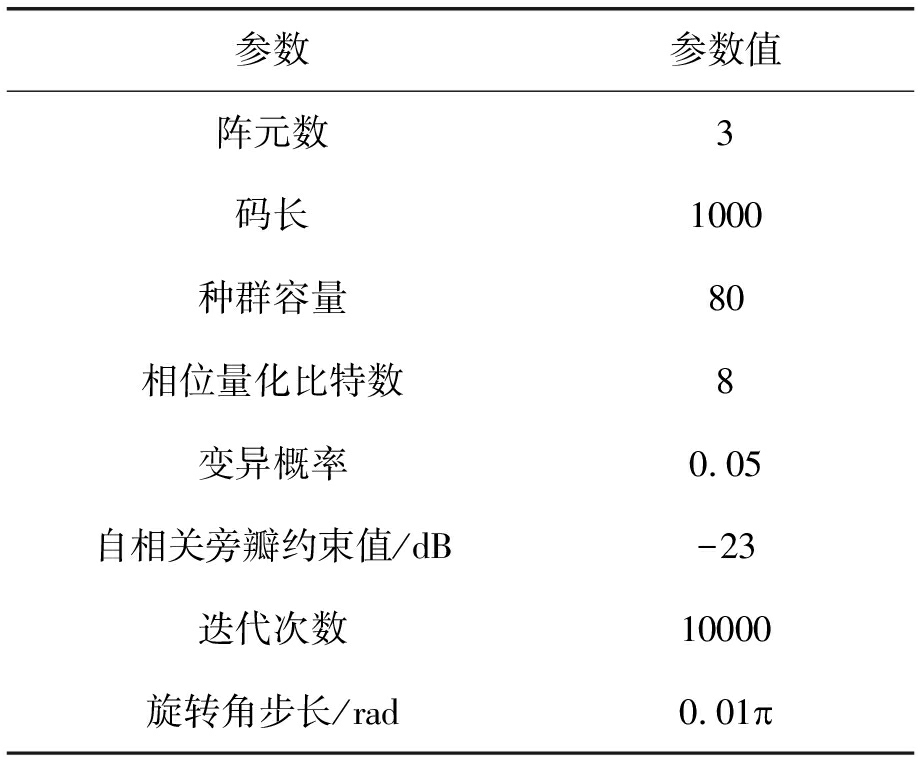
参数参数值阵元数3码长1000种群容量80相位量化比特数8变异概率0.05自相关旁瓣约束值/dB-23迭代次数10000旋转角步长/rad0.01葩
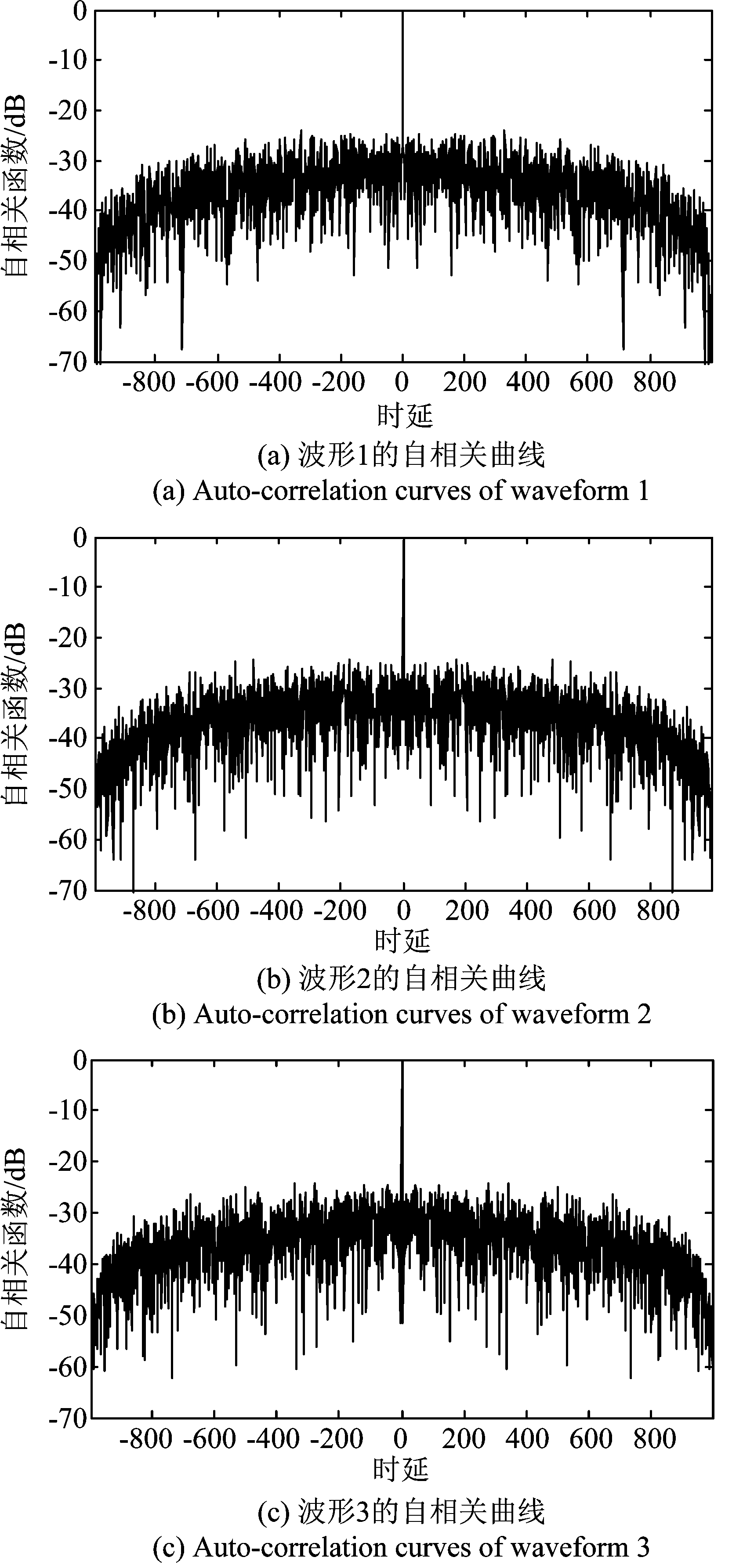
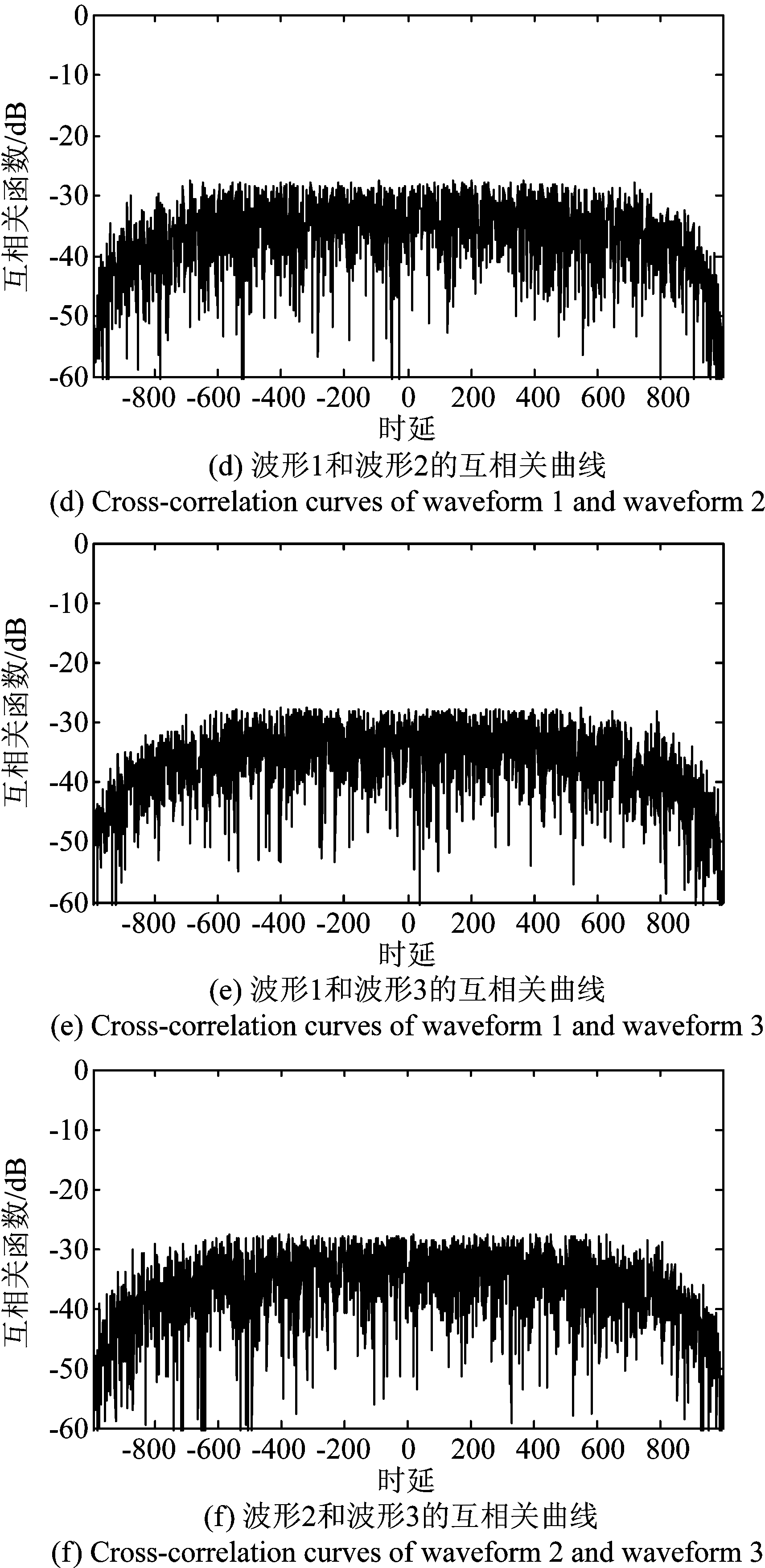
图2 码长为1000的3个波形的自相关曲线和互相关曲线
Fig.2 Auto-correlation and Cross-correlation of three waveforms
然后比较遗传算法与本文使用的量子遗传算法所设计出的正交信号波形的互相关性能。除自相关旁瓣峰值的约束值按照表3给定外,其余参数均使用表2给定参数,然后分别用文献[5]使用的遗传-和声搜索算法、遗传算法和本文使用的量子遗传算法设计码长分别从100到1000的正交信号波形。设计结果的互相关峰值如图3所示,横坐标为正交信号波形的码长,纵坐标为对数形式的互相关峰值。由图3可以观察得到,对于所有码长在100到1000之间的正交信号波形,量子遗传算法所得到的波形的互相关峰值均明显低于随机相位算法和遗传算法所得到的波形。因此可以得出结论,本文使用的量子遗传算法所设计的波形拥有更好的互相关特性。由于适应度函数对自相关旁瓣峰值只是设定了约束值,并没有进行优化,因此没有必要比较几种算法结果的自相关函数峰值。
表3 自相关旁瓣峰值的约束值
Tab.3 The constraint value of autocorrelation sidelobe peak value

码长自相关旁瓣约束值/dB100-14200-15300-16400-17500-18600-19700-20800-21900-221000-23
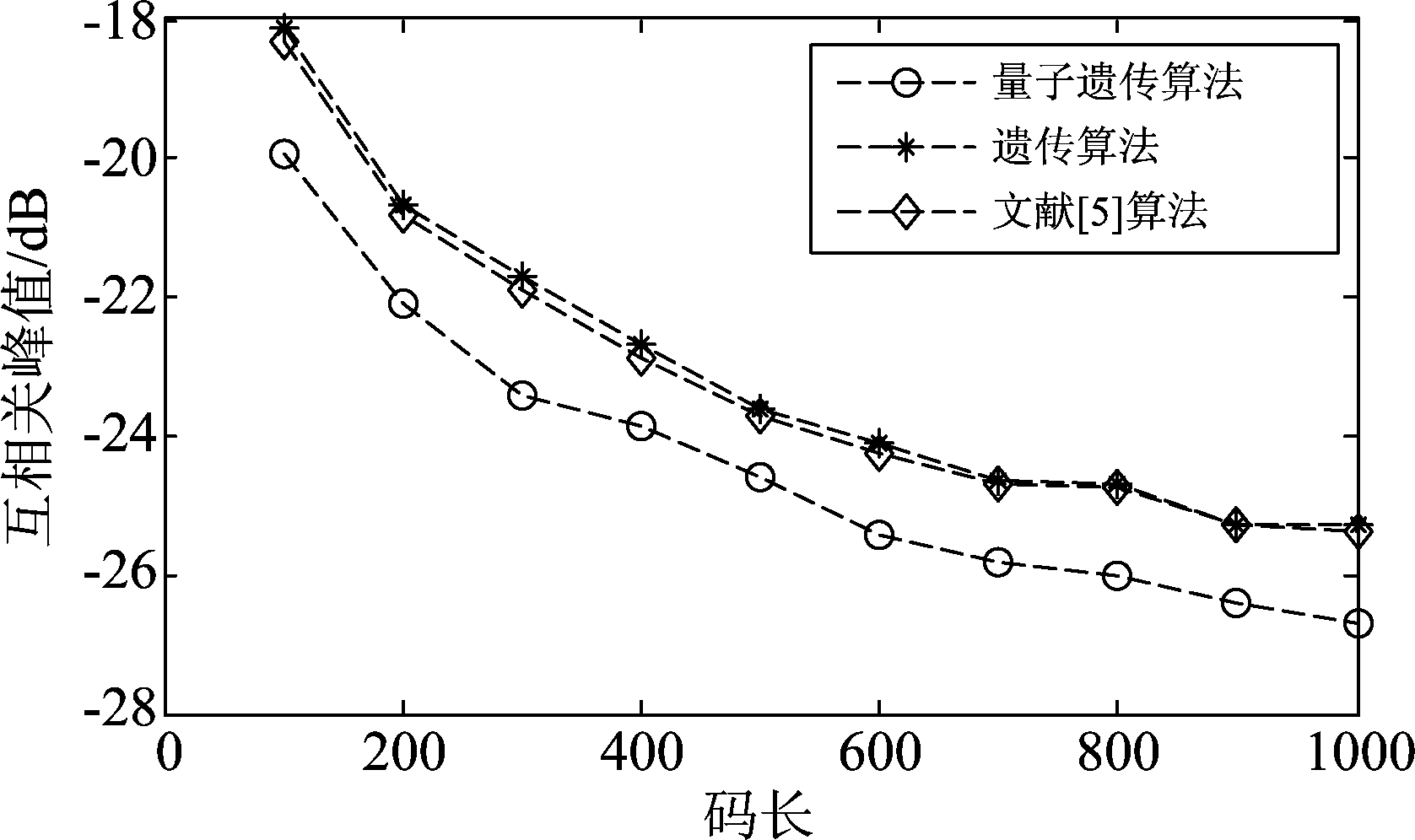
图3 三种算法设计结果的互相关峰值
Fig.3 Cross-correlation peaks of the design results of the three algorithms
为了比较三种算法的优化速度,以码长为100、自相关旁瓣峰值约束为-13 dB为例,分别使用遗传算法、量子遗传算法和文献[5]的算法进行波形设计,并记录其收敛情况。得到的结果如图4所示。从图4中可以得到,在同样的迭代次数下,量子遗传算法的互相关峰值几乎总是低于另外两种算法。
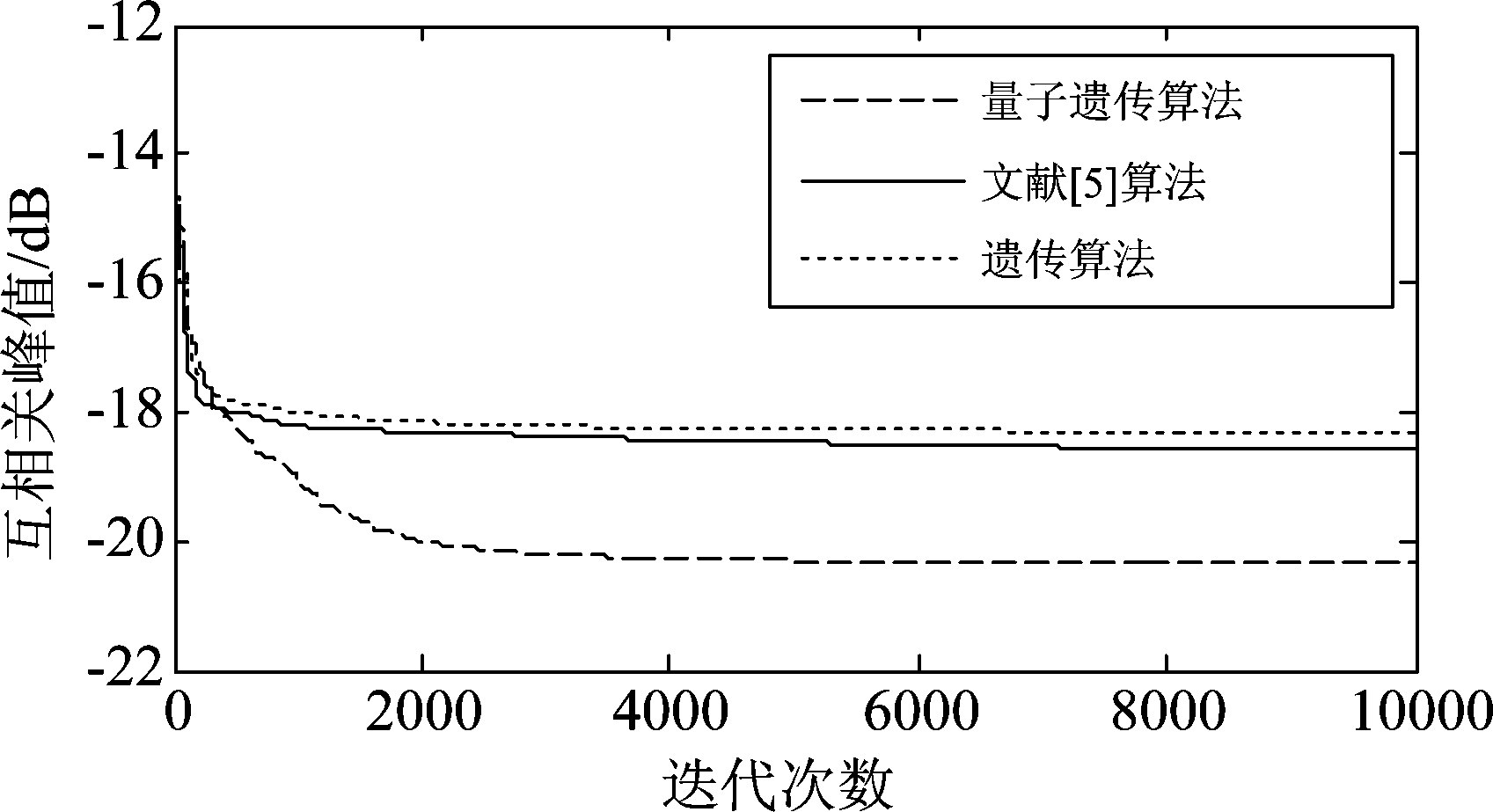
图4 三种算法设计结果的收敛情况
Fig.4 The convergence of the design results of the three algorithms
然后使用量子遗传算法研究不同阵元数对优化波形性能的影响。仍以码长为100、自相关旁瓣峰值约束为-13 dB为例,使用量子遗传算法进行波形设计,其中阵元数为从2到10,并记录其优化结果的互相关峰值。得到的结果如图5所示。从图5中可以得到,随着阵元数的增加,波形的互相关峰值也在增高。因此,阵元数越多,对相关性能的要求也就越高。
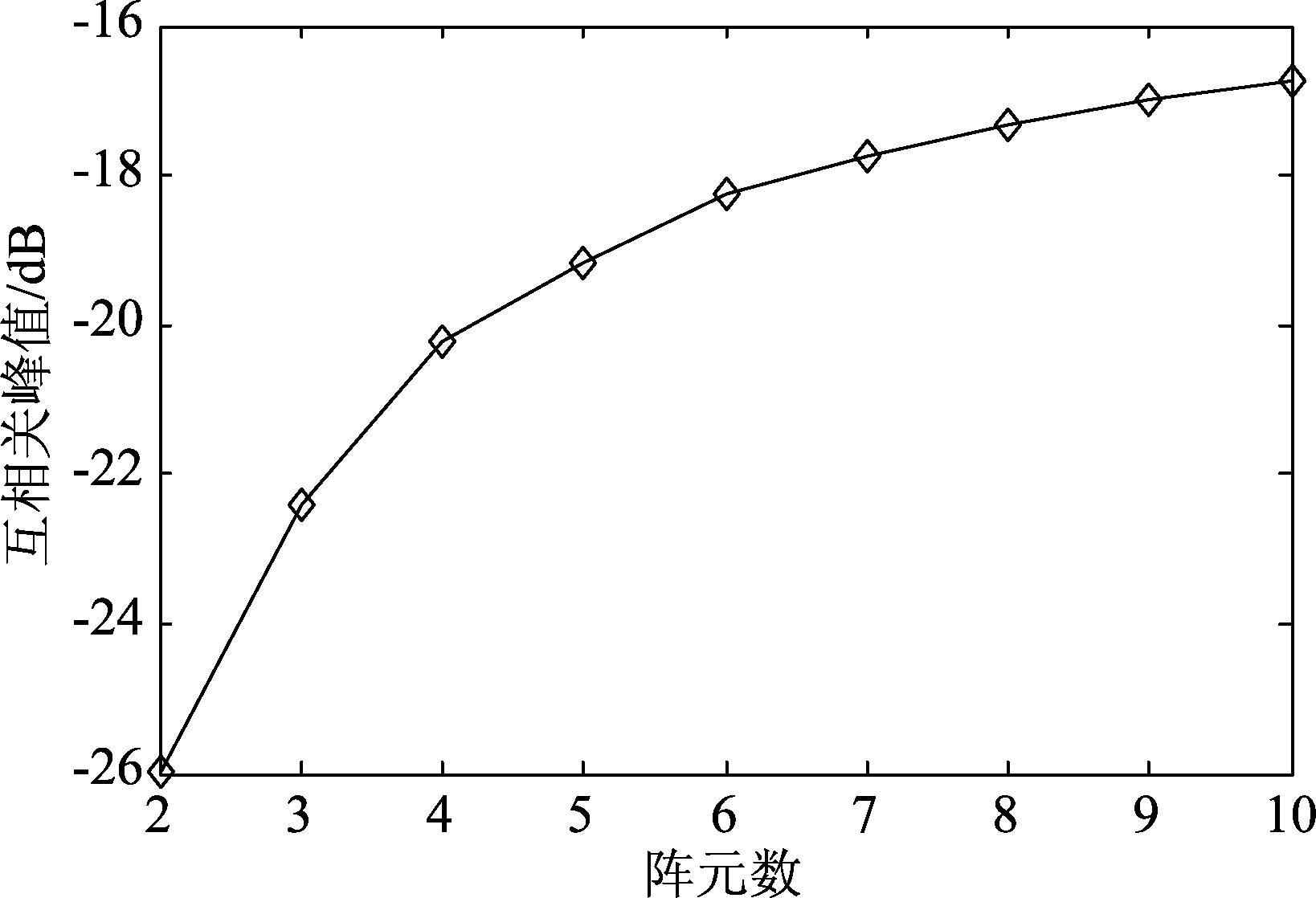
图5 不同阵元数得到的互相关峰值
Fig.5 The cross-correlation peaks of different array elements
5 结论
对于MIMO雷达长码长正交信号波形优化设计的问题,本文在正交多相编码和遗传算法优化的基础上,针对信号的互相关特性,将量子遗传算法引入到正交信号波形优化设计之中,使用量子位编码表示染色体,然后利用量子旋转门和种群最优解对染色体进行更新,并使用量子非门进行染色体变异。最终进一步降低了正交信号波形之间的互相关峰值。仿真部分验证了所得到的MIMO雷达正交信号波形具有良好的自相关特性和互相关特性,相较遗传算法更优,同时优化速度也得到了提升。
[1] 张田仓. MIMO雷达正交连续相位编码波形研究[J]. 现代导航, 2016, 7(4): 299-304.
Zhang Tiancang. Research on orthogonal serial phase-code waveform of MIMO radar[J]. Modern Navigation, 2016, 7(4): 299-304.(in Chinese)
[2] Gartz K J. Generation of uniform amplitude complex code sets with low correlation sidelobes[J]. IEEE Transactions Signal Processing, 1992, 40(2): 343-351.
[3] Deng Hai. Polyphase code design for Orthogonal Netted Radar systems[J]. IEEE Transactions Signal Processing, 2004, 52(11): 3126-3135.
[4] 刘波. MIMO雷达正交波形设计及信号处理研究[D]. 成都: 电子科技大学, 2008.
Liu Bo. Orthogonal waveform design and signal processing of MIMO radar[D]. Chengdu: University of Electronic Science and Technology of China, 2008.(in Chinese)
[5] 谢雷振, 陈怡君, 康乐, 等. 遗传-和声搜索算法下的MIMO雷达正交多相码设计[J]. 电光与控制, 2018, 25(8): 23-27.
Xie Leizhen, Chen Yijun, Kang Le, et al. Design of MIMO radar orthogonal polyphase code based on genetic-harmony search algorithm[J]. Electronics Optics & Control, 2018, 25(8): 23-27.(in Chinese)
[6] 姬媛. 基于相位编码的连续波MIMO雷达波形设计[D]. 西安: 西安电子科技大学, 2017.
Ji Yuan. Waveform design of continuous wave MIMO radar based on phase coding[D]. Xi’an: Xidian University, 2017.(in Chinese)
[7] Sun Jianfeng, Wang Xuefeng, Wang Tianjiao, et al. Quantum genetic search algorithm based on range image of laser radar[P]. Optoelectronics and Microelectronics Technology (AISOMT), 2011 Academic International Symposium on, 2011.
[8] 王海蛟, 贺欢, 杨震. 敏捷成像卫星调度的改进量子遗传算法[J]. 宇航学报, 2018, 39(11): 1266-1274.
Wang Haijiao, He Huan, Yang Zhen. Improved quantum genetic algorithm for scheduling of agile imaging satellites[J]. Journal of Astronautics, 2018, 39(11): 1266-1274.(in Chinese)
[9] 叶培. 一种新的量子遗传算法在阳山金矿GPS卫星信号去噪处理中的应用探讨[J]. 黄金科学技术, 2015, 23(2): 83- 87.
Ye Pei. Application of a new quantum genetic algorithm in GPS satellite signal denoising processing in yangshan gold mine[J]. Gold Science and Technology, 2015, 23(2): 83- 87.(in Chinese)
[10] 王力宝. 多输入多输出合成孔径雷达关键技术研究[D]. 长沙: 国防科学技术大学, 2010.
Wang Libao. Research on challenge technologies of MIMO-SAR[D]. Changsha: National University of Defense Technology, 2010.(in Chinese)
[11] Liu Bo, He Zishu, Zeng Jiankui, et al. Polyphase Orthogonal Code Design for MIMO Radar Systems[C]∥2006 CIE International Conference on Radar, Shanghai, 2006: 1- 4.
[12] 王伟, 赵俊杰, 王辉. 基于混合算法的MIMO雷达正交多相码设计[J]. 系统工程与电子技术, 2013, 35(2): 294-298.
Wang Wei, Zhao Junjie, Wang Hui. Orthogonal polyphase code design of MIMO radar based on hybrid algorithm[J]. Systems Engineering and Electronics, 2013, 35(2): 294-298.(in Chinese)
[13] 薛永华, 李秀友, 关键. MIMO天波雷达非连续谱正交相位编码波形设计[J]. 信号处理, 2015, 31(10): 1255-1262.
Xue Yonghua, Li Xiuyou, Guan Jian. MIMO Skywave Radar Discontinuous Spectra Orthogonal Phase Coded Waveform Design[J]. Journal of Signal Processing, 2015, 31(10): 1255-1262.(in Chinese)
[14] 许国根, 贾瑛, 韩启龙. 模式识别与智能计算的MATLAB实现[M]. 第2版.北京: 北京航空航天大学出版社, 2017: 312-321.
Xu Guogen, Jia Ying, Han Qilong. MATLAB implementation of pattern recognition and intelligent computing[M]. 2nd edition. Beijing: Beihang University Press, 2017: 312-321.(in Chinese)
