1 引言
合成孔径雷达(SAR)作为一种主动成像设备,自上世纪50年代提出以来,成功应用到卫星、飞机、无人机等多种平台,获得了广泛的应用。SAR成像技术不断发展引领着成像算法不断推陈出新,传统的直线轨迹SAR通过“合成孔径”及“脉冲压缩”技术可以获得方位向和距离向的高分辨成像,但该种投影方式会产生遮挡,阴影等问题。为了满足精细化观测需求,1996年美国State University of New York的Mehrdad Soumekh[1]教授首先提出圆迹SAR成像模式,并提出了基于格林函数傅里叶分析的波前重建CSAR成像算法,为之后的CSAR的发展奠定了理论研究基础。螺旋轨迹SAR以雷达随平台作圆周运动、波束始终指向同一场景区域,同时向目标移动靠近,该种模式数据获取几何能够获取目标在多个方向的散射特征,提高目标识别和分类精度,同时提高雷达平台的生存和突防能力,研究螺旋轨迹下的信号模型和成像方法具有重要的应用价值[2- 4]。
后向投影算法(BP)在原理上可以用于任何几何配置进行SAR成像[5- 8],但很低的计算效率使其无法实际应用。中科院林赟等人在2010年提出CSAR极坐标格式算法[9],该算法通过两步相位补偿处理消除了PFA平面波假设带来的二次相位误差[10-11],获得了较大的成像面积。考虑到螺旋轨迹的二维波数频谱在地平面的投影类似于环,它也可以用CSAR极坐标格式算法处理,但是螺旋轨迹变化的斜距使得相位误差补偿操作必须做出改进,本文提出螺旋轨迹SAR的极坐标格式算法,该方法首先需要对数据进行距离向对齐,然后分子孔径进行第一次相位误差滤波,修改二次相位误差补偿函数表达式。通过修改后的两步相位补偿处理,校正了平面波假设带来的二次相位误差,通过实验仿真,获得了边缘聚焦的场景图像,验证了算法的有效性。
2 螺旋轨迹SAR极坐标格式算法
2.1 信号模型
雷达平台沿着半径为R(θ),离地面高度为H(θ)的红色螺旋轨迹移动,雷达平台旋转角度θ定义为慢时间,θ∈[0,2π),慢时间方向即为方位向。雷达平台运动时,雷达视线方向始终指向场景区域中心o,波束俯仰角为α。直角坐标系下雷达平台的坐标为(x(θ),y(θ),z(θ)),
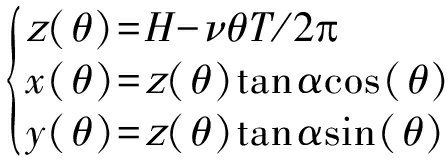
T为雷达平台旋转一周的时间,ν是雷达在y轴方向的速度分量。球坐标系下,雷达平台的坐标系为(R0(θ),α,θ),其中![]() 为雷达平台与场景中心的距离。P为场景区域中任意点目标,散射系数为σp,坐标为(xp,yp,zp)。点目标P球坐标设为(ρ,η,φ)。设雷达与目标场景P之间的瞬时距离为Rp(θ),位置向量瞬时夹角设为β。
为雷达平台与场景中心的距离。P为场景区域中任意点目标,散射系数为σp,坐标为(xp,yp,zp)。点目标P球坐标设为(ρ,η,φ)。设雷达与目标场景P之间的瞬时距离为Rp(θ),位置向量瞬时夹角设为β。
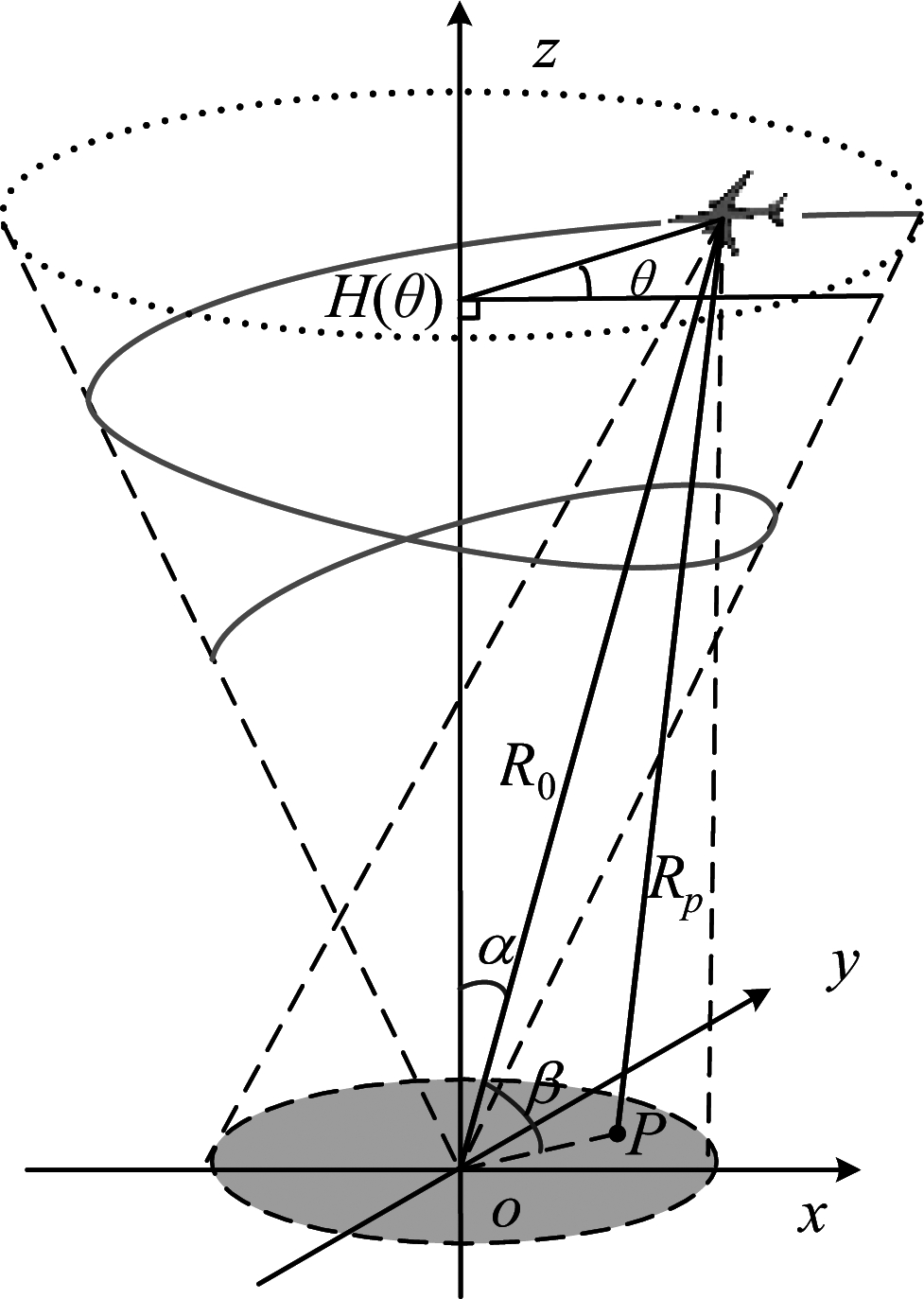
图1 螺旋轨迹SAR成像几何
Fig.1 Spiral SAR imaging geometry
发射雷达信号为Chirp信号,脉宽Tp,调频率γ,雷达接收目标P的回波为:
exp{j2πfc[t-2Rp(θ)/c]+jπγ[t-2Rp(θ)/c]2}
(1)
式中c为光速,t为快时间, fc为中心频率。以区域中心o回波作为解调参考信号
exp{j2πfc[t-2R0(θ)/c]+jπγ[t-2R0(θ)/c]2}
(2)
回波信号与参考信号时域共轭相乘(Dechirping处理),然后脉冲信号傅里叶变换到频域乘以exp(-jπf2/γ),以消除剩余视频相位项(RVP),逆傅里叶变换得到回波信号[12]
(3)
定义波数K(θ)=4π[γ(t-2R0(θ)/c)+fc]/c,中心波束Kc=4πfc/c,Br=4πγTp/c为信号波数域带宽,上式重写为
(4)
其中RΔ=Rp(θ)-R0(θ)为雷达到目标点和原点的距离差,对其幂级数展开,得:
(5)
设点目标P位于z=0平面,η=π/2成立,由几何关系可得
cos β=sin αsin ηcos(θ-φ)+
cos αcos η=sin αcos(θ-φ)
(6)
频谱的相位表达式为:
(7)
其中
Kx=-K(θ)sin αcos θ,Ky=-K(θ)sin αcos θ
(8)
式(6)中第一项确定重建目标位置,当成像距离较远并且成像区域较小时,平面波假设成立,可以考虑不补偿二次相位,直接插值完成传统的PFA成像。插值过程如图2所示,式(3)的数据格式sIF(θ,t)是按照极坐标格式存储的,通过映射关系式(7)二维插值,得到矩形网格上的波数谱,对频谱二维逆傅里叶变换即可以得到成像结果。
为了获取较大场景区域聚焦图像,需要补偿RΔ的二次项带来的相位增量。式中sin2β=1-sin2αcos2(θ-φ)改写为sin2α·sin2(θ-φ)+cos2α,式(3)中相位表达式重新写为
K(θ)RΔ≈2K(θ)ρ sin α cos(θ-φ)-
(9)
通过对相位的拆分,可以分两步对相位误差进行补偿。式(9)第二项是慢时间θ的函数,同时它也和点目标的位置(ρ,η,φ)有关,但是林赟等人通过严谨的分析推导[9],可以将该项通过一个方位向二次相位滤波函数消除掉。第三项与θ和场景中心的距离ρ有关,可考虑在完成极坐标格式到直坐标格式的转化后,分区域进行相位补偿。
2.2 第一次相位补偿
在圆迹SAR极坐标格式算法中,方位第一项的相位增量通过方位向频域滤波消除,相位滤波系统传递函数为:
(10)
式中Na为方位向脉冲数目,推导出该式的前提条件是斜距R0固定,方位向K不随方位向慢时间变化,但是螺旋轨迹SAR模式中显然不成立,R0(θ),K(θ)均是θ的函数,因此我们需要对信号做些处理。对于波数K,我们可以对每个脉冲信号距离向对齐,即就是距离向时延tΔ=2[R0(0)-R0(θ)]/c,式(3)距离向傅里叶变换,乘以Hra(θ, f)=exp(-j2πftΔ)得到信号:
FT[sIF(θ,t-tΔ)]=exp(-j2πftΔ)FT[sIF(θ,t)]
然后距离向逆傅里叶变换,得到时延之后距离对齐的信号

图2 极坐标数据插值到直角坐标系下
Fig.2 Interpolation of Polar coordinate data into Cartesian coordinate system
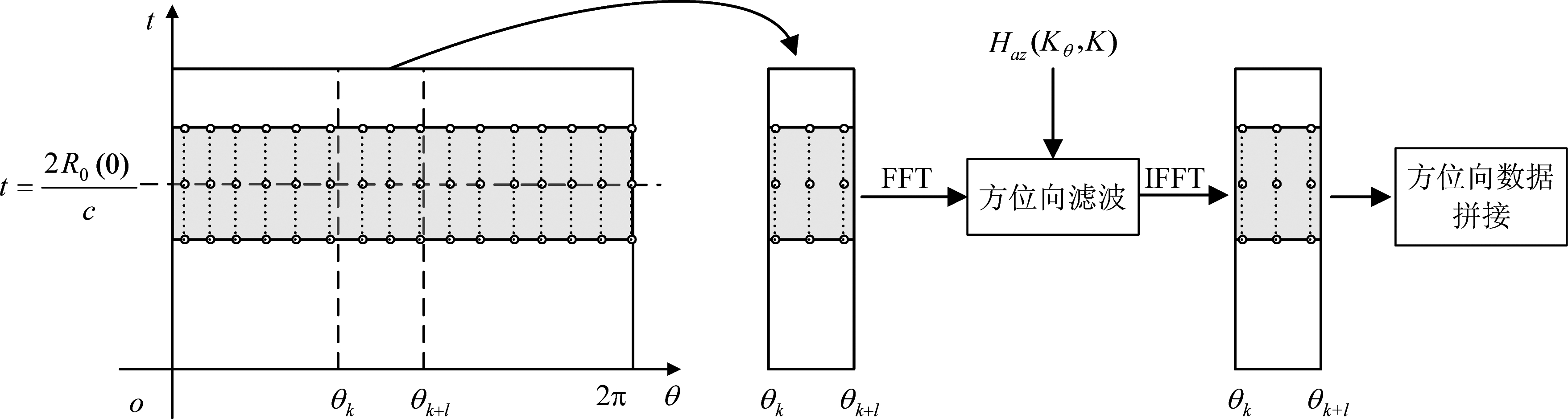
图3 方位向子孔径滤波
Fig.3 Azimuth subaperture filtering
(11)
重新定义波数K=4π[γ(t-2R0(0)/c)+fc]/c,此时波数已经不随方位向慢时间θ而变化。
对于变化的R0我们可以分子孔径进行滤波,截取方位向θk到θk+l中间脉冲数据,定义滤波函数为
(12)
该滤波函数将相位![]() 消除掉,第二项残差相位为
消除掉,第二项残差相位为
Φ1=-K ρ2sin2α sin2(θ-φ)
(13)
当l值取值越小,R0(θk+l/2)和R0(θ)差值很小,可以认为Φ1≈0。所以通过子孔径对数据进行相位滤波,可以有效降低斜距变化带来的式(8)第二项残差相位。
sIF(θ,K) 通过滤波后,输出信号Spo(Kθ,K)的解析表达式为
Spo(θ,K)=IFT(Kθ)[FT(Kθ)(Sa)·Haz(Kθ,K)]≈
(14)
插值得到:
S(Kx,Ky)≈
(15)
2.3 第二次相位补偿
式(14)相位第三项重新写为:
(16)
相位随目标位置半径ρ变化,可以考虑对场景中相同半径处的所有点同时进行相位补偿,即就是圆环分区相位补偿。该方法需要将成像的场景图像按半径分成不同的圆环,对回波数据(15)用圆环对应的相位补偿函数相位补偿,逆傅里叶变换得到场景图像,其中在该圆环中的场景精确聚焦,通过加圆环窗提取出聚焦图像,然后对所有圆环拼接,得到一个完整的场景图像。
式(16)右边第2项引起的相位变化量为:
(17)
R0(2π)是θ=2π的斜距,也是最小斜距,在该时刻Δφ1(ρ)相位变化量最大,为保证图像质量,相位补偿后场景区内所有目标的非线性相位都需控制在π/4内,因此,每个分区的内圈目标和外圈目标的相位变化量Δφ1(ρ)≤π/2,若将Δφ1(ρ)设为π/2,并设第k个分区的半径为rk-1,外圈半径为rk,则rk的表达式为
(18)
对于第k个分区,相位补偿量为内外圈目标相位增量的中值,即:
(19)
将式(15)与相位补偿函数H(Kx,Ky)相乘,可保证半径rk-1,rk圆环区域内每个点目标的相位误差都不超过π/4,相位补偿后得到:
Sk(Kx,Ky)=S·Hk≈exp(-jKxxp-jKyyp),
(20)
对式(20)做二维逆傅里叶变换,加上环状窗后得到环形区域内的聚焦图像,表达式为
sk(x,y)=IFT[Sk]·Wk≈PSF2d(x-xp,y-yp)·Wk
(21)
(22)
其中PSF2d(x,y)代表CSAR的二维点扩展函数。完成各分区的成像处理后,将图像拼接,可得到z=0平面的二维图像。算法流程如图4所示。
3 仿真实验
为了验证算法的有效性,进行点目标仿真验证,系统参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
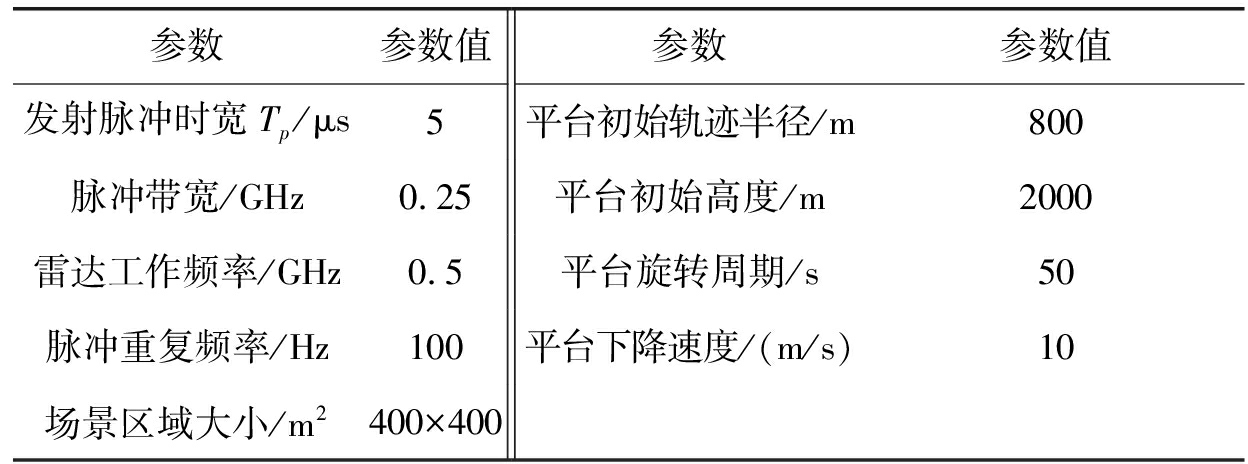
参数参数值参数参数值发射脉冲时宽Tp/μs5平台初始轨迹半径/m800脉冲带宽/GHz0.25平台初始高度/m2000雷达工作频率/GHz0.5平台旋转周期/s50脉冲重复频率/Hz100平台下降速度/(m/s)10场景区域大小/m2400×400
点目标均匀分布在0高度平面,间隔为10的矩形网格中,总共有41×41个点目标参与仿真,场景大小为400 m×400 m,选择BP算法作为结果参照。
图5是点目标成像结果,(a)是只做第一步相位补偿的成像结果,分10个子孔径分别相位滤波,(b)是只做第二步相位补偿的成像结果,可以看出,离场景中心越远,点目标散焦越严重,第二步相位补偿对图像的聚焦影响较大。当完成二步相位补偿后图像完全聚焦,如图(c)所示,图像边缘的点目标也具有良好的聚焦性能,证明了本文螺旋轨迹极坐标格式算法的有效性。
为了量化比较成像质量,对边缘点目标(0,200)进行指标测量,测量内容为第一步相位误差补偿子孔径数目不同时的成像结果,如图6所示,图(a)为子孔径数目为1,即整个方位向不分段,图(b),(c)的子孔径数目分别为4和10,可以看出,随着子孔径数目的增多,相位误差补偿越精确,图像聚焦性能越好。
表2为量化结果,选择BP成像结果作为对比,BP测得成像分辨率=0.285 m,圆迹SAR平面频谱扩展为一个圆环面,圆环面的中空部分控制着扩展函数的旁瓣水平,在表1系统参数,载频0.5 GHz,带宽0.25 GHz条件下,峰值旁瓣比=-9 dB左右,该值高于普通SAR成像扩展函数-13.4 dB水平。PFA划分子孔径数目为1时,第一项相位误差补偿后剩余相位误差较大,成像结果有散焦,测量得到的指标较差。当子孔径数目划分增加时,成像结果变好,当子孔径数目超过10之后成像质量与BP非常接近。结果证明了本文分子孔径补偿第一项相位误差方法的有效性。
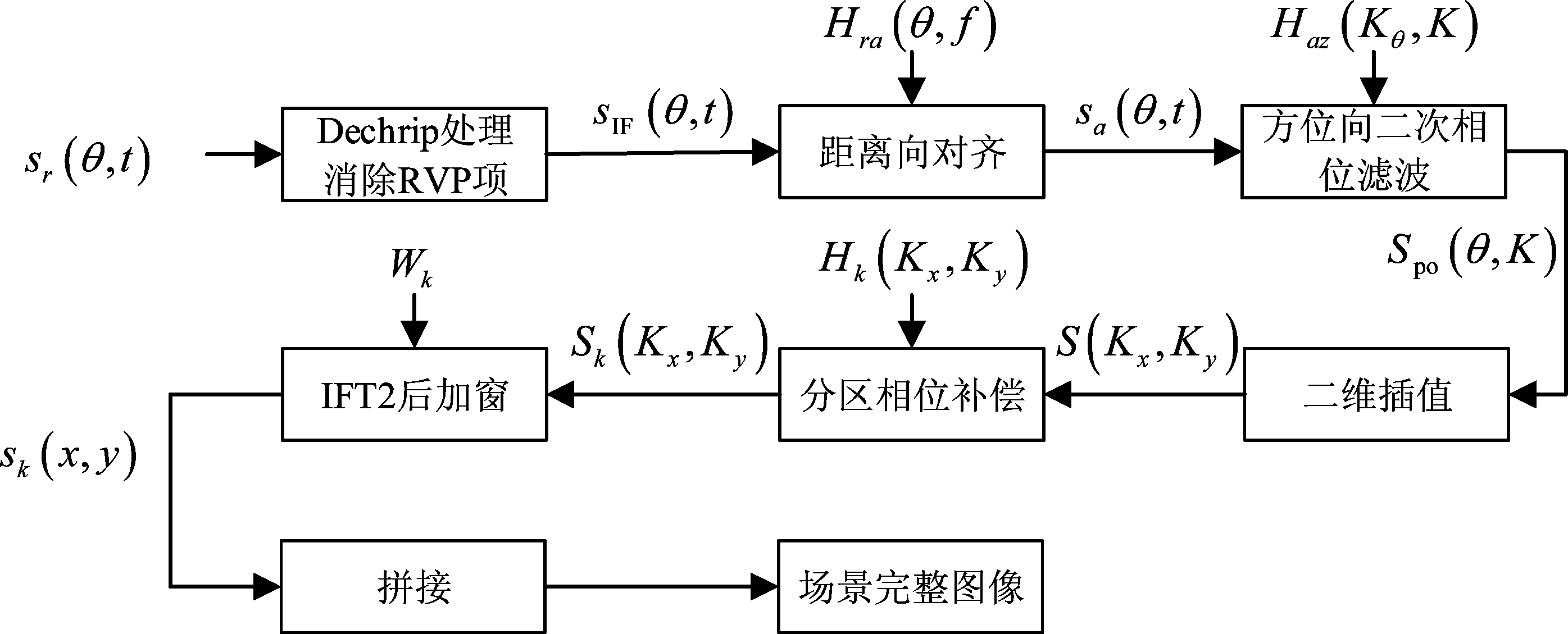
图4 算法流程图
Fig.4 Block diagram of PFA for Spiral SAR
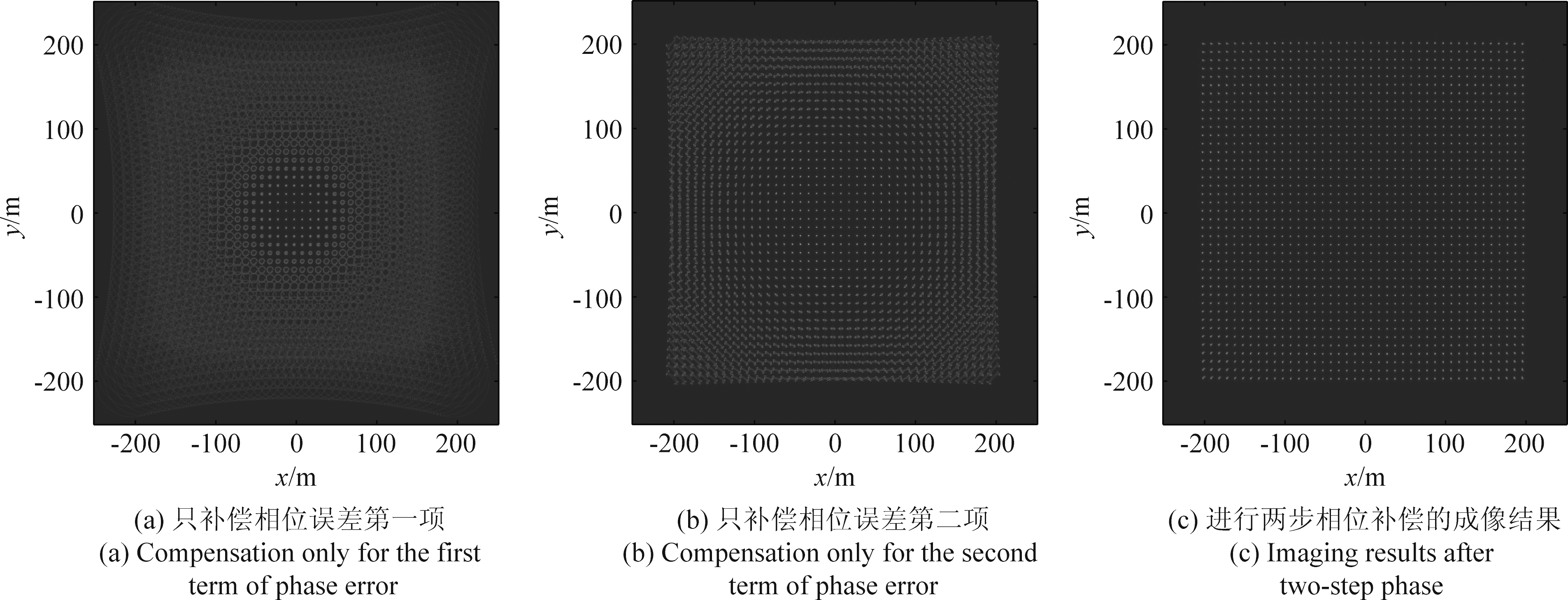
图5 成像结果对比
Fig.5 Comparison of imaging results
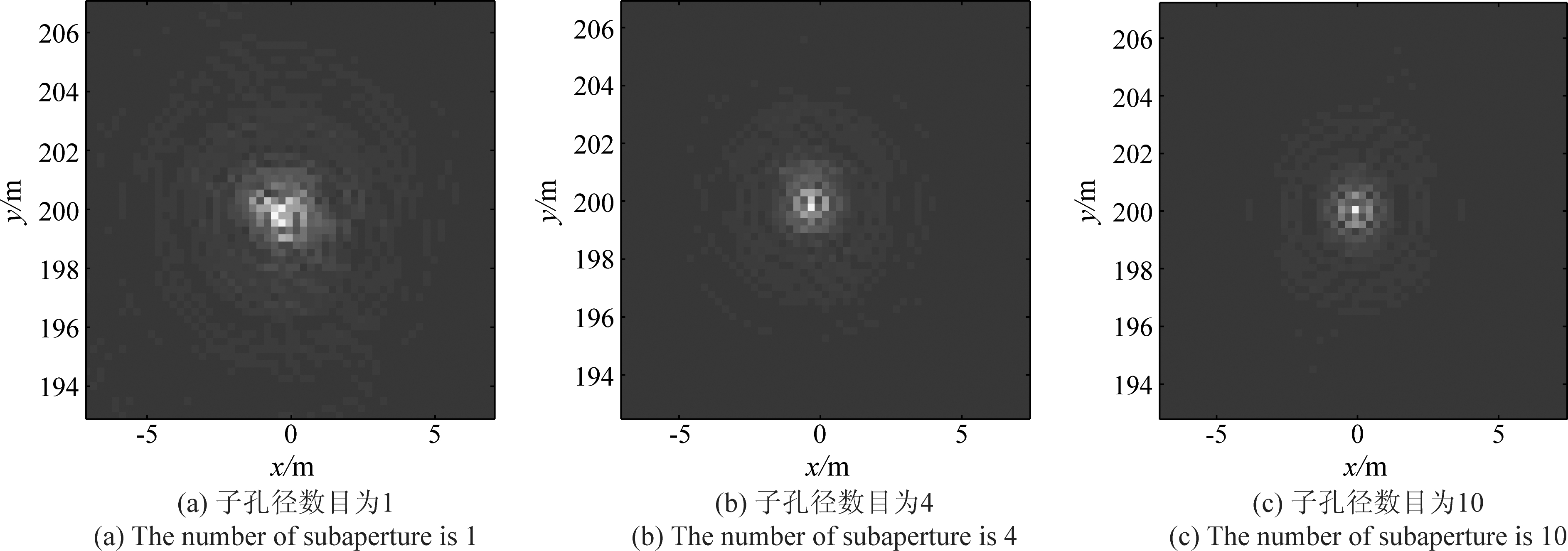
图6 点目标(0,200)成像放大图
Fig.6 Magnified image of point target (0,200)
表2 边缘点目标(0,200)成像性能指标测试结果
Tab.2 Performance of point target (0,200)
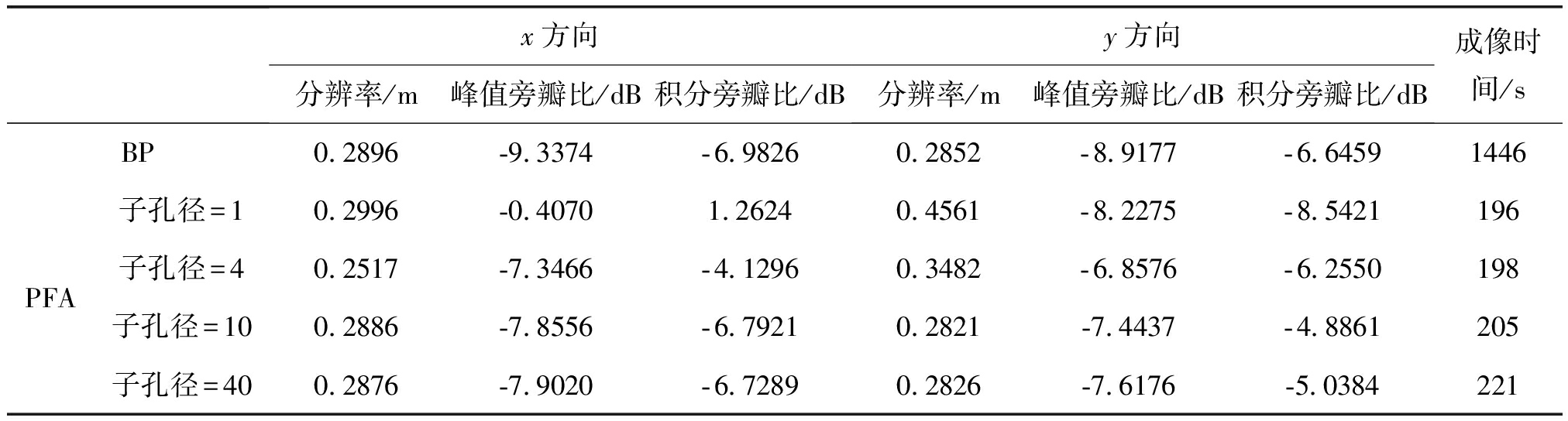
x方向分辨率/m峰值旁瓣比/dB积分旁瓣比/dBy方向分辨率/m峰值旁瓣比/dB积分旁瓣比/dB成像时间/sBP0.2896-9.3374-6.98260.2852-8.9177-6.64591446PFA子孔径=10.2996-0.40701.26240.4561-8.2275-8.5421196子孔径=40.2517-7.3466-4.12960.3482-6.8576-6.2550198子孔径=100.2886-7.8556-6.79210.2821-7.4437-4.8861205子孔径=400.2876-7.9020-6.72890.2826-7.6176-5.0384221
在成像效率方面,本文仿真场景选取3000×3000像素单元,成像时间如表2所示,BP算法耗时1446 s,而PFA在选取40子孔径补偿时,耗时为221 s。PFA经过复杂的相位补偿过程,耗时方面仍是显著优于BP成像算法,不过仍需要后续进一步提高改进。
4 结论
本文基于CSAR极坐标格式算法提出了螺旋轨迹SAR极坐标格式算法,通过距离对齐和两步相位补偿操作校正了波数二次相位误差项,获得了边缘点聚焦良好的大场景成像结果。其中第一步相位误差在每个子孔径内能够近似完全补偿掉,仿真结果证明了当子孔径划分超过一定数目成像质量与BP算法接近。本文还存在不足,后续将通过实测数据对本文算法进行验证。
[1] Soumekh M. Reconnaissance with slant plane circular SAR imaging[J]. IEEE Transactions on Image Processing, 1996, 5(8):1252-1265.
[2] Ponce O, Prats-Iraola P, Scheiber R, et al. First Airborne Demonstration of Holographic SAR Tomography With Fully Polarimetric Multicircular Acquisitions at L-Band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6170- 6196.
[3] Hu C, Li Y, Dong X, et al. Optimal 3D deformation measuring in inclined geosynchronous orbit SAR differential interferometry[J]. Science China(Information Sciences), 2017, 60(6):33- 47.
[4] Yin W, Ding Z, Lu X, et al. Beam scan mode analysis and design for geosynchronous SAR[J]. Science China(Information Sciences), 2017, 60(6): 060306.
[5] Ferrara M, Jackson J A, Austin C. Enhancement of multi-pass 3D circular SAR images using sparse reconstruction techniques[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2010, 7337: 733702-733702-10.
[6] Cantalloube H M J, Colinkoeniguer E, Oriot, Hélène. High resolution SAR imaging along circular trajectories[C]∥IEEE International Geoscience & Remote Sensing Symposium. IEEE, 2007.
[7] Jakowatz C V, Doren N. Comparison of polar formatting and back-projection algorithms for spotlight-mode SAR image formation[C]∥Algorithms for Synthetic Aperture Radar Imagery XIII. International Society for Optics and Photonics, 2006.
[8] Ponce O, Prats-Iraola P, Pinheiro M, et al. Fully Polarimetric High-Resolution 3-D Imaging With Circular SAR at L-Band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6):3074-3090.
[9] 林赟, 谭维贤, 洪文, 等. 圆迹SAR极坐标格式算法研究[J]. 电子与信息学报, 2010, 32(12): 2802-2807.
Lin Yun, Tan Weixian, Hong Wen, et al. Polar Format Algorithm for Circular Synthetic Aperture Radar[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2802-2807.(in Chinese)
[10] Doerry A W. Wavefront curvature limitations and compensation to polar format processing for synthetic aperture radar images[J]. Algorithms, 2006.
[11] Mao X, Zhu D, Zhu Z. Polar Format Algorithm Wavefront Curvature Compensation Under Arbitrary Radar Flight Path[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3):526-530.
[12] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005.
Bao Zheng, Xing Mingdao, Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005.(in Chinese)


