1 引言
雷达技术发明于上个世纪三十年代,其发射与接收具有特定调制形式的电磁波,通过信号处理手段来获得目标的距离、速度、方位等信息,具有全天时、全天候工作的优势,在军事领域和民用领域都得到了广泛的应用。根据雷达波形理论[1],雷达的距离分辨力取决于雷达波形的带宽。因此,现代雷达通常采用脉冲压缩技术,通过在脉冲内进行频率或相位调制获得大时宽带宽积信号来得到高距离分辨力,如使用最广泛的线性调频(Linear Frequency Modulation, LFM)信号。随着雷达技术的发展,在微动测量、目标识别、精确制导等诸多领域,人们对目标高精度测距的需求不断提升,这也意味着需要不断提高雷达波形的瞬时带宽。然而,瞬时带宽的提高对雷达系统硬件提出了很高的要求,主要表现为接收机中频和基带带宽增加、动态范围受限、模数转换模块采样频率提高、信号处理系统负荷增大、易受其他外辐射源干扰等[2]。于是,人们提出了合成带宽雷达体制以解决上述问题,在雷达领域[3- 4]和声纳领域[5]获得了广泛的应用。合成带宽雷达发射一组调制在不同载频上的脉冲串,通过带宽合成技术,在接收信号脉冲间通过逆离散傅里叶变换(Inverse Discrete Fourier Transform, IDFT)处理进行聚焦,来获得一维高分辨距离像(High Range Resolution Profile, HRRP)。合成带宽雷达体制对瞬时带宽要求低,同时可以根据带宽需要,通过带宽合成技术合成超大带宽以获得高距离分辨力,从而有效地解决了传统雷达体制的困扰。但是,合成带宽雷达体制也存在一定局限性,即当目标对雷达有径向运动分量时,径向速度引起的多普勒效应会在回波信号中产生相应的一次相位项和二次相位项,从而使HRRP移位和散焦,严重影响成像效果。
在早期的一些研究中,Gill在[6]中详细推导了径向速度引起的多普勒效应对HRRP的影响。为了估计速度或补偿速度带来的影响,通常雷达需额外发射一组窄带脉冲用来辅助测速,极大浪费雷达资源。文献[7]和[8]提出一种“V”形的频率步进方式,即连续发射两组脉冲串,其中一组载频从小到大顺序步进,另一组载频则从大到小顺序步进,通过对两组回波信号进行特定处理来推算速度信息从而进行补偿。但是,信号形式相对单一固定,容易被干扰;文献[9]给出了另一种求解速度信息的思路,即发射脉冲重复周期(Pulse Repetition Time, PRT)变化的序列,通过特殊设计的PRT解算目标速度信息,但需要在脉冲间改变发射脉冲PRT,对雷达硬件系统有特殊要求;文献[10]给出一种同频点脉冲串脉组间步进频信号,其在同频点脉冲串间通过脉冲多普勒处理进行速度估计,在脉组间来补偿速度的影响以合成具有大带宽的HRRP,但是相比于传统波形其要求更长的相参处理时间;文献[11]给出一种搜索算法,在一定速度范围内分多速度通道对回波信号进行补偿产生HRRP,从而选出最优速度补偿值,但其测速精度却决于算法对速度通道的划分精细程度,从而较高的测速精度会造成较大的计算量;文献[12]则是通过直接拟合回波相位斜率来推算目标运动信息,但利用相位信息进行处理对信噪比要求较高;基于压缩感知模型的速度解算方法在[13]中提出,但算法对目标稀疏性有一定要求,其应用场景有限;文献[14]则提出了一种特定的雷达波形和信号处理算法,可以以较高精度推算目标速度信息,但是与“V”形频率步进方式类似,信号形式单一固定,易被干扰。
本文提出了一种可实现自测速的频率跳变合成带宽波形设计及处理算法,其可以有效估计目标速度信息。在满足一定要求的前提下,波形可根据需求任意设计,相比于现有算法具有更高的通用性和灵活性。同时可以证明,“V”形频率步进方式与[14]中所提波形均为本文所提波形设计的特例。
2 波形设计及处理算法推导
本文考虑设计一种灵活通用的频率跳变方式,设发射信号s(t)为
(1)
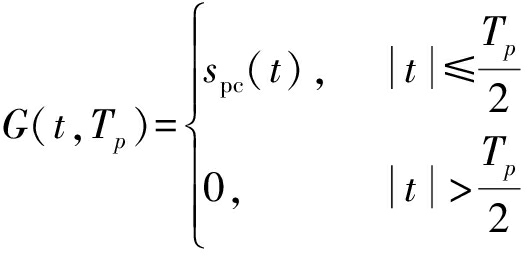
(2)
其中n表示脉冲序列号,N代表发射脉冲总数,t表示快时间轴,Tr表示PRT,Tp表示脉冲宽度, fc表示发射载频, fn为第n个发射脉冲的编码频率,spc(t)为简单脉冲信号或脉冲压缩信号(如LFM信号,相位编码信号等)。其中, fn可以表示为
fn=d(n)·Δf
(3)
其中Δf为脉冲间频率单位跳变量,d(n)为频率编码值,其取值范围为
d(n)∈{0,1,…,N-1}
(4)
为使模型推导过程简洁,以下仅考虑一个距离为R,速度为ν的点散射目标。假设不存在距离模糊情况,对第n个发射脉冲对应的接收信号进行对应频率(fc+fn)的下变频处理,并重新排列快时间轴,则第n个发射脉冲对应回波基带信号(幅度归一化)可以表示为
exp[-j 2πfnτ(n)]·exp[-j 2πfcτ(n)]
(5)
(6)
其中c为光速,ν的正负值代表目标速度方向,此处规定ν为正时表示目标有朝向雷达的径向速度,反之则相反。
设定参考信号为
(7)
则第n个发射脉冲对应的接收信号的匹配滤波结果为
sMF(t,n)=psf[t-τ(n)]·
exp[-j 2πfnτ(n)]·exp[-j 2πfcτ(n)]
(8)
其中
(9)
由上可知,psf(t)由(2)中的spc(t)决定,其代表了spc(t)匹配滤波输出形状,即point spread function, PSF。
接下来,我们考虑把所有或部分回波脉冲分为n1和n2两组等长的序列。我们选择合适的n1和n2,对sMF(t,n1)和sMF(t,n2)进行联合处理,考虑下式
h(t,n1,n2)=sMF(t,n1)·sMF(t,n2)
=psf[t-τ(n1)]·psf[t-τ(n2)]
·exp{-j 2π[d(n1)Δfτ(n1)+d(n2)Δfτ(n2)+
fcτ(n1)+fcτ(n2)]}
(10)
单独考虑上式相位项内中括号内式子,即
d(n1)Δfτ(n1)+d(n2)Δfτ(n2)+fcτ(n1)+fcτ(n2)
(11)
为从h(t,n1,n2)中的相位项推算速度信息,则需要满足式(11)中与ν相关的相位项具有线性性质,而与R相关的相位项为常量。此时即可以通过快速傅里叶变换(Fast Fourier Transform, FFT)聚焦速度信息。由此可得
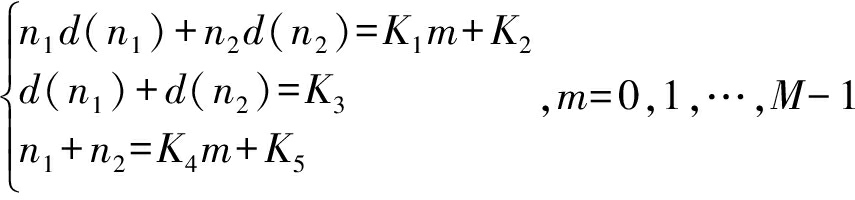
(12)
其中,m为线性变量,M为分成两组等长序列的长度,K1到K5为常量且需满足K1和K4不同时等于0。在实际应用中,一般希望利用到全部的回波数据进行处理,则通常取M=N/2。
将式(12)代入式(11)可得
d(n1)Δfτ(n1)+d(n2)Δfτ(n2)+fcτ(n1)+fcτ(n2)
(13)
将式(13)代入式(10),对m变量进行M点FFT后,目标速度信息会在速度维聚焦成对应的峰值。设聚焦点为kp,则由(13)可得
(14)
则此时可测定目标速度为
(15)
同时我们可以推导出速度分辨率为
(16)
最大不模糊速度为
(17)
同时可以证明,当满足
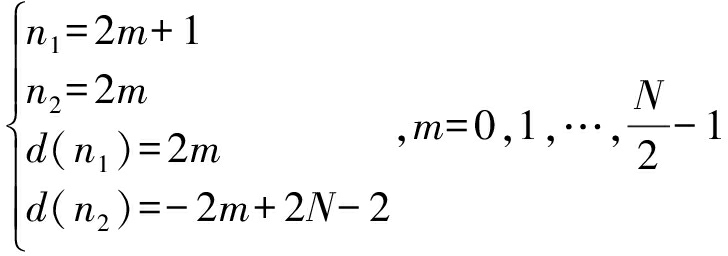
(18)
此时即为[14]中所讨论的特殊设计波形;当满足
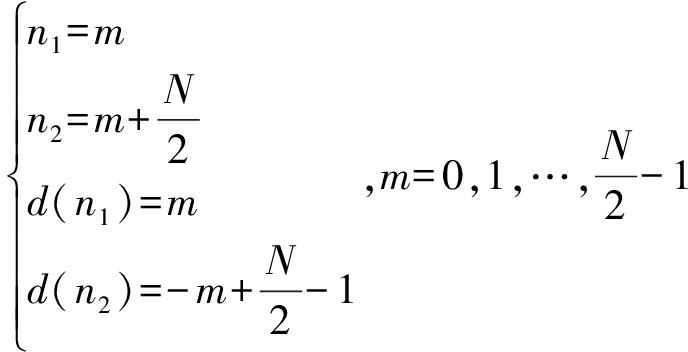
(19)
即为[7]及[8]中所讨论的“V”形频率步进信号。即[7- 8]和[14]中所讨论的波形均为本文波形设计方法特例。事实上,当设计波形满足式(12)形式时,按照本文处理算法均可实现速度的精确推算。
另外,以上模型是基于单点散射目标推导的。当考虑具有多散射点扩展目标时,我们一般假定所有多散射点径向速度一致,则以上模型可较易推广;当考虑多个具有不同速度的目标时,由于式(10)中存在乘法操作,则多目标回波间相乘后会产生交叉项,对速度估计会存在一定影响。由于本文采用先匹配滤波后相乘的处理算法,则每个目标是与其他速度目标的旁瓣进行相乘产生交叉项,因而可以通过设计失配滤波器来降低匹配滤波旁瓣,从而降低多速度目标回波间的相互影响。关于失配滤波器的一些设计方法读者可以参考[15-16]。
综上所述,当满足条件(12)时,所设计波形可通过本文设计算法有效求解目标速度信息,并可根据速度信息补偿对应一次相位项和二次相位项从而获得速度补偿后的HRRP。
3 仿真验证
这里,我们给出以下条件的仿真,设
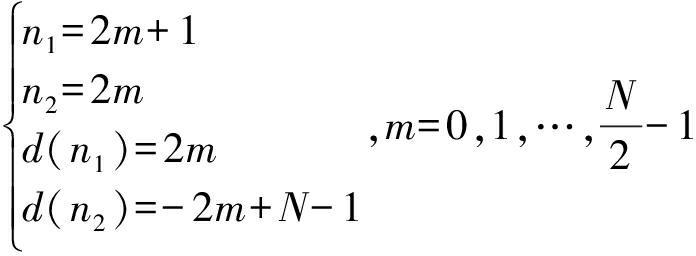
(20)
则对应
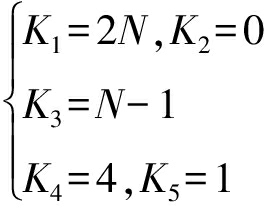
(21)
取![]() 由式(16)和(21)可计算对应速度分辨率为
由式(16)和(21)可计算对应速度分辨率为
(22)
为更简洁地展示该信号形式的时频示意图,这里暂时取N=16,其时频图示意图可表示为图1。
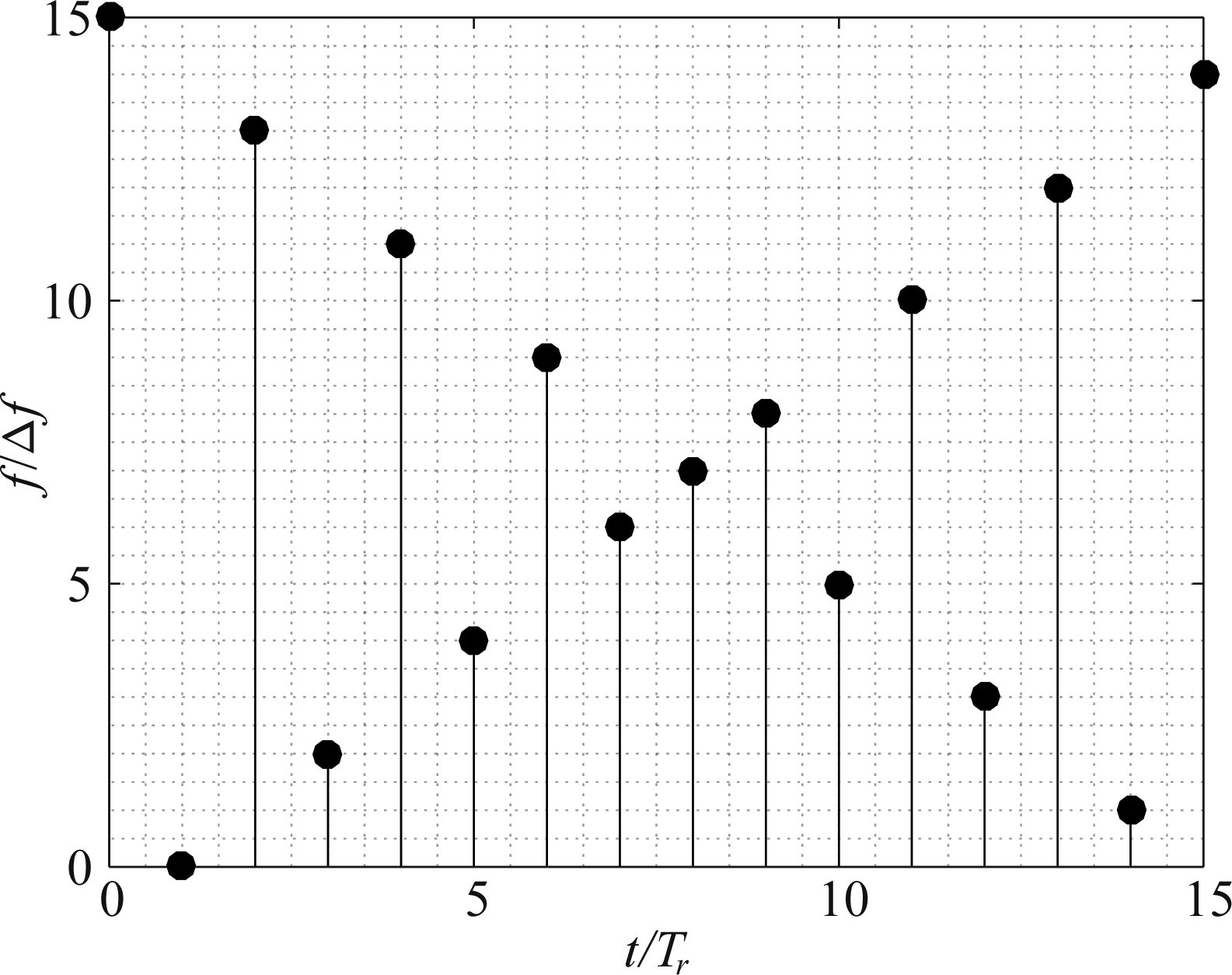
图1 信号时频示意图
Fig.1 Time-frequency schematic of the signal
由式(22)可知,我们可以通过增大N来提高雷达速度分辨力,则在本仿真中N取120。不失一般性的,我们取式(2)中spc(t)为LFM信号,即
spc(t)=exp(jπKt2)
(23)
(24)
其中,K为LFM信号调频斜率,B为LFM信号带宽。仿真实验中,我们设定波形相关参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
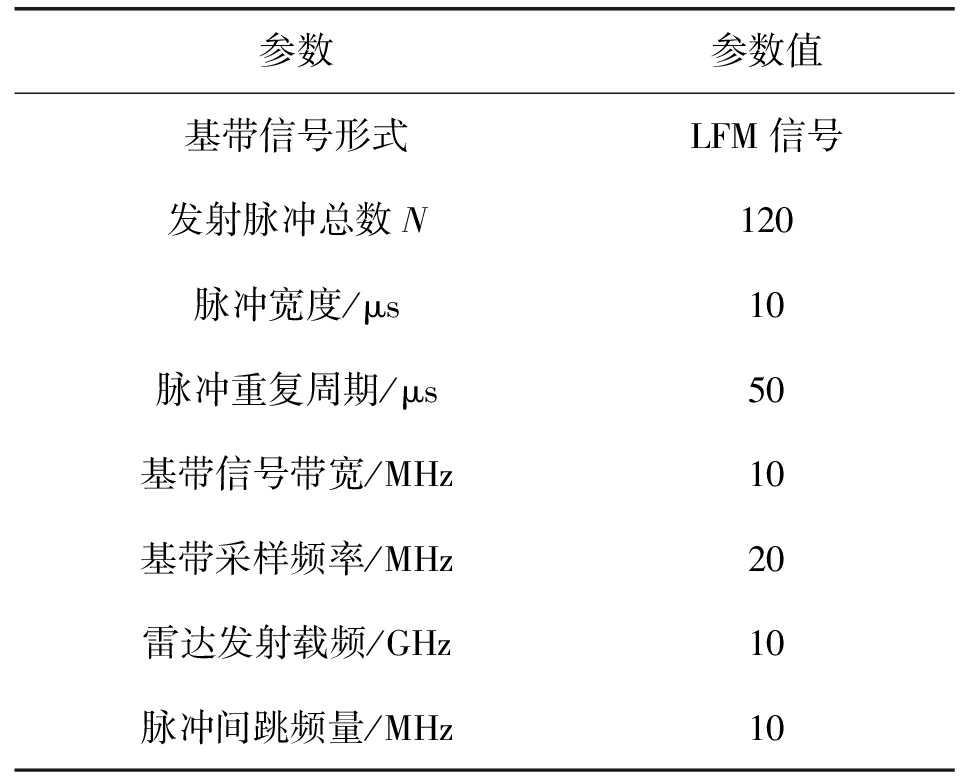
参数参数值基带信号形式LFM信号发射脉冲总数N120脉冲宽度/μs10脉冲重复周期/μs50基带信号带宽/MHz10基带采样频率/MHz20雷达发射载频/GHz10脉冲间跳频量/MHz10
为测试波形及处理算法性能,仿真中设定背景噪声形式为加性高斯白噪声,并设定3个点散射目标,其具体参数如下:
表2 目标参数
Tab.2 Targets parameters

目标序号径向距离/km径向速度/(m/s)脉压前信噪比/dB11.45251022.14-202033.84105
考虑到LFM信号的PSF具有较高距离维旁瓣,且速度维直接聚焦计算结果为多个sinc函数的叠加结果,速度维旁瓣水平同样较高。较高的旁瓣会导致弱散射目标淹没在强散射目标的高旁瓣之中,影响目标检测与识别。则本仿真中,考虑在距离维匹配滤波和速度维聚焦前加权Chebyshev窗函数以降低距离维旁瓣和速度维旁瓣。若已知一定先验信息,读者同样可以参考[15]和[16]中的方法设计特定的失配滤波器或窗函数来降低区域性的旁瓣,具有更低的信噪比损失和更小的主瓣展宽,本文不再赘述。
为比较速度维输出在不同窗函数下算法性能,我们在无噪声条件下对单点目标输出信号的特征(包括输出峰值旁瓣、主瓣宽度等)进行了统计分析,相关结果如图2及表3所示。
由图2可知,对于矩形窗函数而言,其速度维输出为原始辛格函数形式。此时,其峰值旁瓣约为-13.3 dB,对应的速度分辨率可由式(22)计算得到,约为1.2 m/s。为降低速度维输出峰值旁瓣,考虑加权常用的窗函数,其代价为主瓣宽度的不同程度的展宽,即相应的速度分辨率的损失。由图2及表3可知,峰值旁瓣越低,对应的主瓣宽度越宽,即速度分辨率越低。在实际应用中,设计者需权衡二者的关系,选择合适的窗函数进行峰值旁瓣抑制。
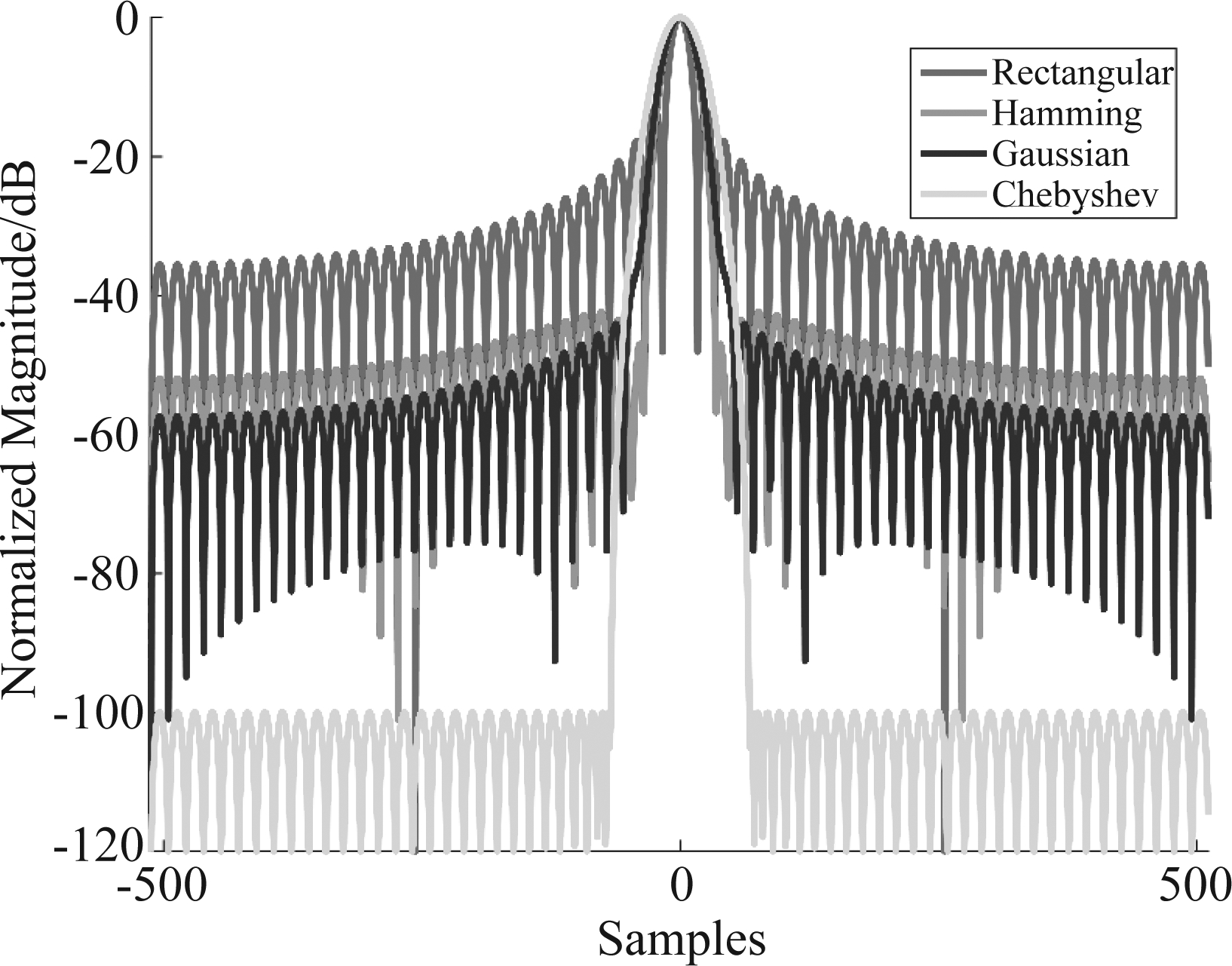
图2 加窗性能比较
Fig.2 Performance comparison with different weights
表3 加窗性能比较
Tab.3 Performance comparison with different weights
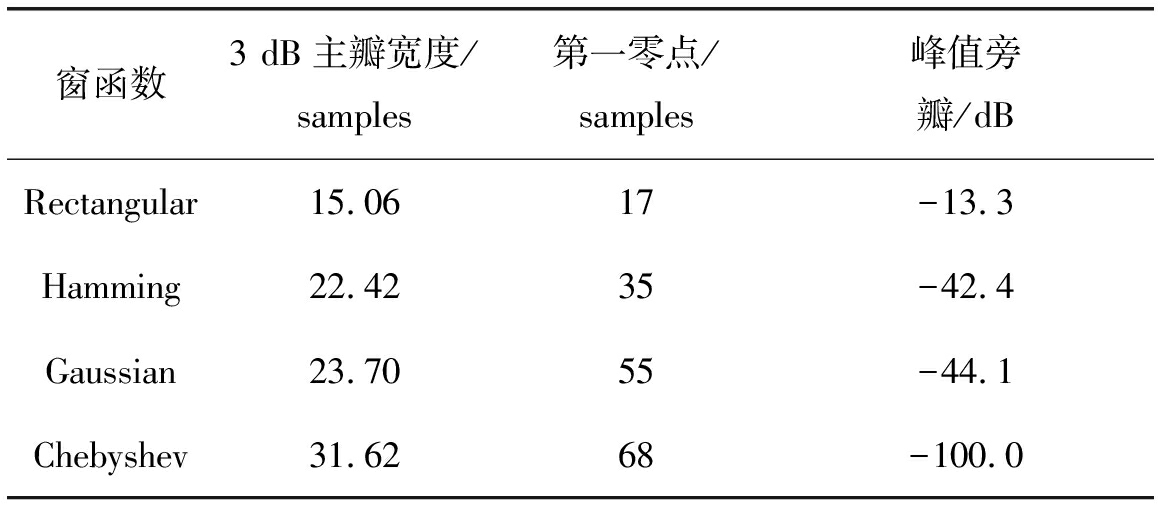
窗函数3dB主瓣宽度/samples第一零点/samples峰值旁瓣/dBRectangular15.0617-13.3Hamming22.4235-42.4Gaussian23.7055-44.1Chebyshev31.6268-100.0
按照第2部分所提波形及对应处理算法,将信号进行基带下变频、匹配滤波等处理后,将n1序列脉冲压缩结果与n2序列脉冲压缩结果相乘,在速度维进行FFT可得结果如下图所示。图3中仿真结果为速度维加权Chebyshev窗函数结果。
根据图3的处理结果可知,三个目标速度信息均以较高信噪比准确测算得到,进而我们可以根据所测速度信息对目标回波进行进一步的处理,包括速度补偿、获得HRRP等。
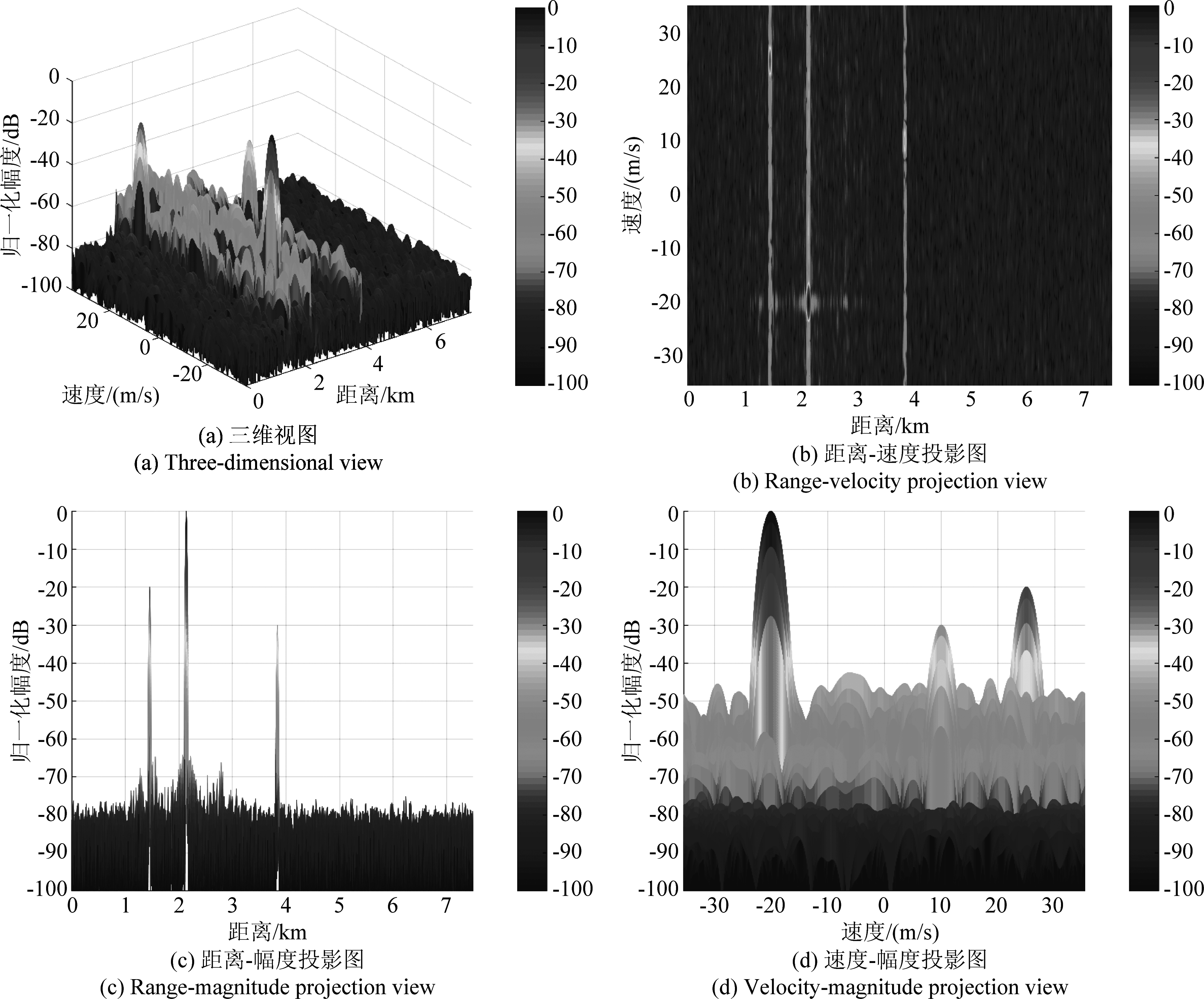
图3 仿真结果
Fig.3 Simulation results
4 结论
本文提出一种可实现自测速的频率跳变合成带宽波形设计及处理算法。该波形设计方法相比于现有算法具有更高的通用性和灵活性,可以通过改变等式(12)相关常数变量快捷灵活地设计波形跳变形式,具有较强的抗干扰能力。可以证明,“V”形频率步进信号与[14]中所提波形仅为本文所提设计方法的特例,故本文设计方法具有更好的普适性。另外,本文所提处理算法可以有效估计目标速度信息。相关仿真结果表明,本文所提设计波形及其处理算法在信噪比为5 dB等较低信噪比下仍可以有效测量目标距离、速度信息,同时具有较高的测量精度和准确度,蕴藏较大实用潜力与价值。
[1] Levanon N, Mozeson E. Radar Signals[M]. Hoboken, New Jersey, USA, John Wiley & Sons, 2004: 7-13.
[2] 刘一民. 合成带宽雷达高分辨成像与目标速度估计[D]. 北京:清华大学, 2009: 1-2.
Liu Yimin. High Range Resolution Profiling and Velocity Estimation in Synthetic Bandwidth Radar[D]. Beijing: Tsinghua University, 2009: 1-2.(in Chinese)
[3] Liu Y, Shan T, Feng Y. Research on the range side lobe suppression method for modulated stepped frequency radar signals[C]∥AIP Conference Proceedings, 2018: 1967.
[4] Huang X, Yang M, Liu M, et al. An efficient and robust frequency estimator dealing with short-observation under-sampled waveforms[J]. IEEE Access, 2018(6): 48021- 48029.
[5] Wang F, Du S, Sun W, et al. A method of velocity estimation using composite hyperbolic frequency-modulated signals in active sonar[J]. Journal of the Acoustical Society of America, 2017, 141(5): 3117-3122.
[6] Gill G S. Simultaneous pulse compression and Doppler processing with step frequency waveform[J]. Electronic Letters, 1996, 32(23): 2178-2179.
[7] 刘峥, 张守宏. 步进频率雷达目标的运动参数估计[J]. 电子学报, 2000(3): 43- 45.
Liu Zheng, Zhang Shouhong. Estimation of Target Motion Parameter in a Stepped Frequency Pulses Radar[J]. Acta Electronica Sinica, 2000(3): 43- 45.(in Chinese)
[8] Wang F, Long T. A new method of velocity estimation for inverse V-shape stepped frequency signal[C]∥2006 CIE International Conference on Radar, 2006: 1-3.
[9] Chen H, Liu Y, Jiang W, et al. A New Approach for Synthesizing the Range Profile of Moving Targets via Stepped-Frequency Waveforms[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 406- 409.
[10] Yang L, Su W, Gu H. Synthetic Ultra-wideband Radar Range Profile Based on Stepped Frequency Pulse Trains[C]∥Proceedings of 2010 IEEE International Conference on Ultra-Wideband, 2010.
[11] Kathree U, Nel W, Van Rensburg V, et al. Investigation of Hopped Frequency Waveforms for Range and Velocity Measurements of Radar Targets[C]∥2015 IEEE Radar Conference, 2015: 475- 480.
[12] Ma C, Xu X. A Motion Compensation Technique for Stepped-frequency Radar with Phase Slope Analysis[C]∥Proceedings of 2011 IEEE CIE International Conference on Radar, 2011(2): 1543-1546.
[13] Liu Z, Wei X, Li X. Low sidelobe robust imaging in random frequency-hopping wideband radar based on compressed sensing[J]. Journal of Central South University, 2013, 20(3): 702-714.
[14] Isoda K, Hara T. Doppler Velocity Measurement Method with a Second-Time-Around Echoes Suppression for Synthetic Bandwidth Radars[C]∥Proceedings of the 8th European Radar Conference, 2011: 134-137.
[15] Sun Y, Liu Q, Cai J, et al. A Novel Weighted Mismatched Filter for Reducing Range Sidelobes[J]. IEEE Transactions on Aerospace and Electronic Systems (Early Access), 2018: 1-1.
[16] Sun Y, Liu Q, Cai J, et al. A Novel Method for Designing General Window Functions with Flexible Spectral Characteristics[J]. Sensors, 2018, 18(9): 3081.



