1 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)技术可以主动发射电磁波信号(微波)且不受云层、雨雪天气的影响,具有全天时、全天候、远距离探测的特点。传统的SAR二维成像算法可对观测区域在方位和斜距平面上进行二维高分辨力成像,其距离向上的高分辨力是通过发射大时宽带宽积的线性调频信号结合脉冲压缩来实现,其方位向上的高分辨力则是通过雷达运动构成虚拟的合成孔径来实现。然而,传统SAR成像系统的观测视角单一、基于点目标模型和采用线性成像处理算法等特点使其不能反演线目标和面目标的完整特性,在对城区等人造目标较多的复杂区域成像时,存在目标边缘不连续、鬼影等现象,与同分辨率光学图像差距较大,不能完全满足实际应用的要求。
复杂场景(特别是城区)中往往存在大量线目标。线目标是指横向尺寸小于分辨单元尺寸的线状结构(如水陆界线,建筑物轮廓等)。为了改善SAR成像的分辨率,文献[2]在层析SAR成像中,利用稀疏重构方法提高了高度维的分辨率;文献[3]针对聚束SAR成像,建立了横向分辨的稀疏模型,讨论了慢时间域的随机采样,利用稀疏重构方法实现成像,考虑在缺失部分雷达回波的情况下,利用稀疏重构方法实现方位向上的良好分辨。然而,上述研究均是基于点散射模型进行的,由于SAR成像所采用的点目标模型不能准确表征线目标的散射特性,这种模型的失配导致目标在SAR图像中表现为一些不连续的散射点。为此,基于散射模型的高分辨成像研究受到了越来越多的重视。Julie Ann 基于几何绕射理论,提出了多种典型几何体的电磁散射模型[6-7]。文献[8-11]基于电磁散射模型开展了散射模型参数反演及高分辨成像的研究。
本文研究了基于多基地SAR的线目标的参数反演与重建方法。线目标具有方向依赖性,其成像结果,很大程度上取决于雷达方位角与线目标的关系。如果雷达经过了直线段的法线方向,则线目标可以完整显现。如果雷达观测位置未经过线的法线方向,则线目标在SAR图像中表现为两个端点。为了解决该问题,本文从空间谱的角度对线目标SAR成像特征进行了分析,并提出了基于多基地SAR的线目标参数反演与图像重建方法。实验表明,在不同信噪比下,该方法可以有效估计出线目标的参数,实现线目标的完整重建。
2 基于几何方法的线目标参数化散射模型
经典的合成孔径雷达采用点散射模型。该模型采用离散点来表示目标,其认为场景回波信号表示为一系列散射点回波信号的叠加。如果设被观测区域散射点的散射强度为ρ(xi,yi),发射信号到接收机的时延为τ,发射信号频谱形式为S0(τ, f),则雷达回波信号可表示为:
(1)
采用离散点表示目标时,散射模型精度随离散点间距减小而提升。可以预见,当离散点间距无限接近时,散射回波模型将具有较好的精度。因此,利用微积分的思想,可以将上式写为:
(2)
在上式的积分结果中,被观测目标的几何信息也包含在其中。若用对应参数表示目标的几何信息,即可得到目标参数化的散射模型。在散射模型建立前,为了简化建模复杂度,采用了如下假设:远场假设,即雷达发射机与接收机到目标距离足够远,其电磁波可视为平面波;忽略雷达接收机与发射机间的同步误差;接收机与发射机间不存在速度扰动;启—停假设,即同一脉冲发射与接收时间内,接收机与发射机不存在相对运动。
场景中的线目标可以用中心点(x,y),直线段长度L,倾角α来表示。其示意图如图1所示,其中θ1与θ2分别为接收机、发射机和原点的连线与x轴夹角。
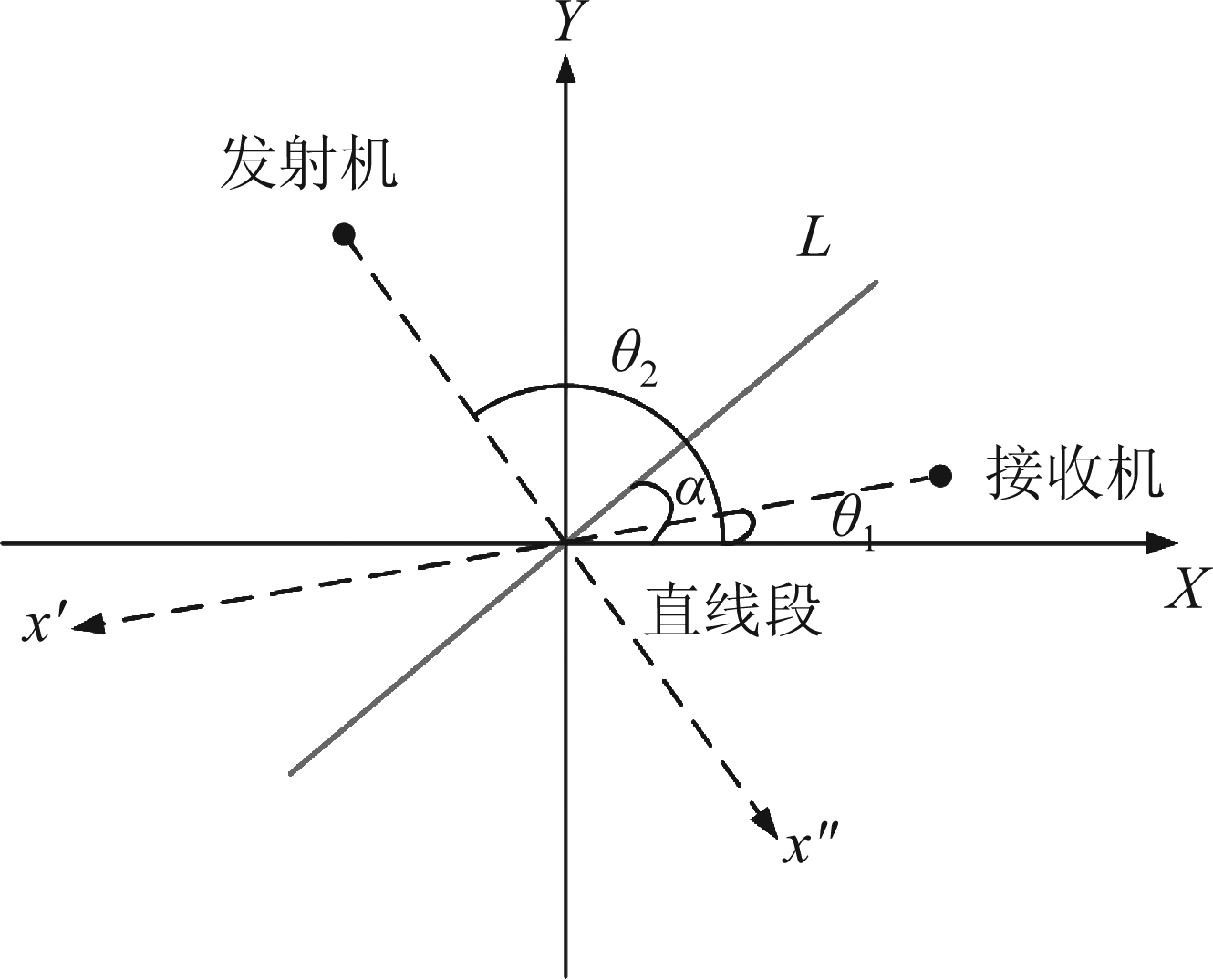
图1 直线段示意图
Fig.1 Linear objects
沿发射机、接收机与原点的连线分别建立局部坐标系x′与x″。在远场假设的条件下,发射信号到目标区域中任意一点的斜距可表示为Rt+x″,Rt为发射机到观测区域中心即原点的距离。同理,目标反射回波与接收机的斜距可表示为Rr+x′。此时式(2)可表示为:
(3)
上式为线积分,化简得到:
exp[-jk(Rt+Rr)]
(4)
其中φ1=180°-θ1+α,φ2=180°-θ2+α,k=2πf/c。
3 多基地SAR线目标参数反演与图像重建
3.1 线目标散射特征
在合成孔径雷达不同观测角度下,线目标的散射特征变化很大。如果雷达经过直线段法线方向则称为主瓣成像,未经过法线方向称为副瓣成像。则主瓣成像时,直线段在SAR图像中为一条完整的直线;在副瓣成像时,直线段在SAR图像中只有两个端点可见。如果在场景中心处放置一长3 m,倾角为10°的直线段,设置雷达方位角分别为85°~105°(主瓣成像),70°~90°(副瓣成像),则SAR仿真结果如下。

图2 直线段成像结果
Fig.2 Linear target SAR image
可以从基于空间谱的SAR成像原理理解这一现象。首先我们假设被成像目标的RCS为σ(x,y),则其空间谱可表示为:
(5)
典型的回波信号可表示为:
(6)
经过正交解调与相位补偿后,其频谱为:
(7)
x′轴为原观测坐标系的x轴经过旋转所获得的。根据直角坐标系旋转公式,x′轴的坐标与原坐标系坐标存在如下关系:
x′=xcos θ-ysin θ
(8)
因此回波频谱可表示为:
(9)
对比式(9)与式(5)可以发现,单基地SAR回波相当于在目标空间谱![]() 处采样的结果,其中θ为雷达的方位角。SAR的回波相当于目标空间谱的部分采样,那么360°圆迹SAR与2直线段空间谱的关系如图3所示。
处采样的结果,其中θ为雷达的方位角。SAR的回波相当于目标空间谱的部分采样,那么360°圆迹SAR与2直线段空间谱的关系如图3所示。

图3 直线段空间谱及SAR对其采样示意图
Fig.3 Linear target spatial spectrum and SAR sampling diagram
接下来讨论单基地情况下直线段空间谱采样与成像结果之间的关系。
表1 单基地SAR仿真参数
Tab.1 Simulation parameters of monostatic SAR
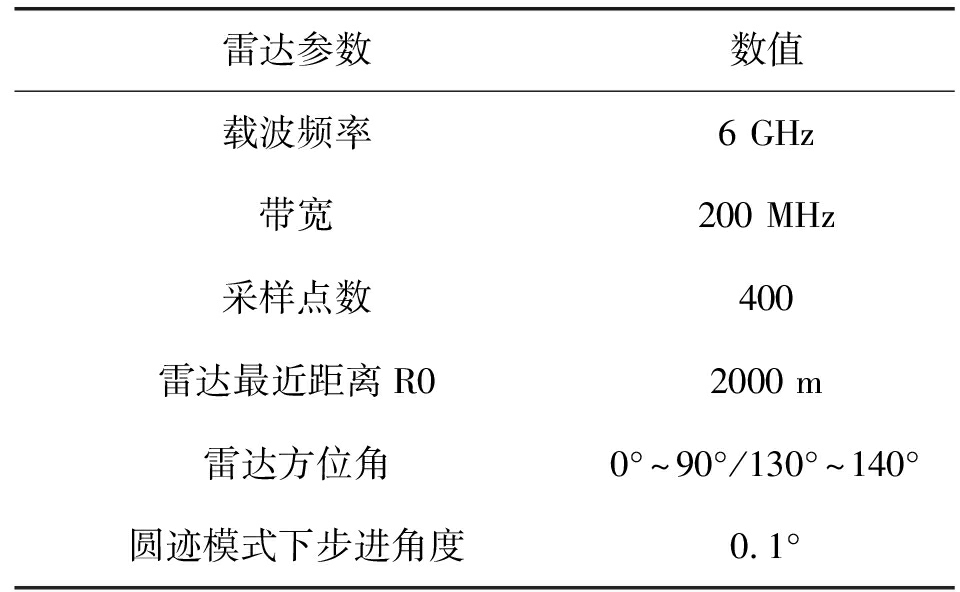
雷达参数数值载波频率6GHz带宽200MHz采样点数400雷达最近距离R02000m雷达方位角0°~90°/130°~140°圆迹模式下步进角度0.1°
当单基地雷达方位角在0°~90°时,其空间谱采样示意图与BP成像结果如图4所示。
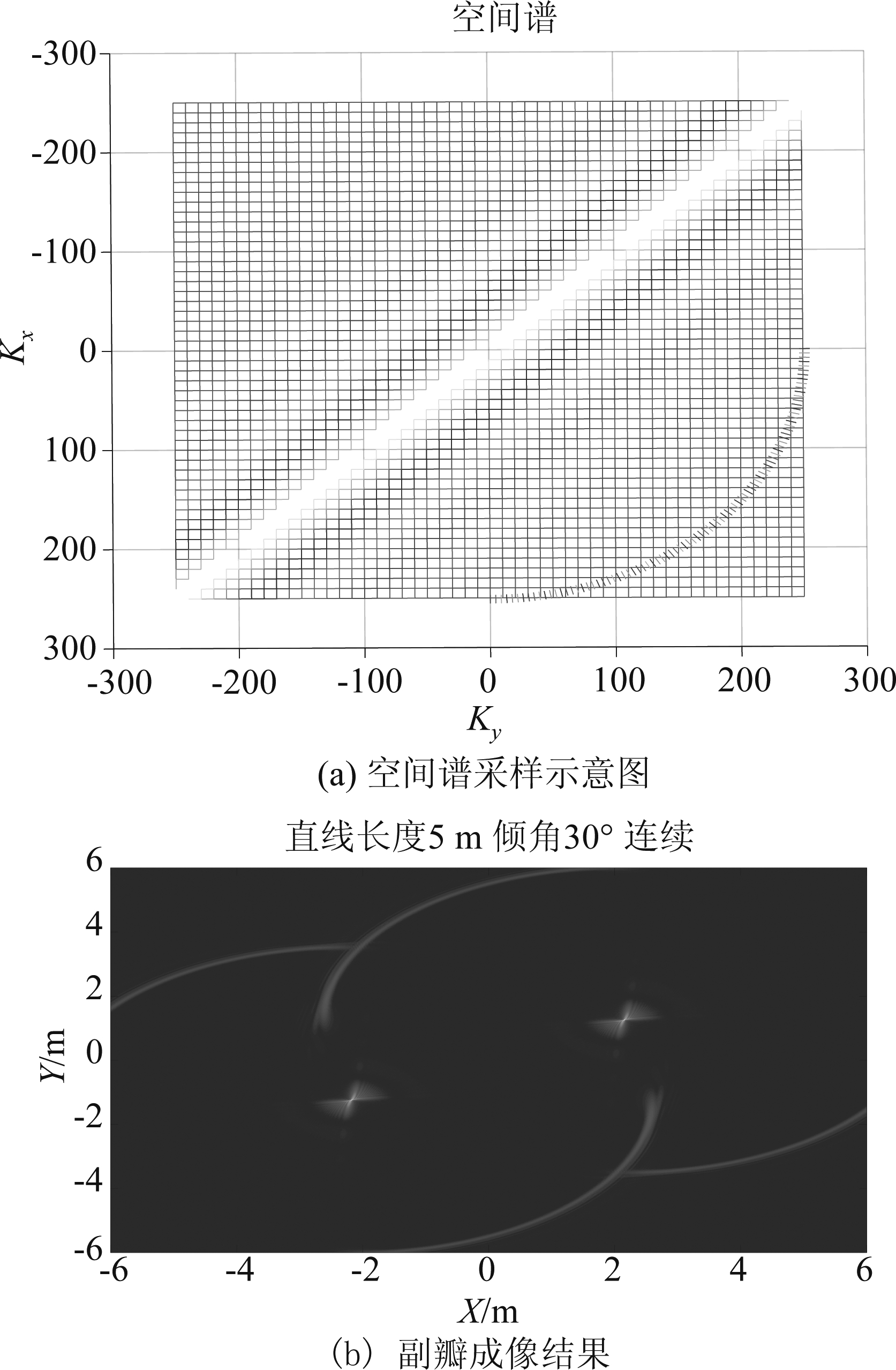
图4 未经过法线时空间谱采样示意图及成像结果
Fig.4 Spatial spectrum sampling diagram and imaging result at sidelobe observation angle
造成成像结果为线段的两个端点的原因是方位角为0°~90°的圆迹SAR只是对空间谱副瓣的部分采样,未能采样到空间谱的主瓣特征。因而成像的结果丢失了大部分直线段的特征。当单基地雷达方位角在130°~140°时,其空间谱采样示意图与BP成像结果如图5。
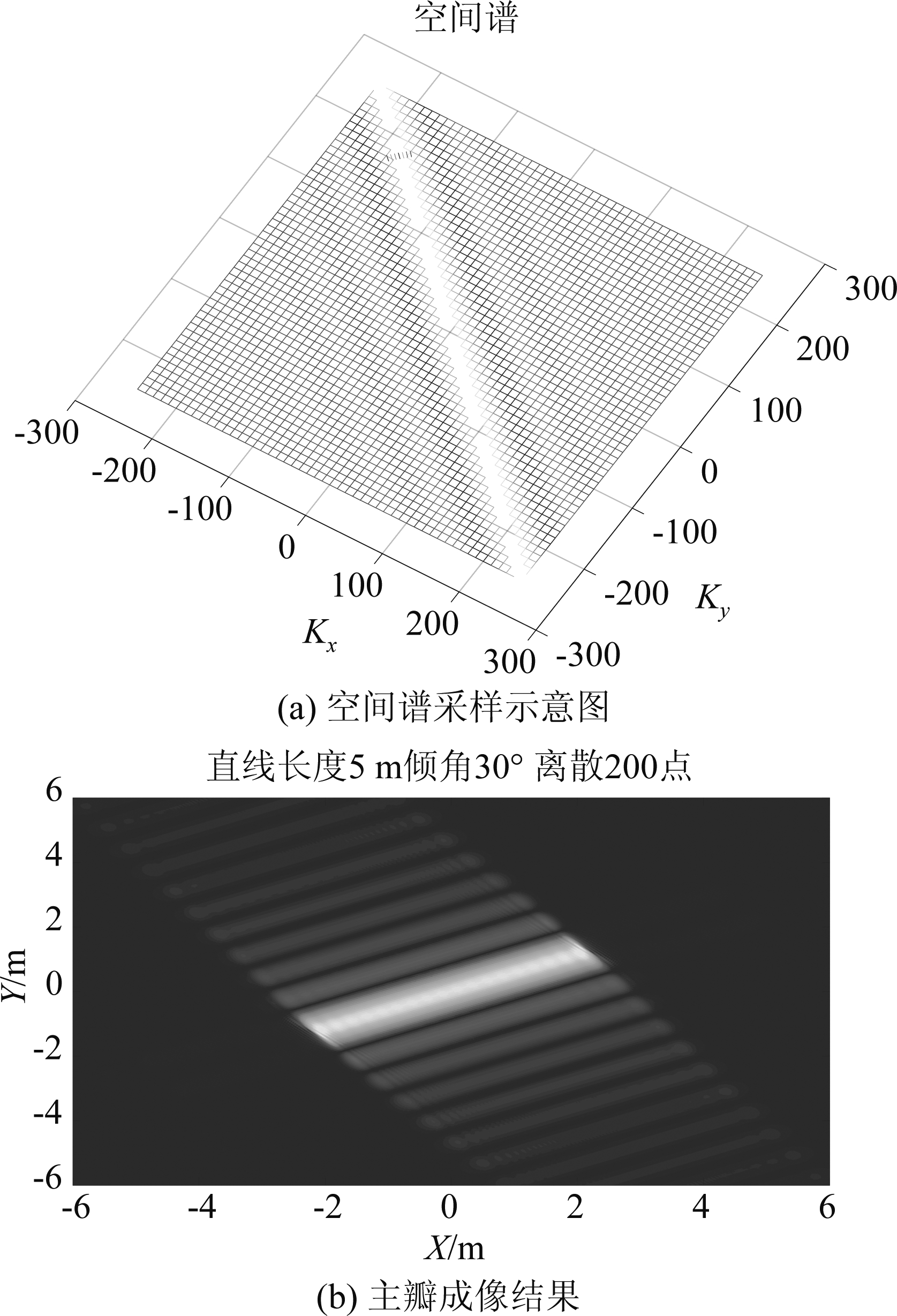
图5 经过法线方向时空间谱采样示意图及成像结果
Fig.5 Spatial spectrum sampling diagram and imaging result at main lobe observation angle
从上述的讨论中我们可知,在雷达系统参数一定的情况下,直线段目标成像的特征,很大程度上取决于雷达方位角与直线段倾角的关系。如果雷达经过了直线段的法线方向,则直线段特征明显。如果雷达未经过直线段的法线方向,则直线特征不明显,仅仅表现为两个端点。因此,要想获得尽可能好的成像效果与反演结果,我们就需要尽可能的使雷达轨迹经过被观测直线段的法线方向。然而在现实观测环境中,直线段的倾角不可能总是满足上述关系,对于复杂的存在大量线目标的观测区域中,直线段的倾角也不尽相同,单基地雷达系统由于视角的单一性,不可能经过所有直线段目标的法线方向。因此对于单基地雷达系统而言,其成像结果往往会丢失线目标的详细特征。由于具有多视角的优势,多基地SAR能在一定程度上克服单基地SAR的局限。双基地回波频谱在经过正交解调与相位补偿后为:
(10)
带入直角坐标系旋转公式,与空间谱的表达式(5)相比较可发现,双基地SAR 回波相当于在目标空间谱![]() 处采样的结果,其中θ′与θ″分别为发射机与接收机的方位向角度。设接收机固定的双基地SAR仿真参数如下:
处采样的结果,其中θ′与θ″分别为发射机与接收机的方位向角度。设接收机固定的双基地SAR仿真参数如下:
表2 双基地SAR仿真参数
Tab.2 Bistatic SAR simulation parameters
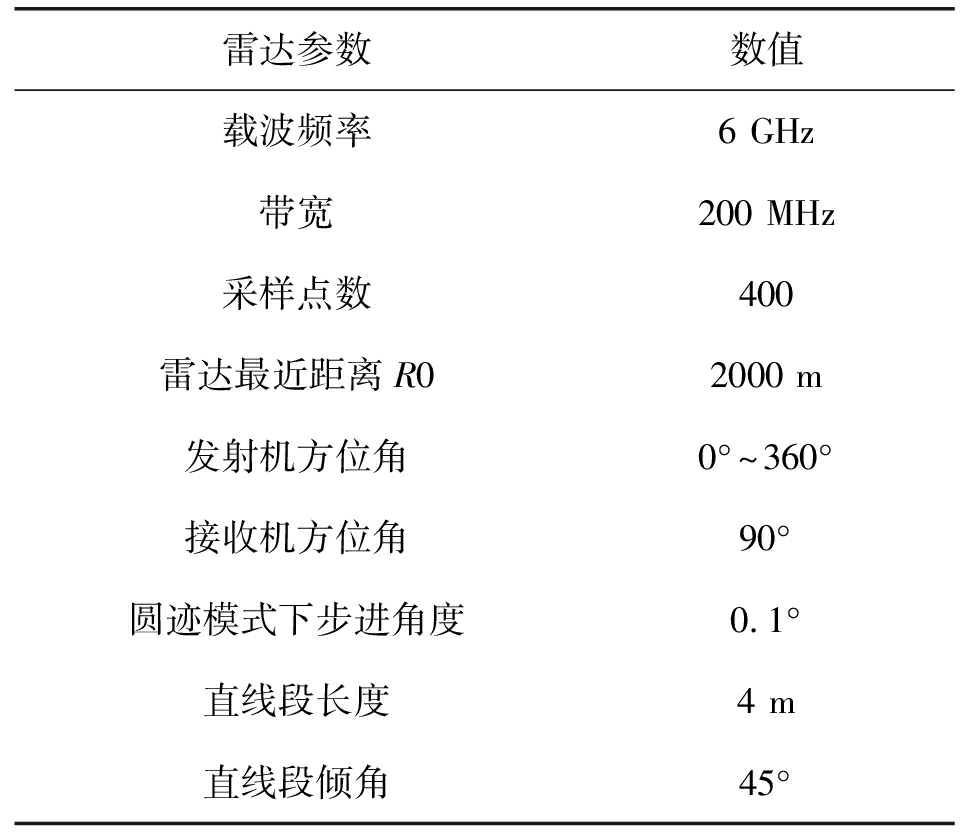
雷达参数数值载波频率6GHz带宽200MHz采样点数400雷达最近距离R02000m发射机方位角0°~360°接收机方位角90°圆迹模式下步进角度0.1°直线段长度4m直线段倾角45°
其空间谱采样示意图如图6。接收机固定的双基地雷达系统对空间谱的采样圆的曲率更低,因而在发射机方位角0°~360°的范围内,可以采集到直线段空间谱主瓣的方位角的范围更大,其所占整个圆环的比例也更大。因此,接收机固定的双基地雷达系统对任意倾角的直线段目标进行采样,有更大的概率采集到直线段空间谱的主瓣,因而更容易获得直线段的特征。
如果我们围绕被成像直线段每隔45°放置一个固定的接收机。则当发射机方位角范围为0°~360°及45°~135°时,对直线段空间谱的采样示意图如图7。
从图7可以看出,接收机固定的一发多收多基地雷达系统,其发射机只需飞行较小范围的方位角即可采集到直线段的主瓣。可以预期,接收机固定的一发多收多基地SAR对直线段的参数估计将会有更好的精度。
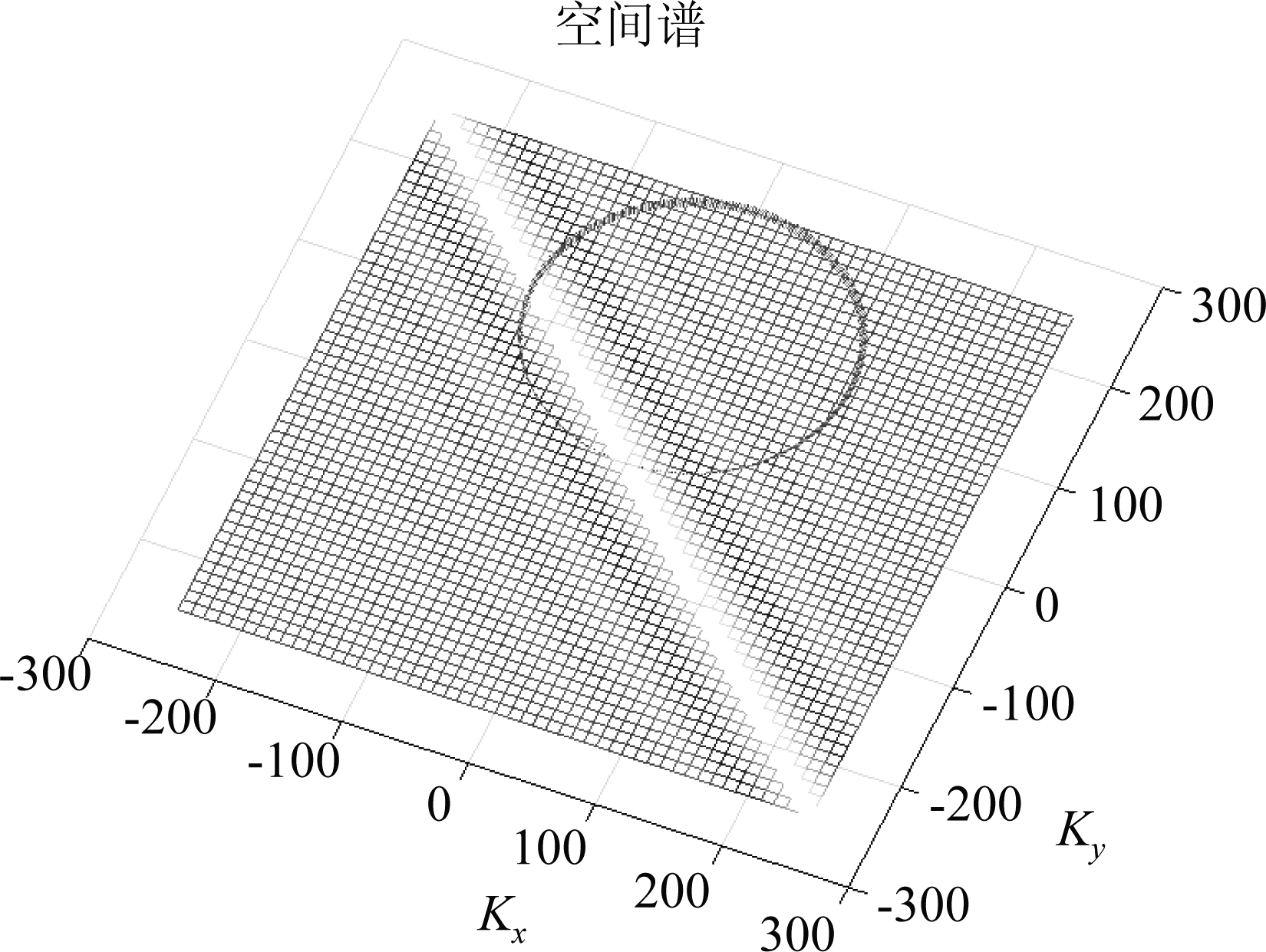
图6 接收机固定的双基地SAR对直线段的空间谱采样示意图
Fig.6 Spatial spectrum sampling diagram of linear segment for bistatic SAR with fixed receiver
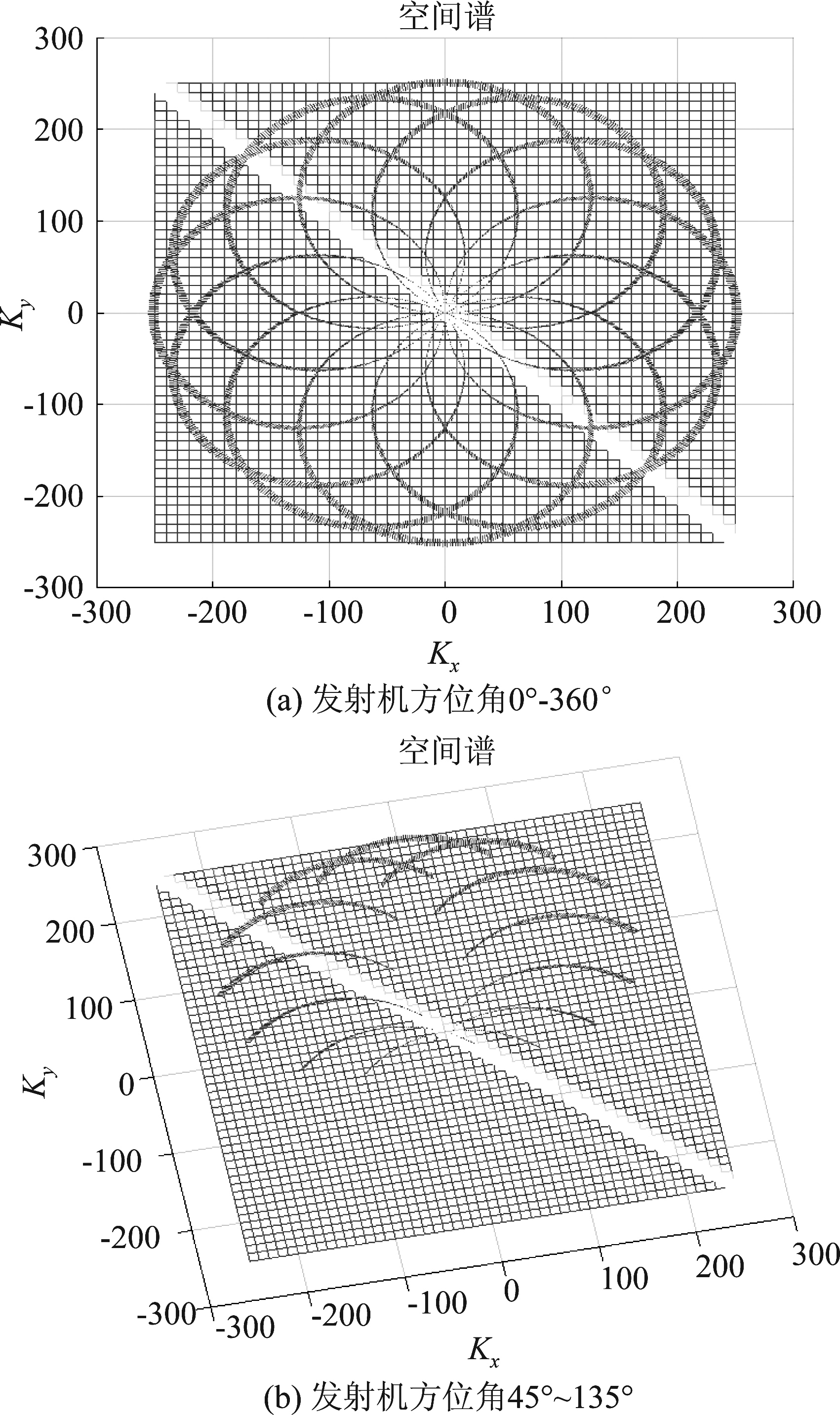
图7 发射机方位角范围为0°~360°及45°~135°的直线段空间谱采样示意图
Fig.7 Spatial spectrum sampling diagram of linear segment in transmitter azimuth range of 0°~360° and 45°~135°
3.2 多基地SAR线目标参数反演
接收机固定的一发多收多基地雷达系统,其发射机只需飞行较小范围的方位角即可采集到直线段的主瓣。可以预期,接收机固定的一发多收多基地SAR对直线段的参数估计将会有更好的精度。多基地SAR可以等效为数组双基地SAR。对于每一个双基地SAR,我们可以依照最小二乘估计方法对直线段进行参数估计。由此获得的多个等效双基地雷达系统的参数估计结果再经过判决等操作即可获得最终的参数估计结果。
对每个等效的双基地雷达系统,设直线段的长度符合高斯分布,直线段的倾角符合均匀分布。设x(φT,φR, f)为雷达接收到的回波信号的频谱,S(φT,φR, f;ϑ)为根据模型所生成的回波模板。其中α,L分别为线目标的倾角与长度。接下来的任务就是寻找最佳的α,L,使下式的值最小:
(11)
其中ϑ={x,y,L,α}。为了减少计算量,利用最小外接矩形法所获得粗参数作为遍历的中值,在中值附近做多点遍历并计算式(11)的值,使(11)最小的α,L 参数即为该等效双基地雷达系统的参数估计结果。在获得了全部的等效双基地雷达系统对直线段的参数估计结果后,选取使式(11)最小的参数集α,L 即为最终的参数估计结果。算法流程图如图8。
设置接收机固定的一发多收多基地SAR的发射机方位向角度75°~105°,接收机固定5部,其方位角分别为0°、45°、90°、135°、180°。雷达系统示意图如图9所示。
在接收机回波中添加高斯白噪声,信噪比的统计采用峰值信噪比。设待估直线段的倾角与长度为随机变量,角度参量为0°~180°的均匀分布,长度参量满足最小值0.4,最大值4,均值2,方差1的高斯分布。错误判决门限为,角度误差大于5°,长度误差大于目标真值长度的10%。每种情况下测试100组数据,仿真参数如表3。
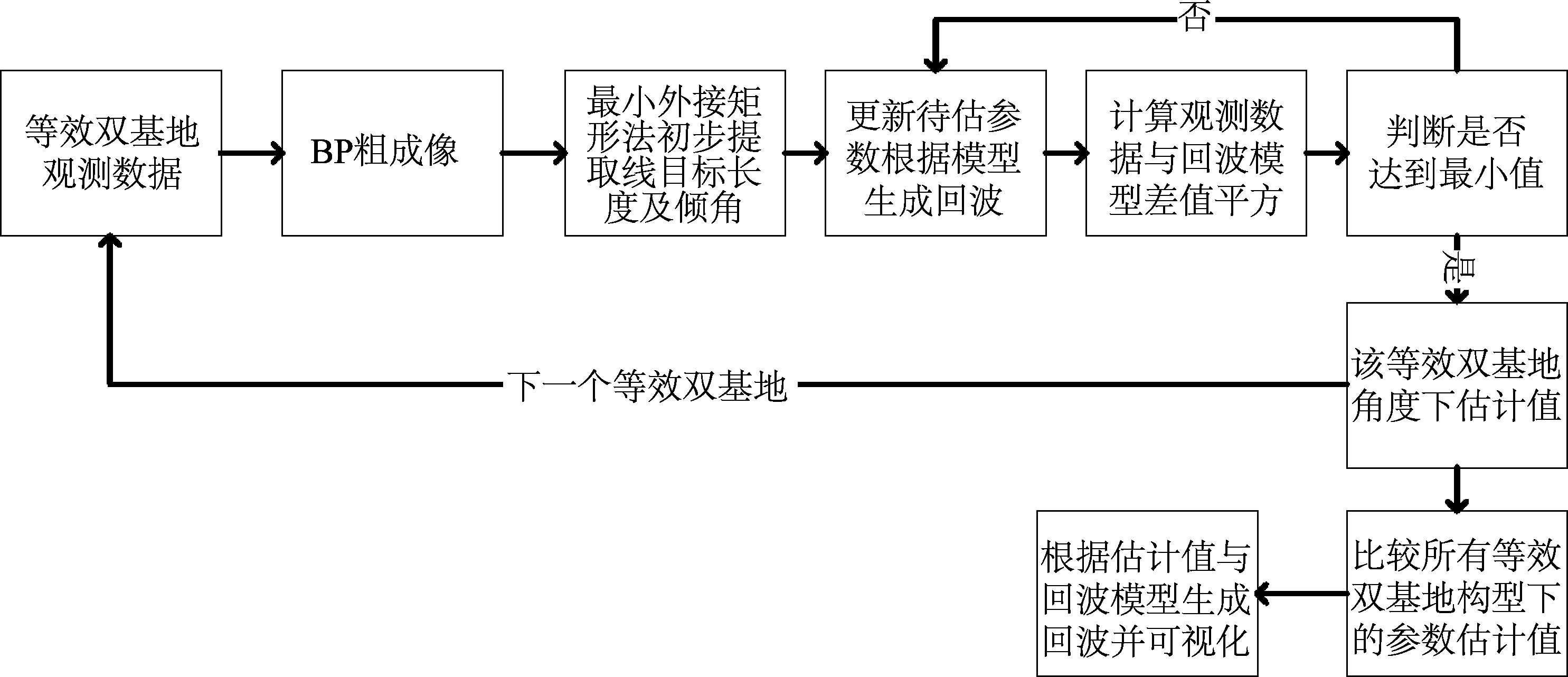
图8 反演算法流程图
Fig.8 Flow chart of inversion algorithm
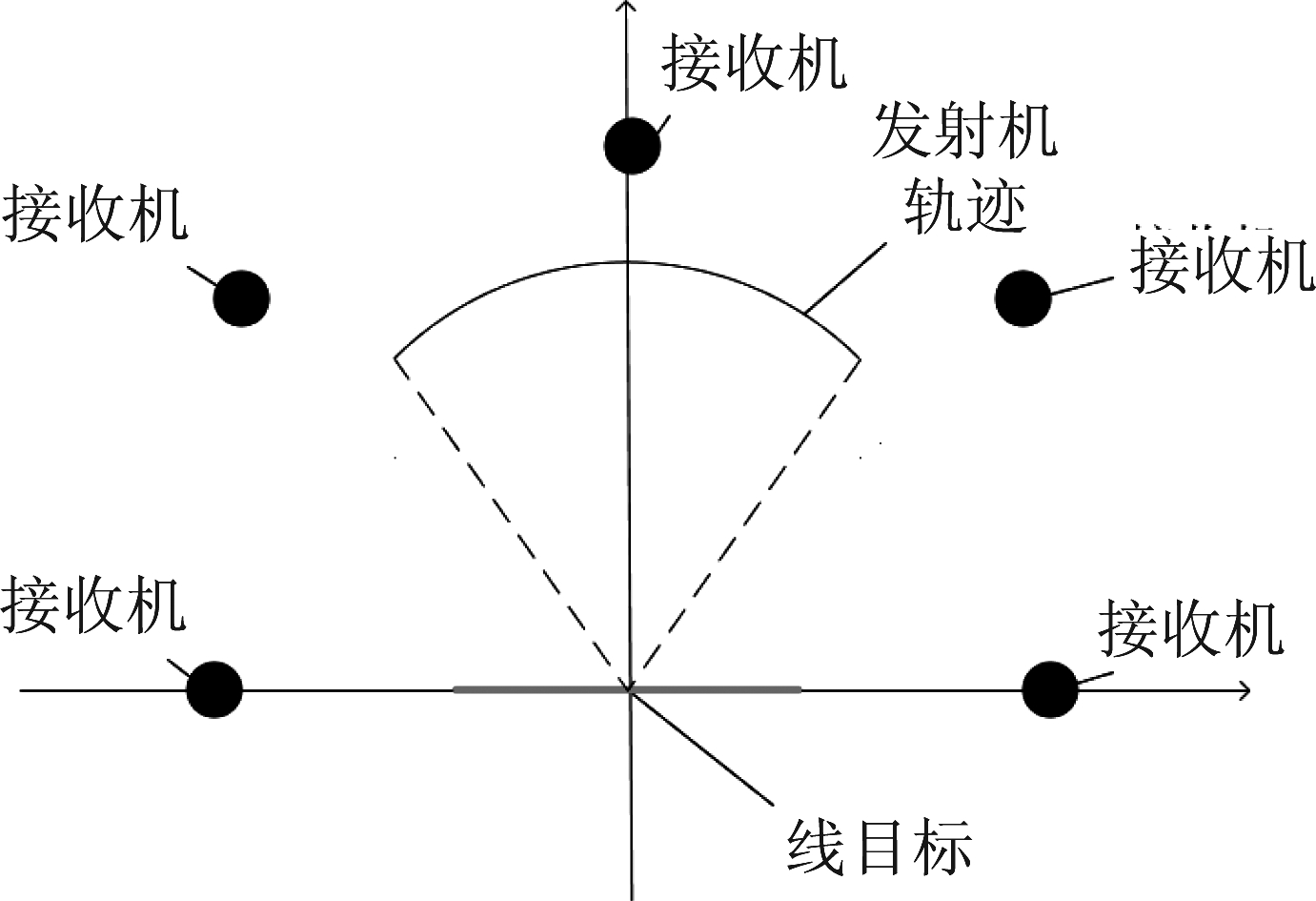
图9 多基地雷达示意图
Fig.9 Multistatic radar diagram
表3 参数反演仿真参数
Tab.3 Parameter inversion simulation parameters
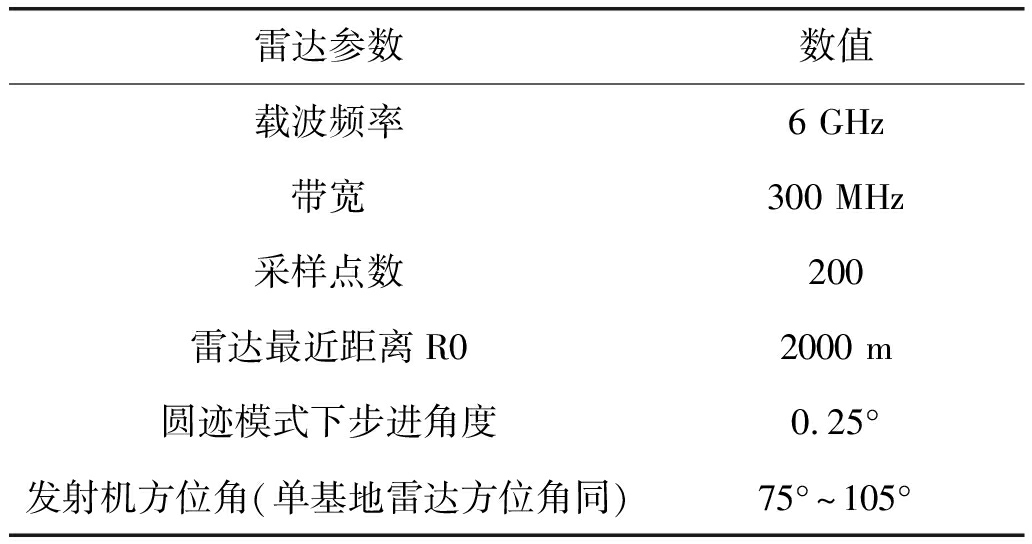
雷达参数数值载波频率6GHz带宽300MHz采样点数200雷达最近距离R02000m圆迹模式下步进角度0.25°发射机方位角(单基地雷达方位角同)75°~105°
在不同峰值信噪比情况下,多基地雷达系统与单基地雷达系统直线段参数估计角度误差小于5°,长度误差小于目标真值长度的10%的概率如表4。
单基地与多基地雷达系统对直线段参数估计的精度与接收机回波的峰值信噪比的关系如图10。
表4 反演精度仿真结果
Tab.4 Simulation results of inversion accuracy
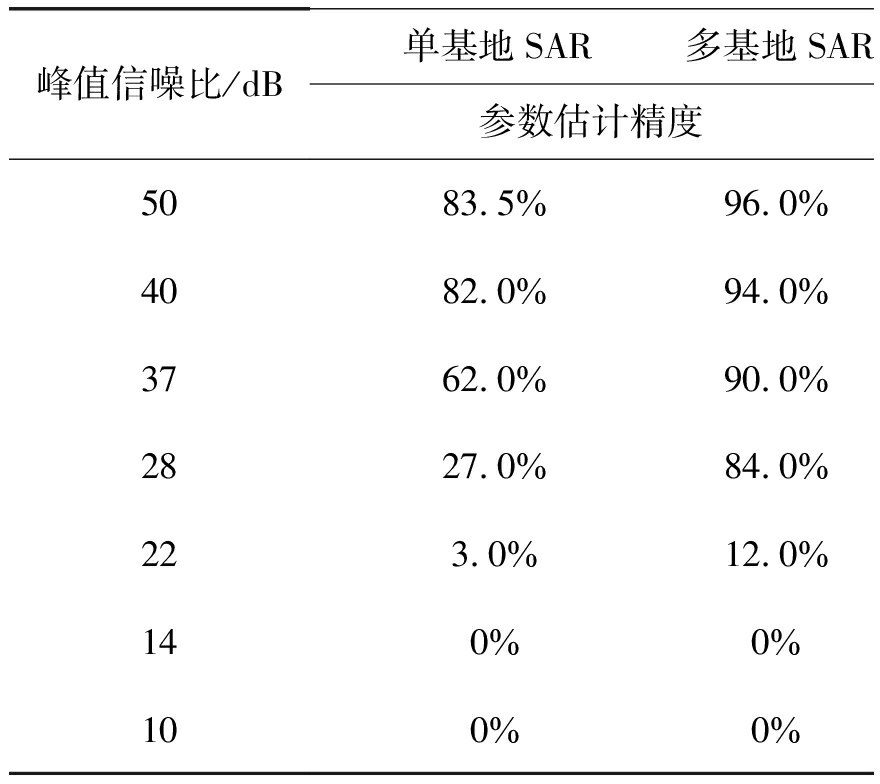
峰值信噪比/dB单基地SAR多基地SAR参数估计精度5083.5%96.0%4082.0%94.0%3762.0%90.0%2827.0%84.0%223.0%12.0%140%0%100%0%
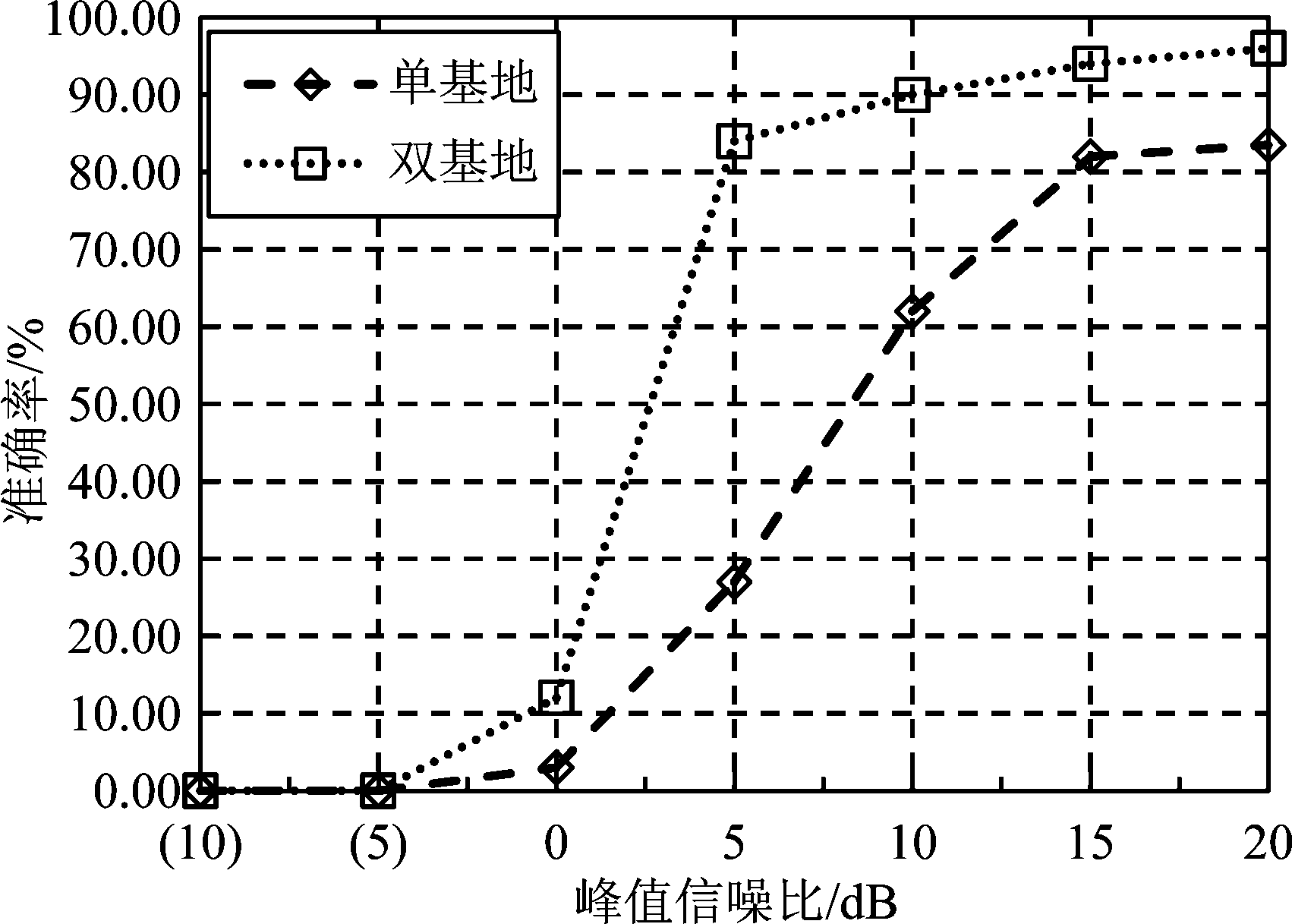
图10 单基地与多基地雷达系统直线段参数估计的精度与图像峰值信噪比的关系
Fig.10 The relationship between the estimation accuracy of line segment parameters and the peak signal-to-noise ratio of images in monostatic and multistatic radar systems
由图10可知,接收机固定的一发多收多基地雷达系统在对直线段目标进行参数估计时具有比单基地雷达系统更高的准确率。利用参数估计算法所估计的参数对其进行图像重建,结果如下,图11(a)为重建前,图11(b)为重建后图像。当观测场景中存在多个线目标时,可根据散射点的位置及回波特征确定线目标的端点并进行图像分割,最后在进行参数反演。

图11 直线段图像重建结果
Fig.11 Result of linear segment image reconstruction
4 结论
针对传统基于点散射模型的单基地SAR对复杂场景中线目标成像时特征丢失的问题,本文基于几何模型详细推导了合成孔径雷达图像中线目标的参数化散射模型表达式,分析了对线目标在不同观测角度下SAR图像从直线段到两端点反复变化的特点,从空间谱采样的角度对这一现象进行了解释,最后根据线目标空间谱的特征,提出了一种基于最小二乘估计的多基地构型下线目标参数反演及图像重建方法。仿真实验结果表明,在回波具有相同的峰值信噪比条件下,本文提出的多基地SAR线目标参数反演与图像重建方法,相对于单一观测角度的单基地SAR具有更高的反演性能,在SAR图像峰值信噪比为28 dB时,线目标朝向与长度的反演误差在10%以内的概率达到了84%,可以基于反演结果实现图像的重建。
[1] Jackson J A, Moses R L. Synthetic aperture radar 3D feature extraction for arbitrary flight paths[J]. IEEE Transaction on Aerospace and Electronic Systems, 2012, 48(3): 2065-2083.
[2] Zhu X X, Bamler R. Tomographic SAR Inversion by L1 Norm Regularization-The Compressive Sensing Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839-3846.
[3] Patel V M, Easley G R, Healy D M, et al. Compressed Synthetic Aperture Radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244-254.
[4] Wang S, Fan C, Huang X, et al. Bistatic ISAR imaging based on BP algorithm[C]∥Progress in Electromagnetic Research Symposium. IEEE, 2016: 2858-2862.
[5] Yang L, Yu W, Zheng S, et al. Efficient Bistatic SAR Raw Signal Simulator of Extended Scenes[J]. International Journal of Antennas & Propagation, 2015, 2014(3): 1-9.
[6] Julie Ann Jackson, Brian D. Canonical Scattering Feature Models for 3D and Bistatic SAR[J]. IEEE Transaction on Aerospace and Electronic Systems, 2010, 46: 525-540.
[7] Jackson J A, Rigling B D, Moses R L. Parametric scattering models for bistatic synthetic aperture radar[C]∥2008 IEEE Radar Conference, Rome, Italy, May, 26-30, 2008.
[8] 李飞, 纠博, 刘宏伟, 等, 基于稀疏表示的SAR图像属性散射中心参数估计算法[J]. 电子与信息学报, 2014, 36(4): 931-937.
Li F, Jiu B, Liu H W. Sparse Representation Based Algorithm for Estimation of Attributed Scattering Center Parameter on SAR imagery[J]. Journal of Electronics and Information, 2014, 36(4): 931-937.(in Chinese)
[9] 钟金荣. 目标三维电磁散射参数化模型反演方法研究[D]. 长沙: 国防科学技术大学研究生院, 2016.
Zhong J R. Inverse Methods for Three Dimensional Parametric Scattering Model of Target[D]. Changsha: Graduate School of National Defense University of Science and Technology, 2016.(in Chinese)
[10] 李增辉. 稀疏激励的极化逆散射理论研究[D]. 北京: 清华大学, 2015.
Li Z H. Research on Polarimetric Inverse Scattering through Enforcing Sparsity[D]. Beijing: Tsinghua University, 2015.(in Chinese)
[11] 高叶盛. 基于信号模型的SAR参数化成像技术研究[D]. 上海: 上海交通大学, 2012.
Gao Y S. Model-Based Parametric SAR Image Formation Technique[D]. Shanghai: Shanghai Jiaotong University, 2012.(in Chinese)






