1 引言
随着超宽带技术的发展,大带宽信号对雷达数据的采集、存储、传输及实时性处理提出了更高的要求。压缩感知(Compressive Sensing,CS)[1-2]在信息采集上提出了新的方向,它利用信号的稀疏性,以低于奈奎斯特率的采样率获取信号的压缩量测值,对信号同时进行采样和压缩,然后通过算法恢复得到原始信号。在雷达目标检测中,目标相对于雷达信号的频谱表现出高度的稀疏性。因此,将CS技术应用于雷达信号系统中,为解决传统雷达采样所面临的信息冗余、低效率和资源浪费等问题提供了新思路,实现了低采样数据量和信号完整性的理想平衡[3]。
AIC是一种基于CS原理,通过对模拟信号处理转换,直接获取稀疏信号的有效信息的采样装置[4]。目前,关于AIC的结构研究主要分为:随机滤波(Random Filter,RF)[5]、随机采样(Random Sampling,RS)[6]、随机解调(Random Demodulation,RD)[7]和调制宽带转换(Modulated Wideband Converter,MWC)[8]。其中,RD是最常用的方案,该方案是由伪随机序列发生器、模拟低通滤波器、ADC和混频器组成的单支路压缩采样结构[7],但是该方案的混频电路仍工作在奈奎斯特频率,且低通滤波器的特性会对原始信号的恢复造成很大干扰。Eldar 团队在RD方案的基础上,提出了并行多路RD结构的MWC方案[8],该模型对各路RD的采样时钟进行了同步,以低频电路完成了对高频稀疏信号的压缩和采样,但是多路结构增加了硬件成本,且RD方案中的问题依旧存在。针对RD和MWC方案中存在的不足,文献[9]提出了一种基于多相分频移相器和累加器结构的多相随机子采样FFT的AIC方案,该方案利用多路低速ADC对信号进行移相采样,避免了混频电路和低通滤波器对信号采样和重构的影响,提高了信号压缩比和信号恢复性能。但是,此方案中的多路并行ADC模块的结构对于硬件实现来说比较复杂。
本文通过分析AIC结构模型,利用了雷达信号连续多个脉冲之间相似性较强的特点,提出了一种单样本压缩采样方法,该方法是在多相随机子采样FFT的AIC方案的基础上,以时间换空间的方式,用时分单路结构替代了空间多路并行ADC采样结构,降低了系统硬件复杂度。通过实验表明,该方案结构简单易实现,以较低的采样率实现了较高的压缩率,能实现对低信噪比环境下的雷达目标检测。
2 多相随机子采样FFT的AIC方案
多相随机子采样FFT的AIC模型是由伪随机序列发生器、多相分频器、多路ADC和累加器组成,首先将多相随机时钟信号和伪随机序列发生器输出的伪随机序列进行与运算,进而控制多路低速ADC的采样时钟对输入信号进行采样,每一路的采样结果都通过累加器计算得到一个压缩量测值,实现了对信号的压缩采样。该AIC结构如图1所示。

图1 多相随机子采样FFT的AIC方案框图
Fig.1 Multiphase random sampling and sub-sampled FFT AIC implement diagram
考虑模拟信号x(t)的奈奎斯特频率为fs(周期为Ts),多相分频器对信号x(t)的采样时钟进行分频,以脉冲重复间隔(Pulse Repetition Interval,PRI)为一个压缩采样周期,输出多路(B路)时钟信号,分别为clk1,clk2,…,clkB,依次以t1,t2,t3,…,tB为采样起始时间进行采样,使得ti=t1+(i-1)Ts,且t1=0,每一路的采样周期为BTs。通过这种空间并行多路ADC低速采样的方式,实现了信号的压缩采样。
该方案虽然实现了压缩采样,但是方案中并行多路ADC的结构复杂,在实际硬件电路实现中所需成本较高。因此,针对如何改进该方案的工作方式,减少ADC数量,节约硬件成本,本文提出了一种基于时分单路的单样本压缩采样方法。
3 单样本压缩采样方法
单样本压缩采样方法利用了雷达连续PRI回波信号的相似性,把多相随机子采样方案中的多路结构变成了时分单路采样结构,以空分变时分的方式,简化了硬件电路。下面对该方法的系统结构和信号理论模型进行分析。
3.1 单样本压缩采样AIC方案
单样本压缩采样的AIC方案框图如图2所示。单样本压缩采样AIC方案由控制器、伪随机序列发生器、采样积分器和ADC模块组成。
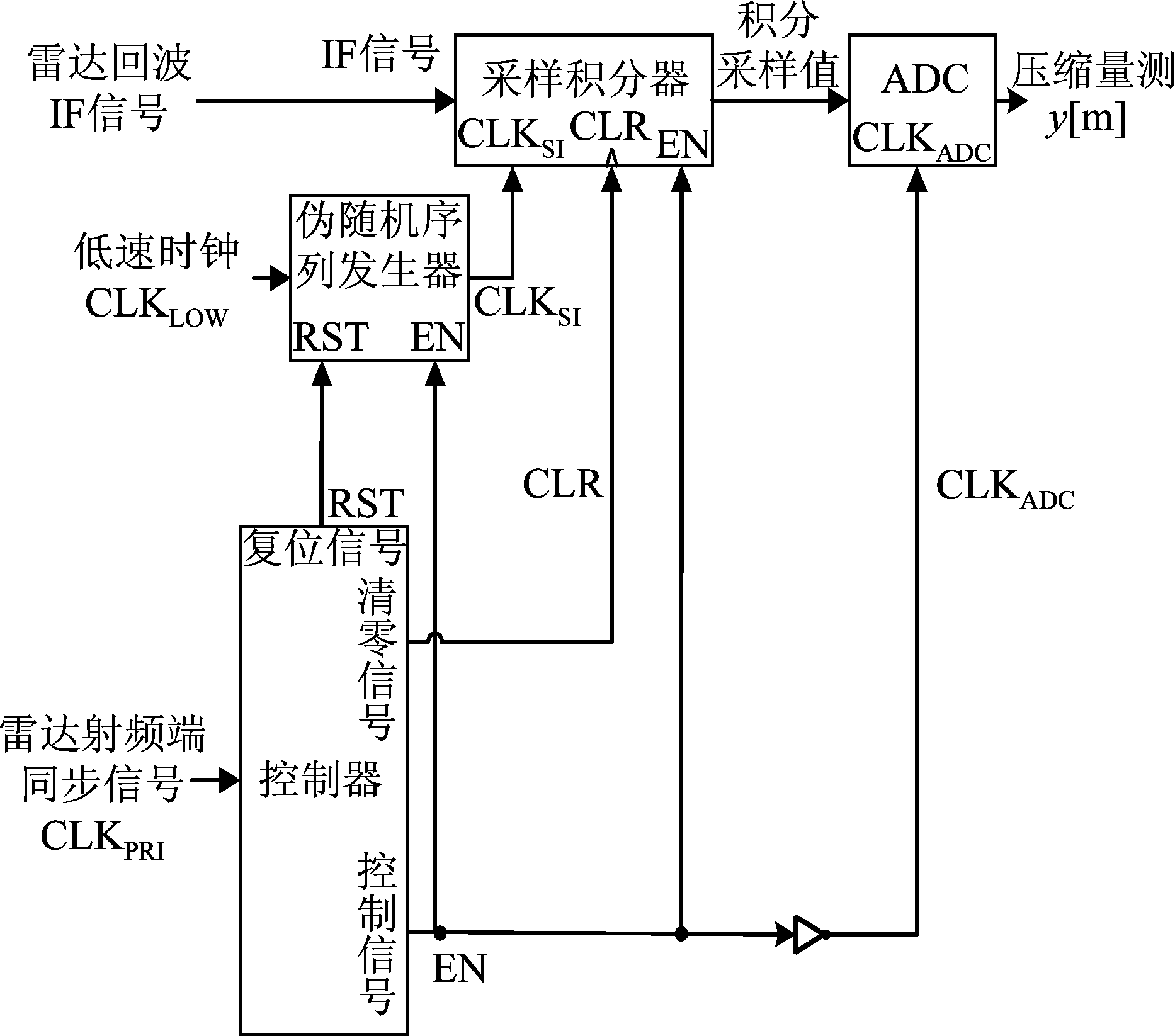
图2 单样本压缩采样AIC方案框图
Fig.2 Diagram of single sample compression sampling AIC
1)控制器与雷达射频端同步,产生控制脉冲信号EN控制积分采样器、伪随机序列发生器和ADC的工作时间,产生清零信号CLR对积分采样器清零,以及复位信号RST对伪随机序列发生器进行复位。
2)伪随机序列发生器由多个D触发器组成,其工作时根据低速采样时钟产生伪随机序列,作为压缩采样中的测量矩阵,并输出随机采样信号CLKSI到采样积分器。
3)采样积分器将雷达回波信号预处理之后的IF信号进行采样积分,其采样持续时间受控制器控制,采样点位置受伪随机序列控制,最终对信号的采样值进行累加。
4)ADC模块的时钟信号为控制信号取反,在时钟信号上升沿到来时,将积分采样器中的信号进行采样量化,输出压缩量测值。
该方案中的各部分信号说明如表1所示。
表1 单样本压缩采样AIC信号说明
Tab.1 Explanation of AIC signals

信号名称信号方向说明CLKPRI输入雷达射频端同步信号CLKLOW输入低速时钟信号RST输出控制器输出的复位信号EN输出控制器输出的控制信号CLKSI输出伪随机序列发生器输出的随机采样信号CLKADC输出控制信号取反CLR输出控制器输出的清零信号
本方案以B个PRI为一个压缩采样周期,考虑采样积分器的采样率为fs(周期为Ts)。伪随机序列发生器产生的随机采样信号CLKSI对B个PRI回波信号依次以t1,t2,t3,…,tB为采样起始时间进行压缩采样,使得ti=t1+(i-1)Ts,i=2,…,B且t1=0。本方案中的信号时序波形如图3所示。
3.2 单样本压缩采样信号模型
考虑运动目标时,设x(t)为第k个发射脉冲与回波混频后的差频信号,其表达式如式(1):
xk(t)=A·exp{j 2π[frν(t-kT0)-fdkT0+θ]}
(1)
其中frν=(Kτ-fd),kT0<t<(k+1)T0, k=1,2,…,B。此外,T0为脉冲周期,A为脉冲的幅度,K为发射信号的斜率,τ=2R0/C表示目标起始位置对应的信号时延, fd=2V0/λ表示目标速度的多普勒频率。
考虑对信号x(t)进行离散化,在满足Nyquist准则的条件下,设采样率为fs,则第k个脉冲信号为:
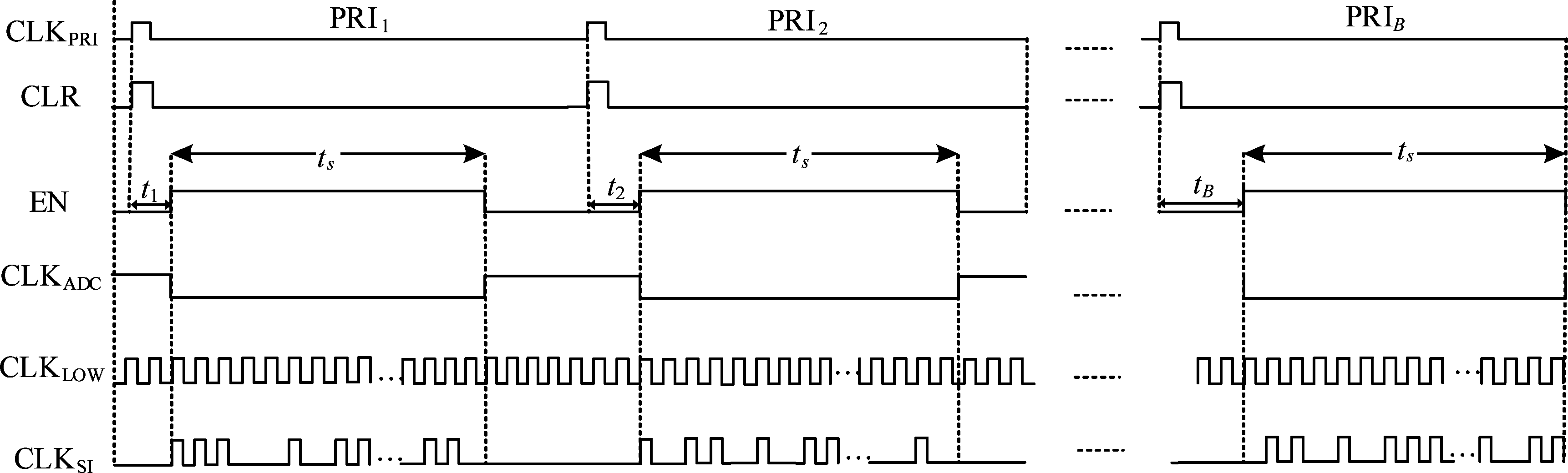
图3 单样本压缩采样AIC的采样时钟波形
Fig.3 The clocking waveform of single sample compression sampling AIC
(2)
若对第k个脉冲的采样长度为N,即:
xk(n)=xk(nTs)=xk(t)|t=nTs
(3)
其中,n=0,1,2,…,N-1。
将式(3)写成向量形式xk∈R1×N:
xk=[xk(0),xk(1),…,xk(N-1)]
(4)
其中,k=1,2,…,B。
经过B个PRI,总采样信号x∈RBN×1可表示为:
(5)
设p(n)为伪随机序列,采样积分器中每一路的采样时钟序列ak∈R1×N为:
⋮
(6)
则测量矩阵Φ∈RB×BN为:
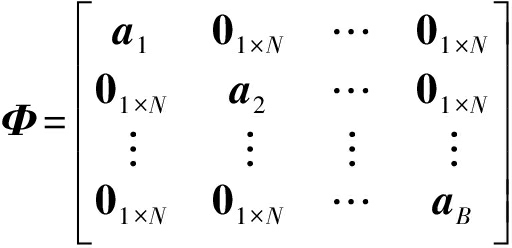
(7)
所以,单样本压缩采样过程可表示为:
y=Φx
(8)
其中,y∈RB×1,Φ∈RB×BN,x∈RBN×1。
因此,B个PRI经过压缩采样之后,得到B个压缩量测,即单个PRI压缩成一个样本。
当目标运动速度较慢,且PRI较小时,连续B个PRI信号相似性较强,稀疏性一致,可以认为这B个PRI完全一样,此时的采样信号为:
x=x1=x2=…=xB∈R1×N
(9)
此时的测量矩阵Φ∈RB×N可表示为:
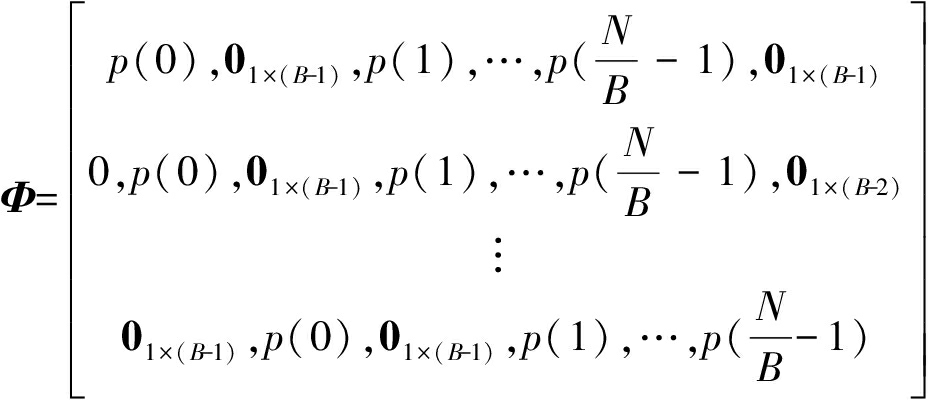
(10)
此时,单样本压缩采样方法与多相随机子采样FFT的AIC方法的测量矩阵和压缩量测值都相等。因此,矩阵Φ符合Toeplitz循环矩阵[10],满足RIP性质,可以实现对稀疏信号的压缩采样。
4 仿真实验及分析
雷达的基本功能是目标检测,因此,本文通过目标检测和参数估计的实验来验证单样本压缩采样方法的有效性。目标检测方法用了基于压缩量测的相关检测方法[11],即不需恢复原始信号,而是通过计算实际量测与估计量测之间的相关性,来估计出目标的参数信息。
本节设计了两个仿真实验,分别针对单目标雷达信号和多目标雷达信号,比较多相随机子采样方案(MRS AIC)和单样本压缩采样方案(SS AIC)在不同信噪比和不同压缩比情况下的目标检测性能。实验中采用了均值为0,方差为σ2的高斯白噪声。相关实验参数如表2所示。
表2 仿真实验相关参数
Tab.2 Simulation parameters
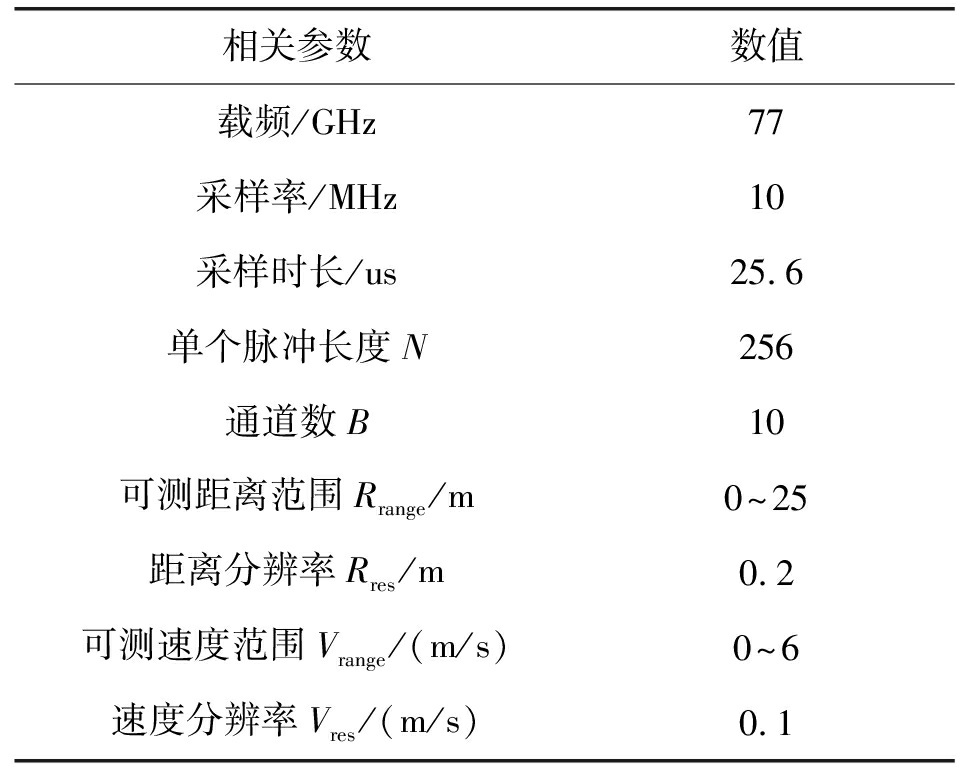
相关参数数值载频/GHz77采样率/MHz10采样时长/us25.6单个脉冲长度N256通道数B10可测距离范围Rrange/m0~25距离分辨率Rres/m0.2可测速度范围Vrange/(m/s)0~6速度分辨率Vres/(m/s)0.1
4.1 单目标检测
为对比不同信噪比和压缩比下两种方案的检测性能,首先对目标T1(R=15.63 m,V=4.25 m/s)在不同的输入信号信噪比和压缩比下,做1000次Monte Carlo实验,定义估计值和真实值的偏差小于一个分辨单元为检测正确,则两种方案的检测概率如图4所示。

图4 不同信噪比的检测概率
Fig.4 The detection probability versus the SNR
由式(9)、(10)可知,当目标径向运动速度较慢时,SS-AIC和MRS-AIC等效。因此,针对![]() 在不同压缩量测信噪比下做了1000次Monte Carlo实验,则两种方案的检测概率如图5所示。
在不同压缩量测信噪比下做了1000次Monte Carlo实验,则两种方案的检测概率如图5所示。
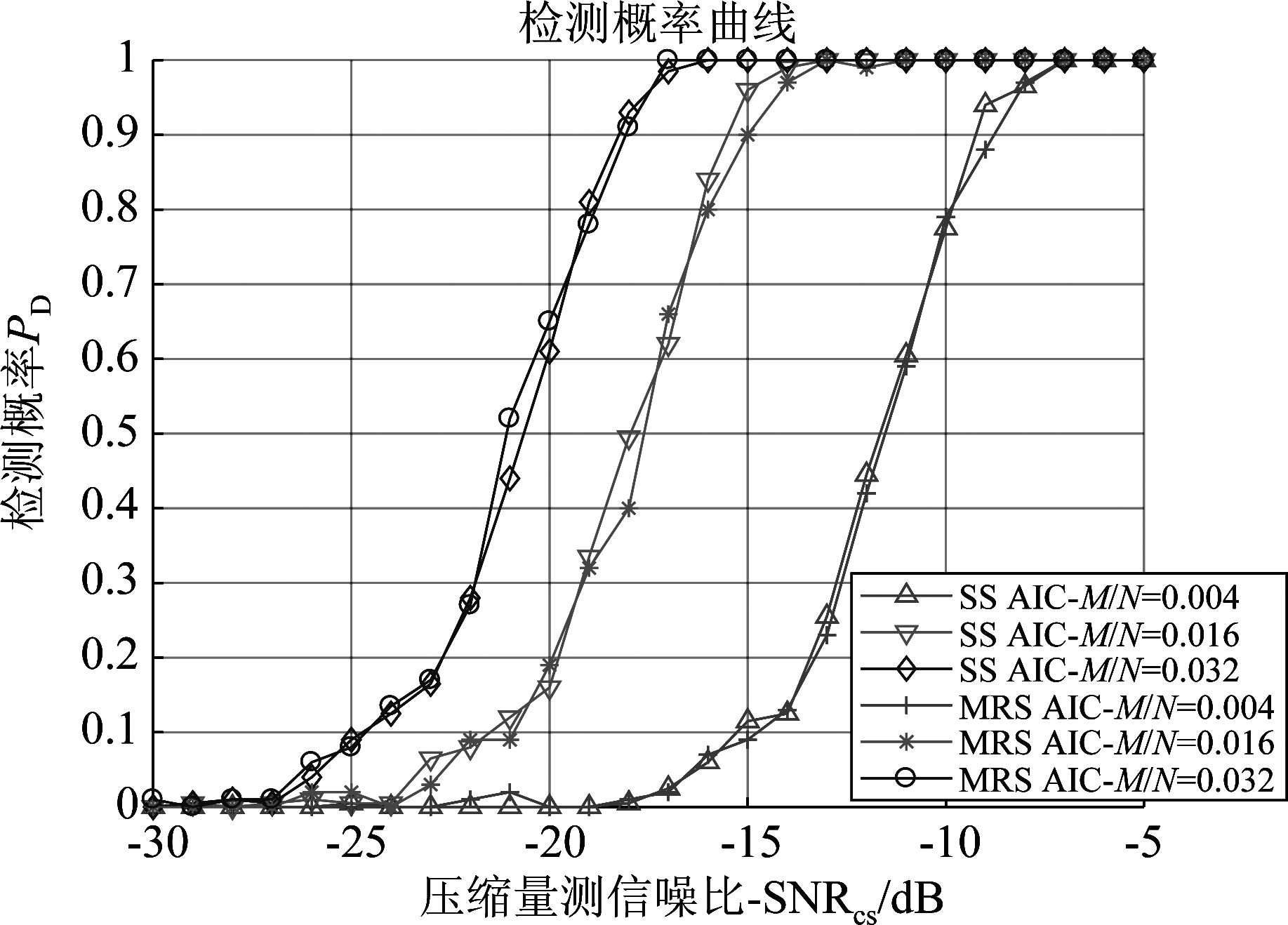
图5 不同信噪比的检测概率
Fig.5 The detection probability versus the SNR
随机选定50个目标,每个目标都在压缩比M/N=0.016和SNR=-10 dB的条件下做500次Monte Carlo实验,统计每个目标的距离和速度的均方根误差如图6和图7所示。

图6 目标距离的均方根误差
Fig.6 RMSE of the target range
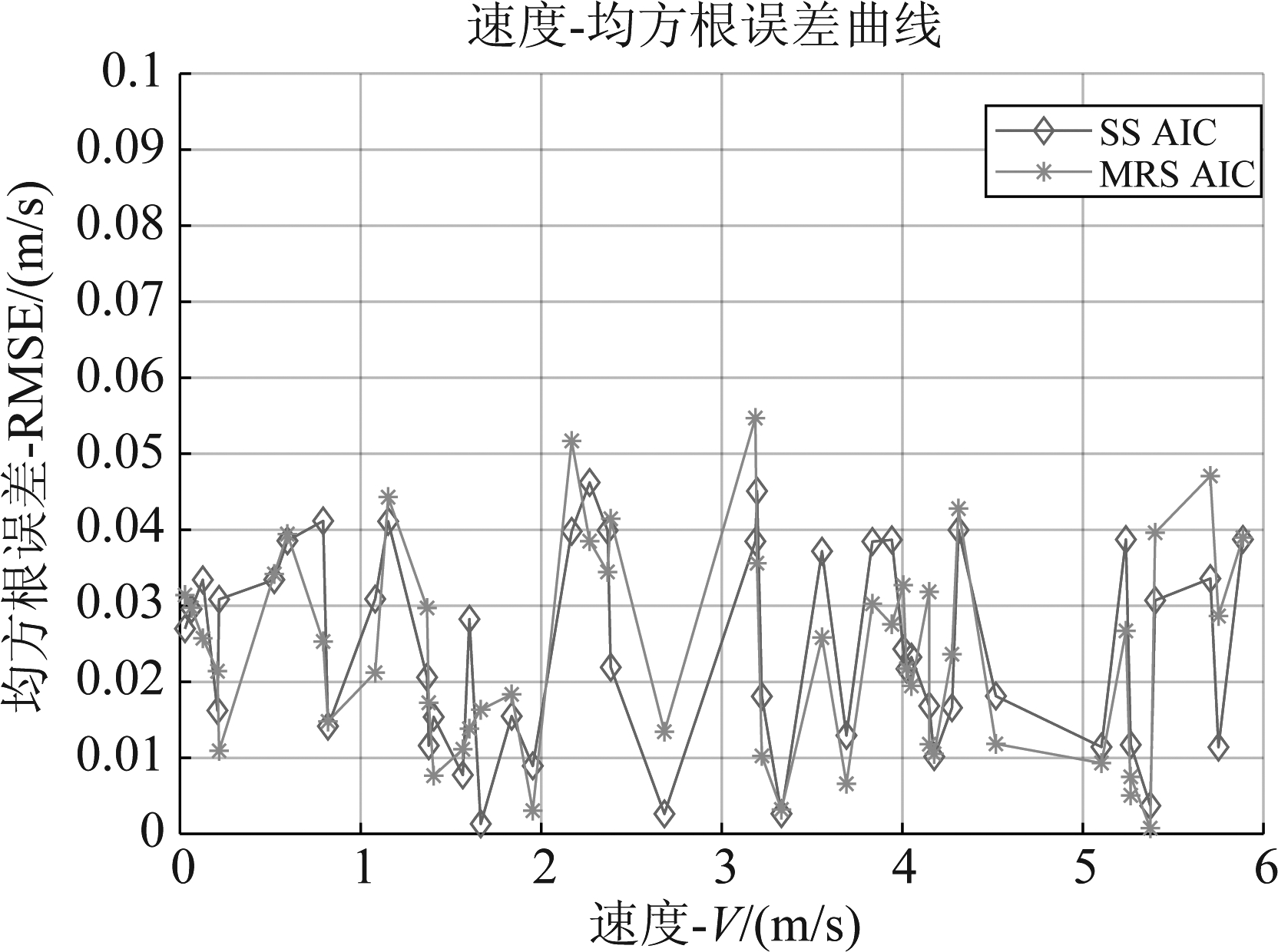
图7 目标速度的均方根误差
Fig.7 RMSE of the target velocity
实验结果表明,对于单目标雷达信号,当目标运动速度较快时,相同输入信号压缩比下,SS-AIC检测效果稍差于MRS-AIC;当目标静止或运动速度较慢时,即连续多个脉冲相似性较强时,相同压缩量测信噪比下,两者检测效果完全一致,SS-AIC等效于MRS-AIC。另外,两种方案目标估计的距离和速度均方根误差均较小,表明了SS-AIC方案在简化了MRS-AIC的硬件结构的基础上,对低速目标还具有与MRS-AIC方案一致的检测准确性和稳定性。因此,实验证明了SS-AIC与MRS-AIC的等效性,能有效地对低信噪比雷达单目标信号进行压缩采样,具有较好的单目标检测性能。
4.2 多目标检测
针对多目标雷达信号的压缩采样,随机选定了3个目标,分别为T2(R=2.071 m,V=2.781 m/s)、T3(R=16.226 m,V=2.367 m/s)、T4(R=23.522 m,V=4.734 m/s),针对不同的输入信号信噪比和不同压缩比,通过1000次的Monte Carlo实验,两种方案的检测概率如图8所示。
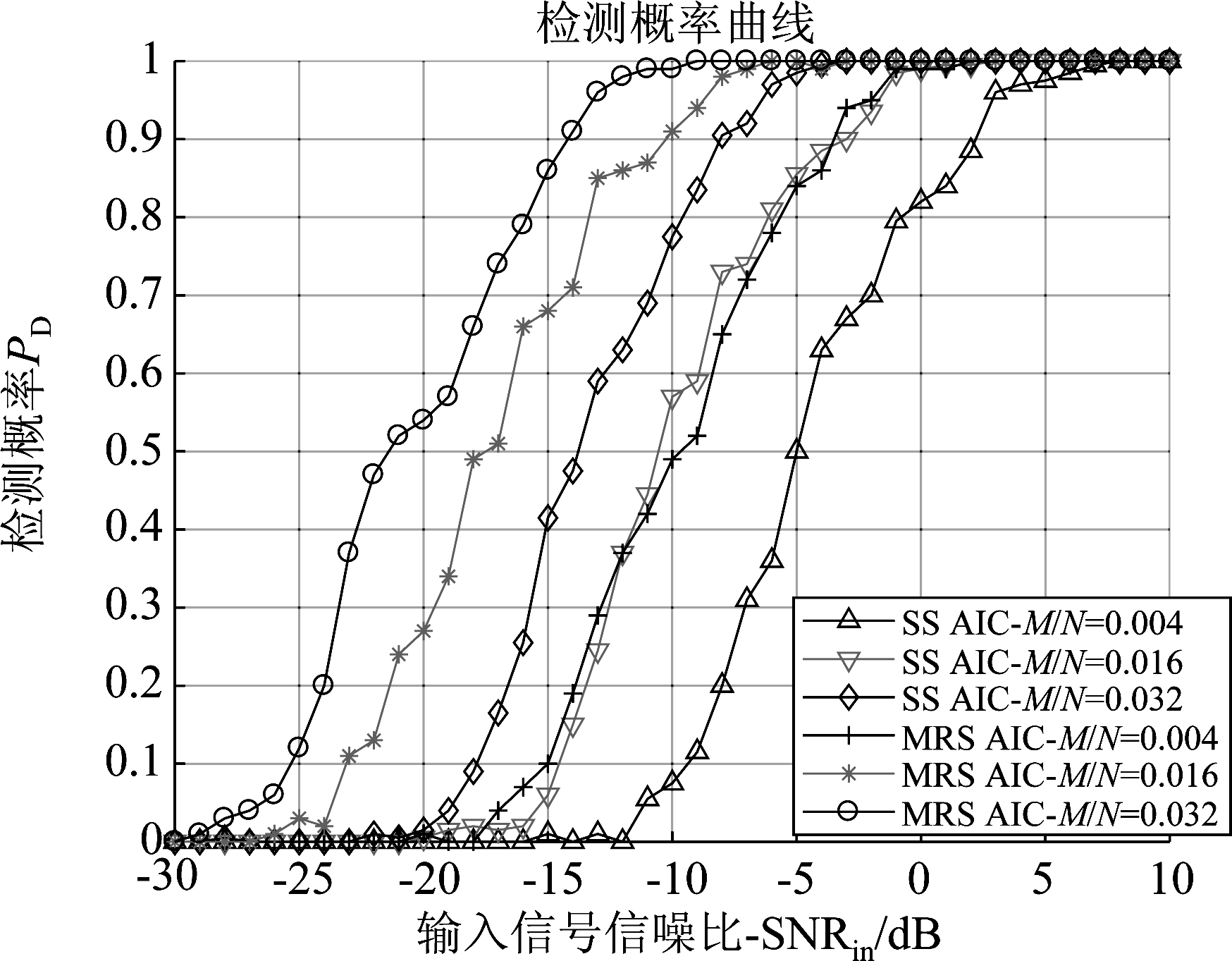
图8 多目标不同信噪比的检测概率
Fig.8 The detection probability versus the SNR
同样地,由式(9)、(10)可知,当目标径向运动速度较慢时,SS-AIC和MRS-AIC等效。因此,针对相同距离、径向速度为0的3个目标![]() 在不同压缩量测信噪比和不同压缩比下做1000次Monte Carlo实验,统计两种方案下的检测概率如图9所示。
在不同压缩量测信噪比和不同压缩比下做1000次Monte Carlo实验,统计两种方案下的检测概率如图9所示。
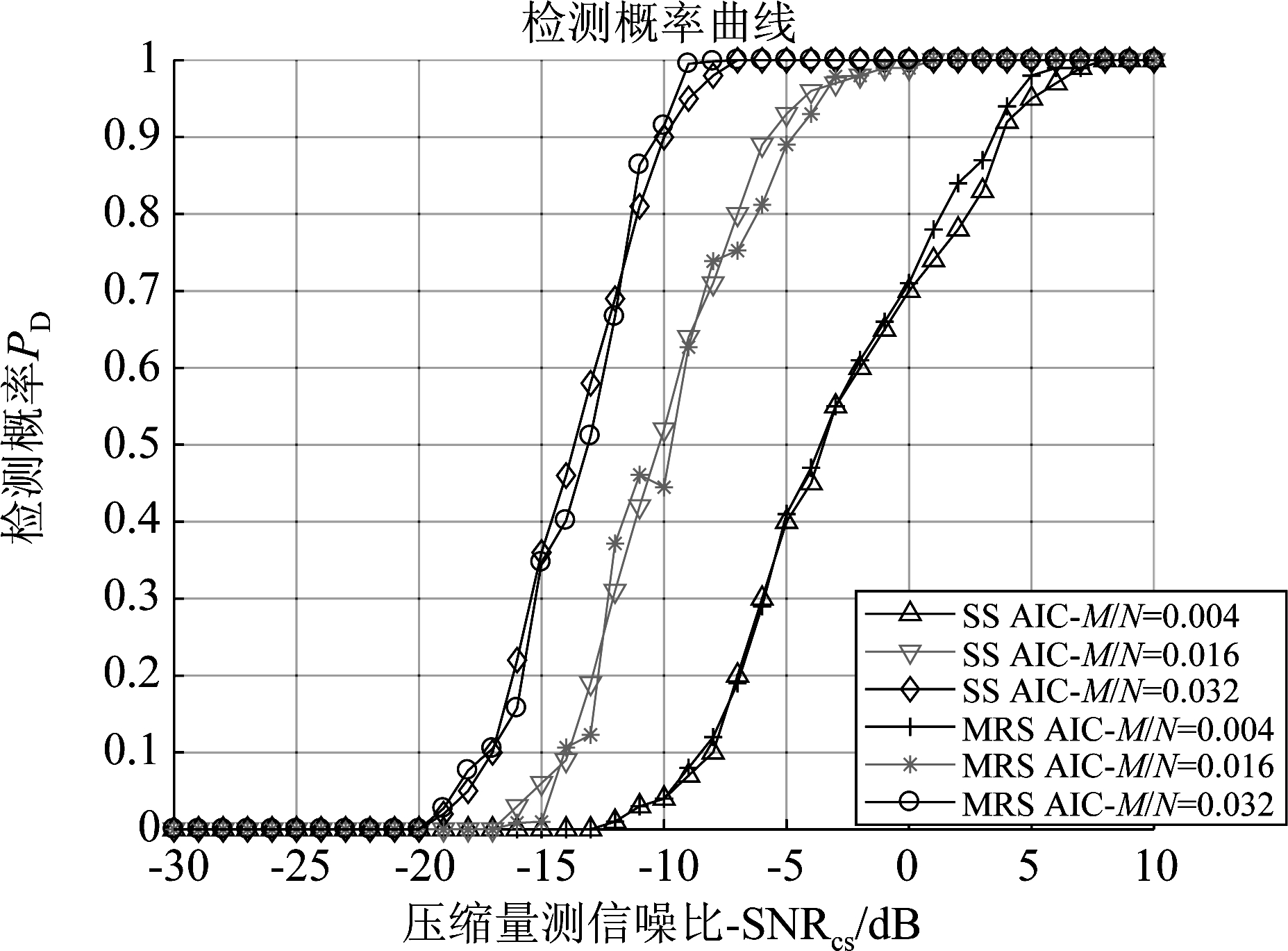
图9 不同信噪比的检测概率
Fig.9 The detection probability versus the SNR
选取参数M/N=0.016和SNR=0 dB,统计两种方案下目标真实参数与估计参数对比如表3和图10所示。
表3 目标真实参数与估计参数对比
Tab.3 Comparison of parameters

目标编号真实参数估计参数SSMRS偏差SSMRST2R2.0712.1482.1060.0770.045V2.7812.7782.7990.0030.018T3R16.22616.21016.2930.0160.067V2.3672.4082.3950.0410.028T4R23.52223.43623.4830.0860.039V4.7344.7234.710.0110.024
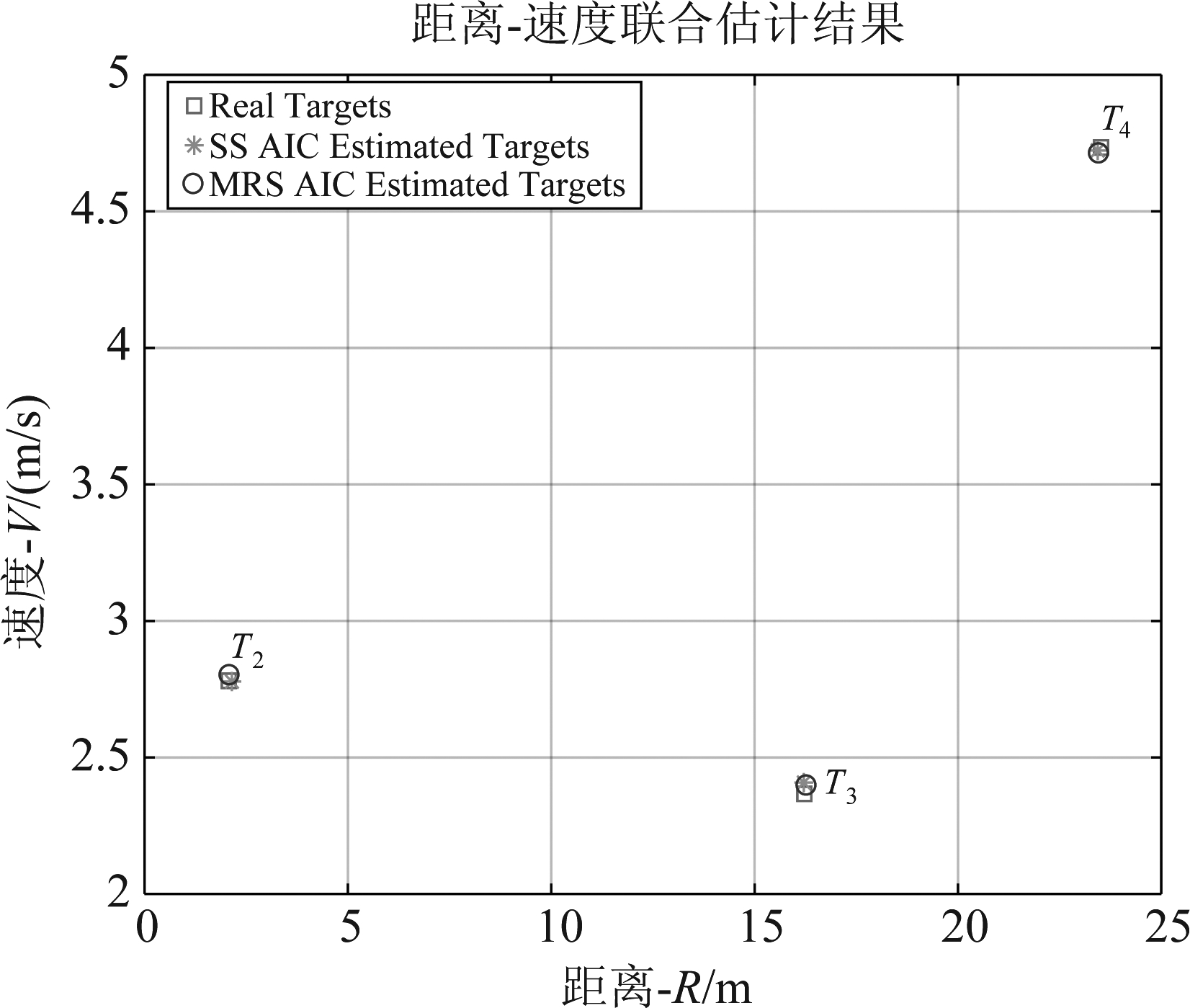
图10 真实目标与估计目标对比
Fig.10 Comparison between real targets and estimated targets
由上述实验结果可知,对于多目标雷达信号,当目标运动速度较慢时,SS-AIC等效于MRS-AIC。另外,估计目标与真实目标的距离和速度偏差都小于一个检测单元,表明了SS-AIC方案在多目标信号检测方面具有与MRS-AIC方案一致的检测性能,目标分辨能力较强。因此,综合上述实验结果,单样本压缩采样方法能对多目标雷达信号进行压缩采样,具有较好的多目标检测性能。
5 结论
本文提出了一种雷达信号的单样本压缩采样方法,该方法简化了多相随机子采样FFT的AIC结构,用时分单路采样的方式替代了空间多路并行采样,在节约了硬件成本的同时,还进一步提高了信号压缩率。本文简要介绍了该方法的系统框架,分析了该方法的信号模型。仿真实验结果表明,该方法能实现对低信噪比下单目标和多目标的准确检测和参数估计,具有检测准确度高、计算量少的优点。
[1] Candes E, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Signal Processing, 2006, 52(2): 489-509.
[2] Donoho D L. Compressed Sensing[J]. IEEE Transactions on Signal Processing, 2006, 52(4): 1289-1306.
[3] 刘明. 基于压缩感知的雷达信号处理技术研究[J]. 信息通信, 2017(12): 8-9.
Liu Ming. Research on Radar Signal Processing Technology Based on Compressed Sensing[J]. Journal of Information and Communications, 2017(12): 8-9.(in Chinese)
[4] 张弓, 文方青, 陶宇, 等. 模拟-信息转换器研究进展[J]. 系统工程与电子技术, 2015, 37(2): 229-238.
Zhang Gong, Wen Fangqing, Tao Yu, et al. Advances in analog-to-information convertor[J]. Journal of Systems Engineering and Electronics, 2015, 37(2): 229-238.(in Chinese)
[5] Baraniuk R G, Wakin M, Duarte M F, et al. Random filters for compressive sampling and reconstruction[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2006, 3: III- 872-III- 875.
[6] Donoho D L, Huo X. Uncertainty principles and ideal atomic decomposition[J]. IEEE Transactions on Information Theory, 2001, 47(7): 2845-2862.
[7] Kirolos S, Laska J, Wakin M, et al. Analog-to-information conversion via random demodulation[C]∥2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software. IEEE, 2006: 71-74.
[8] Smith G E, Diethe T, Hussain Z, et al. Compressed sampling for pulse Doppler radar[C]∥2010 IEEE Radar Conference. IEEE, 2010: 887- 892.
[9] 金磊, 黄建军, 高国星. 多相随机子采样FFT模拟信息转换器[J]. 信号处理, 2016, 32(4): 457- 462.
Jin Lei, Huang Jianjun, Gao Guoxing, Implementation for Analog-to-information Convertor via Multiphase Random Sampling and Sub-sampled FFT[J]. Journal of Signal Processing, 2016, 32(4): 457- 462.(in Chinese)
[10] 李霞丽, 吴立成, 樊艳明. 易于硬件实现的压缩感知观测矩阵的研究与构造[J]. 智能系统学报, 2017, 12(3): 279-285.
Li Xiali. Wu Licheng, Fan Yanming. Study and construction of a compressed sensing measurement matrix that is easy to implement in hardware[J]. Journal of CAAI Transactions on Intelligent Systems, 2017, 12(3): 279-285.(in Chinese)
[11] Davenport M A, Boufounos P T, Wakin M B, et al. Signal Processing With Compressive Measurements[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 445- 460.



