1 引言
在电子战领域,假目标干扰是常见的欺骗干扰方式,尤其是基于数字射频存储器(Digital Radio Frequency Memory, DRFM)产生的转发式假目标干扰,更是获得了广泛的应用。DRFM转发式假目标除能够获得雷达脉冲压缩处理增益外,通常还具有真实目标的典型特征,与雷达回波信号具有相参性,因而具有较强的干扰能力。间歇采样转发干扰[1]是2006年由美国的Sparrow提出,基于DRFM体制且用于对抗线性调频脉冲压缩雷达的新型假目标干扰,具体包括切片组合(Chopping and Interleaving, C&I)干扰与频谱弥散(Smeared Spectrum, SMSP)干扰两种类型。由于干扰机截获雷达信号时不进行全脉冲采集,而是在采集其中的部分信号后立即进行处理转发,从而使该类型的干扰可以在雷达接收端形成大量逼真的假目标,兼具压制和欺骗效果,影响雷达对真实目标的检测。由于此类干扰与雷达回波高度相似,为了抑制此类干扰,往往需要检测、识别出干扰的类型,并且获得其特征参数,以便进行干扰对消,这对准确检测和提取干扰参数提出了迫切需求。
目前针对这两类间歇采样转发式假目标干扰,国内外学者提出了一些基于特征参数的干扰识别与抑制方法。如文献[2]提出了一种基于分数阶傅里叶变换(Fractional Fourier Transform, FRFT)域扫频滤波的 SMSP 干扰抑制方法,但该方法未讨论干扰特征参数的获取;文献[3]提出一种联合时频分布和压缩感知的SMSP干扰抑制算法,在利用分数阶域滤波后,利用正交匹配追踪方法重构目标信号,但该方法在提取目标信号时会导致一定的损失。文献[4]提出利用模糊函数对 SMSP 和C&I干扰进行特征识别,但受噪声影响较大,且难以获得用于干扰重构的特征参数。文献[5]提出一种滑动截断匹配滤波(Sliding-Truncation Matched Filter, STMF)方法对间歇采样转发干扰作识别,该方法能够估计出干扰的切片宽度与转发周期,进而对干扰进行识别,然而该方法不能对SMSP干扰进行区分识别。文献[6]利用组网雷达系统条件与SMSP干扰的调频斜率特性,提出了基于分数阶功率谱的SMSP干扰检测算法。文献[7]同样基于SMSP干扰调频斜率特性,提出了一种基于匹配信号变换(Matched Signal Transform, MST)的干扰识别算法,然而这些方法都难以运用于识别切片组合干扰的场合。文献[8]通过分析干扰的时、频域特征,提取基于时域的盒维数与基于频域的指数熵两种特征参数,运用支持向量机(Support Vector Machine, SVM)对干扰进行分类识别,然而需要提前训练向量机,实时性受到影响。
综上,本文基于短时分数阶傅里叶变换(Short-Time Fractional Fourier Transform, STFRFT)原理,提出了一种针对SMSP和C&I两种典型间歇采样转发干扰的识别与特征参数提取方法。该方法首先对接收信号做分数阶傅里叶变换,得到干扰最优旋转阶次与调频斜率参数;然后在最优旋转阶次下进行短时分数阶傅里叶变换,得到分数阶时频平面;再进行时频平面二值化操作,提取干扰信号时宽、分数阶频率等参数,进而综合判断干扰类型。
2 间歇采样转发干扰模型
2.1 切片组合(C&I)干扰模型
切片组合(C&I)多假目标干扰在干扰发射前对干扰机截获复制的雷达信号进行加工,从而能在脉冲压缩后产生多假目标输出。其产生过程可分为两步:首先,从雷达脉冲中等间隔采样得到若干采样信号片段;之后,将这些信号片段依次顺序重复转发到其右侧相邻的空白时隙中,生成相应的干扰信号。因为C&I信号和雷达信号含有相同的调频斜率,因此它和雷达信号脉冲压缩过程的匹配滤波器是相匹配的,因此可以获得脉冲压缩增益,在雷达接收端产生大量重复虚假目标。C&I干扰生成原理如图1所示。
对于线性调频雷达发射信号,其形式为:
(1)
其中Tp为雷达信号脉冲宽度。设干扰机对信号进行m次等间隔采样(称此阶段为chopping,即切片阶段),每次采样结果转发n次,(称此阶段为Interleaving,即组合阶段),填满两次切片之间的时隙,使得干扰连续。干扰机共将信号分为mn段,每段长度为τ=Tp/mn。切片阶段采样脉冲为
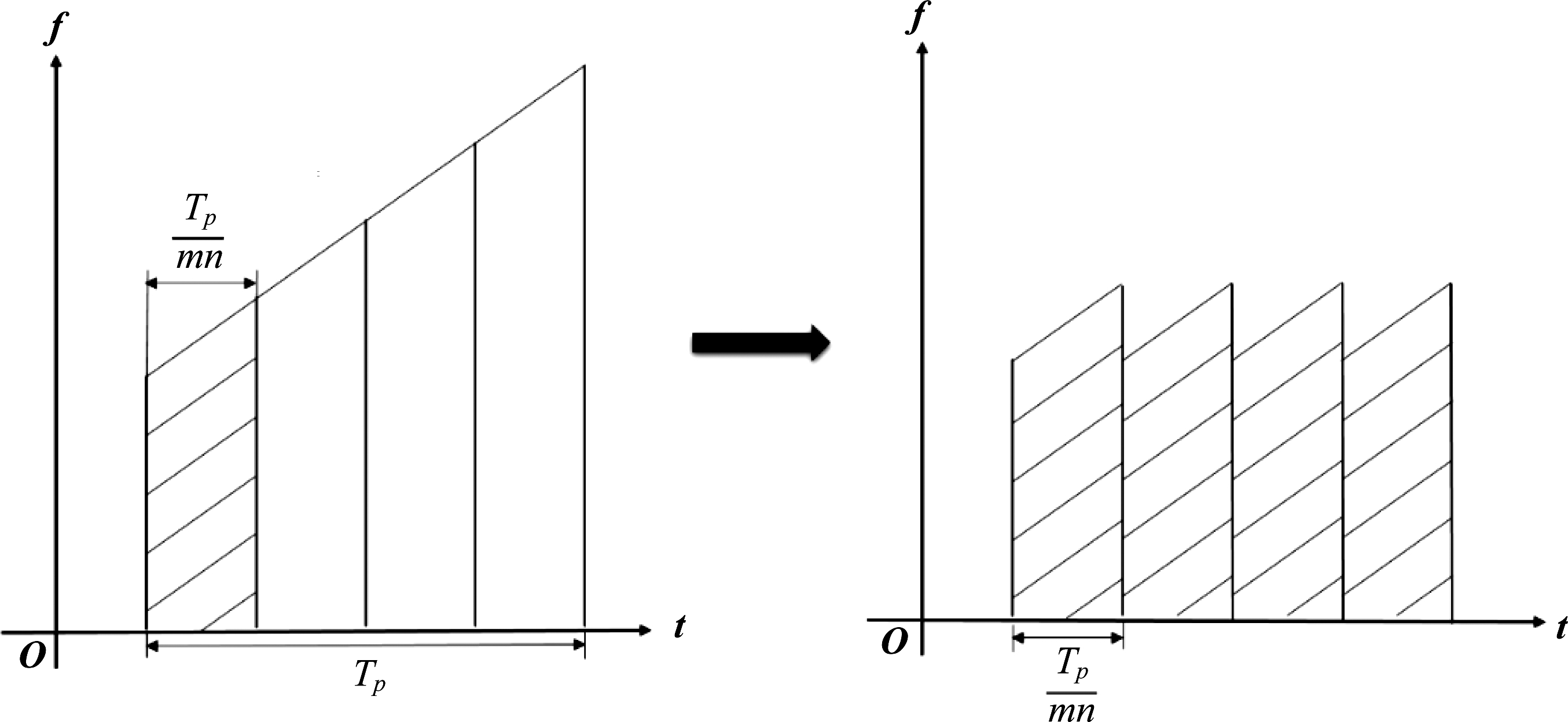
图1 切片组合干扰生成原理示意图
Fig.1 The principle of chopping and interleaving jamming
(2)
则经过组合阶段后,干扰可以表示为
(3)
其中,第p个采样的第q次转发干扰切片可表示为
p=1,…,m q=1,…,n
(4)
图2为切片宽度为1/5脉宽的切片转发干扰在SNR=30 dB,INR=45 dB条件下与目标信号混合,再经接收机脉冲压缩后的时域仿真结果图。图中,红色虚线为目标对应时延。从图中可以看出,干扰形成的脉冲压缩尖峰高于目标信号的脉冲压缩尖峰,使得峰值检测错误将干扰检测为目标;同时,大量重复的干扰信号能够对目标信号形成明显的压制效果。
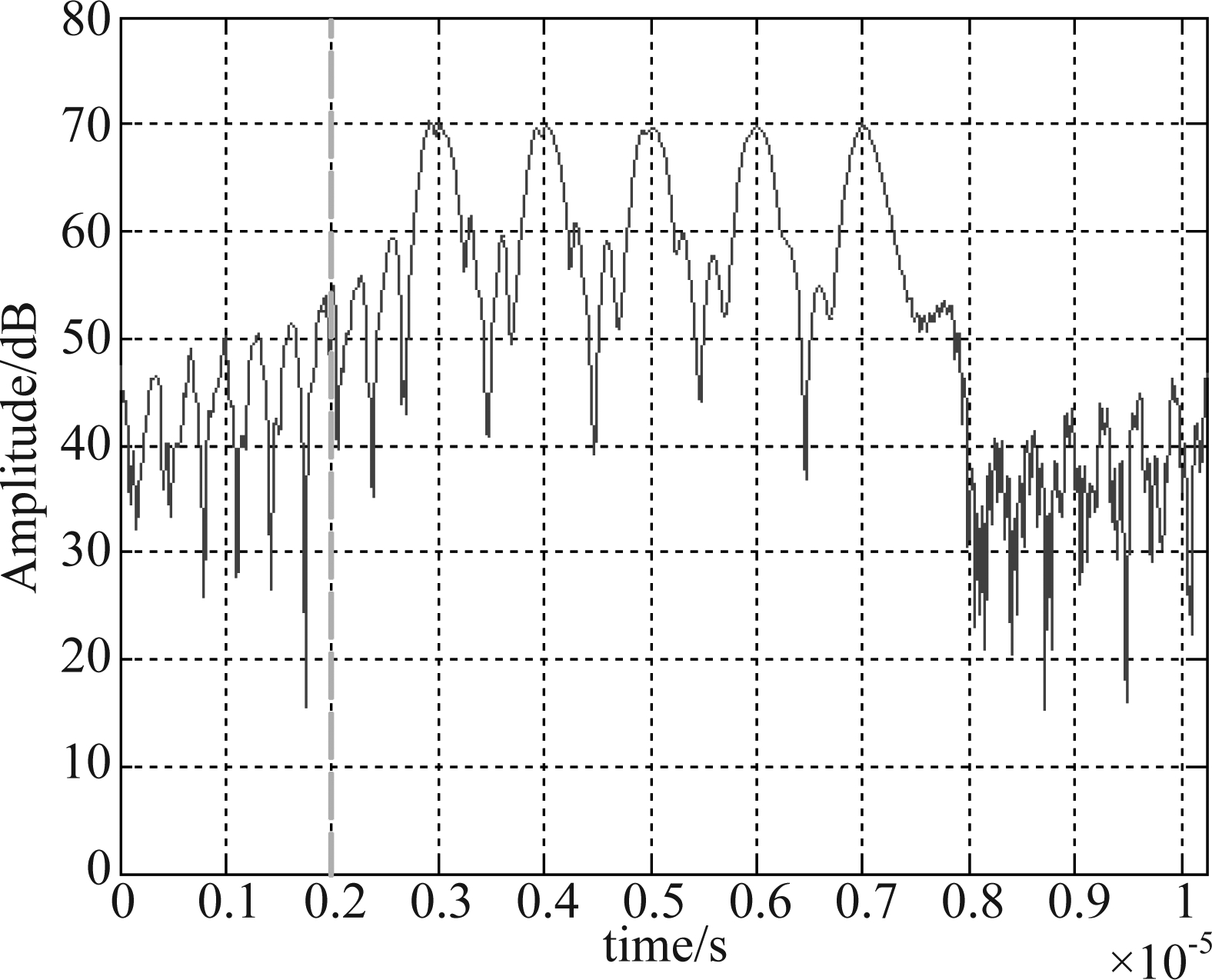
图2 切片转发干扰效果示意图
Fig.2 The effect of chopping and interleaving jamming
从以上分析中可以看出,C&I干扰由雷达信号的部分切片组合而成,其每个切片具有和雷达信号完全相同的形式,时域、频域上都存在耦合性,故难以单纯从时域、频域上对目标与干扰加以区分。反之,C&I干扰的脉冲宽度、间隔以及脉冲个数能够反映出C&I干扰具体的截获-转发策略,而目标回波则拥有和雷达发射信号相同的脉宽等参数。在确定信号形式与回波相同的条件下,通过获得干扰脉冲切片宽度、个数信息,可以将C&I干扰辨识出来。
2.2 频谱弥散(SMSP)干扰模型
与C&I干扰类似,SMSP干扰同样利用了脉冲压缩雷达发射线性调频信号的特性,其产生过程如下:DRFM接收并储存一整段雷达回波信号,并在时域上对其采样,假设采样点数为得到的采样数据对应的频率点,如图3所示。将时钟频率提高到原来的n倍,对采样数据进行抽取,并按原时钟频率将抽取结果排序,然后对排序后的信号复制n次,得到信号的干扰样式,即为SMSP干扰。SMSP干扰与匹配滤波器不完全匹配,然而仍能获得一定的脉冲压缩增益,从而产生与C&I干扰相仿的重复假目标效果,但同样干噪比条件下,其假目标幅度比C&I干扰更低。
对式(1)中雷达发射信号形式,干扰机对其进行n倍时钟频率的采样,得到抽取的干扰单个切片形式为:
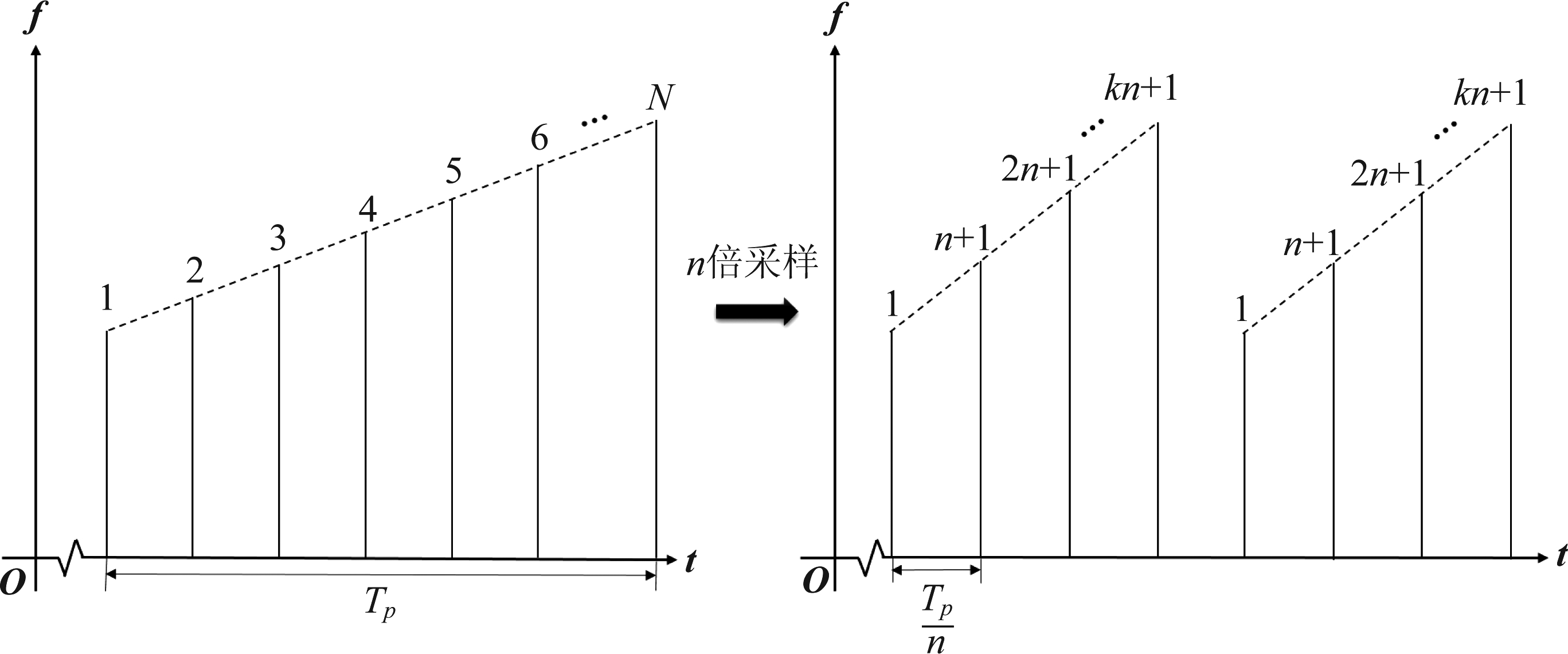
图3 频谱弥散干扰产生原理示意图
Fig.3 The principle of smeared spectrum jamming
(5)
将干扰单个切片在时域上连续复制n次,即可得到SMSP干扰形式为
(6)
SMSP干扰生成原理如图3所示。
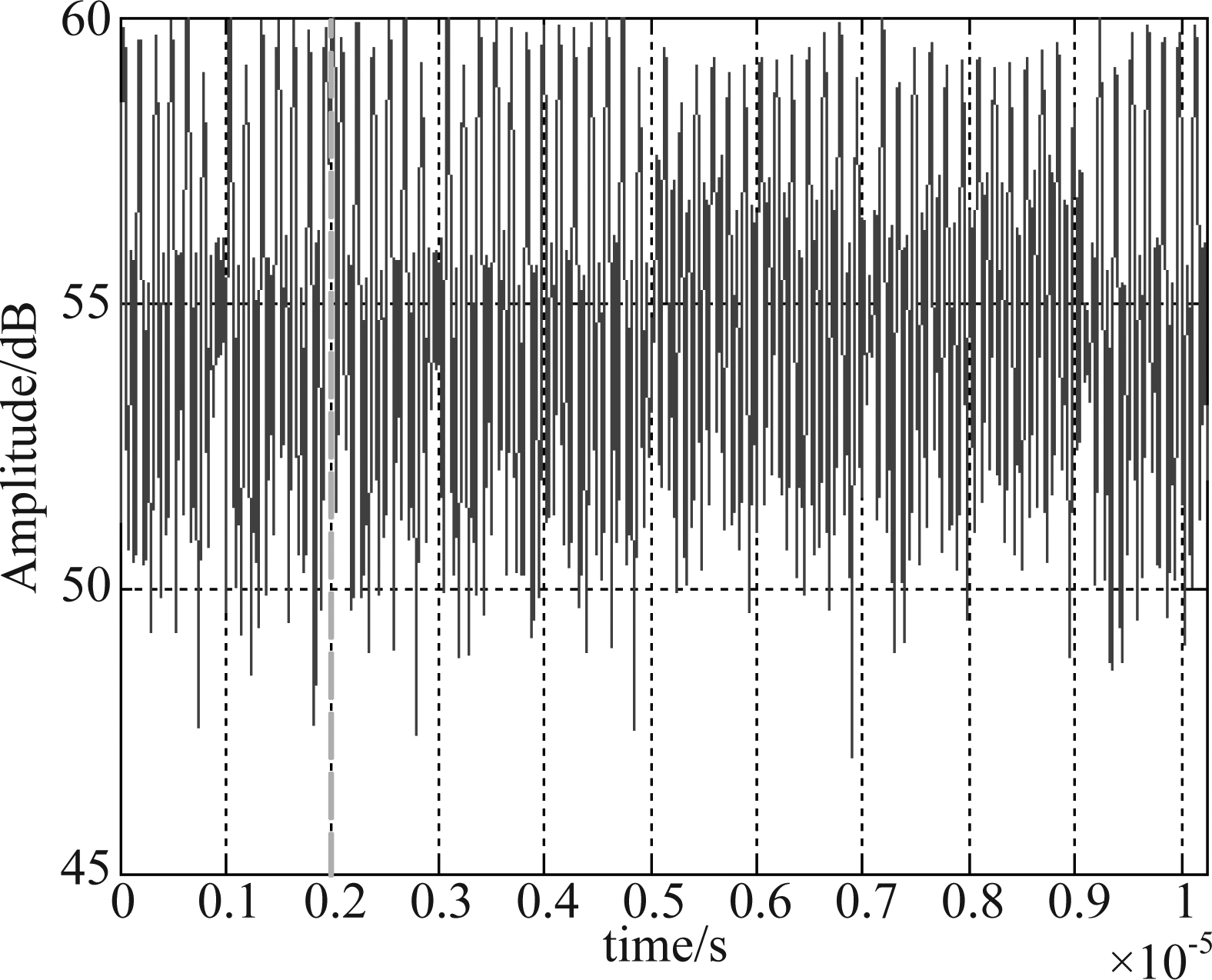
图4 频谱弥散干扰效果示意图
Fig.4 The effect of chopping and interleaving jamming
图4为采样率为信号采样率5倍的频谱弥散干扰在SNR=30 dB,INR=45 dB条件下与目标信号混合,再经接收机脉冲压缩后的时域仿真结果图。图中,红色虚线为目标对应时延。与切片转发干扰类似,图中干扰形成了大量高于目标信号尖峰的脉冲压缩尖峰,兼具欺骗与抑制干扰的效果。
通过对 SMSP 干扰原理的分析可知,此类干扰和目标回波在时域、频域上同样存在耦合性,导致难以通过单一运用时域、频域特征进行辨识;但由于SMSP干扰的调频斜率与目标回波区别明显,从而易于利用时频域特征将其与目标信号加以区别。
3 基于短时分数阶傅里叶变换的干扰辨识方法
3.1 短时分数阶傅里叶变换原理
根据以上对C&I干扰与SMSP干扰的特征分析,本文选择用时频域特征作为C&I干扰与SMSP干扰识别所选用的特征。信号领域常用的时频分析工具有短时傅里叶变换(Short-Time Fourier Transform, STFT)、小波变换、Wigner-Ville分布等。分数阶傅里叶变换(Fractional Fourier Transform, FRFT)是一种重要的时频分析工具,是传统傅里叶变换的推广,对雷达常用的线性调频信号有很好的能量聚集特性,因此本文选择分数阶傅里叶变换以及在此基础上衍生的短时分数阶傅里叶变换(Short-Time Fractional Fourier Transform, STFRFT)[9]作为提取时频域参数的工具。
对信号x(t)的分数阶傅里叶变换定义为:
Xp(u)=![]() Kp(t,u)x(t)dt
Kp(t,u)x(t)dt
(7)
其中Kp(t,u)为FRFT的核函数,p称为信号FRFT的阶数。为便于表征,定义信号FRFT的旋转角度α=pπ/2,则核函数Kp(t,u)的表达式为:
Kp(t,u)=
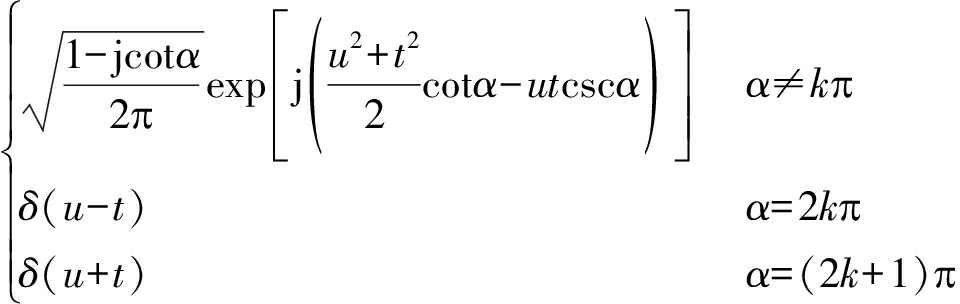
(8)
与傅里叶变换一致,分数阶傅里叶变换所得分数阶频率信号可以通过相应的分数阶傅里叶反变换还原为时域信号。对于角度α=pπ/2的分数阶傅里叶变换,其反变换为角度为α=-pπ/2的分数阶傅里叶变换,即
x(t)=![]() Xp(u)K-p(t,u)du
Xp(u)K-p(t,u)du
(9)
类似于傅里叶变换推广到分数阶傅里叶变换,短时分数阶傅里叶变换也是短时傅里叶变换的推广,可以认为其是一种加窗的分数阶傅里叶变换[9]。参考式(7)、(8),对信号x(t)的短时分数阶傅里叶变换定义为:
STFRFT(x,p)(t,u)=![]() x(τ)g(τ-t)Kp(t,u)dτ
x(τ)g(τ-t)Kp(t,u)dτ
(10)
其中g(τ)为窗函数。不同的窗函数选择会影响STFRFT的聚集性,根据文献[10],本文选择高斯窗作为STFRFT所用窗函数,其在时频域均有较好的聚集性,表达式为
(11)
其中δt为高斯信号时域3 dB宽度,即时域分辨率大小。
3.2 干扰辨识方法实现
分数阶傅里叶变换在处理线性调频信号时具有能量聚集特性,可以据此进行特征提取。对形如式(1)的LFM信号作分数阶傅里叶变换:
(12)
当k=-cotα时,根据FRFT的能量聚集效应,有
sin c[(ucscα-f0)T]
(13)
从上式可见,当
α=-arccotk,α∈(0,π)
(14)
时,LFM信号的FRFT结果会在分数阶频域形成一个尖峰,此时的α称为最佳旋转角度。
类似上述对LFM信号的分数阶傅里叶变换,通过对雷达接收信号(含目标回波与干扰信号)做旋转角度与窗函数适当的滑窗短时分数阶傅里叶变换,能够得到对应的时频平面,在时频平面上能够较为清晰地显示出干扰的切片数目、时宽等特征。由于接收信号中目标回波会对干扰特征提取产生影响,需要选取对于干扰聚集性最好的旋转角度。对于C&I干扰,因其与目标回波调频斜率相同,其最优旋转角度也与目标回波相同,可通过式(14)求得;对于SMSP干扰,其最优旋转角度并不已知。针对此问题,本文采用遍历旋转角度的方法找到干扰最优旋转角度[11]。具体来说,首先以旋转角α为变量,在α∈[0,π]范围内对接收信号进行FRFT,得到[α,u]的二维平面。在该二维平面中,存在目标与SMSP干扰两种峰值,只需排除通过式(14)求得的目标旋转角度上的峰值,则剩余峰值对应的α即为SMSP干扰的最优旋转角度。设遍历旋转角度对应的总点数为M,进行FRFT运算的信号点数为N,考虑到SMSP干扰的调频斜率总是大于目标信号,其对应的最优角度总会落在目标信号最优角度的一侧,即只需遍历一半的角度,则谱峰搜索的运算复杂度为:
(15)
在得到分数阶时频分布图像后,就可以对其中的干扰特征进行提取。在时频分布图像上可以提取到的特征参数中,识别C&I干扰最重要的是切片个数与切片宽度,识别SMSP干扰最重要的是切片个数与调频斜率。我们通常认为只要对以上两种干扰分别准确估计了最重要的两个参数,即可重构出干扰信号。为了对上述过程得到的分数阶时频分布中干扰的切片特征参数进行精确提取,本文引入图像二值化思想。首先对时频分布图像做二值化,再取干扰分数阶频率对应的切片段落长度,从而得到干扰时宽参数,二值化门限根据时频分数图像最高点取一定比例得到。在分数阶时频平面上,通过信号的分数阶频率u0与频率的换算公式:
f0=u0/sin α
(16)
即可将二值化后提取的干扰切片对应的分数阶频率换算回到切片中心频率。
本文提出的间歇采样干扰辨识流程如图5所示,其具体步骤如下:

图5 所提算法流程图
Fig.5 Flowchart of the proposed algorithm
1)对接收信号进行遍历旋转角度的分数阶傅里叶变换,找到干扰尖峰所对应的最优旋转角度;
2)对接收信号在干扰最佳角度作滑窗短时分数阶傅里叶变换,得到分数阶时频分布;
3)将分数阶时频分布图像二值化,提取干扰切片宽度、中心频率等参数,进行干扰辨识。
4 仿真实验与结果分析
根据表1中的仿真参数对所提的干扰辨识方法进行仿真,并与文献[12]中,基于STFT的干扰辨识方法做对比。
首先,通过遍历旋转角度α的FRFT,确定STFRFT所用的最优旋转角度。因C&I干扰最优旋转角度可直接解算,这里仅给出SMSP干扰遍历旋转角度的仿真结果。图6中方框内为干扰尖峰,其对应旋转角度即可作为STFRFT的最优旋转角度。
表1 仿真参数
Tab.1 Simulation parameters
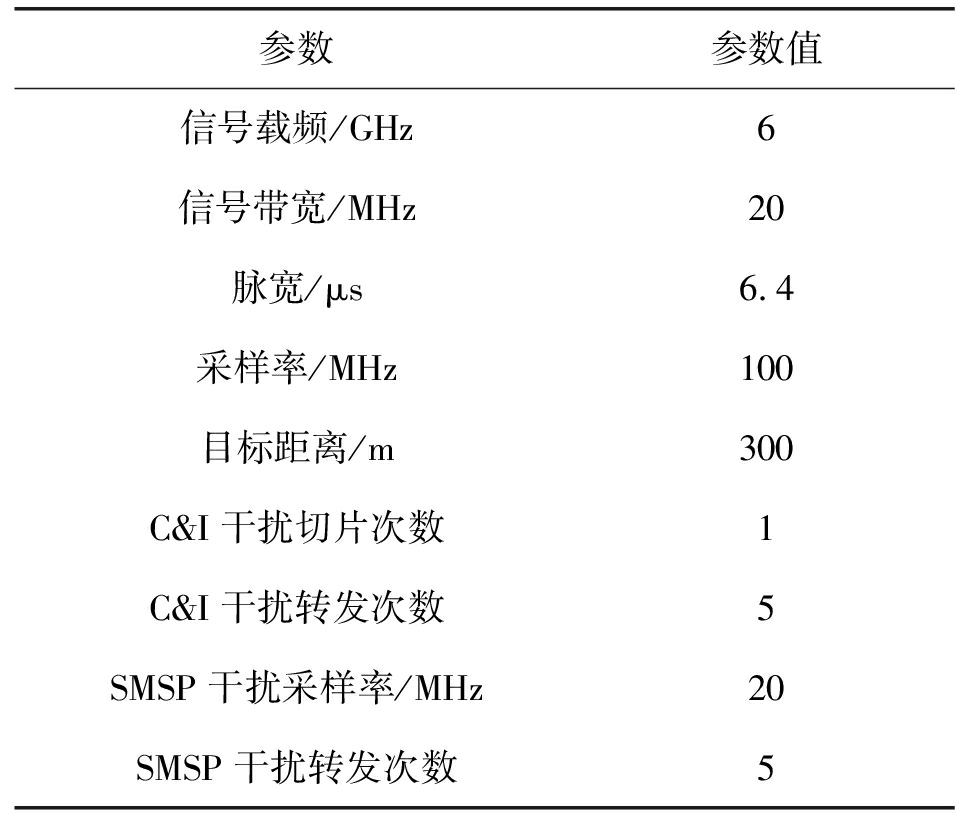
参数参数值信号载频/GHz6信号带宽/MHz20脉宽/μs6.4采样率/MHz100目标距离/m300C&I干扰切片次数1C&I干扰转发次数5SMSP干扰采样率/MHz20SMSP干扰转发次数5
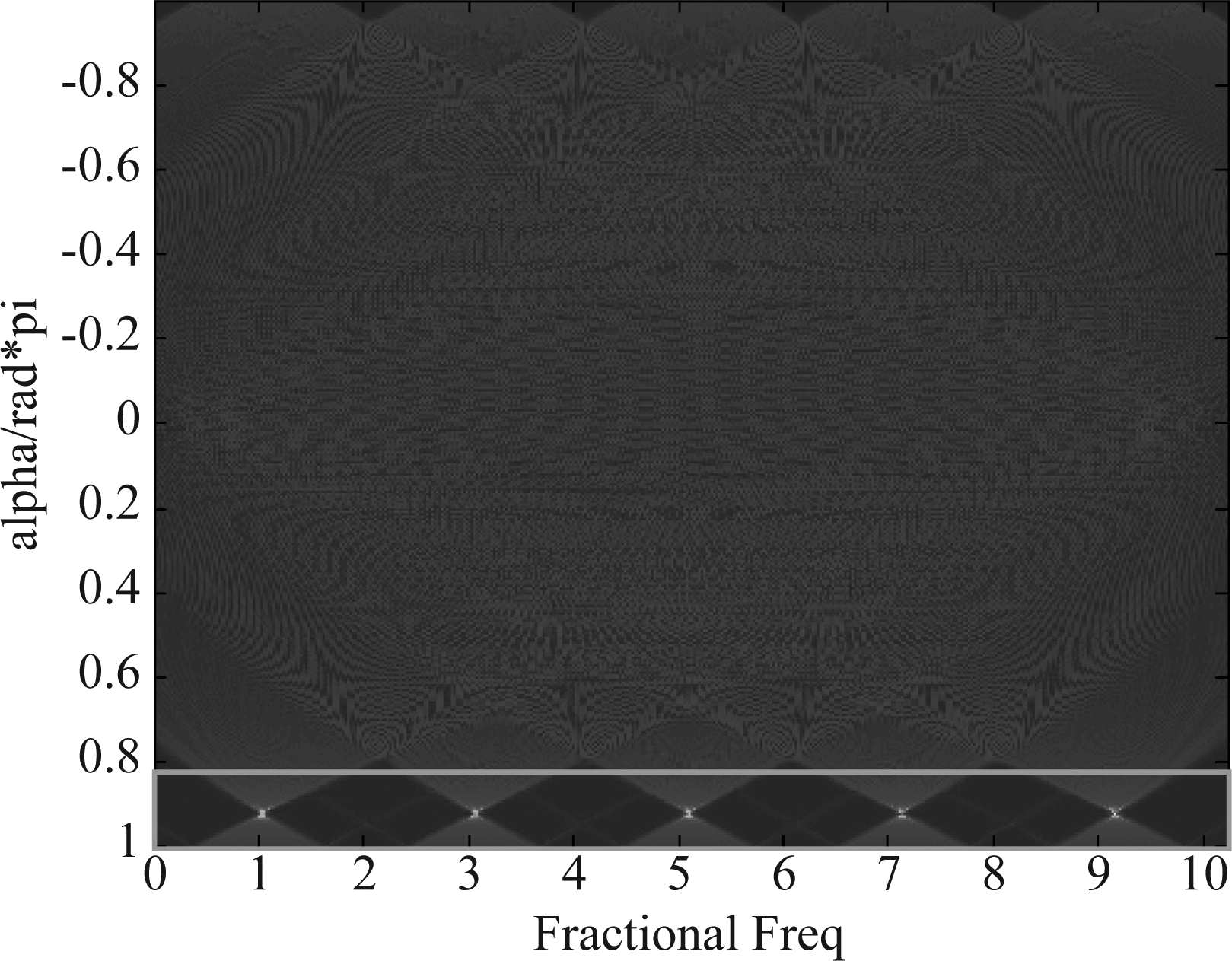
图6 SMSP干扰最优旋转角度提取示意图
Fig.6 Extraction of optimal rotation angle for SMSP Jamming
随后,对接收信号做干扰最优旋转角度的STFRFT,得到分数阶时频分布平面,并以最大值向下3 dB为门限做二值化。在信噪比SNR=30 dB,干噪比INR=30 dB的情况下,对C&I干扰与SMSP干扰分别进行上述仿真,并与STFT方法做对比,结果如图7、图8所示。
从图7、图8中可以看出,STFT提取时频特征的方法在同时存在目标和干扰的条件下,往往会由于目标与干扰时频分布相对接近或存在重叠,导致在二值化后的时频图中,干扰边缘出现毛刺、干扰间或干扰与目标间存在粘连、重叠等情况。尤其是对于SMSP干扰,由于STFT使得时频域上目标回波的聚集性比干扰更强,在干扰的干信比(ISR)较低时,会出现只能提取出目标回波的特征,而提取不到有效的干扰特征的情况,如图8(b)所示。这些情况会使干扰特征如时宽、中心频率的提取准确率受到很大影响。而本文所用的基于STFRFT的方法则能够在视频平面二值化后得到边缘相对整齐的干扰切片,干扰与目标能够有效区分;对于SMSP干扰,由于选择了干扰最优旋转角度,使得ISR较低时,二值化后的时频图中仍存在清晰的干扰切片,能够准确提取干扰特征。
对每个固定的INR,进行100次蒙特卡罗仿真,根据图5给出的干扰辨识流程进行干扰辨识,统计得到该INR条件下的干扰辨识概率。根据以上仿真过程,得到INR与辨识率曲线如图9所示,可以看出,对SMSP干扰,在INR达-3 dB时,干扰检测率可达90%以上,而对C&I干扰,INR达4 dB时,干扰检测率可达90%以上。
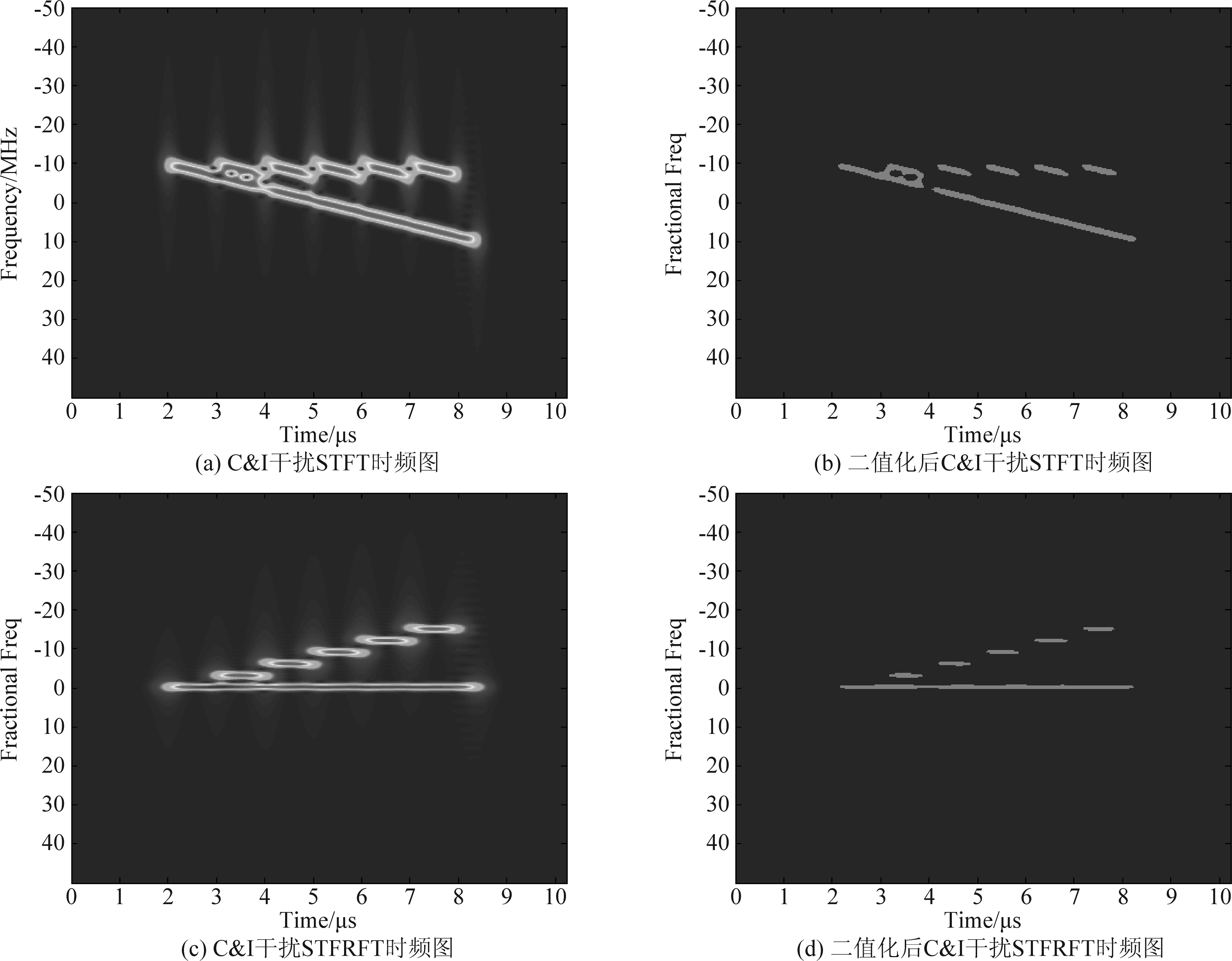
图7 C&I干扰STFRFT与STFT结果对比
Fig.7 Comparison of STFRFT and STFT results for C&I Jamming
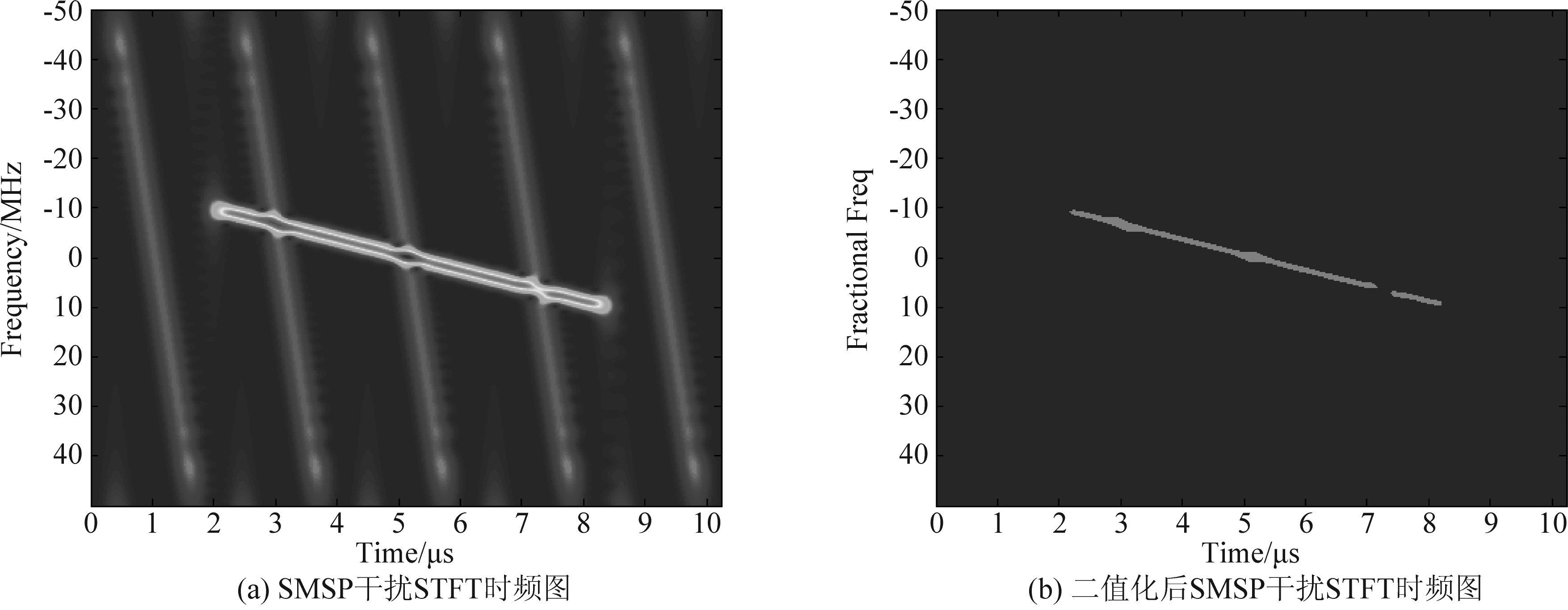
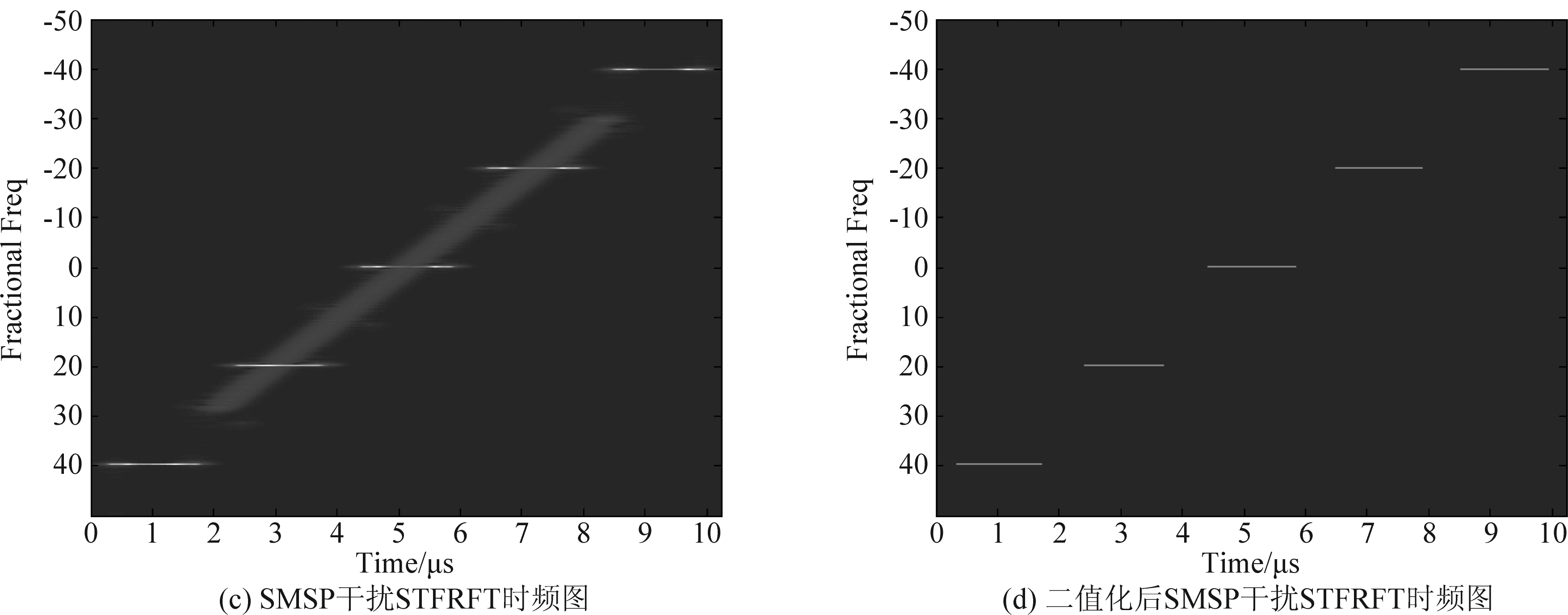
图8 SMSP干扰STFRFT与STFT结果对比
Fig.8 Comparison of STFRFT and STFT results for SMSP Jamming
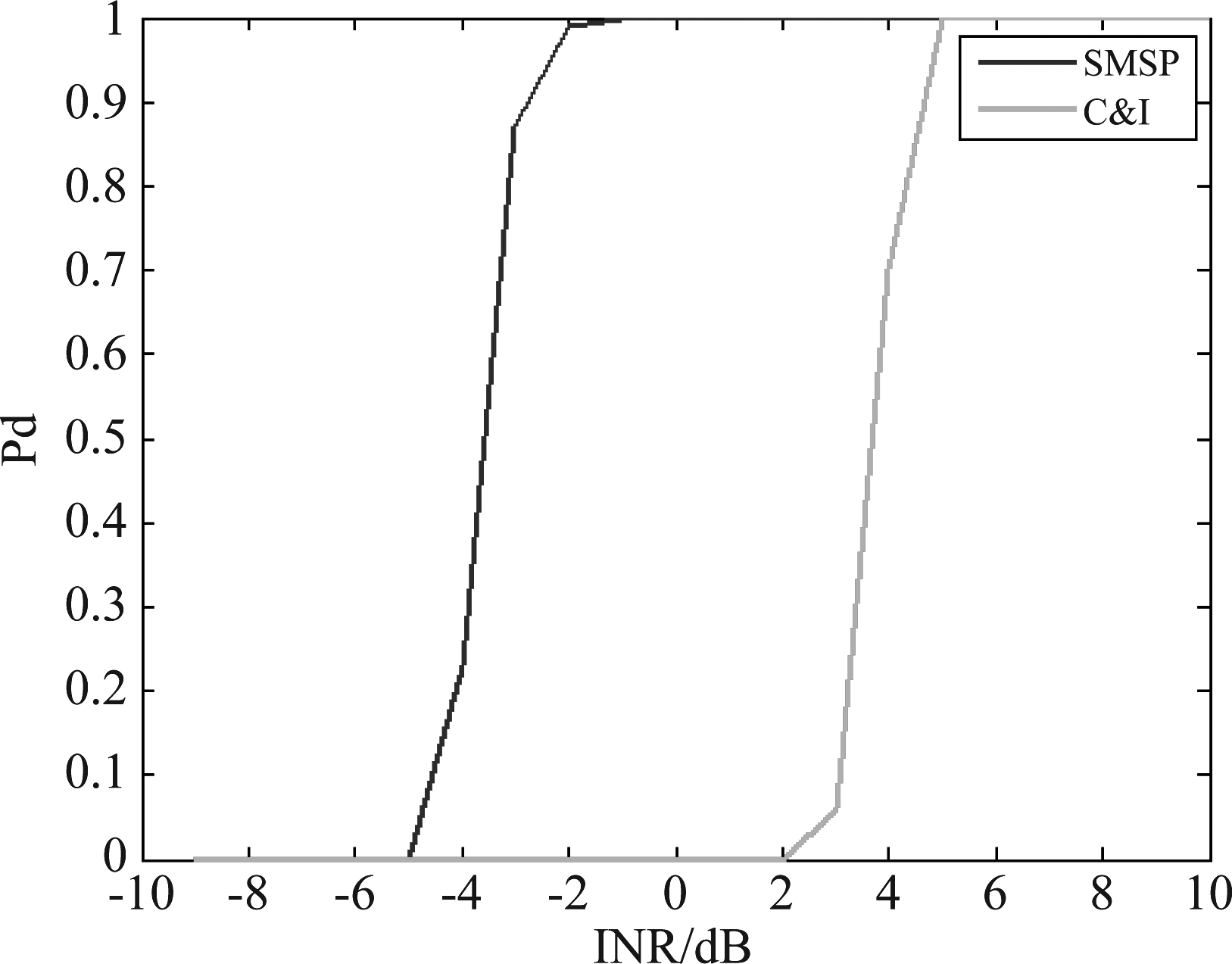
图9 干扰辨识率与INR关系曲线
Fig.9 Relationship between INR and recognition rate
5 结论
基于DRFM的间歇采样转发干扰与雷达回波特征相似,且同时具有压制干扰与欺骗干扰的效果,难以被传统抗干扰手段对抗。本文基于两种典型间歇采样转发干扰:切片组合(C&I)干扰与频谱弥散(SMSP)干扰,提出一种基于短时分数阶傅里叶变换的干扰辨识与参数提取方法,通过选取干扰最优旋转角度进行短时分数阶傅里叶变换,得到干扰时频分布,并通过二值化估计干扰参数,进而实现干扰辨识。仿真结果验证了算法的有效性和其相对于短时傅里叶方法的优势。
[1] Sparrow M J, Cakilo J. ECM techniques to counter pulse compression radar: US, 7081846[P]. 2006.
[2] Sun Minhong, Tang Bin. Suppression of smeared spectrum ECM signal[J]. Journal of the Chinese Institute of Engineers, 2009, 32(3): 407- 413.
[3] 卢云龙, 李明, 曹润清, 等. 联合时频分布和压缩感知对抗频谱弥散干扰[J]. 电子与信息学报, 2016(12): 3275-3281.
Lu Yunlong, Li Ming, Cao Runqing, et al. Jointing Time-frequency Distribution and Compressed Sensing for Countering Smeared Spectrum Jamming[J]. Journal of Electronics & Information Technology, 2016(12): 3275-3281.(in Chinese)
[4] 李永平, 卢刚, 田晓, 等. 基于模糊函数的SMSP和C&I干扰识别算法[J]. 航空兵器, 2011(4): 51-54.
Li Yongping, Lu Gang, Tian Xiao, et al. Jamming Identification Algorithms of SMSP and C&I Based on Ambiguity Function[J]. Aero Weaponry, 2011(4): 51-54.(in Chinese)
[5] 周超, 刘泉华, 曾涛. DRFM间歇采样转发式干扰辨识算法研究[J]. 信号处理, 2017, 33(7): 911-917.
Zhou Chao, Liu Quanhua, Zeng Tao. Research on DRFM Repeater Jamming Recognition[J]. Journal of Signal Processing, 2017, 33(7): 911-917.(in Chinese)
[6] Zhao Yuan, Du Dongping, Ahmed Abdalla Ali, et al. Detection of SMSP Jamming in Netted Radar System Based on Fractional Power Spectrum[C]∥IEEE International Conference on Computational Science & Engineering. IEEE Computer Society, 2014.
[7] Li Yongping, Ying Xiong, Tang Bin. SMSP jamming identification based on matched signal transform[C]∥International Conference on Computational Problem-solving. IEEE, 2011.
[8] 杨少奇, 田波. 频谱弥散和切片组合欺骗式干扰的识别算法[J]. 探测与控制学报, 2016(6): 62- 67.
Yang Shaoqi, Tian Bo. Identification Algorithms of SMSP and C&I[J]. Journal of Detection & Control, 2016(6): 62- 67.(in Chinese)
[9] Tao Ran, Li Yanlei, Wang Yue. Short-Time Fractional Fourier Transform and Its Applications[J]. IEEE Transactions on Signal Processing: A Publication of the IEEE Signal Processing Society, 2010, 58(5): 2568-2580.
[10] 李家强, 金荣洪, 耿军平, 等. 基于高斯短时分数阶傅里叶变换的多分量LFM信号检测与参数估计[J]. 电子与信息学报, 2007, 29(3): 11.
Li Jiaqiang, Jin Ronghong, Geng Junping, et al. Detection and Estimation of Multi-component LFM Signals Based on Gauss Short-Time Fractional Fourier Transform[J]. Journal of Electronic & Information Technology, 2007, 29(3): 11.(in Chinese)
[11] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 2-7.
Tao Ran, Deng Bing, Wang Yue. Fractional Fourier transform and its applications[M]. Beijing: Tsinghua University Press, 2009: 2-7.(in Chinese)
[12] 杨少奇, 田波, 周瑞钊. 利用时频分析的间歇采样干扰对抗方法[J]. 信号处理, 2016, 32(10): 1244-1251.
Yang Shaoqi, Tian Bo, Zhou Ruizhao. ECCM Against Interrupted Sampling Repeater Jamming Based on Time-frequency Analysis[J]. Journal of Signal Processing, 2016, 32(10): 1244-1251.(in Chinese)



