1 引言
单目标跟踪任务[1-2]被广泛应用于视频监控[3],人机交互[4]和自动驾驶[5]等问题中。不同于雷达传感器目标跟踪,视觉目标跟踪具有低成本的优势。视觉目标跟踪问题是:输入一组图像序列,跟踪任务是估计目标运动轨迹。一般跟踪目标可以是任何对象,并且只给定初始位置信息。算法输出后续帧中目标所在位置。
近年来,相关滤波原理被广泛应用于视觉目标跟踪。相关滤波表示的是两个输入信号之间的相似性。它通过相关性结果可以将目标和背景区分开来。最早,Bolme等[8采用相关滤波器来检测视频序列中的对象。Henriques等[10]通过在频域相乘代替相关滤波运算实现快速的目标跟踪。Danelljan等[14]通过空间正则化技术来优化滤波器(后称判别器)。它们被称为基于判别相关滤波器的目标跟踪算法。虽然,基于Discriminative Correlation Filter(DCF)的算法可以通过频域计算实现高速跟踪,但是它容易遭受运动模糊的影响。在实际跟踪环境中,跟踪目标如果发生运动模糊会导致算法接收到模糊或不清晰的图像,此时很难捕获到目标所在位置。
光流技术是图像中物体表观运动速度的分布。它代表着视频序列中物体的运动趋势。最近一些采用光流的工作[7]来实现鲁棒的视觉跟踪和视频目标表示[21]。 这些工作启发了本文融合光流信息到 DCF算法中。
在统计机器学习[18]中,Least Absolute Shrinkage and Selection Operator(Lasso)是一种回归分析方法。它被用于正则化约束和特征稀疏化表示,以提高回归模型的预测精度。由于Lasso可以实现对象的稀疏表示。并且这种稀疏表示可以对特征进行有效降维。因此它可以应用于需要对特征选择的跟踪算法[6]中。
针对一般基于DCF的跟踪算法难以适应于运动模糊场景下的目标跟踪。本文提出了一种Lasso约束下融合光流信息的DCF目标跟踪算法。采用Lasso约束DCF跟踪算法求解目标。在特征提取阶段,不同于之前的DCF跟踪算法,本文对Histogram of Oriented Gradient(HOG)特征和光流特征进行融合。这是由于光流描述了物体的运动信息和HOG表示物体外貌梯度信息。这两种信息的组合可以有效的应对运动模糊下的跟踪问题。在这个融合框架下,本文采用分块坐标梯度下降算法[5]来求解优化目标。本文工作总结如下:(1)与基于DCF的跟踪器不同,该方法不仅使用HOG来表示跟踪对象,而且还融合了光流特征来表示目标。基于这种目标表示,运动模糊对象可以容易地捕获。(2)为了更加有效的约束DCF优化目标函数,本文采用Lasso约束目标函数。(3)由于本文的判别器求解函数中不存在封闭解,故采用分块梯度下降算法来优化目标函数。
本文的其余部分安排如下。第2节主要介绍最近判别式跟踪算法的相关工作。第3节主要介绍DCF算法流程和本文所做算法创新。第4节进行了实验并分析实验结果。最后,第5节总结全文。
2 相关工作
DCF跟踪算法是一种基于相关滤波模式识别理论的目标跟踪算法。它使用图像表示或原始像素作为相关滤波运算的信号输入,并利用逐帧检测出目标位置后合成目标运动轨迹。例如[8,10,12],虽然这些算法只采用传统的滤波方法,但是该方法却拥有着较快的跟踪速度和准确性。最初,文献[8]证明了简单的相关滤波器可以用于有效的视觉跟踪。进一步,为了解决该工作训练样本不足的问题,文献[11]使用循环矩阵来实现丰富的训练样本。并且它采用岭回归训练判别器。同时,为了让DCF跟踪算法特征更加鲁棒。文献[11]和[12]分别在DCF算法中融入了颜色特征和HOG特征作为目标表示,新特征的引入提升了跟踪算法的鲁棒性。在尺度方面,文献[13]提出了一种尺度估计的目标跟踪算法。最近,文献[14]在DCF跟踪算法中引入了空间正则优化,这种优化技术可以约束求解目标从而减轻边界效应。同样文献[17]阐述了一种基于背景感知的图像剪裁技术,用以缓解边界效应。
上述工作体现了,目标表示的鲁棒性和选择适当的优化技术都可以使得跟踪算法具有鲁棒的跟踪能力。得益于这个启发,本文融合光流特征实现更加鲁棒的目标表示,在这个表示下,采用Lasso约束DCF目标函数。通过适当的优化算法,实现鲁棒的判别器求解。
3 光流相关滤波目标跟踪
本节介绍所提出算法的具体细节。首先,介绍基于DCF算法的基本流程,其次阐述了本文算法目标表示方法。然后,介绍本文算法使用分块梯度下降法求解Lasso约束的DCF算法。最后分别介绍了本文算法的模型更新阶段和检测过程。
3.1 基于DCF目标跟踪算法的整体流程
本小节主要介绍DCF跟踪算法的整体流程。基于DCF跟踪算法的整体流程是利用样本x和标签y在当前帧中训练出一个判别器f,然后在下一帧中利用f和下一帧数据做相关滤波运算得到运算结果特征图。最终从特征图中找出目标所在位置,然后依次循环遍历整个视频序列。其流程如图1所示。具体过程可以表示为以下三个步骤:
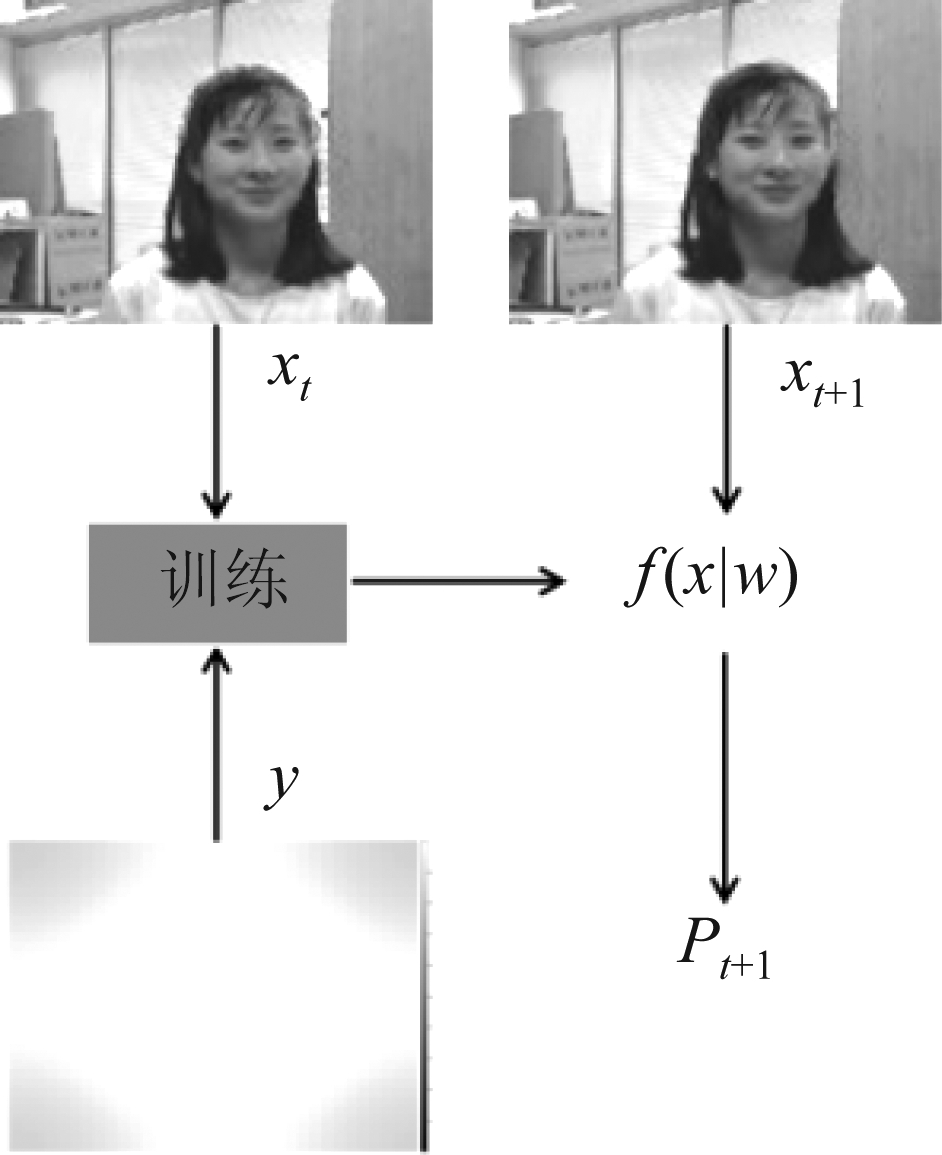
图1 DCF跟踪器跟踪过程
Fig.1 The tracking process of DCF
第一步:从当前帧中抽取目标区域特征。第一帧中剪裁出目标搜索区域并且在搜索区域内抽取出区域特征x。x的大小与训练标签y的大小一致。y一般为均值为0,方差为1的二维高斯分布函数。
第二步:训练判别器。设训练样本为x,高斯型训练标签为y。那么判别器训练可以通过优化最小预测误差得来。其具体的优化目标函数定义如公式(1):
*![]()
(1)
在公式(1)中,ε表示训练误差。w,g,c分别表示判别器f的参数、图像块特征和训练标签。大写的W,G,C分别是w,g,c的频域表示。并且都拥有着同样的大小。第二个等式可以根据帕斯维尔定理[22]得来。训练目标就是求解出f的参数w使ε最小。
第三步:从下一帧中检测目标。在第二步中获得了判别器参数w。那么它具体的检测原理可以定义如下:
S[n]=fn(x)=xn*![]()
(2)
其中S[n]是检测结果。fn表示第n帧训练出来的判别器。*表示相关滤波运算。最终从检测结果特征图中取响应值最大点作为下一帧目标的预测位置Pt+1。
3.2 融合光流信息的目标表示
文献[11]提出了最原始DCF跟踪算法。此后文献[13-14,17]等都采用HOG特征作为目标表示。而HOG特征是一种刚体特征[4],不适应于形变目标。因此本文在文献[11]的基础之上,采取与之前算法不同的目标表示。在特征抽取阶段,提出采用融合光流特征的目标表示方式。
图2展示了本文所提出的一种融合光流的目标表示方法,图中分别抽取HOG特征和光流特征,然后融合。图中第二帧后才融入光流信息。这是由于算法中光流信息的计算需要利用视频序列中间隔的两帧,因此第二帧的光流信息来源于第一帧和第二帧数据。又由于视频序列中不存在第零帧,所以第一帧是不存在光流信息的。而第一帧所抽取出来的矩阵数据与第二帧的矩阵数据在做运算时,会产生矩阵维度不一致问题,进而导致无法进行相关滤波运算。所以,本文在第三帧中使用光流信息。
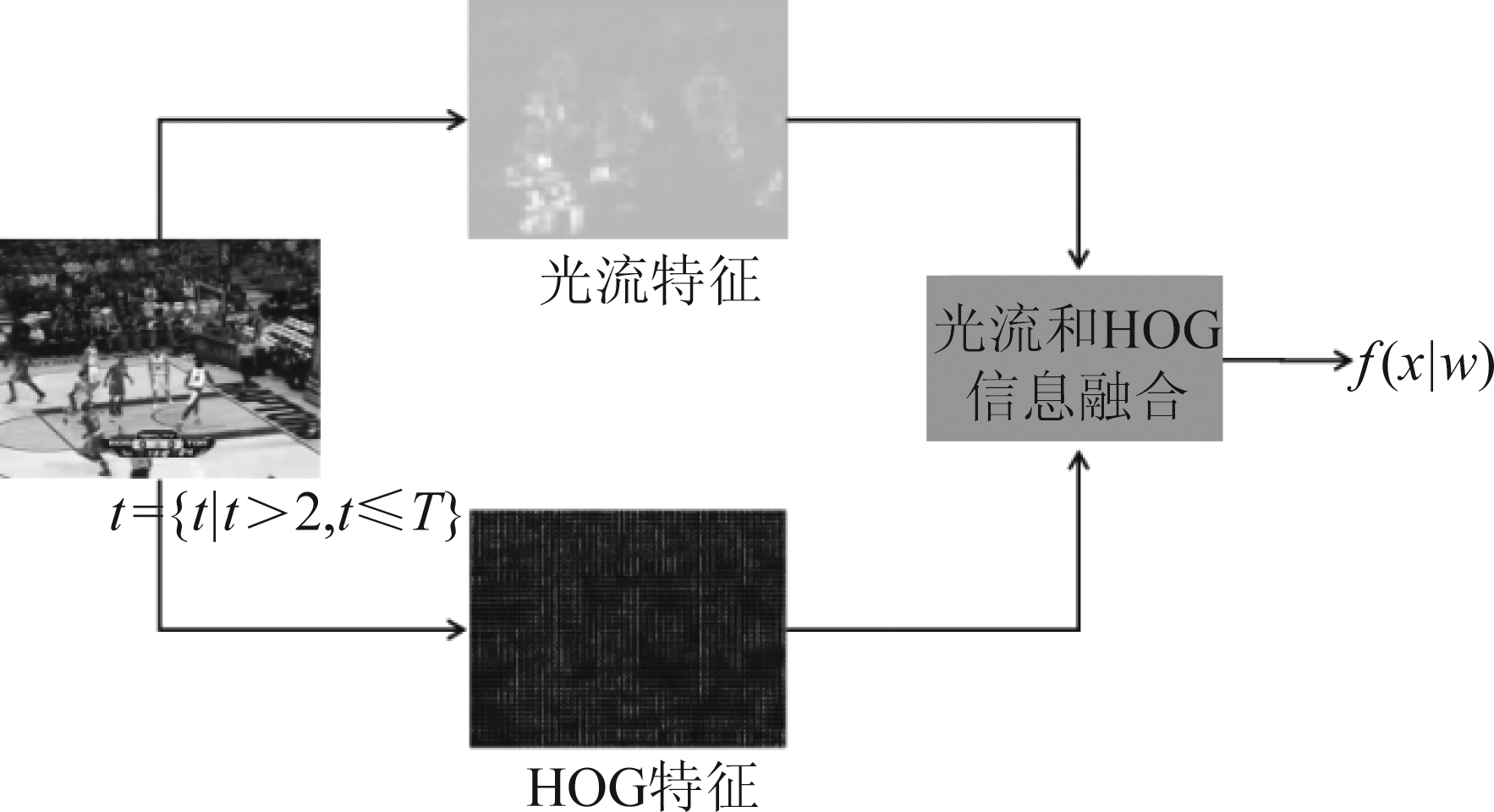
图2 融合光流信息流程
Fig.2 The process of optical flow fusion
假设X表示最终的目标表示结果,那么其计算可以被定义如下:
X=α·fw(Φh(x))+β·fw(Φo(xo))
(3)
在等式(3)中, fw表示傅立叶变换。Φh表示提取HOG特征操作。xo是光流信息。Φo表示光流强度的计算。α梯度信息所占比例,β是运动信息的程度贡献。为了合理的限制α和β的范围。将α+β=1作为约束条件。通过约束项约束,可以将目标表示X稳定的约束在一个固定范围。在这个范围之内,X在跟踪过程中不会发生很大的变化,这样方便后续利用样本X对判别器进行优化。
图3显示了光流特征的处理过程。在抽取光流中,从两个相邻的两帧中计算光流结果。由于提取的光流特征图与原始剪裁后图像块的大小相同,需要将其下采样为M×N,同判别器大小一致。光流特征提取完成后,可以得到大小为M×N×2的数据矩阵。该数据矩阵不能直接用于训练判别器的参数。因此,采用光流强度来表示光流信息并将其作为其输入信号的一部分。光流强度定义如下:
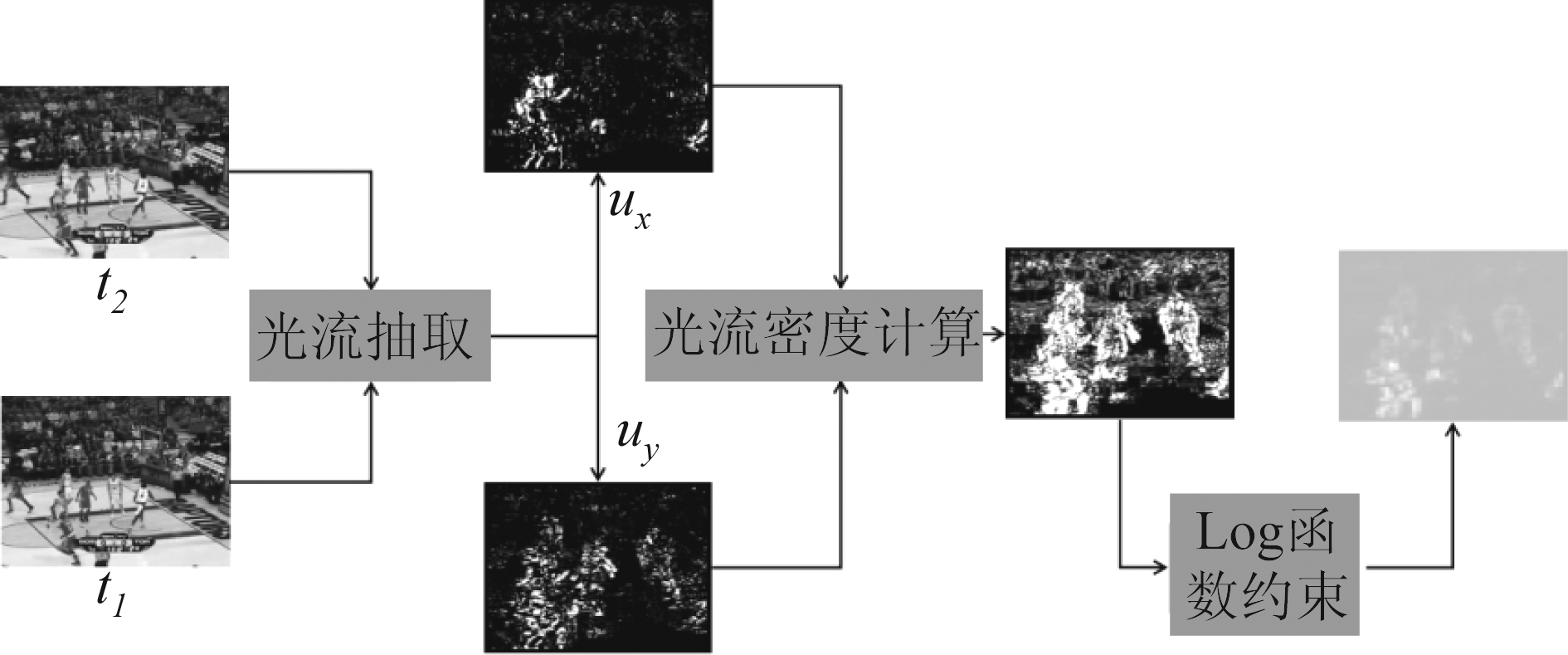
图3 光流特征处理过程
Fig.3 The process of optical flow feature
(4)
在公式(3)中融合的光流是采用公式(4)中光流处理函数。其中ux,uy分别是x方向和y方向的光流信息。Φo(x)是光流处理结果。在实际实现中为了让光流信息准确反映目标变化,本文通过log函数对Φo(x)进行约束。约束后的光流会更加平滑,因此跟踪效果也会更具有鲁棒性。
3.3 分块梯度优化
在具有了上述目标表示后。可以获得一个目标表示的数据矩阵。但是上述数据矩阵维度大,优化难度高。使得判别器的方程解容易产生优化不稳定问题。因此,同文献[5]本文利用LASSO约束技术求解DCF算法的优化目标。如公式(5)所示。
(5)
其中w表示求解滤波器的频域表示,y表示训练标签。f(x)是相关滤波运算的频域表示。m表示一次训练的样本数量。E表示频域滤波器的最小误差。α表示约束正则参数。式(5)在定义域上并不是连续可导的,同时不存在封闭解。在文献[18]对公式(5)的求解过程采用最小角回归。由于其耗时的特点不适用于目标跟踪,本文针对公式(4)采用一种分块拉格朗日松弛松弛的优化过程。同时使用文献[19]中的块坐标梯度下降法来优化目标函数。对式(5)进行具体展开成公式(6)。其中P是对训练样本进行剪裁操作[17],T表示训练样本的数量,d表示模型参数的数量。
(6)
公式(6)利用最优化原理可以转化为式(7)。
(7)
其中,ν是一个辅助变量。矩阵![]() 表示数据块的频域表示。^表示信号的离散傅立叶变换。w表示另一个待优化的变量。其中
表示数据块的频域表示。^表示信号的离散傅立叶变换。w表示另一个待优化的变量。其中![]() ⊗IK)。
⊗IK)。
拉格朗日松弛法:为了对公式(7)进行求解,通过拉格朗日松弛技术。可得公式(8)
(8)
其中λ是拉格朗日乘子。针对式(8),采用分块坐标梯度下降法分块进行求解。
优化子问题w:
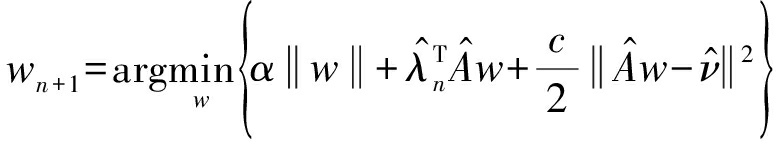
(9)
优化子问题ν:
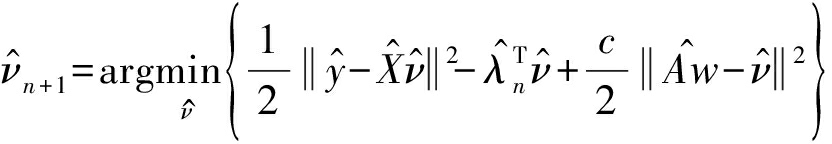
(10)
拉格朗日乘子更新:
(11)
其中W和V是使用拉格朗日更新子问题在n+1步的解。令cn+1=βcn参数选择参考文献[19]其中部分参数设α=1.10, β=2。
3.4 模型更新和检测阶段
为了适应目标在视频序列中的变化,本文与文献[16]一样,采用模型更新策略进行在线跟踪。更新策略定义如下:
wt=(1-η)wt-1+ηwt
(12)
其中η表示学习率。wt代表t的帧中的判别器参数。
检测过程是在当前帧中,目标的位置由公式(2)确定。其中![]() 是从前一帧训练得来的。与[13]类似,跟踪器使用多尺度判别器来检测视频序列中的尺度变化。图像比例的搜索区域和判别器
是从前一帧训练得来的。与[13]类似,跟踪器使用多尺度判别器来检测视频序列中的尺度变化。图像比例的搜索区域和判别器![]() 的大小相同。在相关滤波操作之后,结果是M×N×S矩阵。M×N表示响应图的大小和S表示尺度的数量。为了从S个尺度中估计出目标当前尺度,本文使用插值策略来处理判别器的输出。插值策略与[14]相同。最后输出目标的新坐标和尺度。
的大小相同。在相关滤波操作之后,结果是M×N×S矩阵。M×N表示响应图的大小和S表示尺度的数量。为了从S个尺度中估计出目标当前尺度,本文使用插值策略来处理判别器的输出。插值策略与[14]相同。最后输出目标的新坐标和尺度。
4 实验结果
本节详细介绍了实验结果和参数设置。首先,介绍所使用的测试数据集。接着,介绍本文所使用的评估方法。最后,展示了跟踪器在29个具有运动模糊的视频序列上的测试结果并作了简要的实验分析。
4.1 实验数据、评估指标和参数设置
实验数据:本实验主要测试了文献[15]中29个具有运动模糊情况的视频序列。
评估指标:本文采用三种常用的测试评价准则。所用的评价准则来源于文献[15]。第一种为跟踪对象中心误差准则,其表示如下:
(13)
当P1和P2分别是P1(x1,y1)和P2(x2,y2)。中心错误由Perr表示。它表示实际位置和预测位置之间的误差值。第二种评价指标是跟踪精度,其定义如下式:
(14)
其中Ni表示Perr小于或等于20像素时的帧数,Nsum表示总帧数。第三个评估准则为成功率fs。先定义重叠分数S。其定义如下所示:
(15)
其中,让rt表示预测框,ro表示实际标定框。|·|计算相应的像素数。∩和∪分别是集合的交和并操作。成功率定义如公式(16),其中n表示视频总帧数。
(16)
实验参数设置:本文利用具有31个通道的快速HOG特征提取技术,同方法[11]。然后使用Horn和Schunck运动估计技术[20]作为本文算法的光流特征。惩罚因子λ=0.1。尺度比例设置为5,缩放比例设置为1.01。训练标签为二维高斯分布。学习率η=0.013。本文算法基于Matlab代码,实验平台Intel I7 3.4GH和8G内存台式计算机。
4.2 中心误差分析
中心误差实验在模糊视频序列中选取了具有复杂可变背景环境的视频作为测试序列。测试序列中包含运动模糊情况下同时目标姿态变化、尺度变化、光照变化等多种困难因素。图4表示Human9和Woman的真实场景的跟踪结果。
图5中(a)和(b)显示跟踪目标尺度变化的结果。在整个过程中所有算法都发生了不同程度的误差。即便如此,本文所提出的算法也可以在后续帧中重新定位出目标大体位置,这成功体现了本文算法的先进性。

图4 各算在序列 Woman和Human9上的跟踪结果
Fig.4 Some tracking results of Woman and Human9 sequences
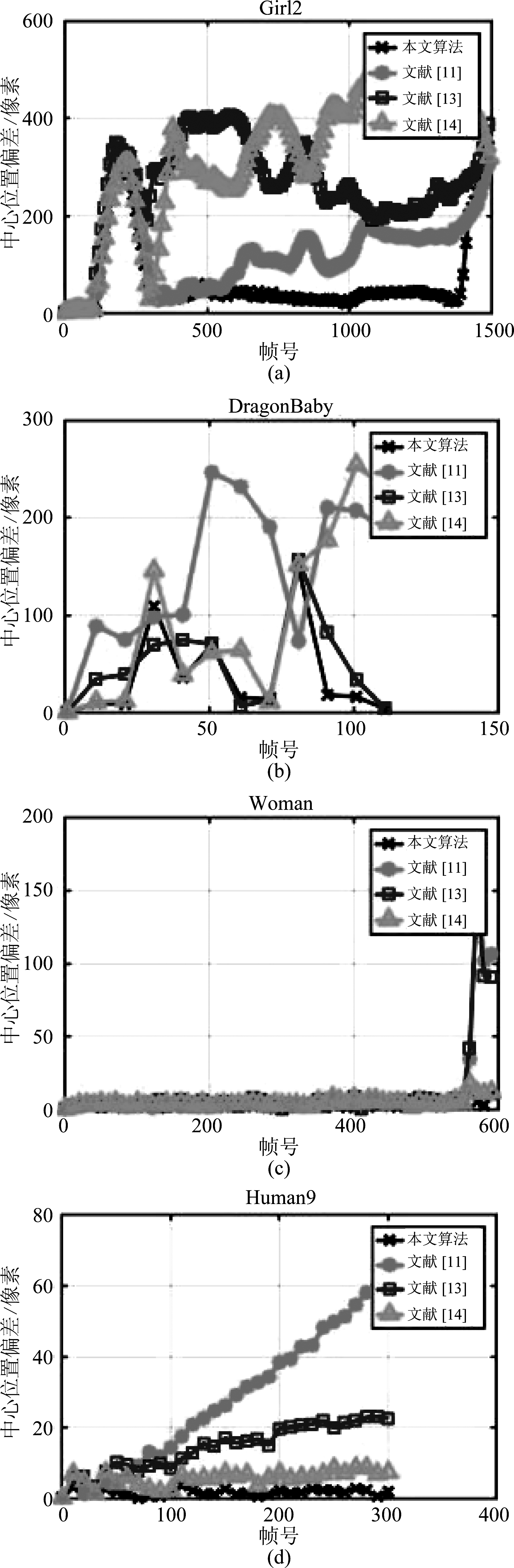
图5 各算法在测试序列上的中心位置定位误差分布图
Fig.5 Center location error plots for the test sequences
图5(c)表示跟踪目标姿态变化的结果。当580帧左右发生了剧烈的尺度变化时,但本文算法仍能准确获得物体位置。这体现了本文算法在追踪形变目标的鲁棒性。
图5(d)中展示了当跟踪器在第50帧中执行时,发生光照变化并且其他文献跟踪算法中心误差逐渐增加。相反本文算法仍然保持较低的中心误差。而文献[11]的误差大幅增加。这是由于其不具有合理的目标表示。
综上所示,本文算法之所以在上述三种情况下要优于其他算法主要原因在于本文算法拥有更加鲁棒的目标表示策略。这种表示策略可以在没有接收到清晰的图片情况下或者剧烈的形变下也能追踪运动目标。最终实现鲁棒的目标跟踪。
4.3 与其他目标跟踪算法比较
表1显示了多个跟踪算法的性能对比。显然,与文献[14]相比,本文提出的算法在29个视频序列上均值跟踪精度和均值成功率分别增加了1.33 % 和2.24%。同时也比文献[17]高出3.6%和2.33%。然而文献[14]和文献[17]分别采用稀疏正则技术和背景剪裁技术来优化判别器。但是对比与其他算法,本文算法更加适用于运动模糊情况。本文算法均值中心位置误差显著小于其他算法。这表明本文在跟踪运动模糊对象方面具有更好的准确性。
表1 各算法在运动模糊序列上的评价指标
Tab.1 Evaluation metrics of the algorithms for the motion blur sequences
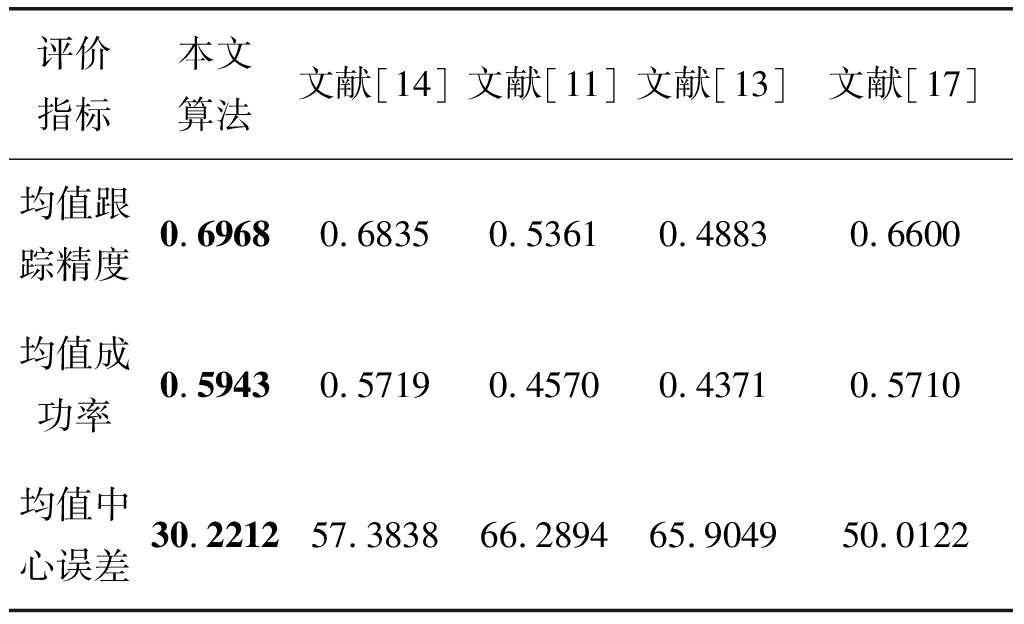
评价指标本文算法文献[14]文献[11]文献[13]文献[17]均值跟踪精度0.69680.68350.53610.48830.6600均值成功率0.59430.57190.45700.43710.5710均值中心误差30.221257.383866.289465.904950.0122
综上所述本文算法在运动模糊场景中具有许多优点。这个主要原因可以归结如下。首先,Lasso约束可以缩小算法目标函数的求解域。提升分块梯度优化算法的求解效率。其次,光流信息的融入有助于目标跟踪。这也有利于捕捉更多的运动模糊对象。上述实验结果虽然验证了本文算法的有效性与优越性,但同时本文算法仍存在一定的不足。分析本文算法在测试序列 Girl2与测试序列 DragonBaby 的中心位置定位误差可知,由于本文算法所融合的仅仅是光流和HOG信息,然而这两种信息难以适应于剧烈形变目标。因此,当目标在相邻帧之间发生较大的形变时,本文算法的中心位置误差上还是出现了较大的偏离。并且光流特征计算需要花费很多时间。这也是本文算法需要改进的地方之一。
表2 消融实验
Tab.2 Ablation experiment
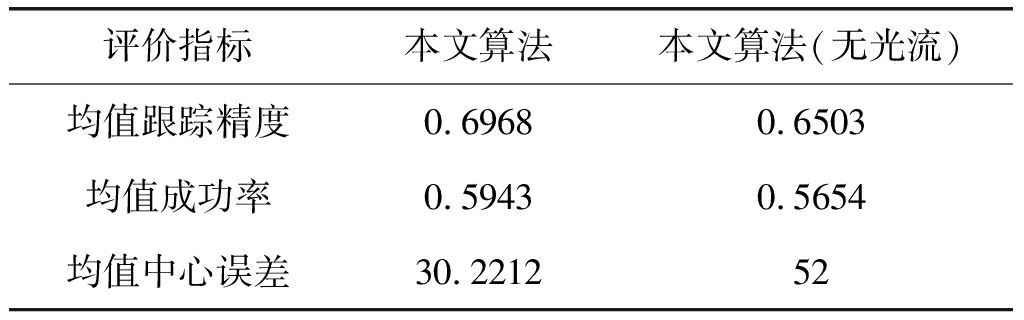
评价指标本文算法本文算法(无光流)均值跟踪精度0.69680.6503均值成功率0.59430.5654均值中心误差30.221252
4.4 消融实验分析
为了分析光流特征在运动模糊视频序列下对跟踪算法的性能影响,本文进行了消融实验。表2展示了在跟踪器中融入光流和没有光流信息的性能变化。在融合光流信息后均值跟踪精度提高了4.6%,均值成功率提高了2.89%,均值中心误差下降了近22个点。通过实验证明了光流信息对运动模糊的有效性。实验中最开始融合光流特征会导致跟踪器不稳定,这是由于提取的光流特征没有经过标准化。因此,判别器的训练变得十分困难。在采用映射函数log函数约束光流特征后,跟踪器可以变得更加鲁棒。
综上所述,融合光流特征有利于跟踪运动模糊对象。这是由于光流定义源于同一像素点亮度恒定不变,对当前点进行三元泰勒展开。分别是x,y,t三个方向。因此对应于物理意义是提取出物体空间的运动趋势信息。反映在某一帧中,也就是运动方向信息。在运动模糊场景下,跟踪器无法准确获取目标位置,此时利用光流信息所提供的运动方向,有助于算法跟踪运动模糊目标。
5 结论
针对视觉目标跟踪中的运动模糊问题,本文提出了一种基于Lasso约束并且融合光流信息的DCF视频跟踪算法。该算法将HOG特征和光流特征进行融合,HOG特征可以表示物体的外貌信息,光流特征可以表示物体的运动信息。这种融合方式有利于在运动模糊的情况下目标跟踪。同时,本文使用Lasso约束跟踪器的目标函数。接着,本文采用块梯度下降算法对Lasso约束下的目标函数进行优化。报告的结果证明了所提出的算法可以跟踪复杂场景的目标并且光流融合到目标表示中对跟踪运动模糊目标具有鲁棒性。至于未来的工作,还可以进一步扩展跟踪器。例如,GPU提取光流信息并使用多线程实现块梯度下降算法,从而加速目标跟踪。
[1] Ojha S, Sakhare S. Image processing techniques for object tracking in video surveillance-A survey[C]∥2015 International Conference on Pervasive Computing(ICPC). IEEE, 2015: 1- 6.
[2] Tong X, Ding D, Li W. Dynamic gesture based short-range human-machine interaction: U.S. Patent 9, 164, 589[P]. 2015-10-20.
[3] Chen T, Wang R, Dai B, et al. Likelihood-field-model-based dynamic vehicle detection and tracking for self-driving[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3142-3158.
[4] Dalal N, Triggs B. Histograms of oriented gradients for human detection[C]∥International Conference on Computer Vision & Pattern Recognition(CVPR′05). IEEE Computer Society, 2005, 1: 886- 893.
[5] Beck A, Tetruashvili L. On the convergence of block coordinate descent type methods[J]. SIAM Journal on Optimization, 2013, 23(4): 2037-2060.
[6] Asvadi A, Girão P, Peixoto P, et al. 3D object tracking using RGB and LIDAR data[C]∥IEEE, International Conference on Intelligent Transportation Systems. IEEE, 2016.
[7] Hua Y, Alahari K, Schmid C. Occlusion and motion reasoning for long-term tracking[C]∥European Conference on Computer Vision. Springer, Cham, 2014: 172-187.
[8] Bolme D S, Beveridge J R, Draper B A, et al. Visual object tracking using adaptive correlation filters[C]∥2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2010: 2544-2550.
[9] Kiani Galoogahi H, Sim T, Lucey S. Correlation filters with limited boundaries[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 4630- 4638.
[10] Henriques J F, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]∥European conference on computer vision. Springer, Berlin, Heidelberg, 2012: 702-715.
[11] Henriques, Rui C, et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern AnalysisMachine Intelligence, 2015, 37(3): 583-596.
[12] Danelljan M, Shahbaz Khan F, Felsberg M, et al. Adaptive color attributes for real-time visual tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2014: 1090-1097.
[13] Danelljan M, Häger G, Khan F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1561-1575.
[14] Danelljan M, Hager G, Shahbaz Khan F, et al. Learning spatially regularized correlation filters for visual tracking[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2015: 4310- 4318.
[15] Wu Y, Lim J, Yang M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
[16] Kiani Galoogahi H, Sim T, Lucey S. Multi-channel correlation filters[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2013: 3072-3079.
[17] Kiani Galoogahi H, Fagg A, Lucey S. Learning background-aware correlation filters for visual tracking[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2017: 1135-1143.
[18] John Lu Z Q. The elements of statistical learning: data mining, inference, and prediction[J]. Journal of the Royal Statistical Society: Series A(Statistics in Society), 2010, 173(3): 693- 694.
[19] Qin Z, Scheinberg K, Goldfarb D. Efficient block-coordinate descent algorithms for the group lasso[J]. Mathematical Programming Computation, 2013, 5(2): 143-169.
[20] Fortun D, Bouthemy P, Kervrann C. Optical flow modeling and computation: A survey[J]. Computer Vision and Image Understanding, 2015, 134: 1-21.
[21] Sun S, Kuang Z, Sheng L, et al. Optical flow guided feature: a fast and robust motion representation for video action recognition[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 1390-1399.
[22] Kumar B V K V, Mahalanobis A, Juday R D. Correlation pattern recognition[M]. Cambridge University Press, 2005.
